Учебное пособие: Основные понятия статистики
ТЕМА 1.4. Законы распределения случайных величин, наиболее часто используемые в экономических приложениях, и их числовые характеристики
1. Основные распределения дискретных случайных величин: биномиальное распределение, распределение Пуассона.
2. Основные распределения непрерывных случайных величин: равномерное распределение, показательное распределение, нормальное распределение.
3. Критериальные случайные величины. Распределение Стьюдента, Пирсона, Фишера - Снедекора.
1. Основные распределения дискретных случайных величин: биномиальное распределение, распределение Пуассона.
1.1 Биноминальное распределение
Дискретная случайная величина Х имеет биноминальный закон распределение, если она принимает значения 0, 1, 2, …m… n с вероятностями
![]() ,
,
0< p <1, q = 1 – p, m = 0, 1, 2, …n
Как видно, вероятность значений
находится по формуле Бернулли. Следовательно, биноминальный закон распределения
представляет собой распределение числа Х = m, количества событий А, произошедших в n испытаниях. Бернулли, в каждом из
которых событие A происходит с вероятностью p, а противоположное событие ![]() с вероятностью 1- p.. Закон распределения
биноминальной случайной величины Х в развёрнутом форме имеет вид:
с вероятностью 1- p.. Закон распределения
биноминальной случайной величины Х в развёрнутом форме имеет вид:
![]()
- верхняя строчка - это совокупность числовых значений, которые может принимать случайная величина;
- нижняя строчка - вероятность события, что случайная величина примет эти значения.
Определение биноминального закона
корректно, так как основное свойство ряда распределения ![]() выполнено, ибо
выполнено, ибо ![]() , как было отмечено выше, есть сумма всех членов
разложения бинома Ньютона:
, как было отмечено выше, есть сумма всех членов
разложения бинома Ньютона:
![]()
Отсюда и название закона – биноминальный.
Числовые характеристики биноминального распределения:
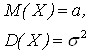
1. М(Х) = np
2. D(X) = npq
1.2 Закон распределения Пуассона
Дискретная случайная величина Х имеет закон распределение Пуассона, если она принимает значения 0, 1, 2, …m,… (бесконечное, но счётное множество значений) с вероятностями
![]() ,
,
где m = 0, 1, 2, …
Числовые характеристики распределения Пуассона:
3. М(Х) = λ
4. D(X) = λ
2. Основные распределения непрерывных случайных величин
Отметим ряд особенностей свойств непрерывных случайных величин.
1. Множество значений непрерывной случайной величины есть совокупность всех точек числовой оси.
2. Функция распределения непрерывной
случайной величины.![]() является непрерывной.
является непрерывной.
3. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число:
![]()
В случае непрерывной случайной величины мы сталкиваемся с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0. Это надо трактовать так, что распределения непрерывных случайных величин дают нам значения вероятности р = f(x) не для данного значения х случайной величины, а для интервала значений Δ х , примыкающего к х. Поэтому возможно такое определение
Определение. Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.
Естественны следствия такого определения.
1.F(b)-F(a) = P(a£ X< b) = P(a£ X £b)
2.Неотрицательная числовая функция f(x) действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:
![]()
Свойства плотности вероятности.
а). 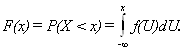
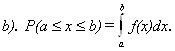
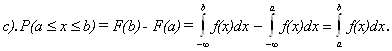
d).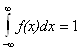
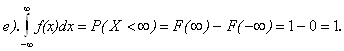
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0.
Примеры непрерывных распределений.
2.1 Равномерное распределение
![]()
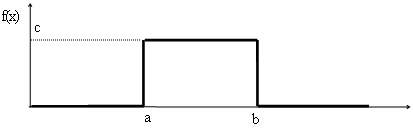
х
Найдём константу с :
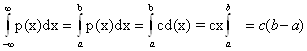
т.к. 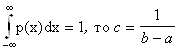 .
.
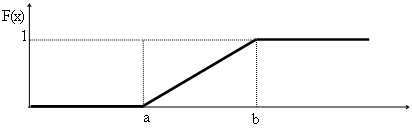
Функция распределения равномерного распределения:
![]()
Математическое ожидание: М(Х) =(а+в)/2, дисперсия D(X) = (b - a)2 /12
x
2.2 Показательный закон распределения
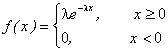
f(x)
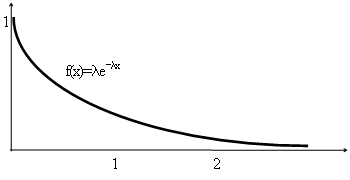
x
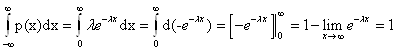
Функция распределения показательного распределения:
![]()
Математическое ожидание: М(Х) = 1/ λ, дисперсия D(X) =1/ λ2
2.3 Нормальное распределение – распределение Гаусса
Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности

По определению функция распределения:

Определение функция плотности
распределения корректно, т.к. основное свойство распределения 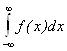 = 1 выполнено,
поскольку интеграл
= 1 выполнено,
поскольку интеграл

|
|
|
|
С нормальным распределением тесно связана функция Лапласа
Функцией Лапласа называется функция вида
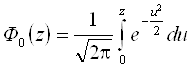
Функция Лапласа при z >0 определяет вероятность попадания стандартной нормальной случайной величины ( M(X) = 0, D(X) =1) в интервал (0, z)
Вероятность того, что значения нормальной случайной величины лежат в интервале (a, b) определяется следующим выражением:.

где ![]()
3. Критериальные случайные величины. Распределение Стьюдента, Пирсона, Фишера - Снедекора
Случайные величины t – Стьюдента, χ2 – Пирсона, F – Фишера – Снедекора задаются табличным способом и используются в качестве критериальных в статистике
Контрольные вопросы
1.Дайте определение биномиальному распределению. Каковы его свойства и основные характеристики?
2. Дайте определение распределению Пуассона? Каковы его свойства и основные характеристики?
3. Какое распределение называется равномерным? Каковы его свойства и основные характеристики?
4. Какое распределение называется нормальным? Каковы его свойства и основные характеристики?
5. Напишите функцию распределения нормально распределенной случайной величины X, если M(Х) =3, D(X) =σ2= 16.
6. Задана случайная величина X, распределенная нормально с параметрами
M(Х) = 0 и σ = 2.
Найдите вероятность того, что эта случайная величина принимает значение
а) из отрезка [-1,2]; б) меньшее -1; в) большее 2; г) отличное от своего среднего значения по абсолютной величине не больше, чем на 1.
7. Задана дискретная случайная величина Z – индикатор испытаний: Z =1, если в соответствующем испытании событие А появилось и Z = 0 в противоположном случае. Закон распределения имеет вид:
| Z | 0 | 1 |
| P | q | p |
Найти математическое ожидание и дисперсию Z.
8. Дискретная пуассоновская случайная величина X p имеет распределение:
![]()
Вычислите математическое ожидание и дисперсию дискретной пуассоновской случайной величины
9. Задана равномерно распределённая на отрезке [a;b] непрерывная случайная величина Х:
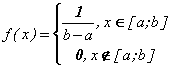
Вычислите математическое ожидание и дисперсию случайной величины Х.
10. Задана непрерывная случайная величина Y, имеющая показательное распределение:
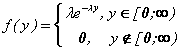
Вычислите математическое ожидание и дисперсию случайной величины Y.
11. Задана непрерывная случайная величина X, имеющая нормальное распределение:

Вычислите математическое ожидание и дисперсию случайной величины X.
Тема 1.5. Системы случайных величин
1. Закон распределения, функция распределения системы случайных величин, их свойства.
2. Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин.
3. Функцией регрессии. Линейная регрессия.
4. Корреляция, свойство коэффициента корреляции. Линейная корреляция
1. Закон распределения, функция распределения системы случайных величин, их свойства
Рассмотренные выше случайные величины были одномерными, т.е. определялись одним числом, однако, существуют также случайные величины, которые определяются двумя, тремя и т.д. числами. Такие случайные величины называются двумерными, трехмерными и т.д.
В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин.
Более подробно рассмотрим системы двух случайных величин.
Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.
![]()
Отметим следующие свойства функции распределения системы двух случайных величин:
1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.
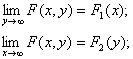
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.
![]()
3) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.
![]()
4) Функция распределения является неубывающей функцией по каждому аргументу.
5) Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
![]()
Плотность распределения системы двух случайных величин.
Определение. Плотностью совместного распределения вероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.
![]()
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:
![]()
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.
![]()
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.
![]()
![]() ;
; ![]() ;
;
2. Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин
Условные законы распределения.
Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.
Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.
В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.
Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.
Все это приводит к необходимости рассмотрения условных законов распределения.
Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:
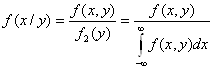
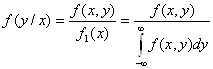
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Условное математическое ожидание.
Определение. Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.
![]()
Для непрерывных случайных величин:
![]() ,
,
где f(y/x) – условная плотность случайной величины Y при X=x.
3. Функцией регрессии. Линейная регрессия
Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
Пример. Найти условное математическое ожидание составляющей Y при
X= x1=1 для дискретной двумерной случайной величины, заданной таблицей:
Y |
X | |||
| x1=1 | x2=3 | x3=4 | x4=8 | |
| y1=3 | 0,15 | 0,06 | 0,25 | 0,04 |
| y2=6 | 0,30 | 0,10 | 0,03 | 0,07 |
![]()
![]()
![]()
![]()
Аналогично определяются условная дисперсия и условные моменты системы случайных величин.
Зависимые и независимые случайные величины.
Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.
Понятие зависимости случайных величин является очень важным в теории вероятностей.
Условные распределения независимых случайных величин равны их безусловным распределениям.
Определим необходимые и достаточные условия независимости случайных величин.
Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.
![]()
Аналогичную теорему можно сформулировать и для плотности распределения:
Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих.
![]()
4. Корреляция, свойство коэффициента корреляции. Линейная корреляция
Определение. Корреляционным моментом mxy случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.
![]()
Практически используются формулы:
Для дискретных случайных величин:
![]()
Для непрерывных случайных величин:
![]()
Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.
Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.
Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.
Определение. Коэффициентом корреляции rxy случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
![]()
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойство: Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.
![]()
Свойство: Абсолютная величина коэффициента корреляции не превышает единицы.
![]()
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.
Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.
Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.
Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:
![]()
Пример. Задана плотность распределения системы случайных величин Х и Y.
![]()
Выяснить являются ли независимыми случайные величины Х и Y.
Для решения этой задачи преобразуем плотность распределения:
![]()
Таким образом, плотность распределения удалось представить в виде произведения двух функций, одна из которых зависит только от х, а другая – только от у. Т.е. случайные величины Х и Y независимы. Разумеется, они также будут и некоррелированы.
Линейная регрессия.
Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины.
Представим приближенно одну случайную величину как функцию другой. Точное соответствие невозможно. Будем считать, что эта функция линейная.
![]()
Для определения этой функции остается только найти постоянные величины a и b.
Определение. Функция g(X) называется наилучшим приближением случайной величины Y в смысле метода наименьших квадратов, если математическое ожидание
![]() принимает наименьшее возможное
значение. Также функция g(x) называется среднеквадратической
регрессией Y на X.
принимает наименьшее возможное
значение. Также функция g(x) называется среднеквадратической
регрессией Y на X.
Теорема. Линейная средняя квадратическая регрессия Y на Х вычисляется по формуле:
![]()
в этой формуле
mx=M(X), my=M(Y), ![]() коэффициент
корреляции величин Х и Y.
коэффициент
корреляции величин Х и Y.
Величина ![]() называется коэффициентом регрессии
Y на Х.
называется коэффициентом регрессии
Y на Х.
Прямая, уравнение которой
![]() ,
,
называется прямой сренеквадратической регрессии Y на Х.
Величина ![]() называется остаточной дисперсией
случайной величины Y относительно случайной величины Х. Эта величина
характеризует величину ошибки, образующейся при замене случайной величины Y линейной функцией g(X)=aХ + b.
называется остаточной дисперсией
случайной величины Y относительно случайной величины Х. Эта величина
характеризует величину ошибки, образующейся при замене случайной величины Y линейной функцией g(X)=aХ + b.
Видно, что если r=±1, то остаточная дисперсия равна нулю, и, следовательно, ошибка равна нулю и случайная величина Y точно представляется линейной функцией от случайной величины Х.
Прямая среднеквадратичной регрессии Х на Y определяется аналогично по формуле:
![]()
Прямые среднеквадратичной регрессии пересекаются в точке (тх, ту), которую называют центром совместного распределения случайных величин Х и Y.
Линейная корреляция.
Если две случайные величины Х и Y имеют в отношении друг друга линейные функции регрессии, то говорят, что величины Х и Y связаны линейной корреляционной зависимостью.
Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.
Контрольные вопросы:
1. Дайте определение закона распределения, функцией распределения системы случайных величин.
2. Что такое условные законы распределения, условные числовые характеристики системы случайных величин?
3. Что такое функция регрессия между случайными величинами ?
4. Что такое корреляционная связь между случайными величинами?
5. Найти условное математическое ожидание составляющей Y при
X= x2=3 и Х= х3=4 для дискретной двумерной случайной величины, заданной таблицей:
Y |
X | |||
| x1=1 | x2=3 | x3=4 | x4=8 | |
| y1=3 | 0,15 | 0,06 | 0,25 | 0,04 |
| y2=6 | 0,30 | 0,10 | 0,03 | 0,07 |
6. Задана плотность распределения системы случайных величин Х и Y.
![]()
Выяснить являются ли независимыми случайные величины Х и Y.
Тема 1.6. Предельные теоремы теории вероятностей
1. Неравенства Чебышева.
2. Закон больших чисел и его следствия.
3. Предельные теоремы теории вероятностей.
1.Неравенство Чебышева
величина распределение вероятность корреляция
На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.
Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.
Рассмотрим дискретную случайную величину Х (хотя все сказанное ниже будет справедливо и для непрерывных случайных величин), заданную таблицей распределения:
X |
x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число e.
Теорема. (Неравенство Чебышева) Вероятность того, что
отклонение случайной величины Х от ее математического ожидания по абсолютной
величине меньше положительного числа e, не меньше чем ![]() .
.
![]()
Доказательство этой теоремы не приводим, т.к. оно имеется в литературе ОЛ [ 3 ], [4].
2.Закон больших чисел и его следствия
Теорема. (Теорема Чебышева) Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства
![]()
будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать:
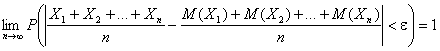
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
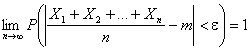
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий. Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно элиминируют.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
Переходим к следующей теореме закона больших чисел.
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р.
Теорема (Теорема Бернулли ). Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.
![]()
Здесь т – число появлений события А. Из всего
сказанного выше не следует, что с увеличением число испытаний относительная
частота неуклонно стремится к вероятности р, т.е. ![]() (сходимость поточечная). В
теореме имеется в виду только сходимость по вероятности, т.е. приближения
относительной частоты к вероятности появления события А в каждом испытании.
(сходимость поточечная). В
теореме имеется в виду только сходимость по вероятности, т.е. приближения
относительной частоты к вероятности появления события А в каждом испытании.
В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.
Теорема (Теорема Пуассона). Если производится п независимых опытов и вероятность появления события А в каждом опыте различна и равна рi, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей рi.
Теорема даёт возможность определить примерно относительную частоту появления события А.
3. Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.
Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.
В рассмотренном выше законе больших чисел нечего не
говорилось о законе распределения случайных величин. Поставим задачу нахождения
предельного закона распределения суммы ![]() , когда число слагаемых п
неограниченно возрастает. Эту задачу решает Центральная предельная теорема
Ляпунова.
, когда число слагаемых п
неограниченно возрастает. Эту задачу решает Центральная предельная теорема
Ляпунова.
В зависимости от условий распределения случайных величин Xi, образующих сумму, возможны различные формулировки центральной предельной теоремы. Рассмотрим один из вариантов.
Допустим, что случайные величины Xi взаимно независимы и одинаково распределены.
Теорема. Если случайные величины Xi взаимно
независимы и имеют один и тот же закон распределения с математическим ожиданием
т и дисперсией s2, причем существует третий абсолютный
момент n3, то при неограниченном увеличении числа испытаний п закон
распределения суммы ![]() неограниченно приближается к
нормальному.
неограниченно приближается к
нормальному.
Контрольные вопросы:
1. Сформулируйте теорему больших чисел Бернулли.
2. Сформулируйте теорему больших чисел Чебышева.
3. Сформулируйте теорему A.M. Ляпунова.
Раздел 2. Математическая статистика
Аннотация
Математическая статистика изучает, как и теория вероятностей, случайные явления, использует одинаковые с ней определения, понятия и методы и основана на той же самой аксиоматике А.Н. Колмогорова. Однако задачи, решаемые математической статистикой , носят специфический характер.
Теория вероятностей исследует явления, заданные полностью их моделью, и выявляет еще до опыта те статистические закономерности, которые будут иметь место после его проведения
В математической статистике вероятностная модель явления определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется тем, что позволяется проводить «пробные» испытания и на их основе восстанавливать недостающую информацию
Тема 2.1. Описательная статистика
1. Два основных направления исследований в статистике.
2. Основные категории статистики.
3. Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
4. Графическое представление вариационных рядов.
1. Два основных направления исследований в статистике
В математической статистике принято выделять два направления: параметрическая статистика и непараметрическая (дескриптивная) статистика.
Первое направление связано с оценкой (определением) неизвестных параметров законов распределения случайных величин на основе экспериментальных наблюдений за значениями случайной величины. Поскольку в качестве оценки выступает число, а числу на числовой прямой соответствует точка, такие оценки называют точечными.
Поскольку точечная оценка получается в результате математических операций над полученными из эксперимента значениями случайной величины она (оценка) сама есть случайная величина, имеющая определенную функцию распределения. Следовательно, точечная оценка должна быть дополнена интервалом, содержащим точечную оценку и возможный разброс её (оценки) значений, которые допустим с наперёд заданной вероятностью, которую называют доверительной. Поэтому наряду с точечными оценками в математической статистике принято определять интервальные оценки или , иными словами, доверительные интервалы, опираясь на уровень доверия или доверительную вероятность
Второе направление в математической статистике связано с проверкой некоторых априорных предположений или статистических гипотез об основных характеристиках экспериментально полученных распределениях случайных величин. Принято называть одну из этих гипотез ( как правило, более важную с практической точки зрения) основной H0, а вторую альтернативной или конкурирующей H1. Индекс 0 буквы H указывает, что гипотеза H0 предполагает несущественное отличие между гипотетическим и истинным значении оцениваемых параметрах, и, наоборот, индекс 1 указывает на существенную разницу между оценкой и истинном значением статистического параметра. Задача проверки статистических гипотез состоит в выборе правила или критерия, позволяющего по результатам наблюдений проверить, справедливость этих гипотез и принять одну из них. Так же, как и при точечной оценке неизвестных параметров, мы не застрахованы от неверного решения, так называемых ошибок первого и второго рода. Ошибка первого рода состоит в том, что мы принимаем конкурирующую гипотезу H1, в то время, как справедлива основная гипотеза H0. Аналогично определяется ошибка второго рода: принимаем основная гипотезу H0, в то время, как справедлива конкурирующая гипотеза H1.
В математической статистике исследуются также байесовские и небайесовские модели. Байесовская модель возникает тогда, когда неизвестный параметр является случайной величиной и имеется априорная информация о его распределении. При байесовском подходе на основе опытных данных априорные вероятности пересчитываются в апостериорные. Этот подход использует формулу Байеса.
Небайесовские модели появляются тогда, когда неизвестный параметр нельзя считать случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели в основном рассматриваются в математической статистике.
В математической статистике употребляют также понятие параметрической и непараметрической модели. Параметрическая модель возникает тогда, когда нам известен вид функции распределения наблюдаемого признака, но неизвестны её параметры и необходимо по результатам испытаний определить эти параметры (задача оценки неизвестного параметра) или проверить гипотезу о принадлежности его некоторому заранее выделенному множеству значений (задача проверки статистических гипотез). Непараметрическая модель – когда неизвестен вид закона распределения и необходимо с помощью специальных критериев определить к какому классу распределений он относится.
2. Основные категории статистики
Основными категориями математической статистики являются: генеральная совокупность, выборка, теоретическая и эмпирическая функции распределения.
Определение 1. Пусть имеется совокупность N объектов любой природы, над которыми проводятся наблюдения или совокупность всех возможных наблюдений. Каждое из наблюдений характеризуется определенным значением хi (среди которых могут быть и одинаковые) некоторого общего для всех объектов признака (характеристики) Х. Назовём множество всех изучаемых объектов генеральной совокупностью, где N - объём генеральной совокупности.
В математической статистике обычно рассматривается генеральная совокупность бесконечно большого объёма.
Определение 2. Выборочной совокупностью или выборкой назовем n объектов, отобранных из генеральной совокупности и подвергнутые исследованию, число n – объёмом выборки.
Выборка должна обладать свойством репрезентативности, В силу закона больших чисел, можно утверждать, что выборка репрезентативна, если каждый её объект выбран из генеральной совокупности случайным образом, т.е. все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.
Определение 3. Эмпирическая функция распределения. Пусть из генеральной совокупности извлечена выборка объёма n , причём количественный признак х1 наблюдался n1 раз, …хk - nk раз. Очевидно,
![]() .
.
Наблюдаемые значения количественного признака хi называются вариантами, а ранжированная (записанная в порядке возрастания) последовательность вариант,, - вариационным рядом. Если исследуемый признак принимает дискретные значения, то такой ряд называется дискретным вариационным рядом; если же значения признака являются непрерывными, то вводят интервалы значений признака [хi, хi+1 ] и вариационный ряд называют интервальным. В вычислительных процедурах с интервальными вариационными рядами интервалы [хi, хi+1 ] заменяются серединами интервалов – х*i.
Числа ni называются частотами, а отношение ni к объёму выборки n –относительной частотой. В случае дискретного ряда ni – число повторения значения признака хi , в случае же интервального вариационного ряда ni число вариант, попавших в интервал [хi, хi+1 ]
![]()
Сумма
относительных частот 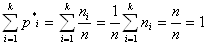
Соответствие между вариантами, записанных в порядке возрастания и относительными частотами называется эмпирическим (статистическим) распределением выборки
| Х | х1 | х2 | ….. | хк |
| P* | p1* | p2* | ….. | pк* |
Существует полная аналогия между эмпирическим распределением и законом распределения дискретной случайной величины, но в данном случае вместо значений случайной величины фигурируют варианты, а вместо вероятностей – относительные частоты. Если обозначить n(x) – число вариант, меньших x, то эмпирическая функция распределения будет иметь вид:
F*(x) = p* ( X < x ) = 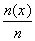
Итак, выборочной (эмпирической) функцией распределения называется функция F*(x), задающая для каждого значения х относительную частоту события Х < x. Выборочную (эмпирическую) функцию распределения можно задать таблично или графически.
Определение 4. Функция распределения генеральной совокупности F (x) называется теоретической функцией распределения.
В отличие от эмпирической функции F*(x) теоретической функцией распределения
F (x) определяет вероятность события X < x , а F*(x) его относительную частоту. Относительные частоты pi* в соответствии с теоремой Бернулли при стремлении объёма выборки n → ∞ сходится по вероятности к вероятности pi. Поэтому в математической статистике эмпирическую функцию F*(x) используют для приближённого представления теоретической функции распределения F (х).
3. Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
Выборочные данные, упорядоченные по возрастанию или убыванию, получают название вариационного ряда.
Важнейшими числовыми характеристиками вариационных рядов являются средние показатели. Средней величиной в статистике называется обобщающая характеристика совокупности однотипных по некоторому количественно варьируемому признаку явлений. Средняя величина отражает то общее, типическое, что характерно для всех этих единиц. Применяют простые и взвешенные средние величины. При вычислении простой средней величины каждый вариант совокупности учитывается один раз. Взвешенная средняя величина вычисляется, когда варианты повторяются. При вычислении средней этого вида вес каждого из вариантов выбираются пропорциональным частоте повторений этого варианта.
В математической статистике используют различные виды средних величин. Наиболее часто применяются средняя арифметическая, средняя гармоническая и средняя геометрическая величины.
Чаще других средних величин используют средние арифметические ![]() . По данным не
сгруппированного вариационного ряда вычисляется средняя арифметическая простая
величина, представляющая собой сумму всех вариантов ряда, деленную на число
вариантов
. По данным не
сгруппированного вариационного ряда вычисляется средняя арифметическая простая
величина, представляющая собой сумму всех вариантов ряда, деленную на число
вариантов
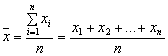 .
(1)
.
(1)
Здесь: x![]() – варианты, n – число вариантов.
– варианты, n – число вариантов.
По данным сгруппированного вариационного ряда рассчитывается средняя арифметическая взвешенная, представляющая сумму попарных произведений вариантов на соответствующие им частоты, деленную на число вариантов
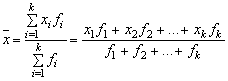 .
(2)
.
(2)
При решении некоторых задач статистики используют понятие доли – отношения числа единиц совокупности, обладающих изучаемым признаком, к общему числу единиц совокупности. Доля единиц совокупности, объединенных по некоторому признаку в i-ю группу, определяется формулой
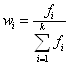 .
.
Формула для средней арифметической, записанная с использованием доли, имеет вид
![]() .
.
Примечание. При расчете средних величин по данным интервального
вариационного ряда вместо варианта x![]() следует использовать значение x*i – абсциссу середины i-го интервала.
следует использовать значение x*i – абсциссу середины i-го интервала.
В теории вероятностей аналогом средней взвешенной величины является математическое ожидание случайной величины.
Помимо средней арифметической в математической статистике применяется средняя
гармоническая величина ![]() . – средняя величина из обратных
значений признака.
. – средняя величина из обратных
значений признака.
Средняя гармоническая простая вычисляется по формуле
 . (3)
. (3)
Средняя гармоническая взвешенная используется тогда, когда статистическая
информация не содержит частот ![]() по отдельным вариантам
по отдельным вариантам ![]() совокупности,
а представлена как их произведение
совокупности,
а представлена как их произведение ![]() , и определяется по формуле
, и определяется по формуле
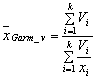 . (4)
. (4)
Пример. В таблице представлены данные о заработных платах.
| Группы рабочих |
Зар. плата ( |
Фонд оплаты труда ( |
| 1 | 1500 | 48000 |
| 2 | 1300 | 58500 |
| 3 | 1700 | 39100 |
Определить среднюю заработную плату по цеху.
Средняя заработная плата по цеху равна суммарному фонду оплаты труда ![]() , деленному на общее
число рабочих
, деленному на общее
число рабочих ![]() , т.е. вычисляется по формуле
(4.4) средней гармонической взвешенной
, т.е. вычисляется по формуле
(4.4) средней гармонической взвешенной
 руб.
руб.
При анализе динамики явлений, когда рассматриваются относительные
величины, используют среднюю геометрическую величину ![]() – корень n-ой степени из произведения n значений признака, позволяющую определить средний
коэффициент роста явления. Средняя геометрическая простая определяется по формуле
– корень n-ой степени из произведения n значений признака, позволяющую определить средний
коэффициент роста явления. Средняя геометрическая простая определяется по формуле
![]() .
(5)
.
(5)
Средняя геометрическая взвешенная вычисляется по формуле
![]() .
(6)
.
(6)
Если какой-либо количественный признак имеет разные значения у различных единиц совокупности, говорят, что он имеет вариацию. Для характеристики размера вариации в статистике применяются показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение (стандарт).
Размах вариации R представляет собой разность между максимальным и минимальным значениями признака в совокупности
R
= ![]() x
x![]() .
.
Среднее линейное отклонение d представляет собой среднее арифметическое абсолютных значений отклонений вариантов от средней арифметической и рассчитывается по формуле
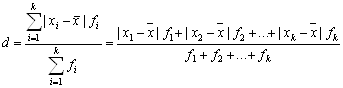 .
.
Дисперсия (от лат. dispersus – рассеянный, рассыпанный) представляет собой среднее арифметическое квадратов отклонений вариантов от среднего значения.
Дисперсия, рассчитанная по данным несгруппированного вариационного ряда, записыва-ется в виде

![]() .
.
Для сгруппированного вариационного ряда формула вычисления дисперсии имеет вид
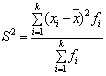
![]() . (7)
. (7)
Преобразовав выражение (7), получим иной вид записи дисперсии
![]() .
.
Среднее квадратическое отклонение (стандарт) S представляет собой квадратный корень из дисперсии
![]() .
.
Коэффициент вариации V – выраженное в процентах отношение среднего квадратического отклонения и среднего арифметического:
![]() .
.
Коэффициент вариации является критерием типичности, достоверности средней. Если коэффициент вариации не велик (не превышает 35%), это значит, что средняя величина характеризует совокупность по признаку, который мало изменяется при переходе от одной единицы совокупности к другой. Типичность такой средней высока, и в последующих вычислениях и выводах вариационный ряд может быть заменён своим средним значением. Если коэффициент вариации превышает 35%, то среднее арифметическое не является типичным значением вариационного ряда, и использование его в качестве средней характеристики некорректно.
Пример. Имеются данные о средней месячной выработке изделий рабочими бригады
|
Средняя месячная выработка Изделий рабочим (штук) (X) |
140-160 | 160-180 | 180-200 | 200-220 |
| Число рабочих (F) | 1 | 3 | 4 | 2 |
Определить показатели вариации.
Сформируем вспомогательную таблицу, обозначив ![]() середину i-го интервала
середину i-го интервала
| X | F |
|
|
|
|
|
|
| 140-160 | 1 | 150 | 150 | -34 | 34 | 1156 | 1156 |
| 160-180 | 3 | 170 | 510 | -14 | 42 | 196 | 588 |
| 180-200 | 4 | 190 | 760 | +6 | 24 | 36 | 144 |
| 200-220 | 2 | 210 | 420 | +26 | 52 | 676 | 1352 |
| Итого | 10 | 1840 | 152 | 3240 |
Cредняя
арифметическая месячная выработка ![]() =
=![]() шт.
шт.
По данным таблицы вычислим показатели вариации
1. Размах вариации R = 210 – 150 = 60 шт.
2.
Среднее
линейное отклонение ![]() =
= ![]() шт.
шт.![]()
3.
Дисперсия
![]()
![]() = 324.
= 324.
4.
Среднее
квадратическое отклонение ![]()
![]() = 18 шт.
= 18 шт.
6. Коэффициент вариации ![]()
![]() % = 9,8%.
% = 9,8%.
Как видно из расчётов, коэффициент вариации составляет 9,8% и, следовательно, типичность среднего значения высока.
В ряде задач статистическая совокупность оказывается разделенной на
несколько групп. В этом случае вычисляют три вида дисперсий: общую ![]() , межгрупповую
, межгрупповую ![]() и среднюю
внутригрупповую дисперсию
и среднюю
внутригрупповую дисперсию ![]() .
.
Рассмотрим статистическую совокупность, которая разделена на m групп. (Это разделение может
совпадать или не совпадать с группировкой той же совокупности, представленной
вариационным рядом, в котором совокупность разделена на k групп). Обозначим количество
элементов, попавших в i-ю
группу через ![]() (
(![]() ).
).
Общая дисперсия ![]() характеризует рассеяние признака
по всей изучаемой совокупности под влиянием всех факторов, формирующих уровень
признака у единиц совокупности, и определяется по формуле (5.1)
характеризует рассеяние признака
по всей изучаемой совокупности под влиянием всех факторов, формирующих уровень
признака у единиц совокупности, и определяется по формуле (5.1)
 ,
(8)
,
(8)
где ![]() –
общая средняя арифметическая для всей изучаемой совокупности.
–
общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия ![]() отражает различия в величине
изучаемого признака, возникающие под влиянием фактора, положенного в основу
группировки, и показывает рассеяние групповых средних вокруг средней величины
признака в совокупности
отражает различия в величине
изучаемого признака, возникающие под влиянием фактора, положенного в основу
группировки, и показывает рассеяние групповых средних вокруг средней величины
признака в совокупности
![]()
 , (9)
, (9)
где ![]() –
средняя арифметическая по i-й
группе.
–
средняя арифметическая по i-й
группе.
Внутригрупповая дисперсия используется для оценки рассеяния признака внутри группы. Она характеризует вариацию, не зависящую от значений признака, положенного в основу группировки (факторного признака), и возникающую под влиянием других факторов. Средняя внутригрупповая дисперсия вычисляется по формуле
![]()
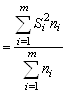 , (10)
, (10)
Здесь 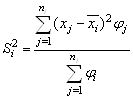 – дисперсия признака в i-й группе, где
– дисперсия признака в i-й группе, где ![]() – частота признака
– частота признака ![]() в i-й группе.
в i-й группе.
Общая, межгрупповая и средняя внутригрупповая дисперсии связаны правилом сложения дисперсий
![]() =
=![]() .
.
Смысл этого соотношения заключается в том, что общая дисперсия, определяемая влиянием всех факторов, равна дисперсии, определяемой фактором группировки, и дисперсии, возникающей под влиянием прочих факторов.
В статистическом анализе вычисляют характеристики, зависящие от распределения частот по вариантам – от структуры распределения. Поэтому эти характеристики получили название структурных средних величин. К таким показателям относятся мода и медиана.
Мода ![]() – значение признака, наиболее
часто встречающееся в ряду распределения. Мода определяется различными
способами в зависимости от вида вариационного ряда. В дискретном вариационном
ряду мода – вариант с максимальной частотой в изучаемой совокупности.
– значение признака, наиболее
часто встречающееся в ряду распределения. Мода определяется различными
способами в зависимости от вида вариационного ряда. В дискретном вариационном
ряду мода – вариант с максимальной частотой в изучаемой совокупности.
Пример. По данным статистического наблюдения получены значения величины X = {5, 3, 1, 2, 1, 4, 1, 5, 2, 1, 4, 2, 1, 1, 6}. Определить моду.
Построим вариационный ряд
| X | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 4 | 5 | 5 | 6 |
Соответствующий сгруппированный вариационный ряд имеет вид:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| F | 6 | 3 | 1 | 2 | 2 | 1 |
Значение признака Х, имеющего наибольшую частоту (6) равно 1.
Следовательно, для данного вариационного ряда ![]() = 1.
= 1.
При отыскании моды в интервальном ряду сначала определяют модальный интервал – интервал, имеющий наибольшую частоту. Затем мода рассчитывается по формуле
![]()
![]() , (11)
, (11)
где ![]() –
нижняя граница модального интервала;
–
нижняя граница модального интервала; ![]() – величина модального интервала;
– величина модального интервала; ![]() – частота
модального интервала, fm-1
– частота интервала, предшествующего модальному, fm+1 – частота интервала, следующего за модальным.
– частота
модального интервала, fm-1
– частота интервала, предшествующего модальному, fm+1 – частота интервала, следующего за модальным.
Пример. По данным статистического наблюдения построен интервальный ряд распределения рабочих по заработной плате
| Зар. плата (руб.) | 1300-1400 | 1400-1500 | 1500-1600 | 1600-1700 | 1700-1800 |
| Число рабочих (частота) | 20 | 40 | 55 | 60 | 35 |
| Кумулятивная частота | 20 | 60 | 115 | 175 | 210 |
Найти моду.
Модальным интервалом является интервал (1600-1700). Подставив данные таблицы в формулу (5.5), получим
o
= ![]() 1616,7
руб.
1616,7
руб.
Медиана ![]() – значение признака (вариант),
которое делит вариационный ряд на две равные части, одна из которых – со
значениями признака меньше медианы, вторая – со значениями признака больше медианы.
– значение признака (вариант),
которое делит вариационный ряд на две равные части, одна из которых – со
значениями признака меньше медианы, вторая – со значениями признака больше медианы.
Медиана для дискретных и интервальных вариационных рядов определяется
по-разному. Если дан дискретный несгруппированный вариационный ряд и число
вариантов n нечетно, то ![]() =
=![]() , где
, где ![]() ; если число вариантов n четное,
; если число вариантов n четное, ![]() = ( x
= ( x![]() + x
+ x ![]() ) / 2, где
) / 2, где![]()
![]() .
.
Пример. По данным примера 5.2 найти медиану дискретного вариационного ряда.
Число вариантов n несгруппированного ряда равно 15, следовательно, k = (n + 1)/2 = 8, и медиана равна 2.
Пример 5.3. Определить медиану по данным, приведенным в таблице
| Размер заработной платы (тыс. руб.) | Число работников (частота) | Накопленная частота | |
| 5800 | 30 | 30 | |
| 6000 | 45 | 75 | |
| 6200 | 80 | 155 | |
| 6400 | 60 | 215 | |
| 6600 | 35 | 250 |
Решение. Сумма частот n
= 250 – четно, ![]() = 125.
= 125. ![]()
![]()
![]() = 6200.
= 6200.
В интервальном вариационном ряду для определения медианы сначала нужно найти медианный интервал – первый по счету интервал, в котором накопленная частота равна или превышает полусумму частот вариационного ряда. После этого медиана определяется по формуле
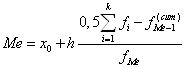 ,
,
где ![]() –
нижняя граница медианного интервала;
–
нижняя граница медианного интервала;
![]() – величина медианного интервала;
– величина медианного интервала;
![]() –
накопленная частота интервала, предшествующего медианному;
–
накопленная частота интервала, предшествующего медианному;
![]() –
частота медианного интервала.
–
частота медианного интервала.
Пример. По данным примера 5.3 определить медиану интервального ряда.
Медианным является интервал (1500-1600), так как это первый по счету интервал, сумма накопленных частот которого (115) больше полусуммы накопленных частот интервального ряда (0.5∙210 = 105). Подставив данные примера в формулу для медианы интервального ряда, получим
![]() .
.
В математической статистике используют структурные характеристики, делящие вариационный ряд на большее число частей, – квантили – показатели дифференциации признаков по частотам. Различают несколько видов квантилей.
Квартили – значения признака, которые делят вариационный ряд на четыре
равные части. Второй квартиль равен медиане, первый и третий вычисляются
аналогично расчету медианы. При расчете i-го квартиля сначала по относительным частотам
определяют соответствующий квартильный интервал – первый по счету интервал,
накопленная частота которого больше ![]() (n – сумма частот). Затем значение квартиля рассчитывают
по формуле, аналогичной формуле для нахождения медианы
(n – сумма частот). Затем значение квартиля рассчитывают
по формуле, аналогичной формуле для нахождения медианы
 ,
i =1, 2, 3,
,
i =1, 2, 3,
где i – номер квартильного интервала;
![]() –
нижняя граница i-го квартильного
интервала;
–
нижняя граница i-го квартильного
интервала;
![]() – величина
i-го квартильного интервала;
– величина
i-го квартильного интервала;
![]() –
накопленная частота интервала, предшествующего i-му квартильному интервалу;
–
накопленная частота интервала, предшествующего i-му квартильному интервалу;
![]() –
частота i-го квартильного интервала.
–
частота i-го квартильного интервала.
Отношение третьего и первого квартилей называется квартильным коэффициентом
![]() =
=![]()
и показывает, во сколько раз значение признака у четверти вариантов, имеющих наибольшие значения признака, превышает значение признака у другой четверти с наименьшими значениями.
Значения признака, которые делят вариационный ряд на десять равных
частей, называются децилями. Расчет значений децилей проводится аналогично
расчету квартилей. Отношение девятого и первого децилей – децильный коэффициент
![]() =
= ![]() показывает, во
сколько раз величина признака у 10% совокупности с наибольшими значениями
превышает такую же величину у 10% совокупности с наименьшими значениями признака.
показывает, во
сколько раз величина признака у 10% совокупности с наибольшими значениями
превышает такую же величину у 10% совокупности с наименьшими значениями признака.
В статистике используются также перцентили – значения признака, которые делят вариационный ряд на сто равных частей.
В ряде случаев в математической статистике вычисляют показатели формы распределения частот по вариантам: асимметрию и эксцесс. Характеристика симметричности распределения – коэффициент асимметрии – рассчитывается по формуле
![]() ,
,
где 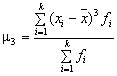 – центральный момент третьего
порядка;
– центральный момент третьего
порядка;
![]() –
куб среднего квадратического отклонения.
–
куб среднего квадратического отклонения.
Если варианты распределены симметрично относительно средней величины ![]() , т.е. равноудаленные
от
, т.е. равноудаленные
от ![]() варианты
имеют одинаковые частоты, коэффициент асимметрии равен нулю. Если
варианты
имеют одинаковые частоты, коэффициент асимметрии равен нулю. Если ![]() < 0, в
вариационном ряду преобладают варианты, которые меньше, чем средняя величина. В
этом случае говорят о наличии левосторонней асимметрии. И, наоборот, при
< 0, в
вариационном ряду преобладают варианты, которые меньше, чем средняя величина. В
этом случае говорят о наличии левосторонней асимметрии. И, наоборот, при ![]() > 0
преобладают варианты, которые больше
> 0
преобладают варианты, которые больше ![]() . Это указывает на правостороннюю
симметрию.
. Это указывает на правостороннюю
симметрию.
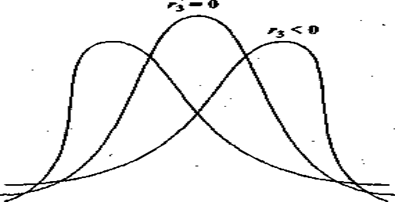
Пример. Рис. 1 иллюстрирует зависимость вида кривой распределения от асимметрии.
|
Рис. 1
Для симметричных распределений рассчитывается также эксцесс распределения – показатель островершинности распределения. Эксцесс рассчитывается по формуле
![]() ,
,
где 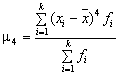 – центральный момент четвертого
порядка.
– центральный момент четвертого
порядка.
При расчете экцесса эталоном является нормальное распределение, для
которого ![]() ,
и, следовательно
,
и, следовательно ![]() . Для распределений, у которых
. Для распределений, у которых ![]() , кривая более
островершинная, чем нормальная кривая. Если
, кривая более
островершинная, чем нормальная кривая. Если ![]() , кривая будет более плосковершинной.
, кривая будет более плосковершинной.
Пример. Рис. 2 иллюстрирует зависимость вида кривой распределения от эксцесса
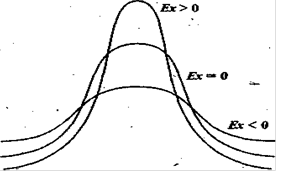
Рис. 2
Контрольные вопросы
1. Что называется средней величиной?
2. Какие виды средних величин вы знаете?
3. Какие виды средней арифметической вам известны?
4. Как вычисляется средняя геометрическая величина?
5. Что представляет собой средняя гармоническая?
6. Чем характеризуется понятие «размах вариации»?
7. Что такое среднее линейное отклонение?
8. Что такое дисперсия и как она может быть вычислена?
9. Что называется средним квадратическим отклонением?
10.Что называется коэффициентом вариации?
11.Что такое мода?
12.Как определяется мода для дискретных и интервальных вариационных рядов?
13.Что такое медиана?
14.Как определяется медиана для дискретных и интервальных вариационных рядов?
4.Графическое представление вариационных рядов
В математической статистике широко используется геометрическая интерпретация результатов первичной статистической обработки экспериментальных данных. Графическое представление сгруппированного дискретного вариационного ряда в осях – признак и частота - называется полигоном частот. Графическое представление интервального вариационного ряда в виде прямоугольников, с основаниями, равными длине интервалов и с высотой, равной соответствующей относительной частоте, называется гистограммой.
Пример. Имеются данные наблюдения над числом посетителей сайта академии в течение 40 дней:
70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100, 120, 120, 100, 75, 75, 70, 70, 100, 100, 75.
Число посетителей Х является дискретным признаком, полученные данные представляют собой выборку из n = 40 наблюдений.
Требуется составить вариационный ряд, найти относительные частоты, построить эмпирическую функцию плотности распределения и эмпирическую функцию распределения.
Сначала составим вариационный ряд:
60, 60, 60, 65, 65, 65 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75, 75, 75, 75, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120, 120, 120.
Сгруппированный вариационный ряд представим в виде таблиц
| Номер группы | i | 1 | 2 | 3 | 4 | 5 | 6 |
| Число посетителей | хi | 60 | 65 | 70 | 75 | 100 | 120 |
| Частота | ni | 3 | 3 | 9 | 8 | 11 | 6 |
| Относительная частота | pi* | 0.075 | 0.075 | 0.225 | 0.2 | 0.275 | 0.15 |
Графическое изображение результатов представлено на рис.1 и рис.2
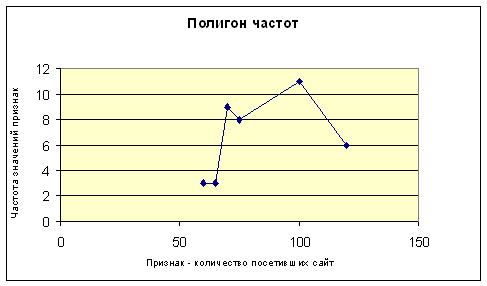
Рис. 3
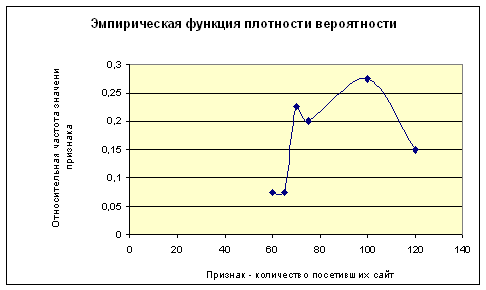
Рис.4
Построим эмпирическую функцию распределения. Исходными данными для её построения являются множество значений признака и множество относительных частот:
| хi | 50 | 60 | 65 | 70 | 75 | 100 | 120 | ||
| pi* | 0 | 0.075 | 0.075 | 0.225 | 0.2 | 0.275 | 0.15 | ||
| xi | 50 | 60 | 65 | 70 | 75 | 100 | 120 | ||
| Pi* | 0 | 0,075 | 0,075 | 0,225 | 0,200 | 0,275 | 0,150 | ||
| F ( xi ) | 0 | 0,075 | 0,15 | 0,375 | 0,575 | 0,85 | 1 | ||
![]()
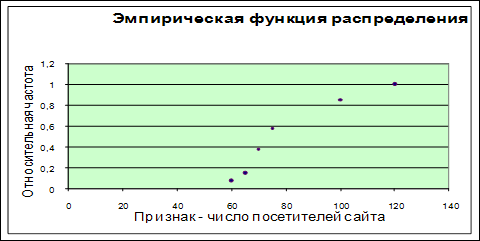
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример. В таблице 1 приведена выборка результатов отчетности однотипных 60 предприятий по прибыли (млн. руб.). Составить интервальный вариационный ряд. Построить гистограмму.
Таблица 1.
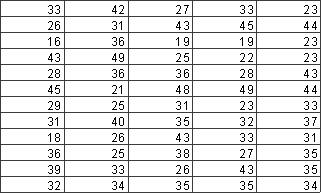
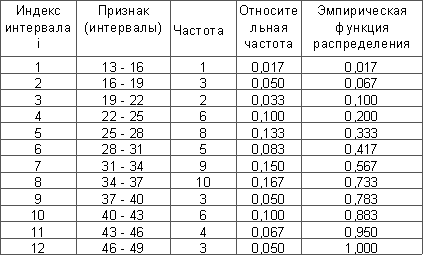
Результаты решения задачи приведены в таблице 2.
Таблица 2.
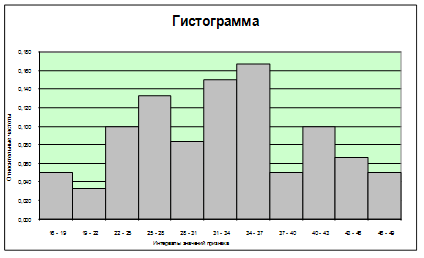
Контрольные вопросы:
1. Дайте определения основным категориям математической статистике: генеральная совокупность, выборка, статистическая совокупность, признак, оценка.
2. Что называется вариационным рядом? Классификация вариационных рядов.
3. Выпишите основные соотношения для вычисления количественных статистических характеристик вариационного ряда: среднего арифметического значения, дисперсии, среднего квадратического значения, коэффициента вариации, коэффициента асимметрии, коэффициента эксцесса, моды, медианы
4. Сформулируйте определения полигона частот, гистограммы и кумуляты.
5.На основе данных о результатах анализа эффективности работы 50‑и предприятий города по изменению реальной заработной платы на этих предприятиях в отчетном году (в % к предыдущему году) сформировать
Таблица 3.
| No | Эр[%] | No | Эр[%] | No | Эр[%] | No | Эр[%] | No | Эр[%] |
| 1 | 91 | 11 | 100 | 21 | 102 | 31 | 104 | 41 | 108 |
| 2 | 93 | 12 | 100 | 22 | 102 | 32 | 104 | 42 | 109 |
| 3 | 95 | 13 | 101 | 23 | 103 | 33 | 105 | 43 | 109 |
| 4 | 96 | 14 | 101 | 24 | 103 | 34 | 105 | 44 | 110 |
| 5 | 97 | 15 | 101 | 25 | 103 | 35 | 106 | 45 | 111 |
| 6 | 97 | 16 | 101 | 26 | 103 | 36 | 106 | 46 | 112 |
| 7 | 97 | 17 | 101 | 27 | 103 | 37 | 106 | 47 | 113 |
| 8 | 97 | 18 | 102 | 28 | 103 | 38 | 107 | 48 | 103 |
| 9 | 98 | 19 | 102 | 29 | 104 | 39 | 107 | 49 | 108 |
| 10 | 98 | 20 | 102 | 30 | 104 | 40 | 107 | 50 | 98 |
интервальный вариационный ряд значений темпов роста реальной заработной платы для равноотстоящих вариант, разбив рассматриваемый отрезок значений исследуемого параметра на 8 равноотстоящих частичных интервалов.
4. Построить таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 8 равноотстоящих частичных интервалов.
5. Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
6. Назовите основные характеристики вариационного ряда и выпишите основные соотношения для их определения.
7. Вычислить выборочную среднюю арифметическую выборки, её дисперсию, выборочное среднее квадратическое отклонение, коэффициент асимметрии и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот. Найти моду, медиану. Накопленные частоты интервалов, построить кумуляты.
Тема 2.2. Статистическое оценивание
1. Статистическое оценивание. Точечные и интервальные оценки. Требование к оценкам: несмещенность, состоятельность и эффективность.
2. Методы оценивания: метод моментов, метод максимального правдоподобия (Фишера), метод наименьших квадратов.
3. Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора.
4. Проверка статистических гипотез Н0 и HI. Уровень значимости. Ошибки 1-го и 2-го рода.
1. Статистическое оценивание
Задача оценивания параметров теоретического распределения состоит в построении приближенных формул для вычисления значений этих параметров, зависящих от выборочных значений х1, ….хn. Любую функцию j = j (х1, ….хn), зависящую от выборочных переменных и поэтому являющуюся случайной величиной, принято называть статистикой. Для того, чтобы оценки неизвестных параметров, т.е. статистики, давали хорошие приближение неизвестных параметров распределения генеральной совокупности, они должны удовлетворять определенным требованиям:
1. Математическое ожидание оценки параметра по всевозможным выборкам данного объёма должно равняться истинному значению определяемого параметра (как предписывает теория вероятностей). Оценку, удовлетворяющую этому требованию, называют несмещенной.
2. При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной.
3. Оценка параметра представляет собой случайную величину, зависящую от выборки, поэтому естественный интерес представляет разброс этой оценки, т.е. её дисперсия. Оценку называют эффективной, если при заданном объёме выборки эта оценка имеет наименьшую дисперсию.
Поскольку в качестве оценки мы ищем число – точку на координатной оси – то такие оценки называются точечными.
2. Методы оценивания: метод моментов, метод максимального правдоподобия (Фишера), метод наименьших квадратов
Известны три основных метода нахождения приближенных формул вычисления точечных оценок: метод максимального правдоподобия, метод моментов и метод наименьших квадратов.
Метод максимального правдоподобия (Фишера)
Пусть исследуемый нами признак Х имеете непрерывное распределение, зависящее от m параметров Θ1….Θm из некоторого множества Θ. В этом случае плотность вероятности генеральной совокупности будет зависеть от значения признака х и этих параметров, т.е. ƒ(х, Θ1….Θm). Пусть теперь из генеральной совокупности получена выборка объёмом n: х1, …..хn. Рассмотрим представленную выборку с позиции того, что каждое значение её хi есть реализация некоторой случайной величины Хi, полученное в i-ом наблюдении, причем в силу репрезентативности выборки Хi имеет то же распределение, что и вся генеральная совокупность. В результате выборку можно рассматривать как n –мерную случайную величину (Х1, …. Хn) или выборочный вектор Х = (Х1…. Хn), все компоненты которого представляют независимые случайные величины с одинаковыми функциями плотности вероятности, совпадающими с плотностью вероятности генеральной совокупности, т.е.
ƒ Хi (хi, Θ1….Θm) = ƒ(хi, Θ1….Θm)
Из теории вероятностей известно, что плотность вероятностей совместного распределения независимых случайных величин равна произведению плотностей вероятностей каждой из случайных величин, т.е.
ƒ(х1, х2, ….хn, Θ1….Θm) = ƒ(х1, Θ1….Θm) ƒ(х2, Θ1….Θm)….. ƒ(хn, Θ1….Θm)
Метод максимального правдоподобия оценки неизвестных параметров распределения
Θ1….Θm основан на свойстве случайной величины реализовывать в эксперименте в основном те свои значения (Х1, …. Хn) , вероятность которых максимальная.
Таким образом, в качестве оценки ![]() неизвестных параметров
распределения Θ1….Θm принимаются
те значения, которые доставляют max функции ƒ(х1, х2, ….хn, Θ1….Θm),
т.е. решения уравнения :
неизвестных параметров
распределения Θ1….Θm принимаются
те значения, которые доставляют max функции ƒ(х1, х2, ….хn, Θ1….Θm),
т.е. решения уравнения :
ƒ(х1, х2, ….хn,
![]() ) = max ƒ(х1, х2, ….хn, Θ1….Θm),
) = max ƒ(х1, х2, ….хn, Θ1….Θm),
( Θ1….Θm )![]() Θ
Θ
если решения этого уравнения существуют.
Во многих случаях вместо функции ƒ(х1, х2, ….хn, Θ1….Θm) рассматривают её натуральный
логарифм, достигающий максимума в тех же точках, что и сама функция ƒ(х1,
х2, ….хn, Θ1….Θm). В результате нахождение оценок ![]() сводится к
известной задаче математического анализа - отыскания максимума функции m переменных. Для отыскания точек
экстремумов получаем уравнения максимального правдоподобия:
сводится к
известной задаче математического анализа - отыскания максимума функции m переменных. Для отыскания точек
экстремумов получаем уравнения максимального правдоподобия:![]()
![]() или
или
![]() i = 1….m
i = 1….m
Пример. Пусть время t до выхода из строя группы компьютеров на испытательном стенде описывается показательным распределением:
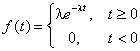 ,
,
единственный параметр которого λ неизвестен. Найти методом максимального правдоподобия оценку параметра λ
Р е ш е н и е. Испытав n компьютеров, мы получим выборку объёмом n : t1, ….tn. Функция плотности вероятности совместного распределения значений t1, ….tn имеет вид:
ƒ(t1, t2, ….tn, λ) = λe-λt1 λe-λt2…. λe-λtn = λn e-λt1 e-λt2…. e-λtn
поскольку выражение для функции плотности вероятности представляет собой произведение экспонент, то лучше воспользоваться логарифмической формой функции правдоподобия:
ln ƒ(t1, t2, ….tn, λ) = ln [λn e-λt1 e-λt2…. e-λtn ] = n lnλ – λ (t1 + t2 + ….+ tn).
Уравнение максимального правдоподобия будет иметь вид:
![]()
![]()
![]() – (t1 + t2 + ….+ tn) = 0
– (t1 + t2 + ….+ tn) = 0 ![]()
![]()
Как было установлено в теории вероятностей, математическое ожидание для
показательного распределения равно М(Х) = ![]() и обозначая
и обозначая ![]() , получим:
, получим:
![]()
Пример. Пусть интересующая нас случайная величина распределена по нормальному закону с неизвестными параметрами Мх и σ (математическое ожидание и среднеквадратическое отклонение) и получена выборка на основе опытов объёмом n : х1, …..хn. Найти методом максимального правдоподобия оценку параметров Мх и σ.
Р е ш е н ие. Плотность вероятности совместного распределения значений х1, …..хn независимых нормально распределённых случайных величин имеет вид:
ƒ(х1, х2, ….хn, Мх, σ) =
![]()
![]() …..
…..![]() =
=
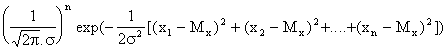 =
=
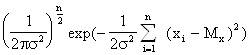
Воспользуемся логарифмической формой представления функции правдоподобия:
ln
ƒ(х1, х2, ….хn, Мх, σ) = - ![]() ln 2π -
ln 2π - ![]() ln σ2
ln σ2 ![]() =
=
- ![]() ln 2π -
ln 2π - ![]() ln D
ln D ![]()
Обозначим σ2 = D – дисперсию распределения признака Х. Уравнения максимального правдоподобия для оценки параметров Мх и σ2 = D имеют вид:
![]()
![]() -
-![]() = 0
= 0
Решения этой системы дают оценки параметров:
![]()
![]()
Пример. Найти методом максимального правдоподобия оценку параметра
λ в распределении Пуассона ![]() на основе проведенных опытов.
на основе проведенных опытов.
Решение. Будем называть опытом группу из n испытаний. При этом в каждом опыте фиксируем число появления рассматриваемого события. Пусть таких независимых опытов будет к. Обозначим число появлений события в i-м опыте mi.Функция плотности вероятности совместного распределения количества появления рассматриваемого события m1, m2,…. mk имеет вид:
ƒ(m1, m2, ….mn, λ) =
![]()
![]() …….
…….![]() =
= 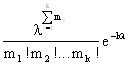
Находим логарифм этой функции:
Ln
ƒ(m1, m2, ….mn,
λ) = 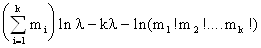
Возьмём первую производную по λ и приравняем её к нулю. Получим уравнение максимального правдоподобия:
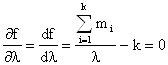 ,
,
откуда ![]()
Если взять вторую производную
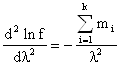
то оказывается, что она отрицательная. Это значит, что
при полученном значении ![]() функция правдоподобия lnƒ(m1, m2, ….mn, λ) достигает
максимума.
функция правдоподобия lnƒ(m1, m2, ….mn, λ) достигает
максимума.
Вывод. Метод максимального правдоподобия является эффективным в случае малых выборок, но часто требует довольно сложных вычислений.
Метод моментов (Пирсона)
Идея метода моментов заключается в приравнивании теоретических и соответствующих им эмпирических моментов, причём число моментов и, следовательно, число уравнений для определения неизвестных параметров распределений берется равным числу параметров. Покажем применение метода на тех же примерах, что и предыдущем пункте.
Напомним, что для случайной величины определены её числовые характеристики – начальные и центральные моменты. Для дискретной случайной величины:
теоретическим моментом к-го порядка называется соотношение вида:
Мкт = ![]() .
.
Эмпирическим моментом к-го порядка для несгруппированных данных называется соотношение вида:
Мкэ = 
Если принять А = 0, то моменты в этом случае называются начальными. Обычно их обозначают малыми латинскими буквами.
![]() ,
, 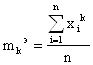 .
.
Например, начальный момент первого порядка m1 - есть математическое ожидание.
Если принять А = m1, то моменты называются центральными. Обычно их обозначают малыми греческими буквами.
μк T =![]() , μк Э =
, μк Э =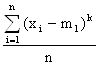 .
.
Например, μ2 - есть дисперсия.
В случае непрерывных случайных величин в теоретических моментах суммы заменяются интегралами с бесконечными пределами.
Пример. Для показательного распределения единственным параметром является λ. Для его оценивания нужно одно уравнения. Возьмем, например, приравняем первые начальные моменты – теоретический и эмпирический.
Первый начальный теоретический момент получается интегрированием по частям выражения:
m1Т
= 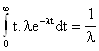
Первый начальный эмпирический момент имеет вид: m1Э =![]()
Приравняем их:
m1Э
= m1Т![]()
![]() =
= ![]()
![]()
![]() =
= 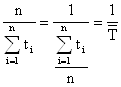
Пример. Для нормального распределения, определенного двумя параметрами, Мх и σ, приравняем теоретический и эмпирический моменты первого порядка и центральные моменты второго порядка: m1T = Mx, μ2T = σ2
m1Э = ![]() , μ2Э =
, μ2Э = 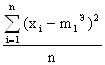
отсюда
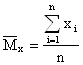 ,
, ![]()
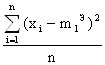 =
= 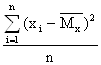
или 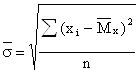
В ы в о д ы. В рассмотренных примерах оценки, полученные методом максимального правдоподобия и моментов, совпали, однако этот факт не является общим. Для других распределений оценки, полученные различными методами, могут не совпадать.
Итак, оценками двух основных параметров генеральной совокупности,– математического ожидания и дисперсии являются:
- для математического ожидания - выборочная средняя, определяемая как среднее арифметическое полученных по выборке значений:
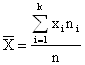 ,
,
где xi – варианта выборки, ni – частота повторяемости варианты, n – объём выборки
- собой среднюю арифметическую квадратов отклонений вариант от их выборочной для дисперсии – выборочная дисперсия, представляющая средней:
d = 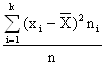 .
.
Для расчетов может быть использована также эквивалентная формула, получающаяся после возведения в квадрат и почленного суммирования:
d
= ![]() ,
,
где ![]() -
выборочная средняя квадратов вариант выборки.
-
выборочная средняя квадратов вариант выборки.
После получения оценок с помощью любого из вышеприведенного метода
остается нерешенным важнейший вопрос о несмещенности и эффективности оценок.
Этот вопрос для математического ожидания решается положительно, т.е. ![]() - несмещенная
оценка для Мх. Для дисперсии – отрицательно, т.е. d является смещенной оценкой для D = σ2.
- несмещенная
оценка для Мх. Для дисперсии – отрицательно, т.е. d является смещенной оценкой для D = σ2.
Для устранения смещенности выборочной дисперсии её следует умножить на величину n/(n-1) и получим:
S2 = 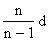 .
.
Величину S2 называют несмещенной или «исправленной» выборочной дисперсией
Пример. Покажем, что оценка математического ожидания с помощью выборочной средней является несмещенной.
Решение. Оценка параметра называется несмещенной, если математическое ожидание оценки равно оцениваемому параметру. Покажем , что математическое ожидание среднего арифметического равно математическому ожиданию генеральной совокупности.
М(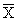 ) = М(
) = М(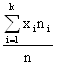 ) =
) = 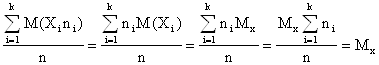 ,
,
т.к. ![]()
Замечание. Мы воспользовались представлением выборочных значений как компонентов к – мерной случайной величины (x1, x2,…..xk) → (X1, X2,….Xk)
( см. начало обсуждение метода максимального правдоподобия).
Пример. Покажем, что оценка дисперсии является смещенной.
Воспользуемся расчётной формулой для вычисления оценки дисперсии, приведенной выше:
d
= ![]() ,
,
![]()
![]()
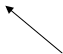
![]()
![]() d =
d = 
здесь n2 слагаемых здесь по n слагаемых
здесь n слагаемых
здесь (n2 – n) слагаемых
= ![]()
Вычислим математическое ожидание d, снова воспользовавшись представлением выборочных данных n –мерной случайной величиной (x1, x2,…..xn) → (X1, X2,….Xn):
М(d) = M(![]() ) =
) = ![]() -
- ![]() .
.
С учётом количества слагаемых (см. выше) и того, что М(Хi) = M(Xj) = M(X) и М(ХiXj) = М(Хi) M(Xj) в силу статистической независимости Хi и Xj получаем:
М(d) = 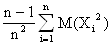 -
-
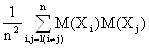 =
=
![]()
![]()
где использована формула для вычисления дисперсии: D =![]()
Из полученного результата следует, что выборочная дисперсия d является смещенной оценкой для D, т.к. её математическое ожидание
не равно D, а несколько меньше. Чтобы
ликвидировать это смещение, достаточно умножить d на ![]() . Результат этого умножения
обозначенный S2 и называется “исправленной
эмпирической дисперсией”.
. Результат этого умножения
обозначенный S2 и называется “исправленной
эмпирической дисперсией”.
Пример. На предприятии изготовляется определённый вид продукции. Ежемесячный объём выпуска этой продукции является случайной величиной, для характеристики которой принят показательный закон распределения.
![]() (
x ≥ 0 )
(
x ≥ 0 )
В течение шести месяцев проводился замер объёмов выпуска продукции, получены следующие данные:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 |
| Объём выпуска | 25 | 34 | 23 | 28 | 32 | 30 |
Найти оценку параметру λ.
Решение. Так как закон распределения содержит лишь один параметр λ, то для его оценке надо составить одно уравнение, например, равенство теоретического и эмпирического первых начальных моментов. Находим выборочную среднюю - эмпирический первый начальный момент:
![]() =
(25+34+23+28+32+30)/6 = 28.7
=
(25+34+23+28+32+30)/6 = 28.7
Определяем математическое ожидание – теоретический первый начальный момент:
М(Х) = 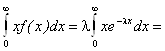
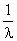 ,
,
Приравниваем теоретический и эмпирический первые начальные моменты:
![]()
откуда получаем оценку параметра λ:
![]()
3. Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
Напомним, что любую функцию j = j (х1, ….хn), зависящую от выборочных переменных и поэтому являющуюся случайной величиной, принято называть статистикой. Таким образом, все оценки являются статистиками, случайными величинами. В связи с таким свойствами оценок, они должны быть проверены на значимость. Для этого используются критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора.
4. Проверка статистических гипотез
Стандартными задачами математической статистики являются задачи определения класса (вида) распределения генеральной совокупности и определение её основных числовых характеристик. Эти задачи математическая статистика решает в виде выдвижения гипотез, а не прямым расчетом. Это связано с тем, исходные данные для статистических расчетов являются случайными величинами и полученные результаты расчета тоже есть случайные величины. Поэтому каждый расчетный результат должен быть дополнен вероятностью его правильности (или ошибки), следовательно, он является гипотетическим.
Определение 1. Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известного распределения.
Наряду с данной гипотезой рассматривают и противоречащую ей гипотезу. В случае, когда выдвинутая гипотеза отвергается, обычно принимается противоречащая ей гипотеза.
Определение 2. Нулевой (основной) называют выдвинутую гипотезу H0. Конкурирующей (альтернативной) называют гипотезу H1, которая противоречит основной.
Пример. Нулевая гипотеза H0 : генеральная совокупность распределена по нормальному закону, тогда гипотеза H1 : генеральная совокупность не распределена по нормальному закону.
Пример. Нулевая гипотеза H0 : Мх = 20 ( т.е. математическое ожидание нормально распределённой
величины равно 20), тогда гипотеза H1 может иметь вид H1: Мх ![]() 20.
20.
Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому различают ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Идея, которая используется при проверке статистических гипотез, заключается в следующем.
Вводится некоторая вычисляемая случайная величина, называемая критерием,
распределение которой заранее известно и которая характеризует отклонение
выборочных характеристик от их гипотетических значений. В предположении о
справедливости гипотезы H0
фиксируем заранее некоторый уровень значимости α (допустимую вероятность
ошибки того, что принимается гипотеза H0, а на самом деле верна гипотеза H1) считая , что в одиночном эксперименте событие с
вероятностью, меньшей α, практически не происходят. По α находим
такое число![]() ,
что бы выполнялось соотношение:
,
что бы выполнялось соотношение:
![]()
Пусть теперь КВ – вычисленное по выборке значение критерия. Если
окажется ![]() ,
то в предположении о справедливости гипотезы H0 произошло «практически» невозможное событие и
поэтому выдвинутую гипотезу H0
следует отвергнуть и принять гипотезу H1. В противном случае, можно считать, что наблюдения не противоречат
гипотезе H0. На приведенных рисунках показано
функция плотности распределения случайной величины – критерия χ2 (Рис. 1 )
и кривая уровню значимости для распределения χ2 ( Рис.2.). Уровень
значимости равен интегралу от функции плотности распределения в пределах от
,
то в предположении о справедливости гипотезы H0 произошло «практически» невозможное событие и
поэтому выдвинутую гипотезу H0
следует отвергнуть и принять гипотезу H1. В противном случае, можно считать, что наблюдения не противоречат
гипотезе H0. На приведенных рисунках показано
функция плотности распределения случайной величины – критерия χ2 (Рис. 1 )
и кривая уровню значимости для распределения χ2 ( Рис.2.). Уровень
значимости равен интегралу от функции плотности распределения в пределах от ![]() до ∞,
т.е.:
до ∞,
т.е.:
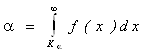
По заданному уровню значимости α находят значение нижнего предела ![]() =
= ![]()
Так, например, при α = 0.05 из графика (Рис. 1.) определяем ![]() = 7.814
= 7.814
Рис. 1.
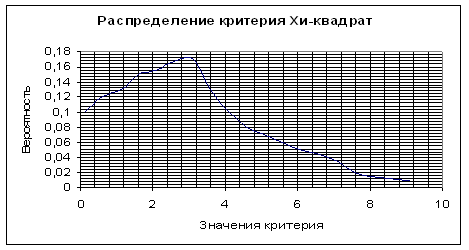
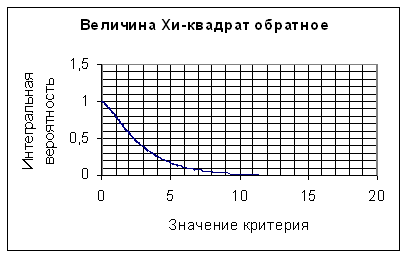
Рис. 2.
Критерий Фишера. Проверка гипотезы о равенстве дисперсий.
Задача проверки «статистического» равенства дисперсий в двух выборках играет в математической статистике большую роль, т.к. именно дисперсия определяет такие исключительные важные конструктивные и технологические и экономические показатели, как точность машин и приборов, погрешность измерительных методик, точность технологических процессов, состояние экономической конъюнктуры. и т.д.
В качестве критерия F (критерий Фишера) для проверки гипотезы о равенстве дисперсий в двух генеральных совокупностях по независимым выборкам из них строится случайная величина, равная отношению двух «исправленных» дисперсий , предполагая, что генеральная совокупность распределена нормально.
![]()
Доказано, что эта случайная величина имеет распределение Фишера с к1 =
n1 – 1 и k2 = n2 – 1 степенями свободы, где n1 и n2
– объёмы первой и второй выборок. Обычно в качестве числителя берут большую из
«исправленных» дисперсий ![]() .
.
Чтобы проверить гипотезу о равенстве дисперсий, надо построить критическую область для критерия F. В качестве критической области принимаются два интервала: интервал больших значений критерия, удовлетворяющий неравенству F >F2 и интервал малых значений 0 < F < F1, причём критические точки занимают такое положение на оси критерия, чтобы удовлетворять следующим равенствам:
![]()
![]()
где ![]() – площади под кривой
распределения (см. Рис.3).
– площади под кривой
распределения (см. Рис.3).
Такой выбор критической области обеспечивает большую чувствительность критерия. Оказывается, что достаточно определить правую критическую точку F2; последнее объясняется тем, что если величина
![]()
имеет распределение Фишера ( с k1 и k2 степенями свободы), то и
![]()
также имеет распределение Фишера (с k1 и k2 степенями свободы). Поэтому в таблицах табулируются только правые точки этого распределения.
Если полученное по выборке значение критерия выходит за правую критическую точку F2, гипотезу о равенстве дисперсий следует отбросить, в противном случае гипотеза о равенстве дисперсий не противоречит наблюдениям.
![]()
|
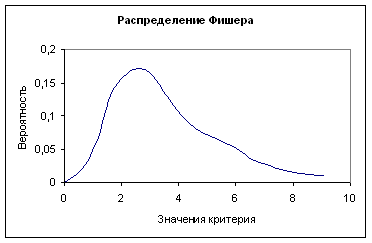
|
Пример. При проведении тестирования на
профессиональную пригодность были подвергнуты испытанию две группы: в первой
группе – 10 человек, во второй группе – 15 человек. По данным этих тестов были
посчитаны «исправленные» эмпирические дисперсии, оказавшиеся равными для первой
группы ![]() и
для второго
и
для второго ![]() .
Требуются проверить с уровнем значимости α=0,1 гипотезу о равенстве дисперсий
– уровнем подготовленности.
.
Требуются проверить с уровнем значимости α=0,1 гипотезу о равенстве дисперсий
– уровнем подготовленности.
Р е ш е н и е.
Вычислим выборочное значение критерия
F
=
![]()
![]()
По таблицам распределения Фишера и при α = 0,05 и степенях свободы k1 = n1 –1 = 9 и k2 = n2 –1 = 14 находим критическую точку
F2 = 2,65. Выборочное значение
критерия оказалось меньше критического, и, следовательно, предположение о
равенстве дисперсий не противоречит наблюдениям. Иными словами, нет оснований
считать, что две группы ![]() обладают разным уровнем
подготовленности.
обладают разным уровнем
подготовленности.
Пример. Оценивается валидность двух различных однотипных тестов. Подвергаются испытанию одна и та же группа с составе 20 человек. По данным тестирования были вычислены исправленные дисперсии, они оказались равными:
![]() ,
, ![]() .
.
Определить валидность однотипных тестов.
Р е ш е н и е.
Вычисляем выборочное значение критерия
![]()
По таблицам распределения Фишера и при α = 0,05 и степенях свободы k1 = n1 –1 = 19 и k2 = n2 –1 = 19 находим критическую точку F2 = 2,16. Таким образом, выборочное значение критерия попадает в критическую область и гипотезу о равенстве дисперсий следует отбросить, т.е. по данным двух выборок испытуемых валидность тестов существенно отличается друг от друга.
Критерий Пирсона χ2. Проверка гипотез о законе распределений .
В предыдущем параграфе были рассмотрены некоторые способы оценки параметров заранее известного закона распределения. Однако в ряде случае сам вид закона распределения является гипотетическим и нуждается в статистической проверке. Гипотезы о виде закона распределения выдвигаются на основе результатов построения эмпирических функций распределения или гистограмм.
Рассмотрим вопрос о критерии проверки по данным выборки гипотезы о том,
что данная случайная величина Х имеет функцию распределения F(х). Необходимо ввести некоторую
случайную величину- критерий К, основанный на выборе определённой меры
расхождения эмпирического и теоретического распределений. Наиболее
распространённым является критерий Пирсона χ2 (хи-квадрат). Суть критерия
Пирсона состоит в следующем.. Область изменения случайной величины разбивается
на конечное число интервалов: ![]()
Δх1, Δx2, …. Δxl (если это вся числовая ось, то первый и последний l-ый интервал будут бесконечными). Пусть mi – число значений выборки n, попавших в интервал Δхi , а pi – вероятность того, что случайная величина Х примет значения, принадлежащие Δхi при данном распределении F(x). Эта вероятность pi вычисляется по известным соотношениям:
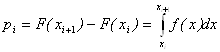
где xi и xi+1 – начальная и конечная точка интервала Δхi. Очевидно, выполняются условия
![]()
По найденным pi находим математические ожидания попаданий случайной величины Х в интервал Δхi. при n испытаниях, которые равны npi. В качестве меры расхождения выборочных m1, m2, ….ml и теоретических np1,np2,….npl характеристик вводится следующая величина:
![]()
Доказано, что введенная таким образом случайная величина при
неограниченном увеличении n распределена
по закону ![]() с
r степенями свободы, где r = l – 1 – k, а k равно числу параметров,
оцениваемых по данным выборке. Если все параметры закона распределения известны
заранее (не на основе выборки!, например, при равномерном распределении), то к
= 0. Остаётся , задавшись определённым уровнем значимости α , указать
критическую область критерия. Обозначим
с
r степенями свободы, где r = l – 1 – k, а k равно числу параметров,
оцениваемых по данным выборке. Если все параметры закона распределения известны
заранее (не на основе выборки!, например, при равномерном распределении), то к
= 0. Остаётся , задавшись определённым уровнем значимости α , указать
критическую область критерия. Обозначим ![]() число, найденное из условия
число, найденное из условия
![]()
В качестве критической области примем интервал ![]() .Определив
.Определив ![]() по данным выборки, мы получим
одно из двух: или
по данным выборки, мы получим
одно из двух: или ![]() (т.е. выборочное значение
критерия попадает в критическую область и тогда расхождение выборочных данных с
гипотетическим законом распределения существенно, а поэтому гипотеза H0 отвергается и принимается
гипотеза H1. Если
(т.е. выборочное значение
критерия попадает в критическую область и тогда расхождение выборочных данных с
гипотетическим законом распределения существенно, а поэтому гипотеза H0 отвергается и принимается
гипотеза H1. Если ![]() , то отличие эмпирического закона
от теоретического считается несущественным и принимается гипотеза H0 о статистическом равенстве
эмпирического и теоретического законов распределения.
, то отличие эмпирического закона
от теоретического считается несущественным и принимается гипотеза H0 о статистическом равенстве
эмпирического и теоретического законов распределения.
Замечание. Случайная величина – критерий ![]() , вычисленная по выборочным
данным, только при n →∞ распределена по
закону
, вычисленная по выборочным
данным, только при n →∞ распределена по
закону ![]() .
Возникает естественный вопрос о правомерности использования этого распределения
при конечном n. Принято считать это приближение
достаточным для практических расчетов, если для всех интервалов npi
.
Возникает естественный вопрос о правомерности использования этого распределения
при конечном n. Принято считать это приближение
достаточным для практических расчетов, если для всех интервалов npi ![]() 10.Если же имеются интервалы, для которых npi <10,
то рекомендуется их объединять с соседними так, чтобы новые интервалы уже
удовлетворяли указанному условию.
10.Если же имеются интервалы, для которых npi <10,
то рекомендуется их объединять с соседними так, чтобы новые интервалы уже
удовлетворяли указанному условию.
Пример. Имеются опытные данные о числе звонков в службу аварийного помощи в течение рабочего дня – таблица 1.
|
Интервалы (часы смены) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Число звонков | 16 | 27 | 17 | 15 | 24 | 19 | 11 | 15 |
Проверить с помощью критерия Пирсона и при уровне значимости α = 0,05 гипотезу о равномерном распределении числа звонков в психологическую службу в течение дня.
Решение. Постоим эмпирическую функцию плотности распределения вызовов. Рис.4.
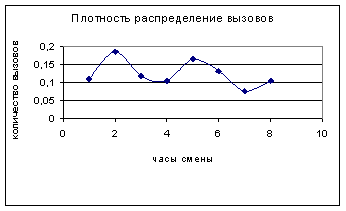
Рис.4
Таблица 2.
|
Интервалы (часы смены) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Число звонков mi | 16 | 27 | 17 | 15 | 24 | 19 | 11 | 15 |
| Математические ожидания npi | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 |
| mi - npi | -2 | 9 | -1 | -3 | 6 | 1 | -7 | -3 |
|
|
0.22 | 4.5 | 0.06 | 0.5 | 2.00 | 0.06 | 2.72 | 0.5 |
Σ =10.56
Число степеней свободы равно r = l – 1 – k = 7 ( k = 0, т.к. единственный параметр распределения – рабочее время смены ,
т.е. длина отрезка b-a – заранее известно). При данном
уровне значимости α = 0,05 по таблице находим соответствующее значение ![]() =14,07. Вычисленное
значение
=14,07. Вычисленное
значение ![]() =
10,56 лежит левее критического значения, т.е. в области допустимых значений, и
поэтому нет оснований считать гипотезу H0 о равномерном распределении противоречащей
наблюдениям.
=
10,56 лежит левее критического значения, т.е. в области допустимых значений, и
поэтому нет оснований считать гипотезу H0 о равномерном распределении противоречащей
наблюдениям.
Пример. Имеются результаты опроса группы молодёжи, состоящей из 200 человек, о возрасте первого употреблении наркотиков. Результаты представлены в виде интервального вариационного ряда (Таблица 1.):
Таблица 1.
| Интервал возрастов | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 | 18-19 | 19-20 | 20-21 |
| Количество человек в группе | 7 | 12 | 14 | 25 | 48 | 42 | 24 | 13 | 10 | 5 |
Требуется с помощью критерия Пирсона и при уровне значимости α = 0,05 оценить гипотезу о нормальном распределении возрастов начала употребления наркотиков, тем самым подтвердив гипотезу, что явление наркомании порождено множеством различных причин.
Решение. Построим экспериментальную функцию плотности распределения распределение. Поскольку вариационный ряд интервальный следует перейти к серединам интервалов и заменить абсолютные частоты – частотами относительными. В результате получим (Таблица 2; Рис 2):
Таблица 2.
| Середины интервалов | 11,5 | 12,5 | 13,5 | 14,5 | 15,5 | 16,5 | 17,5 | 18,5 | 19,5 | 20,5 |
| Относительные частоты | 0,035 | 0,06 | 0,07 | 0,125 | 0,24 | 0,21 | 0,12 | 0,065 | 0,05 | 0,025 |
|
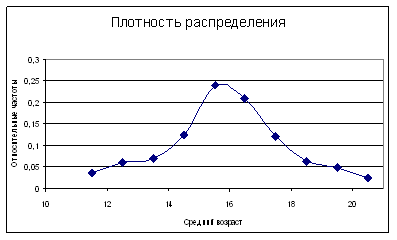
Рис.5
Полученная кривая имеет колоколообразную форму, поэтому есть основания к выдвижению гипотезы о нормальном распределении возрастов начала употребления наркотиков.
Результаты вычислений сведем в таблицу 3.
Таблица 3.
| № интервала | Границы интервала | x*i | mi | νi | pi | npi |
|
| 1 | 11,12 | 11,5 | 7 | 0.035 | 0,0187 | 3,7383 | 2,8458 |
| 2 | 12,13 | 12,5 | 12 | 0.06 | 0,0485 | 9,6940 | 0,5486 |
| 3 | 13,14 | 13,5 | 14 | 0.07 | 0,0984 | 19,6702 | 1,6345 |
| 4 | 14,15 | 14,5 | 25 | 0.125 | 0,1562 | 31,2318 | 1,2435 |
| 5 | 15,16 | 15,5 | 48 | 0.24 | 0,1940 | 38,8031 | 2,1798 |
| 6 | 16,17 | 16,5 | 42 | 0.21 | 0,1886 | 37,7239 | 0,4847 |
| 7 | 17,18 | 17,5 | 24 | 0.12 | 0,1435 | 28,6978 | 0,7690 |
| 8 | 18,19 | 18,5 | 13 | 0.065 | 0,0854 | 17,0829 | 0,9758 |
| 9 | 19,20 | 19,5 | 10 | 0.05 | 0,0398 | 7,9571 | 0,5245 |
| 10 | 20,21 | 20,5 | 5 | 0.025 | 0,0145 | 2,9002 | 1,5203 |
Сумма: 12,72645
Среднее значение возраста, впервые употребляющие наркотики, равно 15,885
Подправленная дисперсия возрастов, впервые употребляющих наркотики, равна 4,077. Стандартное отклонение возрастов, впервые употребляющих наркотики, равно 2,019
Полученные характеристики позволяют с помощью таблиц гауссовой кривой вычислить вероятности средних возрастов, впервые употребляющих наркотики. Результаты вычислений представлены на рисунке 6. Графики экспериментальных относительных частот и теоретических вероятностей практически совпали друг с другом из-за масштабирования. Чтобы показать существующее расхождение между теоретическим и экспериментальным распределением построим графики абсолютных частот средних значений возрастов – рисунок 7.
|

Рис.6
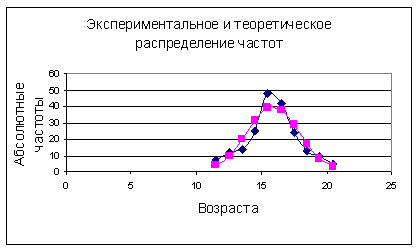
Рис.7.
Вычислим значение критерия – случайной величины χ2. Оно равно сумме значений последнего столбца таблицы - 12,726. Критическое значение χ2 при уровне значимости 0,05 и степенях свободы, равных r = 10 – 1 – k = 10 – 1 – 2 = 7 , определяется значением 14,067. Таким образом, нет оснований отвергать гипотезу H0 о нормальном законе распределения возрастов лиц, впервые употребляющих наркотические вещества, тем самым мы подтверждаем экспериментально мнение специалистов, что проблема наркомании имеет комплексный характер.
Контрольные вопросы:
1 Дайте определение точечной и интервальной оценке.
Сформулируйте основные требования к точечным оценкам и раскройте их смысл
Дайте определения уровню значимости, ошибки первого и второго рода.
4. Для вариационного ряда Темы 2.1. найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
5. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность = 0,95 и 0,99.
6. Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0,01; 0,05.
Тема 2.3. Статистические методы обработки экспериментальных данных
1. Метод наименьших квадратов (МНК).
2. Регрессионный анализ
3. Корреляционный анализ
Конспект лекции
Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:
у = а + bх, (1)
где у - среднее значение результативного признака при определенном значении факторного признака х;
а - свободный член уравнения;
b - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения - вариация у, приходящаяся на единицу вариации х.
Уравнение (1) определяется по данным о значениях признаков х и у в изучаемой совокупности, состоящей из п единиц. Параметры уравнения а и b находятся методом наименьших квадратов (МНК).
Исходное условие МНК для линейной связи имеет вид:
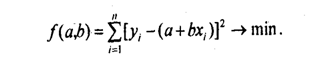
Для отыскания значений параметров а и b, при которых f(a,b) принимает минимальное значение, частные производные функции приравниваем нулю и преобразуем получаемые уравнения, которые называются нормальными уравнениями МНК для линейной формы уравнения регрессии:
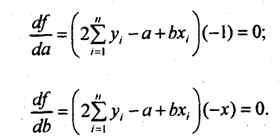
Отсюда система нормальных уравнений имеет вид:
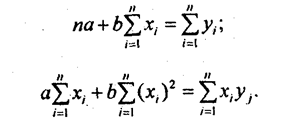
Нормальные уравнения МНК для прямой линии регрессии являются системой двух уравнений с двумя неизвестными а и b. Все остальные величины, входящие в систему, определяются по исходной информации. Таким образом, однозначно вычисляются при решении этой системы уравнений оба параметра уравнения линейной регрессии.
Если первое нормальное уравнение разделить на п, получим:
![]() (2)
(2)
По уравнению (2) обычно на практике вычисляется свободный член уравнения регрессии а. Параметр b вычисляется по преобразованной формуле, которую можно вывести, решая систему нормальных уравнений относительно b:
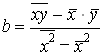 . (3)
. (3)
Так как знаменатель этого выражения есть не что иное, как дисперсия признака х, т. е. σ2, то можно записать формулу коэффициента регрессии в виде:
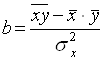 (4)
(4)
Подставив в (3) выражение для s2x, получим:
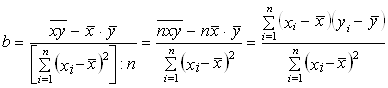 . (5)
. (5)
Параметры уравнения регрессии можно вычислить через определители:
![]() (6)
(6)
где D - определитель системы;
Da - частный определитель, получаемый в результате замены коэффициентов при а свободными членами из правой части системы уравнений;
Db - частный определитель, получаемый в результате замены коэффициентов при b свободными членами из правой части системы уравнений.
Коэффициент парной линейной регрессии, обозначенный ![]() , имеет смысл
показателя силы связи между вариацией факторного признака х и вариацией результативного
признака у. Он измеряет среднее по совокупности отклонение у от его средней
величины при отклонении признака х от своей средней величины на принятую
единицу измерения.
, имеет смысл
показателя силы связи между вариацией факторного признака х и вариацией результативного
признака у. Он измеряет среднее по совокупности отклонение у от его средней
величины при отклонении признака х от своей средней величины на принятую
единицу измерения.
Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением h. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - коэффициент корреляции rxy. Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признакоа в долях среднего квадратического отклонения результативного признака:
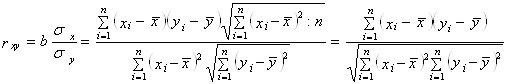 . (7)
. (7)
Коэффициент корреляции был предложен английским статистиком и философом Карлом Пирсоном (1857 - 1936). Его интерпретация такова: отклонение признака-фактора от его среднего значения на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-результата от своего среднего значения на rxy его среднего квадратического отклонения.
В отличие от коэффициента регрессии b коэффициент корреляции не зависит от принятых единиц измерения признаков, а стало быть, он сравним для любых признаков.
Обычно считают связь сильной, если r ³. 0,7; средней тесноты, при 0,5 £ r £ 0,7; слабой при r < 0,5. Квадрат коэффициента корреляции называется коэффициентом детерминации:
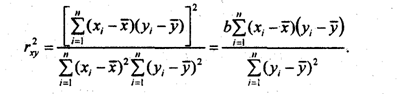
Эта формула используется при. анализе множественной
корреляции. Умножив числитель и знаменатель последнего выражения на ![]() получим:
получим:
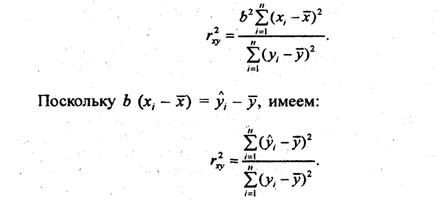
и окончательно, коэффициент корреляции принимает вид:
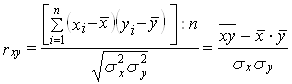 . (8)
. (8)
Эта формула соответствует формуле (7) для коэффициента регрессии.
Средние квадратическое отклонение можно выразить через средние величины признака:
![]() .
.
Подставив эти выражения в (8), получим:
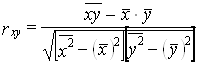 . (9)
. (9)
Эта формула (9) удобнее для расчетов, если средние величины признаков и средние квадраты индивидуальных величин вычислены ранее.
Рассмотрим фактический пример анализа корреляционной парной линии связи по данным 16 сельхозпредприятий о затратах на 10 гектар пашни и о урожайности с 1 гектара. (табл.1).
Средние значения признаков: x̅ = 1605 руб.; у̅ = 35,2 ц/голов.
Сопоставляя знаки отклонений признаков x и у от средних величин, видим явное преобладание совпадающих по знакам пар отклонений: их 14 и только 2 пары несовпадающих знаков.
Таблица 1.
Корреляция между затратами и урожайностью
| Номера единиц сово-куп-ности | Затраты на 10 гектар руб хi |
Урожайность с гектара, ц, yi |
xi - x̅ | yi - y̅ |
(xi - x̅) ´ ´ (yi - y̅) |
(xi - x̅)2 | (yi - y̅)2 | Расчетные значения урожайности , ц |
| 1 | 1602 | 34,2 | -3 | -1,0 | +3,0 | 9 | 1,00 | 35,1 |
| 2 | 1199 | 19,6 | -406 | -15,6 | +6333,6 | 164836 | 243,36 | 21,1 |
| 3 | 1321 | 27,3 | -283 | -7,9 | +2235,7 | 80089 | 62,41 | 25,3 |
| 4 | 1678 | 32,5 | +73 | -2,7 | -197,1 | 5329 | 7,29 | 37,7 |
| 5 | 1600 | 33,2 | -5 | -2,0 | +10,0 | 25 | 4,00 | 35,0 |
| 6 | 1355 | 31,8 | -250 | -3,4 | +850,0 | 62500 | 11,56 | 26,5 |
| 7 | 1413 | 30,7 | -192 | ^,5 | +864,0 | 36864 | 20,25 | 28,5 |
| 8 | 1490 | 32,6 | -115 | -2,6 | +299,0 | 13225 | 6,76 | 31,2 |
| 9 | 1616 | 26,7 | +11 | -8,5 | -93,5 | 121 | 72,25 | 35,6 |
| 10 | 1693 | 42,4 | +88 | +7,2 | +633,6 | 7744 | 51,84 | 38,2 |
| 11 | 1665 | 37,9 | +60 | +2,7 | +162,0 | 3600 | 7,29 | 37,3 |
| 12 | 1666 | 36,6 | +61 | +1,4 | +85,4 | 3721 | 1,96 | 37,3 |
| 13 | 1628 | 38,0 | +23 | +2,8 | +64,4 | 529 | 7,84 | 36,0 |
| 14 | 1604 | 32,7 | -1 | -2,5 | +2,5 | 1 | 6,25 | 35,2 |
| 15 | 2077 | 51,7 | +472 | +16,5 | +7788 | 222784 | 272,25 | 51,6 |
| 16 | 2071 | 55,3 | +466 | +20,1 | +9366,6 | 217156 | 404,01 | 51,4 |
| S 25678 | 563,2 | - | - | +28473,7 | 818533 | 1180,32 | 563,0 |
Вычислим на основе итоговой строки табл1. параметр парной линейной корреляции:
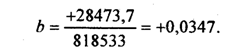
Он означает, что в среднем по изучаемой совокупности отклонение затрат от средней величины на 1 руб. приводило к отклонению с тем же знаком средней урожайности на 0,0347 ц, т. е. на 3,47 кг на 1га. При нестрогой интерпретации говорят: «С увеличением затрат на 1 руб. в среднем урожайность возрасла на 3,47 кг». Свободный член уравнения регрессии : а = 35,2 - 0,0347 • 1605 = - 20,49.
Уравнение регрессии в целом имеет вид:
![]()
Отрицательная величина свободного члена уравнения
означает, что область существования признака у не включает нулевого значения
признакам и близких значений. Если же область существования результативного признака
![]() включает
нулевое значение признака-фактора, то свободный член является положительным и
означает среднее значение результативного признака при отсутствии данного
фактора, например среднюю урожайность картофеля при отсутствии органических
удобрений.
включает
нулевое значение признака-фактора, то свободный член является положительным и
означает среднее значение результативного признака при отсутствии данного
фактора, например среднюю урожайность картофеля при отсутствии органических
удобрений.
Графическое изображение корреляционной связи по данным табл.1. приведено на рис. 1.
Коэффициент корреляции, рассчитанный на основе табл. 8.1,
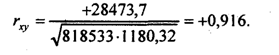
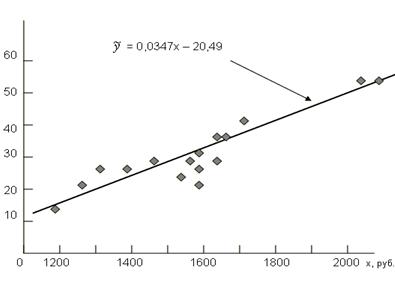
Рис. 1. Корреляция затрат с урожайностью
Контрольные вопросы:
1. Сформулируйте суть метода наименьших квадратов и условия его применимости.
2. Что означает несмещенность, состоятельность и эффективность оценок МНК?
3. Дайте определение регрессионной форме связи.
4. Что такое теснота корреляционной зависимости?
5. Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы
| nij | X | ||||||
| 10 | 15 | 20 | 25 | 30 | 35 | ||
| Y | 30 | 2 | 6 | ||||
| 40 | 4 | 4 | |||||
| 50 | 7 | 35 | 8 | ||||
| 60 | 2 | 10 | 8 | ||||
| 70 | 5 | 6 | 3 |