Реферат: Линейные преобразования случайных сигналов
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ СИГНАЛОВ
При анализе прохождения стационарного СП через линейные электрические цепи (рис. 1) будем полагать, что режим цепи установившийся, т.е. после подачи на вход цепи сигнала все переходные процессы, связанные с включением, закончились. Тогда и выходной СП будет стационарным. Рассматриваемая задача будет состоять в том, чтобы по заданной корреляционной функции входного сигнала или его спектральной плотности мощности определить B(t) или G(w) выходного сигнала.
![]()
Рис. 1
Сначала
рассмотрим решение этой задачи в частотной области. Входной СП задан своей
спектральной плотностью мощности Gх(![]() ). Выходная спектральная
плотность мощности Gy(w) определяется по формуле
). Выходная спектральная
плотность мощности Gy(w) определяется по формуле
Gy(![]() ) = Gх(
) = Gх(![]() )K2(
)K2(![]() ), (1)
), (1)
где
K2(![]() ) - квадрат модуля
комплексной передаточной функции цепи. Возведение в квадрат модуля основано на
том, что искомая характеристика является действительной функцией частоты и
энергетической характеристикой выходного процесса.
) - квадрат модуля
комплексной передаточной функции цепи. Возведение в квадрат модуля основано на
том, что искомая характеристика является действительной функцией частоты и
энергетической характеристикой выходного процесса.
Для определения связи между корреляционными функциями необходимо применить к обеим частям равенства (1) обратное преобразование Фурье:
Bx(![]() ) = F-1[Gx(
) = F-1[Gx(![]() )]; F-1[K2(
)]; F-1[K2(![]() )] = Bh(
)] = Bh(![]() )
)
- корреляционная функция импульсной характеристики исследуемой цепи:
Bh(![]() )=
)= ![]() h(t)h(t
-
h(t)h(t
- ![]() )dt.
)dt.
Таким образом, корреляционная функция выходного СП есть
By(![]() )
= Bx(
)
= Bx(![]() ) Bh(
) Bh(![]() ) =
) = ![]() Bx(t) Bh(t
-
t)dt.
Bx(t) Bh(t
-
t)dt.
ПРИМЕР 1 прохождения стационарного случайного широкополосного сигнала через RC-цепь (фильтр нижних частот), представленную схемой на рис. 2.
Широкополосность
понимается так, что энергетическая ширина спектра входного СП намного больше
полосы пропускания цепи (рис. 3). При таком соотношении между формой K2(![]() ) и Gx(
) и Gx(![]() ) можно не рассматривать
ход характеристики Gx(
) можно не рассматривать
ход характеристики Gx(![]() )
в области верхних частот.
)
в области верхних частот.
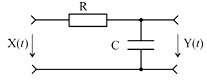
Рис. 2
Учитывая,
что в полосе частот, где K2(w) существенно отличается
от нуля, спектральная плотность мощности входного сигнала равномерна, можно без
существенной погрешности входной сигнал аппроксимировать белым шумом, т.е.
положить Gx(![]() ) = G0 = const. Такое предположение
существенно упрощает анализ. Тогда Gy(
) = G0 = const. Такое предположение
существенно упрощает анализ. Тогда Gy(![]() ) = G0K2(
) = G0K2(![]() )
)
Для заданной цепи
K2(![]() ) = 1/[1 + (
) = 1/[1 + (![]() RC)2], тогда Gy(
RC)2], тогда Gy(![]() ) = G0/[1 + (
) = G0/[1 + (![]() RC)2].
RC)2].
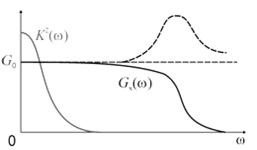
Рис. 3
Определим энергетическую ширину спектра выходного сигнала. Мощность выходного СП
Py = sy2 = (2p)-1![]() Gy(
Gy(![]() )d
)d![]() = G0/(2RC), тогда
= G0/(2RC), тогда
D![]() э = (G0)-1
э = (G0)-1![]() Gy(
Gy(![]() )d
)d![]() = p/(2RC).
= p/(2RC).
На рис. 4 показаны корреляционная функция выходного СП и его спектральная плотность мощности.
Спектральная
плотность мощности по форме повторяет квадрат модуля комплексной передаточной
функции цепи. Максимальное значение Gy(![]() ) равно G0. Максимальное значение
корреляционной функции выходного СП (его дисперсия) равна G0/(2RC). Нетрудно
определить площадь, ограниченную корреляционной функцией. Она равна значению
спектральной плотности мощности при нулевой частоте, т.е. G0:
) равно G0. Максимальное значение
корреляционной функции выходного СП (его дисперсия) равна G0/(2RC). Нетрудно
определить площадь, ограниченную корреляционной функцией. Она равна значению
спектральной плотности мощности при нулевой частоте, т.е. G0:
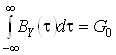 .
.
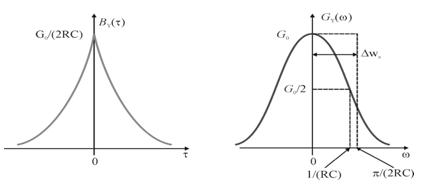
Рис. 4
Энергетической (шумовой) полосой пропускания электрической цепи
называется полоса частот, численно совпадающая с энергетической шириной
спектральной плотности мощности сигнала на выходе цепи при воздействии на вход
цепи белого шума. В заданной случае D![]() э = p/(2RC). Сравним ее
с полосой пропускания
э = p/(2RC). Сравним ее
с полосой пропускания ![]() гр
этой же цепи на уровне 0,707. Так как
гр
этой же цепи на уровне 0,707. Так как ![]() гр
= 1/(RC), то Dwэ = p/2
гр
= 1/(RC), то Dwэ = p/2 ![]() гр, то есть D
гр, то есть D![]() э в p/2 раз больше
э в p/2 раз больше ![]() гр.
гр.
Определим корреляционную функцию сигнала на выходе RC-цепи при воздействии на ее вход белого шума.
Так
как выходная спектральная плотность мощности уже определена, то можно вычислить
искомую функцию обратным преобразованием Фурье. Но в рассматриваемом случае
проще анализ выполнить во временной области, то есть By(![]() ) = Bx(
) = Bx(![]() )Bh(
)Bh(![]() ), но так как Bx(
), но так как Bx(![]() ) = W0d(
) = W0d(![]() ), то By(
), то By(![]() ) = W0Bh(
) = W0Bh(![]() ) (учитывая фильтрующее
свойство дельта-функции).
) (учитывая фильтрующее
свойство дельта-функции).
Таким образом, при воздействии на вход цепи белого шума, корреляционная функция выходного сигнала совпадает с точностью до постоянного множителя с корреляционной функцией импульсной характеристики рассматриваемой цепи. Так как
h(t) = 1/(RC) exp[-t/(RC)], t ³ 0, то
Bh(![]() ) =
) = ![]() h(t)h(t -
h(t)h(t - ![]() )dt = 1/(2RC)exp[-|
)dt = 1/(2RC)exp[-|![]() |/(RC)], -¥ <
|/(RC)], -¥ < ![]() < ¥.
< ¥.
На
рис. 5 представлены корреляционные функции (рис. 5а) и спектральные плотности
мощности (рис. 5б) для двух значений постоянной времени заданной цепи (RC)1
< (RC)2. Дисперсия выходного СП ![]() y2 = By(0) = = G0/(2RC).
y2 = By(0) = = G0/(2RC).
Площадь
под кривой By(![]() ) равна
значению спектральной плотности мощности при
) равна
значению спектральной плотности мощности при ![]() =
0, есть G0. Из сравнения графиков на рис. 5 следует, что с уменьшением
полосы пропускания цепи начальное (максимальное) значение корреляционной
функции By(0) уменьшается, что связано с уменьшением
мощности выходного сигнала, и корреляционная функция изменяется медленнее с
увеличением RC заданной цепи.
=
0, есть G0. Из сравнения графиков на рис. 5 следует, что с уменьшением
полосы пропускания цепи начальное (максимальное) значение корреляционной
функции By(0) уменьшается, что связано с уменьшением
мощности выходного сигнала, и корреляционная функция изменяется медленнее с
увеличением RC заданной цепи.
Нетрудно рассчитать интервал корреляции выходного СП
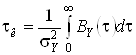 =
= 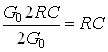 .
.
Откуда следует, что интервал корреляции выходного СП равен постоянной времени цепи.
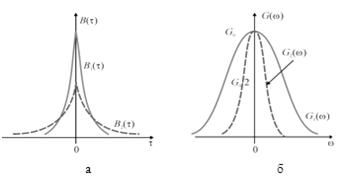
Рис. 5
ПРИМЕР 2 анализа прохождения белого шума через колебательный контур (рис. 6). Чтобы придать этой задаче физический смысл, сводим задачу, как и предыдущую, к аппроксимации входного сигнала белым шумом.
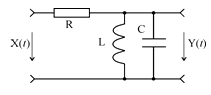
Рис. 6
Чтобы
использовать такой прием, входной сигнал должен иметь спектральную плотность
мощности, неизменную в пределах практически значимых значений ординат АЧХ цепи.
Тогда Gx(![]() ) можно считать
равной G0, а входной СП – белым шумом (рис. 7).
) можно считать
равной G0, а входной СП – белым шумом (рис. 7).
Передаточная
функция такой цепи K(j![]() )=Kр/[1+j2(
)=Kр/[1+j2(![]() -
-![]() р)/(
р)/(![]() рQэ)];
0 <
рQэ)];
0 < ![]() < ¥, где Kр
-
коэффициент передачи цепи при резонансной частоте
< ¥, где Kр
-
коэффициент передачи цепи при резонансной частоте ![]() р,
то есть Kр = Rэр/(Rэр + R);
Qэ = Q/(1 + Rэр/R) - добротность
шунтированного нагрузкой R колебательного контура, его постоянная
времени
р,
то есть Kр = Rэр/(Rэр + R);
Qэ = Q/(1 + Rэр/R) - добротность
шунтированного нагрузкой R колебательного контура, его постоянная
времени ![]() к = 2Qэ/
к = 2Qэ/![]() р = 2/(D
р = 2/(D![]() )0,7, то есть
обратная половине полосы пропускания контура на уровне 0,707. Квадрат модуля
передаточной функции K2(
)0,7, то есть
обратная половине полосы пропускания контура на уровне 0,707. Квадрат модуля
передаточной функции K2(![]() )
=Kр2/[1 + (
)
=Kр2/[1 + (![]() -
- ![]() р)2
р)2![]() к2].
Найдем дисперсию процесса на выходе цепи
к2].
Найдем дисперсию процесса на выходе цепи
![]() y2 = G0Kр2/(p
y2 = G0Kр2/(p![]() к) (p/2 + arctg2Qэ)
»
G0Kр2/(2
к) (p/2 + arctg2Qэ)
»
G0Kр2/(2![]() к) при Qэ
>> 1.
к) при Qэ
>> 1.
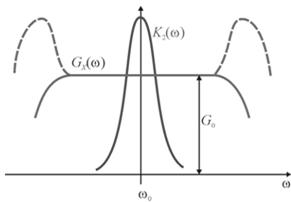
Рис. 7
Оценим
энергетическую полосу пропускания колебательного контура (рис. 6) D![]() э = (G0Kр2)-1
э = (G0Kр2)-1![]() Gy(
Gy(![]() )d
)d![]() » p/
» p/![]() к. Сравним с
полосой пропускания по уровню 0,707 (-3 дБ). Так как
к. Сравним с
полосой пропускания по уровню 0,707 (-3 дБ). Так как ![]() к = 2Qэ/
к = 2Qэ/![]() р, то D
р, то D![]() э = p/2 (D
э = p/2 (D![]() )0,7.
)0,7.
Вычислим корреляционную функцию выходного процесса (рис. 8):
By(![]() ) = G0Kр2/(2
) = G0Kр2/(2![]() к) exp(-|
к) exp(-|![]() |/
|/![]() к) cos
к) cos ![]() р
р![]() ; -¥ <
; -¥ < ![]() < ¥.
< ¥.
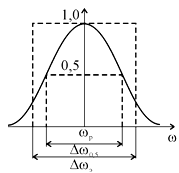
Рис. 8
Если рассматривать анализ контуров с разными добротностями, то можно увидеть различия в реализациях выходных процессов: рис. 9 при добротности Q1 и рис. 10 при добротности Q2.
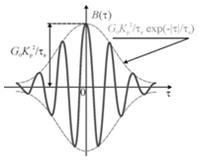
Рис. 9
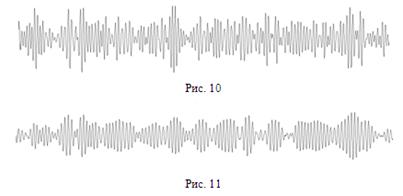
Сравнительный анализ показывает, что увеличение добротности приводит к снижению полосы пропускания контура, а значит, к снижению средней скорости изменения огибающей во времени (можно сравнить с влиянием на огибающую АМК снижения частоты модулирующего колебания). белый шум сигнал линейный преобразование
1. Расчет плотности вероятности стационарного случайного сигнала на выходе линейной цепи
Если для многих электрических цепей в установившемся режиме просто рассчитать энергетический спектр и корреляционную функцию, то задача расчета плотности вероятности в произвольном случае не имеет общего решения. Расчет плотности вероятности на выходе такой цепи является сложной задачей, не имеющей аналитического решения. Трудности анализа обусловлены тем, что мгновенные значения сигнала на выходе линейной цепи зависят не только от мгновенных значений входного сигнала в данный момент времени, но и от значений сигнала в предыдущие моменты (поскольку цепь обладает инерционностью, вызванной наличием катушек индуктивности и конденсаторов в цепи). Однако имеет место единственный случай, когда законы плотности вероятности на входе и выходе цепи совпадают. Это случай, когда входной сигнал имеет нормальный закон распределения. Основным свойством нормального закона является то, что при прохождении сигнала с нормальной плотностью вероятности сам вид закона не изменяется, а меняются лишь его параметры, то есть математическое ожидание, дисперсия, корреляционная функция. Здесь можно выявить аналогию с гармоническим колебанием в линейной цепи.
Прохождение нормального стационарного СП через линейную
электрическую цепь. Задан входной СП X(t), у которого плотность вероятности
в каждый момент времени f(x) = (![]() x2
x2![]() )-1 exp [-x2/(2
)-1 exp [-x2/(2![]() x2)], -¥<x<¥, математическое ожидание
считаем равным нулю. Поэтому средний квадрат такого СП равен дисперсии.
Корреляционная функция Bx(
x2)], -¥<x<¥, математическое ожидание
считаем равным нулю. Поэтому средний квадрат такого СП равен дисперсии.
Корреляционная функция Bx(![]() ) и, следовательно, Gx(
) и, следовательно, Gx(![]() ) известны. Вычислить
плотность вероятности сигнала на выходе цепи, заданной или импульсной
характеристикой h(t), или передаточной функцией K(j
) известны. Вычислить
плотность вероятности сигнала на выходе цепи, заданной или импульсной
характеристикой h(t), или передаточной функцией K(j![]() ). Учитывая, что при
прохождении случайного сигнала через линейную цепь нормальный закон распределения
не изменяется, можно записать: f(y) = (
). Учитывая, что при
прохождении случайного сигнала через линейную цепь нормальный закон распределения
не изменяется, можно записать: f(y) = (![]() y2
y2![]() )-1 exp [-y2/(2
)-1 exp [-y2/(2![]() y2)], т.е. сама форма
закона известна. Необходимо определить дисперсию
y2)], т.е. сама форма
закона известна. Необходимо определить дисперсию ![]() y2, а она связана с мощностью
процесса: By(0) = sy2 = (2p)-1
y2, а она связана с мощностью
процесса: By(0) = sy2 = (2p)-1![]() Gy(
Gy(![]() )d
)d![]() . Чтобы найти либо By(
. Чтобы найти либо By(![]() ), либо Gy(
), либо Gy(![]() ), требуется знать Bx(
), требуется знать Bx(![]() ) или Gx(
) или Gx(![]() ).
).
В частотной области
Gy(![]() ) = Gx(
) = Gx(![]() )K2(
)K2(![]() ), тогда
), тогда
![]() y2 = (2p)-1
y2 = (2p)-1![]() Gx(
Gx(![]() ) K2(
) K2(![]() )d
)d![]() .
.
Во
временной области By(![]() )
= Bx(
)
= Bx(![]() )×Bh(
)×Bh(![]() ). Полагая
). Полагая ![]() = 0 и учитывая, что Bh(-
= 0 и учитывая, что Bh(-![]() ) = Bh(
) = Bh(![]() ), можно записать
), можно записать
sy2 = ![]() Bx(
Bx(![]() ) Bh(
) Bh(![]() )d
)d![]() .
.
2. Нормализация случайных сигналов в узкополосных электрических цепях
Допустим есть устройство, имеющее структурную схему, показанную на рис. 12.
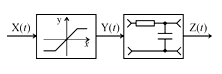
Рис. 12
Если СП с нормальным законом подвергнуть какому-либо нелинейному преобразованию (например, двухстороннему ограничению), то его закон распределения изменится (рис. 13).
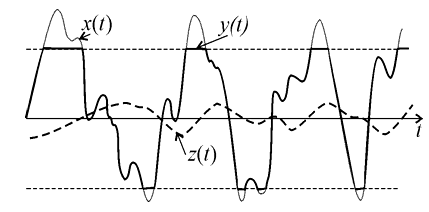
Рис. 13
На выходе узкополосной цепи опять получим сигнал с нормальным распределением, и этот закон тем ближе будет к нормальному, чем ýже полоса пропускания используемой линейной цепи.
3. Исследование на LabVIEW линейных преобразований случайных процессов и явления нормализации
Исследование влияния полосы фильтра на вид и параметры реализации случайного процесса
Количество реализаций: 200.
Тип фильтра: НЧ Баттерворта.
Порядок фильтра НЧ: 50.
Выполнение:
а) Частота среза фильтра НЧ: 3 МГц
Полученные данные показаны на рис. 1
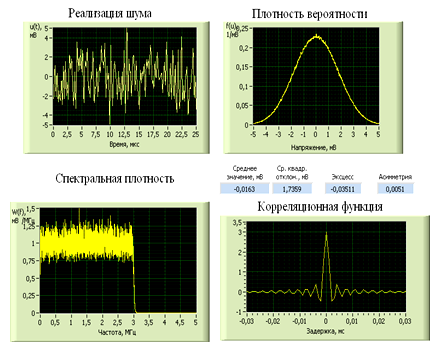
Рис. 14
Погрешность
оценки спектральной плотности мощности составляет: ![]() мВ2/МГц (оценка
методом экспресс-анализа).
мВ2/МГц (оценка
методом экспресс-анализа).
Дисперсия процесса может быть определена по площади под кривой спектральной плотности мощности, которая приблизительно равна 3 мВ2.
Среднеквадратическое
отклонение оценки составит ![]() мВ;
значение практически соответствует полученным данным (1,7359 мВ).
мВ;
значение практически соответствует полученным данным (1,7359 мВ).
б) Частота среза фильтра НЧ: 2 МГц.
Полученные данные показаны на рис. 15.
Погрешность
оценки спектральной плотности мощности процесса на выходе фильтра составляет: ![]() мВ2/МГц.
мВ2/МГц.
Среднеквадратическое
отклонение процесса составит ![]() мВ –
значение практически соответствует полученным данным.
мВ –
значение практически соответствует полученным данным.
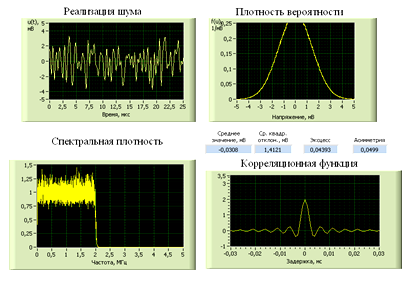
Рис. 15
в) Частота среза фильтра НЧ: 4 МГц.
Полученные данные показаны на рис. 16.
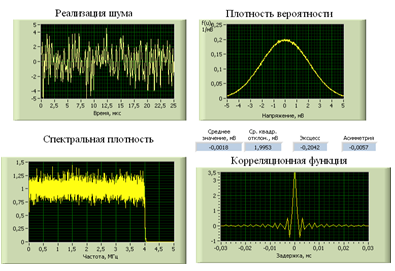
Рис. 16
Погрешность
фильтра составляет: ![]() мВ2/МГц.
мВ2/МГц.
Среднеквадратическое
отклонение, вычисленное по площади, ограниченной усредненной спектральной
плотности мощности, составит ![]() мВ;
значение практически соответствует полученным данным.
мВ;
значение практически соответствует полученным данным.
Выводы. При увеличении полосы ФНЧ
корреляционная функция уменьшается (из-за уменьшения дисперсии), при этом
главный лепесток расширяется и уменьшается плотность распределения вероятности.
Вид корреляционной функции соответствует кривой ![]() .
Скорость изменения мгновенных значений в реализации увеличивается с ростом
верхней граничной частоты фильтра. Увеличивается и размах реализации. С увеличением
дисперсии уменьшается максимальное значение плотности
вероятности.
.
Скорость изменения мгновенных значений в реализации увеличивается с ростом
верхней граничной частоты фильтра. Увеличивается и размах реализации. С увеличением
дисперсии уменьшается максимальное значение плотности
вероятности.
Влияние полосы П полосового фильтра на вид и параметры реализации входного случайного процесса
Количество реализаций: 200.
Частота среза ФНЧ: 3 МГц.
Тип фильтра: НЧ Баттерворта.
Порядок фильтра НЧ: 50.
а) Нижняя частота среза: 1,2 МГц.
Верхняя частота среза: 1,8 МГЦ.
Центральная частота: 1,5 МГц.
Полученные результаты показаны на рис. 17.
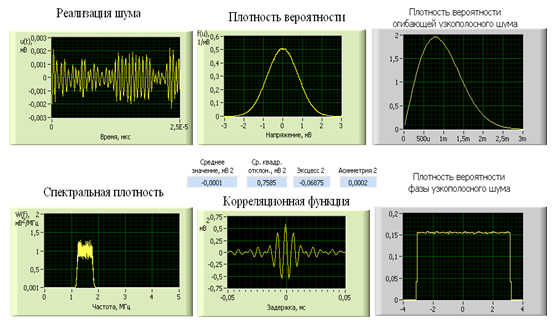
Рис. 17
Погрешность
оценки спектральной плотности СП на выходе фильтра составляет: ![]() мВ2/МГц.
мВ2/МГц.
Среднеквадратическое
отклонение, вычисленное по площади ограниченной усредненной спектральной
плотности мощности, составит ![]() , мВ;
значение практически соответствует полученным ранее результатам.
, мВ;
значение практически соответствует полученным ранее результатам.
б) Нижняя частота среза: 1,0 МГц;
Верхняя частота среза: 2,0 МГЦ;
Центральная частота: 1,5 МГц.
Полученные результаты показаны на рис. 18.
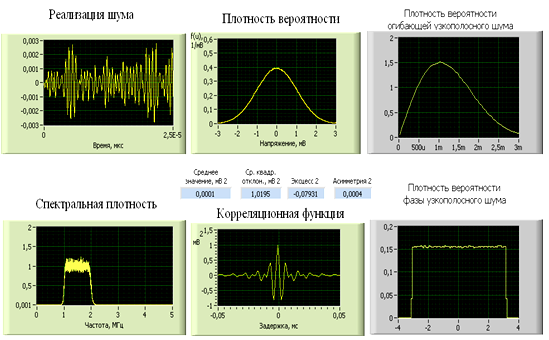
Рис. 18
Погрешность
фильтра составляет: ![]() мВ2/МГц.
мВ2/МГц.
Среднеквадратическое отклонение, вычисленное по площади, ограниченной усредненной спектральной плотности мощности, составит 1 мВ; значение практически соответствует полученным результатам.
в) Нижняя частота среза: 0,5 МГц.
Верхняя частота среза: 2,5 МГЦ.
Центральная частота: 1,5 МГц.
Полученные результаты показаны на рис. 19.
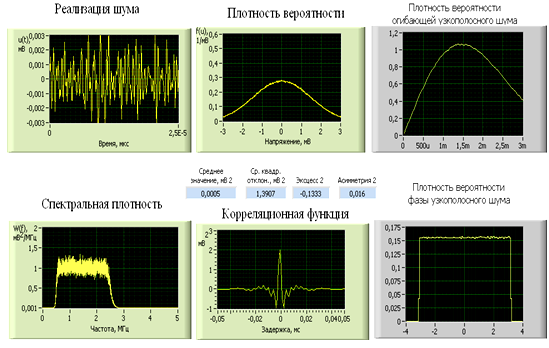
Рис. 19
Погрешность
фильтра составляет: ![]() мВ2/МГц.
мВ2/МГц.
Среднеквадратическое
отклонение, вычисленное по площади, ограниченной усредненной спектральной
плотности мощности, составит ![]() мВ;
значение практически соответствует полученным данным.
мВ;
значение практически соответствует полученным данным.
Выводы. При увеличении полосы П полосового фильтра боковые лепестки корреляционной функции уменьшаются как по амплитуде, так и по количеству, при этом максимальное значение плотности вероятности уменьшается, а площадь плотности вероятности огибающей узкополосного шума увеличивается. В реализации с ростом полосы пропускания фильтра увеличивается скорость изменения огибающей и возрастает размах реализации. Растет максимальное значение корреляционной функции при нулевом значении ее аргумента.
Исследование нормализации случайного процесса
а) Полоса пропускания: 1 МГц. Центральная полоса: 1,5 МГц.
Полученные результаты показаны на рис. 20.
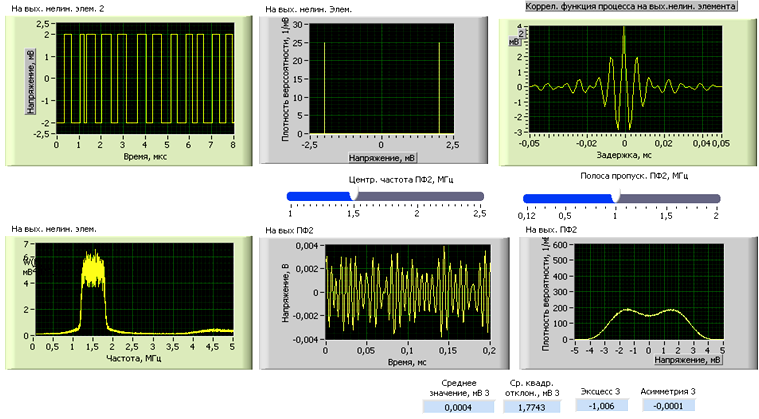
Рис. 20
б) Полоса пропускания: 0,75 МГц.
Центральная полоса: 1,5 МГц.
Полученные результаты показаны на рис. 21.
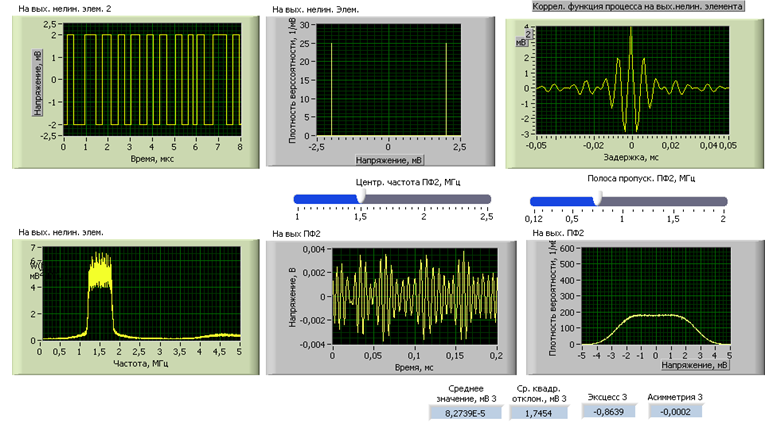
Рис. 21
в) Полоса пропускания: 0,5 МГц.
Центральная полоса: 1,5 МГц.
Полученные данные показаны на рис. 22.
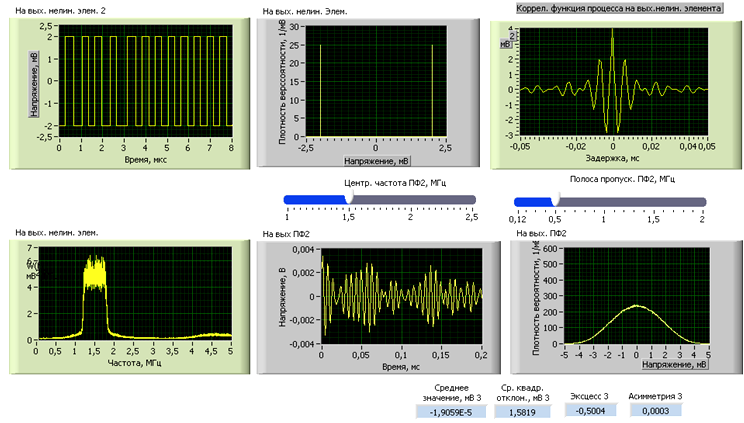
Рис. 22
г) Полоса пропускания: 0,5 МГц.
Центральная полоса: 1,5 МГц.
Полученные данные показаны на рис. 23.
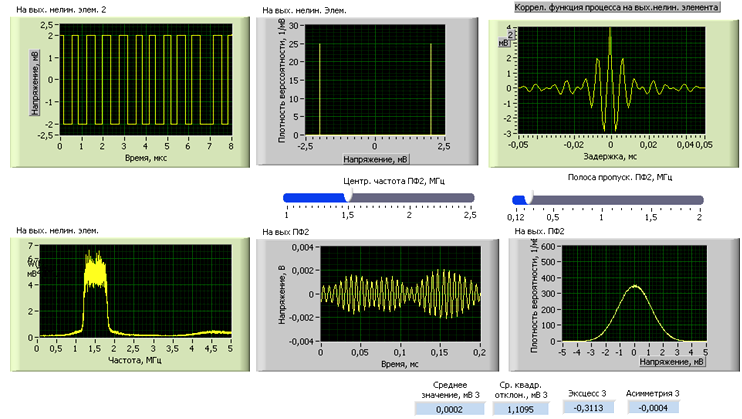
Рис. 23
д) Полоса пропускания: 0,125 МГц. Центральная полоса: 1,5 МГц.
Полученные данные показаны на рис. 2
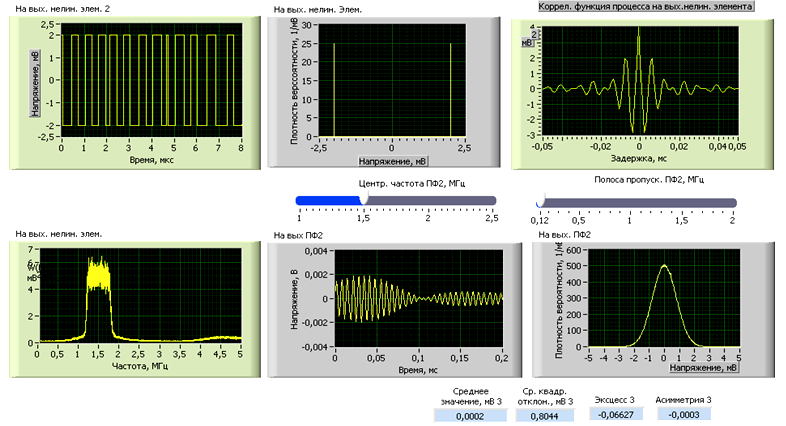
Рис. 24
Для наглядности данные сведены в табл. 1, а график зависимости коэффициента эксцесса от полосы пропускания полосового фильтра показан на рис. 25.
Таблица 1 Результаты исследований
| Полоса пропускания, МГц | Коэффициент эксцесса |
| 1,0 | -1,006 |
| 0,75 | -0,8639 |
| 0,5 | -0,5004 |
| 0,25 | -0,3113 |
| 0,125 | -0,06627 |
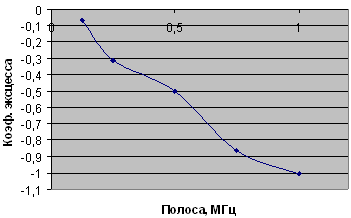
Рис. 25
Выводы
В
спектральной плотности мощности СН на выходе нелинейного элемента наблюдаются
отличающиеся от нуля значения при частотах ![]() и
3
и
3![]() . При уменьшении полосы
пропускания плотность вероятности стремится к нормальной, а коэффициент эксцесса
уменьшается (возрастает острота вершины плотности вероятности), а значит,
плотность вероятности стремится к нормальной, что соответствует центральной
предельной теореме теории вероятности. При увеличении полосы пропускания нормализующего
фильтра плотность вероятности стремится к двум d-функциям.
. При уменьшении полосы
пропускания плотность вероятности стремится к нормальной, а коэффициент эксцесса
уменьшается (возрастает острота вершины плотности вероятности), а значит,
плотность вероятности стремится к нормальной, что соответствует центральной
предельной теореме теории вероятности. При увеличении полосы пропускания нормализующего
фильтра плотность вероятности стремится к двум d-функциям.
Библиографический список
1. Жовинский, В.Н. Инженерный экспресс-анализ случайных процессов [Текст] / А.Н. Жовинский, В.Н. Жовинский. – М. : Энергия, 2009. – 112 с.
2. Манжос, В.Н. Теория и техника обработки радиолокационной информа-ции на фоне помех [Текст] / Я.Д. Ширман, В.Н. Манжос. – М. : Радио и связь, 2011. – 416 с.
1. Математические основы современной радиоэлектроники [Текст] / И.А. Большаков [и др.]. – М. : Радио и связь, 2009. – 208 с.
3. Гнеденко, Б.Н. Курс теории вероятности [Текст] / Б.Н. Гнеденко. – М. : Физматгиз, 2011. – 203 с.
4. Фомичев, К.И. Моноимпульсная радиолокация [Текст] / А.И. Леонов, К.И. Фомичев. – М. : Энергия, 2010. – 370 с.
2. Федосов, В.П. Статистическая радиотехника [Текст] : конспект лекций / В.П. Федосов, В.П. Рыжов. – Таганрог : Изд-во ТРТИ, 2008. – 76 с.
5. Царьков, Н.М. Многоканальные радиолокационные измерители [Текст] / Н.М. Царьков. – М. : Физматгиз, 2010. – 192 с.
3. Гоноровский, И.С. Радиотехнические цепи и сигналы [Текст] / И.С. Го-норовский. – М. : Радио и связь, 2006. – 608 с.
