Контрольная работа: Расчет статистических показателей
УСЛОВИЕ:
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млрд. руб. | Объем продукции в сопоставимых ценах, млрд. руб. |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
3,4 3,1 3,5 4,1 5,8 5,2 3,8 4,1 5,6 4,5 4,2 6,1 6,5 2,0 6,4 4,0 8,0 5,1 4,9 4,3 5,8 7,2 6,6 3,0 6,7 |
3,5 3,3 3,5 4,5 7,5 6,9 4,3 5,9 4,8 5,8 4,6 8,4 7,3 2,1 7,8 4,2 10,6 5,8 5,3 4,9 6,0 10,4 6,9 3,5 7,2 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1. число заводов;
2. среднегодовую стоимость основных производственных фондов - всего и в среднем на один завод;
3. объем продукции - всего и в среднем на один завод;
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
РЕШЕНИЕ
Сначала рассчитываем шаг интервала по формуле:
 , где
, где
Xmax максимальное значение среднегодовой стоимости ОПФ, Xmax= 8,0;
Xmin - минимальное значение среднегодовой стоимости ОПФ, Xmin = 2,0;
n- Количество групп, n = 4
![]() млн. руб.
млн. руб.
Результаты представим в виде групповой таблицы № 1.
В колонку «Номера заводов» записываем номера заводов, которые попадают в интервалы по группам, затем считаем ОПФ (их среднегодовую себестоимость). Считаем колонку «Всего»: складываем среднегодовую себестоимость по заводам групп, затем « В среднем на 1 завод». Считаем «Валовой продукт» - значения объемов продукции в сопоставимых ценах складываем по заводам групп.
Считаем фондоотдачу:

Разбиваем на 4 групп:
I гр.: 2,0 – 3,5 (2,0; 3,0; 3,1; 3,4; 3,5) = 15/5 = 3
Валовой продукт: (2,1; 3,5; 3,3; 3,5; 3,5) = 15,9/4 = 3,98 млрд. руб.;
II гр.: 3,5 – 5,0 (3,8; 4,0; 4,1; 4,1;4,2; 4,3; 4,5; 4,9; 5,1) = 39/9 = 4,3;
Валовой продукт: (4,3; 4,2; 4,5; 5,9; 4,6; 4,9; 5,8; 5,3; 5,8) = 45,3 / 4 = 11,33 млрд. руб.;
III гр.: 5,0 – 6,5(5,2; 5,6; 5,8; 5,8; 6,1; 6,4; 6,5; 6,6; 6,7) = 54,7/9 = 6,08;
Валовой продукт: (6,9; 4,8; 7,5; 6,0; 8,4; 7,8; 7,3; 6,9; 7,2) = 62,8/4 = 15,7 млрд. руб.;
IV гр.: 6,5 – 8,0 (7,2; 8,8) = 15,2 / 2 = 7,6;
Валовой продукт: (10,4; 10,6) = 21 / 4 = 5,25 млрд. руб.;
Используя метод группировок для решения поставленной задачи можно сделать следующие выводы:
1. Параметры фондоотдачи наиболее эффективны в группе предприятий № IV, поскольку максимальное значение этого коэффициента свидетельствует о наиболее эффективном использовании основных фондов в производстве продукции.
2. На этом основании министерству указанной отрасли, куда входят представленные заводы, необходимо рекомендовать проводить группировку предприятий для каждой группы с максимальным числом заводов равным 2.
Таблица № 1
| Величина интервала | № заводов | Число заводов | ОПФ | Валовой продукт | ФОср = ВПср/ОПФср | ||
| Всего | На 1 завод | Всего | На 1 завод | ||||
| 2,0 - 3,5 | 13,23,2,1,3 | 5 | 15 | 3 | 15,9 | 3,98 | 1,06 |
| 3,5 - 5,0 | 7,16,4,8,11,20,10,19,18 | 9 | 39 | 4,33 | 45,3 | 11,33 | 1,16 |
| 5,0 - 6,5 | 6,9,5,21,12,15,13,23,25 | 9 | 54,7 | 6,08 | 62,8 | 15,7 | 1,15 |
| 6,5 - 8,0 | 22,17 | 2 | 15,2 | 7,6 | 21 | 5,25 | 1,38 |
Задача № 2
УСЛОВИЕ:
Имеются следующие данные по областям Центрально-Черноземного района:
| Область | Валовой сбор, Ц. | Урожайность, Ц. / га. |
| 1 | 63000 | 21,0 |
| 2 | 38000 | 19,6 |
| 3 | 29000 | 18,4 |
| 4 | 68000 | 23,2 |
| 5 | 51000 | 19,5 |
Вычислите среднюю урожайность в целом по району. Укажите, какой вид средней нужно применить.
РЕШЕНИЕ
Задача составлена на применение средней арифметической и средней гармонической взвешенных. Выбор вида средней зависит от исходной статистической информации и экономического содержания показателя.
Если в условии задачи даны показатели урожайности по видам сельскохозяйственных культур и валовой сбор, то средняя урожайность будет вычислена по формуле средней гармонической взвешенной:
 , где
, где
Wi = Xi*fi

Вывод: Средняя урожайность в среднем по району 20,6 ц / га.
Задача № 3
УСЛОВИЕ:
Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
| Количество слов в телеграмме | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Итого |
| Число телеграмм | 18 | 22 | 34 | 26 | 20 | 13 | 7 | 140 |
Рассчитайте абсолютные и относительные показатели вариации.
РЕШЕНИЕ
Найдем абсолютные показатели вариации
1. Найдём размах вариации по формуле:
![]() , где
, где
Xmax – максимальное значение признака в совокупности
Xmin - минимальное значение признака в совокупности
18 – 12 = 6 слов.
2. Найдем средне арифметическую взвешенную по формуле

![]()
3. Рассчитаем средне линейное отклонение взвешенное так как данные сгруппированы, по формуле

 4. Взвешенная
дисперсия рассчитывается по формуле
4. Взвешенная
дисперсия рассчитывается по формуле

![]()
5. Найдем среднее квадратическое отклонение (взвешенное) по формуле
![]() =
=![]() слова
слова
1. Найдем относительные показатели вариации
А). Коэффициент
осцилляции по формуле ![]()
![]()
Б).
Линейный коэффициент вариации по формуле ![]()
![]()
В).
Коэффициент вариации по формуле ![]()
![]()
Задача № 4
УСЛОВИЕ:
По нижеследующим данным вычислите моду и медиану:
| Группы деталей по весу, г | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | Итого |
| Число деталей | 2 | 4 | 12 | 18 | 21 | 24 | 11 | 8 | 100 |
РЕШЕНИЕ
Задача № 4 состоит в определении структурных средних – моды и медианы. Для интервальных вариационных рядов структурные средние определяются по формулам.
1. Мода вычисляется по формуле
![]() , где
, где
Хо - нижняя граница модального интервала (интервала, встречающегося с наибольшей частотой)
i - величина модального интервала
fмо - частота модального интервала
fмо-1 - частота интервала, предшествующего модальному
fмo+1 - частота интервала, следующего за модальным
У нас получается, что мода = 24 деталям и находится в интервале (90-100)
![]()
2. Медиана вычисляется по формуле
![]() , где
, где
Xо – нижняя граница медианного интервала (интервала, сумма накопленных частот которого впервые превышает половину суммы всех частот)
i - величина медианного интервала
1/2åfi - половина суммы всех частот
Sмe-1 - сумма накопленных частот интервала, предшествующего медианному
Fмe - частота медианного интервала
С учётом накоплений получили, что медиана = 21 детали в интервале(80-90)
![]()
ИТОГ: Мода = 91,88 гр., Медиана = 86,67 гр.
Задача № 5
УСЛОВИЕ:
В порядке механической выборки обследован возраст 100 студентов ВУЗа из общего числа 2000 человек. Результаты обработки материалов наблюдения приведены в таблице:
| Возраст, лет | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Число студентов, чел. | 11 | 13 | 18 | 23 | 17 | 10 | 8 |
Установите:
а) средний возраст студентов по выборке;
б) величину ошибки при определении возраста студентов на основе выборки;
в) вероятные пределы колебания возраста для всех студентов при вероятности 0,997;
г) определите долю студентов старше 20 лет;
д.) рассчитайте ошибку выборочной доли и установите пределы удельного веса студентов старше 20 лет в генеральной совокупности.
РЕШЕНИЕ
мода медиана вариация динамика
Нам известно n = 100 чел, N = 2000 чел, F(t) = 0,997 = 3
1. Определим среднюю по выборочной совокупности (по формуле средней арифметической)


Мы видим, что студенты в возрасте 20 лет встречаются чаще, их количество составляет 23 человека.
2. Найдем дисперсию по формуле


3. Определим предельную ошибку по формуле
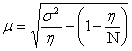 , где
, где
s2 – дисперсия варьирующего признака
n - объем выборочной совокупности
N - объем генеральной совокупности

4. После этого устанавливаются пределы, в которых находится генеральная средняя, рассчитывается по формуле
![]() , где
, где
t – коэффициент доверия (определяется по заданному уровню вероятности)
µ– средняя ошибка.
![]() - предельная
ошибка.
- предельная
ошибка.
5.
Рассчитаем пределы в которой находится генеральная средняя по формуле ![]()
![]()
ИТОГ: вероятные пределы колебания возраста для всех студентов при вероятности 0,997 составляют в пределах от 19,3 % до 20,4 %
6. Определим долю студентов старше 20 лет.
m= 17+10+8 = 35
![]()
7. Определим предельную ошибку по формуле

 8.
устанавливаются пределы, в которых находится генеральная доля, рассчитывается
по формуле
8.
устанавливаются пределы, в которых находится генеральная доля, рассчитывается
по формуле
![]()
9. Рассчитаем пределы в которой находится генеральная средняя по формуле

ИТОГ: пределы удельного веса студентов старше 20 лет в генеральной совокупности находятся в промежутке от 22 % до 49 %
Задача № 6
УСЛОВИЕ: Производство чугуна в стране характеризуется следующими данными:
| Годы | Производство чугуна, млн. т. |
| 1990 | 107 |
| 1991 | 108 |
| 1992 | 107 |
| 1993 | 110 |
| 1994 | 111 |
| 1995 | 110 |
Для анализа динамики производства чугуна вычислите:
1. абсолютные приросты (или снижения), темпы роста и темпы прироста (или снижения) по годам и к 1990г.; абсолютное значение одного процента прироста (или снижения). Полученные данные представьте в таблице;
2. среднегодовое производство чугуна;
3. среднегодовой темп роста и прироста производства чугуна.
РЕШЕНИЕ
1. Для того чтоб понять, как развивалось производство чугуна, мы построили график и заметили, что производство чугуна имело и темпы роста, и темпы снижения.

Расчет показателей рядов динамики (табл.1-3):
1.1. Абсолютный прирост Таблица 1
| Базисные, млн. т. | Цепные, млн. т. |
|
|
|
1.2. Темп роста Таблица 2
| Базисные, % | Цепные, % |
|
|
|
1.3. Темп прироста Таблица 3
| Базисные, % | Цепные, % |
|
|
|
1.4. Абсолютное значение одного % прироста Таблица 4
| Базисные, % | Цепные, % |
|
|
|
Все расчетные показатели сведем в общую итоговую таблицу (табл.5).
Таблица 5
|
Наименование показателя |
Тип показа- теля |
Год | ||||
| 1981 | 1982 | 1983 | 1984 | 1985 | ||
| Абсолютный прирост |
|
1 | 0 | 3 | 4 | 3 |
|
|
1 | -1 | 3 | 1 | -1 | |
| Темп роста |
|
100,93 | 100 | 102,8 | 103,74 | 102,8 |
|
|
100,93 | 99,07 | 102,8 | 100,91 | 99,1 | |
| Темп прироста |
|
0,93 | 0 | 2,8 | 3,74 | 2,8 |
|
|
0,93 | -0,93 | 2,8 | 0,91 | -0,9 | |
| Абсолютное значение 1 % прироста |
|
1,08 | 1,07 | 1,1 | 1,11 | 1,1 |
|
|
1,08 | 1,08 | 1,07 | 1,1 | 1,11 |
Анализ расчетных показателей подтвердил:
1). Что производство чугуна имело и темпы роста, и темпы снижения.
2). На участках 1991-1992года было заметно снижение производства чугуна, а на участке 1992-1994 годов было улучшение производства, в остальном видено снижение, что мы видим на графике
2. Поскольку представленный ряд динамики интенсивный и имеет равные годовые интервалы, среднегодовое производство чугуна будем исчислять по простой среднеарифметической формуле:
![]()
Среднегодовое производство чугуна соответствует типичному производству в 1991 году, которое составило 108 млн. т.
3. Среднегодовой темп роста производства чугуна исчисляется по формуле:
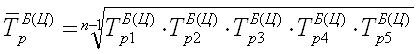 ,%
,%
![]() - базисный
- базисный
![]() - цепной
- цепной
4. Среднегодовой темп прироста производства чугуна
![]() ,%
,%
![]() - базисный
- базисный
![]() - цепной
- цепной
Задача № 7
УСЛОВИЕ:
Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Вид продукции | Выраб-но продукции, тыс.ед. | Себес-ть единицы продукции, руб. | ||
| Базисный период | Отчётный период | Базисный период | Отчётный период | |
| ЗАВОД № 1 | ||||
| МП - 25 | 4,5 | 5 | 5 | 4,8 |
| ММ - 29 | 3,2 | 3 | 8 | 8,2 |
| ЗАВОД № 2 | ||||
| МП - 25 | 10,6 | 10 | 7 | 6,6 |
На основании имеющихся данных вычислите:
Для завода № 1 (по двум видам продукции вместе)
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Покажите взаимосвязь между исчисленными индексами.
Для двух заводов вместе (по продукции МП-25):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов постоянного и переменного состава.
РЕШЕНИЕ:
1 часть.
Допустим, что g – выработано продукции, z – себестоимость продукции, тогда производим расчет и заносим в таблицу 1:
Таблица № 1
| Исходные данные | Расчет | ||||||
| Вид продукции |
|
|
|
|
|
|
|
|
Завод №1 МП-25 ММ-25 |
4,5 3,2 |
5,0 3,0 |
5,0 8,0 |
4,8 8,2 |
22,5 25,6 |
24,0 24,6 |
25,0 24,0 |
| Итого | 7,7 | 8,0 | 13,0 | 13,0 | 48,1 | 48,6 | 49,0 |
1). Общий индекс затрат на производство продукции:

![]()
б). Общий индекс себестоимости продукции:

![]()
в). Общий индекс физического объема производства продукции:

![]()
Вывод: использование индексного метода при решении задачи по анализу себестоимости позволило получить следующий результат:
1. Общий индекс затрат для завода №1, выпускающего 2 вида продукции на основании исчисления общего индекса затрат показал, что затраты увеличились на 1,04 %, что в стоимостном эквиваленте увеличили затраты на производство на 0,5 тыс. руб.
2. Фактор-анализ, проведенный по двум последовательным индексам (Iz и Ig ) показал:
а). Затраты, связанные с себестоимостью продукции снизились на 0,82 %, что позволило сэкономить 0,4 тыс. руб.
б). Физический объем производства продукции увеличился на 1,87 % и увеличил затраты на 0,9 тыс. руб., что можно объяснить следующей сложившейся ситуацией на рынке:
-выпускаемая продукция пользуется спросом и конкурентоспособна;
ПРОВЕРКА: Izg = Iz * Ig = 0, 99 * 1, 02 = 1, 0098
∆zg = ∆z + ∆g = -0,4 + 0,9 = 0,5 тыс. руб.
2 часть.
Таблица 2
| Исходные данные | Расчет | ||||||
| Вид продукции |
|
|
|
|
|
|
|
|
Завод №1 МП-25 Завод №2 МП-25 |
4,5 10,6 |
5,0 10,0 |
5,0 7,0 |
4,8 6,6 |
22,5 74,2 |
24,0 66,0 |
25,0 70,0 |
| Итого | 15,1 | 15,0 | 12,0 | 11,4 | 96,7 | 99,0 | 95,0 |
а) Индекс переменного состава:

∆перем = 6,6 - 6,401 = 0,199 = 0,2 * 1000 = 200 тыс. руб.
б) Индекс себестоимости постоянного состава:

∆пост = 6,6 - 6,3 = 0,3 * 1000 = 300 тыс. руб.
в) Индекс средней себестоимости:

∆с.с = 6,3 – 6,4 = -0,1 * 1000 = -100 тыс. руб.
Вывод: использование индексного метода для оценки себестоимости по двум предприятиям для однородной продукции МП-25 показал:
1). Что общая себестоимость на этих двух заводах увеличилась на3,11 %, что в денежном эквиваленте составило 200 тыс. руб.
2). Факторный анализ, проведенный путем расчета индекса постоянного состава и структурных сдвигов показал, что в целом изменение себестоимости произошло за счет увеличения себестоимости на 4,8 %, что в денежном эквиваленте составило 300 тыс. руб., а изменение удельного веса уменьшилось на 1,6 % , что позволило сэкономить 100 тыс. руб.
ПРОВЕРКА:

∆перем = ∆пост + ∆с.с = 0,3 + (-0,1) = 0,2 = 200 тыс. руб.
| Улучшение финансового состояния предприятия на базе системы принятия ... | |
|
АННОТАЦИЯ Пояснительная записка к магистерской работе на тему "Улучшение финансового состояния предприятия на базе системы принятия управленческих ... Прирост производства продукции по сравнению 2004 годом по чугуну составил 58,8 тыс. тонн ( или 1,1%), по стали - 52,4 тыс. тонн ( или 0,8%), по готовому прокату - 174,1 тыс. тонн ... 103,1%) были меньше темпов прироста себестоимости (109,5%). Аналогичная ситуация наблюдалась и в2006г.: превышение темпов роста себестоимости реализованной продукции (работ, услуг ... |
Раздел: Рефераты по финансовым наукам Тип: дипломная работа |
| Затраты и себестоимость продукции предприятия ОАО "Корпорация ... | |
|
Министерство высшего и профессионального образования РФ Новгородский государственный университет имени Ярослава Мудрого Институт экономики и ... в)индекс фактического снижения себестоимости единицы продукции в отчетном периоде по сравнению с базисным Для определения себестоимости из себестоимости валовой продукции вычитается прирост или прибавляется уменьшение остатка незавершенного производства полуфабрикатов, инструментов и ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Механизмы снижения себестоимости производства молока | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ АГРОБИЗНЕСА КАФЕДРА ЭКОНОМИКИ И ОРГАНИЗАЦИИ ... Если в 1999 - 2001 г.г. среднегодовой темп прироста в сельском хозяйстве составлял 6,8%, то в 2002 - 2006 г.г. только 2,3%. Если рассматривать данные таблицы 2.20., необходимо отметить, что себестоимость 1 ц молока из года в год увеличивается (особенно в 2003 году, когда валовой надой молока уменьшился ... |
Раздел: Рефераты по ботанике и сельскому хозяйству Тип: дипломная работа |
| Снижение себестоимости продукции предприятия на примере ОАО " ... | |
|
РЕФЕРАТ Объём пояснительной записки 107 стр., рис. 6, табл. 38, источников 30, приложений 6. Тема: Снижение себестоимости продукции предприятия (на ... в) себестоимость сравнимой товарной продукции (сравнимой продукцией считают ту, которая производилась в базисном периоде); Группировка затрат по элементам позволяет определить себестоимость валовой и товарной продукции, спроектировать план по себестоимости и скоординировать план себестоимости с другими ... |
Раздел: Рефераты по экономике Тип: дипломная работа |
| Снижение себестоимости продукции путем использования организационно ... | |
|
Содержание Введение 1. Себестоимость как экономическая категория 2. Аналитический раздел: ПТ ЧУП "Вланик", его характеристика и анализ работы 2.1 ... Он позволяет выяснить тенденции изменения данного показателя, выполнения плана по его уровню, определить влияние факторов на его прирост, установить резервы и дать оценку работы ... Для этого необходимо рассчитаны базисные и цепные темпы роста (по сравнению с предыдущим годом или за анализируемый период). |
Раздел: Рефераты по экономике Тип: дипломная работа |



