Контрольная работа: Математичне програмування

Завдання 1

Зібраний врожай зерна трьох сільськогосподарських артілей повинен бути перевезений на три елеватори, а саме: елеватор А₁ потужністю 100 тис. тонн, елеватор А₂ – 80 тис. тонн; А₃ – 90 тис. тонн. Визначити план перевезення зерна на елеватори, який мінімізує транспортні витрати.

Розв’язок

Побудова математичної моделі. Нехай x_ij — кількість продукції, що перевозиться з і-го пункту виробництва до j-го споживача .

Перевіримо необхідність і достатність умов розв'язання задачі:

Оскільки 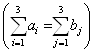, то умова балансу дотримується. Запаси рівні потребам. Отже, модель транспортної задачі є закритою.

Занесемо вихідні дані у таблицю.

Розпочинаємо будувати математичну модель даної задачі:

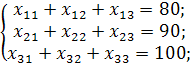
Економічний зміст записаних обмежень полягає в тому, що весь вантаж потрібно перевезти по пунктах повністю.

Аналогічні обмеження можна записати відносно замовників: вантаж, що може надходити до споживача від чотирьох баз, має повністю задовольняти його попит. Математично це записується так:

Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Тому формально це можна записати так:

minZ=12,5x₁₁+24x₁₂+18,4x₁₃+28,3x₂₁+14,5x₂₂+25,7x₂₃+15,7x₃₁+20,6x₃₂+16,3x₃₃.

Загалом математична модель сформульованої задачі має вигляд:

minZ=12,5x₁₁+24x₁₂+18,4x₁₃+28,3x₂₁+14,5x₂₂+25,7x₂₃+15,7x₃₁+20,6x₃₂+16,3x₃₃.

за умов:

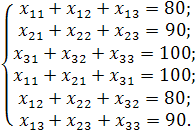
Запишемо умови задачі у вигляді транспортної таблиці та складемо її перший опорний план у цій таблиці методом «північно-західного кута».

В результаті отримано перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 5, а має бути m+n-1=5. Отже, опорний план є не виродженим.

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0:

u₁=0, u₂=15,8, u₃=21,9, v₁=12,5, v₂=-1,3, v₃=-5,6. Ці значення потенціалів першого опорного плану записуємо у транспортну таблицю.

Потім згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності u_i + v_j ≤ c_ij(для порожніх клітинок таблиці).

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(3;1): 21.9 + 12.5 > 15.7; ∆₃₁ = 21.9 + 12.5 - 15.7 = 18.7

Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці. Вибираємо максимальну оцінку вільної клітини (3;1): 15.7. Для цього в перспективну клітку (3;1) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

Тепер необхідно перемістити продукцію в межах побудованого циклу. З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (3, 2) = 20. Додаємо 20 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 20 з х_ij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.

Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n + m – 1).

Отже, другий опорний план транспортної задачі матиме такий вигляд:

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(2;3): 15.8 + 13.1 > 25.7; ∆₂₃ = 15.8 + 13.1 - 25.7 = 3.2

Вибираємо максимальну оцінку вільної клітини (2;3): 25.7

Для цього в перспективну клітку (2;3) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (2, 1) = 0. Додаємо 0 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 0 з Х_ij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.

Перевіримо оптимальність опорного плану, тобто повторюємо описані раніше дії.

Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний.

Розрахуємо значення цільової функції відповідно до другого опорного плану задачі:

F(x) = 12.5*80 + 14.5*90 + 15.7*20 + 16.3*80 = 3923

За оптимальним планом перевезень загальна вартість перевезень всієї продукції є найменшою і становить 3923 грн.

Завдання 2

математична модель екстремум транспортна задача

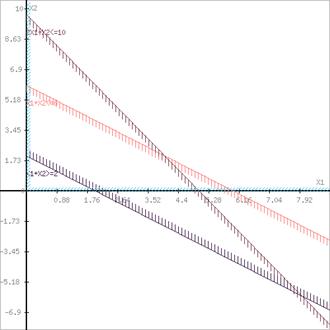
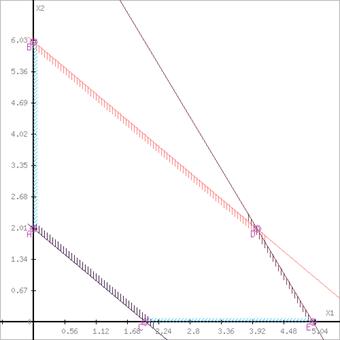
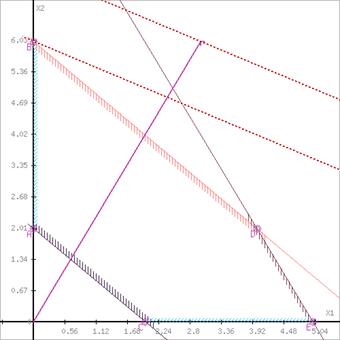
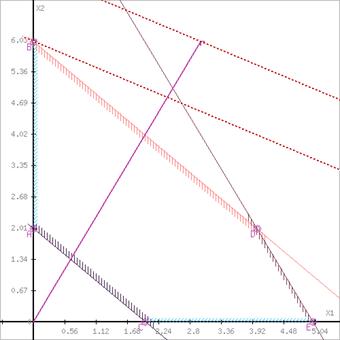
Записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну із задач симплексним методом і визначити оптимальний план іншої задачі. Оптимальні результати перевірити графічно.

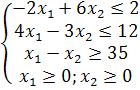
Розв’язок

Розв’яжемо задачу лінійного програмування симплексним методом.

Визначимо максимальне значення цільової функції F(X) = 3x₁+x₂ за таких умов-обмежень.

-2x₁+6x₂≤2

4x₁-3x₂≤12

x₁-x₂≥3

Для побудови першого опорного плану систему нерівностей наведемо до системи рівнянь шляхом введення додаткових змінних (перехід до канонічної форми).

-2x₁ + 6x₂ + 1x₃ + 0x₄ + 0x₅ = 2

4x₁-3x₂ + 0x₃ + 1x₄ + 0x₅ = 12

1x₁-1x₂ + 0x₃ + 0x₄-1x₅ = 3

Введемо штучні змінні x.

-2x₁ + 6x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 2

4x₁-3x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 12

1x₁-1x₂ + 0x₃ + 0x₄-1x₅ + 1x₆ = 3

Для постановки завдання на максимум цільову функцію запишемо так:

F(X) = 3x₁+x₂ - Mx₆ =>max

Отриманий базис називається штучним, а метод рішення називається методом штучного базису.

Причому штучні змінні не мають відношення до змісту поставленого завдання, однак вони дозволяють побудувати стартову точку, а процес оптимізації змушує ці змінні приймати нульові значення та забезпечити допустимість оптимального рішення.

З рівнянь висловлюємо штучні змінні:

x₆ = 3-x₁+x₂+x₅

які підставимо в цільову функцію:

F(X) = 3x₁ + x₂ - M(3-x₁+x₂+x₅) =>max

або

F(X) = (3+1M)x₁+(1-1M)x₂+(-1M)x₅+(-3M) =>max

Матриця коефіцієнтів A = a(ij) цієї системи рівнянь має вигляд:

Базисні перемінні це змінні, які входять тільки в одне рівняння системи обмежень і притому з одиничним коефіцієнтом.

Вирішимо систему рівнянь відносно базисних змінних:

x₃, x₄, x₆,

Вважаючи, що вільні змінні рівні 0, отримаємо перші опорний план:

X1 = (0,0,2,12,0,3)

Переходимо до основного алгоритму симплекс-методу.

Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х₁, оскільки значення коефіцієнта за модулем найбільше.

Остаточний варіант симплекс-таблиці оптимальний, тому що в індексному рядку знаходяться позитивні коефіцієнти.

Оптимальний план можна записати так:

x₃ = 8

x₁ = 3

x₆ = 0

F(X) = 3*3 = 9

Складемо двоїсту задачу до прямої задачі.

-2y₁+4y₂+y₃≥3

6y₁-3y₂-y₃≥1

2y₁+12y₂+3y₃ =>min

y₁ ≥ 0

y₂ ≥ 0

y₃ ≤ 0

Рішення двоїстої задачі дає оптимальну систему оцінок ресурсів.

Використовуючи останню ітерацію прямої задачі знайдемо, оптимальний план двоїстої задачі.

З першої теореми двоїстості випливає, що Y = C*A^-1.

Складемо матрицю A з компонентів векторів, що входять в оптимальний базис.

Визначивши зворотну матрицю А^-1 через алгебраїчні доповнення, отримаємо:

Як видно з останнього плану симплексного таблиці, зворотна матриця A^-1 розташована в стовпцях додаткових змінних .

Тоді Y = C*A^-1 =

Оптимальний план двоїстої задачі дорівнює:

y₁ = 0

y₂ = 0.75

y₃ = 0

Z(Y) = 2*0+12*0.75+3*0 = 9

Завдання 3

Розв’язати транспортну задачу.

Розв’язок

Побудова математичної моделі. Нехай x_ij — кількість продукції, що перевозиться з і-го пункту виробництва до j-го споживача . Оскільки 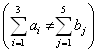, то задачу треба закрити, тобто збалансувати (зрівняти) поставки й потреби:

У нашому випадку робиться це введенням фіктивного постачальника, оскільки 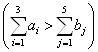. З уведенням фіктивного споживача транспортній таблиці додатково заявляється n робочих клітинок.

Ціни, додатковим клітинкам, щоб фіктивний стовбець був нейтральним щодо оптимального вибору планових перевезень, призначаються усі рівні нулю.

Занесемо вихідні дані у таблицю.

Забезпечивши закритість розв'язуваної задачі, розпочинаємо будувати математичну модель даної задачі:

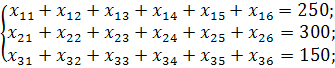
Економічний зміст записаних обмежень полягає в тому, що весь вантаж потрібно перевезти по пунктах повністю.

Аналогічні обмеження можна записати відносно замовників: вантаж, що може надходити до споживача від чотирьох баз, має повністю задовольняти його попит. Математично це записується так:

Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Тому формально це можна записати так:

minZ=1x₁₁+4x₁₂+7x₁₃+9x₁₄+1x₁₅+0x₁₆+2x₂₁+3x₂₂+1x₂₃+2x₂₄+4x₂₅+0x₂₆+2x₃₁+1x₃₂+3x₃₃+1x₃₄+ +4x₃₅+0x₃₆.

Загалом математична модель сформульованої задачі має вигляд:

minZ=1x₁₁+4x₁₂+7x₁₃+9x₁₄+1x₁₅+0x₁₆+2x₂₁+3x₂₂+1x₂₃+2x₂₄+4x₂₅+0x₂₆+2x₃₁+1x₃₂+3x₃₃+1x₃₄+ +4x₃₅+0x₃₆.

за умов:

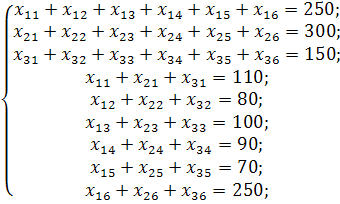
Запишемо умови задачі у вигляді транспортної таблиці та складемо її перший опорний план у цій таблиці методом «північно-західного кута».

В результаті отримано перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 8, а має бути m+n-1=8. Отже, опорний план є не виродженим.

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0:

u₁ + v₁ = 1; 0 + v₁ = 1; v₁ = 1

u₁ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₁ + v₃ = 7; 0 + v₃ = 7; v₃ = 7

u₂ + v₃ = 1; 7 + u₂ = 1; u₂ = -6

u₂ + v₄ = 2; -6 + v₄ = 2; v₄ = 8

u₂ + v₅ = 4; -6 + v₅ = 4; v₅ = 10

u₂ + v₆ = 0; -6 + v₆ = 0; v₆ = 6

u₃ + v₆ = 0; 6 + u₃ = 0; u₃ = -6

Ці значення потенціалів першого опорного плану записуємо у транспортну таблицю.

Потім згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності u_i + v_j ≤ c_ij(для порожніх клітинок таблиці).

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(1;5): 0 + 10 > 1; ∆₁₅ = 0 + 10 - 1 = 9

(1;6): 0 + 6 > 0; ∆₁₆ = 0 + 6 - 0 = 6

(3;4): -6 + 8 > 1; ∆₃₄ = -6 + 8 - 1 = 1

Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці. Вибираємо максимальну оцінку вільної клітини (1;5): 1. Для цього в перспективну клітку (1;5) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

Тепер необхідно перемістити продукцію в межах побудованого циклу. З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (1, 3) = 60. Додаємо 60 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 60 з х_ij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.

Для цього у порожню клітинку (1;5) переносимо менше з чисел х_ij, які розміщені в клітинках зі знаком «–». Одночасно це саме число х_ij додаємо до відповідних чисел, що розміщені в клітинках зі знаком «+», та віднімаємо від чисел, що розміщені в клітинках, позначених знаком «–».

Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n + m – 1).

Отже, другий опорний план транспортної задачі матиме такий вигляд:

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(2;1): 3 + 1 > 2; ∆₂₁ = 3 + 1 - 2 = 2

(2;2): 3 + 4 > 3; ∆₂₂ = 3 + 4 - 3 = 4

(3;1): 3 + 1 > 2; ∆₃₁ = 3 + 1 - 2 = 2

(3;2): 3 + 4 > 1; ∆₃₂ = 3 + 4 - 1 = 6

(3;4): 3 + -1 > 1; ∆₃₄ = 3 + -1 - 1 = 1

Вибираємо максимальну оцінку вільної клітини (3;2): 1

Для цього в перспективну клітку (3;2) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (2, 5) = 10. Додаємо 10 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 10 з Х_ij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(1;6): 0 + 3 > 0; ∆₁₆ = 0 + 3 - 0 = 3

(3;4): -3 + 5 > 1; ∆₃₄ = -3 + 5 - 1 = 1

Вибираємо максимальну оцінку вільної клітини (1;6): 0

Для цього в перспективну клітку (1;6) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (1, 2) = 70. Додаємо 70 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 70 з Х_ij, що стоять в мінусових клітинах.

В результаті отримаємо новий опорний план.

Перевіримо оптимальність опорного плану. Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких u_i + v_i>c_ij

(3;4): 0 + 2 > 1; ∆₃₄ = 0 + 2 - 1 = 1

Вибираємо максимальну оцінку вільної клітини (3;4): 1

Для цього в перспективну клітку (3;4) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-». Цикл наведено в таблиці.

З вантажів х_ij що стоять в мінусових клітинах, вибираємо найменше, тобто у = min (3, 6) = 70. Додаємо 70 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 70 з Х_ij, що стоять в мінусових клітинах.

В результаті отримаємо новий опорний план.

Перевіримо оптимальність опорного плану, тобто повторюємо описані раніше дії.

Знайдемо потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний.

Мінімальні витрати складуть:

F(x) = 1*110 + 1*70 + 0*70 + 1*100 + 2*20 + 0*180 + 1*80 + 1*70 = 470

За оптимальним планом перевезень загальна вартість перевезень всієї продукції є найменшою і становить 470 грн.

Завдання 4

Знайти графічним методом екстремуми функцій в області, визначеній нерівностями.

.

Розв’язок

Побудуємо область допустимих рішень, тобто вирішимо графічно систему нерівностей. Для цього побудуємо кожну пряму і визначимо півплощини, задані нерівностями (півплощини позначені штрихом).

Межі області

Цільова функція F(x) =>max

Розглянемо цільову функцію завдання F = 3X₁+6X₂ =>max.

Побудуємо пряму, що відповідає значенню функції F = 0: F = 3X₁+6X₂ = 0. Будемо рухати цю пряму паралельним чином. Оскільки нас цікавить максимальне рішення, тому рухався прямо до останнього торкання позначеної області. На графіку ця пряма позначена пунктирною лінією.

Рівний масштаб

Перетином півплощини буде область, яка представляє собою багатокутник, координати точок якого задовольняють умові нерівностей системи обмежень задачі.

Пряма F(x) = const перетинає область у точці B. Оскільки точка B отримана в результаті перетину прямих 1 i 5, то її координати задовольняють рівнянням цих прямих:

x₁+x₂≤6

x₁=0

Вирішивши систему рівнянь, одержимо: x₁ = 0, x₂ = 6

Звідки знайдемо максимальне значення цільової функції:

F(X) = 3*0 + 6*6 = 36