Курсовая работа: Методы распознавания образов

Федеральное агентство по образованию

Дальневосточный государственный университет

Институт математики и компьютерных наук

Кафедра процессов управления

Курсовая работа

тема: Методы распознавания образов

Владивосток 2010

Теория распознавания образов является одним из важнейших разделов кибернетики как в теоретическом, так и в прикладном плане. Она является полезнейшим инструментом в научных исследованиях и в ряде областей практической деятельности. Владение методами распознавания образов необходимо каждому специалисту по прикладной информатике, занимающемуся обработкой результатов экспериментов, что является востребованным в последние годы. В данной курсовой работе более подробно будет изучен такой способ решения задачи распознавания, как непараметрические парзеновские оценки плотностей.

1. Задача распознавания

Сформулируем задачу распознавания. Пусть имеется несколько классов объектов. Каждый объект характеризуется значениями нескольких его параметров – признаков. В результате некоторого эксперимента можно получить наборы (векторы) признаков для последовательности объектов, при этом известно, из какого класса взят каждый объект. Затем появляется новый объект с его описанием, но неизвестно, какому классу он принадлежит. Необходимо на основе полученной ранее информации вынести решение о принадлежности этого объекта.

Так как объекты изображаются векторами в многомерном пространстве (пространстве признаков), то мы приходим к геометрической формулировке задачи распознавания: необходимо построить поверхность, которая разделяет множества, соответствующие в пространстве признаков различным классам объектов. Если множества в пространстве признаков, описывающие разные классы, не пересекаются, то возможно точное разделение классов; если же они пересекаются, то любое решающее правило неизбежно будет ошибаться, поэтому необходимо искать правило классификации, доставляющее минимум ошибок.

Информация, которой обладает исследователь до эксперимента – априорная информация – служит для выбора конкретного типа алгоритма распознавания. Та информация, которую получают в результате эксперимента (векторы признаков и указания о принадлежности объектов классам), называется обучающей выборкой и служит для построения наилучшего правила классификации.

Сам процесс построения этого правила и есть обучение распознающей системы. Возможна и такая ситуация, когда указания о принадлежности объектов обучающей выборки отсутствует, в этом случае мы имеем дело с задачей самообучения.

1.1 Основные понятия и определения

Пусть имеется множество объектов , элементы которого мы будем обозначать буквами А, В, … (возможно с индексами). Множество  разбито на М непересекающихся подмножеств

которые называются классами объектов. Над каждым объектом А производится N измерений, результаты которых  называются признаками данного объекта. Таким образом, каждый объект изображается вектором признаков  в N-мерном пространстве, которое называется пространством признаков.

На вход распознающей системы поступает последовательность векторов признаков соответствующих набору объектов А1, …, Аn,… из . Последовательность (1.1) называется обучающей последовательностью, или обучающей выборкой.

x1,…xn,…,xk = x(Ak) (1.1)

Задача распознавания может быть в общем виде сформулирована следующим образом: необходимо по обучающей выборке построить решающее правило, то есть правило, которое для любого объекта А (возможно, не совпадающего ни с одним из А1, …, Аn) позволяло бы на основе вектора х(А) указать, какому из классов  принадлежит объект А.

Постановку задачи можно еще более детализировать, рассматривая отдельно три случая: детерминированная задача распознавания, вероятностная задача распознавания и самообучение (автоматическая классификация). Остановимся подробнее на вероятностной задаче распознавания.

1.2 Вероятностная задача распознавания

Дадим строгую математическую формулировку вероятностной задачи распознавания. Пусть на вероятностном пространстве  задана случайная величина , принимающая конечное число значений, . Будем интерпретировать значение случайной величины  как номер класса, которому принадлежит объект, появившийся на входе распознающей системы. Тогда вероятность  есть априорная вероятность .

Пусть, кроме того, имеется векторная случайная величина , принимающая значения в пространстве признаков ; значение х случайной величины  есть вектор признаков объекта, поступившего на вход распознающей системы. Предположим, что существуют условные плотности распределений для каждого из классов, то есть для множества В:

Очевидно, распределение случайной величины  будет иметь плотность:

(этот факт следует из формулы полной вероятности).

Наша задача состоит в том, чтобы наилучшим образом провести классификацию объекта, заданного вектором признаков, то есть необходимо построить такое правило, которое по вектору признаков указывало бы, к какому из классов  относится соответствующий объект. Слова «наилучшим образом» предполагают, что у нас есть способ количественной оценки построенного правила классификации. Определим, что мы будем понимать под качеством классифицирующего правила.

Байесовским решающим правилом называется решающее правило, минимизирующее средний риск отнесения объектов k-го класса в i-й класс.

Пусть нам задана вероятностная схема:  и матрица потерь , элемент  которой имеет смысл потерь, связанных с отнесением объекта, принадлежащего k-му классу, в i-ый класс.  - разбиение пространства  на М непересекающихся подмножеств. Тогда байесовское решающее правило определяется разбиением:

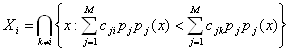
Рассмотрим один очень важный частный случай построения оптимального решающего правила. Пусть матрица потерь имеет вид:

Тогда оптимальное разбиение состоит из множеств:

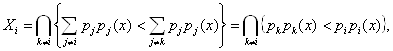
что соответствует решающему правилу: х относится к если

 для всех  (1.2)

Итак, мы имеем вид решающего правила, минимизирующего функционал среднего риска.

Однако, при решении задачи распознавания мы не имеем достаточно информации для использования этого правила, так как могут быть неизвестны ни плотности , ни априорные вероятности . Иначе говоря, мы должны принимать решения, имея неполную априорную информацию. Для преодоления этой неопределенности и служит обучающая выборка. При этом возможны два пути использования эмпирических данных:

-  оценивание плотностей распределения,

-  непосредственное восстановление параметров оптимального решающего правила.

Рассмотрим в отдельности оценивание плотностей распределения.

Оценивание плотностей распределения представляет собой классическую задачу, решаемую в математической статистике. А именно, пусть имеется повторная выборка (то есть, последовательность независимых одинаково распределенных случайных величин)  с плотностью распределения p(x). Необходимо построить оценку функции p(x). Известно много методов решения этой задачи, например, метод максимального правдоподобия, байесовские методы оценивания, непараметрические оценки плотностей.

Схема обучения распознавания в таком случае строится следующим образом. Обучающая выборка разбивается на подвыборки, соответствующие отдельным классам. Оцениваются плотности распределений для каждого класса  и априорные вероятности классов . Полученные оценки подставляются в байесовское решающее правило (1.2), которое и используется для классификации. Рассмотрим подробно такой метод решения задачи распознавания, как парзеновские оценки плотностей.

Методы оценивания, в которых не делается предположений об аналитическом виде неизвестной плотности, называются непараметрическими.

Пусть  - повторная выборка с плотностью p(x). Парзеновская оценка плотности p(x) есть функция

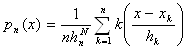, (2.1)

где k(y) – некоторая заданная функция, называемая ядром оценки (2.1),  - неотрицательная числовая последовательность.

Если ядро k(y) удовлетворяет условиям

то (2.1) есть плотность распределения.

Докажем следующие теоремы:

Теорема (2.1):

Пусть выполнены условия на ядро k и :

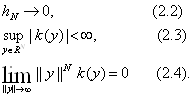
Если функция p(x) непрерывна в точке х, то

геометрический распознавание непараметрический парзеновский

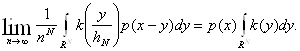
Доказательство.

Рассмотрим величину:

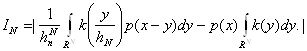
Справедлива формула:

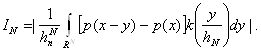
Разобьем здесь область интегрирования на два множества  и  - произвольное положительное число.

Первое слагаемое не превосходит величины

а второе не превосходит

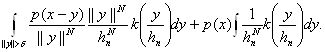
Отсюда следует, что

Устремляя n к бесконечности, получаем в силу условий (2.2)-(2.4) получаем:

а так как  может быть взято произвольно малым, то это и означает сходимость .

Теорема доказана.

Теорема (2.2).

Пусть х – точка непрерывности плотности p(x) и выполнены условия теоремы (2.1). тогда  - асимптотически несмещенная оценка величины p(x), то есть

Если, кроме того

то  - состоятельная оценка, то есть

Доказательство.

Соотношение (2.5) непосредственно следует из теоремы (1).

Справедливо равенство

второе слагаемое в правой части стремиться к нулю при .

Введем обозначения:

;

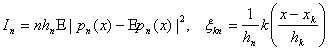тогда

а так как  - независимые одинаково распределенные случайные величины, то

При больших n:

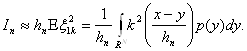
Так как функция  удовлетворяет условиям теоремы (2.1), то

Теорема доказана.

При N=1 следующие функции удовлетворяют условиям (2.7)

Многомерные ядра могут быть получены из одномерных следующим образом:

,

где x – вектор с компонентами . Условия (2.4), (2.6) выполнены для последовательностей вида

где а – некоторая константа.

2.2 Исследование парзеновских оценок плотностей на практике

В данном исследовании была поставлена задача смоделировать повторную выборку, соответствующую плотности распределения

() и применить к ней парзеновскую оценку, а также сравнить графически найденную оценку с истинной плотностью.

Работа выполняется в пакете Microsoft Excel, так как этот пакет один из наиболее пригодных для решения подобных задач.

На интервале [-4;9] с шагом 0,2 построим графическое изображение истинного значения плотности распределения по заданной нам функции при .

Полученный результат представлен на рис. 1:

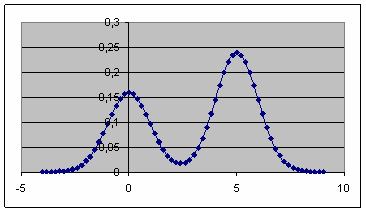
Рис. 1. График заданной плотности распределения

Для оценивания ее строим повторную (обучающую) выборку, соответствующую данной плотности распределения. В качестве ядра k(y) выберем функцию

.

Проверим, удовлетворяет ли при N=1 функция  условиям теорем (2.1) и (2.2).

(a) 

где а – некоторая константа,

(b)  ,

(c) 

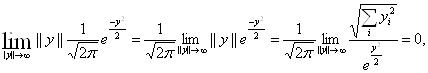
(d)  Функция непрерывна во всех точках х,

(e)  .

Таким образом, условия теорем выполнены, и оценка является асимптотически несмещенной оценкой величины p(x) (в силу условий (а)-(d)), то есть

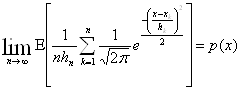
и состоятельной оценкой (в силу условий (а)-(е)), то есть

В зависимости от выбора множителя  оценки будут принимать различный вид. Графики сравнения оценки с истинным значением функции при различных  представлены на рис. 2-5.

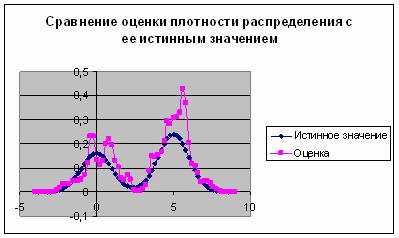
Рис. 2. График сравнения оценки плотности распределения с ее истинным значением при

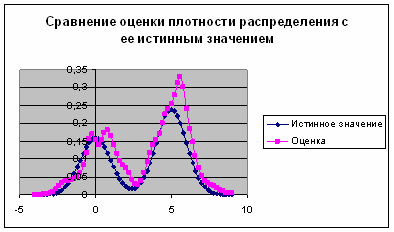
Рис. 3. График сравнения оценки плотности распределения с ее истинным значением при

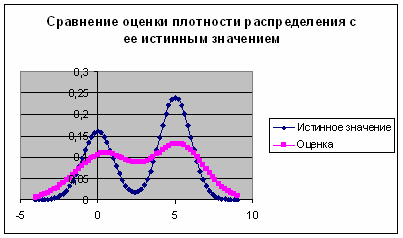
Рис. 4. График сравнения оценки плотности распределения с ее истинным значением при

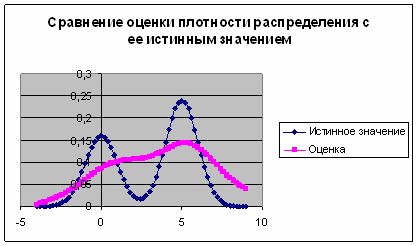
Рис. 5. График сравнения оценки плотности распределения с ее истинным значением при

Наиболее удачная оценка получается при  (см. рис. 6)

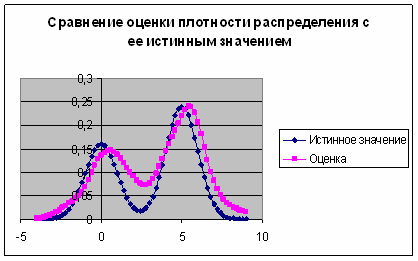
Рис. 6. График сравнения оценки плотности распределения с ее истинным значением при

Также вид оценки зависит от повторной выборки. Графики, полученные при изменении значений обучающей выборки при неизменном  представленны на рис. 6-8.

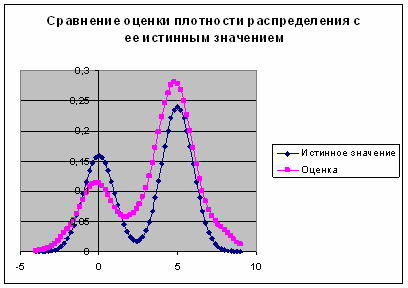
Рис. 7. График сравнения оценки плотности распределения с ее истинным значением для повторной выборки (1)

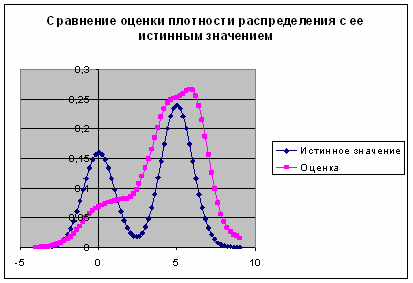
Рис. 8. График сравнения оценки плотности распределения с ее истинным значением для повторной выборки (2)

Таким образом, для каждой новой повторной выборки необходимо подбирать свое , максимально приближающее оценку к истинной плотности распределения.

Таким образом, в процессе выполнения курсовой работы мною было исследовано теоретически и на практике построение непараметрических парзеновских оценок. В ходе работы мною сделаны выводы, что хорошо выполненная оценка достаточно достоверно отображает поведение заданной функции и что в результате изменения значений повторной выборки и неотрицательной числовой последовательности  можно построить оценку, максимально приближенную к истинному значению функции.

1.  Лиховидов В.Н. Практический курс распознавания образов. – Владивосток: издательство ДВГУ, 1983.

2.  Невельсон М. Б., Хасьминский Р.З. Стохастическая аппроксимация и рекуррентное оценивание. М.: «Наука», 1972.

3.  Булдаков В. М., Кошкин Г. М. Рекуррентное оценивание условной плотности вероятности и линии регрессии по зависимой выборке. Материалы V научн. конф. По математике, I. Томск, 1974, 135-136.

4.  Воронцов К. В. Лекции по статистическим (байесовским) алгоритмам классификации, 2008.