Курсовая работа: Нахождение полиноминальной аппроксимации методом наименьших квадратов
Московский Авиационный Институт
(государственный технический университет)
Курсовая работа по
«теории вероятностей и математической статистике»
на тему:
Нахождение полиноминальной аппроксимации методом наименьших квадратов
Вариант №2
Выполнила: Студентка группы 05-202
Андреева Виктория
Принял: Преподаватель кафедры 804
Молчанов Игорь Иванович
Москва
2010 г.
ЗАДАНИЕ (вариант № 2) : Даны результаты измерений случайного процесса в равноотстоящие моменты времени (реализация временного ряда).
13,393 13,207 13,477 11,911 14,311 14,979 14,437 14,957 13,044 12,142
12,000 11,496 12,927 11,849 11,612 10,401 8,755 8,185 9,681 9,644
9,073 8,535 9,062 7,602 9,164 6,913 7,749 5,543 5,901 5,901
6,760 4,593 6,131 3,651 3,796 3,663 3,068 3,008 2,809 0,333
1,730 -0,072 0,479 -3,180 -2,962 -5,849 -6,153 -7,911 -10,134 -11,662
Измерения производятся с шагом по аргументу 0,08
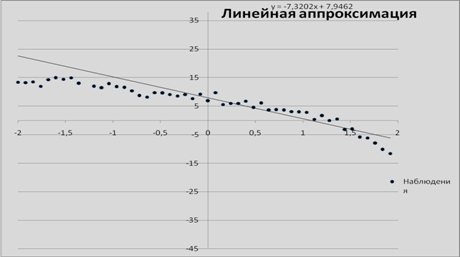
ЦЕЛЬ РАБОТЫ: Требуется найти полиноминальную аппроксимацию этого процесса методом наименьших квадратов.
Теоретическая часть
Математическая статистика – наука о математических методах, позволяющих по статистическим данным, например по реализацией случайной величины (СВ), построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики являются, в некотором смысле, обратными к задачам теории вероятностей. Центральным понятием математической статистики является выборка.
Выборка
Однородной выборкой
(выборкой) объема n при ![]() называется случайный вектор
называется случайный вектор ![]() , компоненты
которого
, компоненты
которого ![]() ,
называемые элементами выборки, являются независимыми СВ с одной и той же
функцией распределения F(x). Будем говорить, что выборка
,
называемые элементами выборки, являются независимыми СВ с одной и той же
функцией распределения F(x). Будем говорить, что выборка ![]() соответствует функции
распределения F(x).
соответствует функции
распределения F(x).
Реализацией выборки называется неслучайный вектор ![]() , компонентами
которого являются реализации соответствующих элементов выборки
, компонентами
которого являются реализации соответствующих элементов выборки ![]() .
.
Из вышеописанных определений
вытекает, что реализацию выборки ![]() можно также рассматривать как
последовательность
можно также рассматривать как
последовательность ![]() из n реализаций одной и той же СВ X, полученных в серии из n независимых одинаковых опытов, проводимых в одинаковых
условиях. Поэтому можно говорить, что выборка
из n реализаций одной и той же СВ X, полученных в серии из n независимых одинаковых опытов, проводимых в одинаковых
условиях. Поэтому можно говорить, что выборка![]() порождена наблюдаемой СВ X, имеющей распределение
порождена наблюдаемой СВ X, имеющей распределение![]() .
.
Если компоненты вектора![]() независимы, но
их распределения
независимы, но
их распределения ![]() различны, то такую выборку
называют неоднородной.
различны, то такую выборку
называют неоднородной.
Множество S всех реализаций выборки ![]() называется выборочным
пространством.
называется выборочным
пространством.
Выборочное пространство
может быть всем n-мерным
евклидовым пространством ![]() или его частью, если СВ X непрерывна, а также может состоять
из конечного или счетного числа точек из
или его частью, если СВ X непрерывна, а также может состоять
из конечного или счетного числа точек из ![]() , если СВ X дискретна.
, если СВ X дискретна.
На практике при
исследовании конкретного эксперимента распределения ![]() СВ
СВ ![]() редко бывают известны полностью.
Часто априори (до опыта) можно лишь утверждать, что распределение
редко бывают известны полностью.
Часто априори (до опыта) можно лишь утверждать, что распределение ![]() случайного
вектора
случайного
вектора ![]() принадлежит
некоторому классу (семейству)
принадлежит
некоторому классу (семейству) ![]() .
.
Пара (S,F) называется статистической моделью описания серии
опытов, порождающих выборку ![]() .
.
Если распределение ![]() из класса F определены с точностью до некоторого
векторного параметра
из класса F определены с точностью до некоторого
векторного параметра ![]() , то такая статистическая модель
называется параметрической и обозначается
, то такая статистическая модель
называется параметрической и обозначается ![]() .
.
В некоторых случаях
выборочное пространство может не зависеть от неизвестного параметра ![]() распределения
распределения ![]() .
.
В зависимости от вида статистической модели в математической статистике формулируются соответствующие задачи по обработке информации, содержащейся в выборке.
СВ ![]() , где
, где ![]() - произвольная функция,
определенная на выборочном пространстве S и не зависящая от распределения
- произвольная функция,
определенная на выборочном пространстве S и не зависящая от распределения ![]() , называется статистикой.
, называется статистикой.
Кривая регрессии.
регрессия вероятность статистический опыт
Условное математическое
ожидание ![]() СВ
СВ
![]() как
функция параметра
как
функция параметра ![]() называется регрессией
называется регрессией ![]() на
на ![]() . График
функции
. График
функции ![]() называется
кривой регрессии
называется
кривой регрессии ![]() на
на ![]() .
.
Точечная оценка.
Точечной (выборочной)
оценкой неизвестного параметра распределения ![]() называется произвольная
статистика
называется произвольная
статистика ![]() построенная
на выборке
построенная
на выборке ![]() и
принимающая значения в множестве
и
принимающая значения в множестве ![]() .
.
Оценка ![]() параметра
параметра ![]() называется
несмещенной, если ее МО равно
называется
несмещенной, если ее МО равно ![]() , т. е.
, т. е. ![]() для любого
для любого ![]() .
.
Оценка ![]() параметра
параметра ![]() называется
состоятельной, если она сходится по вероятности к
называется
состоятельной, если она сходится по вероятности к ![]() , т. е.
, т. е. ![]() при
при ![]() для любого
для любого ![]() .
.
Оценка ![]() параметра
параметра ![]() называется
сильно состоятельной, если она сходится почти наверное к
называется
сильно состоятельной, если она сходится почти наверное к ![]() , т. е.
, т. е. ![]() при
при ![]() для любого
для любого ![]() .
.
Очевидно, что если оценка сильно состоятельная, то она является также состоятельной.
Доверительный интервал.
Чтобы дать представление
о точности и надежности оценки ![]() , в математической статистике
пользуются так называемыми доверительными интервалами и доверительными
вероятностями.
, в математической статистике
пользуются так называемыми доверительными интервалами и доверительными
вероятностями.
Пусть для параметра ![]() получена из
опыта несмещенная оценка
получена из
опыта несмещенная оценка ![]() . Назначим некоторую достаточно
большую вероятность
. Назначим некоторую достаточно
большую вероятность ![]() (например,
(например, ![]() или 0,99) такую, что
событие с вероятностью
или 0,99) такую, что
событие с вероятностью ![]() можно считать практически
достоверным, и найдем такое значение
можно считать практически
достоверным, и найдем такое значение ![]() , для которого
, для которого
![]()
Тогда диапазон
практически возможных значений ошибки, возникающей при замене ![]() на
на ![]() , будет
, будет ![]() ; большие по абсолютной
величине ошибки будут появляться только с малой вероятностью
; большие по абсолютной
величине ошибки будут появляться только с малой вероятностью ![]()

Вероятность ![]() принято
называть доверительной вероятностью, а интервал
принято
называть доверительной вероятностью, а интервал ![]() - доверительным интервалом.
Границы интервала
- доверительным интервалом.
Границы интервала ![]() :
: ![]() и
и ![]() называются доверительными
границами.
называются доверительными
границами.
Интервальные оценки.
Пусть имеется
параметрическая статическая модель ![]() , и по выборке
, и по выборке ![]() , соответствующей
распределению
, соответствующей
распределению ![]() наблюдаемой СВ
наблюдаемой СВ ![]() , требуется определить
неизвестный параметр
, требуется определить
неизвестный параметр ![]() . Вместо точечных оценок,
рассмотренных ранее, рассмотрим другой тип оценок неизвестного параметра
. Вместо точечных оценок,
рассмотренных ранее, рассмотрим другой тип оценок неизвестного параметра ![]() .
.
Интервал ![]() со случайными концами,
«накрывающий» с вероятностью
со случайными концами,
«накрывающий» с вероятностью ![]() ,
, ![]() , неизвестный параметр
, неизвестный параметр ![]() , т. е.
, т. е.
![]() ,
,
называется доверительным
интервалом (или интервальной оценкой) уровня надежности ![]() параметра
параметра ![]() .
.
Число ![]() называется доверительной
вероятностью или уровнем доверия.
называется доверительной
вероятностью или уровнем доверия.
Уровень значимости.
Уровнем
значимости статистического критерия
называется вероятность ошибки 1-го рода ![]() . Вероятность ошибки 1-го рода
. Вероятность ошибки 1-го рода ![]() может быть
вычислена, если известно распределение
может быть
вычислена, если известно распределение ![]() .
.
Ошибки 1 и 2-го рода.
Ошибкой 1-го рода называется событие, состоящее в том,
что гипотеза ![]() отвергается, когда она верна.
отвергается, когда она верна.
Ошибкой 2-го рода называется событие, состоящее в том,
что принимается гипотеза ![]() , когда верна гипотеза
, когда верна гипотеза ![]() .
.
Проверка статистических гипотез.
Статистической
гипотезой H или просто гипотезой
называется любое предположение относительно параметров или закона распределения
СВ ![]() ,
проверяемое по выборке
,
проверяемое по выборке ![]() .
.
Проверяемая гипотеза
называется основной (или нулевой) и обозначается ![]() . Гипотеза,
конкурирующая с
. Гипотеза,
конкурирующая с ![]() , называется альтернативной
и обозначается
, называется альтернативной
и обозначается ![]() .
.
Статистическая гипотеза ![]() называется простой,
если она однозначно определяет параметр или распределение СВ
называется простой,
если она однозначно определяет параметр или распределение СВ ![]() . В противном случае
гипотеза
. В противном случае
гипотеза ![]() называется
сложной.
называется
сложной.
Статистическим
критерием (критерием
согласия, критерием значимости или решающим правилом) проверки гипотезы ![]() называется правило, в соответствии с которым по реализации
называется правило, в соответствии с которым по реализации ![]() статистики
статистики ![]() гипотеза
гипотеза ![]() принимается или отвергается.
принимается или отвергается.
Критической областью ![]() статистического критерия
называется область реализаций
статистического критерия
называется область реализаций ![]() статистики
статистики ![]() , при которых
гипотеза
, при которых
гипотеза ![]() отвергается.
отвергается.
Доверительной областью ![]() статистического критерия
называется область значений
статистического критерия
называется область значений ![]() статистики
статистики ![]() , при которых
гипотеза
, при которых
гипотеза ![]() принимается.
принимается.
Практическая часть.
Этап 1 (Вычисление оценок ![]() ,
, ![]() неизвестных
коэффициентов регрессии
неизвестных
коэффициентов регрессии ![]() ,
, ![]() ):
):
![]() ;
;
![]() ;
;
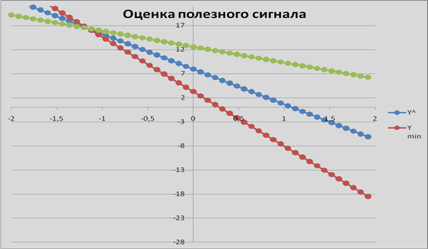
![]() - оценка полезного сигнала (кривая регрессии);
- оценка полезного сигнала (кривая регрессии);
![]() - ошибка;
- ошибка;
Формулируем все ошибки:
 .
.
Находим наименьшую ошибку. Для этого продифференцируем уравнение по a и по b, приравняем к 0, получив систему:
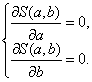 - система нормальных уравнений.
- система нормальных уравнений.
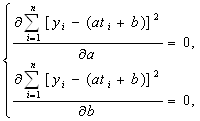
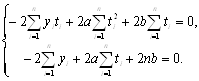
Решаем систему методом Крамера:

Расчетная схема для
оценок ![]() по
методу наименьших квадратов.
по
методу наименьших квадратов.
| Номер | Y | X | y^2 | X*Y | x^2 | δ^2=(y-at-b)^2 |
| 1 | 13,393 | -2 | 179,37245 | -26,786 | 4 | 84,52154547 |
| 2 | 13,207 | -1,92 | 174,42485 | -25,3574 | 3,6864 | 77,33345969 |
| 3 | 13,477 | -1,84 | 181,62953 | -24,7977 | 3,3856 | 63,01706699 |
| 4 | 11,911 | -1,76 | 141,87192 | -20,9634 | 3,0976 | 79,54344995 |
| 5 | 14,311 | -1,68 | 204,80472 | -24,0425 | 2,8224 | 35,20165139 |
| 6 | 14,979 | -1,6 | 224,37044 | -23,9664 | 2,56 | 21,89755599 |
| 7 | 14,437 | -1,52 | 208,42697 | -21,9442 | 2,3104 | 21,49126227 |
| 8 | 14,957 | -1,44 | 223,71185 | -21,5381 | 2,0736 | 12,46267515 |
| 9 | 13,044 | -1,36 | 170,14594 | -17,7398 | 1,8496 | 23,59662672 |
| 10 | 112,142 | -1,28 | 12575,828 | -143,542 | 1,6384 | 8991,966406 |
| 11 | 12 | -1,2 | 144 | -14,4 | 1,44 | 22,3767305 |
| 12 | 11,496 | -1,12 | 132,15802 | -12,8755 | 1,2544 | 21,61124277 |
| 13 | 12,927 | -1,04 | 167,10733 | -13,4441 | 1,0816 | 6,928339322 |
| 14 | 11,849 | -0,96 | 140,3988 | -11,375 | 0,9216 | 9,762864991 |
| 15 | 11,612 | -0,88 | 134,83854 | -10,2186 | 0,7744 | 7,705858746 |
| 16 | 10,401 | -0,8 | 108,1808 | -8,3208 | 0,64 | 11,56902772 |
| 17 | 8,755 | -0,72 | 76,650025 | -6,3036 | 0,5184 | 19,90687251 |
| 18 | 8,185 | -0,64 | 66,994225 | -5,2384 | 0,4096 | 19,76777254 |
| 19 | 9,681 | -0,56 | 93,721761 | -5,42136 | 0,3136 | 5,590769531 |
| 20 | 9,644 | -0,48 | 93,006736 | -4,62912 | 0,2304 | 3,29736681 |
| 21 | 9,073 | -0,4 | 82,319329 | -3,6292 | 0,16 | 3,244500827 |
| 22 | 8,535 | -0,32 | 72,846225 | -2,7312 | 0,1024 | 3,075233208 |
| 23 | 9,062 | -0,24 | 82,119844 | -2,17488 | 0,0576 | 0,410905071 |
| 24 | 7,602 | -0,16 | 57,790404 | -1,21632 | 0,0256 | 2,296447057 |
| 25 | 9,164 | -0,08 | 83,978896 | -0,73312 | 0,0064 | 0,399692323 |
| 26 | 6,913 | 0 | 47,789569 | 0 | 0 | 1,067444888 |
| 27 | 9,749 | 0,08 | 95,043001 | 0,77992 | 0,0064 | 5,704661232 |
| 28 | 5,543 | 0,16 | 30,724849 | 0,88688 | 0,0256 | 1,517679181 |
| 29 | 5,901 | 0,24 | 34,821801 | 1,41624 | 0,0576 | 0,083131718 |
| 30 | 5,901 | 0,32 | 34,821801 | 1,88832 | 0,1024 | 0,088381223 |
| 31 | 6,76 | 0,4 | 45,6976 | 2,704 | 0,16 | 3,034234095 |
| 32 | 4,593 | 0,48 | 21,095649 | 2,20464 | 0,2304 | 0,025766932 |
| 33 | 6,131 | 0,56 | 37,589161 | 3,43336 | 0,3136 | 5,217278758 |
| 34 | 3,651 | 0,64 | 13,329801 | 2,33664 | 0,4096 | 0,151906494 |
| 35 | 3,796 | 0,72 | 14,409616 | 2,73312 | 0,5184 | 1,255222992 |
| 36 | 3,663 | 0,8 | 13,417569 | 2,9304 | 0,64 | 2,474275069 |
| 37 | 3,068 | 0,88 | 9,412624 | 2,69984 | 0,7744 | 2,444839854 |
| 38 | 3,008 | 0,96 | 9,048064 | 2,88768 | 0,9216 | 4,364814626 |
| 39 | 2,809 | 1,04 | 7,890481 | 2,92136 | 1,0816 | 6,129731157 |
| 40 | 0,333 | 1,12 | 0,110889 | 0,37296 | 1,2544 | 0,342745729 |
| 41 | 1,73 | 1,2 | 2,9929 | 2,076 | 1,44 | 6,59493426 |
| 42 | -0,072 | 1,28 | 0,005184 | -0,09216 | 1,6384 | 1,827027788 |
| 43 | 0,479 | 1,36 | 0,229441 | 0,65144 | 1,8496 | 6,191594234 |
| 44 | -3,18 | 1,44 | 10,1124 | -4,5792 | 2,0736 | 0,34233389 |
| 45 | -2,962 | 1,52 | 8,773444 | -4,50224 | 2,3104 | 0,047752061 |
| 46 | -5,849 | 1,6 | 34,210801 | -9,3584 | 2,56 | 4,338314281 |
| 47 | -6,153 | 1,68 | 37,859409 | -10,337 | 2,8224 | 3,244489064 |
| 48 | -7,911 | 1,76 | 62,583921 | -13,9234 | 3,0976 | 8,842481446 |
| 49 | -10,134 | 1,84 | 102,69796 | -18,6466 | 3,3856 | 21,26146404 |
| 50 | -11,662 | 1,92 | 136,00224 | -22,391 | 3,6864 | 30,84025156 |
| Сумма | 411,949 | -2 | 16631,368 | -504,296 | 66,72 | 9666,40808 |
Подставив найденные суммы
в систему, получаем оценки ![]() :
:
![]() =-7,320193878
=-7,320193878
![]() =7,946172245
=7,946172245
Этап 2 (Вычисление оценки
![]() неизвестной дисперсии
неизвестной дисперсии ![]() шумов
шумов ![]() ):
):
![]()
![]()
![]() , где
, где
n – число измерений;
m – число неизвестных параметров.
Этап 3:
По таблице находим квантиль Стьюдента.
| m/a | 0.85 | 0.9 | 0.95 | 0.975 |
| 47 | 1.0480 | 1.2998 | 1.6779 | 2.0117 |
| 48 | 1.0478 | 1.2994 | 1.6772 | 2.0106 |
| 49 | 1.0475 | 1.2991 | 1.6766 | 2.0096 |
| 50 | 1.0473 | 1.2987 | 1.6759 | 2.0086 |
Фрагмент таблицы 1
При λ=0,975 , квантиль Стьюдента 2.0086

Уровень доверия ![]()
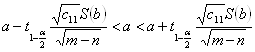 ;
;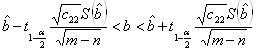 ;
;
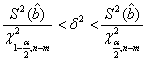 ;
;
|
|
|
|
| 0,95 | 69,0225 | 30,7545 |
| ymin | ymax |
| 25,9848632 | 19,188257 |
| 25,077453 | 18,924436 |
| 24,1700428 | 18,660615 |
| 23,2626327 | 18,396794 |
| 22,3552225 | 18,132973 |
| 21,4478123 | 17,869153 |
| 20,5404021 | 17,605332 |
| 19,632992 | 17,341511 |
| 18,7255818 | 17,07769 |
| 17,8181716 | 16,813869 |
| 16,9107614 | 16,550048 |
| 16,0033513 | 16,286227 |
| 15,0959411 | 16,022407 |
| 14,1885309 | 15,758586 |
| 13,2811208 | 15,494765 |
| 12,3737106 | 15,230944 |
| 11,4663004 | 14,967123 |
| 10,5588902 | 14,703302 |
| 14,703302 | |
| 9,65148007 | 14,439482 |
| 8,7440699 | 14,175661 |
| 7,83665973 | 13,91184 |
| 6,92924956 | 13,648019 |
| 6,02183939 | 13,384198 |
| 5,11442921 | 13,120377 |
| 4,20701904 | 12,856556 |
| 3,29960887 | 12,592736 |
| 2,3921987 | 12,328915 |
| 1,48478853 | 12,065094 |
| 0,57737835 | 11,801273 |
| -0,3300318 | 11,537452 |
| -1,237442 | 11,273631 |
| -2,1448522 | 11,009811 |
| -3,0522623 | 10,74599 |
| -3,9596725 | 10,482169 |
| -4,8670827 | 10,218348 |
| -5,7744928 | 9,9545271 |
| -6,681903 | 9,6907063 |
| -7,5893132 | 9,4268854 |
| -8,4967234 | 9,1630646 |
| -9,4041335 | 8,8992437 |
| -10,311544 | 8,6354229 |
| -11,218954 | 8,371602 |
| -12,126364 | 8,1077812 |
| -13,033774 | 7,8439603 |
| -13,941184 | 7,5801395 |
| -14,848595 | 7,3163186 |
| -15,756005 | 7,0524978 |
| -16,663415 | 6,788677 |
| -17,570825 | 6,5248561 |
| -18,478235 | 6,2610353 |
Список литературы
1. Е.С. Кочетков “Метод наименьших квадратов”, Москва, МАИ, 1993.
2. А.И. Кибзун “Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами”, Москва, «Физматлит», 2002.
3. Е.С. Вентцель “ Теория вероятностей ”, Москва, «Высшая школа», 1999.