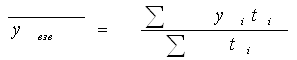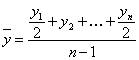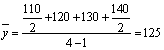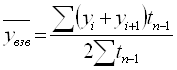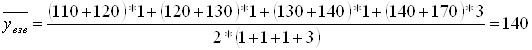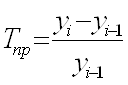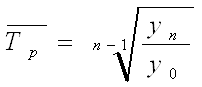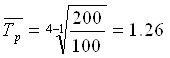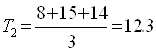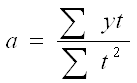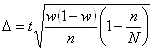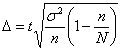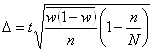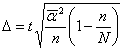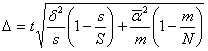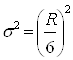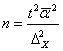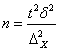Учебное пособие: Статистические наблюдения
ТЕМА 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ
Gegenstand, Methoden und Aufgaben der Statistik
Subject matter, methods and tasks of statistics
1.1. Предмет статистики
Статистика (Statistik, Statistics) – это самостоятельная наука, которая изучает количественную сторону социально-экономических явлений и процессов, их закономерности, влияние общественной жизни на окружающую среду и обратное влияние.
В научный обиход термин "статистика" был введен в середине ХVIII века немецким ученым Г. Ахенвалем.
Статистика занимается анализом, представлением и интерпретацией числовых данных.
Своеобразие статистических закономерностей проявляется в том, что:
1) мы имеем дело с массой случаев. В единичных случаях они могут и не действовать;
2) механизм действия статистических закономерностей не всегда ясен, но они настолько устойчивы, что мы можем ими пользоваться.
Пример. На 12 девочек рождается 13 мальчиков.
При исследовании тенденций и закономерностей статистика опирается на закон больших чисел. Сущность закона больших чисел: при суммировании данных по достаточно большому числу случаев (единиц статистической совокупности) различия отдельных единиц взаимно погашаются и в общих средних числах выступают существенные, характерные черты и взаимосвязи явления в целом. Т.е. совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Место статистики среди других экономических дисциплин: с одной стороны, является вспомогательной по отношению к экономической теории, экономике предприятия, менеджменту (приводит первичные данные в удобную для анализа и принятия решений форму), с другой стороны, является базовой по отношению к частным разделам статистики, например, отраслевым статистикам – макроэкономической, статистики промышленности, населения и др.
Статистика делится на две составные части: дескриптивную (описательную, descriptive, descriptive) и индуктивную (выводную или аналитическую, induktive, inferential)). Исторически развитие статистики связано с потребностями государства (status – политическое состояние, stato – государство). Описание явлений, связанных с деятельностью государства – хозяйственного механизма, функционирования экономики, результатов социально-экономического развития – дало название одному из двух основных разделов общей теории статистики – описательной статистике.
Индуктивная или выводная статистика отражает математическое направление в статистике. С ее помощью по части данных определяются показатели всей совокупности.
![]()
![]() Статистика
Статистика
Дескриптивная Индуктивная
(описательная) (выводная)
Статистика изучает только совокупность явлений.
Совокупность (Statistische Masse, Statistical population) – это множество однокачественных варьирующих единиц.
Единица (Statistische Einheit, Statistical unit)– это предел дробления совокупности, при котором сохраняются все свойства рассматриваемого явления или процесса.
Единицы совокупности обладают свойствами или признаками.
Признак (Merkmal, Feature)– это то, с помощью чего статистика изучает явление или процесс.
Результатами измерения признаков являются статистические показатели (Kennzahlen, Indicators). Показатель – это количественная оценка свойств изучаемого явления.
Пример. Студенты МИЭПМ ННГАСУ на потоковой лекции по статистике образуют статистическую совокупность. Единицами совокупности являются отдельные студенты, признаком – например, возраст, показателем – средний возраст студента на потоке.
Количественные изменения значений признака при переходе от одной единицы совокупности к другой называется вариацией (Streuung, Variation). Именно вариация обуславливает необходимость статистики.
Классификация признаков:
1) По характеру выражения: количественные признаки (выражаются в числовом значении)
- дискретные (количество автомобилей в семье, ед.)
- постоянные (непрерывные) (возраст)
качественные признаки (атрибутивные) выражают смысл понятиями (наличие театров в Нижнем Новгороде по видам)
2) По роли в статистическом исследовании: основные и второстепенные
3) По способу измерения: первичные и вторичные. Первичные признаки характеризуют абсолютные размеры социально-экономических явлений (протяженность заасфальтированных дорог в муниципальном образовании или численность сотрудников хозяйствующего субъекта). Вторичные (расчетные) признаки образуются в результате соотношения первичных признаков (например, отношение объема собранного урожая к размеру посевной площади дает показатель урожайности).
4) По отношению ко времени: моментные (объем вкладов населения в Сбербанке РФ на 1.01.200 __ г.) и интервальные (объем инвестиций в регионе N за 200__ г.)
5) По измеримости признаки делятся на:
- номинально измеряемые, (можно ответить только на вопрос: есть ли данный признак или нет);
- ординально измеряемые, порядковая шкала (можно провести ранжирование);
- метрически измеряемые, интервальная шкала (можно не только ранжировать, но и определить расстояние между отдельными значениями признака, т.е. величину интервала).
Пример.
Таблица 1.1.
Сведение о сотрудниках консалтинговой фирмы ООО "Зефиров и компания"
| Табельный номер сотрудника | Возраст | Пол | Стаж работы, мес. | Почасовая оплата, $ | Мотивация | Подразделение |
| 1 | 23 | М | 12 | 4,8 | Высокая | Бухгалтерия |
| 2 | 34 | М | 3 | 4,7 | Высокая | Финансы |
| 3 | 35 | Ж | 17 | 7,2 | Очень высокая | Управление |
| 4 | 45 | М | 56 | 4,5 | Низкая | Консалтинг |
| 5 | 21 | Ж | 23 | 5,0 | Средняя | Реклама |
В приведенных в табл. 1.1 сведениях статистической совокупностью являются все сотрудники фирмы, единицей совокупности – отдельные работники. Пол, подразделение - номинально измеряемые признаки, мотивация – ординально измеряемый, возраст, стаж и зарплата – метрически измеряемые признаки.
Процесс изучения социально-экономических явлений посредством системы статистических методов и системы показателей называется статистическим исследованием (Statistische Untersuchung, Statistical investigation, inquiry).
Статистическое исследование представляет собой определение потребностей заказчика исследования, целей и задач; проведение наблюдения; обработку и анализ данных; интерпретацию и презентацию результатов исследования. В случае необходимости статистическое исследование может содержать дополнительный этап – статистический прогноз.
1.2 Методы статистики
На стадии сбора информации используются различные методы наблюдения.
На стадии обработки информации - методы сводки, группировки, построения таблиц и графиков.
На стадии анализа и интерпретации данных – методы абсолютных и относительных величин, корреляционный и регрессионный анализ, анализ рядов динамики, индексный метод и т. д.
Индуктивная (выводная) статистика широко использует методы теории вероятностей, теорию выборки, статистическую проверку гипотез.
В последнее время используются также методы высшей математики: методы оптимального программирования, теория распознавания образов и др.
1.3 Задачи статистики
Главной целью статистики является подготовка обозримой, надежной и достоверной информации для принятия управленческих решений.
К основным задачам статистики относятся:
1) обеспечение хозяйствующих субъектов надежной информацией;
2) выявление ресурсов развития и резервов повышения эффективности;
3) обобщение и прогнозирование тенденций развития экономики;
4) всестороннее исследование происходящих в обществе процессов;
5) обеспечение достоверности, качества и доступности информации.
Областями применения статистических методов служат:
- национальная экономика (макроэкономические показатели, например, ВВП и ВНП, индексы цен, показатели занятости, экспорта-импорта и т.д.),
- экономика предприятия (микроэкономические показатели, например, по производству, сбыту, управлению персоналом, контролю качества и т.д.),
- общественные науки (методы эмпирического исследования, например, в социологии – поведение в группе, в психологии – тесты на проверку гипотез, в педагогике – измерение результата обучения),
- естественные науки (химия, физика – экспериментальные исследования, биология, медицина - классификации, экспериментальные исследования),
- инженерные науки (экспериментальные исследования, контроль качества).
1.4 Организация статистики
Выделяют следующие организационные составляющие статистики:
1) государственная и муниципальная статистика;
2) ведомственная статистика;
3) частная и неофициальная статистика.
Первые две составляющие образуют официальную статистику. Нижний уровень официальной статистики – это районные отделы и управления статистики. Далее следуют статистические комитеты субъектов федерации (в Нижегородской области, например, Нижегородский областной комитет государственной статистики), Госкомстат РФ, Статкомитет СНГ, Евростат, Статистическая комиссия ООН.
Ведомственная статистика ведется на предприятиях, в организациях, ведомствах, министерствах, например, в Центральном банке (банковская статистика) или в Таможенном комитете (таможенная статистика).
Основными статистическими продуктами являются:
ü макроэкономические показатели,
ü отраслевые данные,
ü социальные статистика и статистика уровня жизни,
ü межрегиональные международные сравнения.
Они выходят в виде докладов, сборников, бюллетеней, аналитических записок, экспресс-информации.
В процессе сбора и предоставления статистических данных роль официальной статистики можно интерпретировать как посредническую. Она собирает данные на микроуровне, агрегирует их и предоставляет на макроуровне в распоряжение конечных потребителей для анализа и расчетов (см. рис. 1.1.)
|
|
|
микроданные макроданные
Рис.1.1. Посредническая роль официальной статистики
Источник: П. фон дер Липпе (1995), с.16
Важная особенность официальной статистики состоит в том, что обследования проводятся на основе законодательных и нормативных актов, что дает возможность требовать от респондентов предоставления необходимых сведений при одновременной обязанности конфиденциальности индивидуальных данных.
Неофициальная статистика, напротив, занимается статистическим анализом данных официальной статистики для специальных целей. К организациям, занимающимся неофициальной статистикой относятся научно-исследовательские организации, консалтинговые агентства по изучению общественного мнения и проведению опросов, союзы и объединении предприятий. Примеры: Рейнско-Вестфальский институт экономических исследований RWI (Эссен), Российский союз предпринимателей и промышленников (Москва), НФ ВЦИОМ (Нижний Новгород) являются представителями неофициальной статистики.
ТЕМА 2. СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ
2.1 Формы, виды и способы статистического наблюдения
Наблюдение является первой важной стадией статистического исследования и одновременно – одним из главных методов статистики.
Наблюдение (Erhebung, Observation)– это планомерно организованный сбор массовых данных о явлениях и процессах общественной жизни.
Наблюдение осуществляется в трех организационных формах:
1) Отчетность;
2) Обследование;
3) Регистр.
Отчетность – основная форма. Представляет собой изучение документов с различными статистическими сведениями. Пример: формы статистической отчетности предприятий, организаций, учреждений № П-1, № 5-з и др.
Обследование – специально организованное наблюдение. Пример: перепись населения.
Регистр – форма непрерывного наблюдения за статистическими совокупностями с фиксированным началом и концом. Пример: Единый государственный регистр предприятий, организаций, учреждений и объединений, созданный с целью обеспечения единого государственного учета хозяйствующих субъектов. (ЕГРПО).
Виды статистического наблюдения:
I. По времени регистрации фактов
1) текущее наблюдение (непрерывное) – ведется постоянно, по мере возникновения, наступления явления. Пример: ЗАГС;
2) периодическое – через одинаковые промежутки времени. Пример: определение уровня цен в розничной торговле;
3) единовременное (разовое) - служит для решения каких-либо отдельных задач, повторяется через неопределенный промежуток времени по мере надобности. Пример: единовременный учет студенческих эстрадных театров.
II. По охвату единиц совокупности
1) сплошное – обследуются все единицы совокупности. Пример: перепись населения;
2) несплошное – обследуется определенная часть единиц совокупности, возможно распространение результатов на всю совокупность. К несплошным видам наблюдения относятся:
ü выборка – отбор изучаемой части совокупности с помощью специальных методов (см. тему 11). Пример: опрос общественного мнения;
ü основной массив – обследуется та часть единиц совокупности, которая вносит наибольший вклад в изучаемое явление. Пример: изучение особенностей урбанизации по городам-миллионникам.
ü монографическое обследование – обследуется одна единица совокупности ради самой этой единицы, очень подробно. Пример: одна семья при предварительном бюджетном обследовании.
3) частичное (изучение части совокупности ради самой этой части). Пример: обследование крупных городов.
Преимущества и недостатки сплошного и несплошного наблюдений:
- Сплошное наблюдение:
охватывает все единицы совокупности. Собранный материал точно соответствует цели обследования;
оно более дорогостоящее и занимает больше времени;
оно не всегда может охватить все элементы совокупности.
сравнительно продолжительное время обработки результатов сплошного наблюдения может понизить актуальность выводов.
- Несплошное наблюдение:
опасность плохой репрезентативности (часть неточно представляет всю совокупность);
могут быть упущены некоторые существенные признаки и таким образом искажены результаты.
Первичная и вторичная статистика. С первичной статистикой (Primärforschung, Field research) мы имеем дело, когда материал для статистического обследования собирается специально. Вторичная статистика (Sekundärforschung, Desk research) использует уже собранный материал, даже если он собран для других целей.
Пример: Предприятие розничной торговли хочет открыть филиал в новом микрорайоне. Информацию о структуре населения микрорайона оно может получить по результатам собственного опроса (первичная статистика), или по документам паспортного стола (вторичная статистика).
Данные первичной статистики точно совпадают с целью исследования, но требуют высоких временных и финансовых затрат в отличие от данных вторичной статистики.
Способы статистического наблюдения (регистрации данных): непосредственное, документальное, опрос и эксперимент.
Непосредственное наблюдение (unmittelbare Beobachtung, direct observation) осуществляется путем регистрации фактов лично исследователем. Пример: изучение счетчиками интенсивности пассажиропотока.
При документальном наблюдении (dokumentale Beobachtung, documentary observation) источниками являются документы первичного учета (например, инвентарные карточки).
Опрос (Befragung, Census) – это получение сведений со слов респондента. Выделяют
- анкетный – вопросники письменно заполняют сами респонденты, как правило, анонимно и добровольно.,
- корреспондентский – сведения сообщают добровольные корреспонденты,
- экспедиционный или устный опрос – счетчики получают устные ответы и сами фиксируют их в формуляре,
- явочный опрос – предоставление сведений в явочном порядке, например, при регистрации брака.
В последнее время все шире применяются интерактивные формы опроса – по телефону, электронной почте, в сети Internet.
Эксперимент (Experiment) – получил распространение в естественных науках.
2.2 Программа статистического наблюдения
Она включает в себя две основные части:
1) методическую (что мы хотим изучить?)
2) организационную (кто, когда, где и как будет проводить наблюдение?)
В методической части определяются:
Цель - получение достоверной информации о развитии явлений и процессов;
задачи – пути достижения цели;
объект и единица наблюдения. Объект – это исследуемая статистическая совокупность. Единица наблюдения – первичный элемент объекта или элемент совокупности, по которому собираются необходимые данные. Необходимо отличать единицу наблюдения от отчетной единицы. Отчетная единица – единица, предоставляющая статистические данные, может состоять из нескольких единиц совокупности, а может и совпадать с единицей совокупности. Например, при обследовании населения единицей может быть член домашнего хозяйства, а отчетной единицей – само домохозяйство.
перечень признаков (вопросов), подлежащих регистрации в процессе наблюдения, т.е. так называемая программа наблюдения.
Пример программы наблюдения: переписные листы при проведении переписи населения осенью 2002 г.
Важное значение имеет формулировка вопросов наблюдения. Обычно соблюдают следующие правила:
- не задают вопросов "на всякий случай";
- не задают вопросов, на которые заведомо нельзя получить ответ;
- не задают вопросы, вызывающие настороженность и подозрение.
Пример: прямой вопрос о Вашей заработной плате за месяц лучше заменить на косвенный вопрос о размере расходов за месяц.
Далее, рекомендуется формулировать вопросы как можно более проще и понятнее. Вопросов должно быть ровно столько, чтобы достичь цели наблюдения. По возможности вопросы формулируются коротко и точно. Контрольные вопросы дополняют обычные вопросы так, чтобы из ответов на них можно было сделать вывод о правдивости всех ответов. Вопросы располагаются в порядке, облегчающем оценку ответов. Вид анкеты (бумага, шрифт, оформление и т.д.) должны соответствовать целевым группам наблюдения.
В организационной части (организационном плане):
- указываются органы, выполняющие наблюдение, четко определяются и разграничиваются их права и обязанности,
- формируется кадровый состав,
- устанавливается время и срок проведения наблюдения (время, в течение которого заполняются статистически формуляры). Пример: 9 -16 октября 2002 года – Всероссийская перепись населения,
- критическая дата, критический момент – для величин состояния, запаса. Это момент времени, на который регистрируют явление. Пример: 0 часов 9 октября 2002 года во время переписи населения;
- интервал времени – для потоковых величин;
- определяется список объектов и их местонахождение;
- подготавливаются бланки, инструкции, формы, переписные листы и т.п.;
- расписывается бюджет наблюдения.
2.3 Ошибки и контроль статистического наблюдения
Ошибки (Fehler, Errors) – это расхождение между расчетным и действительным значениями изучаемой величины.
Существуют ошибки:
1) регистрации – ошибки наблюдения, которые всегда могут произойти. Они в массе случаев погашаются. Пример: описка регистратора ЗАГСа.
2) репрезентативности – ошибки, которые встречаются при несплошном обследовании, когда часть плохо представляет целое.
3) случайные – ошибки под влиянием случайных факторов. Пример: ошибка счетчика вследствие усталости;
4) систематические – ошибки, ведущие по тенденции к завышению или занижению значений показателей. Пример: округление возраста на цифрах, оканчивающихся на 5 и 0.
Систематические ошибки бывают преднамеренными и непреднамеренными.
И ошибки регистрации, и ошибки репрезентативности бывают случайными и систематическими
Существуют два способа контроля над ошибками: логический и арифметический.
Логический предусматривает использование логических, качественных взаимосвязей. Пример: у 8-летнего ребенка не может быть собственных детей. Логический контроль применяется, когда невозможен арифметический.
Арифметический использует количественные зависимости между значениями показателей. Пример: гр.3 = гр.1 + гр. 2.
2.4 Источники информации
Источниками информации для проведения и первичных, и вторичных статистических исследований служат данные
а) внутрипроизводственной и
б) внепроизводственной статистики
В качестве первичных источников информации в первую очередь рассматриваются опросы, интервью.
Вторичными источниками данных являются:
- для внутрипроизводственной статистики: калькуляции, прайс-листы, ведомости выдачи зарплаты, больничные листы, балансы, отчеты о производственно-хозяйственной деятельности, планы предприятий и организаций;
- для внепроизводственной статистики:
материалы государственной и муниципальной статистики (справочники, бюллетени, доклады и т.д.),
журналы,
материалы ведомственной статистики (ЦБ РФ, ГТК, Федеральной службы занятости и т.д.),
частная статистика (союзы и объединения предприятий, ТПП),
материалы научно-исследовательских институтов.
Некоторые национальные и международные источники информации приведены в таблице 2.1.
Таблица 2.1.
Национальные и международные источники информации
| Национальные источники | Международные источники |
| Журнал «Вопросы статистики» | Zeitschrift “Wirtschaft und Statistik" |
| Российский статистический ежегодник | Statistisches Jahrbuch für die Bundesrepublik Deutschland |
| Россия в цифрах | Monatsberichte der Deutschen Bundesbank |
|
Госкомстат РФ www.gks.ru |
Statistisches Bundesamt (BRD) www.statistik-bund.de |
| Журнал «Статистическое обозрение» |
Deutsche Bundesbank www.bundesbank.de |
|
Межгосударственный статистический комитет СНГ http://www.cisstat.com |
Bundesministerium für Wirtschft und Technologie (BRD) www.bmwi.de |
| Russian Economic Trends http://cep.lse.ac.uk/datalib/ret/ |
Organisation for Economic Co-operation and Development www.oecd.org |
| Summaries of GOSCOMSTAT's monthly reports prepared in English by IC RATING and put on INTERNET http://feast.fe.msk.ru/koi/informarket/emn/rating/gstat.php |
USA. Bureau of Labor Stats http://stats.bls.gov http://stats.bls.gov/cpihome.php |
|
Всероссийская перепись населения 2002 г. http://www.perepis2002.ru |
USA. Department of Commerce, Bureau of Economic Analysis http://www.stat-usa.gov |
|
USA. Census Bureau http://www.census.gov |
|
|
World Trade Organisation (WTO) www.wto.org |
|
|
Eurostat http://europa.eu.int/en/comm/eurostat/eurostat.php |
|
|
United Kingdom. Office for National Stats http://www.emap.co.uk/ons http://www.ons.gov.uk |
|
|
United Nations, Statistics Division (UNSD) http://www.un.org/depts/unsd |
ТЕМА 3. СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
Statistische Aufbereitung von Daten Statistical data processing
3.1 Статистическая сводка
Сводка – это второй этап статистического исследования после наблюдения. Он заключается в превращении индивидуальных значений признаков, полученных в ходе наблюдения, в систему статистических показателей, т.е. обобщающих характеристик статистической совокупности по определенному признаку.
Этапы сводки:
1) формулировка задачи;
2) группировка:
- определение количества групп;
- определение величины интервала;
- определение группировочного признака.
3) техническое осуществление сводки;
4) проверка полноты и качества сводки.
Существуют следующие способы сводки:
по форме обработки материала: - централизованный (информация идет снизу вверх по иерархической лестнице, обрабатывается в одном месте);
- децентрализованный (информация собирается на нижнем уровне и там же полностью обрабатывается),
по технике выполнения: - механизированный (с помощью компьютеров);
- ручной.
3.2 Группировка
Это важная часть сводки и один из самых распространенных методов статистики.
Группировка (Gruppierung, Grouping)– это разделение статистической совокупности на части (группы) по определенным существенным признакам.
В отличие от группировки, классификация – это распределение явлений и объектов на определенные группы, классы на основе заранее установленных стандартизированных качественных признаков.
Примеры классификации: международные правила заключения сделок Incoterms, товарная номенклатура внешнеэкономической деятельности ТН ВЭД и др.
Виды группировки:
1) Типологическая группировка
Означает разделение качественно разнородной совокупности на однородные группы. При этом каждая группа будет представлять собой отражение какого-либо одного типа, аспекта исследуемого явления. Выделяется столько групп, сколько существует типов данного явления. Границы интервалов проходят там, где один тип сменяется другим.
Типологическая группировка дает хорошие результаты, если удалось идентифицировать типы явления и найти точки перехода одного типа в другой.
Пример (см. табл.3.1).
Таблица 3.1.
Структура объема платных услуг населению Нижнего Новгорода по их видам в 2000 г.
| Вид услуг | Доля в % |
| Пассажирского транспорта | 28,6 |
| Бытовые | 4,7 |
| Системы образования | 10,7 |
| Медицинские | 3,0 |
| Связи | 15,7 |
| Жилищные | 10,6 |
| Коммунальные | 18,6 |
| Санаторно-оздоровительные | 3,2 |
| Прочие | 4,9 |
Источник: Нижний Новгород. Краткий статистический сборник. – Нижний Новгород:
Нижегородский областной комитет государственной статистики, 2001.
2) Аналитическая группировка
Применяется для выявления взаимосвязи между явлениями, т. е. отвечает на вопрос: есть или нет связь?
Признак, по которому все единицы совокупности делятся на группы в аналитической группировке, называется группировочным или факторным, а по которому судят о наличии или отсутствии связи – результативным.
С аналитической группировкой мы встретимся еще в теме корреляционно-регрессионный анализ.
Как правило, при аналитической группировке применяют неравные, все время увеличивающиеся или уменьшающиеся интервалы.
Пример (см. табл.3.2) Установить наличие или отсутствие связи между стажем и производительностью труда. В данном случае факторным признаком х будет стаж, результативным y – производительность труда.
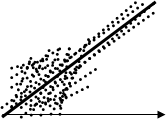
Один из сложных вопросов аналитической группировки – определить количество групп и границы интервалов между группами. Применяют различные методы, например, метод координатной сетки.
В системе координат наносят по оси OX стаж, по оси OY производительность труда (рис.3.1). Всего на рисунке получается 710 точек. Затем ищут так называемые сгущения. Между ними и проводят границы интервалов. Недостаток метода: рисунок сгущений меняется с изменением масштаба.
Таблица 3.2.
Распределение работников по средней производительности труда
|
Группы работников по стажу в годах |
Число работников в группе, чел. | Средняя производи-тельность труда в группе (изделий/час) | Плотность распределения |
| 0-1 | 200 | 2 | 200 |
| 1-3 | 300 | 4 | 150 |
| 3-10 | 150 | 5 | 21 |
| 10-20 | 50 | 3 | 5 |
| 20 и более | 10 | 1 | (1) |
| N = 710 |
3) Структурная (вариационная) группировка
Широко применяется для простого сжатия информации по какому-либо признаку. Принципиально отличается от типологической тем, что содержит группы, отличающиеся друг от друга количественно, а не качественно. Пример структурной группировки (табл. 3.3):
Интервалы при структурной группировке, как правило, равные.
Величина равного интервала определяется по формуле:
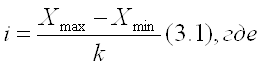
Xmax и Xmin – максимальное и минимальное значения признака.
Таблица 3.3
Данные о денежных доходах населения Нижегородской области в 1996 г.
|
Группы населения (по 10% каждая) |
Доля оплаты труда и дохода от предпринимательской деятельности ко всем доходам, % |
| 1 (группа с низшим доходом) | 68,4 |
| 2 | 75,8 |
| 3 | 76,1 |
| 4 | 75,6 |
| 5 | 76,4 |
| 6 | 77,8 |
| 7 | 79,8 |
| 8 | 79,9 |
| 9 | 81,7 |
| 10 (группа с высшим доходом) | 78,0 |
Источник: данные НОКГС
Число же групп можно определить разными способами:
ü по формуле Стерджесса
![]()
k – число групп;
N – объем ряда (число единиц совокупности).
Применение формулы Стерджесса дает хорошие результаты при большом объеме ряда и распределении, близком к нормальному.
ü на основе применения среднего квадратического отклонения – например, при величине интервала i = 0,5 σ совокупность разбивается на 12 групп, при i = σ – на 6 групп со следующими интервалами:
от ![]() - 3σ до
- 3σ до ![]() - 2σ
- 2σ
от ![]() - 2σ до
- 2σ до ![]() - σ
- σ
от ![]() - σ до
- σ до ![]()
от ![]() до
до ![]() + σ
+ σ
от ![]() + σ до
+ σ до ![]() +2 σ
+2 σ
от ![]() + 2σ до
+ 2σ до ![]() +3σ
+3σ
ü с помощью заранее установленных норм. Пример: согласно нормам DIN ориентировочное минимальное число групп составляет (табл.3.4):
Таблица 3.4
Число групп по нормам DIN
| Число наблюдений | Число групп |
| до 100 | min 10 |
| до 1000 | min 13 |
| до 10000 | min 16 |
При этом величина интервала выбирается таким образом, чтобы в каждой группе было хотя бы одно значение признака, т.е. не было "пустых" групп. Кроме того, величина интервала по возможности должна выражаться нечетным числом, чтобы середина интервала являлась бы целым числом.
Количество групп зависит также от того, на какую потерю информации согласен исследователь (заказчик). Обычно приемлемым считается уровень 1-5 % величины показателя.
Точное установление границ интервалов
Если признак дискретный, то следующий интервал будет на одну единицу больше предыдущего:
0-2 (+1)
3-5 (+1)
6-8 (+1) и.т.д.,
где, например, 6 – нижняя граница; 8 – верхняя граница интервала.
Если же имеем непрерывный признак, то интервалы выглядят так:
0-2 (-)
2-5
5-8,
и возникает вопрос: в какую группу включать единицу наблюдения, значение признака у которой совпадает с границами интервалов. Существует 2 способа: "включительно" и "исключительно". По способу "включительно" единица наблюдения со значением 2 попадает в первую группу, по способу "исключительно" – во вторую.
Далее, интервалы бывают открытые и закрытые. У закрытых интервалов обозначены обе границы, у открытых – только одна граница, верхняя или нижняя, например,
"менее 2" или
"5 и более"
Ширина открытого интервала принимается равной ширине смежного с ним интервала (последующего или предыдущего).
4) Сложная группировка
Если в основу группировки положено несколько признаков, то мы имеем дело со сложной группировкой. Она может выполняться как комбинационная (группы, выделенные по одному признаку, затем подразделяются на подгруппы по другому признаку) или как многомерная (группы или кластеры выделяются одновременно по нескольким признакам). В последнем случае единица совокупности рассматривается как точка в m-мерном пространстве, а задачей группировки является выделение точек, составляющих однородные группы (кластеры) единиц. Изучение многомерных группировок (кластерный анализ) проводится с помощью средств вычислительной техники.
После проведения группировки строится ряд распределения, а затем обработанный статистический материал представляется в виде таблиц, графиков, диаграмм и т.д..
3.3 Статистические ряды
Статистический ряд – это упорядоченное распределение единиц совокупности по группам. Его нужно отличать от ряда динамики. Ряд распределения характеризует структуру явления. Ряд динамики – развитие явления во времени.
Ряд распределения называют ранжированным, если признак стоит в порядке возрастания или убывания.
Ряд распределения всегда имеет 2 элемента:
х – варианта или значение признака,
f – частота или числовое значение варианты.
Если значение признака выражается числом, то ряд распределения является количественным или вариационным, если словом – атрибутивным или качественным.
Количественные ряды делятся, в свою очередь, на дискретные (варьирующий признак дискретен) и непрерывные (варьирующий признак непрерывен, значения признака задаются в виде интервала).
Пример (табл.5) .
Таблица 3.5
Дискретный ряд распределения
| X | f | F |
| 0 | 10 | 10 |
| 1 | 20 | 30 |
| 2 | 15 | 45 |
| 3 | 5 | 50 |
| 4 | 3 | 53 |
| 5 | 2 | 55 |
где X – число забитых в чемпионате мячей;
f – число игр с таким числом голов;
F – накопленная частота.
На плоскости дискретный ряд распределения изображается графиком, называемым полигоном распределения – das Häufigkeitspolygon, the frequency polygon (рис.3.2.).
![]() f
f
 20 -
20 -
 15 -
15 -
10 -
![]() 5 -
5 -
![]()
![]() │ │ │ │ │
│ │ │ │ │
0 1 2 3 4 5 x
Рис. 3.2 Пример полигона распределения
Примером интервального ряда распределения может служить таблица распределения семей по размеру жилой площади на одного человека.
Таблица 3.6
Интервальный ряд распределения
| Группы семей по размеру жилой площади на человека (кв. м.) | Число семей с данным размером жилой площади | Накопленное число семей |
| 3-5 | 10 | 10 |
| 5-7 | 20 | 30 |
| 7-9 | 30 | 60 |
| 9-11 | 40 | 100 |
| 11-13 | 15 | 115 |
| N=115 |
Для графического изображения интервального ряда распределения (непрерывный признак) применяется гистограмма – das Histogramm, the histogram.
Если в ряду распределения интервалы не равны, то гистограмма строится с использованием еще одной величины – плотности распределения. Плотность распределения – это частота, падающая на единицу интервала.
Построим гистограмму для ряда с неравными интервалами (см. табл.3.2. и рис.3.4.)
![]() плотность
плотность
![]()
![]() 200-
200-
![]()
![]() 150-
150-
![]()
![]() 20-
20-
![]()
![]()
![]() 10-
10-
|![]()
![]() | | | |
| | | |
0 1 3 10 20 30 стаж
Рис. 3.4. Гистограмма ряда распределения с неравными интервалами
В целом выделяют следующие основные типы распределения:
![]()
![]() f
f
![]()
![]()
![]()
![]()
![]() ТИП
1 ТИП
2
ТИП
1 ТИП
2
 в
в
 а в
а в
а
![]()
![]()
![]()
![]()
![]() x
x
![]()
ТИП 3 ТИП 4
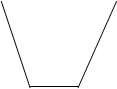
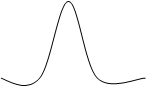
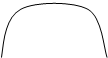
Рис. 3.5. Основные типы распределения
ТИП 1 – симметричное распределение (а – плосковершинное, в - островершинное);
ТИП 2 – асимметричное распределение (а – правосторонняя асимметрия, в – левосторонняя асимметрия);
ТИП 3 – многовершинное распределение (статистическая совокупность неоднородна);
ТИП 4 – симметричная кривая распределения с двумя экстремальными значениями.
Часто возникает вопрос не о том, какова частота отдельной варианты, а о том, сколько значений признака выше (или ниже) определенной величины.
В таких случаях применяют два особых вида кривых для изображения ряда распределения: кумуляту и огиву. Кумулята отвечает на вопрос “менее чем”, огива – “более, чем”.
Пример (табл. 3.7, рис.3.5).
Таблица 3.7.
Договоры предприятия N в 200_ г.
| Группы договоров | Количество договоров | Количество договоров в процентах | |||
| Абсолютное значение | Накопленная величина по возрастанию | Накопленная величииа по убыванию | Доля | Накоплен-ная вели-чина по воз-растанию | |
| 0-150 | 50 | 50 | 1000 | 5 | 5 |
| 150-300 | 150 | 200 | 950 | 15 | 20 |
| 300-450 | 180 | 380 | 800 | 18 | 38 |
| 450-600 | 260 | 640 | 620 | 26 | 64 |
| 600-750 | 220 | 860 | 360 | 22 | 86 |
| 750-900 | 90 | 950 | 140 | 9 | 95 |
| 900-1050 | 50 | 1000 | 50 | 5 | 100 |
| 1000 | 100 |
Построим по этим данным огиву и кумуляту (рис. 3.6)
В таблице 200 договоров имеют сумму менее 300 у. е., 950 – менее 900 у. е., 800 – от 300 у. е. и более, 50 – от 900 у. е. и более и т.д.
Кроме полигона распределения, гистограмм, огивы и кумуляты существуют другие статистические графики:
столбиковые,
круговые (радиус круга = ![]() ,
,
ленточные,
квадратные (сторона
квадрата = 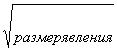 ,
,
радиальные
cекторные (все явление = 100 % = 360°, значит 1% явления = 3,6° )
и фигурные диаграммы.
Таким образом, величина явления всякий раз равна площади фигуры. Для построения диаграмм и графиков удобно использовать стандартные программные пакеты, например, MS Office/Excel.
![]() накопленная
частота
накопленная
частота
![]()
![]() 1000
кумулята
1000
кумулята
![]()
![]() 950
950
900
 850
850
 800
800
750
700

 650
650
600
550
500
450
 400
400
350
300
250
![]() 200
200
![]() 150
150
100 огива
![]() 50
50
![]() 0
0
50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950 1000 1050 варианта ряда
Рис. 5. Кумулята и огива
3.4 Статистические таблицы
Каждая таблица должна соответствовать макету.
(Таблица №)
(наименование таблицы)
|
П |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
АИсточник: Примечания: Каждая таблица имеет подлежащее и сказуемое. Подлежащее – это группы и подгруппы, на которые разбиваются статистические совокупности для изучения. Если единицы совокупности просто перечисляются в подлежащем, то таблица называется перечневой или простой. Если совокупность делится на определенные группы, то таблица будет групповая. Если совокупность делится по группам по двум или более признакам, таблица будет называться комбинационной. Сказуемое – это показатель, с помощью которого мы изучаем подлежащее. Сказуемое бывает простым и сложным. Если показатель разбивается на две или более части, то это будет сложное сказуемое. Правила заполнения таблиц: 1) все данные в таблице должны измеряться с одной точностью (0; 0.0; 0.00; 0.000 и т. д.); 2) если значение признака мало по сравнению с выбранной нами точностью измерения, то вместо него пишут 0 (0.0; 0.00 и т. д.); 3) если явление отсутствует, ставят прочерк (-); 4) если явление не имеет смысла, ставят крест (x); 5) если нет сведений, то пишут либо ”нет сведений”, либо ставят многоточие (…); После таблицы пишется: Источник: Примечания: ТЕМА 4. СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ И СРЕДНИЕ Statistische Kennzahlen und Mittelwerte Statistical indices and Means 4.1 Статистические показатели Таблицы и графики дают только первый обзор характера распределения. Чтобы кратко охарактеризовать эмпирические данные, используют количественные величины, которые представляют все данные так, что можно отказаться от отдельных, попавших под наблюдение значений признака. Эти количественные величины называются статистическими показателями (Kennzahlen, Indices). К ним относятся абсолютные показатели, относительные показатели и средние. Отличие статистического показателя от признака заключается в том, что он получается расчетным путем. Абсолютные показатели (Absolute Kennzahlen, Absolute indices). Абсолютные показатели выражают абсолютные размеры явлений и процессов и получаются в результате сводки статистической информации. Это масса, площадь, объем, протяженность и т. д. Все абсолютные показатели имеют определенную размерность. Единица измерения может быть выражена: 1) натуральными измерителями (кг); 2) условно- натуральными измерителями (условная консервная банка); 3) составными натуральными показателями (т/км, чел/дн, кВт/ч); 4) стоимостными показателями (руб., $); 5) трудовыми показателями (трудодень).
Проблема может выражаться в сопоставлении показателей, особенно это касается стоимостных единиц измерения (индекс-дефлятор, в котором применяются цены базисного года, а физический объем – текущего года). Относительные показатели (Verhältniszahlen, Relative indices). Относительные показатели представляют собой частное от деления двух статистических величин и характеризует количественное соотношение между ними. Относительный показатель
= Если база сравнения равна единице, то относительный показатель является коэффициентом. Если она равна ста, то относительный показатель выражается в процентах (%), если она равна тысяче, то - в промилле (‰). Виды относительных показателей: 1) выполнение договорных обязательств Макет показателя = 2) относительный показатель структуры (Gliederungszahl, Relativ index of structure) Макет показателя = 3) относительный показатель сравнения (Beziehungszahl) показывает соотношение одних и тех же данных, но относящихся к разным объектам наблюдения (например, отношение ВВП двух стран) Макет показателя =
Макет показателя = 5) Макет показателя =
6) цепные и базисные показатели динамики (Messzahlen) Цепные показатели рассматривают по сравнению с предыдущими, а базисные – по сравнению с периодом, выбранным за базу. Макет показателя = Пример. Таблица 4.1. Вычисление цепных и базисных показателей динамики (1993 г. - базисный)
С показателем динамики связаны показатели темпов роста и темпов прироста. Темп роста – это отношение текущего показателя к показателю, выбранному за базу сравнения. Темп прироста – это темп роста минус единица (или минус 100 %). В нашем примере темп роста производства в 1994 г. по сравнению с 1993 г. равен (250 / 200)*100 % = 125 %, а темп прироста – 125 % - 100 % = 25 %. При анализе показателей динамики нужно всегда смотреть на базу сравнения. Если она разная, то эти показатели вообще нельзя сравнивать. Если она одинаковая, то сравнивать можно, но не в процентах, а в процентных пунктах. Пример (см. табл.4.1.). На сколько выросло производство продукции в 1995 г. по сравнению с 1994 г.? Неправильный ответ: на 25%. Правильный ответ: на 25 процентных пунктов или на (300-250)/250= (150-125)/125=20 % 4.2 Средние Средняя (Mittelwert, Mean)– это обобщающий показатель, отражающий наиболее типичный уровень варьирующего признака качественно однородных единиц совокупности. Данный показатель может вычисляться только у качественно однородных величин. Общий макет = Виды средних: 1) степенные 2) структурные (мода, медиана); 4.2.1 Степенные средние Степенными средними являются средние, исчисляемые по формуле:
где Хi – индивидуальное значение признака каждой единицы совокупности; n - число единиц совокупности
Для взвешенной имеем: где fi – частота повторения индивидуальных значений признака (вес).
При k = 1 получаются формулы средней арифметической (Arithmetisches Mittel, Arithmetic mean) простой и взвешенной: Средняя арифметическая простая используется тогда, когда значение признака относится к отдельным единицам наблюдения или к равновеликим группам единиц. Пример (см. таблицы 4.2, 4.3). Таблица 4.2. Заработная плата работников бригады
или Таблица 4.3. Заработная плата по цехам предприятия
Тогда
Средняя арифметическая взвешенная применяется тогда, когда отдельные значения признака встречаются с разной частотой или когда группы не являются равновеликими. Пример (см. табл.4.4). Таблица 4.4. Заработная плата по цехам предприятия
При k = - 1 степенная средняя называется средней гармонической (Harmonisches Mittel, Harmonic mean):
Средняя гармоническая взвешенная тогда будет равна: где Wi – вес средней гармонической, равный произведению индивидуального значения признака на его частоту (обычную). Пример (см. таблицы 4.5, 4.6). Таблица 4.5. Данные о заработной плате по отделам организации
Тогда среднюю зарплату по организации можно найти по формуле средней арифметической взвешенной: Однако часто данные имеются в другом виде (табл. 4.6).Тогда для расчета средней зарплаты по организации применяется средняя гармоническая взвешенная: Таблица 4.6. Данные о заплате по отделам организации
Всегда, когда в качестве веса уже имеем произведение значения признака на частоту, средняя арифметическая не работает – применяют формулу средней гармонической. Чтобы не ошибиться в расчетах, нужно постоянно следить за смыслом числителя и знаменателя.
При k = 0 получаем формулу средней геометрической (Geometrisches Mittel, Geometric mean) простой и взвешенной:
Средняя геометрическая применяется тогда, когда используются операции, связанные умножением/ делением, а не сложением/ вычитанием. Пример (см. табл.4.7).Найти среднегодовой темп роста и прироста по следующим данным. Таблица 4.7. Темпы роста объема сбыта по фирме N
Среднегодовой темп роста (Wachstumstempo, Rate of Growth): Среднегодовой темп прироста (Zuwachsrate, Rate of increment):
В нашем примере: Примечание: среднегодовой темп роста и среднегодовой темп прироста можно получить исходя и из абсолютных значений. Видоизменим предыдущий пример (табл. 4.8). Таблица 4.8. Объем оказанных услуг по фирме N
Тогда получим:
При k = 2 получаем формулу средней квадратической (Quadratisches Mittel, Quadratic mean) простой и взвешенной:
При k = 3 получаем формулу средней кубической (Kubisches Mittel, Cubic mean) простой и взвешенной и т.д:. Средняя квадратическая и средняя кубическая применяются, если нужно сохранить неизменной сумму квадратов или сумму кубов исходных величин. Правило мажорантности средних
Если на одном и том же фактическом материале рассчитать разные средние, то все они будут иметь разные значения, причем эти значения будут тем меньше, чем меньше k. Получаем следующее неравенство: Свойства средней арифметической Средняя арифметическая обладает некоторыми свойствами, облегчающими ее применение на практике и упрощающими ее расчеты. 1) сумма отклонений индивидуальных значений признаков от средней арифметической равна нулю:
2) если все значения признака увеличить или уменьшить на какое-либо число, то средняя арифметическая увеличится (уменьшится) на это же число:
3) если все значения признака умножить (поделить) на какое-либо число, то средняя арифметическая изменится во столько же раз:
4) сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть величина минимальная:
5) если вес каждого значения признака разделить (умножить) на какое-либо постоянное число А, то средняя арифметическая от этого не изменится:
6) средняя суммы (разности) двух величин равна сумме (разности) средних этих величин
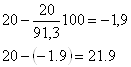
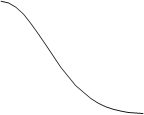
Условия применения средних величин в анализе - однородность статистической совокупности. Действительно, допустим, что отдельные элементы совокупности, вследствие подверженности влиянию некоторого случайного фактора, имеют слишком большие (или слишком малые) величины изучаемого признака, существенно отличающиеся от остальных. Такие элементы повлияют на размер средней для данной совокупности, поэтому средняя не будет выражать наиболее характерную для совокупности величину признака. Если исследуемое явление не является однородным, то его разбивают на группы, содержащие только однородные элементы. Для такого явления рассчитываются сначала средние по группам, которые называются групповые средние, – они будут выражать наиболее типичную величину явления в каждой группе. Затем рассчитывается для всех элементов общая средняя величина, характеризующая явление в целом, – она рассчитывается как средняя из групповых средних, взвешенных по числу элементов совокупности, включенных в каждую группу. На практике, однако, выполнение данного условия не является безусловным. Пример: расчет величины средней заработной платы по всем секторам экономики, включая высокооплачиваемые (банки, финансы) и низкооплачиваемые (народное образование, сельское хозяйство). - достаточное количество единиц в совокупности, по которой рассчитывается среднее значение признака. Достаточность анализируемых единиц обеспечивается корректным определением границ исследуемой совокупности, т.е. закладывается еще на начальном этапе статистического исследования. Данное условие становится решающим при применении выборочного наблюдения, когда необходимо обеспечить репрезентативность выборки. - нежелательность большого расхождения максимального и минимального значения признака в изучаемой совокупности также является условием применения средней величины в анализе. В случае больших отклонений между крайними значениями и средней, необходимо проверить принадлежность экстремумов к исследуемой совокупности. Если сильная изменчивость признака вызвана случайными, кратковременными факторами, то, возможно, крайние значения не характерны для совокупности. Следовательно, их следует исключить из анализа, т.к. они оказывают влияние на размер средней величины. 4.2.2 Структурные средние Мода (Modus, Mode)– это наиболее часто встречающееся значение признака. Медиана (Median) – это значение признака у серединной единицы ранжированного ряда. При нормальном распределении средняя арифметическая, мода и медиана совпадают (рис.4.1а). Условия нормального распределения довольно широки, оно часто встречается, следовательно, можно и не считать среднюю арифметическую, а брать моду или медиану.
Рис. 4.1. Средняя арифметическая, мода и медиана при нормальном и деформированном распределении При деформированном распределении показатели "разбегаются": мода остается почти на месте, медиана сдвигается в сторону асимметрии, туда же, но еще дальше убегает средняя арифметическая (рис. 4.1б). Медиана ближе к средней арифметической, расстояние от моды до медианы при умеренно деформированном распределении в 2 раза больше, чем от медианы до средней арифметической, поэтому в этом случае среднюю арифметическую лучше заменять медианой. Расчет моды и медианы в дискретном ряду (по несгруппированным данным) Пусть дан ранжированный ряд распределения: Ряд: 10, 20, 20, 25, 30 (35) Порядковый номер значения признака: 1 2 3 4 5 (6) Чаще всего повторяется значение признака 20, оно и будет модой: Мо=20 Медианой будет центральное значение ряда 20: Ме=20 Если ряд содержит четное число единиц, то медиана определяется как средняя из двух центральных значений. Предположим, что в нашем ряду 6 значений, добавлено значение 35. Тогда Ме = (20+25) /2= 22,5. Расчет средней арифметической, моды и медианы по данным интервального ряда (сгруппированные данные). Расчет средней арифметической, моды и медианы по данным интервального ряда (сгруппированным данным) проведем на основе сведений табл. 4.9. Для того, чтобы рассчитать среднюю арифметическую, берем середины интервалов в качестве значений признаков, что несколько искажает результат, так как мы априори исходим из того, что внутри групп распределение равномерное. Допущение: в случае открытых интервалов расчет, строго говоря, не возможен, но чаще всего берут величины предыдущих (последующих) интервалов либо используют в качестве средней арифметической моду или медиану. Таблица 4.9. Производительность труда на предприятии N
Расчет моды. По таблице видим, что она находится во втором интервале, т.е. имеет значение между 10 и 20. Для точного расчета применяется формула:
А0 – нижняя граница модального интервала; i – величина модального интервала; fМ0 - частота модального интервала; f М0-1– частота интервала, предшествующего модальному; f Mo+1- частота интервала, следующего за модальным.
Расчет медианы. По таблице видим, что накопленная частота превышает половину суммы накопленных частот (в нашем случае – 50) в третьем интервале, т.е. имеет значение между 20 и 30. Для точного расчета применяется формула: А0 – нижняя граница медианного интервала; i - величина медианного интервала; N – объем ряда; FМе-1 – накопленная частота интервала, предшествующего медианному; f Ме – частота медианного интервала.
Квартили (Quartile, Quartile)– значения признаков, разбивающие ряд на 4 равные части. Децили (Dezentile, Deciles) – значения признаков, разбивающие ряд на 10 равных частей. Перцентили (Perzentile, Percentiles)- значения признаков, делящие ряд на 100 равных частей. 4.3 Математическое ожидание Математическое ожидание (Erwartungswert, Expected value) ТЕМА 5. ПОКАЗАТЕЛИ ВАРИАЦИИ Streuungsmaße Variation 5.1 Понятие вариации Вариация (Variation)– это колеблемость или изменчивость изучаемого признака. При исследовании социально-экономических явлений и процессов мы почти всегда имеем дело с вариацией. Причина вариации – множественность действующих факторов, не поддающихся устранению (элиминированию). Показатели вариации нужны для определения степени диффузии (рассеивания) признака. Ряды распределения могут иметь одинаковые средние значения, один и тот же центр группирования, симметричное расположение частот вокруг него, но разные степени рассеивания. Пример (см. также рис. 5.1.): дано два ряда: 1)
2) -9; -8; -6; 0; 1; 1; 2; 2; 3; 14; X = 0 Вывод: необходимо использовать показатели вариации, т.е. мы должны изучать и оценивать вариацию и оперировать колеблющимися величинами.
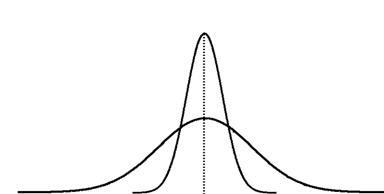
Рис. 5.1. Ряды распределения с разной степенью диффузии 5.2 Показатели вариации 1) Размах вариации (Spannweite, Variation range) – это разница между максимальным и минимальным значениями признака.
Показатель легко исчисляется, но недостаточно информативен, зависит только от крайних значений признака. 2) Среднее линейное отклонение (Durchschnittliche absolute Abweichung, Mean absolute deviation)– арифметическая сумма отклонений значений признака от средней. В качестве средней чаще всего берут среднюю арифметическую, но можно брать также другие средние, например, медиану.
Недостаток показателя – мы вынуждены брать модуль отклонений, т.к. алгебраическая сумма отклонений значений признака от средней арифметической всегда равна 0. 3) Дисперсия (Varianz, Variance)– средняя из квадратов отклонений значений признаков от средней арифметической
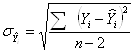
4) Среднее квадратическое отклонение (или стандартное) отклонение (Mittlere quadratische (Standard-) Abweichung, Standard deviation)– корень квадратный из дисперсии:
Преимущество среднего квадратического отклонения перед дисперсией состоит в том, что оно является именованной величиной, т.е. имеет ту же единицу измерения, что и значения признака. И среднее квадратическое отклонение, и дисперсия – показатели, широко применяемые в статистике, математической статистике и теории вероятностей. Пример расчета показателей вариации. Дан ряд:
1; 2; 3; 4; 5 Тогда: X = 3, R = 5-1 = 4 Пример расчета дисперсии и среднего квадратического отклонения по сгруппированным данным: Таблица 5.1. Расчет σ2 и σ по сгруппированным данным
X = 15 разрядов ; σ2 = 118/132 = 0,89; и σ = Для оценки характера распределения используют следующие взаимосвязи: 1) среднее квадратическое отклонение при нормальном или умеренно деформированном распределении примерно в 1,25 раза больше линейного отклонения
2) коэффициент вариации (Variationskoeffizient, Coefficient of variation) – это отношение среднего квадратического отклонения к средней
Здесь критическим значением выступает V = 35 %. Если V ≤ 35 %, то считаем, что наша совокупность однородна. Если V > 35 %, то совокупность разнородна и это автоматически накладывает ограничения на расчет средней (расчет просто не имеет смысла). В нашем первом примере отношение σ/l =1,18 , т.е. распределение близко к нормальному, а V = 47 %, т.е. совокупность разнородна. Свойства дисперсии. Правило сложения дисперсии 1) дисперсия постоянной величины равна 0 2) уменьшение всех значений признака на одну и ту же величину А не меняет дисперсии: σ2(х - А) = σ2х 3) уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз, а среднее квадратическое отклонение – в k раз. σ2(х / k) = σ2х : k2 σ(х / k) = σх : k 4) дисперсия равна средней из квадратов значений признака минус квадрат средней значений признака:
5)
6) дисперсию, в отличие от среднего квадратического отклонения, можно собирать по частям и делить на части.
Существует так называемое правило сложения дисперсии, которое заключается в следующем: δ² - межгрупповая дисперсия;
Межгрупповая дисперсия – это дисперсия, характеризующая влияние фактора, положенного в основу группировки. Ее расчет производится по следующей формуле:
m – количество групп.
Средняя из внутригрупповых дисперсий отражает влияние прочих факторов и определяется, как: k – объем k-ой группы. Исчисление среднеарифметической и показателей вариации для качественных (атрибутивных или номинально измеряемых) признаков Наряду с вариацией количественных признаков может ставиться задача оценки вариации качественных признаков, например, при изучении качества продукции вся она делится на годную и бракованную. В таком случае за эквивалент наличия признака (ответ "да") принимается 1, отсутствие признака обозначается 0 (ответ “нет”). Общее число единиц совокупности примем за n, тогда число единиц совокупности, обладающих данным признаком, будет f, а число единиц, не обладающих данным признаком, будет (n - f). Ряд распределения по качественному признаку представлен в табл. 5.2. таблице: Таблица 5.2. Пример ряда распределения по качественному признаку
Тогда средняя арифметическая равна:
Фактически, это доля единиц, обладающих данным признаком. Соответственно, доля единиц, не обладающих данным признаком равна:
Так как p + q = 1, то для дисперсии альтернативного признака имеем:
На практике это означает, что дисперсия по альтернативным или качественно изменяющимся признакам подчиняется следующему правилу
Среднее квадратическое отклонение по альтернативному признаку:
Коэффициент вариации:
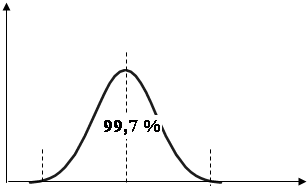
Пример. В результате контроля качества из 1000 готовых изделий 20 оказались бракованными. Нужно вычислить дисперсию и среднеквадратическое отклонение по данному номинально измеряемому признаку. 5.3 Свойства нормального распределения Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин, которые не зависят друг от друга и ни одна из которых не имеет преобладающего влияние над другими.
1) Кривая распределения симметрична относительно максимальной ординаты: 2) кривая нормального распределения имеет две точки перегиба х ±σ
3) В промежутках между:
5.4 Моменты Показатели вариации характеризуют ряд с точки зрения рассеивания, колеблемости значений признака. Ряд распределения, помимо рассеивания, может быть симметричным (асимметричным), остро- и плосковершинным. Универсальными характеристиками ряда распределения являются моменты (Momente, Moments) – средняя арифметическая тех или иных степеней отклонений значений признака от определенной исходной величины А. Их общая формула:
Если А = 0, то момент называется начальным.
Если А = условной величине, то момент называется условным. В таблице 5.3. представлены формулы моментов первых четырех порядков. Таблица 5.3. Начальные, центральные и условные моменты первых четырех порядков
Большое значение имеют центральные моменты, обозначаемые μi. Центральный момент 2-го порядка – это дисперсия:
С помощью центральных моментов 3-го порядка
исчисляются показатели симметричности (асимметричности) ряда. Так, если μ3 = 0, то ряд распределения симметричен, μ3 < 0, то ряд имеет левостороннюю асимметрию, μ3 >0, то у ряда правосторонняя асимметрия (см. рис.5.3).
Кроме того, степень асимметрии можно определить с помощью коэффициента асимметрии Аs (Schiefemaß nach 3. zentralen Moment):
Асимметрия выше 0,5 (независимо от знака) считается значительной, меньше 0,25 – незначительной. Существенность коэффициента асимметрии оценивается на основе средней квадратической ошибки σAs:
Если Для симметричных рядов по моментам 4-го порядка рассчитывается показатель остро- или плосковерщинности - эксцесса Ex (Wölbungskoeffizient):
Ecли Ex = 0, то распределение признается нормальным, при Ex > 0 распределение островершинное, при Ex < 0 распределение плосковершинное (см. рис.5.4). При Ex = -2 и менее распределение "рассыпается", статистическая совокупность разнородна.
 

Рис. 5.4. Ряды с нормальным, остро- и плосковершинным распределением Среднеквадратическая ошибка эксцесса σEx рассчитывается по формуле:
ТЕМА 6. ИНДЕКСЫ Indizes Indices 6.1 Понятие об индексах Индексы (Index)– это относительные величины (динамики, структуры или сравнения), полученные в результате сопоставления сложных показателей во времени и в пространстве. Сложными являются такие показатели, отдельные элементы которых не подлежат непосредственному суммированию. Пример. Таблица 6.1.
Для получения итогового изменения стоимости продуктов питания нужно перейти к общей мере. Следовательно, вводят особый соизмеритель. Выбор соизмерителя зависит от цели исследования. Это может быть цена, себестоимость, трудоемкость и т.д. Большинство экономических показателей являются сложными или несоизмеримыми, поэтому индексы широко применяются на практике. При построении индекса отвечают на следующие три вопроса: 1) какая величина будет индексируемой? 2) что будет весом при расчете индекса? 3) по какому составу разнородных элементов необходимо исчислить индекс? С помощью индексов решаются следующие задачи: 1) характеризуется общее изменение уровня сложного экономического показателя (так называемая синтетическая функция); 2) выделяют влияние одного из факторов на изменение изучаемого показателя (аналитическая функция). В теме индексы приняты следующие обозначения: q – количество (физический объем продаж); p – цена; z – себестоимость; t – трудоемкость и т. д. Индексы бывают: I. По степени охвата явления: - индивидуальные; - сводные. II. По базе сравнения: - динамические а) базисные – текущий (отчетный) уровень показателя сопоставляется с уровнем периода, принятого за базу сравнения; б) цепные – текущий (отчетный) уровень показателя сопоставляется с предшествующим уровнем; - территориальные – сравниваются показатели территорий. III. По виду весов: 1) постоянным состава; 2) переменного состава. IV. По характеру объекта исследования: 1) Качественные – индексы цен, себестоимости, зарплаты, производительности труда и др.; 2) количественные – индекс физического объема; 6.2 Индивидуальные индексы Индивидуальные индексы отражают изменение только одного элемента сложного показателя.
Так, индивидуальный индекс физического объема: отражает изменение только физического объема, индивидуальный индекс цен – изменение цен на конкретные продукты..
Пример (на основе таблицы 6.1.): Вывод: цена на хлеб возросла на 50%, цена на пиво – на 20%. 6.3 Сводные индексы Сводные индексы определяют изменение всех элементов сложного показателя. Макет сводного индекса выглядит следующим образом:
Пример сводного индекса – индекс стоимости (Wertindex, Value index):
По таблице 6.1.: Вывод: расходы возросли на 55,6%. Если индекс охватывает не все элементы, а только их часть, то он называется групповым или субиндексом. Если в индексе сравниваемая величина (ставится в числитель) берется за текущий период, а база сравнения (в знаменателе) за базисный, то такой индекс называется базисным. Если же в индексе сравниваемая величина берется за текущий период, а база сравнения за предыдущий, то индекс называется цепным. В экономике широко применяются индексы цен и физического объема. Индекс цен и физического объема по Э. Ласпейресу и Г.Пааше: Индекс цен по Э.Ласпейресу (Preisindex nach Laspeyres, Laspeyres price index):
Индекс физического объема по Э. Ласпейресу (Mengenindex nach Laspeyres, Laspeyres quantity index):
Индекс физического объема по Г. Пааше (Mengenindex nach Paasche, Paasche quatity index): Индекс цен по Г. Паше (Preisindex nach Paasche, Paasche price index):
Следующее уравнение отражает взаимосвязь между индексами цен, физического объема и стоимости: В целом отметим, что: - индекс по формуле Ласпейреса (например, цен) дает ответ на вопрос: как изменились бы цены, если бы структура производства (потребления) осталась прежней? Преимущество этого индекса: веса определяются один раз на длительный период времени. Недостаток: чем больше времени прошло с базисного года, тем больше вероятность изменения структуры производства (потребления) товаров и тем больше вероятность неточности индекса. Пример применения: индекс стоимости жизни (Lebenshaltungskostenindex, cost of living index) - индекс Пааше (например, цен) дает ответ на вопрос: как изменились бы цены при данной (текущей) структуре производства (потребления) товаров и услуг? Преимущество: отражает реальную сложившуюся на сегодня ситуацию. Недостаток: требует более высоких затрат на исчисление весов. Пример применения: проверка и корректировка индекса стоимости жизни, а также расчет макроэкономических показателей (индекса – дефлятора и др.). Индекс-дефлятор служит для приведения важнейших стоимостных макроэкономических показателей (ВВП, ВНП, национального дохода, выпуска по регионам, по отдельным отраслям экономики и др.) в сопоставимый вид путем их измерения по стоимости базисного периода. Т.е. индекс-дефлятор рассчитывается как отношение фактической стоимости выпуска к стоимости выпуска в ценах базисного года при сохранении структуры выпуска отчетного года. Для индекса-дефлятора ВВП имеем:
Средний арифметический индекс Бывает, что имеется информация по одним элементам сложных показателей и не имеется по другим. Например, при расчете индекса физического объема продаж есть данные по индивидуальным индексам, тогда сводный индекс применяется в виде среднего арифметического .
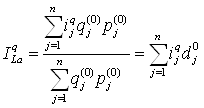
Гармонический индекс Аналогично при наличии данных, например, о динамике физического выпуска продукции ijq и стоимости каждого вида продукции в текущем (отчетном) периоде pj1 qj1, удобно применять сводный индекс физического объема Паше в виде гармонического индекса:
В нашем примере: Другие индексы (по Лоу и Фишеру)
Предпринимались неоднократные попытки избавиться от недостатков индексов по Пааше и Ласпейресу с помощью изобретения "идеального" индекса. Американский экономист И.Фишер вывел среднюю геометрическую из этих индексов – изящный расчетный пример, лишенный, однако, экономического содержания. Индекс Лоу привязан к условной структуре выпуска продукции, что обуславливает трудности его исчисления на практике. Некоторые правила исчисления индексов 1) Произведение рядом стоящих цепных индексов дает базисный индекс.
2) Частное от деления двух рядом стоящих базисных индексов дает цепной.
Эти правила работают для индивидуальных индексов, для сводных они будут верным только в случае постоянных весов. Пример индекса с постоянными весами: Пример индекса с переменными весами: 3) Установление иной базы сравнения (Umbasierung, determining of another base for index). Таблица 6.2.
|
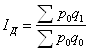
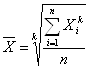
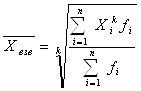
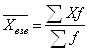
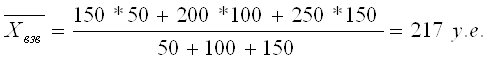
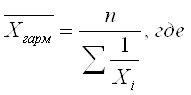
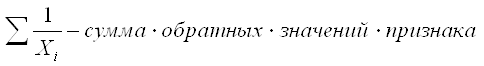
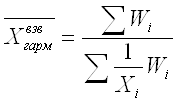
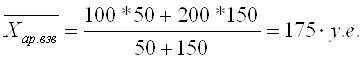
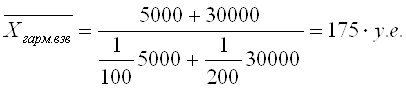
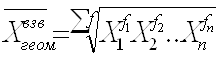
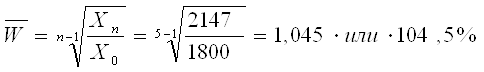
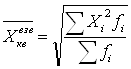
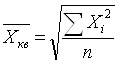

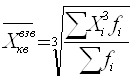
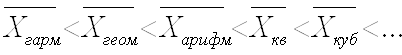
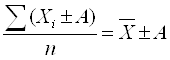
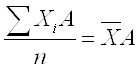
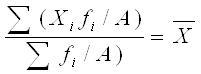


 а) б)
а) б)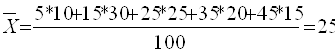
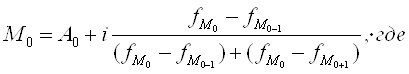
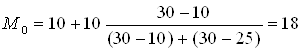 В нашем примере:
В нашем примере: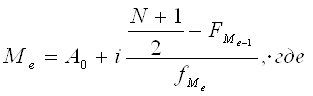
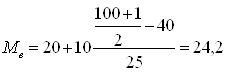 В нашем примере:
В нашем примере: 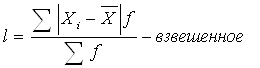
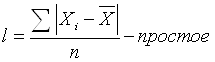
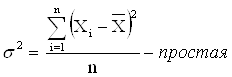
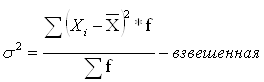
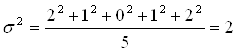
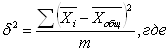
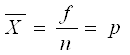
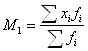
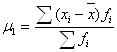
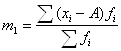
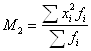
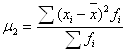
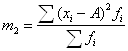

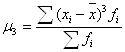
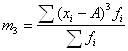
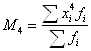
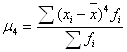

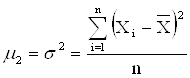
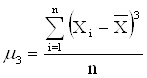

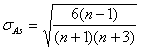
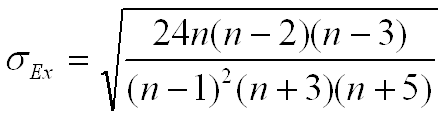
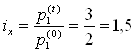
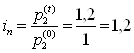
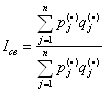
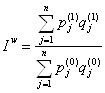
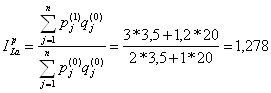
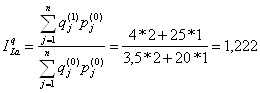
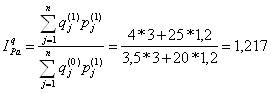
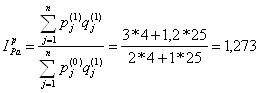
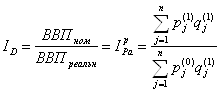
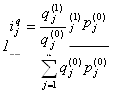
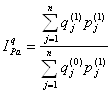
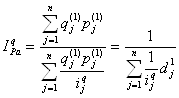
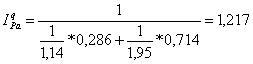
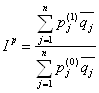
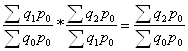
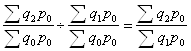
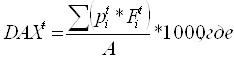

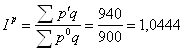
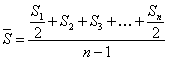
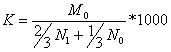
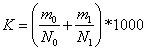

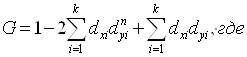
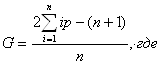
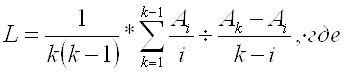

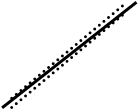
 нет связи экстремально
негативная связь
нет связи экстремально
негативная связь



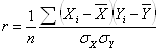
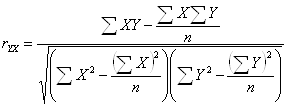
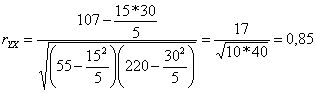
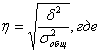
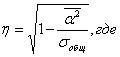
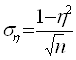
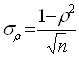
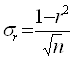

 aX+b
aX+b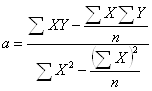
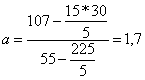
 9
9