Курсовая работа: Преобразование параллельного двоичного кода в код Хэмминга
Министерство образования Республики Беларусь
Белорусский государственный университет
информатики и радиоэлектроники
Кафедра метрологии и стандартизации
К защите допускаю
" __" 2009г.
преподаватель Гурский А.Л.
Пояснительная записка
к курсовой работе на тему:
" Преобразование параллельного двоичного
кода в код Хэмминга "
Выполнила: Проверил:
ст. группы 762101 Гурский А.Л.
Лазарева Е.О.
Минск 2009
Преобразователь кодов (кодопреобразователь) – логическая схема, которая изменяет данные, представленные в одном двоичном виде, в другой вид, также двоичный. Наиболее часто используемые кодопреобразователи: двоично-десятичный код в семисегментный; двоично-десятичный код в двоичный; двоичный код в двоично-десятичный; двоичный код в код Грея; двоичный код в код Хэмминга; двоичный код в код Айкена.
Преобразователи кодов (ПК) могут быть весовыми и невесовыми. Весовые ПК преобразуют информацию из одной системы счисления в другую. Основное назначение невесовых - преобразование информации для ее дальнейшего отображения.
Информация в цифровых устройствах может быть представлена в последовательном и параллельном кодах. При использовании последовательного кода каждый такт соответствует одному разряду двоичного кода. Номер разряда определяется номером такта, отсчитываемого от такта, совпадающего с началом представления кода. Параллельный код позволяет существенно сократить время обработки и передачи информации.
Цифровые устройства по характеру информации на входах и выходах подразделяют на устройства последовательного, параллельного и смешанного действия. В последних, например, входное слово может представляется в параллельной форме, а выходное - в последовательной.
В данной работе используется преобразователь параллельного двоичного кода в код Хэмминга, который является помехоустойчивым. Помехоустойчивое кодирование основано на введении определенным образом избыточной информации в передаваемые сообщения. Помехоустойчивыми называются коды, позволяющие обнаруживать и (или) исправлять ошибки в кодовых словах, которые возникают при передаче по каналам связи. Преднамеренное введение избыточной информации в передаваемые информационные сообщения обеспечивает возможность обнаружения по определенным алгоритмам и коррекции ошибочных информационных символов.
В настоящее время помехоустойчивое кодирование широко используется во многих областях техники: в системах обработки информации, в устройствах памяти ЭВМ, в системах записи на магнитные ленты, компакт-диски, в системах управления ракетами, сжатия информации и т.д. Таким образом, помехоустойчивое кодирование играет немаловажную роль в процессе передачи и хранения информации.
1. ОСНОВНЫЕ СВЕДЕНИЯ О ПРИНЦИПАХ ПОСТРОЕНИЯ КОДОВ ХЭММИНГА
В курсовом проекте для графического изображения кодера кода Хэмминга используются три основных вида схем:
- структурная схема;
- функциональная схема;
- принципиальная схема.
Различаются они своим назначением и степенью детализации изображения устройств.
Структурная схема отображает принцип работы устройства в самом общем виде. На схеме изображаются все основные функциональные блоки, а также основные взаимосвязи между ними, указывающие на последовательность взаимодействия функциональных блоков в схеме. Функциональные блоки на схеме изображаются в виде прямоугольников или условных графических обозначений. Наименования, типы или обозначения блоков вписываются внутрь прямоугольников.
Функциональная схема служит для разъяснения и конкретизации видов процессов, происходящих в отдельных функциональных блоках. Функциональная схема представляет собой гибрид структурной и принципиальной. Некоторые наиболее простые блоки отображаются на ней, как на структурной схеме, а остальные — как на принципиальной схеме. Функциональная схема дает возможность понять всю логику работы устройства, все его отличия от других подобных устройств, но не позволяет без дополнительной самостоятельной работы воспроизвести это устройство.
Принципиальная схема является наиболее полной электрической схемой устройства. Она обязательно показывает все использованные в устройстве элементы и все связи между ними. Принципиальная схема должна позволять полностью воспроизвести устройство.
При построении корректирующих кодов используют следующие параметры:
- основание кода (q) – число элементарных символов, выбранных для передачи сообщений;
- длина кода (n) – число символов, выбранных для передачи сообщений;
- количество информационных символов (k) – количество двоичных символов, несущих полезную информацию;
- кодовое расстояние (d) – количество позиций, которыми отличаются две сравнимые кодовые последовательности;
- кратность (количество) исправляемых (tисп) и обнаруживаемых (tоб) ошибок;
- скорость передачи кода (R) – характеризует количество избыточных символов приходящиеся на один информационный символ. Чем больше R, т.е. R→1 (R всегда меньше 1), тем эффективнее помехоустойчивый код, так как передается меньше избыточной информации;
- число проверочных позиций в коде (r) – r = n - k;
- мощность (М) – число различных кодовых комбинаций. Максимальное число кодовых комбинаций при заданных q и n равно Мmax=qn.
Код Хэмминга с параметрами (n; k) = (2m-1; 2m-1-m) относится к разделимым кодам, следовательно, он задается с помощью проверочной матрицы. Проверочную матрицу Н можно задавать несколькими способами. Она должна содержать все ненулевые двоичные числа длиной m = r.
В курсовом проекте проверочную матрицу будем задавать с помощью элементов поля Галуа. Для формирования поля выбирается примитивный неприводимый порождающий полином степени r. Элементы поля находятся путем деления многочлена степени меньшей, чем n-1, на полином, являющийся неприводимым. Поскольку в качестве столбцов матрицы Н кода Хэмминга выбираются все ненулевые двоичные числа, то матрица Н – матрица степеней элемента поля α, где α – примитивный элемент поля, т.е H = [α0, α1, α2, α3,…αn-1].
Главной функцией кодера является формирование проверочных уравнений, правило формирования которых определено проверочной матрицей H.
Правило формирования проверочного символа для любой кодовой последовательности одинаково и определяется номерами позиций логических единиц в каждой строке проверочной подматрицы проверочной матрицы H. Используя систему формирования проверочных символов, составляем структурную схему кодера.
2. РАСЧЕТ ПАРАМЕТРОВ КОДОВ ХЭММИНГА
Заданы исходные параметры кода Хэмминга:
- кодовое расстояние d0 = 3;
- число информационных символов k = 8 бит;
Используя эти параметры, рассчитаем основные параметры кода Хэмминга. Код является двоичным, следовательно, основание кода q = 2, т.е. используются двоичные символы "1" и "0" .
Кратность (количество) исправляемых ошибок вычисляем по формуле
d0 = 2tи + 1, (1)
где d0 – кодовое расстояние;
tи – количество исправляемых ошибок.
Кратность (количество) обнаруживаемых ошибок вычисляется по формуле
d0 = tоб + 1, (2)
где tоб – количество обнаруживаемых ошибок.
Таким образом, получаем, что данный код исправляет одиночную ошибку, т.е. tи = 1, и обнаруживает двойную, т.е. tоб = 2.
Для кодов Хэмминга, с d0 = 3, т.е. корректирующих одиночные ошибки, количество информационных символов должно удовлетворять следующему равенству:
k = n – log2(n + 1). (3)
Используя это равенство, длина кода n = 12.
Число проверочных позиций r :
r = n – k, (4)
Следовательно, r = 4.
Итак, укороченный код Хэмминга имеет параметры (n; k) = (12,8).
Для r = 4 полный код Хэмминга имеет параметры
(n; k) = (2r – 1; 2r – 1 – r) = (15,11).
Скорость передачи кода R вычисляется по формуле
R = k/n. (5)
Таким образом, R=8/12≈0.67.
3. РАЗРАБОТКА СТРУКТУРНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЫ КОДЕРА
Код Хэмминга с параметрами (n; k) = (2m-1; 2m-1-m) относится к разделимым кодам, следовательно, он задается с помощью проверочной матрицы. Проверочную матрицу Н можно задавать несколькими способами. Она должна содержать все ненулевые двоичные числа длиной m = r.
В курсовой работе проверочную матрицу будем задавать с помощью элементов поля Галуа. Для формирования поля выбирается неприводимый порождающий полином степени r:
q(x) = x4 + x3 + 1.
Элементы поля находятся путем деления многочлена степени меньшей, чем n-1, на полином, являющийся неприводимым, т.е. на q(x).
Таким образом, получившиеся элементы поля приведены в таблице 1.
таблица 1 – Элементы поля Галуа
|
αi |
R(x) |
HT |
|
α0 |
1 | 1 0 0 0 |
|
α1 |
x | 0 1 0 0 |
|
α2 |
x2 |
0 0 1 0 |
|
α3 |
x3 |
0 0 0 1 |
|
α4 |
1+ x3 |
1 0 0 1 |
|
α5 |
1+x+ x3 |
1 1 0 1 |
|
α6 |
1+x+x2+x3 |
1 1 1 1 |
|
α7 |
1+x+x2 |
1 1 1 0 |
|
α8 |
x+x2+x3 |
0 1 1 1 |
|
α9 |
x2+x3 |
0 0 1 1 |
|
α10 |
x+ x3 |
0 1 0 1 |
|
α11 |
1 +x2+x3 |
1 0 1 1 |
|
α12 |
1+x | 1 1 0 0 |
|
α13 |
x+x2 |
0 1 1 0 |
|
α14 |
x2+x3 |
0 0 1 1 |
Поскольку в качестве столбцов матрицы H кода Хэмминга выбираются все ненулевые двоичные числа, то матрица H – матрица степеней элемента поля α, т.е. H = [α0, α1, α2, α3,…αn-1].
Итак, получаем проверочную матрицу полного кода Хэмминга (15, 11):

Чтобы в матрице информационные и проверочные двоичные символы были разделены, приведем проверочную матрицу H(15,11) к приведено-ступенчатому виду:

Чтобы получить матрицу Н кода Хэмминга с нужным числом информационных символов, в нашем случае k = 8, необходимо в проверочной матрице полного кода исключить любые T = 3 столбцов, относящиеся к информационным разрядам, т.е. исключить нужное число столбцов весом w≥2. Итак, исключим из матрицы H(15, 11) три столбца с максимальным весом.
Чем больше логических единиц в приписываемых строках проверочной матрицы, тем большей корректирующей способностью обладает разрабатываемый код, но тем больше будет иметь кодек сумматоров по модулю два и тем больше сложность его реализации. Следовательно, вычеркивание столбцов с максимальным весом приводит к уменьшению сложности вышеуказанных блоков. Проверочная матрица H укороченного кода (12, 8) имеет вид:

Главной функцией кодера является формирование проверочных уравнений, правило формирования которых определено проверочной матрицей H(12, 8). В матрице H(12, 8) символы a1, a2, a3…a8 – информационные, а a9, a10, a11, a12 – проверочные, которые могут быть получены путем суммирования по модулю два определенных информационных символов.
Правило формирования проверочного символа для любой кодовой последовательности одинаково и определяется номерами позиций логических единиц в каждой строке проверочной подматрицы проверочной матрицы H(12, 8). Так символ a1 формируется путем суммирования по модулю два информационных символов. Итак, устройство кодирования (кодер) реализует нижеследующие уравнения:
a9 = a1 + a2 + a3 + a6,
a10 = a2 + a3 + a5 + a6 + a7,
a11 = a3 + a4 + a7 + a8,
a12 = a1 + a2 + a4 + a5 + a8,
где под знаком "+" подразумевается суммирование по модулю два.
Используя полученную выше систему формирования проверочных символов, составим структурную схему кодера, представленную на рисунке 2:
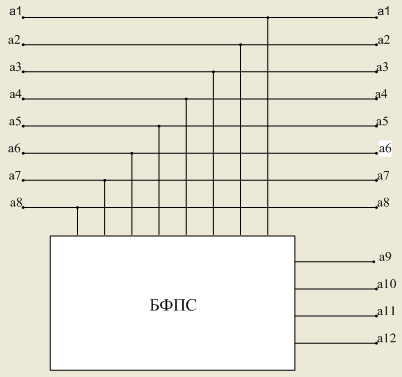
Рисунок 2 – Структурная электрическая схема кодера кода Хэмминга
Рассмотрим принцип работы структурной схемы.
На вход кодирующего устройства передаются в параллельном виде информационные символы a1, a2, a3…a8 . Затем они поступают на блок формирования проверочных символов (БФПС), где из восьми информационных символов формируется 4 проверочных разряда в соответствии с уравнениями кодирования. Закодированная информация из кодирующего устройства передается в параллельном виде.
4. РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЫ КОДЕРА
Так как функциональная схема служит для разъяснения и конкретизации видов процессов, происходящих в отдельных функциональных блоках, то в данном разделе основное внимание должно быть обращено на выбор и обоснование принципа построения каждого функционального блока кодека, представленного на структурной электрической схеме кодека.
Функциональная схема представляет собой гибрид структурной и принципиальной. Некоторые наиболее простые блоки отображаются на ней, как на структурной схеме, а остальные — как на принципиальной схеме. Функциональная схема дает возможность понять всю логику работы устройства, все его отличия от других подобных устройств, но не позволяет без дополнительной самостоятельной работы воспроизвести это устройство.
Функциональная схема кодера представлена на рисунке 4:
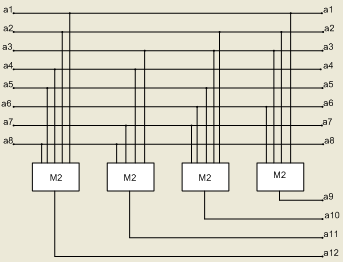
Рисунок 4 – Функциональная электрическая схема кодера кода Хэмминга
Таким образом, кодер состоит из четырёх сумматоров по модулю два, выходы которых соответствуют четырём проверочным символам. В функциональной схеме кодера используется параллельный интерфейс (совокупность средств и методов взаимодействия между элементами системы) ввода и вывода данных. Если один из проверочных символов равен единицы, то в данном канале присутствует ошибка, и, глядя на проверочные уравнения, можно сказать, в каком именно разряде произошла ошибка, если же равно нулю, то ошибки нет в канале информации. В соответствии на выходе кодера формируется наше сообщение (а1..а8) и проверочные символы (а9..а12).
5. РАЗРАБОТКА ПРИНЦИПИАЛЬНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЫ
КОДЕКА
5.1 ОБОСНОВАНИЕ ВЫБОРА ЭЛЕМЕНТНОЙ БАЗЫ
С целью минимизации веса, габаритов и объема оборудования кодера принципиальная схема кодера выполняется с использованием современных интегральных микросхем (ИМС).
Номенклатура выпускаемых интегральных микросхем обширна. Для построения устройств автоматики и вычислительной техники широкое применение находят цифровые микросхемы, которые изготавливают по стандартной технологии биполярных микросхем транзисторно-транзисторной логики (ТТЛ).
При выборе элементной базы, т.е. конкретной серии и типа ИМС, для разработки принципиальной схемы кодера кода Хэмминга необходимо, чтобы выполнялись следующие условия:
- потребление кодеком электроэнергии должно быть минимальным;
- ИМС должны иметь высокую степень интеграции, что обеспечит минимальный объем оборудования кодека;
- минимальная стоимость ИМС;
- ИМС должны обеспечивать надежную работу кодека и др.
В данной работе выбраны микросхемы серии К555. Отличие их от микросхем серии К155 – использование транзисторов с коллекторными переходами, зашунтированными диодами Шотки. В результате транзисторы микросхем серии К555 не входят в насыщение, что существенно уменьшает задержку выключения транзисторов. К тому же они значительно меньших размеров, что уменьшает емкости их р-n-переходов.
5.2 РАЗРАБОТКА ПРИНЦИПИАЛЬНЫХ СХЕМ ФУНКЦИОНАЛЬНЫХ БЛОКОВ КОДЕРА
Распишем функциональные блоки для построения принципиальной схемы преобразования параллельного двоичного кода в код Хэмминга.
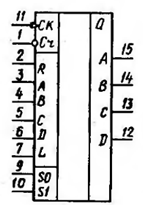
Код параллельно поступает на информационные входы регистра, который представляет собой линейку из триггеров и применяется для накопления (хранения) и сдвига данных. В данном случае используется восьмиразрядный регистр с разрешением записи К555ИР27. Его условное графическое обозначение представлено ниже
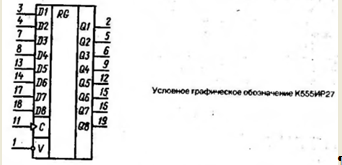
1 – вход разрешения записи; 2 – выход информационный первого разряда; 3 – вход информационный первого разряда; 4 – вход информационный второго разряда; 5 – выход информационный второго разряда; 6 – выход информационный третьего разряда; 7 – вход информационный третьего разряда; 8 – вход информационный четвёртого разряда; 9 – выход информационный четвёртого разряда; 12 – выход информационный пятого разряда; 13 – вход информационный пятого разряда; 14 – вход информационный шестого разряда; 15 – выход информационный шестого разряда; 17 – вход информационный седьмого разряда; 18 – вход информационный восьмого разряда; 19 – выход информационный восьмого разряда.
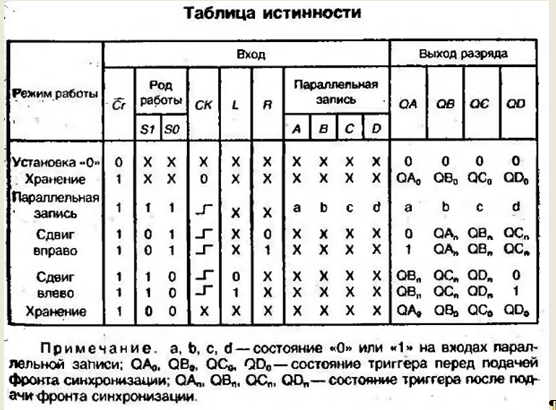
Таблица истинности К555ИР27
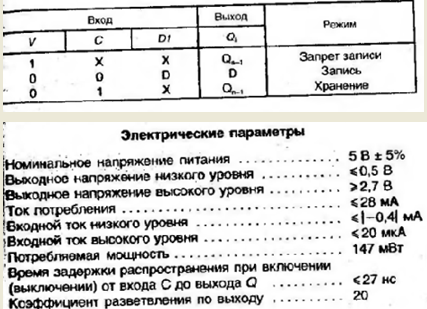
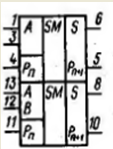
В итоге информационные и сформированные проверочные символы поступают на ряд регистров (3), на выходе получаем параллельный код. В этом случае используются четырёхразрядные универсальные регистры К555ИР11А.
Условное графическое обозначение К555ИР11А


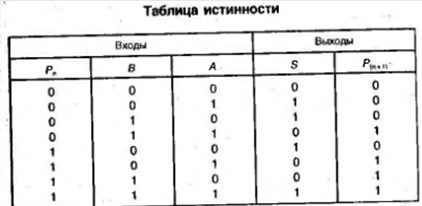
Для построения принципиальной схемы блока формирования проверочных символов (БФПС) используются сумматоры серии К555ИМ5. Микросхема представляет собой два одноразрядных полных сумматора.
Условно-графическое изображение
![]()


| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... Два символа деления / (косая черта (по английски - slash)) и \ (обратная косая че-рта (backslash)) используются в двух случаях, когда неизвестная матрица появляется слева или ... Поскольку матрица коэффициентов R содержит небольшие по величине целые числа, целесообразно представить решение в формате rational (в виде отношения двух целых чисел). |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Техническая диагностика средств вычислительной техники | |
|
ГОУ СПО Астраханский колледж вычислительной техники М.В. Васильев преподаватель специальных дисциплин Астраханского колледжа вычислительной техники ... Рг сдв - регистр сдвига, преобразующий параллельный код строки матрицы символа в последовательность яркостных точек в строке экрана. Схемотехническая реализация функции деления двоичного информационного полинома на образующий полином типа P(a) = x0 + x3 + x8 + x9 |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Технология цифровой связи | |
|
НЕКОММЕРЧЕСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО АЛМАТИНСКИИ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ Кафедра автоматической электросвязи ТЕХНОЛОГИИ ЦИФРОВОЙ СВЯЗИ Конспект ... Чтобы разобраться с этим вопросом, предположим, что кодированная информационная последовательность должна передать один бит за определённое время с постоянной скоростью R бит/с ... Для формирования линейных сигналов используется блочные коды вида nBmB, где n означает число кодируемых цифровых разрядов, B определяет двоичное основание системы счисления ... |
Раздел: Рефераты по коммуникации и связи Тип: учебное пособие |
| Методы позиционирования и сжатия звука | |
|
Современные звуковые карты. Аннотация В данной курсовой работе изучаются различные аспекты применения звуковых карт. Рассматриваются способы получения ... В качестве EDC популярен циклический избыточный код CRC (Cyclic Redundancy Check), суть которого состоит в сложном перемешивании исходной информации в блоке и формированию коротких ... ЦАП в основном строятся по трем принципам: взвешивающие - с суммированием взвешенных токов или напряжений, когда каждый разряд входного слова вносит соответствующий своему ... |
Раздел: Рефераты по информатике, программированию Тип: дипломная работа |
| Кодирующее устройство для кода Файера | |
|
Министерство общего и профессионального образования РФ Московский энергетический институт (Технический Университет) Филиал в городе Смоленске Кафедра ... Любой групповой (n, k) - код может быть записан в виде матрицы, включающей k линейно-независящих строк по n символов, и, наоборот, любая совокупность k линейно-независящих n ... С помощью схем второго типа вычисляют значения проверочных символов как линейную комбинацию информационных символов, т. е. построены на основе систематических кодов. |
Раздел: Рефераты по коммуникации и связи Тип: реферат |