Дипломная работа: Методика обучения решению текстовых задач алгебраическим способом
Дипломная работа
По теме:
«Методика обучения решению текстовых задач алгебраическим способом»
Содержание
Введение
Глава 1. Научно-методические основы обучения решению текстовых задач
§1. Что такое задача? Что значит решить задачу?
§2. Этапы процесса решения задачи
§3. Решение задач выделением 3-х этапов математического моделирования
Глава 2. Методика обучения построению математических моделей в соответствии с сюжетом задачи
§1. Роль аналитико-синтетических рассуждений в формировании умений решать задачи алгебраическим способом
§2. Система упражнений учебника «Математика» 5-6 класс Зубарева И.И., Мордкович А.Г. по формированию умений составления математических моделей
§3. Задания по формированию умений составления математических моделей
Заключение
Список литературы
Введение
Актуальность выбранной нами темы определяется тем, что далеко не все ученики основной школы осваивают алгебраический метод решения текстовых задач даже на базовом уровне. Причин тому великое множество. Одни из них носят общий характер: устоявшийся страх перед задачей, отсутствие общих представлений о рассматриваемых в задачах процессах, неумение устанавливать, что дано в задаче, что надо найти, выявлять по тексту взаимосвязи рассматриваемых в задаче величин и т.п. Другие свидетельствуют о несформированности определенных умений и навыков: незнание этапов решения задачи, непонимание содержания и цели собственной деятельности на каждом из них, неумение решать уравнения или неравенства (или их системы) определенного вида, неумение производить отбор корней уравнения или решений неравенства в соответствии с условием задачи и т.д. Недостатки в овладении необходимыми приемами рассуждений, незнание общих методов решения задач не дают возможности многим школьникам успешно работать над конкретной задачей.
Следует отметить и недостатки в методике построения различных моделей обучения как на этапе текущего обучения решению текстовых задач, так и на этапе работы с задачами в процессе обобщающего повторения по отдельной теме или по целому курсу. Работая над конкретной задачей в классе, учитель дает пояснения, сущность и значимость которых понимают и запоминают в классе лишь отдельные ученики. Как правило, эти пояснения не систематизированы учителем и носят локальный характер. Учитель не требует записи этих пояснений, их запоминания, что большей частью школьников воспринимается как сигнал: «это не столь важно, это можно забыть». А поэтому опыт этих учеников по решению задач носит неполный и бессистемный характер, а значит и воспользоваться им – дело почти безнадежное.
К субъективным причинам можно отнести влияние индивидуальных особенностей школьников на процесс усвоения материала и формирование необходимых умений. Затрудненное восприятие, плохая память, слабое владение анализом и синтезом, отсутствие достаточного опыта в решении простейших задач оказывают несомненное влияние на освоение такими учениками алгебраического метода решения текстовых задач.
Известно, что решение сюжетной задачи алгебраическим методом состоит в последовательной реализации трех этапов:
- перевод текста задачи на алгебраический язык – составление математической модели данной сюжетной задачи;
- решение полученной математической задачи – внутримодельное решение;
- ответ на вопрос задачи, перевод полученного результата на язык исходной ситуации – интерпретация внутримодельного решения.
Процесс обучения решению текстовых задач в контексте алгебры в основной школе построен так, что сначала школьники осваивают эту деятельность в пределах одной темы, а затем – на этапе обобщения и систематизации в пределах более крупного раздела.
Когда речь идет о решении текстовых задач в пределах одной темы, то сначала осваивается решение определенной математической задачи: решение уравнений определенного вида, системы уравнений, неравенства, системы неравенств или смешанной системы. После рассмотрения решения математической задачи определенного вида, например, решения уравнений второй степени с одной переменной (квадратных уравнений) ученикам предлагается решить ряд текстовых задач, решение каждой из которых сводится к только что изученной математической задаче – к уравнению второй степени с одной переменной. Таким образом, в контексте обучения решению текстовых задач в пределах определенной темы сначала ведется работа над вторым этапом – решением математической задачи (модели текстовой задачи), т.е. над внутримодельным решением. Это служит определенной подсказкой ученику при работе над задачей: у него есть четкий ориентир – вид модели. На этом этапе ученики довольно успешно справляются с решением текстовых задач. Значит, при обучении решению задач в пределах определенной темы акцент в работе над задачей можно и нужно перенести на первый и третий этапы: переводе задачи на математический язык и интерпретации полученного на втором этапе результата. Практика показывает, что существенные затруднения возникают у «средних» и «слабых» школьников именно на первом этапе, хотя и на этапе интерпретации тоже встречаются определенные ошибки, связанные как с невнимательностью, так и с неумением производить отбор решений.
Когда же требуется перенос знаний в новую ситуацию и отсутствует предопределенность вида математической модели, учащиеся часто не справляются с решением даже совсем несложных задач, хотя при работе над темой могли решать и более сложные задачи.
Поскольку наиболее сложным для учащихся является этап составления математической модели (уравнения или системы уравнений) целью исследования стала разработка комплекса упражнений, предназначенных для обучения составлению математических моделей реальных ситуаций, т.е. переводу сюжета задачи на математический язык.
Для достижения указанной цели необходимо решить следующие задачи:
1) проанализировать психолого-педагогическую литературу по данной теме;
2) изучить педагогический опыт учителей по данному вопросу;
3) изучить научно-методическую литературу, направленную на обучение решению текстовых задач;
4) разработать требования к упражнениям, подводящим к составлению математической модели ситуации, описываемой в задаче;
5) разработать комплекс упражнений, направленных на обучение составлению математический моделей.
Глава 1. Научно-методические основы обучения решению текстовых задач
§1. Что такое задача? Что значит решить задачу?
Понятие задачи имеет различные трактовки. Их обстоятельное исследование в психологической литературе было проведено Г.А. Баллом [1]. Термин «задача», отмечает Г.А. Балл, употребляется для обозначения объектов, относящихся к трем различным категориям:
1) к категории цели действий субъекта, требования, поставленного перед субъектом;
2) к категории ситуации, включающей, наряду с целью, условия, в которых она должна быть достигнута;
3) к категории словесной формулировки этой ситуации.
Г.А Балл отмечает, что в психологической литературе наиболее распространено употребление термина «задача» для обозначения объектов второй категории. Для объектов первой категории, Указывает Г.А. Балл, вполне подходит выражение «цель действия», «требование задачи», а для объектов третьей категории – «формулировка задачи».
Сторонники трактовки задачи как ситуации, в которой должен действовать субъект, явно включают субъекта в само понятие задачи. В методике обучения математике подобное толкование задачи особенно характерно для работ Ю.М. Колягина [11]. Без субъекта, отмечает он, нет задачи. То, что для одних является задачей, для других может ею не быть.
Сторонниками другой трактовки задачи субъект не включается в понятие задачи. Наиболее четко и последовательно эта точка зрения реализуется в работах Л.М. Фридмана, который определяет задачу как модель проблемной ситуации, выраженную с помощью знаков некоторого естественного или искусственного языка [21,24]. Проблемная ситуация, отмечает Фридман, возникает тогда, когда субъект в своей деятельности, направленной на некий объект, встречает какое-то затруднение, преграду. Однако проблемная ситуация – это не просто затруднение, преграда в деятельности субъекта, а осознанное субъектом затруднение, способ устранения которого он желает найти. Таким образом, в понятие проблемной ситуации Л.М. Фридман включает субъект. Значит, задача есть модель ситуации, элементом которой является субъект, осознавший затруднение в своей деятельности. Отсюда следует, что возникновение задачи обязано деятельности субъекта. Другими словами, Л.М. Фридман наделил понятие задачи «субъективными генами» [21, 24]. Заметим, что различные авторы по-разному подходят к соотношению понятий «задача» и «проблемная ситуация». Одни (Л.М. Фридман) считают первичным понятие проблемной ситуации [24], причем некоторые психологи считают субъекта элементом проблемной ситуации. Другие (С.Л. Рубинштейн) под проблемной ситуацией понимают некоторую объективную ситуацию, в которой берет начало процесс мышления [21]. Задача, по Рубинштейну, есть результат того, что проблемная ситуация, содержащая какие-то нераскрытые звенья, подвергается анализу со стороны человека. То есть, субъект рассматривается как элемент задачи. Существует и противоположная точка зрения, при которой первичным считается понятие задачи, а вторичным – понятие проблемной ситуации. Проблемная ситуация оценивается как фактор, рассматриваемый в отношении субъекта, тогда как задача признается существующей объективно.
Наиболее распространенным является использование термина «задача» для обозначения ситуации, включающей цель и условия ее достижения. Для понятия задачи характерны две стороны: объективная и субъективная. К первой относятся предмет действия, требование, место в системе задач, логическая структура решения задачи, определенность или неопределенность или неопределенность условия и т.д., ко второй – способы и средства решения.
В методике обучения математике многие годы была распространена классификация, основу которой составлял характер требования: а) задачи на доказательство; б) задачи на построение; в) задачи на вычисление. Длительный успех этой классификации обеспечивало то, что она в какой-то степени предопределяла метод решения каждого типа задач. В связи с расширением целей обучения и роли задач в их обеспечении в школьный курс математики начали проникать задачи, не укладывающиеся в традиционную типологию. Функции задач в обучении подчеркиваются в следующей классификации: а) задачи с дидактическими функциями; б) задачи с познавательными функциями; в) задачи с развивающими функциями (К.И. Нешков и А.Д. Семушкин). Данная классификация позволяет обоснованно осуществлять отбор задач, хотя на практике довольно трудно отделить друг от друга указанные типы задач. Задачи с дидактическими функциями предназначены для усвоения теоретического материала, в процессе решения второго типа задач учащиеся углубляют теорию и методы решения задач, задачи третьего типа характеризуют то, что их содержание может отходить от основного курса. Соглашаясь с авторами в целесообразности широкого использования задач в обучении, нельзя согласиться с тем, что развивающие функции присущи только задачам, содержание которых отходит от обязательного курса, расширяя его. Отметим, что указанная публикация является первой теоретической работой, в которой исследуются функции задачи (1971г)
В последнее время получила распространение типология задач, в которой каждый тип задач соотносится с компонентами учебной деятельности: организационно-действенным, стимулирующим и контрольно-оценочным. Указанное сопоставление выделяет следующие типы задач:
1) задачи, стимулирующие учебно-познавательную деятельность;
2) задачи, организующие и осуществляющие учебно-познавательную деятельность школьников;
3) задачи, в процессе решения которых осуществляется контроль и самоконтроль эффективности учебно-познавательной деятельности.
В зависимости от конкретизации учебной деятельности классификация будет наполняться более конкретным содержанием:
1) задачи, стимулирующие усвоение знаний, умений и навыков;
2) задачи, в процессе решения которых осуществляется усвоение знаний, умений и навыков;
3) задачи, контролирующие усвоение знаний, умений и навыков.
Теперь мы немножко поговорим о методике обучения решению математических задач. Методика решения задач впервые в достаточно общем виде была разработана Д. Пойа и представлена в известной книге «Как решать задачу?». Автор выделяет в решение задачи четыре этапа:
1) понимание постановки задачи;
2) составление плана решения;
3) осуществление плана;
4) взгляд назад (изучение и анализ плана решения).
Итак, методика обучения решению задач предполагает выделение спектра умений решать задачи. Первый этап составляют действия: выделение условия и требования задачи, объектов и отношений между ними, выполнение рисунка, отметка на нем данных и искомых элементов, краткая запись условия и заключения задачи. Содержание этого этапа решения, как правило, реализуется на практике. Второй этап включает в себя анализ условия и требования задачи. Под анализом условия задачи будем понимать выявление такой информации, которая непосредственно не задана условием, но присуща ему. Анализ требования задачи предполагает выяснение возможных путей ответа на вопрос задачи. Информация, являющаяся результатом анализа условия задачи, может быть получена следующими способами:
1) выведением следствий непосредственно из условия задачи;
2) переосмысливанием объектов (фигур, отношений между ними) с точки зрения других понятий;
3) заменой термина его определением;
4) использованием характеристических свойств понятия;
5) интерпретацией символических записей;
6) переводом содержания задачи на язык специальной теории и наоборот.
Важнейшим компонентом умения анализировать требование задачи является умение преобразовывать требование задачи в равносильное ему. Проблема формирования этого умения непосредственно связана с вооружением учащихся как можно большим числом признаков и свойств понятий. Выполнение анализа требования задачи предполагает наличие ассоциаций: осознание термина, обозначающего понятие, – осознание определения этого понятия и термина, обозначающего понятие, – осознание его характеристических свойств. Важными компонентами анализа требования задач является умение составлять вспомогательные задачи и умение видеть различные пути решения задачи.
Обобщая все то, что было сказано выше, отметим, что обучение решению задач включает формирование умений школьников выполнять действия, адекватные поиску способа решения задачи.
Следующий этап – осуществление плана решения – Д. Пойа характеризует так: осуществляя план решения, контролируйте каждый свой шаг. Особое значение имеет четвертый этап – взгляд назад. Его особенность обусловлена тем, что он является хорошим полигоном для развития творческой инициативы учащихся, самостоятельности их мышления. Несмотря на большие возможности этого этапа в развитии ученика, он почти не используется учителями на практике. Решение задачи, как правило, заканчивается получением ответа или, в лучшем случае, обсуждением базиса и идеи решения. Между тем реализация этого этапа должна включать, кроме изучения полученного решения, составление задач – аналогов данной, задачи-обобщения, задачи-конкретизации, задач, решаемых тем же способом, что и основная задача, поиск различных способов решения данной задачи, их оценку, выбор наиболее простого. Исследование задачной ситуации может осуществляться со стороны: а) способа поиска решения задачи; б) способа развития ученика; в) способа систематизации знаний. Каждое из указанных направлений будет служить основой составления новых задач. Учитывая сказанное, можно заключить, что сущность рассматриваемого этапа заключается не столько «во взгляде назад», сколько «во взгляде вперед».
В своих работах Фридман Л.М.[1] отмечал, решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Если приглядеться к любой задаче, то увидим, что она представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче. Поэтому, приступая к решению какой-либо задачи, надо ее внимательно изучить, установить, в чем состоят ее требования (вопросы), каковы условия, исходя из которых, надо решать задачу. Все это называется анализом задачи.
Получив задачу, мы сначала внимательно ее читаем. Первое, что можно заметить при чтении любой задачи, это то, что в ней есть определенные утверждения и требования. Часто требование формулируется в виде вопроса. Но всякий вопрос предполагает требование найти ответ на этот вопрос, а поэтому всякий вопрос можно заменить требованием. Как мы знаем из любой задачи, что формулировка состоит из нескольких утверждений и требований. Утверждения задачи называются условиями задачи.
Отсюда ясно, что первое, что нужно сделать при анализе задачи, - это расчленить формулировку задачи на условия и требования. Будем иметь в виду, что в задаче обычно не одно условие, а несколько независимых элементарных условий, требований в задаче также может быть не одно. Поэтому необходимо расчленить все утверждения и требования задачи на отдельные элементарные условия и требования. Но, производя анализ задачи, вычленяя из формулировки задачи ее условия, мы все время должны соотносить этот анализ с требованием задачи, как бы постоянно оглядываться на требование. Иными словами, анализ задачи всегда направлен на требования задачи. Анализируя условия задач, можно заметить, что каждое из них состоит из одного или нескольких объектов и некоторой их характеристики. Если в условии один объект, то указывается его характеристика в виде некоторого свойства этого объекта; если же объектов два, то характеристикой служит некоторое отношение этих объектов. После того, как задача проанализирована, ее условие надо как-то записать. Но записывать ее словесно, описательно малоудобно, так как это займет много места и времени. Поэтому надо найти более удобную, более компактную и в то же время достаточно наглядную форму записи результатов анализа задач. Такой формой является схематическая запись задачи.
Заметим, что не для всякой задачи надо делать схематическую запись. Так, например, для задач по решению уравнений, неравенств, преобразований выражений анализ проводится обычно устно и никак не оформляется. Вообще для задач, которые записаны на символическом языке, схематическая запись не нужна.
Первой отличительной особенностью схематической записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей и т.д. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематической записи фиксируется лишь только то, что необходимо для решения задачи; Все другие подробности, имеющиеся в задаче, при схематической записи отбрасываются.
Для схематической записи геометрической и некоторых других задач полезно использовать чертеж той фигуры, которая рассматривается в задаче.
Задачи, которые решаются в школе, различаются в первую очередь характером своих объектов. В одних задачах объектами являются реальные предметы, в других – все объекты математические (числа, геометрические фигуры, функции и т.д.). Первые задачи, в которых хотя бы один объект есть реальный предмет, называются текстовыми (практическими, житейскими, сюжетными), вторые, все объекты которых математические, называются математическими задачами.
В связи с тем, что нашей темой является рассмотрение текстовых задач, мы будем рассматривать именно их.
В следующем примере мы произведем анализ задачи, вычленяя из формулировки задачи ее условия, и соотнесем этот анализ с требованиями задачи.
Задача.
Катер прошел 20 км по течению реки и 20 км против течения реки. Затратит ли он на весь путь больше времени, чем ему требуется на прохождение 40 км в стоячей воде, меньше или столько же?
Первичный анализ этой задачи позволяет вычленить такие условия:
1) катер прошел 20 км по течению реки;
2) он прошел 20 км против течения реки;
3) он же прошел 40 км в стоячей воде.
Но, сопоставив эти условия с требованием задачи: узнать больше, меньше или столько же времени затратил катер на первый и второй пути вместе по сравнению с третьим, мы обнаруживаем недостаточность произведенного анализа. Эта недостаточность проявляется хотя бы в том, что в условиях ничего не говориться о времени, а требование задачи сводится к сравнению промежутков времени. Поэтому нужно продолжить анализ. Для этого вдумаемся в требование задачи. Надо сравнить время движения катера в стоячей воде. От чего зависит это время? Очевидно, от собственной скорости катера, от скорости течения реки и, конечно, пройденных расстояний. Но если пройденное расстояние в формулировке задачи даны, то скорости катера и реки даже не упоминаются. Как же быть? В таких случаях эти величины, без которых решение задачи невозможно, принимаются за неопределенные параметры. Положим, например, что собственная скорость катера равна v км/ч, а скорость течения реки a км/ч. Теперь мы можем вычленить такие условия:
1) собственная скорость катера v км/ч;
2) скорость течения реки a км/ч;
3) катер проплыл 20 км по течению реки;
4) он же проплыл 20 км против течения реки;
5) на весь путь туда и
обратно по реке катер затратил ![]() ч;
ч;
6) в стоячей воде катер проплыл 40 км;
7) на этот путь он
затратил ![]() ч;
ч;
Требование задачи:
сравнить ![]() и
и
![]() ч, и
установить, равны ли они или нет, а если нет, то, что больше.
ч, и
установить, равны ли они или нет, а если нет, то, что больше.
Следующий пример приведем для того, чтобы рассмотреть схематическую запись задачи, которая является очень важным этапом в решение задач, во-первых она наиболее краткая из-зи использования в ней различных обозначений, символов, чертежей и др., во-вторых в ней наиболее четко выделены все условия и требования, и в-третьих в схематической записи фиксируется только то, что требуется для решения, все остальное отбрасывается.
Задача.
С одного участка 1440 ц. пшеницы, а с другого, площадь которого на 12 га меньше, - 1080 ц. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором.
Анализ задачи
показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при
этом этот сбор характеризуется тремя величинами: массой собранной пшеницы,
площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу
для схематической записи условий и требований задачи. Неизвестные величины,
встречающиеся в задаче, запишем в таблице буквами, притом искомое обозначим
буквой ![]() :
:
| участки | Масса собранной пшеницы, ц | Урожай с 1 га, ц | Площадь участка , га |
| первый | 1440 | а+2 | х |
| второй | 1080 | а | х-12 |
В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти площадь первого участка. В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задачи.
Задачи, которые были приведены выше – практические задачи, т.е. задачи в которых объектами являются реальные предметы, их еще называют житейские, текстовые, сюжетные. Приведем пример еще одной такой задачи.
Задача.
Телефонная проволока длиной 15 м протянута от столба, где она прикреплена на высоте 8 м от поверхности земли, к дому, где ее прикрепили на высоте 20 м. Найти расстояние между домом и столбом, если проволока не провисает
Объектами этой задачи являются вполне реальные предметы: проволока, столб, дом. Поэтому это практическая задача. Чтобы ее решить с помощью математики, надо построить соответствующую ей математическую задачу, которая получается путем отвлечения от конкретных особенностей реальных предметов и заменой их математическими объектами. В данном случае проволоку, столб и дом (точнее стену дома) можно рассматривать как отрезки. Считая, что поверхность земли есть прямая, а отрезки, изображающие столб и дом, перпендикулярны к этой прямой, получаем такую математическую задачу.
Отрезки длиной 8 м и 20 м перпендикулярны к прямой, соединяющей их концы, и расположены по одну сторону от этой прямой. Отрезок, соединяющий другие концы этих отрезков, имеет длину 15 м. Найти расстояние между отрезками.
Мы рассмотрели составные части задачи, то, как надо производить анализ задач. Теперь рассмотрим сущность решения задачи, структуру процесса ее решения. Но сначала, ответим на вопрос, что значит решить математическую задачу. Решить математическую задачу, это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется в задаче.
§2. Этапы процесса решения задачи
Если под процессом решения задач понимать процесс, начинающийся с момента получения задачи до момента полного завершения ее решения, то очевидно, что этот процесс состоит не только из изложений уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.
Из каких же этапов состоит процесс решения задачи?
Очевидно, получив задачу, первое, что нужно сделать, это разобраться в том, что это за задача, каковы ее условия, в чем состоят ее требования, т.е. провести анализ задачи. Этот анализ и составляет первый этап процесса решения задачи.
В ряде случаев этот анализ надо как-то оформить, записать. Для этого используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения.
Анализ задачи и построение ее схематической записи необходимы главным образом для того, чтобы найти способ решения данной задачи. Поиск этого способа составляет третий этап процесса решения.
Когда способ решения задачи найден, его нужно осуществить, - это будет четвертый этап процесса решения – этап осуществления (изложения) решения.
После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.
При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом, сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д. Все это составляет шестой этап процесса решения.
Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи, - это будет седьмой этап процесса решения.
Наконец, в учебных и познавательных целях полезно также произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т.д. Все это составляет последний, конечно не обязательный, восьмой этап решения.
Итак, весь процесс решения задачи можно разделить на восемь этапов:
1 этап – анализ задачи;
2 этап – схематическая запись задачи;
3 этап – поиск способа решения задачи;
4 этап – осуществление решения задачи;
5 этап – проверка решения задачи;
6 этап – исследование задачи;
7 этап – формулирование ответа задачи;
8 этап – анализ решения задачи.
Приведенная схема дает лишь общее представление о процессе решения задачи, поэтому приведем пример решения задачи.
Задача.
Лодка прошла по течению реки расстояние между двумя пристанями за 6 часов, а обратный путь она совершила за 8 часов. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки?
1. Анализ задачи. В задаче речь идет о двух объектах: лодка и плот. Лодка имеет какую-то собственную скорость, а река, по которой плывут и лодка, и плот, имеет определенную скорость течения. Именно поэтому лодка совершает путь между пристанями по течению реки за меньшее время (6ч), чем против течения (8ч). Но эти скорости (собственная скорость лодки и скорость течения реки) в задаче не даны (они неизвестны), так же как неизвестно расстояние между пристанями. Однако требуется найти не эти неизвестные скорости и расстояние, а время, за которое плот проплывет неизвестное расстояние между пристанями.
2. Схематическая запись задачи.
|
А В |
|
8 ч |
3. Поиск способа
решения задачи. Нужно найти время, за которое плот проплывет расстояние между
пристанями А и В. Для того чтобы найти это время, надо знать расстояние АВ и
скорость течения реки. Оба они известны, поэтому обозначим расстояние АВ буквой
![]() (км), а
скорость течения реки примем равной
(км), а
скорость течения реки примем равной ![]() км/ч. Чтобы связать эти
неизвестные с данными задачи (время движения лодки по и против течения реки),
нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что
она равна
км/ч. Чтобы связать эти
неизвестные с данными задачи (время движения лодки по и против течения реки),
нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что
она равна ![]() км/ч.
Отсюда естественно возникает план решения, заключающийся в том, чтобы составить
систему уравнений относительно введенных неизвестных.
км/ч.
Отсюда естественно возникает план решения, заключающийся в том, чтобы составить
систему уравнений относительно введенных неизвестных.
4. Осуществление
решения задачи. Итак, пусть расстояние АВ равно s км,
скорость течения реки ![]() км/ч, собственная скорость лодки
км/ч, собственная скорость лодки ![]() км/ч, а
искомое время движения плота на пути в
км/ч, а
искомое время движения плота на пути в ![]() км равно
км равно ![]() часов.
часов.
Тогда скорость лодки по
течению реки равна ![]() км/ч. За 6 ч лодка, идя с этой
скоростью, прошла путь АВ в
км/ч. За 6 ч лодка, идя с этой
скоростью, прошла путь АВ в ![]() км. Следовательно.
км. Следовательно.
![]() (1)
(1)
Против течения эта
лодка идет со скоростью ![]() км/ч и путь АВ в
км/ч и путь АВ в ![]() км она проходит за 8 ч,
поэтому
км она проходит за 8 ч,
поэтому
![]() (2)
(2)
Наконец, плот, двигаясь
со скоростью ![]() км/ч, покрыл расстояние
км/ч, покрыл расстояние ![]() км за
км за ![]() ч,
следовательно,
ч,
следовательно,
![]() (3)
(3)
Уравнения (1), (2) и
(3) образуют систему уравнений относительно неизвестных ![]() и
и ![]() . Так как требуется
найти лишь
. Так как требуется
найти лишь![]() ,
то остальные неизвестные постараемся исключить.
,
то остальные неизвестные постараемся исключить.
Для этого из уравнений (1) и (2) найдем
![]() .
.
Вычитая из первого уравнения второе, получим:
решение задача текстовый алгебраический
![]() , отсюда
, отсюда ![]() .
.
Поставим найденное
выражение для ![]() в уравнение (3)
в уравнение (3)
![]() .
.
Так как, очевидно, ![]() не равно нулю,
то можно обе части полученного уравнения разделить на
не равно нулю,
то можно обе части полученного уравнения разделить на ![]() . Тогда найдем:
. Тогда найдем: ![]() .
.
5. Проверка решения.
Итак, мы нашли, что плот проплывает расстояние между пристанями за 48 ч.
Следовательно, его скорость, равная скорости течения реки, равна ![]() км/ч. Скорость же лодки
по течению равна
км/ч. Скорость же лодки
по течению равна ![]() км/ч, а против течения
км/ч, а против течения ![]() км/ч. Для того
чтобы убедиться в правильности решения, достаточно проверить, будут ли равны
собственные скорости лодки, найденные двумя способами:
км/ч. Для того
чтобы убедиться в правильности решения, достаточно проверить, будут ли равны
собственные скорости лодки, найденные двумя способами:
1) от скорости лодки по
течению отнять скорость течения реки, т.е. ![]() ,
,
2) к скорости лодки
против течения реки прибавить скорость течения реки, т.е. ![]() .
.
Произведя вычисления,
получаем верное равенство: ![]() .
.
Значит, задача решена правильно.
6. Исследование задачи. В данном случае этот этап решения не нужен.
7. Ответ: плот проплывет расстояние между пристанями за 48 ч.
8. Анализ решения. Мы свели решение этой задачи к решению системы трех уравнений с четырьмя неизвестными. Однако найти-то надо было нам лишь одно из этих неизвестных. Поэтому, естественно, возникает мысль, что проведенное решение не самое удачное, хотя и достаточно простое. Можно предложить другое решение.
Зная, что лодка
проплыла расстояние АВ по течению реки за 6 ч, а против – за 8 ч, найдем, что в
1 ч лодка, идя по течению, проходит ![]() часть этого расстояния, а против
течения
часть этого расстояния, а против
течения ![]() .
Тогда разность между ними
.
Тогда разность между ними ![]() есть удвоенная часть расстояния
АВ, проплываемая плотом за 1 ч. Значит, плот за 1 ч проплывет
есть удвоенная часть расстояния
АВ, проплываемая плотом за 1 ч. Значит, плот за 1 ч проплывет ![]() часть расстояния АВ,
следовательно, все расстояние АВ он проплывет за 48 ч.
часть расстояния АВ,
следовательно, все расстояние АВ он проплывет за 48 ч.
Как видим, при таком решении нам не понадобилось составлять систему уравнений. Однако, несомненно, это решение сложнее приведенного выше, хотя бы потому, что не всякий догадается найти разность скоростей лодки по течению и против течения реки. Часто также эту разность принимают не за удвоенную часть расстояния АВ, проплываемую плотом за 1 ч, а за скорость плота, что, конечно, приводит к ошибочному результату.
Как мы уже знаем, решение задачи состоит из последовательности шагов (действий). Поэтому отыскание этой последовательности шагов есть самое главное, что нужно сделать для того, чтобы решить задачу.
Вот этим и занимается математика, установлением для многих видов задач правил, пользуясь которыми можно найти указанную последовательность шагов для решения любой задачи.
Приведем некоторые такие правила.
1. Словесное правило. Примером такого правила может служить правило нахождения степени произведения, которое изучается в 6 классе: степень произведения равна произведению степеней сомножителей.
Это правило позволяет составить такую последовательность шагов: 1) установить все сомножители произведения; 2) найти данную степень каждого из этих сомножителей; 3) результаты второго шага перемножить.
2. Правило-формула.
Примером такого правила служит формула корней квадратного уравнения. В курсе
алгебры 7 класса эта формула дается в таком виде: корни уравнения ![]() , если
, если ![]() и
и ![]() , где
, где ![]() , можно
вычислить по формуле
, можно
вычислить по формуле ![]() .
.
В этом правиле легко
указать последовательность шагов на основе указанного правила-формулы:
1)проверим условие: ![]() ; 3) находим:
; 3) находим: ![]() ; 3) проверяем условие
; 3) проверяем условие ![]() ; если эти
условия выполнены, то вычисляем корни по формуле
; если эти
условия выполнены, то вычисляем корни по формуле ![]() .
.
3. Правило-тождество.
Примером такого правила может служить тождество квадрата двучлена, которое
изучается в 6 классе: ![]() .
.
Словесная формулировка этого тождество такова: квадрат двучлена равен сумме квадрата первого члена на удвоенное произведение первого и второго членов и квадрата второго члена.
В соответствии с этим тождеством можно составить такую последовательность шагов: 1) найти первый член двучлена; 2) найти второй член двучлена; 3) возвести первый член в квадрат; 4) возвести второй член двучлена в квадрат; 5) составить произведение первого и второго членов двучлена; 6) результат пятого шага удвоить; 7) результаты 3, 4, и 6-го шагов сложить.
4. Правило-теорема. Многие теоремы могут служить правилами для решения задач соответствующего вида. Например, теорема: средняя линия трапеции параллельна ее основаниям, и длина ее равна полусумме длин оснований, изучается в курсе геометрии в 7классе. Последовательность шагов очень простая: 1) устанавливаем длину основания трапеции; 2) находим их полусумму. Это и будет длина средней линии.
5. Правило-определение. Иногда основой для правила решений задач некоторого вида может служить определение соответствующего понятия. Например определение решения систем неравенств с одной переменной. Это определение дано в учебнике алгебры 7 класса в таком виде: решением систем неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Последовательность шагов к данному правилу будет такова: 1) решить каждое из неравенств системы, получим для каждого неравенства числовой промежуток – его решение; 2) найти пересечение полученных числовых промежутков. Найденное пересечение и будет решением системы неравенств.
Математические задачи, для решения которых в школьном курсе математики имеются готовые правила или эти правила непосредственно следуют из каких-либо определений или теорем, определяющих программу решения этих задач в виде последовательности шагов, назовем стандартными. При этом предполагается, что для выполнения отдельных шагов решения стандартных задач в курсе математики также имеются вполне определенные правила.
Что такое стандартная задача понятно, но если есть стандартная, значит, есть и нестандартная. Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения.
Задача.
Расстояние от реки до турбазы туристы рассчитывали пройти за 6 ч. Однако после 2 ч пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 минут. С какой скоростью шли туристы первоначально?
Решение. Эта задача является текстовой. Для подобных задач никакого общего правила, определяющего точную программу их решения, не существует. Однако общие указания для решения таких задач есть.
Обозначим искомую
первоначальную скорость туристов через ![]() км/ч. Тогда за 6 ч, за которые
они рассчитывали пройти расстояние от реки до турбазы, они прошли
км/ч. Тогда за 6 ч, за которые
они рассчитывали пройти расстояние от реки до турбазы, они прошли ![]() км. Фактически
этот путь они прошли следующим образом: 2 ч они шли с первоначальной скоростью,
а затем еще 4,5 ч (т.к. они опоздали на 0,5 ч к сроку) – с уменьшением скорости
км. Фактически
этот путь они прошли следующим образом: 2 ч они шли с первоначальной скоростью,
а затем еще 4,5 ч (т.к. они опоздали на 0,5 ч к сроку) – с уменьшением скорости
![]() км/ч.
Следовательно, они прошли
км/ч.
Следовательно, они прошли ![]() км и
км и ![]() км, а всего
км, а всего ![]() км, что равно
расстоянию от реки до турбазы, т.е.
км, что равно
расстоянию от реки до турбазы, т.е. ![]() км. Получаем уравнение:
км. Получаем уравнение: ![]() .
.
Решив это уравнение,
найдем: ![]() Значит,
первоначальная скорость туристов равна 4,5 км/ч.
Значит,
первоначальная скорость туристов равна 4,5 км/ч.
Итак, процесс решения нестандартной задачи состоит в последовательном применение двух основных операций:
1) сведение нестандартной задачи к другой ей эквивалентной, но уже стандартной задаче;
2) разбиение нестандартной задачи на несколько стандартных подзадач.
В зависимости от характера нестандартной задачи мы используем либо одну из этих операций, либо обе. При решении более сложных задач эти операции приходиться использовать многократно.
Существуют различные методы решения текстовых задач [6]: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей. Например при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом – строятся диаграммы ил графики. Решение задачи логическим методом начинается с составления алгоритма. Различные методы решения конкретной задачи будем называть способами решения.
Арифметический метод. Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.
Пример. Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем то одним?
Решение.
1 способ.
1) 82+32+78=192 чел. – удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192÷2=96 чел. – поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96_32=64 чел. – поют в хоре;
4) 96-78=18 чел. – занимаются танцами;
5) 96-82=14 чел. – занимаются художественной гимнастикой.
2 способ.
1) 82-32=50 чел. – на столько больше студентов поют в хоре, чем занимаются художественной гимнастикой;
2) 50+78=128 чел. – удвоенное число студентов поющих в хоре;
3) 128÷2=64 чел. – поют в хоре;
4) 78-64=14 чел. – занимаются художественной гимнастикой;
5) 82-64=18 чел. – занимаются танцами.
Ответ: 64 студента поют в хоре; 14 студентов занимаются художественной гимнастикой; 18 студентов занимаются танцами.
Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Одну и ту же задачу можно также решить различными алгебраическими способами, если для ее решения составлены различные уравнения или системы уравнений, в основе составления которых лежат различные соотношения меду данными и искомыми.
Пример. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справиться с заданием за 2 дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?
Решение.
1 способ. Пустьx д./день – первоначальная производительность рабочего. Тогда (x+10) д./день – новая производительность, 3x д. – число деталей, которые он должен сделать. По условию получаем уравнение 3x=2(+10), решив, которое найдем x=20. Первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.
2 способ. Пусть x д. – число деталей, которое должен сделать рабочий. Тогда x/2 д./день – новая производительность, (x/2-10) д./день – первоначальная производительность рабочего. По условию получаем уравнение x=3(x/2-10), решив которое найдем x=60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.
Ответ: 20 деталей в день, 60 деталей.
Геометрический метод. Решить задачу геометрическим методом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами. Задача считается решенной различными способами, если для ее построения используются различные построения или свойства фигур.
Логический метод. Решить задачу логическим методом – это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения. Примерами таких задач могут служить задачи «на переправы», классическим представителем которых является задаче о волке, козе и капусте, или задачи «на взвешивание».
Практический метод. решить задачу практическим методом – значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т.д.)
Т.к. тема нашей курсовой решение текстовых задач алгебраическим способом, именно его рассмотрим более подробно.
Алгебраический метод решения задачи позволяет легко показать, что некоторые задачи, отличаются друг от друга лишь фабулой, имеют не только одни и те же соотношения между данными и искомыми величинами, но и приводят к типичным рассуждениям, посредством которых устанавливаются эти соотношения. Такие задачи дают лишь различные конкретные интерпретации одного и того математического рассуждения, одних и тех же соотношений, т.е. имеют одну и туже математическую модель.
Рассмотрим классификацию задач решаемых алгебраическим способом по фабуле, из-за многообразия уравнений и неравенств [6].
Задачи на движение
К этой группе задач относятся задачи, в которых говорится о трех величинах: пути, скорости и времени. Как правило, в них речь идет о равномерном прямолинейном движении. В этих задачах весьма полезно делать иллюстрированный чертеж, который помогает в составлении уравнений и неравенств.
Данную группу задач, можно разбить на задачи, в которых рассматриваются движения тел: 1) навстречу друг другу, 2) в одном направлении(«вдогонку»), 3) в противоположных направлениях, 4) по замкнутой траектории, 5) по течению реки.
Задачи на работу.
К этой группе задач относятся задачи, в которых говорится о трех величинах: работе, времени, в течение которого производится работа, производительности – работе, произведенной в единицу времени. К задачам на работу относят и задачи, связанные с наполнением и опорожнением резервуаров с помощью труб, насосов и других приспособлений. В качестве произведенной работы в этом случае рассматривают объем перекачанной воды.
Задачи на работу можно отнести к группе задач на движение, т.к. в задачах такого типа можно считать, что вся работа или полный объем резервуара играют роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения. Однако по сюжету, фабуле эти задачи совершенно отличаются.
Задачи на смеси и проценты.
К этой группе задач относятся задачи, в которых речь идет о смешении различных веществ в определенных пропорциях, а также задачи на проценты
Мы рассмотрели некоторые классификации задач, а сейчас мы бы хотели рассмотреть более подробно решение задач с помощью математического моделирования.
§3. Решение задач выделением 3-х этапов математического моделирования
Математики отличаются друг от друга тем, что говорят друг с другом и пишут на особом «математическом языке». Используя математический язык можно составлять математические модели реальных ситуации. В процессе решения задачи выделяются три этапа математического моделирования: 1) составление математической модели, 2) работа с математической моделью, 3) ответ на вопрос задачи. Рассмотрим некоторые примеры, в которых рассматриваются этапы математического моделирования.
Задача.
Турист шел 2 ч пешком из пункта А в пункт В, затем в В он сел на катер, скорость которого в 4 раза больше скорости туриста как пешехода, и ехал на катере 1,5 ч до пункта С. В С он сел на автобус, скорость которого в 2 раза больше скорости катера, и ехал на нем 2 ч до пункта D. С какой скоростью ехал турист на автобусе если известно, что весь его путь от А до D составил 120 км?
Решение.
Первый этап. Составление математической модели.
пусть х км/ч – скорость пешехода. За 2 ч он пройдет 2х км.
Из условия следует, что скорость катера 4х км/ч. За 1,5 ч катер пройдет путь 4х×1,5 км, т.е. 6х км.
Из условия следует, что скорость автобуса равна 2×4х км/ч, 8х км/ч. За 2 ч автобус пройдет 8х×2 км, т.е. 16х км.
Весь путь от А до D равен: 2х+6х+16х, что составляет, по условию, 120 км. Таким образом, 2х+6х+16х=120.
Это математическая модель задачи.
Второй этап. Работа с составленной моделью.
Сложив одночлены 2х, 6х, 16х, получим 24х. Значит, 24х=120, откуда находим х=5.
Третий этап. Ответ на вопрос задачи.
За х мы приняли скорость пешехода, она равна 5 км/ч. Скорость катера в 4 раза больше, т.е. 20 км/ч, а скорость автобуса еще в 2 раза больше, т.е. 40 км/ч.
Ответ: скорость автобуса 40 км/ч.
Задача.
Пункты А, В и С расположены на шоссе друг на другом. Расстояние между А и В равно 16 км. Из В по направлению к С вышел пешеход. Через 2 ч после этого из А по направлению к С выехал велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Через 4 ч после своего выезда велосипедист догнал пешехода в пункте С. Чему равно расстояние от В до С?
Решение.
Первый этап. Составление математической модели.
Пусть х км/ч – скорость пешехода, тогда (х+6) км/ч – скорость велосипедиста.
Расстояние от А до С велосипедист проехал за 4 ч, значит, это расстояние выражается формулой 4(х+6) км; иными словами, АС=4(х+6).
Расстояние от В до С пешеход прошел за 6 ч (ведь до выезда велосипедиста он уже был в пути 2 ч), следовательно, это расстояние выражается формулой 6х км, иными словами, ВС=6х.
По условию мы знаем, что пункты А, В и С следуют друг за другом, поэтому АС-ВС=АВ, т.е. АС-ВС=16. Это основа для составления математической модели задачи. Напомним, что АС=4(х+6), ВС=6х; следовательно,
4(х+6)–6х=16.
Второй этап. Работа с составленной математической моделью.
Для решения уравнения придется, во-первых, умножить одночлен 4 на двучлен х+6, получим 4х+24. Во-вторых, придется из двучлена 4х+24 вычесть одночлен 6х:
4х+24-6х=24-2х.
После этих преобразований уравнение принимает более простой вид:
24-2х=16.
Далее имеем:
-2х=16-24,
-2х=-8,
х=4.
Третий этап. Ответ на вопрос задачи.
Мы получили, что х=4, значит, скорость пешехода 4 км/ч. Но нам нужно найти не это, в задаче требуется найти расстояние от В до С. Мы установили, что ВС=6х, значит, ВС=6×4=24.
Ответ: расстояние от В до С равно 24 км.
Задача.
Лодка плыла по течению реки 3 ч 12 мин, а затем против течения 1,5 ч. Найти собственную скорость лодки, если известно, что скорость течения реки 2 км/ч, а всего лодкой пройден путь 41 км.
Решение.
Первый этап. Составление математической модели.
Пусть х км/ч – собственная скорость лодки, тогда по течению она плывет со скоростью (х+2) км/ч, а против течения – со скоростью (х_2) км/ч.
По течению реки лодка плыла 3ч 12 мин. Поскольку скорость выражена в км/ч, это время надо записать в часах. Имеем: 12 мин=12/60 ч=1/5 ч=0,2 ч. Значит, 3 ч 12 мин=3,2 ч. За это время со скоростью (х+2) км/ч лодкой пройден путь 3,2(х+2) км.
Против течения лодка плыла 1,5 ч. За это время со скоростью (х-2) км/ч лодкой пройден путь 1,5(х-2) км.
По условию весь ее путь составил 41 км. Так как он состоит из пути по течению и пути против течения, то получаем:
3,2(х+2)+1,5(х-2)=41.
Это уравнение – математическая модель задачи.
Второй этап. Работа с составленной математической моделью.
Как всегда, на этом этапе думаем только о том, как решить модель – уравнение, а не о том, откуда эта модель взялась. Выполним в левой части уравнения умножение одночлена 3,2 на двучлен х+2, одночлена 1,5 на двучлен х-2, а затем полученные многочлены сложим:
3,2х+6,4+1,5х-3=41;
4,7х+3,4=41;
4,7х=41-3,4;
4,7х=37,6;
х=8.
Третий этап. Ответ на вопрос задачи.
Спрашивается, чему равна собственная скорость лодки, т.е. чему равен х? Но ответ на этот вопрос уже получен: х=8.
Ответ: собственная скорость лодки 8 км/ч.
Задача.
В седьмом классе в понедельник не пришли в школу одна девочка и пять мальчиков. При этом число девочек в классе оказалось в 2 раза больше числа мальчиков. Во вторник не пришли один мальчик и девять девочек. При этом число мальчиков оказалось в 1,5 раза больше числа девочек. В среду на уроки пришли все ученики. Сколько школьников присутствовало на уроках в среду в седьмом классе?
Решение.
Первый этап. Составление математической модели.
Пусть х – число девочек, у – число мальчиков в седьмом классе.
В понедельник было (х-1) девочек, (у-5) мальчиков. При этом оказалось, что девочек вдвое больше, т.е.
![]() .
.
во вторник было (х-9) девочек, (у-1) мальчиков. При этом оказалось, что мальчиков в 1,5 раза больше, т.е.
![]() .
.
Математическая модель ситуации составлена:
![]()
Второй этап. Работа с составленной математической моделью.
Сначала упростим каждое уравнение системы.
Для первого уравнения имеем:

Для второго уравнения имеем:
![]()
(обе части уравнения умножили на 2); далее,
![]()
Итак, получили следующую систему двух линейных уравнений с двумя переменными:
![]()
Решаем систему методом подстановки. Из первого уравнения системы находим: х=2у-9. Подставим этот результат вместо х во второе уравнение системы находим: х=2у-9. Подставим это результат вместо х во второе уравнение системы. Получим:

Так как х=2у-9, то х=2×13-9=17.
Итак, х=17, у=13 – решение системы.
Третий этап. Ответ на вопрос задачи.
Спрашивается, сколько школьников было в седьмом классе на уроках в среду, когда пришли все ученики. Поскольку х=17, у=13, т.е. в классе было 17 девочек и 13 мальчиков, делаем вывод: всего в классе 17+13=30 учеников.
Ответ: 30 учеников.
Глава 2. Методика обучения построению математических моделей в соответствии с сюжетом задачи
§1. Роль аналитико-синтетических рассуждений в формировании умений решать задачи алгебраическим способом
Многие учителя математики, работая с текстовыми задачами, стремятся в процессе обучения как можно быстрее перейти к решению их алгебраическим способом, не понимая, что решение текстовой задачи арифметическим способом (т.е. по действиям, с постановкой вопросов к каждому действию или с пояснением) учит детей особому способу мышления – синтезу (от данных к искомому), в то время как «алгебраический» способ решения задачи учит анализу (от искомого к данным). Если учесть, что после прохождения курса математики 5-6 класса учащиеся в курсе алгебры основной школы длительное время решают текстовые задачи только алгебраическим способам, т.е. составлением уравнения (или системы уравнений), и тем самым учатся мыслить аналитически, становится ясно, что исключение или сокращение числа текстовых задач, решаемых арифметически из практики обучения в 5-6 классах (и в начальной школе) не только обедняет само обучение математике, но и лишает учащихся разностороннего математического развития. Подчеркнем, что при решении текстовой задачи арифметическим способом на уровне поиска решения идет обучение детей не только синтезу (зная …, можно узнать … ), но и анализу (чтобы узнать …, нужно знать …).
В виду методической значимости заявленной проблемы рассмотрим более подробно в данном параграфе взаимосвязь анализа и синтеза, которая ярко иллюстрируется при решении текстовых задач курса математики 5-6 класса.
В психологии установлено, что полноценное мышление человека формируется только тогда, когда он владеет аналитико-синтетическим способом рассуждений. Всякая составная текстовая задача представляет собой логически связанную последовательность простых задач. Структура этой последовательности и определяет ход решения задачи, ведущего от условия к искомому результату. Трудность решения задачи, которая не является стандартной (задачей с известным ходом решения) и состоит в обнаружении этой последовательности действий. Явно или неявно всякий человек, решающий поставленную задачу использует аналитико-синтетический способ рассуждений.
Проиллюстрируем этот метод рассуждений на примере задачи 5 класса.
Задача. «Из пунктов А и В одновременно навстречу друг другу выехали два автобуса. Первый шел со скоростью 50 км/ч, а второй – 40 км/ч. Их встреча произошла в 20 км от середины пути АВ. Найти расстояние между пунктами А и В.»
Представим условие задачи на схеме:
![]()
![]() 2 автобус – 40
км/ч 1 автобус – 50 км/ч
2 автобус – 40
км/ч 1 автобус – 50 км/ч
| А | В |
20км 20км
1) Проведем рассуждения аналитически, сопровождая их схемой и записью решения.
|
Чтобы узнать расстояние, пройденное автомобилем до встречи, нужно знать скорость их сближения и время сближения. скорость сближения находится действием: 50+40=90 (км/ч) Чтобы узнать время сближения, нужно узнать разницу в пройденном пути и в скоростях движения, из-за которой один путь оказался меньше другого. Оба результата находятся так: 50-40=10 (км/ч), 20+20=40 (км). Теперь нетрудно получить результат: 40÷10=4 (ч), 90×4=360 (км). |
Расстояние АВ
скорость время сближения сближения
разность разность расстояния скорости 20+20=40 50-40=10 |
Решение
Пусть x(км) – расстояние АВ, тогда x/2+20 (км) – расстояние, пройденное 1 автобусов до встречи, а x/2-20 (км) – расстояние, пройденное 2 автобусом до встречи.
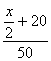 (ч) – время движения 1
автобуса, а
(ч) – время движения 1
автобуса, а 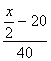 (ч)
– время движения 2 автобуса.
(ч)
– время движения 2 автобуса.
Составляем уравнение:
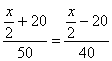
x = 360 (км).
2) Проведем теперь рассуждения синтетически, также сопровождая их схемой и записью решения.
|
Зная скорость движения автомобилей, можно узнать скорость сближения (50+40=90(км/ч)). Зная место встречи, можно узнать на сколько один автомобиль проехал больше другого (20+20=40(км)); зная скорости автомобилей, можно узнать разность скоростей, которая обусловила разность пройденных до встречи путей (50-40=10 (км/ч)). Зная оба различия, можно узнать время сближения – время пути до встречи (40÷10=4(ч)). Зная время сближения и скорость сближения, можно найти путь АВ (90×4=360 (км)). |
скорость разность сближения расстояния 50+40=90 20+20=40 разность скоростей 50-40=10 время сближения 40÷10=4 Расстояние АВ 90×4=360 |
Решение
1) 20+20=40(км),
2) 50-40=10 (км/ч),
3) 40÷10=4(ч),
4) 50+40=90(км/ч),
5) 90×4=360 (км).
Анализ открывает путь решения задачи, а синтез осуществляет это решение. Поэтому анализ иногда называют методом открытия. А синтез методом обоснования. Решая любую текстовую задачу арифметическим способом, ученик (и учитель) обязательно намечают план решения (а это и есть скрытый анализ), и уже затем формулируют первый вопрос (или записывают первое действие). Решение многих текстовых задач методом уравнений, несомненно, легче, чем их решение арифметическим методом. Вместе с тем, следует помнить, что только анализ не имеет доказательной силы и поэтому всегда соседствует с синтезом. Поэтому решение задачи методом уравнений нуждается в смысловой проверке, а выкладки, полученные аналитическим путем (от искомого к данным) нуждаются в синтетическом подтверждении (от данных к искомому).
При работе с текстовыми задачами, необходимо, прежде всего, помнить, что важно не столько решить задачу, сколько научить учащихся решать задачи, догадываться, рассуждать, обосновывать или опровергать свои догадки и уметь проверять полученный результат.
Работа по формированию умений перевода сюжета задачи на математический язык разбивается на несколько этапов.
1 этап. Составление и расшифровка числовых выражений
2 этап. Составление буквенных выражений
3 этап. Расшифровка буквенных выражений в соответствии с данной ситуацией.
4 этап. Составление равенств.
5 этап. Расшифровка равенств.
§2. Система упражнений учебника «Математика» 5-6 класс Зубарева И.И., Мордкович А.Г. по формированию умений составления математических моделей
Для рассмотрения этапов формирования умений перевода сюжета задачи на математический язык проанализируем учебник И.И. Зубаревой, А.Г. Мордковича «Математика, 5 класс».
1 этап. Составление и расшифровка числовых выражений.
§ 2. Числовые и буквенные выражения.
№32
Стоимость батона хлеба - 5р., а стоимость плитки шоколада – 15р. Запишите в виде выражения:
1) на сколько плитка шоколада дороже батона хлеба;
2) Во сколько раз плитка шоколада дороже батона хлеба;
3) стоимость плитки шоколада и батона хлеба вместе;
4) стоимость двух плиток шоколада;
5) стоимость трех батонов хлеба;
6) стоимость двух плиток шоколада и трех батонов хлеба вместе;
7) на сколько две плитки шоколада дороже трех батонов хлеба;
8) во сколько раз две плитки шоколада дороже трех батонов хлеба.
Найдите значения полученных выражений.
Начинаем разбор задачи с вопроса «Что нам известно в задаче?». Известно, что батон хлеба стоит 5 р., а плитка шоколада – 15 р. Мы должны записать выражения и найти их значения. Дети это делать умеют.
1) 15-5=на 10р. плитка шоколада дороже батона хлеба;
2) 15÷5=в 3 раза плитка шоколада дороже батона хлеба;
3) 15+5=20р. стоят батон хлеба и плитка шоколада вместе;
4) 15×2=30р.стоят две плитки шоколада;
5) 5×3=15р. стоят три батона хлеба;
6) 15×2+5×3=45р. стоят 2 плитка шоколада и 3 батона хлеба вместе;
7) 15×2-5×3=на 15р. две плитки шоколада дороже трех батонов хлеба;
8) (15×2)÷(5×3)= в 2 раза две плитки шоколада дороже трех батонов хлеба.
Мы ответили на все вопросы задачи. Нашли значения полученных выражений.
После этой задачи учащимся сообщается: все выражения, которые у вас получились, содержат только числа и знаки действий, такие выражения называются числовыми.
Дальше идет задача №33. Она другая, но при записи решения выясняется, что это то же самое, что и предыдущая задача, только в буквенном варианте.
2 этап. Составление и расшифровка буквенных выражений
№33.
Цена груш - ![]() р. за 1 кг, а
цена моркови -
р. за 1 кг, а
цена моркови - ![]() р. за 1 кг. Запишите в виде
выражения:
р. за 1 кг. Запишите в виде
выражения:
1) на сколько 1 кг груш дороже 1 кг моркови;
2) во сколько раз 1 кг груш дороже, чем 1 кг моркови;
3) стоимость 1 кг груш и 1 кг моркови вместе;
4) стоимость 2 кг груш;
5) стоимость 3 кг моркови;
6) стоимость 2 кг груш и 3 кг моркови вместе;
7) на сколько 2 кг груш дороже 3 кг моркови;
8) во сколько раз 2 кг груш дороже 3 кг моркови.
Чем отличаются эти выражения от тех, которые были получены в предыдущем задании? Как бы вы назвали эти выражения?
В задаче нам известно:
Цена 1 кг груш - ![]() р., цена 1 кг
моркови -
р., цена 1 кг
моркови - ![]() р.
р.
Отличие этой задачи от предыдущей в том, что в задаче №32 были даны числовые значения. В этой задаче даны буквенные значения, получаются такие выражения:
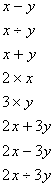
Разбирается с детьми то, что эти выражения отличаются от выражений, полученных в предыдущем задании, тем, что они записываются с помощью букв и можно было бы их назвать буквенными.
Сразу после этой задачи идут выводы о том, что это действительно буквенные выражения. А также о том, что найти значения буквенных выражений можно, зная значения входящих в них букв.
Рассмотрим более сложное задание для 1-го этапа.
№39
Саша и Миша – братья. Саша любит ходить за грибами, а Миша ловить рыбу. Обычно, рано утром из дома они выходят одновременно, но идут в противоположных направлениях. Саша, собирая грибы, идет медленно, со скоростью 2 км/ч, а Миша торопится поскорее дойти до озера и идет быстро, со скоростью 6 км/ч.
Запишите выражения для следующих величин:
1) расстояние между грибником и рыболовом через час после начала движения;
2) скорость, с которой грибник и рыболов удаляются друг от друга;
3) расстояние между грибником и рыболовом через 2 ч после выхода;
4) расстояние, пройденное грибником за 2 ч;
5) расстояние, пройденное рыболовом за 2 ч;
6) на сколько расстояние, пройденное рыболовом за 2 ч, больше расстояния, пройденного за то же время грибником;
7) во сколько раз расстояние, пройденное рыболовом за 2 ч, больше расстояния, пройденного за то же время грибником.
Найдите значения полученных выражений.
Что нам известно?
Саша ходит за грибами, со скоростью 2 км/ч,
Миша ходит ловить рыбу со скоростью 6 км/ч.
1) 6×1-2×1=4 км расстояние между ребятами через 1 ч;
2) 6-2=4 км/ч скорость удаления;
3) 6×2-2×2=8 км расстояние меду ребятами через 2 ч;
4) 2×2=4 км прошел Саша за 2 ч;
5) 6×2=12 км прошел Миша за 2 ч;
6) 12-4= на 8 км расстояние, пройденное Мишей больше расстояния пройденного Сашей.
7) 12÷4= в 3 раза расстояние, пройденное Мишей больше расстояния пройденного Сашей.
Следующий №40 из 2 этапа.
Из одного гаража
одновременно в противоположных направлениях выехали автомобиль и автобус.
Скорость автомобиля - ![]() км/ч, а автобуса -
км/ч, а автобуса - ![]() км/ч, причем автомобиль
едет быстрее, чем автобус.
км/ч, причем автомобиль
едет быстрее, чем автобус.
Запишите в виде выражения:
1) расстояние между автомобилем и автобусом через час после начала движения;
2) скорость, с которой автомобиль и автобус удаляются друг от друга;
3) расстояние между автомобилем и автобусом через 2 ч после начала движения;
4) расстояние, которое прошел автомобиль за 2 ч;
5) расстояние, которое прошел автобус за 2 ч;
6) на сколько расстояние, пройденное автомобилем за 2 ч, больше расстояния, пройденного за то же время автобусом;
7) во сколько раз расстояние пройденное автомобилем за 2 ч, больше расстояния , пройденного за то же время автобусом.
Нам известно, что
скорость автомобиля - ![]() км/ч, а автобуса -
км/ч, а автобуса - ![]() км/ч.
км/ч.
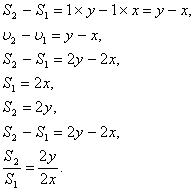
Сравнивая №39 и №40
понимаем, что выражения с 1 по 7 получились одинаковые, только в №39 числовые
выражения, а в №40 буквенные выражения. И если заменить скорости Миши и Саши на
буквенные обозначения ![]() и
и ![]() , то выражения станут одинаковыми.
, то выражения станут одинаковыми.
№49
Какое число больше, a или b, если:
а)![]() b;
b;
б) ![]() a;
a;
в)![]() b;
b;
г)![]() a.
a.
№50
Какое число больше, ![]() или
или ![]() , если:
, если:
а) ![]() m
m
б) ![]() m
m
в) ![]() n
n
г) ![]() n
n
№51
а) число m на 8 больше числа n: m-8=n;
б) число a в четыре раза больше числа b: 4×b=a;
в) число c на 3 меньше числа d: d-3=c;
г) число e в шесть раз меньше числа g: 6×e=g.
Постепенно ситуация усложняется.
№60. Движение навстречу (числовые выражения)
Из пунктов А и В, расстояние между которыми 260 км, одновременно навстречу друг другу выехали велосипедист и мотоциклист. Скорость велосипедиста – 13 км/ч, а мотоциклиста – 52 км/ч.
Запишите в виде выражения:
1) на сколько скорость велосипедиста меньше скорости мотоциклиста: 52-13= на 29 км/ч скорость велосипедиста меньше скорости мотоциклиста;
2) во сколько раз скорость велосипедиста меньше скорости мотоциклиста: 52÷13= в 4 раза скорость велосипедиста меньше скорости мотоциклиста;
3) время, которое потребуется велосипедисту на весь путь из А в В: 260÷13=20 часов потребуется велосипедисту на весь путь;
4) время, которое потребуется мотоциклисту на весь путь из А в В: 260÷52=5 часов потребуется на весь путь мотоциклисту;
5)на сколько меньше времени потребуется на весь путь мотоциклисту, чем велосипедисту: 20-5=на 15 часов меньше потребуется мотоциклисту, чем велосипедисту;
6)во сколько раз меньше времени потребуется на весь путь М., чем В.: 20÷5=в 4 раза меньше времени потребуется М., чем В.
7) скорость сближения В. и М.: 13+52=65 км/ч;
8) через какое время после начала движения В. и М. встретятся: 260÷(13+52)= через 4 ч.
№61. Движение навстречу (буквенные выражения).
Из пунктов А и В,
расстояние между которыми 260 км, одновременно навстречу друг другу выехали
автобус и автомобиль. Скорость автобуса – x
км/ч, а скорость автомобиля – y
км/ч ![]() .
Запишите в виде выражения:
.
Запишите в виде выражения:
1) на сколько скорость автобуса меньше скорости автомобиля:
![]() ;
;
2) во сколько раз
скорость автобуса меньше скорости автомобиля: ![]() ;
;
3) время, которое
потребуется автобусу на весь путь из А в В: ![]() ;
;
4) время, которое
потребуется автомобилю на весь путь из А в В:![]() ;
;
5) на сколько меньше
потребуется времени на весь путь из А в В автомобилю, чем автобусу: ![]() ;
;
6) во сколько раз
меньше потребуется времени на весь путь из А в В автомобилю, чем автобусу: ![]() ;
;
7) скорость сближения
автобуса и автомобиля: ![]() ;
;
8) через какое время
после начала движения автобус и автомобиль встретятся: ![]() .
.
Если сравнивать условия последних двух задач, то в них описаны похожие реальные ситуации на движение навстречу, только в первом случае выражения, которые мы составляли, были числовые, а во втором случае – буквенные.
№75. Движение вдогонку.
Вини-Пух был в гостях у Пятачка. Уходя, он забыл у него свой воздушный шарик. Пятачок заметил это только через 12 минут после ухода Вини-Пуха и сразу побежал за ним вдогонку, чтобы отдать шарик. Ему удалось догнать Вини-Пуха довольно быстро, поскольку тот шел не торопясь, со скоростью 50 м/мин, а Пятачок бежал быстро – со скоростью 200 м /мин.
Запишите на математическом языке:
1) какое расстояние Вини-Пух прошел за 12 минут: 50×12=600 метров;
2) на какое расстояние Пятачок приближался к Вини-Пуху за одну минуту: на 200 м;
3) сколько времени понадобилось Пятачку, чтобы догнать Вини-Пуха: 600÷200=3 минуты.
Следующая задача №76 такая же, только вместо числовых выражений составляются буквенные и вместо Винни-Пуха и Пятачка – волк с зайцем.
Задачи на движение по реке
№81
Скорость течения реки 2 км/ч, а собственная скорость катера 15 км/ч. Составьте выражения для следующих величин и найдите их значения:
1) скорость катера при движении по течению реки: 15+2=17 км/ч;
2) скорость катера при движении против течения реки: 15-2=13 км/ч;
3) расстояние, которое пройдет катер за 3 ч, двигаясь по течению реки: 17×3=51 км;
4) расстояние, которое пройдет катер за 3 ч, двигаясь против течения реки: 13×3=39 км;
5) время, которое потребуется катеру на путь 68 км при движении по течению реки: 68÷17=4 ч;
6) время, которое потребуется катеру на путь 78 км при движении против течения: 78÷13=6 ч;
7) на сколько скорость катера при движении по течению больше его скорости при движении против течения: 17-13=на 4 км/ч.
Полезно давать задания на составление буквенных и числовых выражений на геометрическом материале.
№92.
Длина отрезка АВ равна 50 см. Точки M и N лежат на этом отрезке. Найдите длину отрезка MN, если:
а) AM=15 см, NB=19 см, значит MN=50-15-19=16 см;
б) AN= 38 см, MB=26 см, значит MN=38+26-50=14 см;
в) AM=23 см, NB=21 см, значит MN=50-23-21=6 см;
г) AN=42 см, MB=34 см, значит MN=42+34-50=26 см.
№93.
Длина отрезка АВ равна ![]() см. Запишите
выражение для длины отрезка:
см. Запишите
выражение для длины отрезка:
а) MN,
который в 3 раза длиннее AB:
MN=3![]() ;
;
б) KL,
который на 25 см длиннее AB:
KL=![]() +25;
+25;
в) CD,
который в 4 раза короче AB:
CD=![]() ÷4;
÷4;
г) EF,
который на 8 см короче AB:
EF=![]() -8.
-8.
№108.
Запишите выражение для длины ломаной ABCD, если:
а) AB=x, DC в 2 раза больше AB , а CD на 6 см меньше AB: AB=x, BC=2x, CD=x-6, тогда ABCD=x+2x+(x-6);
б) AB=y, BC в 3 раза меньше AB, а CD на 8 больше BC: AB=y, BC=y÷3, CD=y÷3+8, тогда ABCD=y+ y÷3+(y÷3+8).
Далее переходим к следующему 3 этапу расшифровке буквенных выражений в соответствии с данной ситуацией
№113
Книга стоит x р., а альбом – y р. Какой смысл имеет выражение:
а) 3x – стоимость трех книг;
б) 2y – стоимость двух альбомов;
в) y-x – разница между стоимостью альбома и стоимостью книги;
г) 5x+4y – стоимость пяти книг и четырех альбомов.
№114
Скорость пассажирского
поезда - ![]() км/ч,
а товарного -
км/ч,
а товарного - ![]() км/ч. Что записано на
математическом языке:
км/ч. Что записано на
математическом языке:
а) ![]() - скорость сближения
пассажирского и товарного поездов;
- скорость сближения
пассажирского и товарного поездов;
б) 1750÷![]() - время, за
которое пассажирский поезд пройдет расстояние в 1750 км;
- время, за
которое пассажирский поезд пройдет расстояние в 1750 км;
в) 1750÷![]() - время, за
которое товарный поезд пройдет расстояние в 1750 км;
- время, за
которое товарный поезд пройдет расстояние в 1750 км;
г) 1750÷(![]() ) – время,
через которое два поезда встретятся.
) – время,
через которое два поезда встретятся.
§12. Формулы.
На этом этапе большое значение имеет введение понятия «формула», т.к. это тоже перевод в математический язык.
§13. Законы арифметических действий.
Словесная и буквенная формулировка законов сложения и умножения.
§16. Математический язык.
Математическая модель.
Второй и третий этапы не отделяются четко друг от друга, например, когда мы переходим к расшифровке выражения, это не значит, что мы перестаем составлять выражение.
После того как дети получили элементарное представление о составление выражений и их расшифровке целесообразно ввести такие понятия как математический язык и математическая модель, что авторы и делают.
№260
Переведите на обычный язык:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Проверьте себя
|
1) |
произ-ние суммы чисел |
|
2) |
частное числа 10 и разности чисел |
|
3) |
сумма числа 5 и произ-ния чисел |
|
4) |
разность утроенного числа |
Обращается внимание на то, что чтение выражений начинается с последнего выполняемого действия.
№ 261
Переведите на обычный язык:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Проверьте себя.
|
1) |
произведение суммы чисел |
|
2) |
частное числа 10 и разности чисел |
|
3) |
сумма числа 5 и произведения чисел |
|
4) |
разность утроенного числа |
Следующие задания обратные двум предыдущим, теперь дана фраза, и надо записать ее на математическом языке.
№262
Запишите на математическом языке такие «слова»:
1) сумма первых четырех натуральных чисел;
2) произведение первых четырех натуральных чисел;
3) частное наибольшего двузначного и наибольшего однозначного чисел;
4) разность наименьшего трехзначного и наименьшего двузначного чисел,
В результате дети получают такие выражения:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
№263
Запишите на математическом языке предложения:
1) сумма первых четырех натуральных чисел равна десяти;
2) произведение первых четырех натуральных чисел равно двадцати четырем;
3) частное наибольшего двузначного и наибольшего однозначного чисел равно одиннадцати;
4) разность наименьшего трехзначного и наименьшего двузначного чисел равна девяноста.
В результате дети получают такие выражения
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Следующее задание на составление выражения.
№264.
Цена хризантемы - ![]() р. за один
цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:
р. за один
цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:
а) цену розы;
Если цена хризантемы - ![]() р, а цена розы
на 30р. больше, тогда ответ цена розы – (30+
р, а цена розы
на 30р. больше, тогда ответ цена розы – (30+![]() )р.
)р.
б) стоимости пяти хризантем;
Если цена одной
хризантемы - ![]() р., то ответ цена пяти
хризантем –5
р., то ответ цена пяти
хризантем –5![]() р.
р.
в) стоимости трех роз;
Если цена одной розы -
(30+![]() )р.,
тогда ответ цена трех роз –3(30+
)р.,
тогда ответ цена трех роз –3(30+![]() ) р.
) р.
г) стоимость букета из пяти хризантем и трех роз.
Если цена пяти
хризантем - 5![]() р. и цена трех роз – (3(30+
р. и цена трех роз – (3(30+![]() ))р., то ответ
букет из этих цветов будет стоить – (5
))р., то ответ
букет из этих цветов будет стоить – (5![]() +3(30+
+3(30+![]() ))р.
))р.
Переходим к 4 этапу: составление равенств и неравенств.
№266.
Цена хризантемы - ![]() р. за один
цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:
р. за один
цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:
а) букет из пяти
хризантем и трех роз стоит 250 р.: ответ ![]() ;
;
б) три розы дороже пяти
хризантем на 50 р.: ответ ![]() ;
;
в) стоимость букета из
семи хризантем меньше трехсот рублей: ответ ![]() ;
;
г) стоимость букета из
семи роз больше трехсот рублей: ответ ![]() .
.
§17. Математическая модель
С целью дальнейшего формирования представлений о том, что с помощью одной и той же математической модели могут быть описаны различные с обыденной точки зрения ситуации, учащимся предлагаются следующие задачи.
№273.
Расстояние 180 км легковой автомобиль может преодолеть за 2 ч, а грузовому автомобилю на то же расстояние требуется 3 ч. Через какое время они смогут встретиться, если выедут навстречу друг другу из пунктов, расстояние между которыми 300 км?
Решение
180 км легковой автомобиль - за 2 ч, значит за 1 ч – 90 км. 180 км грузовой автомобиль – за 3 ч, значит за 1 ч – 60км.
300÷(90+60)= через 2 ч автомобили встретятся.
Ответ: через 2 часа.
№274
Одной бригаде трактористов, чтобы вспахать 180 а, требуется 2 дня, а другой – 3 дня. За какое время эти бригады смогут вспахать 300 а, работая одновременно?
Решение
300÷(180÷2+180÷3)=за 2 ч эти бригады могут вспахать 300 а.
Ответ: за 2 часа.
Для решения этих двух задач требуется найти значение одного и того же числового выражения: 300÷(180÷2+180÷3). Но это не является для учеников чем-то совершенно новым и необычным. Они уже сталкивались с тем, что на математическом языке различные с точки зрения обыденной жизни ситуации описываются совершенно одинаково.
В учебнике рассказывается о том, что полученное в процессе решения выражение – это математическая модель реальной жизненной ситуации, о которой говорится в задаче. В первой задаче рассматривается встречное движение, во второй – совместная работа, и обе эти ситуации описываются одинаковыми математическими моделями.
Ученики, выполняя задания из предыдущих пунктов по «переводу» обычной речи на математический язык каждый раз составляли математическую модель данной ситуации.
§27. Определение угла. Развернутый угол.
№509
Прочитайте задачу. Постарайтесь найти разные способы решения.
В двух коробках 16 кг печенья. Найдите массу печенья в каждой коробке, если в одной из них печенья на 4 кг больше, чем в другой.
Проверьте так ли вы решали задачу:
1 способ.
Если из первой коробки достать 4 кг печенья, то в обеих коробках печенья станет поровну, а всего останется 16-4=12 кг – печенья. Тогда в каждой коробке будет 12÷2=6 кг печенья. Но это как раз та масса печенья, которая была во второй коробке: 6+4=10 кг.
Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.
2 способ.
Если во вторую коробку добавить 4 кг печенья, то в обеих коробках печенья станет поровну, а всего в двух коробках станет 16+4=20 кг печенья. Тогда в каждой коробке станет 20÷2=10 кг печенья. Но это как раз та масса печенья, которая была в первой коробке. Теперь можем узнать массу печенья во второй коробке: 10-4=6кг.
Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.
3 способ.
Обозначим массу печенья во второй коробке буквой x кг.
Тогда масса печенья в первой коробке будет равна (x+4) кг, а масса печенья в двух коробках – ((x+4)+x) кг.
Но, по условию задачи, в двух коробках было 16 кг печенья. Значит, можем составить уравнение
(x+4)+x=16.
Решив его получаем x=6.
Итак, мы получили, что во второй коробке было 6 кг печенья, значит, в первой было 6+4=10 кг печенья.
Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.
4 способ.
Обозначим массу печенья в первой коробке буквой x кг.
Тогда масса печенья во второй коробке будет равна (x-4) кг, а масса печенья в двух коробках – (x+(x-4)) кг.
По условию задачи, в двух коробках было 16 кг печенья. Составим уравнение
x+(x-4)=16.
Отсюда x=10.
Итак, мы получили, что в первой коробке было 10 кг печенья, значит, во второй было 10-4=6 кг печенья.
Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.
3 и 4 способы решения задачи – это один и тот же способ: алгебраический. Решая задачу алгебраическим способом, обозначают неизвестную величину буквой, составляют уравнение по условию задачи и решают его.
№510.
С трех участков земли собрали 156 ц картофеля. С первого и второго участков картофеля собрали поровну, а с третьего – на ц больше, чем с каждого из первых двух. Сколько картофеля собрали с каждого участка?
| 1 поле |
|
|
| 2 поле | ||
| 3 поле | 2 ц |
Всего 156 ц
1 способ.
Если на двух первых полях количество собранного картофеля одинаковое, на третьем на 12 ц больше, то мы можем из общей суммы 156 ц вычесть 12ц, чтобы получить количество картофеля на трех полях 156-12=144 ц картофеля на трех полях. А теперь мы можем 144÷3=48 ц картофеля собрали с первого и второго поля, а с третьего поля собрали 48+12=60 ц картофеля.
Ответ: с первого и второго поля собрали по 48 ц картофеля, а с третьего поля собрали 60 ц картофеля.
2 способ.
Обозначим количество картофеля собранного с первого поля буквой x ц. Тогда со второго собрали тоже x ц картофеля, а с третьего поля собрали картофеля на 12 больше, значит обозначим (x+12) ц. Количество собранного картофеля с трех полей x+x+(x+12).
По условию задачи с трех полей собрали 156 ц картофеля. Составим уравнение
x+x+(x+12)=156.
Отсюда 3x=144, а x =48.
Итак, мы получили, что с первого и второго полей собрали по 48 ц картофеля, а с третьего 48+12=60 ц картофеля.
Ответ: с первого и второго поля собрали по 48 ц картофеля, а с третьего поля собрали 60 ц картофеля.
В следующих задачах уровень сложности повышается.
№544.
1) Решите задачу.
На первом элеваторе зерна в три раза больше, чем на втором. Если с первого элеватора вывезти 850 т, а со второго – 150 т, то на обоих элеваторах зерна останется поровну. Какое количество зерна было на первом элеваторе?
Если вы догадались составить к задаче такую схему, то возможно, вы смогли решить ее устно:
| 1 элеватор |
|
850 | |
| 2 элеватор |
|
||
850-150=600 т зерна в двух частях 1 элеватора;
600÷2=300 т зерна на втором элеваторе;
600+300=900 т зерна на первом элеваторе.
2) Обозначьте буквой x количество зерна на втором элеваторе. Подумайте, для каких величин можно составить выражения с этой буквой, и запишите их.
3) составьте математическую модель задачи
Пусть х – количество зерна на втором элеваторе, тогда 3х – количество зерна на первом элеваторе.
Если с первого вывезли 850 т зерна (3х-850), а со второго вывезли 150 т (х-150), то в обоих элеваторах зерна останется поровну, тогда получаем 3х-850=х-150.
Это уравнение учащиеся решить не могут, но такая задача перед ними и не ставиться, еще раз подчеркнем, что в 5 классе, главная задача научить составлять математические модели. Работать с математическими моделями они будут в следующих классах.
Следующие задачи авторы учебника предлагают решить двумя способами: арифметическим и алгебраическим. Если будут затруднения с решением уравнения, подставьте в него найденный арифметическим способом результат и проверьте справедливость составленного вами равенства. В 6-м классе дети познакомятся с методом, который позволит без труда решить все составленные ими уравнения.
№636.
Стоимость автомобиля с гаражом составляет 355600р. Сколько стоит автомобиль, если он на 97300р дороже удвоенной стоимости гаража?
Первый способ.
| автомобиль | 97300 р. | ||
| гараж |
Вся стоимость автомобиля с гаражом 355600р.
1) 355600–97300=258300 р. цена трех гаражей;
2) 258300÷3=86100 р. стоимость гаража;
3) 355600–86100=269500 р. стоимость машины.
Ответ: стоимость автомобиля 269500 р.
2 способ.
Пусть стоимость гаража – х рублей, тогда стоимость машины – (2х+97300) р. Стоимость гаража и автомобиля вместе составляет 355600 р.
Составим уравнение:
х+2х+97300=355600,
3х=258300,
х=86100 р. – стоимость гаража, тогда стоимость автомобиля 86100×2+97300=269500р.
Ответ: стоимость автомобиля 269500 р.
№637.
В двух кусках поровну ткани. После того как от первого куска продали 14 м, а от второго – 22 м, в первом куске осталось втрое больше ткани, чем во втором. Сколько метров ткани было в каждом куске первоначально?
Решение:
1 способ.
14 м
| 1 кусок | ||||
| 2 кусок |
22 м
| 1 кусок | ||||
| 2 кусок |
Нам известно, что ткани первоначально было поровну, затем от 1 куска отрезали 14 м, а от 2ого – 22 м, и тогда в первом куске осталось втрое больше, чем во втором. Поэтому если мы из 22 вычтем 14, то получим 8 м, а это составляет 2 одинаковых части в первом куске, значит если 8÷2=4 м осталось во втором куске, после того как от него отрезали 22 м. Значит первоначально в нем было 26 м. Можно проверить, посчитав сколько было м в первом куске: 4×3=12 м осталось в первом куске после того, как от него отрезали 14 м, и для того, чтобы найти, сколько было мы должны 14+12=26 м было в первом куске первоначально.
Ответ: первоначально в каждом куске ткани было 26 м
2 способ.
Пусть во втором осталось х м ткани, тогда в первом осталось 3х м ткани.
Мы знаем, что от первого куска отрезали 14 м, а от второго – 22 метра, тогда в 1 куске было (3х+14) м ткани, а во втором было – (х+22) м ткани.
В условии сказано, что ткани изначально было поровну, значит можем составить уравнение:
1) 3х+14=х+22,
2х=8,
х=4 м ткани осталось во втором куске,
2) 4×3=12 м ткани осталось в первом куске,
3) 4+22=26 м было в первом куске изначально.
Мы знаем, что в первом и втором кусках ткани было поровну, следовательно, и во втором куске было 26 м ткани.
Ответ: первоначально в каждом куске ткани было 26 м
№638.
У двоих братьев было вместе 112р. После того как старший отдал младшему 14 р., у него осталось все же денег больше, чем у младшего, но всего лишь на 10 р.Сколько денег было у каждого мальчика первоначально?
Решение:
1 способ.
10р. 14р.
| 1 брат | ||||
| 2 брат |
14р.
Всего у двух братьев 112 р.
10р.
| 1 брат | ||||
| 2 брат |
14р
1) 112-24=88 р у двух мальчиков, после того как 1ый отдал 2ому – 14 р, и если у 1ого забрать 10 р.
2) 88÷2=44 р. стало у 2ого мальчика, когда 1ый отдал ему 14 р.,
3) 44-14=30 р. было у 2ого мальчика первоначально,
4) 44+10+14=68 р. было у первого мальчика вначале.
Ответ: у первого брата было 68 р., а у второго – 30 р.
6 класс.
§20.
В 6 классе после того как дети познакомились с действиями над положительными и отрицательными числами, научились решать уравнения, можно приступать к решению задач выделением трех этапов математического моделирования. Но решать с шестиклассниками задачи таким способом без предварительной подготовки преждевременно. Поэтому решение каждой такой задачи следует предварять специальной системой упражнений.
Например, №593.
В одном бидоне x л, а в другом – y л молока.
а) что означают
выражения ![]() ?
?
б) что означают
равенства ![]() ?
?
Эта задача предварительного этапа, затем следует задача №594:
В одном бидоне молока в 3 раза больше, чем в другом. когда из одного бидона перелили в другой 5 литров, молока в бидонах стало поровну. Сколько литров было в каждом бидоне первоначально?
Решите задачу алгебраическим способом.
Решение.
Пусть x л – количество молока, которое было до переливания во втором бидоне. Тогда в первом бидоне его было 3x л.
После переливания в первом бидоне осталось (3x-5) л молока, а во втором стало (x+5) л.
Поскольку после переливания в обоих бидонах молока стало поровну, можно составить уравнение:
3x-5=x+5.
Учитель сообщает, что эту часть рассуждений при решении задачи называют составлением математической модели. На этом этапе переводят текст задачи с обыденного языка на математический язык. В результате получают математическую модель ситуации, описанной в условии задачи. Такой математической моделью и является составленное уравнение. После этого приступают ко второму этапу, который называют работой с математической моделью. На этом этапе нам надо решить составленное уравнение 3x-5=x+5.
Решение (учащиеся выполняют самостоятельно):
3x-x=5+5,
2x=10,
x=5.
Уравнение решено, теперь надо приступить к третьему этапу – ответу на вопрос задачи: сколько литров было в каждом бидоне первоначально?
Мы получили x=5, а за x было принято количество молока (в литрах), которое было во втором бидоне. Итак, во втором бидоне было 5 л молока. По условию задачи, в первом бидоне молока было в 3 раза больше, значит, в первом бидоне было 15 л молока.
Ответ: в одном бидоне было 5 л, а в другом – 15 л молока.
После этого в 7 классе повторяются этапы математического моделирования и они уже к этому подготовлены, но тем не менее нулевой этап своей актуальности не теряет, т.к. появляются более сложные задачи.
Рассмотрим задачник математика «Алгебра, 7» авторов Мордковича А.Г. и др. и составим к задачам, данным в этом учебнике, упражнения подводящие к их решению.
№95
Расстояние между городами мотоциклист проехал за 2 часа, а велосипедист – за 5 часов. Скорость велосипедиста на 18 км/ч меньше скорости мотоциклиста. найдите скорости велосипедиста и мотоциклиста и расстояние между городами.
Решение.
Т.к. скорости велосипедиста и мотоциклиста неизвестны, то мы можем взять за x – скорость мотоциклиста, а скорость велосипедиста – (x-18). Мотоциклист двигался в течение 2-х часов со скоростью x км/ч, а велосипедист – 5 ч со скоростью (x-18) км/ч. Зная, что велосипедист и мотоциклист преодолели одно и то же расстояние, составим уравнение:
2x=5(x-18),
3x=90,
x=30 км/ч скорость М.,
30-18=12 км/ч скорость В.
Ответ: За 2 часа мотоциклист и за 5 ч велосипедист пройдут путь в 60 км.
Но перед тем как решать эту задачу можно рассмотреть другие задачи, направленные на подготовку к ее решению:
Пешеход идет со скоростью x км/ч, велосипедист на 10 км/ч быстрее. Расстояние от точки А до точки В пешеход преодолел за 3 ч, а велосипедист за 1 час.
Что обозначают выражения:
(x+10) – скорость велосипедиста;
3x – расстояние, которое прошел пешеход за 3 часа;
Что обозначает равенство:
3x=x+10
– пешеход и велосипедист преодолели одинаковое расстояние.
№96.
В одном доме на 86 квартир больше, чем в другом. Сколько квартир в каждом доме, если в двух домах 792 квартиры?
Решение
1 дом – x кв.
2 дом – (x+86)кв.
Всего 792 кв.
x+x+86=792,
2x=706,
x=353 кв. в 1 доме, 439 кв. во 2 доме.
Задача нулевого этапа.
В одной деревне x домов, а в другой на 112 домов больше. Всего в двух деревнях 504 дома. Что обозначают выражения и равенства:
x+112 – столько домов во второй деревне;
2x+112 - столько домов в двух деревнях;
2x+112=504 – всего в двух деревнях 504 дома.
№97.
В жилом доме всего 215 квартир. Сколько из них однокомнатных, если известно, что трехкомнатных квартир на 10 меньше, чем двухкомнатных, и на 5 больше, чем однокомнатных?
Решение
Пусть x – число трехкомнатных квартир, тогда
число однокомнатных кв. – (x-5),
число двухкомнатных – (x+10),
Составим уравнение:
x+x-5+x+10=215,
3x=210,
Ответ: x=70 кв. трехкомнатных, 80 кв. – двухкомнатных, 65 кв. – однокомнатных.
Нулевой этап: на огороде выросло всего 220 кг овощей. Картошки – x кг, капусты на 10 кг меньше, свеклы на 15 кг больше. Что означают выражения и равенства:
x+15 – количество кг свеклы;
x-10 – количество кг капусты;
x+15+x-10 – количество кг свеклы и капусты;
x+x+15 – количество кг картошки и свеклы;
x+x-10 – количество кг картошки и капусты;
x+x+15+x-10=220 – сколько всего кг овощей выросло на огороде.
№98.
В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нем в 3 раза больше мест, чем в малом?
Малый зал – x мест, большой зал – 3x мест.
Решение
Составим уравнение:
x+3x=460,
4x=460,
x=115 мест в малом зале,
115×3=345 мест в большом зале.
Ответ 345 мест в большом зале.
Нулевой этап к этой задаче.
В двух книгах 580 страниц. В одной книге x страниц, а в другой книге – в 3 раза больше. Что обозначают эти выражения:
3x – страниц в во второй книге,
x+3x – число страниц в двух книгах,
x+3x=580 – уравнение из которого следует, что в двух книгах 580 страниц.
№309.
В магазин завезли апельсины и бананы, причем бананов в 3 раза больше. Когда продали половину бананов и 2/3 апельсинов, оказалось, что бананов осталось на 70 кг больше, чем апельсинов. Сколько бананов и апельсинов завезли в магазин?
Пусть в магазин завезли x кг апельсинов, тогда бананов – 3x кг. После продажи апельсинов стало 2/3x кг, а бананов – 3/2x кг. Но бананов осталось на 70 кг больше, чем апельсинов.
Решение
Составляем уравнение:
![]() x+70=
x+70=![]() x,
x,
4x-9x+420=0,
5x=420,
x=84 кг апельсинов завезли в магазин.
Бананов в 3 раза больше, значит, 84×3=252 кг бананов завезли в магазин.
Ответ: 252 кг бананов завезли в магазин.
Нулевой этап.
В игрушечный магазин завезли x штук машин, а кукол в 3 раза больше. Когда продали половину кукол и 2/3 машин, оказалось, что кукол осталось на 70 больше, чем машин.
Что значат выражения:
3x – столько кукол завезли в магазин,
![]() x
– осталось машинок после продажи,
x
– осталось машинок после продажи,
![]() x – осталось кукол после продажи,
x – осталось кукол после продажи,
![]() x
+70 – на столько больше осталось кукол, чем машин,
x
+70 – на столько больше осталось кукол, чем машин,
![]() x
+70=
x
+70=![]() x – столько стало кукол и машин после продажи вместе.
x – столько стало кукол и машин после продажи вместе.
№412.
Из пункта А в пункт В со скоростью 12 км/ч выехал велосипедист, а через полчаса вслед за ним выехал другой велосипедист, проезжавший в час 14 км и прибывший в пункт В одновременно с первым велосипедистом. Найдите расстояние между А и В.
Решение
Пусть 1ый велосипедист был в пути x ч, тогда второй велосипедист (x-0,5)ч. Скорость 1ого велосипедиста 12 км/ч, значит, расстояние, которое он прошел 12x км, а второй велосипедист 14(x-0,5) км. Т.к. прибыли они одновременно, то можно составить уравнение:
12x=14(x-0,5);
12x=14x-7;
2x=7;
x=3,5 часа 1ый велосипедист был в пути, тогда 2ой - был в пути 3 часа.
Расстояние которое они прошли от пункта А до пункта В составляет 42 км.
Ответ: расстояние 42 км.
Нулевой этап.
Из пункта А в пункт В вышел пешеход со скоростью 6 км/ч и был в пути x часов, через 30 минут из пункта А вышел 2ой пешеход и шел со скоростью 8 км/ч. Пришли в пункт В они одновременно.
Что обозначают выражения:
6x – расстояние, которое прошел 1 пешеход,
(x-0,5) – столько времени 2ой пешеход был в пути
8(x-0,5) – расстояние, которое прошел 2ой пешеход.
№413.
Лодка плыла 6 ч по течению реки, а затем 4 ч против течения. Найдите собственную скорость лодки (т.е. скорость в стоячей воде), если известно, что скорость течения реки равна 3 км/ч, а всего лодкой пройдено расстояние 126 км.
Решение
Пусть x км/ч – собственная скорость лодки, тогда по течению она плывет со скоростью (x+3) км/ч (течение помогает), а против течения – со скоростью (x-3) км/ч (течение препятствует).
По течению реки лодка плыла 6 ч. За это время со скоростью (x+3) км/ч лодкой пройден путь 6(x+3) км.
Против течения лодка плыла 4 ч. За это время со скоростью (x-3) км/ч лодкой пройден путь 4(x-3) км.
По условию весь ее путь составил 126 км. Т.к. он состоит из пути по течению и пути против течения, то получаем:
6(x+3)+4(x-2)=126,
6x+18+4x+8=126,
10x=116,
x=11,6 км/ч собственная скорость лодки.
Ответ: собственная скорость лодки 11,6 км/ч.
Нулевой этап:
Лодка плыла 3 ч по течению реки, а затем 2 ч против течения. Собственная скорость лодки x км/ч, скорость течения реки равна 1,5 км/ч, всего лодкой пройдено 63 км. Что обозначают следующие выражения:
(x+1,5) км/ч – скорость лодки по течению реки,
(x-1,5) км/ч – скорость лодки против течения реки,
3(x+1,5) км – путь, пройденный лодкой по течению реки,
2(x-1,5) км – путь, пройденный лодкой против течения реки,
3(x+1,5)+ 2(x-1,5) км – весь пройденный путь.
№414.
От поселка до станции велосипедист ехал со скоростью 10 км/ч, а возвращался со скоростью 15 км/ч, поэтому он затратил на обратный путь на 1 ч меньше. Найдите расстояние от поселка до станции.
Решение
Пусть x ч велосипедист был в пути от поселка до станции, тогда если он затратил на обратный путь на 1 ч меньше, то он был в пути (x-1) ч.
Т.к. он ехал туда со скоростью 10 км/ч , то он проехал 10x км, а обратно он ехал со скоростью 15 км/ч, тогда он проехал 15(x-1) км.
Т.к. путь туда и обратно был одинаковым, то мы можем записать уравнение:
10x=15(x-1);
10x=15x-15;
5x=15;
x=3 ч время которое он потратил на путь туда, а обратно он ехал на 1 ч быстрее, значит 2 часа.
Отсюда можно найти расстояние умножив 10 км/ч на 3 ч или 15 км/ч на 2 ч, получаем 30 км.
Ответ: расстояние 30 км.
Нулевой этап:
Из пункта А в пункт В мотоциклист проехал со скоростью 20 км/ч и потратил на весь путь x ч, а обратно ехал со скоростью 25 км/ч и затратил на обратный путь на 1 ч меньше. что обозначают эти выражения:
(x-1) ч – время, потраченное на обратный путь,
20x км – путь туда,
25(x-1) км – путь обратно,
20x=25(x-1) км – путь туда и обратно.
№1135
Для учащихся приобрели футбольные и волейбольные мячи, причем волейбольных в 5 раз больше, чем футбольных. На следующий год приобрели новую партию мячей, причем футбольных стало в 6 раз больше, чем было, волейбольных – в 4 раза больше, чем было, а всего мячей стало 52. Сколько мячей закупили в первый год?
Решение
Пусть x – число футбольных мячей, приобретенных в первый год, а y – число волейбольных мячей, приобретенных в первый год. По условию задачи y=5x.
Далее, на второй год футбольных мячей приобрели в 6 раз больше и их стало 6x, а волейбольных мячей приобрели в 4 раза больше и их стало 4y. По условию всего стало 52 мяча, т.е. 6x+4y=52. Итак наша математическая модель готова, она состоит из двух линейных уравнений с двумя переменными x и y:
![]() ,
,
Подставляем первое уравнение во второе, получаем
6x+20x=52,
26x=52,
x=2, т.е. 2 футбольных мяча закупили в первый год, тогда волейбольных мячей закупили10 штук. Вопрос задачи : сколько мячей закупили в первый год?
Ответ: 12 мячей.
Нулевой этап.
Света и Гоша посадили на балконе цветы. Света в первый раз посадила x цветков, Гоша y цветков, у Гоши цветов получилось в 3 раза больше, чем у Светы. Во второй раз Света посадила в 2 раза больше, чем было, а Гоша в 5 раз больше, чем было. Всего они посадили 34 цветка.
Что обозначают следующие выражения:
y=3x – во столько раз число цветов у Гоши было больше цветов Светы в первый раз,
2x – столько цветов стало у Светы,
5y – столько цветов стало у Гоши,
15x – столько цветов стало у Гоши,
2x+15x –общее количество цветов у детей и оно равно 34.
8 класс
№893
Из пункта А в пункт В, удаленный от А на расстояние 100 км, отправился междугородный автобус. Из-за ненастной погоды он ехал со скоростью на 10 км/ч меньшей, чем предполагалось по расписанию, и поэтому прибыл в пункт в пункт В с опозданием на 30 минут. С какой скоростью должен был ехать автобус по расписанию?
Решение
Пусть x
км/ч – скорость автобуса по расписанию. Так как расстояние от А до В равно 100
км, то время отведенное на данное расстояние составляет ![]() ч.
ч.
Фактически автобус
прошел расстояние в 100 км со скоростью ![]() км/ч, значит время затраченное на
прохождение пути, равно
км/ч, значит время затраченное на
прохождение пути, равно ![]() ч.
ч.
Из двух величин ![]() ч и
ч и ![]() ч вторая больше
первой на 30 минут, т.е. на
ч вторая больше
первой на 30 минут, т.е. на ![]() ч. Значит, мы приходим к уравнению
ч. Значит, мы приходим к уравнению
![]() - это рациональное
уравнение,
- это рациональное
уравнение,
![]() ,
,
Преобразуем левую часть уравнения
![]() ,
,
Приравняв числитель
этой дроби нулю, получим квадратное уравнение ![]() , находим,
, находим,
![]() .
.
Оба значения
удовлетворяют условию ![]() , следовательно, эти значения
корни составленного рационального уравнения.
, следовательно, эти значения
корни составленного рационального уравнения.
В задаче спрашивается, с какой скоростью должен был ехать автобус по расписанию? Именно эту величину мы обозначили буквой x. Получилось, что x = 50, либо x = –40. Второе значение нас явно не устраивает, поскольку скорость движения поезда не может выражаться отрицательным числом. Значит, выбираем значение x = 50.
Ответ: 50 км/ч.
Нулевой этап.
Из пункта А в пункт В расстояние между которыми 100км, отправился автомобиль, который шел со скоростью x км/ч. Из-за сильного снегопада водитель ехал со скоростью на 20 км/ч меньше, чем он рассчитывал и поэтому прибыл в пункт В с опозданием на 1 час.
Что обозначают следующие выражения:
![]() - время, за которое
водитель должен был доехать до пункт В;
- время, за которое
водитель должен был доехать до пункт В;
![]() - время, затраченное на
прохождение пути;
- время, затраченное на
прохождение пути;
![]() - первое время больше
второго времени на 1 час.
- первое время больше
второго времени на 1 час.
В этой главе мы рассмотрели задачи из учебника «Математика» 5, 6 класс, а также рассмотрели учебники «Алгебра» 7, 8 класс, в которых сделали нулевые этапы к задачам, который нужен для того, чтобы ребенок был подготовлен к составлению математических моделей.
Заключение
В ходе работы были решены все поставленные задачи:
1) Изучена психолого-педагогическая литература, по данной теме. В ходе ее анализа было изучено, что такое задача, классификации задач. Были рассмотрены несколько определений задачи. Например «задача» по Баллу употребляется для обозначения объектов. Другие, например Колягин рассматривают задачи как ситуации, в которых должен действовать субъект, которого включают в само понятие задачи. Еще в одном определение по Фридману субъект не включается в понятие задачи.
2) Изучена учебно-методическая литература, направленная на обучение решению текстовых задач. Было рассмотрено несколько классификаций задач. В одной из которых основу составляет характер требования, другая рассматривается по функциям задачи, еще одна классификация по компонентам учебной деятельности.
3) Изучен педагогический опыт учителей по вопросу решения текстовых задач. Рассмотрена методика решения задач, которая была представлена в книге Д. Пойя «Как решать задачу». Методика обучения решению задач предполагает выделение спектра умений решать задачи. Весь процесс решения задачи можно разделить на 8 этапов представленных в нашей дипломной работе. В ней также рассмотрены правила, пользуясь которыми можно найти последовательность шагов для любой задачи. Рассмотрены методы решения текстовых задач, в основе которых лежат различные виды математических моделей. Рассмотрена классификация задач, решаемых алгебраическим способом по фабуле, из-за многообразия уравнений и неравенств. В процессе решения текстовых задач выделяются 3 этапа математического моделирования. Самые большие трудности у детей появляются при составлении математической модели.
4) был разработан комплекс упражнений, предназначенных для обучения составлению математических моделей реальных ситуаций, т.е. переводу сюжета задачи на математический язык. В этот комплекс включены линейные уравнения, системы уравнений, дробно-рациональные уравнения.
Подводя итоги проделанной работы, можно утверждать, что цели дипломной работы достигнуты.
Библиография
1. Балл, Г.А. О психологическом содержании понятия «задача» [Текст] / Г.А. Балл // Вопросы психологии.– 1970.– № 5.– С. 81-87.
2. Бобровская, А.В. Текстовые задачи курса алгебры средней школы. [Текст] / А.Б. Бобровская.– 3-е изд., доп. и перераб.– Шадринск: Исеть, 1999.– 64 c: ил.
3. Ванцян, А.Г. Эти непростые "простые задачки" [Текст] / А.Г. Ванцян // Практика образования.– 2007.– № 3.– C. 20-22.
4. Гороховцева, Л.А. Процесс решения текстовой задачи при изучении математики в средней школе . [Текст] / Л.А. Гороховцева // Теория и практика высш. проф. обр.– 2003.– № 9.– С. 14-21.
5. Дашинимаева, Ц.Д. Текстовые задачи [Текст]: учеб. пособие по математике для 7-11 кл. / Ц.Д. Данишимаева.– М.: Спутник, 2006.– 50 с: ил.
6. Демидова, Т.Е. Теория и практика решения текстовых задач [Текст]: пособие для студ. высш. пед. учеб. заведений / Т.Е. Демидова, А.П. Тонких.– М.: Академия, 2002.– 288 с.
7. Демидова, Т.Е. Текстовые задачи и методы их решения [Текст] / Т.Е. Демидова, А.П. Тонких.– М.: изд-во Моск. ун-та, 1999.– 261 с.: ил.
8. Зайцева, С.А. Организация работы над текстовой задачей на основе модели. [Текст] / С.А. Зайцева, И.И. Целищева // Начальное образование.– 2007.– № 4.– C. 9-15
9. Зубарева, И.И. Математика [Текст]: 5 кл.: Учеб. для общеобразоват. учреждений / И.И. Зубарева, А.Г. Мордкович.– 3-е изд., добав. и испр.– М.: Мнемозина, 2004.– 270 с.: ил.
10. Зубарева, И.И. Математика [Текст]: 6 кл.: Учеб. для общеобразоват. учреждений. / И.И. Зубарева, А.Г. Мордкович.– 4-е изд.– М.: Мнемозина, 2005.– 264 с.: ил.
11. Колягин, Ю.М. Задачи в обучении математике. [Текст] / Ю.М. Колягин.– М.: Просвещение, 1977.– 267 с.: ил.
12. Крутецкий, В.А. Психология математических способностей школьников [Текст] / В.А. Крутецкий.– М.: Просвещение, 1968.– 432 с.
13. Кузнецов, С.А. Научим учеников решать текстовые задачи по алгебре [Текст]: из опыта работы учителя математики Кузнецова С. А. / С.А. Кузнецов // М-лы метод. каб. Ромодан. отд. обр.– Б.М., 2000. – 32 с.
14. Кулагина, И.Ю. Возрастная психология [Текст]: Учебное пособие / И.Ю. Кулагина.– 3-е изд.– М.: УРАО, 1997.–176 с.
15. Мордкович, А.Г. Алгебра. 7 кл. [Текст]: Учеб для общеобразоват. учреждений / А.Г. Мордкович.– 3-е изд., доработ.– М.: Мнемозина, 2000.– 160 с.: ил.
16. Мордкович, А.Г. Алгебра. 8 кл. [Текст]: Учеб для общеобразоват. учреждений / А.Г. Мордкович.– 3-е изд., доработ.– М.: Мнемозина, 2001.– 223 с.: ил.
17. Мордкович, А.Г. Алгебра. 7 кл. [Текст]: Задачник для общеобразоват. учреждений / А.Г. Мордкович и др.– 3-е изд., доработ.– М.: Мнемозина, 2000.– 160 с.: ил.
18. Мордкович, А.Г. Алгебра. 8 кл. [Текст]: Задачник для общеобразоват. учреждений. / А.Г. Мордкович.– 3-е изд., испр.– М.: Мнемозина, 2001.– 239 с.: ил.
19. Панкова, О.А. Текстовые задачи в учебниках Л.Г. Петерсон [Текст] : учеб. пособие к курсу методики преподавания математики в нач. кл. / О.А. Панкова.– М.: СМУ, 2005.– 76 с.
20. Панкова, О.А. Текстовые задачи начального курса математики в разных системах обучения [Текст]: учеб. пособие к курсу методики преподавания математики в нач. кл. / О.А. Панкова.– Магадан: изд-во Север. междунар. ун-та, 2002.– 97 с.: ил.
21. Саранцев, Г.И. Методика обучения математике в средней школе [Текст]: Учеб. пособие для студентов мат. спец. пед. вузов и ин-тов / Г.И. Саранцев.– М.: Просвещение, 2002.– 224 с.: ил.
22. Сафонова, Л.А. О действиях, составляющих умение решать текстовые задачи [Текст] / Л.А. Сафонова // Математика в шк.– 2000.– № 8.– С. 34-36.
23. Захарова, А.Е. Как помочь школьникам преодолеть некоторые затруднения в овладении решением текстовых задач. [Текст] / А. Захарова // Сборник научных трудов математического факультета МГПУ. М.:МГПУ, 2005.- С. 119-124.
24. Савинцева, Н.В. О текстовых задачах в современном курсе математики 5-6 класса. [Текст] / Н. Савинцева // Сборник научных трудов математического факультета МГПУ. М.:МГПУ, 2005.- С. 144-148.
25. Фридман, Л.М. Как научиться решать задачи [Текст] : Кн. для учащихся ст. кл. средн. шк. / Л.М. Фридман, Е.Н. Турецкий.– 3-е изд., дораб.– М.: Просвещение, 1989.– 192 с.: ил.
26. Целищева, И. Как помочь каждому ученику самост-но решать текстовые задачи [Текст] / И. Целищева, С. Зайцева // Нач. шк.: еженед. прил. к газ. "Первое сентября".– 2001.– 00.05 (№ 18).– С. 2-5.
27. Шавернева, Л.А. Решение текстовых математических задач разными способами в системе развивающего обучения Л. В. Занкова [Текст] /Л.А. Шавернева.– Самара: Федоров, 2007.– С. 268-294.
28. Шевкин, А.В. Текстовые задачи [Текст]: 7-11 кл.: Учеб. пособие по математике / А.В. Шевкин.– М. : Русское слово, 2003.– 182 с.: ил.
29. Шикова, Р.Н. Использование моделирования в процессе обучения решению текстовых задач. [Текст] / Р.Н. Шикова // Начальная школа: ежемес. науч.-метод. журн.– 2004.– № 12.– С. 32-41.