Курсовая работа: Механизм привода поворотной части робота
Министерство высшего и профессионального образования РФ
Ижевский государственный технический университет
Воткинский филиал
Кафедра «Техническая механика»
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по курсу «Детали машин»
Вариант Т-7-5: «Механизм привода поворотной части робота»
Выполнил: студент Бегеев А. М.
группа Т–712
Руководитель проекта: Юрченко С. А.
2002
Содержание
ВВЕДЕНИЕ
1 ИСХОДНЫЕ ДАННЫЕ
2 КИНЕМАТИЧЕСКИЕ РАСЧЕТЫ
2.1 Выбор электродвигателя
2.2 Определение передаточных чисел привода
2.3 Определение вращающих моментов на валах привода
3 РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
3.1 Выбор твердости, термической обработки и материала колес
3.2 Допускаемые напряжения
3.3 Расчет межосевого расстояния
3.4 Предварительные основные размеры колес
3.5 Диаметры валов
3.6 Модуль передач
3.7 Суммарное число зубьев и угол наклона
3.8 Число зубьев шестерни и колеса
3.9 Фактическое передаточное число
3.10 Диаметры колес
3.11 Размеры заготовок колес
3.12 Силы в зацеплении
3.13 Проверка зубьев колес по напряжениям изгиба
3.14 Проверка зубьев колес по контактным напряжениям
4 РАСЧЕТ ЭЛЕМЕНТОВ КОРПУСА РЕДУКТОРА
5 ПОДБОР ПОДШИПНИКОВ ПО ДИНАМИЧЕСКОЙ ГРУЗОПОДЪЁМНОСТИ
5.1 Определение радиальных реакций
5.2 Определение осевых нагрузок
6 ПРОВЕРОЧНЫЙ РАСЧЕТ ВАЛОВ
7 ПРОВЕРКА ПРОЧНОСТИ ШПОНОЧНОГО СОЕДИНЕНИЯ
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Технический уровень всех отраслей народного хозяйства в значительной мере определятся уровнем развития машиностроения. На основе развития машиностроения осуществляется комплексная механизация и автоматизация производственных процессов в промышленности, строительстве, сельском хозяйстве, на транспорте.
В данном проекте разрабатывается привод поворотной части робота, состоящий из поворотной колонны и редуктора.
Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи мощности от двигателя к рабочей машине. Назначение редуктора – понижение угловой скорости и повышение вращающего момента ведомого вала по сравнению с валом ведущим.
1 ИСХОДНЫЕ ДАННЫЕ
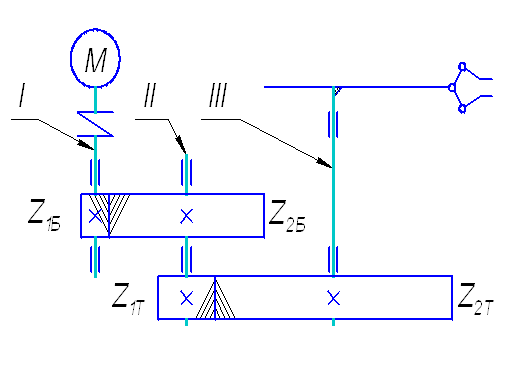
Рис. 1. Кинематическая схема привода
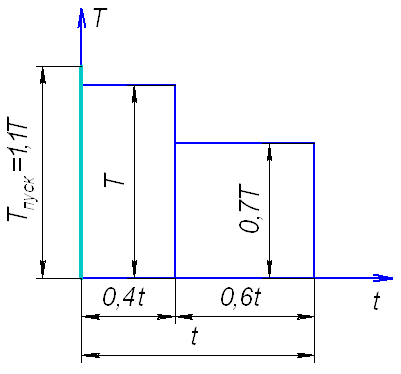
Рис. 2. График загрузки
2 КИНЕМАТИЧЕСКИЕ РАСЧЕТЫ
2.1 Выбор электродвигателя
Потребную мощность электродвигателя определим по формуле:
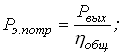
где ![]()
Здесь ![]() – КПД цилиндрической
передачи;
– КПД цилиндрической
передачи;
![]() – КПД пары подшипников качения;
– КПД пары подшипников качения;
![]() – КПД соединительной муфты.
– КПД соединительной муфты.
Вычисляем общий КПД привода:
![]()
Потребная мощность электродвигателя:
![]() .
.
Определим частоту вращения вала электродвигателя по формуле
![]() ,
,
где ![]() ,
, ![]() – передаточные числа
тихоходной и быстроходной ступеней, соответственно.
– передаточные числа
тихоходной и быстроходной ступеней, соответственно.
Рекомендуемые значения
передаточных чисел ![]() принимаем по таблице 1.2 [1],
получаем:
принимаем по таблице 1.2 [1],
получаем:
![]()
![]()
Вычисляем частоту вращения электродвигателя:
![]()
По справочнику [2] подбираем электродвигатель 4А112МА8 со следующими характеристиками:
![]()
![]()
2.2 Определение передаточных чисел привода
Определим окончательное общее передаточное число привода по формуле:
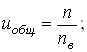
получим
![]()
Полученное расчетом общее передаточное число распределим между ступенями привода, пользуясь соотношениями, приведенными в таблице 1.3 [1]:
![]()
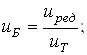
где ![]() – передаточное число
редуктора, в нашем случае равное
– передаточное число
редуктора, в нашем случае равное ![]() .
.
Вычисляем передаточные отношения ступеней
![]()
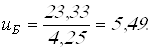
2.3 Определение вращающих моментов на валах привода
Частота вращения вала
колеса тихоходной ступени ![]()
![]() .
.
Частота вращения вала
колеса быстроходной ступени ![]()
![]() .
.
Момент на приводном валу ![]()
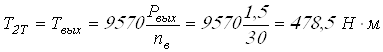 .
.
Момент на валу колеса
быстроходной ступени редуктора ![]()
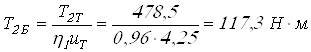 .
.
3 РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
3.1 Выбор твердости, термической обработки и материала колес
Для колес быстроходной ступени выберем сталь 40ХН и термическую обработку по II варианту [1] – т.о. колеса – улучшение, твердость HB 269…302; т.о. шестерни – улучшение и закалка ТВЧ, твердость поверхности HRC 48…53.
Для колес тихоходной ступени выберем тоже сталь 40ХН и термическую обработку по I варианту [1] – т.о. колеса – улучшение, твердость HB 235…262; т.о. шестерни – улучшение, твердость HB 269…302.
3.2 Допускаемые напряжения
Расчет передач проведем по допускаемым напряжениям
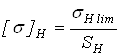
и 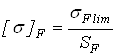
соответствующим длительной контактной и изгибной выносливостям:
![]() и
и ![]() – пределы выносливостей;
– пределы выносливостей;
![]() и
и ![]() – коэффициенты безопасности по
контактным (индекс ) и изгибным (индекс F) напряжениям.
– коэффициенты безопасности по
контактным (индекс ) и изгибным (индекс F) напряжениям.
Допускаемые контактные
напряжения и напряжения изгиба определим отдельно для колеса ![]() ,
, ![]() и шестерни
и шестерни ![]() ,
, ![]() .
.
Значения ![]() и
и ![]() принимаем по таблице 2.2
[1], в которой
принимаем по таблице 2.2
[1], в которой ![]() и
и ![]() – средняя твердость для двух
предельных значений, приведенных в вариантах т.о. и в таблице 2.1.
– средняя твердость для двух
предельных значений, приведенных в вариантах т.о. и в таблице 2.1.
Для тихоходной ступени принимаем
![]()
![]() ,
,
и получаем следующие значения
для колеса
![]() ;
;
![]() ,
,
для шестерни
![]() ;
;
![]() ,
,
для быстроходной ступени принимаем
![]()
![]()
![]()
![]() ,
,
и получаем следующие значения
для колеса
![]()
![]()
для шестерни
![]()
![]() .
.
Для зубчатых передач при II варианте т.о. определяют расчетное допускаемое контактное напряжение
![]()
это напряжение не должно
превышать ![]() .
.
Вычисляем
![]()
условие
![]() .
.
выполняется. В расчетную
формулу вместо ![]() подставим меньшее из значений
подставим меньшее из значений ![]() и
и ![]() ,
следовательно, для дальнейших расчетов будем использовать, следующие значения
допустимых напряжений:
,
следовательно, для дальнейших расчетов будем использовать, следующие значения
допустимых напряжений:
для тихоходной ступени
![]() ;
;
![]() ,
,
для быстроходной ступени
![]() ;
;
![]() .
.
3.3 Расчет межосевого расстояния
Межосевое расстояние определяется по формуле:
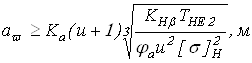
где коэффициент![]() – для
косозубых колес.
– для
косозубых колес.
Коэффициент концентрации
нагрузки ![]() принимаем
для прирабатывающихся колес при переменной нагрузке:
принимаем
для прирабатывающихся колес при переменной нагрузке:
![]()
где ![]() – начальный коэффициент
концентрации нагрузки;
– начальный коэффициент
концентрации нагрузки;
![]() – коэффициент режима нагрузки.
– коэффициент режима нагрузки.
При ступенчатом графике
режима нагружения коэффициент ![]() вычисляем по формуле:
вычисляем по формуле:
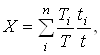
где ![]() – момент при i-м режиме
нагружения;
– момент при i-м режиме
нагружения;
![]() – наибольший момент из числа
длительно действующих;
– наибольший момент из числа
длительно действующих;
![]() – время работы передачи (ч) при
i-м режиме;
– время работы передачи (ч) при
i-м режиме;
![]() – время работы передачи, ч.
– время работы передачи, ч.
Вычисляем коэффициент режима нагрузки
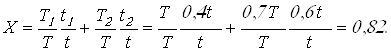
Начальный коэффициент
концентрации нагрузки ![]() принимаем по таблице 2.3 [1] в
зависимости от коэффициента
принимаем по таблице 2.3 [1] в
зависимости от коэффициента 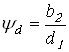 . Так как ширина колеса
. Так как ширина колеса ![]() и диаметр
шестерни
и диаметр
шестерни ![]() ещё
не определены, коэффициент
ещё
не определены, коэффициент ![]() определяем ориентировочно:
определяем ориентировочно:
![]() ,
,
где коэффициент ![]() принимаем из
ряда стандартных чисел в зависимости от положения колес относительно опор,
равным:
принимаем из
ряда стандартных чисел в зависимости от положения колес относительно опор,
равным:
для тихоходной передачи, при консольной расположении колес
![]() ,
,
для быстроходной передачи, при симметричном расположении колес
![]() .
.
Вычисляем коэффициенты для передач:
![]() ;
;
![]()
По таблице 2.3 [1] в
зависимости от коэффициента ![]() находим
находим ![]() .
.
Получаем
![]() ;
;
![]() .
.
При коэффициенте ![]() целесообразно
применять колеса с бочкообразными зубьями, для которых
целесообразно
применять колеса с бочкообразными зубьями, для которых ![]() , тогда получим
, тогда получим
![]() ;
;
![]() .
.
Вычисляем коэффициенты концентрации нагрузки
![]() ;
;
![]() .
.
![]() – эквивалентный момент на колесе,
где
– эквивалентный момент на колесе,
где
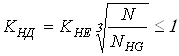 – коэффициент долговечности.
– коэффициент долговечности.
Здесь: ![]() – коэффициент
эквивалентности, зависящий от режима нагружения;
– коэффициент
эквивалентности, зависящий от режима нагружения; 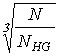 – коэффициент циклов, учитывающий
различие в числе циклов нагружений зубчатых колес в разных ступенях передач;
– коэффициент циклов, учитывающий
различие в числе циклов нагружений зубчатых колес в разных ступенях передач; ![]() – базовое
число циклов нагружений.
– базовое
число циклов нагружений.
При ступенчатом графике режима нагружения коэффициент эквивалентности
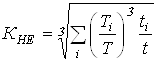 ,
,
где ![]() ;
; ![]() ;
; ![]() и
и ![]() определяются также как
и при вычислении коэффициента режима
определяются также как
и при вычислении коэффициента режима ![]() .
.
Базовое число циклов нагружения
![]() ;
;
![]() .
.
Число циклов нагружения
![]() ,
,
где ![]() – число зацеплений
колеса;
– число зацеплений
колеса;
![]() – время работы передачи,
определяется так
– время работы передачи,
определяется так
![]() ,
,
где ![]() – срок службы привода;
– срок службы привода;
![]() – коэффициент годовой загрузки
привода;
– коэффициент годовой загрузки
привода;
![]() – сменность работы привода;
– сменность работы привода;
![]() – коэффициент сменной загрузки
привода.
– коэффициент сменной загрузки
привода.
Вычисляем числа циклов нагружения
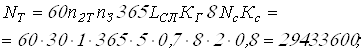
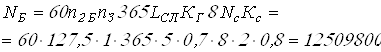
Вычисляем коэффициент эквивалентности
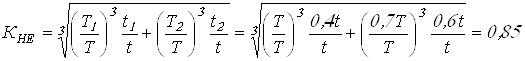 .
.
Вычисляем коэффициенты долговечности
 , принимаем
, принимаем ![]() ;
;
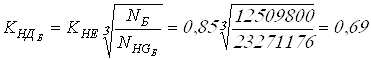 .
.
Вычисляем эквивалентные моменты на колесах
![]() ;
;
![]() .
.
Вычисляем межосевые расстояния
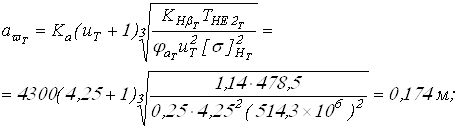

Вычисленные межосевые расстояния округляем в большую сторону до стандартных значений и окончательно получаем:
![]() ;
;
![]() .
.
3.4 Предварительные основные размеры колес
Делительный диаметр зубчатых колес
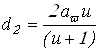 ;
;
![]() .
.
Ширина зубчатых колес
![]() .
.
Вычисляем основные размеры колес
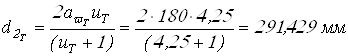 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3.5 Диаметры валов
Диаметры различных участков валов редуктора определим по формулам:
для быстроходного вала
![]() ;
;
![]() ;
;
![]() ,
,
для промежуточного вала
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
для тихоходного вала
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
где ![]() – высота буртика;
– высота буртика;
![]() – фаска подшипника;
– фаска подшипника;
![]() – размер фаски
– размер фаски
принимаемые в зависимости
от диаметра ![]() посадочной
поверхности.
посадочной
поверхности.
Вычисляем диаметры валов и округляем их в ближайшую сторону до стандартных значений:
быстроходный вал
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ,
,
для промежуточного вала
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ;
;
![]() .
.
тихоходный вал
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ;
;
![]() ;
;
![]() принимаем
принимаем ![]() ;
;
![]() .
.
3.6 Модуль передач
Модуль передач определим по формуле:
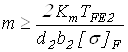 ,
,
где коэффициент ![]() – для
косозубых колес.
– для
косозубых колес.
![]() – эквивалентный момент на колесе,
– эквивалентный момент на колесе,
где 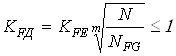 – коэффициент
долговечности.
– коэффициент
долговечности.
Здесь: ![]() – базовое число циклов
– базовое число циклов
При ступенчатом графике режима нагружения коэффициент эквивалентности
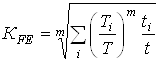 ,
,
где ![]() при т.о. колес –
улучшение.
при т.о. колес –
улучшение.
Вычисляем коэффициент
эквивалентности ![]()
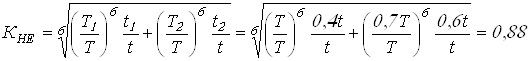
Вычисляем коэффициенты
долговечности ![]()
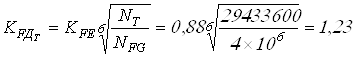 , принимаем
, принимаем ![]() ;
;
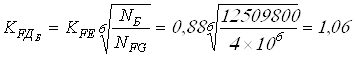 , принимаем
, принимаем ![]() .
.
Вычисляем эквивалентные
моменты на колесах ![]()
![]() ;
;
![]() .
.
Вычисляем модули передач
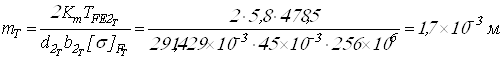 ;
;
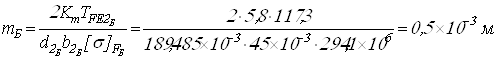 .
.
Значения модуля, полученные расчетом, округляем до стандартной величины и получаем
![]() ;
;
![]() .
.
3.7 Суммарное число зубьев и угол наклона
Минимальный угол наклона зубьев косозубых колес
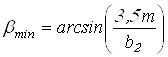
Вычисляем
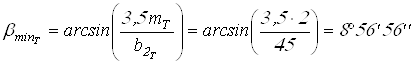 ;
;
 .
.
Суммарное число зубьев
![]()
Вычисляем суммарное число зубьев
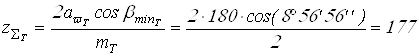 ;
;
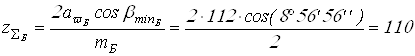 .
.
Определяем действительное значение угла
 ;
;
Вычисляем
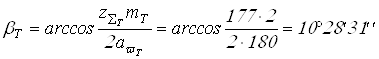 ;
;
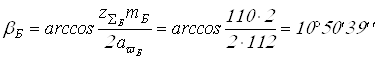 .
.
3.8 Число зубьев шестерни и колеса
Число зубьев шестерни
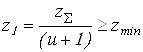
Вычисляем числа зубьев шестерен
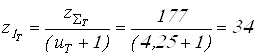 ;
;
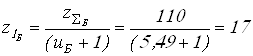 .
.
Для косозубых колес ![]()
Вычисляем минимально допустимое число зубьев
![]() ;
;
![]() .
.
Условие
![]()
выполняется для обеих передач.
Число зубьев колеса
![]()
Вычисляем числа зубьев колес
![]() ;
;
![]() .
.
3.9 Фактическое передаточное число
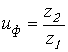
Вычисляем фактические передаточные числа
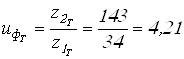 ;
;
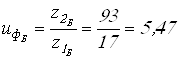 .
.
Общее передаточное число привода
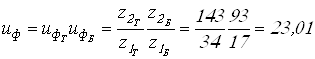
Отклонение от заданного передаточного числа
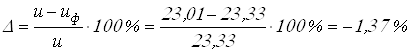
Условие
![]()
выполняется.
3.10 Диаметры колес
Делительные диаметры ![]() :
:
шестерни
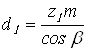 ;
;
колеса
![]() ;
;
Диаметры окружностей
вершин ![]() и
впадин
и
впадин ![]() зубьев
зубьев
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
где ![]() и
и ![]() – коэффициенты смещения
у шестерни и колеса;
– коэффициенты смещения
у шестерни и колеса; ![]() – коэффициент воспринимаемого
смещения.
– коэффициент воспринимаемого
смещения.
Вычисляем диаметры колес и полученные результаты заносим в таблицу 1.
Делительные диаметры
шестерен ![]()
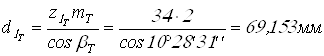 ;
;
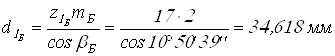 .
.
Делительные диаметры
колес ![]()
![]() ;
;
![]() .
.
Диаметры окружностей
вершин зубьев ![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Диаметры впадин ![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Параметры зубчатых колес Таблица 1
| Параметр |
|
|
|
|
| Число зубьев | | | | |
| Модуль, мм | | | ||
| Угол наклона, град | ¢¢¢ | ¢¢¢ | ||
| Делительный диаметр, мм | | | | |
| Диаметр впадин, мм | | | | |
| Диаметр вершин зубьев, мм | | | | |
| Межосевое расстояние, мм | | | ||
| Ширина венца, мм | | |
3.11 Размеры заготовок колес
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, вычислим предельные размеры заготовок и проверим выполнение условий
![]() ;
;
![]() ;
;
Диаметр заготовки
![]() ;
;
для колеса с выточками принимаем меньшее из
![]() ;
;
![]() ,
,
для колеса без выточек
![]() .
.
По таблице 2.1 [1] находим следующие предельные размеры заготовок
электродвигатель привод вал
для ![]() ,
, ![]() ,
, ![]() –
– ![]() ;
; ![]() ;
;
для ![]() –
– ![]() ;
; ![]() .
.
Вычисляем размеры заготовок
для ![]() (без выточки)
(без выточки)
![]() ;
;
![]() ,
,
для ![]() (с выточкой)
(с выточкой)
![]() ;
;
![]() ,
,
для ![]() (без выточки)
(без выточки)
![]() ;
;
![]() ,
,
для ![]() (с выточкой)
(с выточкой)
![]() ;
;
![]()
проверяем условия ![]() и
и ![]() – все
выполняются.
– все
выполняются.
3.12 Силы в зацеплении
Окружная сила ![]()
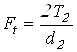 ;
;
Радиальная сила ![]()
 ;
;
Осевая сила ![]()
![]() .
.
Вычислим уточненные крутящие моменты и частоты вращения
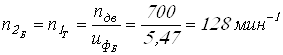 ;
;
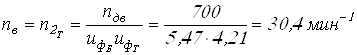 ;
;
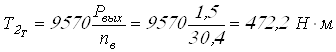 ;
;
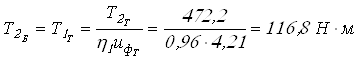 ;
;
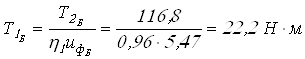 ;
;
Вычисляем силы в зацеплениях и результаты заносим в таблицу 2.
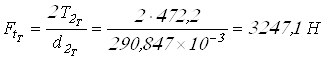 ;
;
 ;
;
 ;
;
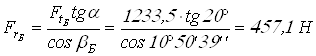 ;
;
![]() ;
;
![]() .
.
Силы в зацеплении, в Н Таблица 2
| Ступень |
Окружная сила |
Радиальная
сила |
Осевая сила |
Крутящий момент
|
Частота вращения
|
| Быстроходная | | | | | |
| Тихоходная | | | | | |
3.13 Проверка зубьев колес по напряжениям изгиба
Расчетное напряжение изгиба в зубьях колеса определим по формуле
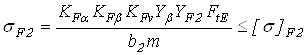 ;
;
в зубьях шестерни по формуле
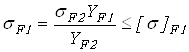 .
.
Степень точности передач принимаем по таблице 2.5 [1] в зависимости от окружной скорости колеса (м/с)
![]() ;
;
Вычисляем окружные скорости колес
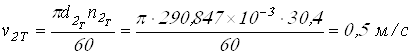 ;
;
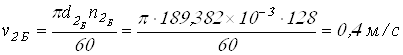 .
.
По таблице 2.5 [1] принимаем 9-ю степень точности для всех колес.
Для косозубых колес при
выбранной степени точности коэффициент ![]() .
.
Коэффициент концентрации
нагрузки ![]() принимаем
для прирабатывающихся колес по формуле
принимаем
для прирабатывающихся колес по формуле
![]() ,
,
где ![]() – начальный коэффициент
концентрации нагрузки;
– начальный коэффициент
концентрации нагрузки;
![]() – коэффициент режима.
– коэффициент режима.
По таблице 2.6 [1] в
зависимости от 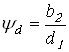 принимаем
принимаем
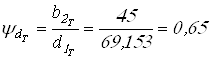 ;
; ![]() ;
;
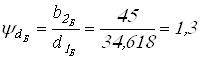 ;
; ![]() .
.
Вычисляем коэффициенты
концентрации нагрузки ![]()
![]() ;
;
![]() .
.
Коэффициент динамической
нагрузки ![]() принимаем
по таблице 2.7 [1]
принимаем
по таблице 2.7 [1]
![]() .
.
Коэффициент ![]() вычисляют по
формуле
вычисляют по
формуле
![]() .
.
Вычисляем коэффициенты ![]()
![]() ;
;
![]() .
.
Коэффициенты формы зуба ![]() принимаем по
таблице 2.8 [1]
принимаем по
таблице 2.8 [1]
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
![]() – эквивалентная окружная сила.
– эквивалентная окружная сила.
Вычисляем эквивалентную
окружную силу ![]()
![]() ;
;
![]() .
.
Вычисляем напряжения изгиба действующие в передачах
для колес
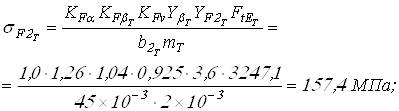
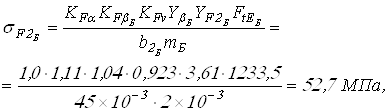
для шестерен
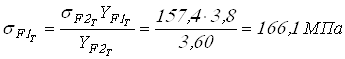 ;
;
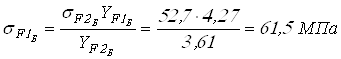 .
.
Все условия
![]()
выполняются.
Проверим зубья колес на
статическую прочность по кратковременно действующим пиковым моментам ![]()
![]()
Значение ![]() берем из таблицы 2.2
[1]
берем из таблицы 2.2
[1]
![]() – при т.о. колеса улучшение;
– при т.о. колеса улучшение;
![]() – при сквозной закалке зубьев
ТВЧ.
– при сквозной закалке зубьев
ТВЧ.
Получаем
для ![]()
![]() ;
;
для ![]() и
и ![]()
![]() ;
;
для ![]()
![]() .
.
Вычисляем напряжения изгиба при кратковременно действующих пиковых моментах
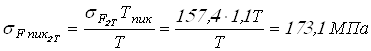 ;
;
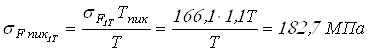 ;
;
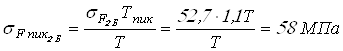 ;
;
 .
.
Все условия
![]()
выполняются.
3.14 Проверка зубьев колес по контактным напряжениям
Расчетное контактное напряжение определим по формуле
 ,
,
где для косозубых колес ![]() ;
; ![]() . Коэффициент
. Коэффициент ![]() принимаем по
таблице 2.9 [1] и получаем
принимаем по
таблице 2.9 [1] и получаем
![]() .
.
Вычисляем контактные напряжения, действующие в колесах
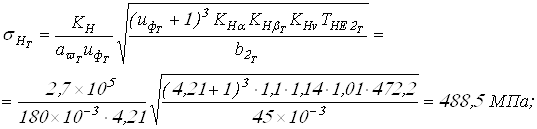
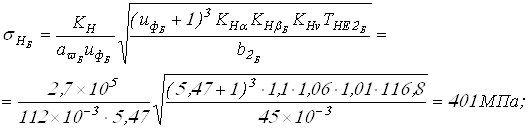
Условия
![]()
выполняются.
Проверим зубья колес на
статическую прочность при кратковременных действующих пиковых моментах ![]() по формуле
по формуле
 .
.
Значения ![]() берем из таблицы 2.2
[1]
берем из таблицы 2.2
[1]
![]() – при т.о. колеса улучшение;
– при т.о. колеса улучшение;
![]() – при сквозной закалке зубьев
ТВЧ.
– при сквозной закалке зубьев
ТВЧ.
Получаем
для ![]()
![]() ,
,
для ![]() и
и ![]()
![]() ,
,
для ![]()
![]() .
.
Вычисляем контактные напряжения при кратковременно действующих пиковых моментах
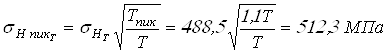 ;
;
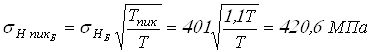 .
.
Все условия
![]()
выполняются.
4 РАСЧЕТ ЭЛЕМЕНТОВ КОРПУСА РЕДУКТОРА
Чтобы поверхности
вращающихся колес не задевали за внутренние поверхности стенок корпуса, между
ними оставляют зазор ![]() , который определяют по формуле
, который определяют по формуле
![]() ,
,
где ![]() – наибольшее расстояние
между внешними поверхностями деталей передач, мм.
– наибольшее расстояние
между внешними поверхностями деталей передач, мм.
Вычисляем зазор ![]()
![]() .
.
Толщину стенки ![]() , отвечающую
требованиям технологии литья и необходимой жесткости корпуса редуктора,
рекомендуется определять по формуле
, отвечающую
требованиям технологии литья и необходимой жесткости корпуса редуктора,
рекомендуется определять по формуле
![]() ,
,
где ![]() – вращающий момент на
тихоходном валу,
– вращающий момент на
тихоходном валу, ![]() .
.
Вычисляем толщину стенки ![]()
![]() принимаем
принимаем ![]() .
.
Радиусы для сопряжения стенок корпуса редуктора определим по соотношению
![]() ;
; ![]()
где ![]() – радиус внутреннего
сопряжения, а
– радиус внутреннего
сопряжения, а ![]() – наружного.
– наружного.
Вычисляем радиусы ![]() и
и ![]()
![]() ;
; ![]() .
.
Предварительно выберем
для обеих опор роликовые конические подшипники средней серии ![]() со следующими характеристиками:
со следующими характеристиками:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Требуемая долговечность подшипников в часах
![]()
полученное значение
округляем по таблице 70 [3] до ![]() .
.
5.1 Определение радиальных реакций
Радиальная реакция
подшипника ![]() считается
приложенной к оси вала в точке пересечения с ней нормалей, проведенных через
середины контактных площадок. Для роликовых конических подшипников расстояние
«а» между этой точкой и торцом подшипника определяется по формуле:
считается
приложенной к оси вала в точке пересечения с ней нормалей, проведенных через
середины контактных площадок. Для роликовых конических подшипников расстояние
«а» между этой точкой и торцом подшипника определяется по формуле:
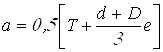 ,
,
где ![]() – монтажная высота
кольца;
– монтажная высота
кольца;
![]() – диаметр внутреннего кольца
подшипника;
– диаметр внутреннего кольца
подшипника;
![]() – диаметр наружного кольца
подшипника;
– диаметр наружного кольца
подшипника;
![]() – коэффициент осевого нагружения.
– коэффициент осевого нагружения.
Вычисляем расстояние «а»
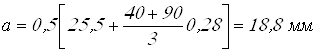 .
.
С учетом монтажной высоты
кольца ![]() и
расстояния «а» построим расчетную схему для определения радиальных сил
действующих на подшипники (рис. 3).
и
расстояния «а» построим расчетную схему для определения радиальных сил
действующих на подшипники (рис. 3).

Рис. 3. Схема к определению реакций опор
Приведем плоскости действия известных сил к двум взаимно перпендикулярным плоскостям. Реакции опор определим из условия равновесия всех сил относительно каждой опоры.
Плоскость X–X
![]() ;
;
![]() , откуда реакция
, откуда реакция ![]() равна
равна
![]() .
.
![]() ;
;
![]() , откуда реакция
, откуда реакция ![]() равна
равна
![]() .
.
Плоскость Y–Y
![]() ;
;
![]() , откуда реакция
, откуда реакция ![]() равна
равна
![]() .
.
![]() ;
;
![]() , откуда реакция
, откуда реакция ![]() равна
равна
![]() .
.
Результирующие радиальные силы, максимально длительно действующие на подшипники, вычислим по формуле
![]() ,
,
где ![]() и
и ![]() – соответственно
горизонтальная и вертикальная составляющие радиальной силы.
– соответственно
горизонтальная и вертикальная составляющие радиальной силы.
![]() ;
;
![]() .
.
5.2 Определение осевых нагрузок
Результирующая осевая сила, действующая на подшипники от косозубых зубчатых колес равна
![]() .
.
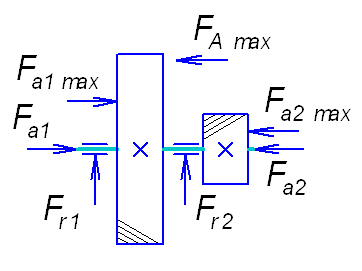
Рис. 4. Схема нагружения подшипников
При установке вала на
радиально-упорных подшипниках осевые силы ![]() , нагружающие подшипники, находят
с учетом осевых составляющих S от
действия радиальных сил
, нагружающие подшипники, находят
с учетом осевых составляющих S от
действия радиальных сил ![]() :
:
для конических роликовых подшипников
![]() ,
,
где ![]() – коэффициент осевой
нагрузки.
– коэффициент осевой
нагрузки.
Вычисляем осевые
составляющие ![]()
![]() ;
;
![]() .
.
В таблице 7.2 [1] исходя
из условий нагружения ![]() ;
; ![]() получаем формулы для вычисления
получаем формулы для вычисления ![]() и
и ![]() :
:
![]() ;
;
![]() .
.
Вычисляем осевые силы ![]() , нагружающие
подшипники
, нагружающие
подшипники
![]() ;
;
![]() .
.
Эквивалентную
динамическую нагрузку ![]() для подшипников определим по
формуле
для подшипников определим по
формуле
![]() ,
,
где ![]() и
и ![]() – коэффициенты
радиальной и осевой нагрузок;
– коэффициенты
радиальной и осевой нагрузок;
![]() – коэффициент вращения;
– коэффициент вращения;
![]() – коэффициент безопасности;
– коэффициент безопасности;
![]() – коэффициент, зависящий от
рабочей температуры подшипника.
– коэффициент, зависящий от
рабочей температуры подшипника.
Вычисляем эквивалентные
динамические нагрузки ![]()
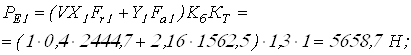
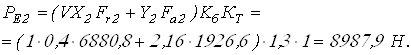
Требуемую грузоподъёмность подшипников определим по самой нагруженной опоре 2 по формуле
 ,
,
где ![]() – частота вращения
кольца, мин-1;
– частота вращения
кольца, мин-1;
для роликовых подшипников
![]() .
.
Требуемая
грузоподъёмность подшипников ![]() равна
равна
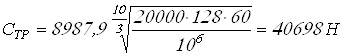 .
.
Так как
![]() ,
,
то предварительно намеченный подшипник подходит.
6 ПРОВЕРОЧНЫЙ РАСЧЕТ ВАЛОВ
При расчете примем, что насаженные на вал детали передают силы и моменты валу на середине своей ширины.
Под действием постоянных по величине и направлению сил во вращающихся валах возникают напряжения, изменяющиеся по симметричному циклу.
Построим расчетную схему для II вала: нанесем на неё все внешние силы нагружающие вал (рис. 5).
Расчет произведем в форме проверки коэффициента запаса прочности. Для каждого из установленных предположительно опасных сечений определим расчетный коэффициент запаса прочности «S» и сравним его с допускаемым значением [S], которое обычно принимают [S]=1,3…2.
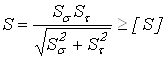 ,
,
где ![]() и
и ![]() – коэффициенты запаса
по нормальным и касательным напряжениям, определяемые по зависимостям:
– коэффициенты запаса
по нормальным и касательным напряжениям, определяемые по зависимостям:
 – для напряжений изменяющихся по
симметричному циклу.
– для напряжений изменяющихся по
симметричному циклу.
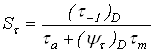
Здесь ![]() и
и ![]() – амплитуды напряжений
цикла;
– амплитуды напряжений
цикла;
![]() – среднее напряжение цикла.
– среднее напряжение цикла.
![]() ;
; ![]() .
.
Напряжение в опасных сечениях определим по формулам
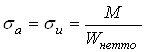 ;
; 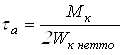 ,
,
где ![]() – результирующий
изгибающий момент;
– результирующий
изгибающий момент;
![]() – крутящий момент;
– крутящий момент;
![]() и
и ![]() – осевой и полярный моменты сопротивления
сечения вала.
– осевой и полярный моменты сопротивления
сечения вала.
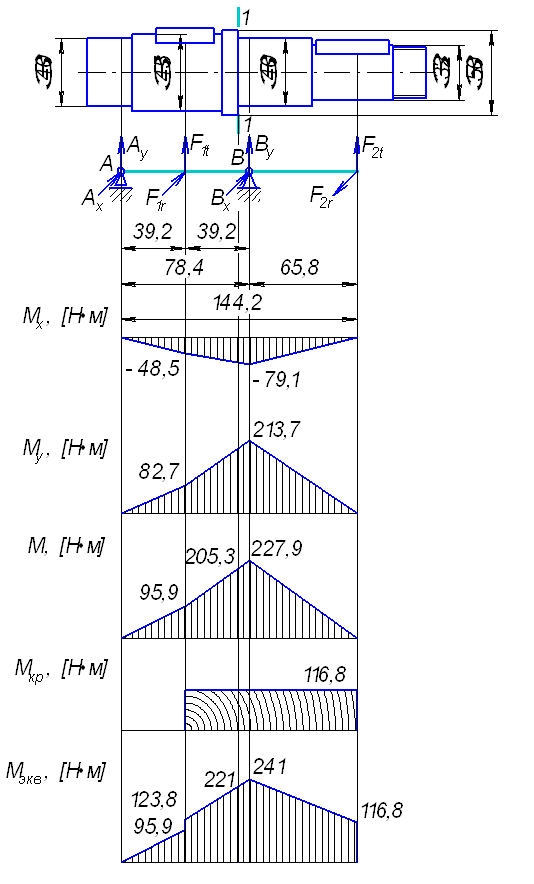
Рис. 5. Расчетная схема II вала
Пределы выносливости вала в рассматриваемом сечении
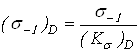 ;
;
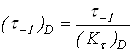
где ![]() и
и ![]() – пределы выносливости
гладких образцов при симметричном цикле изгиба и кручения;
– пределы выносливости
гладких образцов при симметричном цикле изгиба и кручения;
![]() и
и ![]() – коэффициенты концентрации
напряжений для данного сечения вала.
– коэффициенты концентрации
напряжений для данного сечения вала.
Значения ![]() и
и ![]() находят по
зависимостям:
находят по
зависимостям:
 ;
;
 ,
,
где ![]() и
и ![]() – эффективные
коэффициенты концентрации напряжений;
– эффективные
коэффициенты концентрации напряжений;
![]() – коэффициент влияния абсолютных
размеров поперечного сечения;
– коэффициент влияния абсолютных
размеров поперечного сечения;
![]() – коэффициент влияния
шероховатости;
– коэффициент влияния
шероховатости;
![]() – коэффициент влияния
поверхностного упрочнения.
– коэффициент влияния
поверхностного упрочнения.
Коэффициент влияния асимметрии цикла для рассматриваемого сечения вала
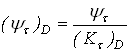 ,
,
где ![]() – коэффициент
чувствительности материала к асимметрии цикла напряжений.
– коэффициент
чувствительности материала к асимметрии цикла напряжений.
По эпюрам эквивалентного
момента ![]() (рис.
5) видно, что самым опасным сечением является сечение 1–1.
(рис.
5) видно, что самым опасным сечением является сечение 1–1.
Материал вала выберем
сталь 45 со следующими характеристиками: HB 270, ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Осевой ![]() и полярный
и полярный ![]() моменты
сопротивления сечения 1‑1
моменты
сопротивления сечения 1‑1
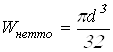 ;
;
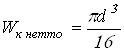 .
.
где ![]() – диаметр сечения
равный 40 мм.
– диаметр сечения
равный 40 мм.
Вычисляем моменты сопротивления
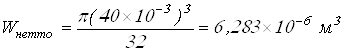 ;
;
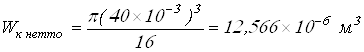 .
.
Вычисляем напряжения в опасном сечении
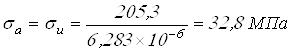 ;
;
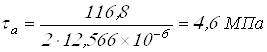 ,
,
По таблицам 10.3…10.6 [1] находим значения следующих коэффициентов
![]() ;
; ![]() ; при
; при ![]() ;
; ![]() .
.
![]() ; при
; при ![]() .
.
![]() – без упрочнения.
– без упрочнения.
Вычисляем коэффициенты концентрации напряжений
при ![]()
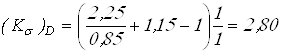 ;
;
при ![]()
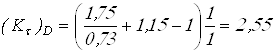 .
.
Вычисляем коэффициент влияния асимметрии цикла
![]() .
.
Вычисляем пределы выносливости вала в рассматриваемом сечении
![]() ;
;
![]() .
.
Вычисляем коэффициенты запаса по нормальным и касательным напряжениям
![]() ;
;
![]() .
.
Вычисляем коэффициент запаса прочности
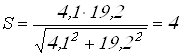 .
.
Запас прочности обеспечен достаточный так как
![]() .
.
7 ПРОВЕРКА ПРОЧНОСТИ ШПОНОЧНОГО СОЕДИНЕНИЯ
Рекомендуется назначать одинаковые шпонки для всех ступеней вала исходя из ступени наименьшего диаметра, имеющего шпоночный паз. Наличие на одном валу шпоночных пазов, одинаковых по сечению и длине, улучшает технологичность конструкции вала.
Предварительно выберем сечение шпонки, рекомендуемое ГОСТ 23360‑78, исходя из величины диаметра вала.
Получаем шпонку 12´8´40 ГОСТ 23360‑78.
Проверим рабочие грани шпонки на смятие. Условие прочности на смятие
![]() ,
,
где ![]() – наибольший
допускаемый крутящий момент;
– наибольший
допускаемый крутящий момент;
![]() – диаметр вала;
– диаметр вала;
![]() – рабочая длина шпонки;
– рабочая длина шпонки;
![]() – выступ шпонки от шпоночного
паза;
– выступ шпонки от шпоночного
паза;
![]() – допускаемое напряжение на
смятие.
– допускаемое напряжение на
смятие.
Вычисляем наибольший
допускаемый крутящий момент ![]()
![]()
так как наибольший
продолжительно действующий крутящий момент на валу ![]() , то выбранная шпонка проходит
проверку на смятие
, то выбранная шпонка проходит
проверку на смятие
![]()
Проверим шпонку на срез. Условие прочности сечения шпонки на срез
![]() ,
,
где ![]() – ширина шпонки;
– ширина шпонки;
![]() – допускаемое напряжение на срез.
– допускаемое напряжение на срез.
Вычисляем наибольший
допускаемый крутящий момент ![]()
![]() ,
,
так как ![]() , то выбранная шпонка
проходит проверку на срез.
, то выбранная шпонка
проходит проверку на срез.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Дунаев П. Ф., Леликов О. П. Конструирование узлов и деталей машин. ‑М.: Высшая школа, 1985.
2. Асинхронные двигатели серии 4А: Справочник/ под ред. Кравчика А. Э., Шлафа М. М. и др. ‑М.: Энергоиздат, 1982.
3. Справочник конструктора-машиностроителя/ под ред. Анурьева В. И. т. 2 – М.: Машиностроение, 1982.