Контрольная работа: Математическое моделирование финансовых операций
Министерство образования и науки РФ
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Всероссийский заочный финансово-экономический институт
Филиал в г. Туле
Факультет финансово-кредитный
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
Финансовая математика
Вариант №6.
Тула-2009 г.
Содержание:
Задание №1
Задание №3
Список использованной литературы
Задание №1
В каждом варианте приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах, табл. 1.1) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).
Таблица 1.1
Исходные данные
| Вариант №6 | ||||||||||||||||
| Квартал | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Данные | 36 | 46 | 55 | 35 | 39 | 50 | 61 | 37 | 42 | 54 | 64 | 40 | 47 | 58 | 70 | 43 |
Требуется:
1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания α1=0,3, α2=0,6, α3=0,3.
2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной модели на основе исследования:
- случайности остаточной компоненты по критерию пиков;
- независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и по первому коэффициенту автокорреляции при критическом значении r1=0,32;
- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить на графике фактические, расчетные и прогнозные данные.
Решение:
1) Модель Хольта-Уинтерса имеет вид:
![]()
где k – период упреждения, k=1;
at, bt, Ft — коэффициенты модели;
L — период сезонности, L=4.
Адаптация к новому значению параметра времени t коэффициентов модели Хольта-Уинтерса производится по формулам
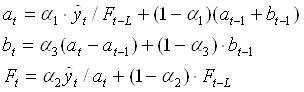
Для оценки начальных значений a0 и b0 применим линейную модель к первым 8-ми значениям заданного ряда (табл. 1.2.)
Таблица 1.2
Расчет параметров линейной модели a0 и b0
| t |
yt |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 | 36 | -8,875 | -3,5 | 12,25 | 31,0625 | 41,90 |
| 2 | 46 | 1,125 | -2,5 | 6,25 | -2,8125 | 42,75 |
| 3 | 55 | 10,125 | -1,5 | 2,25 | -15,1875 | 43,60 |
| 4 | 35 | -9,875 | -0,5 | 0,25 | 4,9375 | 44,45 |
| 5 | 39 | -5,875 | 0,5 | 0,25 | -2,9375 | 45,30 |
| 6 | 50 | 5,125 | 1,5 | 2,25 | 7,6875 | 46,15 |
| 7 | 61 | 16,125 | 2,5 | 6,25 | 40,3125 | 47,00 |
| 8 | 37 | -7,875 | 3,5 | 12,25 | -27,5625 | 47,85 |
|
|
359 | 42 | 35,5 | |||
| 4,5 | 44,875 |
Расчет a0 и b0 произведем по формулам:
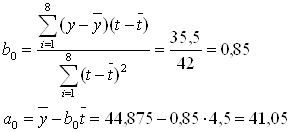
Таким образом, линейная модель имеет вид
![]() .
.
Подставив фактические
значения времени, найдем ![]()
Оценим приближенные значения коэффициентов сезонности F-3; F-2; F-1; F0 по формулам:

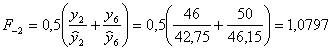
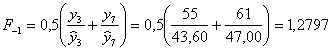
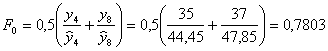
1. Тогда для момента времени t=0, и k=1 имеем
![]()
2. Для t=1, k=1,
![]()
![]()
![]()
![]()
3. Для t=2, k=1,
![]()
![]()
![]()
![]()
4. Для t=3, k=1,
![]()
![]()
![]()
![]()
5. Для t=4, k=1,
![]()
![]()
![]()
![]()
6. Для t=5, k=1,
![]()
![]()
![]()
![]()
7. Для t=6, k=1,
![]()
![]()
![]()
![]()
8. Для t=7, k=1,
![]()
![]()
![]()
![]()
9. Для t=8, k=1,
![]()
![]()
![]()
![]()
10. Для t=9, k=1,
![]()
![]()
![]()
![]()
11. Для t=10, k=1,
![]()
![]()
![]()
![]()
12. Для t=11, k=1,
![]()
![]()
![]()
![]()
13. Для t=12, k=1,
![]()
![]()
![]()
![]()
14. Для t=13, k=1,
![]()
![]()
![]()
![]()
15. Для t=14, k=1,
![]()
![]()
![]()
![]()
16. Для t=15, k=1,
![]()
![]()
![]()
![]()
17. Для t=16, k=1
![]()
![]()
![]()
Сведем полученные данные с таблицу (табл. 1.3.)
адаптивный мультипликативный коммерческий сглаживание
Таблица 1.3
Расчетные данные по модели Хольта-Уинтерса
|
|
y |
at |
bt |
Ft |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
-3 |
0,8601 | ||||||
|
-2 |
1,0797 | ||||||
|
-1 |
1,2797 | ||||||
|
0 |
41,05 | 0,85 | 0,7803 | ||||
|
1 |
36 | 41,90 | 0,85 | 0,8601 | 36,04 | -0,04 | 0,0011 |
|
2 |
46 | 42,75 | 0,85 | 1,0797 | 46,16 | -0,16 | 0,0035 |
|
3 |
55 | 43,60 | 0,85 | 1,2796 | 55,79 | -0,79 | 0,0144 |
|
4 |
35 | 44,45 | 0,85 | 0,7802 | 34,68 | 0,32 | 0,0091 |
|
5 |
39 | 45,30 | 0,85 | 0,8601 | 38,96 | 0,04 | 0,0010 |
|
6 |
50 | 46,15 | 0,85 | 1,0797 | 49,83 | 0,17 | 0,0034 |
|
7 |
61 | 47,00 | 0,85 | 1,2796 | 60,14 | 0,86 | 0,0141 |
|
8 |
37 | 47,85 | 0,85 | 0,7802 | 37,33 | -0,33 | 0,0089 |
|
9 |
42 | 48,70 | 0,85 | 0,8601 | 41,89 | 0,11 | 0,0026 |
|
10 |
54 | 49,55 | 0,85 | 1,0797 | 53,50 | 0,50 | 0,0093 |
|
11 |
64 | 50,40 | 0,85 | 1,2796 | 64,49 | -0,49 | 0,0077 |
|
12 |
40 | 51,25 | 0,85 | 0,7801 | 39,98 | 0,02 | 0,0005 |
|
13 |
47 | 52,10 | 0,85 | 0,8601 | 44,81 | 2,19 | 0,0466 |
|
14 |
58 | 52,95 | 0,85 | 1,0797 | 57,17 | 0,83 | 0,0143 |
|
15 |
70 | 53,80 | 0,85 | 1,2796 | 68,84 | 1,16 | 0,0166 |
|
16 |
43 | 54,65 | 0,85 | 0,7801 | 42,63 | 0,37 | 0,0086 |
|
Σ |
4,76 | 0,1617 | |||||
|
ср. |
0,30 | 0,0101 |
2) Оценим точность построенной модели Хольта-Уинтерса с использованием средней относительной ошибки аппроксимации, которую найдем по формуле (расчеты произведем в табл. 1.3. графы 7,8)
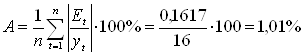
Так как средняя относительная ошибка аппроксимации А меньше 5%, то модель точная.
3) Проверим адекватность модели.
а) Для адекватной модели характерно равенство математического ожидания ряда остатков 0. Проверка осуществляется на основе t-критерия Стьюдента. Расчеты произведем в табл. 1.4.
Таблица 1.4
Проверка адекватности модели
|
|
|
Тп |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
| 1 | -0,04 | 0,1139 | - | - | 0,0016 | - |
| 2 | -0,16 | 0,2093 | 0 | 0,0144 | 0,0256 | 0,0064 |
| 3 | -0,79 | 1,1827 | 1 | 0,3969 | 0,6241 | 0,1264 |
| 4 | 0,32 | 0,0005 | 1 | 1,2321 | 0,1024 | -0,2528 |
| 5 | 0,04 | 0,0663 | 1 | 0,0784 | 0,0016 | 0,0128 |
| 6 | 0,17 | 0,0163 | 0 | 0,0169 | 0,0289 | 0,0068 |
| 7 | 0,86 | 0,3164 | 1 | 0,4761 | 0,7396 | 0,1462 |
| 8 | -0,33 | 0,3938 | 1 | 1,4161 | 0,1089 | -0,2838 |
| 9 | 0,11 | 0,0352 | 0 | 0,1936 | 0,0121 | -0,0363 |
| 10 | 0,50 | 0,0410 | 1 | 0,1521 | 0,2500 | 0,0550 |
| 11 | -0,49 | 0,6202 | 1 | 0,9801 | 0,2401 | -0,2450 |
| 12 | 0,02 | 0,0770 | 0 | 0,2601 | 0,0004 | -0,0098 |
| 13 | 2,19 | 3,5816 | 1 | 4,7089 | 4,7961 | 0,0438 |
| 14 | 0,83 | 0,2836 | 1 | 1,8496 | 0,6889 | 1,8177 |
| 15 | 1,16 | 0,7439 | 1 | 0,1089 | 1,3456 | 0,9628 |
| 16 | 0,37 | 0,0053 | - | 0,6241 | 0,1369 | 0,4292 |
| 7,6870 | 10 | 12,5083 | 9,1028 | 2,7794 | ||
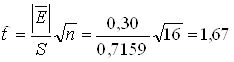
где
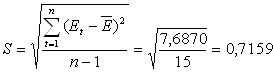
Сравним tрасч с табл t0,05; 15= 2,13. Т.к. 1,67<2,13, то на уровне значимости α=0,05 гипотеза о том, что математическое ожидание ряда остатков Et=0 принимается.
б) Проверим условие случайности уровней остаточной компоненты по критерию пиков.
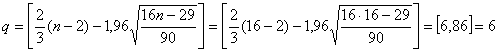
р=10, т.к. р>q (10>6), то условие случайности уровней остаточной компоненты выполняется.
в) Проверку независимости уровней ряда остатков (отсутствия автокорреляции) проведем с помощью критерия Дарбина-Уотсона. Расчеты произведем в табл. 1.4.
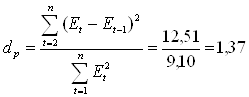
Т.к. d1<dp=1,37=d2, то для проверки независимости уровней ряда остатков используем первый коэффициент автокорреляции.
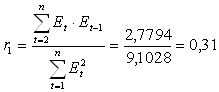
rтабл=0,34, так как r1<rтабл (0,31<0,34), то автокорреляция уровней ряда остатков отсутствует.
г) Проверку соответствия ряда остатков нормальному закону распределения выполним по R/S-критерию.
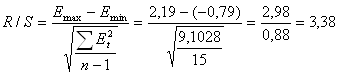
3 < 3,38< 4,21
d1<R/S<d2, значит условие подчинения ряда остатков нормальному закону распределения выполняется.
Так как все 4 условия выполнены, то модель является адекватной и ее можно использовать для прогнозирования.
4) Построим точечный прогноз на 4 шага вперед, т.е. на 1 год.
![]()
![]()
![]()
![]()
![]()
5) Отобразим на графике фактические, расчетные и прогнозные данные (Рис. 1).
Задание №2
Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:
1. экспоненциальную скользящую среднюю;
2. момент;
3. скорость изменения цен;
4. индекс относительной силы;
5. %R, %К, %D.
Расчеты проводить для тех дней, для которых эти расчеты можно выполнить на основании имеющихся данных (табл. 2.1.).
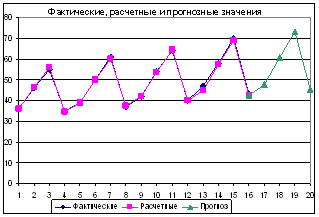
Рис. 1.1 График
Табл. 2.1
Исходные данные
| Вариант №6 | ||||
| Дни | Цены | |||
| макс. | мин. | закр. | ||
| 1 | 600 | 550 | 555 | |
| 2 | 560 | 530 | 530 | |
| 3 | 536 | 501 | 524 | |
| 4 | 545 | 521 | 539 | |
| 5 | 583 | 540 | 569 | |
| 6 | 587 | 562 | 581 | |
| 7 | 582 | 561 | 562 | |
| 8 | 573 | 556 | 556 | 573 |
| 9 | 610 | 579 | 592 | |
| 10 | 645 | 585 | 645 |
Решение:
1) Рассчитаем экспоненциальную скользящую среднюю по формуле
![]() , где
, где
ЕМАt — значение экспоненциальной скользящей средней текущего дня t;
Сt — цена закрытия t-го дня;
k – коэффициент,
![]() ;
;
n – интервал сглаживания, n=5.
![]()
![]()
![]()
![]()
![]()
![]()
Отобразим полученные данные на графике (рис. 2.1.)
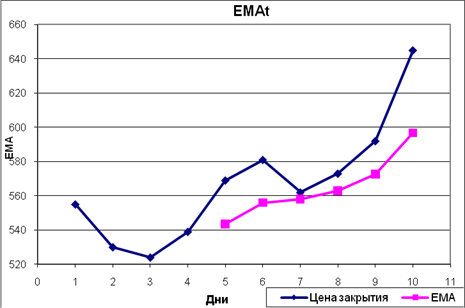
Рис. 2.1 График цен закрытия и ЕМА
На основании графика (рис. 2.1.) нельзя сделать выводов, так как графики цен закрытия и ЕМА не пересекаются.
2) Найдем момент по формуле
![]() , где
, где
Сt – цена закрытия текущего дня;
Ct-n – цена закрытия торгового дня n дней назад.
![]()
![]()
![]()
![]()
![]()
Построим график ![]()
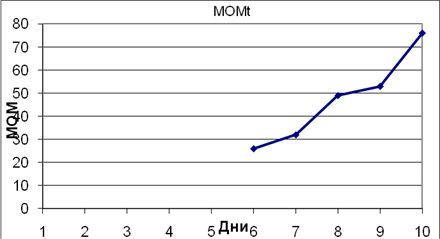
Рис. 2.2 График изменения момента МОМt.
График МОМt не пересекает нулевую линию, поэтому нет сигналов ни к покупке, ни к продаже акций, однако положительные значения МОМt свидетельствуют об относительном росте цен.
3) Найдем скорость изменения цен по формуле
![]()
![]()
![]()
![]()
![]()
![]()
Отобразим ![]() на графике
(рис. 2.3.)
на графике
(рис. 2.3.)
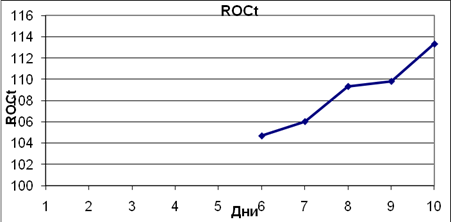
Рис. 2.3 График изменения скорости изменения цен ROCt.
График ROC (рис. 2.3.) нигде не пересекает уровень 100%, что означает, что нет сигналов ни к покупке, ни к продаже.
4) Найдем индекс относительной силы торгов по формуле
![]() , где
, где
AU – сумма приростов конечных цен за n дней;
AD – сумма убытков за n дней.
Таблица 2.2
Расчет значений параметров RSI
| Дни |
Сt |
∆Сt↑ |
∆Сt↓ |
∑∆Сt↑ |
∑∆Сt↓ |
RSI |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 | 555 | - | - | |||
| 2 | 530 | 25 | ||||
| 3 | 524 | 6 | ||||
| 4 | 539 | 15 | ||||
| 5 | 569 | 30 | ||||
| 6 | 581 | 12 | 57 | 31 | 64,77 | |
| 7 | 562 | 19 | 57 | 25 | 69,51 | |
| 8 | 573 | 11 | 68 | 19 | 78,16 | |
| 9 | 592 | 19 | 72 | 19 | 79,12 | |
| 10 | 645 | 53 | 95 | 19 | 83,33 |
![]()
![]()
![]()
![]()
![]()
Построим график индекса относительной силы торгов RSI (рис. 2.4).
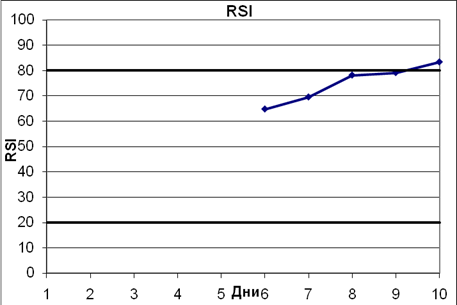
Рис. 2.4 График индекса относительной силы торгов RSI
Из графика RSI (рис. 2.4.) видно, что индекс относительной силы входит в «зону перекупленности» (от 80 до 100) на 9-й день. Значит, цены сильно выросли, надо ждать падения и подготовиться к продаже. Сигналом к продаже будет служить момент выхода графика RSI из «зоны перекупленности».
5) Рассчитаем осцилляторные индексы %R, %К, %D по формулам
![]()
![]()
 , где
, где
Kt, Rt, Dt – значения индексов текущего дня t;
H5 (L5) – максимальная (минимальная) цена за 5 предшествующих дней, включая текущий.
Расчеты произведем в табл. 2.3.
Таблица 2.3
Расчет значений осцилляторов %Rt, %Kt, %Dt.
| Дни |
Сt |
Сmax |
Сmin |
H5 |
L5 |
H5- Сt |
H5-L5 |
%Rt |
Ct-L5 |
%Kt |
∑за 3 дня (графа 10) | ∑за 3 дня (графа 8) |
%Dt |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 1 | 555 | 600 | 550 | ||||||||||
| 2 | 530 | 560 | 530 | ||||||||||
| 3 | 524 | 536 | 501 | ||||||||||
| 4 | 539 | 545 | 521 | ||||||||||
| 5 | 569 | 583 | 540 | 600 | 501 | 31 | 99 | 31,31 | 68 | 68,69 | |||
| 6 | 581 | 587 | 562 | 587 | 501 | 6 | 86 | 6,98 | 80 | 93,02 | |||
| 7 | 562 | 582 | 561 | 587 | 501 | 25 | 86 | 29,07 | 61 | 70,93 | 209 | 271 | 77,12 |
| 8 | 573 | 573 | 556 | 587 | 521 | 14 | 66 | 21,21 | 52 | 78,79 | 193 | 238 | 81,09 |
| 9 | 592 | 610 | 579 | 610 | 540 | 18 | 70 | 25,71 | 52 | 74,29 | 165 | 222 | 74,32 |
| 10 | 645 | 645 | 585 | 645 | 556 | 0 | 89 | 0,00 | 89 | 100,00 | 193 | 225 | 85,78 |
![]() ;
;
![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
Сведем полученные данные в таблицу (табл. 2.3.) и отобразим на графике расчетные значения осцилляторов (рис. 2.5.)
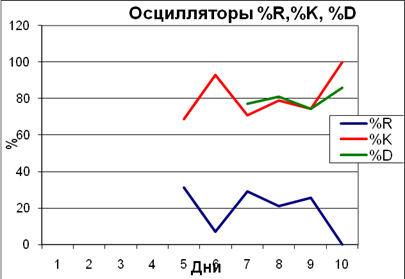
Рис. 2.5 Графики изменения осцилляторов %Rt, %Kt, %Dt.
Задание №3
Таблица 3.1
Исходные данные
| Вариант | Сумма | Дата начальная, | Дата конечная | Время в днях | Время в годах | Ставка | Число начислений |
| S |
Тн |
Тк |
Тдн |
Тлет |
i | m | |
|
6 |
3000000 | 14.01.02 | 18.03.02 | 90 | 5 | 35 | 4 |
Выполнить различные коммерческие расчеты, используя данные, приведенные в табл. 3.1.
В условии задачи значения параметров приведены в виде переменных. Например, S означает некую сумму средств в рублях, Тлет – время в годах, i – ставку в процентах и т. д. По именам переменных из таблицы необходимо выбрать соответствующие численные значения параметров и выполнить требуемые расчеты.
3.1 Банк выдал ссуду размером S руб. Дата выдачи ссуды - Tн, возврата - Тк. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой ставке i% годовых. Требуется найти:
а) точные проценты с точным числом дней ссуды;
б) обыкновенные проценты с точным числом дней ссуды;
в) обыкновенные проценты с приближенным числом дней ссуды.
3.2 Через Тдн дней после подписания договора должник уплатил S руб. Кредит выдан под i% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
3.3 Через Тдн дней предприятие должно получить по векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.
3.4 В кредитном договоре на сумму S руб. и сроком на Тлет лет, зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму.
3.5 Ссуда, размером S руб. представлена на Тлет лет. Проценты – сложные, ставка - i% годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму.
3.6 Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i% годовых.
3.7 Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.
3.8 Через Тлет предприятию будет выплачена сумма S руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставска i% годовых.
3.9 Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i% годовых. Определить дисконт.
3.10 В течение Тлет лет на расчетный сет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного срока.
3.1 Известны:
P=3000000 руб.
Тн=14.01.02
Тк=18.03.02
i=35%, или 0,35
Найти: I1, I2, I3.
Решение:
Используем формулы
![]()
а) точные проценты с точным числом дней ссуды.
k=365
t=63
![]()
б) обыкновенные проценты с точным числом дней ссуды.
k=360
t=63
![]()
в) обыкновенные проценты с приближенным числом дней ссуды.
k=360
t=64
![]()
Ответ: I1=181232,88 руб.; I2=183750,00 руб.; I3=186666,67 руб.
3.2 Известны:
S=3000000 руб.
Тдн=90
n=t/k=90/360=0,25
i%=35, или 0,35
Найти: Р=?, D=?.
Решение:
Первоначальная сумма и дисконт находятся по следующим формулам:
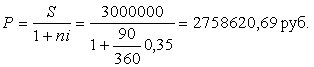
![]()
Ответ: Р=![]() ; D=
; D=![]()
3.3 Известны:
S=3000000 руб.
i%=35, или 0,35.
Тдн=90
Найти: Р-?, D-?.
Решение:
Применим следующие формулы:
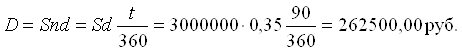
![]()
Ответ: предприятие получило 2737500,00 руб., дисконт составил 262500,00 руб.
3.4 Известны:
Р = 3000000 руб.
n = 5 лет
iсл=35, или 0,35
Найти: S-?
Решение:
1) Для расчета наращенной суммы применим формулу
![]()
Ответ: S= 13452100,31 руб.
3.5 Известны:
Р=300000 руб.
j=35%, или 0,35
m=4
n=5
Найти: S-?
Решение:
1) Наращенную сумму можно найти по формуле
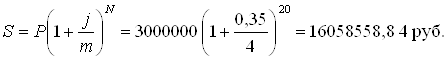
Ответ: S=16058558,84 руб.
3.6 Известны:
j=35% или 0,35
m=4
Найти: iэ-?
Решение:
Эффективную ставку процента можно найти по формуле
![]() или 39,87%
или 39,87%
Ответ: эффективная ставка процента составляет 39,87%.
3.7 Известны:
iэ=35%, или 0,35
m=4
Найти: j-?
Решение:
Применим формулу
![]()
Ответ: номинальная ставка составляет 31,16%.
3.8 Известны:
n=5
S=3000000 руб.
i=35 %, или 0,35.
Найти: Р-?
Решение:
Используем формулу
![]()
Ответ: Р = 669040,51 руб.
3.9 Известны:
n=5
S=3000000 руб.
dcл=35%, или 0,35
Найти: D-?
Решение:
1) Дисконт можно найти по формуле
![]()
Ответ: D= 2651912,81 руб.
3.10 Известны:
n=5
R=3000000 руб.
m=4
j=0,35
Найти: S-?
Решение:
Используем формулу
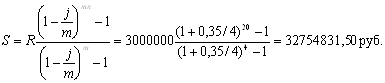
Ответ: сумма на расчетном счете к концу срока составит 32754831,50 руб.
Список использованной литературы:
1. Финансовая математика: математическое моделирование финансовых операций: учеб. пособие/ под ред. Половникова В.А., Пилипенко А.И.. — М.: Вузовский учебник, 2004.
2. Финансовая математика: методические указания по изучению дисциплины и контрольные задания./ ВЗФЭИ. — М.: Финстатинформ, 2002.