Контрольная работа: Расчет развозочно-сборочных маршрутов
ИСХОДНЫЕ ДАННЫЕ
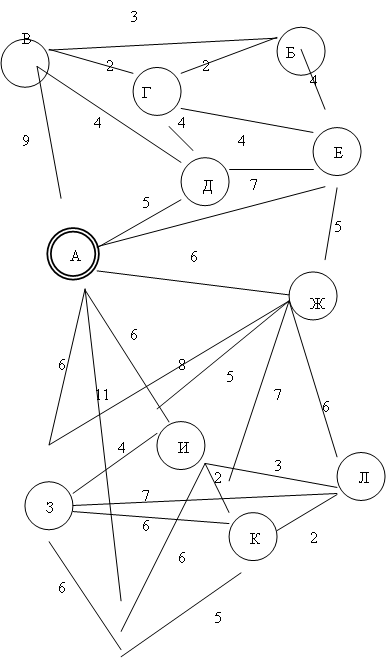
Из пункта А (база) доставляется груз в 11 других пунктов, перечисленных в исходных данных, из которых в свою очередь необходимо в пункт А доставить груз, например возвратную тару (рисунок 1). Количество единиц груза доставляемого из пункта А в каждый из них, дан в исходных данных.
Вместимость одного автомобиля составляет не более 250 ед. груза. Необходимо организовать перевозки между пунктами наименьшим пробегом автомобиля.
Таблица 1 – Исходные данные
| Пункт | Ввоз | Вывоз |
| Б | 10 | 30 |
| В | 30 | 20 |
| Г | 50 | 55 |
| Д | 20 | 80 |
| Е | 15 | 40 |
| Ж | 70 | 30 |
| З | 45 | 70 |
| И | 20 | 25 |
| К | 100 | 40 |
| Л | 50 | 20 |
| М | 30 | 30 |
| ИТОГ | 440 | 440 |
 |
|||
 |
Рисунок 1 – Схема размещения пунктов и расстояния между ними
РЕШЕНИЕ:
Решение находится путем последовательного расчета по нескольким этапам.
1 этап – нахождение кратчайшей связывающей сети.
Пусть все пункты, указанные на рисунке 1, называются вершинами сети, а линия, соединяющая две соседние вершины, - звеном; незамкнутая сеть, связывающая две и более вершины с минимальной суммарной длиной всех соединяющих их звеньев; кратчайшей связывающей сетью.
Она определяется следующим образом:
1) на сети находим меньшее звено В-Г=2 км;
2) рассмотрим все звенья, связанные с одной из своих вершин с выбранным звеном, т. Е. звенья В-А=9; В-Б=3; В-Д=4; Г-Б=2; Г-Д=4; Г-Е=4;
3) из них выбираем звенья с наименьшим расстоянием Г-Б=2;
4) рассмотрим звенья, связанные с вершинами полученной линии В-Г-Б, и из них выберем наименьшее (при этом нельзя выбирать звено, соединяющее две ранее включенные в сеть вершины), такое звено – В-Б;
5) другими звеньями связанными своими вершинами с уже выбранной сетью являются звенья В-А, В-Д, Г-Д, Г-Е, Б-Е (последние 4 имеют = наименьшие расстояния);
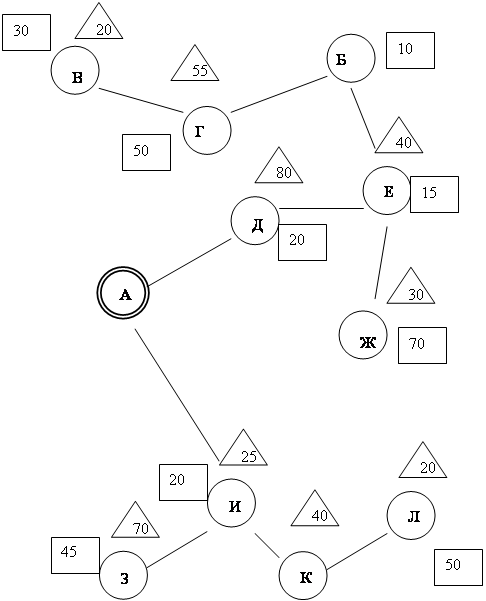
6) примем наименьшее Б-Е и получим сеть В-Г-Б-Е. На рисунке 2 представлена кратчайшая связывающая сеть;
 |
|||||||||
|
|||||||||
 |
|||||||||
|
|||||||||
 |
|||||||||
Рисунок 2 – Кратчайшая связывающая сеть
7) условиями задачи установлено, что вместимость автомобиля – 250 ед. груза; исходя из этого пункты, указанные на рисунке 2 можно сгруппировать, так как это сделано в таблице 2;
Таблица 2 – Группировка маршрутов
| Пункты | Маршрут №1 | Пункты | Маршрут №2 | ||
| Количество груза, ед. | Количество груза, ед. | ||||
| Ввоз | Вывоз | Ввоз | Вывоз | ||
| Б | 10 | 30 | Д | 20 | 80 |
| В | 30 | 20 | И | 20 | 25 |
| Г | 50 | 55 | К | 100 | 40 |
| Ж | 70 | 30 | Л | 50 | 20 |
| Е | 15 | 40 | М | 30 | 30 |
| З | 45 | 70 | ИТОГО | 220 | 195 |
| ИТОГО | 220 | 245 |
2 этап - набор пунктов в маршруты
По каждой ветви сети, начиная с той, которая имеет наибольшее число звеньев, группируют пункты в маршруты с учетом количества ввозимого и вывозимого груза и вместимости подвижного состава. Если все пункты данной ветви не могут быть включены в один маршрут, то ближайшие к другой ветви пункты группируются вместе с пунктами этой ветви.
В нашем случае условиями задачи установлено, что максимальная вместимость автомобиля составляет 250 ед. груза. Исходя из этого пункты, указанные на рисунке 2, можно сгруппировать так, как это сделано в таблице 2.
3 этап – определение очередности объезда пунктов маршрута
На этом этапе все пункты маршрута, начиная с А, связываются тонкой замкнутой линией, которая соответствует кратчайшему пути объезда этих пунктов.
Для маршрута №1
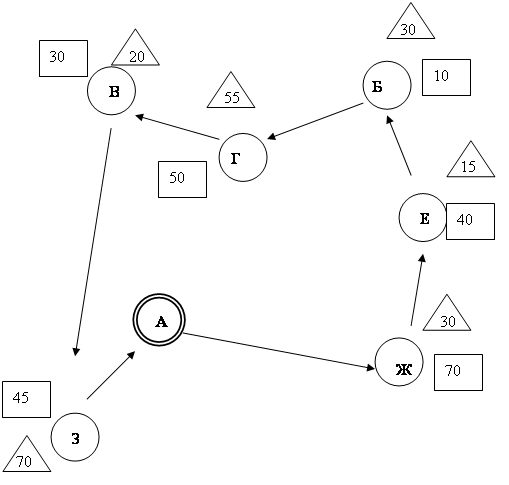
Рисунок 3 – Маршрут №1
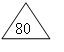 Для маршрута №2
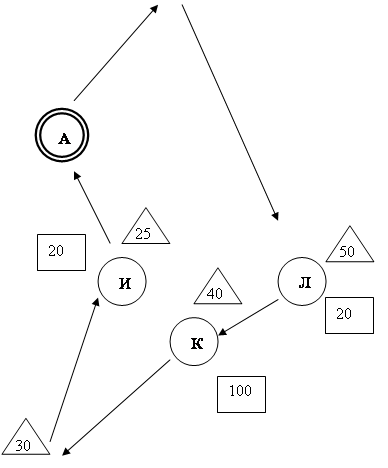
Для маршрута №2
|
|||||||||
 |
|||||||||
 |
|||||||||
|
|||||||||
 |
|||||||||
Рисунок 4 – Маршрут№2
Известно несколько методов расчета кратчайшего пути объезда заданных пунктов. Как правило, все они являются приближенными. Одним из наиболее простых является так называемый метод сумм, с помощью которого строится таблица, называемая симметричной матицей. На главной диагонали в ней располагаются пункты, включаемые в маршрут.
Для маршрута №1 симметричная матрица представлена в таблице 3.
Таблица 3 – Симметричная матрица для маршрута №1
| А | 6 | 7 | 11 | 9 | 9 | 6 |
| 6 | Ж | 5 | 9 | 9 | 11 | 8 |
| 7 | 5 | Е | 4 | 4 | 6 | 13 |
| 11 | 9 | 4 | Б | 2 | 3 | 17 |
| 9 | 9 | 4 | 2 | Г | 2 | 15 |
| 9 | 11 | 6 | 3 | 2 | В | 15 |
| 6 | 8 | 13 | 17 | 15 | 15 | З |
| 48 | 48 | 39 | 46 | 41 | 46 | 74 |
Цифры показывают расстояние между этими пунктами. Дополнительно в этой матрице имеется итоговая строка — строка сумм. В ней проставляется сумма расстояний по каждому столбцу.
Затем строим начальный маршрут из 3 пунктов имеющих максимальную сумму, в нашем случае – АЖЗА. В него включаем следующий пункт с максимальной суммой – Б. Чтобы определить, между какими пунктами его ставить необходимо поочередно включать его между каждой соседней парой.
При этом находим величину прироста пробега автомобиля на маршруте при его включении.
![]()
![]()
![]()
Из
полученных значений выбираем минимальную и между соответствующими ей пунктами
вставляем данный. В нашем случае это - ![]() = 14 км, поэтому получаем маршрут – АБЖЗА.
= 14 км, поэтому получаем маршрут – АБЖЗА.
![]() км.
км.
Вновь находим в таблице 3 пункт не принимавшийся в расчете, в нашем случае это – В. Все дальнейшие расчеты производим аналогично.
![]() - min
- min
![]()
![]()
![]()
![]() км.
км.
Затем в полученную последовательность вставляем пункт Г
![]()
![]() - min
- min
![]()
![]()
![]()
![]() км.
км.
Затем в полученную последовательность вставляем пункт Е
![]()
![]()
![]()
![]() - min
- min
![]()
![]()
![]() км.
км.
Можно утверждать, что полученная последовательность объезда пунктов маршрута дает наименьший или весьма близкий к наименьшему путь движения, так как при движении автомобиля по ранее выбранному маршруту общее расстояние равно 48 км, а скорректированный – 36 км, что дает уменьшение расстояния на 12 км.
По маршруту № 2 проводим аналогичные расчеты.
Составляем симметричную матрицу для маршрута №2, которая представлена в таблице 4.
Таблица 4 – Симметричная матрица для маршрута №2
| А | 5 | 9 | 8 | 11 | 6 |
| 5 | Д | 14 | 13 | 16 | 11 |
| 9 | 14 | Л | 2 | 7 | 3 |
| 8 | 13 | 2 | К | 5 | 2 |
| 11 | 16 | 7 | 5 | М | 6 |
| 6 | 11 | 3 | 2 | 6 | И |
| 39 | 59 | 35 | 30 | 45 | 28 |
Строим начальный маршрут из 3 пунктов имеющих максимальную сумму, в нашем случае – АДМА. В него включаем следующий пункт с максимальной суммой – Л. Чтобы определить, между какими пунктами его ставить необходимо поочередно включать его между каждой соседней парой.
При этом находим величину прироста пробега автомобиля на маршруте при его включении.
![]()
![]() - min
- min
![]()
Из
полученных значений выбираем пункт с минимальным значением и между
соответствующими ей пунктами вставляем данный. В нашем случае это - ![]() = 5 км, поэтому получаем маршрут – АДЛМА.
= 5 км, поэтому получаем маршрут – АДЛМА.
![]() км.
км.
Вновь находим в таблице 4 пункт не принимавшийся в расчете, в нашем случае это – К. Все дальнейшие расчеты производим аналогично.
![]()
![]()
![]() - min
- min
![]()
![]() км.
км.
Затем в полученную последовательность вставляем пункт И
![]()
![]() - min
- min
![]()
![]()
![]()
![]() км.
км.
Можно утверждать, что полученная последовательность объезда пунктов маршрута дает наименьший или весьма близкий к наименьшему путь движения, так как при движении автомобиля по ранее выбранному маршруту общее расстояние равно 39 км, а скорректированный – 37 км, что дает уменьшение расстояния на 2 км.
На рисунках 5 и 6 представлены скорректированные схемы движения автомобилей по маршрутам № 1 и 2 (выделены пунктирной линией).
Для маршрута №1
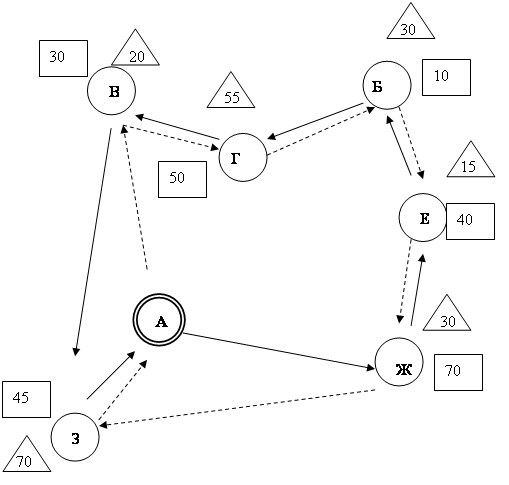
Рисунок 5 – Маршрут №1
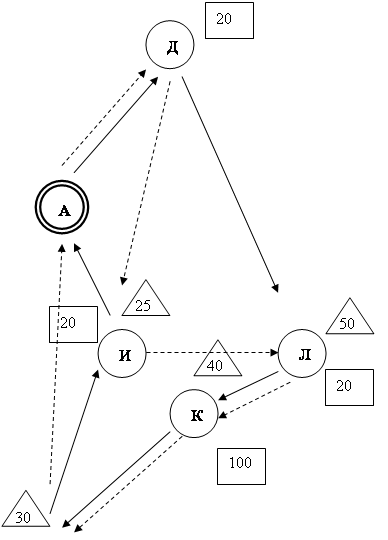
 Для маршрута №2
Для маршрута №2
 |
|||||
|
|||||
 |
|||||
Рисунок 6 – Маршрут№2
автомобиль пробег маршрут
Если бы указанные маршруты являлись только развозочными или только сборными, то на этом все расчеты заканчивались.
В нашем случае же по маршруту одновременно осуществляется развоз и сбор груза, поэтому необходимо провести дополнительный четвертый этап расчетов.
4 этап – определение возможности одновременного развоза и сбора груза на маршруте
Так как вместимость подвижного состава ограничена, необходимо проверить возможность его использования для одновременного развоза и сбора груза на маршруте в той последовательности объезда пунктов, которая получена на предыдущем этапе расчетов. Покажем это на примере расчета скорректированных маршрутов № 1 и 2.
Маршрут № 1 по полученному решению должен иметь следующую последовательность объезда пунктов: АВГБЕЖЗА. Проверяем, какое при этом количество груза будет находиться в автомобиле на протяжении всего маршрута. Сделаем это в таблице 5, где даны пункты маршрута в полученной последовательности и расчет наличия груза в автомобиле после погрузки и выгрузки в каждом пункте. Из этой таблицы видно, что на протяжении всего маршрута автомобиль не будет перегружен, так как максимальная загрузка автомобиля — 250 ед. груза.
Таблица 5 – Определение количества груза в автомобиле при движении его по маршруту №1
| Пункты | Количество груза, ед. | Пункты | Количество груза, ед. | ||||
| Прибытие | Отправление | Всего в автомобиле | Прибытие | Отправление | Всего в автомобиле | ||
| А | - | 70 | 70 | Б | 10 | 30 | 85 |
| В | 30 | 20 | 60 | Е | 15 | 40 | 110 |
| Г | 50 | 55 | 65 | Ж | 70 | 30 | 70 |
| З | 45 | 70 | 95 |
В таблице 6 сделаем то же самое для маршрута № 2: АДИЛКМА.
Таблица 6 – Определение количества груза в автомобиле при движении его по маршруту №2
| Пункты | Количество груза, ед. | Пункты | Количество груза, ед. | ||||
| Прибытие | Отправление | Всего в автомобиле | Прибытие | Отправление | Всего в автомобиле | ||
| А | - | 185 | 185 | Л | 50 | 20 | 220 |
| Д | 20 | 80 | 245 | К | 100 | 40 | 160 |
| И | 20 | 25 | 250 | М | 30 | 30 | 160 |
ВЫВОД:
принятые маршруты обеспечат наименьшее расстояние перевозки, а также автомобиль в процессе движения по этим маршрутам не будет перегружен, что и требовалось доказать.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Витязев, М. В. Экономико-математические методы в управлении перевозками [Текст] : курс лекций / М. В. Витязев. – Архангельск, 2007.
2 Геронимус, Б. Л. Экономико-математические методы в планировании на автомобильном транспорте [Текст] : учебник для вузов / Б. Л. Геронимус. – М.: Транспорт, 1977.
3 Кожин, А. П. Математические методы в планировании и управлении грузовыми автомобильными перевозками [Текст] : учебник / А. П. Кожин. – М.: Высшая школа, 1979. – с. 94-102.