Дипломная работа: Разработка автоматизированной системы для исследования устойчивости и автоколебаний в электромеханической следящей системе
Оглавление
Введение
1. Математическая модель следящей системы
2. Исследование нелинейной следящей системы аналитическими методами
3. Разработка требований к интерфейсу пользователя диалоговой системы
4. Разработка программного обеспечения АИС
5. Результаты испытания АИС
Заключение
Приложение
Введение
Настоящая дипломная работа посвящена проблеме разработки автоматизированной системы синтеза нелинейных систем методом гармонического баланса.
В теории автоматического управления особое место занимают методы исследования нелинейных систем.
Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики звена (произведение переменных или их производных, корень, квадрат или более высокая степень переменной любая другая нелинейная связь переменных и их производных).
Следовательно, к нелинейным системам относятся, в частности, все системы, в звеньях которых имеются статические характеристики любого из многих видов. К ним же относятся и все системы релейного действия.
Нелинейными могут быть, разумеется, также и системы с переменными параметрами, с распределительными параметрами, с запаздыванием, импульсные и цифровые системы, если в них где-либо нарушается линейность уравнений динамики (в цифровых системах это связано с квантованием сигнала по уровню).
При исследовании, расчете и синтезе автоматических систем нужно иметь в виду, что наиболее полно разработана теория и различные прикладные методы для обыкновенных линейных систем. Поэтому в интересах расчета и его простоты всегда желательно (там, где это допустимо) сводить задачу к такой форме, чтобы максимально использовать методы исследования обыкновенных линейных систем.
Обычно уравнения динамики всех звеньев системы стараются привести, обыкновенно, к линейным, и только для некоторых звеньев, где это недопустимо или где специально вводится особое линейное или нелинейное звено, учитываются их особые свойства. Тогда при наличии одного такого звена система при расчете разбивается на два блока, а одном из которых объединяется весь комплекс обыкновенных линейных звеньев.
Однако это вовсе не значит, что при проектировании новых автоматических систем нужно стремится к обыкновенности линейным системам. Наоборот, уже из приведенных выше определений совершенно очевидно, что обыкновенные линейные системы обладают ограниченными возможностями.
Введение особых линейных и нелинейных звеньев может придать системе лучшие качества.
Особенно богатыми возможностями обладают системы со специально вводимыми нелинейностями и дискретные системы. В том числе с цифровыми вычислительными устройствами, а также адаптивные, то есть, самонастраивающиеся, экстремальные, самоорганизующиеся системы.
Разрабатываемая система может быть использована в качестве методического пособия для студентов ВУЗов при изучении ими методов исследования нелинейных систем автоматического управления.
Перечислим некоторые из них:
• метод фазового пространства или фазовых траекторий;
• метод точечных преобразований;
• метод изоклин;
• частичный метод В.М. Попова;
• метод гармонического баланса;
• частотный метод определения устойчивости и автоколебаний.
Из известных автору систем автоматизированного проектирования автоматических систем управления наибольшими возможностями обладают системы SIAM и CSSE. Однако эти средства расчета систем управления имеют ограниченные возможности графического представления информации.
В то же время перечисленные выше методы исследования нелинейных систем удобны, когда решение реализуется именно графическими методами.
Существует чрезвычайно большое разнообразие автоматических систем, выполняющих те или иные функции по управлению самыми различными физическими процессами во всех областях техники. В этих системах сочетаются весьма разнообразные по конструкции механические, электрические и другие устройства, составляя, в общем, сложный комплекс взаимодействующих друг с другом звеньев.
Примерами автоматических систем могут служить:
а) автомат включения освещения, в котором имеется фотоэлемент, реагирующий на силу дневного света, и специальное устройство для включения освещения, срабатывающее от определенного сигнала фотоэлемента;
б) автомат, выбрасывающий какие-либо определенные предметы (билеты, шоколад) при опускании в него определенной комбинации монет;
в) станок-автомат, автоматические линии станков и автоматические цехи на заводах;
г) системы телеуправления, в которых от нажатия кнопки или от легкого поворота ручки на пульте управления совершается определенная комбинация мощных и сложных операций в управляемом объекте;
д) автоматический регулятор скорости вращения двигателя,
поддерживающий постоянную угловую скорость двигателя независимо от внешней нагрузки (аналогично регуляторы температуры, давления, напряжения, частоты и пр.);
е) автопилот, поддерживающий определенный курс и высоту полета самолета без помощи летчика;
ж) следящая система, на выходе которой с определенной точностью копируется произвольное во времени изменение какой-нибудь величины, поданной на вход;
з) система сопровождения, в которой ствол наземного орудия автоматически поворачивается за летящим самолетом;
и) вычислительное устройство, выполняющее определенную математическую операцию (дифференцирование, интегрирование, решение уравнений и т. п.);
к) измерительные приборы, работающие по так называемому компенсационному принципу;
л) система самонаведения снаряда на цель и пр.
Все эти и им подобные автоматические системы можно разделить на два больших класса:
1) автоматы, выполняющие определенного рода одноразовые или многоразовые операции; сюда относятся, например, автомат включения освещения, билетный автомат, станок-автомат, ружье-автомат, автомат переключения скоростей и т.п.
2) автоматические системы, которые в течение достаточно длительного времени нужным образом изменяют (или поддерживают неизменными) какие-либо физические величины (координаты движущегося объекта, скорость движения, электрическое напряжение, частоту, температуру, давление, громкость звука и пр.) в том или ином управляемом процессе. Сюда относятся автоматические регуляторы, следящие системы, автопилоты, некоторые вычислительные устройства, некоторые измерительные приборы, системы дистанционного управления, телеуправления, самонаведения и т. п.
Естественным дальнейшим усовершенствованием автоматической системы является замыкание ее выхода (контрольные приборы) со входом (источник воздействия) таким образом, чтобы контрольные приборы, измерив некоторые величины, характеризующие определенный процесс в управляемом объекте, сами служили бы одновременно и источником воздействия на систему, причем величина этого воздействия зависела бы от того, насколько отличаются измеренные величины на управляемом объекте от требуемых значений.
Таким образом, возникает замкнутая автоматическая система. Очевидно, что в замкнутой автоматической системе имеется полная взаимозависимость работы всех звеньев друг от друга. Протекание всех процессов в замкнутой системе коренным образом отличается от процессов в незамкнутой системе. Замкнутая система совершенно по-другому реагирует на внешние возмущающие воздействия.
Различные ценные свойства замкнутых автоматических систем, делают их незаменимыми во многих случаях, когда требуется точность и быстродействие для управления, измерения или для производства математических вычислений. Поэтому при создании всяких замкнутых автоматических систем особое значение приобретают динамические расчеты.
Замкнутые автоматические системы существуют в технике в виде различных автоматических систем управления, систем автоматического регулирования, следящих систем, вычислительных систем, компенсационных систем измерения, систем автоматического пилотирования, систем стабилизации, систем самонаведения, телеуправления, автономного управления и т. п.
В следящей системе выходная величина у (t) воспроизводит изменение входной величины g (t), причем, автоматическое устройство реагирует на рассогласование (t) между выходной и входной величинами. Условимся величины у и g называть соответственно регулируемой величиной и задающим воздействием.
Следящая система имеет обратную связь выхода со входом, которая, по сути дела, служит для измерения результата действия системы. На входе системы производится вычитание х – h-z. Устройство, производящее это вычитание, будем называть датчиком рассогласования.
Величина рассогласования х и воздействует на промежуточные устройства, а через них – на управляемый объект. Система работает так, чтобы все время сводить к нулю рассогласование х. Источником воздействия на задающее устройство может быть либо человек, либо специальное устройство, либо изменение внешних условий, в которых работает система.
Для систем автоматического регулирования введем следующую терминологию.
Агрегат, в котором происходит процесс, подлежащий регулированию, называется регулируемым объектом. Величина у, которую необходимо в этом агрегате регулировать, т. е. поддерживать постоянной или изменять по заданной программе, называется регулируемой величиной.
Автоматически действующее устройство, предназначенное для выполнения задачи регулирования, называется автоматическим регулятором. Автоматический регулятор включает в себя измерительное устройство, т. е. чувствительный элемент, реагирующий на отклонение регулируемой величины у.
Далее ставится усилительно-преобразовательное и исполнительное устройства. Они служат для формирования регулирующего воздействия u(t) на объект, для возможно более точного выполнения задачи регулирования при реально имеющемся возмущающем воздействии f(t).
Автоматический регулятор вместе с регулируемым объектом называется системой автоматического регулирования.
Системы автоматического регулирования, поддерживающие постоянное частности, нулевое значение регулируемой величины, называют также системами стабилизации. Система автоматического регулирования, изменяющая значения регулируемой величины по заранее заданной программе, называется системой программного регулирования.
Регулятор, в котором имеется усилительно-преобразовательное устройство, питаемое извне, от добавочного источника энергии называется регулятором непрямого действия.
В простейших регуляторах, как увидим ниже, усилительно- преобразовательного устройства и привода может и не быть вовсе, т. е. измерительное устройство может непосредственно (без дополнительного источника энергии) воздействовать на регулирующий орган. Такой регулятор называется регулятором прямого действия. Питание регулятора прямого действия энергией идет не извне, а целиком за счет энергии самого регулируемого объекта, подаваемой через измерительное устройство.
Но существуют, наоборот, и более сложные регуляторы. Так, кроме одиночных систем регулирования, о которых здесь идет речь, состоящих из одного регулируемого объекта и одного регулятора, существуют так называемые связанные или многомерные системы регулирования.
Многомерными системами регулирования называются такие, в которых имеется несколько регулируемых величин или в единый автоматически работающий комплекс связаны несколько регуляторов на одном объекте или несколько регуляторов и несколько объектов с перекрестными связями между ними.
Система автоматического управления может решать любую из этих задач: регулирование, стабилизация, слежение, ориентация, наведение, но может решать также и совокупность такого рода задач и иметь различные дополнительные функции. Те же общие принципы используются в разного рода системах автоматического управления.
Большое значение в технике управления имеют системы комбинированного действия с регулированием по возмущению. Все большую роль начинают играть адаптивные системы, т.е. самонастраивающиеся, самооптимизирующиеся и самоорганизующиеся системы, а также системы с переменной структурой.
Для систем автоматического регулирования и для следящих систем (равно как и для всех замкнутых автоматических систем вообще) существуют практически единые методы динамических расчетов.
Большое различие в теорию систем вносят не только функциональные признаки, но и характер внутренних процессов: непрерывный – дискретный (импульсный), линейный – нелинейный и т. п.
Классифицируются автоматические системы по характеру внутренних динамических процессов.
Каждая автоматическая система состоит из целого ряда блоков или звеньев, различно соединенных между собой. Каждое отдельно взятое звено имеет вход и выход. В общем случае звено может иметь несколько входов и выходов. Входная величина Xi и выходная Х2 могут иметь любую физическую природу (ток, напряжение, перемещение, температура, освещенность и т. п.). В процессе работы автоматической системы величины Xi и Х2 изменяются во времени.
Динамика процесса преобразования сигнала в данном звене описывается некоторым уравнением, связывающим выходную переменную Х2 с входной переменной Х\. Совокупность уравнений и характеристик всех звеньев описывает динамику процессов управления или регулирования во всей системе в целом. Существуют различные характеристики звеньев: статические, переходные, частотные и др.
Основными признаками деления автоматических систем на большие классы по характеру внутренних динамических процессов являются следующие:
1. непрерывность или дискретность (прерывистость) динамических процессов во времени;
2. линейность или нелинейность уравнений, описывающих динамику процессов регулирования.
По первому признаку автоматические системы делятся на системы непрерывного действия, системы дискретного действия (импульсные и цифровые) и системы релейного действия.
По второму признаку каждый из указанных классов, кроме релейного, делится на системы линейные и нелинейные. Системы же релейного действия относятся целиком к категории нелинейных систем.
Системой непрерывного действия называется такая система, в каждом из звеньев которой непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины. При этом закон изменения выходной величины во времени может быть произвольным, в зависимости от формы изменения входной величины и от вида уравнения динамики (или характеристики) звена.
Чтобы автоматическая система в целом была непрерывной, необходимо, прежде всего, чтобы статические характеристики всех звеньев системы были непрерывными.
Системой дискретного действия называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина изменяется не непрерывно, а имеет вид отдельных импульсов, появляющихся через некоторые промежутки времени. Звено, преобразующее непрерывный входной сигнал в последовательность импульсов, называется импульсным.
Если последующее звено системы тоже дискретное, то для него не только выходная, но и входная величина будет дискретной (импульсной). К дискретным автоматическим системам относятся системы импульсного регулирования (т. е. системы с импульсным звеном), а также системы с цифровыми вычислительными устройствами.
Эти последние дают результат вычисления на выходе дискретно, через определенные промежутки времени, в виде чисел для отдельных дискретных числовых значений входной величины.
Системой релейного действия называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторых точках процесса, зависящих от значения входной величины, изменяется скачком. Такое звено называется релейным звеном. Обратимся теперь ко второму признаку классификации автоматических систем.
Линейной системой называется такая система, динамика всех звеньев которой вполне описывается линейными уравнениями (алгебраическими и дифференциальными или разностными).
Для этого необходимо прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т. е. имели вид прямой линии.
Если динамика всех звеньев системы описывается обыкновенными линейными дифференциальными (и линейными алгебраическими) уравнениями с постоянными коэффициентами, то систему называют обыкновенной линейной системой.
Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики звена (произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных и их производных).
Следовательно, к нелинейным системам относятся также и системы с переменными параметрами, с распределенными параметрами, с запаздыванием, импульсные и цифровые системы, если в них где-либо нарушается линейность уравнений динамики (в цифровых системах это связано, в частности, с квантованием сигнала по уровню). К ним же относятся и все системы релейного действия.
При исследовании, расчете и синтезе автоматических систем нужно иметь в виду, что наиболее полно разработаны теория и различные прикладные методы для обыкновенных линейных систем. Поэтому в интересах простоты расчета всегда желательно (там, где это допустимо) сводить задачу к такой форме, чтобы максимально использовать методы исследования обыкновенных линейных систем.
Обычно, уравнения динамики всех звеньев системы стараются привести к обыкновенным линейным, и только для некоторых звеньев, где это недопустимо или где специально вводится особое линейное или нелинейное звено, учитываются эти особые их свойства. Тогда при наличии одного такого звена система при расчете разбивается на два блока, в одном из которых объединяется весь комплекс обыкновенных линейных звеньев.
Однако это вовсе не значит, что при проектировании новых автоматических систем нужно стремиться к обыкновенным линейным системам. Наоборот, уже из приведенных выше определений совершенно очевидно, что обыкновенные линейные системы обладают ограниченными возможностями.
Введение особых линейных и нелинейных звеньев может придать системе лучшие качества. Особенно богатыми возможностями обладают системы со специально вводимыми нелинейностями и дискретные системы, в том числе с цифровыми вычислительными устройствами, а также адаптивные, т.е. самонастраивающиеся, экстремальные, самоорганизующиеся системы.
В настоящее время во многих областях техники существует необозримое количество самых разнообразных систем автоматического управления, использующих принцип следящих систем. Он применяется почти везде, где нужно добиться высокой точности и надежности автоматического управления.
Качество работы любой системы регулирования, в конечном счете, определяется величиной ошибки, равной разности между требуемым и действительным значениями регулируемой величины: x(t) g(t)-y(t). В системах стабилизации при g(t) О ошибка x(t) ^-y(t).
Знание мгновенного значения ошибки в течение всего времени работы регулируемого объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако в действительности, вследствие случайности задающего и возмущающего воздействий, такой подход не может быть реализован. Поэтому приходится оценивать качество системы регулирования по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы регулирования в этом случае используются так называемые критерии качества.
В настоящее время разработано большое число различных критериев качества систем регулирования. Все их можно разбить на четыре группы.
К первой группе относятся критерии, в той или иной степени использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем регулирования.
Ко второй группе относятся критерии, определяющие величину запаса устойчивости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система регулирования.
Почти всегда опасной для системы является колебательная граница устойчивости. Это определяется тем, что стремление повысить общий коэффициент усиления в системе, как правило, приводит к приближению системы именно к колебательной границе устойчивости и затем к возникновению незатухающих автоколебаний.
Третья группа критериев качества определяет так называемое быстродействие систем регулирования. Под быстродействием понимается быстрота реагирования системы регулирования на появление задающих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы.
К четвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстродействие. Обычно, это делается при помощи рассмотрения некоторых интегральных свойств кривой переходного процесса.
При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения.
Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полюсов и нулей передаточной функции замкнутой системы и т. п.
Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и другие.
Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот, и другой подход требует изучения условий эксплуатации построенных систем автоматического регулирования, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем.
Связь между временными и частотными свойствами системы автоматического регулирования имеет сложный характер и может быть определена в общем виде только в простейших случаях, например, для систем, описываемых дифференциальным уравнением второго порядка.
Однако отсутствие зависимостей, связывающих в общей форме свойства системы во временном и частотном представлениях, не может служить препятствием для развития и независимого использования критериев качества того или иного направления.
Использование того или иного подхода при формулировании критериев качества определяется в настоящее время удобствами его применения в системах конкретного вида, а также, в известной мере, сложившимися в данной области традициями.
К числу общих методов повышения точности систем автоматического регулирования относятся:
1) увеличение коэффициента усиления разомкнутой цепи;
2) повышение степени астатизма;
3) применение регулирования по производным от ошибки.
Увеличение общего коэффициента усиления разомкнутой цепи является наиболее универсальным и эффективным методом. Увеличить общий коэффициент усиления можно обычно за счет введения в систему регулирования усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.
Увеличение общего коэффициента усиления благоприятно сказывается, в смысле уменьшения ошибок, практически во всех типовых режимах. Это вытекает, в частности, из того, что общий коэффициент усиления разомкнутой цепи входит в качестве делителя во все коэффициенты ошибок.
Однако увеличение общего коэффициента усиления ограничивается устойчивостью системы регулирования. При повышении коэффициента усиления, как правило, система приближается к колебательной границе устойчивости.
При некотором предельном его значении в системе возникают незатухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы регулирования.
В связи с этим повышение общего коэффициента усиления до значения, при котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повышении запаса устойчивости системы, что осуществляется при помощи так называемых корректирующих средств
Под улучшением качества процесса регулирования, помимо повышения точности в типовых режимах, понимается изменение динамических свойств системы регулирования с целью получения необходимого запаса устойчивости и быстродействия.
В этой проблеме основное значение имеет обеспечение запаса устойчивости. Это объясняется тем, что стремление снизить ошибки системы регулирования приводит, как правило, к необходимости использовать такие значения общего коэффициента усиления, при которых без принятия специальных мер, система вообще оказывается неустойчивой.
При решении задачи повышения запаса устойчивости проектируемой системы регулирования, прежде всего, необходимо попытаться рациональным образом изменить ее параметры (коэффициенты передачи отдельных звеньев, постоянные времени и т.п.) так, чтобы удовлетворить требованиям качества регулирования, которые определяются критериями качества.
При невозможности решить эту задачу в рамках имеющейся системы приходится идти на изменение ее структуры. Для этой цели обычно используется введение в систему регулирования так называемых корректирующих средств, которые должны изменить динамику всей системы в нужном направлении.
К корректирующим средствам относятся, в частности, корректирующие звенья, представляющие собой динамические звенья с определенными передаточными функциями.
В тех случаях, когда корректирующие звенья используются именно для получения устойчивости системы регулирования или для повышения ее запаса устойчивости, они называются иногда демпфирующими или стабилизирующими звеньями. При этом имеется в виду, что звенья демпфируют колебания, которые возникают в системе регулирования. Термин «корректирующие звенья» является более широким и используется для звеньев, которые вводятся в систему для изменения статических и динамических свойств с различными целями.
Получение требуемого быстродействия обычно обеспечивается при проектировании системы регулирования посредством выбора соответствующих элементов цепи регулирования (исполнительных органов, усилителей, серводвигателей и т. п.). Однако возможно улучшение быстродействия системы посредством использования корректирующих средств.
До сих пор поведение систем автоматического регулирования исследовалось при определенных, заданных во времени задающих и возмущающих воздействиях (ступенчатая функция, импульсная функция, гармоническое воздействие и т. д.)
Однако во многих случаях характер воздействия бывает таким, что его нельзя считать определенной функцией времени. Оно может принимать с течением времени самые разнообразные случайные значения. В таких случаях можем оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени.
Это происходит не потому, что оно неизвестно заранее, а потому, что сама природа реального задающего или возмущающего воздействия такова, что величина его в каждый момент времени, и процесс его изменения с течением времени, зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом, появляться одновременно, или с любым сдвигом во времени и т.д.
Следящие системы – это системы, на вход которых попадают вместе с полезным сигналом, помехи. Например, в радиолокационной системе сопровождения отраженный от цели сигнал содержит в себе помехи в виде многочисленных флуктуации, происходящих от вибраций и поворотов цели, замирания сигнала и т. п.
Аналогичные помехи случайной природы имеют место в других автоматических устройствах.
В следящих системах не только возмущающие воздействия и помехи являются случайными, но и сам полезный сигнал, который должен воспроизводиться (задающее воздействие), как правило, носит случайный характер.
Система автоматического регулирования, которая содержит хотя бы одно звено, описываемое нелинейным уравнением, называется нелинейной.
Перечислим виды нелинейных звеньев:
1) звено релейного типа;
2) звено с кусочно-линейной характеристикой;
3) звено с криволинейной характеристикой любого очертания;
4) звено, уравнение которого содержит произведение переменных, их производных и другие их комбинации;
5) нелинейное звено с запаздыванием;
6) нелинейное импульсное звено;
7) логическое звено;
8) звенья, описываемые кусочно-линейными дифференциальными уравнениями, в том числе переменная структура.
Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, а вторые – в виде нелинейных дифференциальных уравнений.
Общий метод составления уравнений для нелинейных систем состоит, в следующем. Сначала, производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно нелинейных звеньев (чаще всего одного-двух).
Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.
В результате получается система обыкновенных линейных уравнений, к которым добавляется одно-два (иногда более) нелинейных. В соответствии с этим, обобщенную структурную схему любой нелинейной системы автоматического регулирования в случае одного нелинейного звена, можно представить в виде, где линейная часть может иметь структуру любой сложности (с обратными связями и т п.). В случае двух нелинейных звеньев могут быть разные комбинации, в зависимости от того, в какие цепи системы они входят.
Часто при исследовании нелинейных систем автоматического регулирования удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами и может иметь любую форму (релейного типа, кусочно-линейного или криволинейного). Но иногда, не удается этого сделать и приходится исследовать нелинейные дифференциальные зависимости.
Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах. Благодаря этим существенным особенностям, даже вопрос об устойчивости системы становится здесь более сложным.
Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значение здесь, в отличие от линейных систем, также и начальные условия. Возможен новый вид установившегося процесса – автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий.
Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным. Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше:
1) область устойчивости равновесного состояния с постоянным значением регулируемой величины;
2) область устойчивых автоколебаний;
3) область неустойчивости системы;
3) области, соответствующие другим, более сложным случаям. Если процессы в системе имеют вышеуказанный, то равновесное состояние неустойчиво. В том случае, когда колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте, система будет обладать устойчивыми автоколебаниями с амплитудой а.
Разрабатываемая система должна удовлетворять следующим требованиям:
1. интерфейс пользователя должен быть прост в обращении, и представлять собой диалоговую многоуровневую систему в виде вопрос-ответ;
2. программная оболочка должна обеспечивать выполнение следующих функций:
• доступ к текстовым файлам, содержащих справочные материалы;
• графическое отображение структурных схем и формул исследуемой системы;
• выполнение программ, реализующих различные методы исследования нелинейных систем;
• вывод результатов расчетов в виде графиков и таблиц;
3. система должна быть открытой для дополнения ее другими методами расчета и видами представления результатов эксперимента.
С учетом изложенных требований необходимо выбрать инструментальные средства, которые позволят решить поставленную задачу.
Предполагается функционирование разрабатываемой системы под управлением MS-DOS. Подготовка графических файлов требует наличие графического редактора, как правило, работающего в среде WINDOWS, как, например, редактор PAINT BRUSH.
Для создания текстовых файлов справочников и исходных текстов программ можно использовать любой редактор, работающий в MS-DOS, например: EDIT или MULTY EDIT. Для разработки программного обеспечения удобно использовать язык высокого уровня PASCAL, так как он имеет средства для графического режима отображения информации и средства для быстрого построения оболочек TURBO-VISION.
Для демонстрации графических файлов необходимо использовать средства визуализации их типа VIEWER. Конфигурация инструментальных средств для решения поставленной задачи приведена на рисунках.
Всю работу над дипломным проектом разделили на пять основных этапов.
1 этап. Разработка математической модели и структурных схем, исследуемых объектов.
2 этап. Исследование объектов аналитическими методами.
3 этап. Разработка алгоритмического программного обеспечения АИС.
4 этап. Исследование объектов методом математического машинного моделирования на ПЭВМ.
5 этап. Сравнение результатов математического и машинного моделирования и подтверждение эффективности разработанного АИС.
На первом этапе разрабатываются как подробные математические модели и структурные схемы, в частности, электромеханического привода, так и частичные случаи, например:
• отсутствие обратной связи по скорости:
• отсутствие релейного усилителя;
• отсутствие инерционности цепи якоря электропривода;
• управление двигателя по цепи обмотки возбуждения и управления двигателем по цепи якоря.
На втором этапе аналитическими методами (алгебраическими и частотными) исследуются устойчивость системы и определяются возможности автоколебаний в системе и их параметры.
На третьем этапе разрабатывается алгоритмическое и программное обеспечение АИС с использованием выше перечисленных инструментальных средств операционной системы ПЭВМ.
На четвертом и пятом этапах проверяется эффективность разрабатываемой ЭВМ путем сравнения результатов, полученных при аналитическом и машинном исследованиях.
1. Математическая модель следящей системы
нелинейный следящий автоматизированный
Структурная схема электромеханической следящей системы на базе электропривода постоянного тока приведена на рис 1.1.
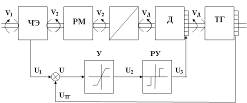
Рис. 1.1
На схеме обозначены:
V1 и V2 – углы поворота командной и исполнительной оси;
V1=V1-V2 – рассогласование (ошибка);
ЧЭ – чувствительный элемент (датчик угла рассогласования);
У – усилитель и его статическая характеристика;
РУ – релейный усилитель;
Д – двигатель;
Р – редуктор;
ТГ – тахогенератор;
РМ – рабочий механизм (объект управления);
Статическая характеристика релейного усилителя показана на рис. 1.2
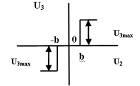
Рис. 1.2
По данной структурной схеме составим дифференциальные уравнения звеньев системы.
1. Уравнение чувствительного элемента
U1=K1V, (1.1)
V=V1-V2,
Где U1 – напряжение на выходе чувствительного элемента.
2. Уравнение линейного усилителя в операторной форме.
(T1p+)U2=K2U, (1.2)
U=U1-UТГ,
Где U2 – напряжение на выходе усилителя, UТГ – напряжение тахогенератора,
![]() – оператор Лапласа
– оператор Лапласа
Статическая характеристика усилителя с учетом насыщения представлена на рис 1.3.
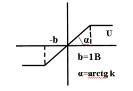
Рис. 1.3
3. Уравнение релейного усилителя записывается в следующем виде:
U3=F(U2) (1.3),
где U3 – напряжение на выходе усилителя (У);
F(U2) – нелинейная функция, заданная статической характеристикой (см. рис. 1.2).
4. Уравнение исполнительного двигателя.
Составим обобщенное дифференциальное уравнение движения постоянного тока, управляемого по цепям якоря обмотки возбуждения.
За входные величины принять напряжение цепи якоря UЯ и обмотки возбуждения UВ и момент нагрузки на валу двигателя MН=МН(t), за выходную – угловую скорость якоря двигателя W.
Насыщением магнитных цепей и реакцией якоря можно пренебречь.
Двигатель работает в системе стабилизации частоты вращения. Составим уравнение равновесия напряжения:
![]() (1.4)
(1.4)
и цепи якоря
![]() (1.5)
(1.5)
а также уравнение равновесия моментов
![]() (1.6)
(1.6)
Индексами «В» и «Я» отмечены параметры – индуктивность L, активное сопротивление R и переменные напряжения U, ток i возбуждения и якоря.
Электромагнитный момент двигателя М и ЭДС якоря l имеют вид:
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
где dE, dM – постоянные коэффициенты;
MH, J – момент нагрузки и момент инерции, приведенные к валу двигателя.
Уравнения цепи якоря и уравнения равновесия моментов (1.7) и (1.8) – нелинейные, так как в них входят произведения переменных величин iЯ, iB и iBW.
![]()
![]()
Линеаризуем выражения для M и l разложением их в ряд Тейлора с учетом лишь линейных составляющих ряда.
В результате получим соотношения для малых приращений:
∆![]() ∆
∆![]() +
+![]() ∆
∆![]() , (1.9)
, (1.9)
∆λ=![]() ∆Ω+
∆Ω+![]() ∆
∆![]() , (1.10)
, (1.10)
Здесь и далее верхним индексом «0» обозначаются установившиеся значения переменных, относительно которых изменяются их приращения. После подстановки ∆M и ∆λ в уравнение цепи якоря (1.5) и уравнение равновесия моментов (1.6) получим уравнение в малых приращениях (знак приращения ∆ отбросим).
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
Найдем из выше
написанного уравнения (1.7) ток ![]() .
.
Подставим его в уравнение (1.11) и после преобразования получим

где
![]()
![]()
![]() ,
, ![]() ,
,
![]() ,
, 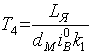 ,
,
|
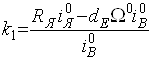 ,
, 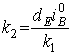 ,
,
![]()
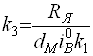 ,
, ![]() ;
;
Определим коэффициенты ![]() и
и ![]() .
.
В режиме короткого
замыкания (Ω = 0) при ![]() и
и ![]() ,
,
![]() =
= ![]() ,
, ![]() ,
,
где ![]() - пусковой момент,
- пусковой момент,
![]() – ток короткого замыкания цепи
якоря.
– ток короткого замыкания цепи
якоря.
Тогда из уравнения цепи якоря получим
![]()
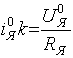
С другой стороны из уравнения
![]() и
и ![]()
Получим следующее выражение уравнения для пускового момента
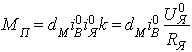 ,
, 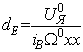
Подставив ![]() в уравнение (1.4) и
сделав соответствующие преобразования, окончательно получим следующее:
в уравнение (1.4) и
сделав соответствующие преобразования, окончательно получим следующее:
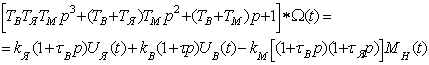 (1.14)
(1.14)
где ![]() ;
;
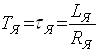 ;
; 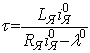 ;
;
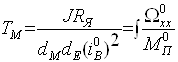 ;
;
 ; ;
; ; 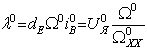
 ;
;
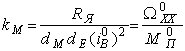 ;
;
Далее из обобщенного дифференциального уравнения двигателя постоянного тока (1.14) получим частотные уравнения для следующих случаев:
1)
управление
двигателем по цепи обмотки возбуждения, когда ![]() , где
, где ![]() – напряжение сети;
– напряжение сети;
2)
то же, но при ![]()
3)
управление
двигателем по цепи якоря, когда ![]() ;
;
4)
то же, но при ![]() ;
;
Рассмотрим эти случаи:
1)
В этом случае
приращение, ∆![]() , тогда и обобщенное
, тогда и обобщенное
уравнение движения принимает вид:
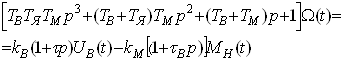
![]() (1.15)
(1.15)
2)
Если ![]() , то
, то ![]() ,
, ![]() =0 И уравнение
(1.15) упрощается и имеет вид:
=0 И уравнение
(1.15) упрощается и имеет вид:
![]()
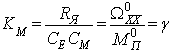 ,
, 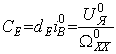 ,
,
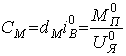 ,
, ![]() ;
;
Коэффициенты ![]() и
и ![]() определены в
формуле (1.14)
определены в
формуле (1.14)
Механические характеристики при этом имеют вид, показанный на рис. 1.4.
a) ![]() б)
б) ![]()
![]()
![]()
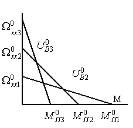
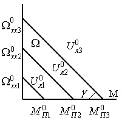
Рис. 1.4
Из этого видно, что
коэффициент наклона механических характеристик γ=const при ![]() =var.
=var.
Дифференциальное
уравнение движения и передаточная функция двигателя с независимым возбуждением,
управляемого по цепи якоря относительно угла поворота вала λ при ![]() =0 имеет вид:
=0 имеет вид:
![]()
![]()
Передаточные функции двигателя постоянного тока с независимым возбуждением выражены в уравнении
![]() (1.16)
(1.16)
Коэффициенты уравнений (1.15) и (1.16) определены в формуле (1.14). Механические характеристики при этом имеют вид как показано на рисунке (1.3).
3)
В этом случае
приращение ∆![]() и обобщенное уравнение движения принимает вид
и обобщенное уравнение движения принимает вид
![]() (1.17)
(1.17)
4)
Если ![]() , то
, то ![]() и уравнение (1.17)
упрощается
и уравнение (1.17)
упрощается
![]() (1.18),
(1.18),
а коэффициенты уравнений принимают следующий вид:
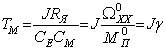
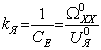
то цепи якоря, если пренебречь электромагнитными процессами цепи якоря, имеют вид:
![]() ;
;
![]()
5) Уравнение тахогенератора имеет вид
![]()
6) Уравнение редуктора
![]() ,
,
где ![]() – коэффициент передачи редуктора.
– коэффициент передачи редуктора.
Полученные дифференциальные уравнения представляют собой математическую модель электропривода (следящей системы). В дальнейшем для проверки методик исследования нелинейных систем мы будем пользоваться этой моделью с учетом некоторых ограничений.
Например, можно пренебречь влиянием статического момента нагрузки и переходного процесса в цепи якоря, тогда структурная схема следящей системы может быть представлена в виде той, которая приведена на рис 1.5
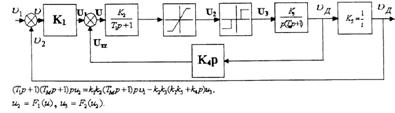
Рис. 1.5
Согласно этой схеме дифференциальное уравнение линейной части системы, записанное относительно входной величины нелинейного звена релейного усилителя U2, имеет следующий вид:
![]() (1.19)
(1.19)
Уравнение линейной части дополняется уравнениями нелинейных звеньев. Уравнения имеют вид:
U2=F1(U), U3=F2(U2).
2. Исследование нелинейной следящей системы аналитическими
методами
Найдем область устойчивого состояния равновесия и область автоколебаний, и определим амплитуду и частоту автоколебаний для следящей системы, схема которой изображена на рис 1.2 при учете нелинейности типа насыщения в предварительном усилителе и отсутствии релейного усилителя и обратной связи по напряжению тахогенератора.
Исходные данные:
Т 1=0,1 с – постоянная времени усилителя;
Т2=1 с – электромеханическая постоянная времени двигателя;
Кл=20 с-1 – общий коэффициент передачи линейной части системы;
К1=50 В/рад – коэффициент передачи чувствительного элемента. Исследование проведем для к2=1 и к2=2;
Составляем структурную схему с учетом допущений рис. 1.6.
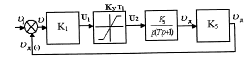
Рис. 1.6
Согласно этой схеме дифференциальное уравнение линейной части системы при V1(t)=0 запишется в следующем виде:
(T2p+1)pU1=-kЛU2 (1.20)
где kЛ=k1k3k5
Дифференциальное уравнение нелинейного звена имеет вид:
(T1p+1)U2=kyU1 (1.21)
Коэффициент усиления усилителя ky является нелинейной функцией, заданной графически (рис. 1.5).
Поэтому согласно методу гармонической линеаризации, запишем для него гармонически линеаризованное выражение
![]() (1.22)
(1.22)
где коэффициенты гармонической линеаризации для характеристики с насыщением имеют значение:
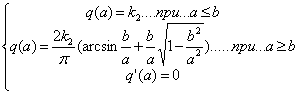 (1.23)
(1.23)
Из уравнений (1.21) – (1.23) получим линеаризованное уравнение замкнутой нелинейной системы
[(T1p+1)(T2p+1)p+kЛq(a)]U1= 0, (1.24)
которому соответствует характеристическое уравнение. Оно имеет вид:
T1T2p3+(T1+T2)p2+p+kЛq(a)=0 (1.25)
Для отыскания условий существования периодического решения
![]() (1.26)
(1.26)
из характеристического
полинома после подстановки p=j![]() выделим вещественную и мнимую части и приравняем их к
нулю:
выделим вещественную и мнимую части и приравняем их к
нулю:
![]()
![]()
![]() (1.27)
(1.27)
Частота периодического решения находится из второго уравнения (1.27)
![]() (1.28)
(1.28)
Из первого уравнения(1.27), с учетом (1.28), получим формулу, связывающую амплитуду периодического решения с параметрами системы
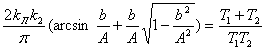 (1.29)
(1.29)
Для исследования устойчивости периодического решения найдем частные производные от выражений
 (1.30)
(1.30)
Для устойчивости периодического решения (1.26) требуется, чтобы выполнялось следующее неравенство
![]() (1.31)
(1.31)
или с учетом выражений
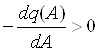 (1.32)
(1.32)
то есть частная производная должна быть отрицательной.
Для определения знака этой производной по выражению (1.23) построим график q(A) рис 1.7 согласно которому
dq(A) dA
<0 при А>b (1.33)
Следовательно, амплитуда периодического решения (1.27) будет амплитудой автоколебаний лишь при выполнении следующего условия, когда А>b
При А<b автоколебания в системе отсутствуют, что и понятно, так как при этом, согласно рис. 1.5, нелинейная система превращается в линейную, которая является устойчивой.
Определим амплитуду автоколебаний. Уравнение (1.29), связывающее ее с параметрами системы, является трансцендентным. Поэтому для определения амплитуды воспользуемся графоаналитическим методом. Для этого решим уравнение (1.29) относительно следующего равенства k = kЛk2:
 (1.34)
(1.34)
и построим график, в котором k = k(A) рис. 1.7,
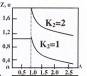
Рис. 1.7
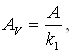
где Av – является амплитудой колебаний относительно исполнительной оси системы (рис. 1.8).
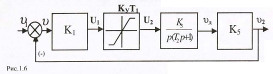
Рис. 1.8
Что касается частоты автоколебаний Q, то она остается неизменной для любой переменной системы и, согласно выражению (1.28), не зависит от коэффициента k.
Граничный коэффициент передачи системы k,p определяется из выражения (1.34) при следующем равенстве А=b и равен
![]() (1.35)
(1.35)
Автоколебания в системе возникают лишь тогда, когда k>kГР.
Нетрудно убедиться, что граничный коэффициент (1.33) совпадает с коэффициентом передачи, найденным из условия границы устойчивости линейной системы. Но, в отличие от линейной системы, у которой за областью устойчивости лежит область неустойчивости, в системе с нелинейностью типа насыщения за областью устойчивости лежит область автоколебаний, т.е. устойчивых периодических колебаний с вполне определенной амплитудой и частотой.
На рис. 1.3 также изображены графики, связывающие амплитуду и частоту автоколебаний с шириной b зоны линейности статической характеристики нелинейного звена при равенстве К2=1
Для заданных значений параметров системы по графику рис. 1.9
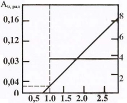
Рис. 1.9
определяем частоту и амплитуду автоколебаний:
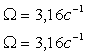

Рассмотрим случай, когда в системе не учитывается нелинейность электронного усилителя. Исследуем устойчивость состояния электромеханической следящей системы, структурная схема которой, изображена на рис. 1.10 частотным методом определения автоколебаний.
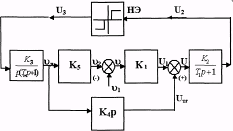
Рис. 1.10
Пусть заданы следующие параметры линейных звеньев:
K1=57,3 В/рад – крутизна статической характеристики чувствительного элемента;
к2:=2,5 – коэффициент усиления линейного усилителя;
к3=5,7 – коэффициент передачи двигателя;
k4=10-2 В с/рад – крутизна статической характеристики тахогенератора;
k5=0,001 – коэффициент передачи редуктора;
Т j =0,05 с – постоянная времени линейного усилителя; и статическая характеристика нелинейного звена (уравнение релейного усилителя) 1.11, для которой b=0,25 В
V3max=c=110B
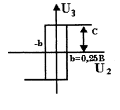
Рис. 1.11
По заданной структурной схеме определим передаточную функцию линейной части системы WЛ(p) и гармонически линеаризованную передаточную функцию нелинейного звена WH(a).
Для этого структурную схему нелинейной системы представим в виде последовательного соединения нелинейного звена и линейной части системы рис. 1.10.
Согласно рис. 1.10 мы получим следующее:
![]()
Гармонически линеаризованная передаточная функция нелинейного звена, имеющего однозначную статическую характеристику, может быть записана в следующем виде:
WH(a)=q(a) (1.37)
Где 
По передаточной функции (1.36) определим частотную передаточную функцию:
![]() (1.38)
(1.38)
ее модуль:
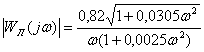 (1.39)
(1.39)
и фазу:
![]() (1.40)
(1.40)
По формуле (1.39) и (1.40) строим амплитудно-фазовую характеристику линейной части системы рис. 1.11 и годограф нелинейного звена.
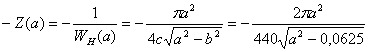 (1.41)
(1.41)
при
значениях амплитуд ![]()
В данном случае этот годограф совпадает с отрицательной вещественной полуосью и имеет две ветви.
Минимальное значение модуля функции – Z(a) равно следующему
![]()
Достигается
при ![]()
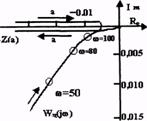
Рис. 1.12
Как
видно из рис. 1.12, годографы ![]() и
-Z(a) не имеют общих точек пересечения.
и
-Z(a) не имеют общих точек пересечения.
Следовательно, состояние равновесия рассматриваемой системы устойчиво. Эту же систему рассмотрим, если статическая характеристика нелинейного звена имеет петлю гистерезиса рис. 1.12.
Согласно структурной схемы рис. 1.10 передаточная функция линейной части системы при исходных данных задачи равна:
![]()
частотная передаточная функция нелинейного звена, имеющего неоднозначную статическую характеристику, может быть записана в виде:
WH (a)=q(a)=jq’(a),
где для релейной характеристики с гистерезисной петлей рис. 1.11 мы получаем следующее:
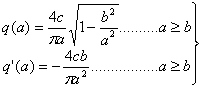
Годограф нелинейного звена -Z(a), построенный по выражению, имеющему вид:
WH(a) 4с![]() ,
,
изображен на рис. 1.13.
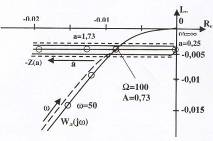
Рис. 1.13
На этом
же рисунке построена амплитудно-фазовая характеристика линейной части системы ![]() , которая
полностью совпадает с построенной на рис. 1.11.
, которая
полностью совпадает с построенной на рис. 1.11.
Точка пересечения этих двух кривых определяет периодическое решение в системе:
![]() ,
,
где ![]() . Согласно рис. 1.13, найденное периодическое решение является устойчивым,
т.е. А и Ω являются амплитудой и частотой автоколебаний.
. Согласно рис. 1.13, найденное периодическое решение является устойчивым,
т.е. А и Ω являются амплитудой и частотой автоколебаний.
Полученные результаты аналитических исследований нелинейной системы в следующих разделах будут сравнены с результатами, полученными при математическом машинном моделировании на ЭВМ.
3. Разработка требований к интерфейсу пользователя диалоговой
системы
Проектируемая система состоит из двух практически самостоятельных частей.
Во-первых, что программа – оболочка, и, во-вторых, что это некоторый набор самостоятельных модулей, реализующих различные математические методы исследования нелинейных САУ.
Программа-оболочка предназначена для связи в единое целое вычислительных задач (методы исследования САУ), текстовых файлов (справочные материалы), графических файлов (иллюстрации).
Она должна обеспечивать доступ к этим компонентам системы. Очевидно, что программа-оболочка по своей сути диалоговая.
В настоящее время по принципу оболочка-приложение строится большинство программных систем, предназначенных для решения научно-технических, экономических и других задач.
Понятие диалоговую по отношению к программной системе подразумевает тесное взаимодействие человека-пользователя с ЭВМ.
Аспекты этого взаимодействия в настоящее время тщательно изучаются, результатом чего являются практические рекомендации по разработке диалоговых систем.
Целесообразно кратко рассмотреть основные вопросы, связанные с этим. Пользователь программного обеспечения рассмотрен в двух аспектах:
• пользователь, как человек;
• пользователь в процессе общения с системой.
Такой подход приводит к выделению ряда важных факторов.
А. Пользователь, как человек. Потребности.
Навыки.
Свойства личности.
Б. Диалоговая подготовка пользователя. Обучение диалогу.
Опыт работы с диалоговыми системами.
В. Подготовка пользователя в прикладной области.
Г. Отношение пользователя к системе.
Причины пользования системой.
Отношение и ожидания.
Цели пользователя.
Д. Аспекты, связанные с задачей.
Структура задачи. Ограничения по времени.
Эти факторы могут быть описаны подробнее.
Человеческие потребности означают, например, потребность быть понятым партнером по диалогу. Пользователь хочет иметь возможность двустороннего разрешения конфликта. Он не хочет обходится ограниченным в своем поведении в процессе общения и вдобавок у него есть физические и психические потребности.
Навыки пользователя состоят из физических и моторных навыков, лингвистических навыков, навыков общения.
Свойства личности это, например, подверженность ошибкам, терпеливость, неустойчивое внимание.
Диалоговая подготовка – здесь приходится делать различие между программистом и не программистом, и во второй группе оказываются параметрические пользователи и пользователи языков запросов.
Выделим три класса пользователей:
• оперирующие языком программирования и знающие организацию базы данных;
• оперирующие языком запросов и использующие модели данных;
• оперирующие параметрическим вводом с почти «естественным видом» данных.
Опыт работы с диалоговыми системами определяется частотой и методом взаимодействия с одной или несколькими диалоговыми системами, мы проводим различие между опытом работы с интерфейсом определяемой базы данных.
Причина пользования системой может быть :
• обязательной, как неотъемлемая часть работы;
• необязательной, как часть работы;
• обязательной в частной жизни (пользование библиотекой).
В литературе обычно принимают во внимание только профессиональных пользователей. Отношение к системе и ожидания от работы с ней являются следствиями типа диалогового обучения.
Оно может быть:
• нейтральным (пользователь воспринимает компьютер, как рабочий инструмент);
• положительным;
• негативным (пользователь предпочел бы не пользоваться компьютером).
Целями пользователя могут быть: решить определенную задачу с помощью компьютера или как научиться работать с системой.
По своей структуре задача может быть отнесена в зависимости от природы проблемы к одному из классов, а именно:
• хорошо структурированные задачи, где данные и методы известны;
• плохо структурированные задачи, где решение может быть получено лишь приближенно.
Кроме того, можно выделить пять различных категорий:
• простой запрос;
• принятие решения после системного запроса;
• систематический сбор данных;
• непрерывное построение и перестройка на основе правил ограничений;
• обнаружение взаимосвязей.
Ограничения по времени.
Независимо от временных условий, заданных системой, пользователь может быть вынужден приспосабливаться к ограничениям времени.
На основе анализа этих факторов можно определить требования к диалоговой системе:
• Поведение системы по отношению к пользователю должно быть гибким, так чтобы пользователь не был вынужден действовать строго предписанным образом.
• Должна существовать процедура отказа от услуг системы.
Система должна быть способна различать пользователей и приспосабливаться к ним.
• Поведение системы и его результаты должны быть ясны пользователю.
• В любой момент времени терминал находится в некотором конкретном состоянии, которое характеризуется набором возможных входных сообщений и интерпретаций.
• Система должна быть всегда готова помочь пользователю; никогда не следует ставить пользователя в затруднительное положение.
• Должно складываться впечатление, что управление всеми аспектами системы принадлежит пользователю.
• Взаимодействие человека с машиной должно напоминать, по возможности, человеческое общение.
• Проект системы должен принимать во внимание физические и психические особенности пользователя во время его работы с машиной.
• Скорость обмена не должна выходить из диапазона без стрессовой работы. Всегда должно казаться, что скоростью управляет пользователь.
Подготовленность людей.
Для пользователя системой не должны требоваться специальные навыки. Система должна подстраиваться к возможностям пользователя.
Для работы с системой не следует требовать специальных физических и моторных навыков. Обычных лингвистических навыков пользователя и навыков общения должно хватать для ведения простых диалогов.
Система должна вести себя логично, так, чтобы пользователь мог научиться предвидеть ее поведение. Система не должна ограничивать разнообразие способов решения задач.
Несмотря на многообразие и сложность использования и на количество требований к диалоговой системе, можно предположить ряд мероприятий, которые при своей простоте помогут решить поставленные задачи.
Взаимодействие пользователя с ЭВМ осуществляется через систему экранных окон (независимость от операционной системы DOS или WINDOWS), связанных через меню.
Управление может осуществляться с помощью клавиатуры или манипулятором «мышь». Один и тот же результат может быть достигнут различным путем:
• использование меню;
• использование функциональных или «горячих клавиш»;
• указание и запуск с помощью «мыши».
• Наличие на экране строки «статуса», содержащей краткую информацию о состоянии системы и возможных на данный момент командах, облегчает диалог.
Управление цветом и звуком также способствует удобству диалога. Описанные мероприятия стали практически стандартными при описании диалоговых систем. Они составляют основу пользовательского интерфейса. Компания IBM определила свой стандарт, которого придерживаются большинство разработчиков программного обеспечения.
В стандарте определено, что основой интерфейса является «панель» – информация, сгруппированная и расположенная на экране определенным способом.
Определены панели: меню, ввода, информационная, списковая, идентификации, приложения. Каждая панель состоит из трех частей, каждая из которых содержит свою информацию. Это меню действий с выпадающими меню, тело панели и область функциональных клавиш.
Меню действий представляет доступ к основным функциям приложения и отображается вверху экрана. При выборе действия на экране появляется расширенное меню действий – выпадающее меню.
Тело панели располагается под меню действий и может быть разделено на несколько областей. Область функциональных клавиш располагается внизу панели. Она содержит список назначений функциональных клавиш. Панели, расположенные в отдельных ограниченных частях экрана, называются окнами.
Краткое описание типов панели.
Панель меню.
Содержит один и более список объектов, из которых пользователь выбирает один или несколько. Для этой цели есть поля выбора.
Панель ввода.
Она отображает поля, в которые пользователь вводит информацию и из которых выбирает объекты. Имеется три типа панелей ввода:
• панель ввода параметров отображает поля для ввода значений параметров и указания режимов действий. Содержит поля ввода и выбора.
• Панель ввода с заголовками представляет форму документов на бумаге и на каждой строке, и на каждой строке может содержать несколько панелей;
• Панель ввода с табуляцией содержит поля с заголовками, организованные по столбцам и строкам.
Информационная панель.
Отображает защищенную информацию: данные, сообщения, справки.
Списковая панель.
Отображает список объектов, из которых пользователь выбирает один или несколько и запрашивает одно или несколько действий над ними. Для каждого объекта одновременно запрашивается только одно действие, но для различных объектов – различные действия.
Панель идентификации приложения.
Отображает информацию, идентифицирующую приложение и авторские права разработчиков. Панели имеют различные рабочие области. К ним относятся:
• разделители областей;
• идентификатор панели;
• заголовок панели;
• инструкция;
• заголовок столбца и группы;
• заголовок поля;
• указатель протяжки;
• область сообщений;
• область команд.
Панель обладает рядом свойств, которые позволяют открывать и закрывать их различными способами (клавиатура или мышь), перемещать их на экране или изменять их размер.
Стандарт фирмы ШМ также предлагает для цветового решения приложения несколько палитр, разработанных с учетом требований эргономики и санитарии.
Из изложенного видно, что круг задач, который должен решить программист при разработке диалоговых программ, весьма обширен. Поэтому для эффективной работы необходимо пользоваться современными инструментальными средствами. В качестве такого может быть выбран язык программирования BORLAND PASCAL в комплекте с библиотекой TURBO VISION.
Эта библиотека использует объектно-ориентированный подход в программировании и содержит большое количество объектов, позволяющих эффективно строить диалоговые программы с использованием оконного интерфейса.
Разрабатываемая программа-оболочка должна обеспечивать следующее:
• отображения в окне текстовых файлов, содержащих справочную информацию;
• отображение в окне графических файлов в формате PCX, содержащих иллюстрации;
• запуск на выполнение исследовательских программ и отображение результатов в окне.
Основное окно программы-оболочки содержит главное меню, тело и область функциональных клавиш.
Главное меню имеет следующий вид:
| Справки | Демонстрация | Исследование | Выход |
Выбор пункта меню «справки» приводит к появлению выпадающего меню второго уровня, которое имеет вид:
| Методы исследования |
| Нелинейные элементы |
| Инструкция программисту |
| Инструкция пользователю |
Выбор пункта меню «демонстрация» вызывает запуск демонстрационной задачи, содержащей текст описания и графическое представление результатов.
Выбор пункта меню «Исследование» вызывает запуск программ, реализующих методы исследования САУ, и имеет вид:
| Метод 1 |
| Метод 2 |
| Метод 3 |
| Метод 4 |
| Метод N |
Где «Метод» – конкретное название метода анализа САУ. Выбор пункта меню «Выход» приводит к завершению работы.
4. Разработка программного обеспечения АИС
Библиотека TURBO VISION основана на объектно-ориентированном подходе к программированию, который базируется на трех основных понятиях: инкапсуляция, наследование, полинорфаза.
Инкапсуляция – объединение данных с процедурами и функциями, которые манипулируют этими данными. Примером может служить перемещаемый по экрану отрезок, определяемый координатами своих концов (данные), и процедурой, обеспечивающей это перемещение (метод).
Наследование – возможность использования уже определенных объектов для построения иерархии объектов, начиная с некоторого простого первоначального (предка) и кончая более сложными, но включающими свойства предшествующих элементов (потомки). В качестве такой иерархии можно рассмотреть точку на экране дисплея, задаваемую своими координатами (предок), отрезок, задаваемый координатами двух точек – его концов (потомок точки), перемещаемый отрезок, задаваемый координатами своих концов и процедурой, обеспечивающей его перемещение (потомок неперемещаемого отрезка).
Полиморфизм – возможность определения единого по имени действия, принимаемого одновременно по всем объектам иерархии наследования, т.е. для различных родственных объектов можно задать единый класс действий.
Под объектом понимается такая структура, компонентами которой являются взаимосвязанные данные различных типов и использующие эти данные процедуры и функции. Компоненты – данные называются полями объекта, а компоненты – процедуры и функции называются методами. Дальнейшее описание диалоговой программы будет базироваться на этих понятиях.
Разработка системы меню с использованием TURBO VISION, базируется на применении объектов TMenu Bar и Tmenu Box, которые отличаются от абстрактного типа Tmenu View.
Объекты TMenu Bar представляют полосы горизонтального меню, пункт которого может быть выбран через:
• прямую отметку;
• клавишу F10;
• выбор (подсветку) и нажатие ENTER;
• горячие клавиши.
Объект TMenu Bar обычно принадлежит TApplication. Перекрывая Tapplication Tnit Menu Bar соответствующим набором вложенных видов New, NewSubMenu, Newltem и NewLine, можно сформировать объект меню.
Объекты MenuBox представляют вертикальные прямоугольники меню. Они могут содержать произвольный характер выполняемых действий.
Функция NewSubMenu распределяет и возвращает указатель на новую запись TMenuItem, которая представляет собой подменю. Функция Newltem распределяет и возвращает указатель на новую запись THenaltem, которая представляет собой меню. Реализация системы меню диалоговой программы осуществлена в процедуре TMyAPP.InitMenu Bar.
Функция, которая будет выполнена диалоговой программой; определяется выбором пункта меню. В TURBO VISION для обработки событий меню предназначен метод HandleEvent (процедура) объекта TmenuView. Он определяет, какой элемент меню был выбран «мышью» или клавиатурой, и генерирует соответствующее командное событие. Реализация обработки событий осуществлена в процедуре Тту Арр. HandleEvent.
Кроме описанных процедур в состав диалоговой программы входят также:
TmyApp. TnitStatusLine – привязка функциональных клавиш к пунктам меню.
• TmyApp. PrintFile – вывод текста в окно без возможности прокрутки;
• TmyApp. PrintFileScr – вывод текста в окно с возможностью прокрутки
• TmyApp. ShowFile – вывод графического файла в формате PCV в окно;
• TmyApp. RunMetod I, TmyApp. RimMetod2,..., TmyApp. RunMetod N – запуск программы исследования САУ.
На следующих страницах приведены рисунки, иллюстрирующие вышеизложенное.
5. Результаты испытания АИС
Во второй главе специальной части дипломного проекта для подтверждения работоспособности АИС были получены результаты аналитического исследования электромеханического привода для нескольких конкретных примеров, характеризующиеся различными видами нелинейности (зоны нечувствительности и насыщения, релейная, петли гистерезиса) и различиями в структуре привода. После завершения разработки АИС были проведены вычислительные эксперименты по расчету рассмотренных ранее моделей приводов.
Результаты показали адекватность разработанной АИС. Результаты испытаний АИС приведены на рисунках.
Заключение
В дипломной работе рассматривались вопросы, связанные с разработкой учебно-методического комплекса для исследования нелинейных систем.
Разработана диалоговая программа, позволяющая объединить в рамках одной системы различные методы исследования САУ.
Для доказательства работоспособности автоматизированной системы были проведены аналитические исследования некоторых контрольных примеров, а затем они же были рассчитаны с помощью АИС. Сравнительный анализ полученных результатов подтверждает адекватность системы.
Приложение
Program Diplom; uses
Forms,
Main in 'Main.pas' {MainForm},
Unitl in'Unitl.pas' {Forml},
Unit2 in 'Unit2.pas' {AboutBox}; ($R *.RES begin
Application. CrateForm (TmainForm, MainForm);
Application. CrateForm (TForml, Forml);
Application. CrateForm (TAboutBox, AboutBox);
Forml.Show;
Application.Run; end.
unit Main;
interface
uses
SysUtils, Windows, Messages, Classes, Graphics, Controls, Fornis, Dialogs,
StdCtris, Buttons, ExtQik, Menus, Grids, Unitl; type
TMainForm=dass (TForm); StringGridl:TStringGrid;
procedure FormCreate (Sender TObject);
procedure SttingGridlClick (Sender TObject); ant
TMass=aiay[l J6,136]ofByte; var
MainForm TMainForm; MassTMass В1:Всх*щ
implementation fSR *DFM)
procedure TMainFomiFomCreate (Sender TObject); var
I, J, К : Integer; begin
Bl: =False; For i:=l to 36 do For j=l to 36 do
Mass [i, j] :=4; with StringGridl do begin K:=0;
forl:=l to 31 do begin
К :=К+1;
Cells [I,0]:=IntToStr(K); end; К -0;
for I :=lto31do begin
К :=К+1;
Cells [0,1] :=IntToStr(K); end;
k:=0;
for I :=lto31do forJ =1 to 31 do
Cells P,J]-IntToStr(K);
k:=l;
Cells [7,2] : =IntToStr (K);
Cells [13,4]: =IntToStr (K);
Cells [21,4] : = IntToStr (K);
Cells[3,6]: = IntToStr (K);
Cells [15,6] : = IntToStr(K);
Cells [14,8] : = InfToStr(K);
Cells [9,10]: = InfToSlr(K);
Cells [29,10] : = IntToStr(K);
Cells [17,9] : = IntToStr(K);
Cells [16,9] : = IntToStr(K);
Cells [15,10] : = lntToStr(K);
Cells [16,10] : = IntToStr(K);
Cells [17,10] : =IntToSlr(K);
Cells [18,10] : =lntToStr(K);
Cells [14,11] : = JntToStr(K);
Cells [15,11] : = IntToStr(K);
Cells [16,11] : = IntToStr(K);
Cells [17,11] : = IntToStr(K);
Cells [18,11] : =IntToStr (K);
Cells [19,11]: = IntToStr(K);
Cells [7,12] := InrToStr (К);
Cells[13,12]: = InrToStr(K);
Cells [15,12]: = InrToStr (K);
Cells [16,12] : = IntToStr (K);
Cells [17,12] : = IntToSlr(K);
Cells [18,12] : = IntToStr(K);
Cells [19,12] : = IntToStr (K);
Cells [20,12] : = IntToStr(K);
Cells [21,12]: = IntToStr (K);
Cells [12,13] : = IntToStr(K);
Cells [13,13] : = IntToSlr(K);
Cells [14,13] : = IntToStr(K);
Cells [15,13]: = IntToStr (K);
Cells [16.13] : = lnfToSlr(K);
Ceils [17,13] : = lntToStr(K),
Cells [18,13] :=IntToStr(K);
Cells [19,13] : = IntToStr (K);
Cells [11,14] : = IntToSlr(K);
Cells [12,14] : = IntToStr(K);
Cells [13,14] : = IntToStr(K);
Cells [14,14] : = IntToSlr(K);
Cells [15,14] : = IntToStr(K);
Cells [16,14]: = IntToStr (K);
Cells [17,14] : = IntToSlr(K);
Cells [18,14] : = IntToStr (K);
Cells [9,15]: = IntToStr (K);
Cells [10,15]: = IntToStr (K);
Cells [11,15]: = IntToStr (K);
Cells [12,15]: = IntToStr (K);
Cells [13,15]: = IntToStr (K);
Cells [14,15]: = IntToStr (K);
Cells [15,15]: = IntToStr (K);
Cells [16,15]: = IntToStr (K);
Cells [17,15]: = IntToStr (K);
Cells [23,15] : = brfToStr(K);
Cells [10,16] : = IntToStr (K);
Cells [11,16] : = IntToStr (K);
Cells [12,16] : = IntToStr (K);
Cells [13,16] : = IntToStr(K);
Cells [14,16]: = IntToStr (K);
Cells [15,16]: = IntToStr (K);
Cells [16,16]: = IntToStr (K);
Cells [9,17] : = InrToStr (K);
Cells [12,17]: = IntToStr (K);
Cells [13,17]: = IntToStr (K);
Cells [14,17]: = IntToStr (K);
Cells [15,17]: = IntToStr (K);
Cells [10,18] : = IntToStr(K);
Cells [H,18]: = IntToSlr(K);
Celk [12,18]: = IntToStr (K);
Cells [13,18]: = IntToStr (K);
Cells [14,18]: = IntToStr (K);
Cells [8,19] : = IntToStr(K);
Celk [11,19]:=IntToStr (K);
Cells[12,19]: = InfToSlr(K);
Cells [13,19]: = IntToStr (K);
Cells [14,19]: = IntToStr (K);
Cells [12,20]: = IntToStr (K);
Cells [22,20]: = IntToStr (K);
Cells [27,20] : = IntToStr (K);
Cells [5,2З]: = IntToStr (K);
Cells [18,23]: = IntToStr (K);
Cells [24,23] : = IntToSlr(K),
Cells [13,25]: = IntToStr (K);
Cells [29,26]: = IntToStr (K),
Cells [14,27]: = IntToSlr(K);
Cells [16,27]: = IntToSlr(K);
Cells [27,27]: = IntToStr(K);
Cells [2,29] : = IntToSlr(K);
Cells [8,29] : = IntToStr(K);
Cells [10,30] : = IntToStr(K);
Cells [30,30] : = IntToStr (K);
end;
For i:=l to 31 do For j=l to 31 do
Mass [i, j]:=0; end;
procedure TMainForm.StringGridl Click (Sender:TObject);
Procedure Show Mass: Varij:byte; begin
Application. ProcessMessages; Fori:=lto36do Forj:=lto36do begin
If (Mass [L j] = 3) then StringGridl. Cells [i, j] := 'X' else If (Mass [i, j] = 4) then StringGridl.Cells [i, j] :=?'
else StringGridl.Cells [i, j] := IntToStr (Mass [i, j]); end; end;
procedure Stepl; Var Lj: Byte; begin
Fori:=lto31 do For j: = 1 to 31 do
Mass[I,j]:=0; Mass [16,9]:=1;
Mass [17,9]:=1;
Mass [15,10]:=1;
Mass [16,10]:=1;
Mass [17,10]:=1;
Mass [18,10]:=1;
Mass [14,11]:=1;
Mass [15,11]:=1;
Mass [16,11]:=1;
Mass [17,11]:=1;
Mass [18,11]:=1;
Mass [19,11]:=1;
Mass [12,12]:=1;
Mass [13,12]:=1;
Mass [14,12]:=1;
Mass [15,12]:=1;
Mass [16,12]:=1;
Mass [17,12]:=1;
Mass [18,12]:=1;
Mass [19,12]:=1;
Mass [20,12]:=1;
Mass [11,13]:=1;
Mass [12,13]:=1;
Mass [13,13]:=1;
Mass [14,13]:=1;
Mass [15,13]:=1;
Mass [16,13]:=1;
Mass [17,13]:=1;
Mass [18,13]:=1;
Mass [19,13]:=1;
Mass [11,14]:=1;
Mass [12,14]:=1;
Mass [13,14]:=1;
Mass 14,14]:=1;
Mass [15,14]:=1;
Mass [16,14]:=1;
Mass [17,14]:=1;
Mass [18,14]:=1;
Mass [10,15]:=1;
Mass [11,15]:=1;
Mass [12,15]:=1;
Mass [13,15]:=1;
Mass [14,15]:=1;
Mass [15,15]:=1;
Mass [16,15]:=1;
Mass [17,15]:=1;
Mass [9,16]:=1;
Mass [10,16]:=1;
Mass [11,16]:=1;
Mass [12,16]:=1;
Mass [13,16]:=1;
Mass [14,16]:=1;
Mass [15,16] :=1;
Mass [16,16]:=1;
Mass [9,17]:=1;
Mass [10,17]:=1;
Mass [11,17]:=1;
Mass [12,17]:=1;
Mass [13,17] :=1;
Mass [14,17]:=1;
Mass [15,17]:=1;
Mass [10,18]:=1;
Mass [11,18]:=1;
Mass [12,18]:=1;
Mass [13,18]:=1;
Mass [14,18]:=1;
Mass [11,19]:=1;
Mass [12,19]:=1;
Mass [13,19]:=1;
Mass [12,20]:=1; ShowMass;
end;
procedure StepX; Var i,j:Byte;
begin
For i:=l to 31 do
For j:=l to 31do
If Mass [i, j]=3 then StringGridl.Cells [i, 0]:= 'X'; ShowMass;
end;
procedure Step2; begin
Mass[16,9]:=3;
Mass[16,10]:=3;
Mass[16,ll]:=3;
Mass[16,12]:=3;
Mass[16,13]:=3;
Mass[15,14]:=3;
Mass[14,15]:=3;
Mass[13.16]:=3;
Mass[12,17]:=3;
Mass[12,18]:=3;
Mass[12,19]:=3;
Mass[12.20]:=3;
StepX;
end;
procedure Step31;
Var i,j,k,l,:Byte;
Begin
For i:=l to31do
For j :=33 to 36 do
For i:=33 to 36 do For j:=1 to 31 do
Mass[i,j]:=0; For i:=l to31 do
For j :=1 to 31 do
If Mass [I,j]>0 then begin
Mass[i,33]:=l; Mass[i,34]:=l;
end;
For i:=l to31do
For j:=l to31 do
If Mass [i,j]>0 then begin
Mass[33,j]:=l;
Mass[34,j]:=l;
end;
end;
procedureStep32; Var i, j, k, l: Byte; begin
For i:=l to 31 do
if Mass [33, i]=1 then begin
Mass[34,i]:=0;
Break;
end;
For i:=15 to31do
if Mass [i, 33] =0 then
begin
Mass[i-l,34]:=0;
Break;
end;
K:=0;
l:=0;
For i:=1 to31do
if Mass[34,i]=l then
begin
inc(k);
l:=I;
end;
k:=Round (k/2); l:=l-k+l;
Mass [1,35]:=l;
K:=0;
l:=0;
For i:=1 to31do
if Mass [i, 34] =1 then begin
inc(k);
l:=i;
end;
k:=Round(k/2);
l:=l-k+l;
Mass [1,35] :=1;
ShowMass ;
end;
Procedure Step4; Var i,j :Byte; begin
Forml.ListBoxl.Items.Add(‘Начинаем расчёт’)
For i:=l to31do
For j:=1 to31 do
Mass[i,j]:=0;
For i:=14 to 18 do
For j:=11 to 21 do
Mass[i,j] :=1; For i:=11 to 21 do
Mass[16,i] :=3;
Form1. ListBox1. Items. Add ('Очистка от помех");
Form1. ListBox1. Items. Add ('Построение проекции");
Form1. ListBox1. Items. Add ('Нахождение центра проекции');
Form1. ListBox1. Items. Add ('Расчет окончен');
Step31;
StepX;
Mass [16,35 ]:=1;
Mass [35,16] :=1;
ShowMass;
end;
begin
If Bl then
begin
Step4;
Bl:=False;
Exit;
end
else Bl:=True;
Form1.ListBox1.Items. Add ('Начинаем расчет'); Step1;
Form1.ListBox1.Items. Add ('Очистка от помех'); Step2;
Form1.ListBox1.Items.Add ('Построение проекции'); Step31;
Step32;
Form1.ListBox1.Items.Add ('Нахождение центра проекции"); Form1.ListBox1.Items.Add ('Расчет окончен');
end;
end.
Unit Until;
interface uses
Windows, Messages, SysLftils, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls, Buttons;
type
TForml = class (TForm)
ListBox1:TlistBox;
BitBtn1:TBitBtn;
procedure BitBtn1Click (Sende: TObject); private
{Private declarations}
public
{Public declarations}
end;
var
Form1:TForm1; implementation uses Unit2;
{$R*.DFM}
Procedure TForm1.BitBtn1Click (Sender: TObject); begin
AboutBox.ShowModal;
end;
end.
unit Unit2; interface uses
Windows, SysUtils, Classes, Graphics, Forms, Controls,
StdCtrls, Buttons, ExtCtrls;
type
TAboutBox = class (TForm)
Pane1: TPanel;
ProgramIcon: TImage;
ProductName: TLabel;
Version: TLabel;
Copyright: TLabel;
Comments: TLabel;
OKButton: TButton; private
{Private declarations} public
{Public declarations}
end;
var
AboutBox: TAboutBox; implementation
{$R*.DFM}
end.
| Организация документооборота с помощью "Visual Basic for ... | ||
|
СОДЕРЖАНИЕ АНОТАЦИЯ ВВЕДЕНИЕ 1. ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ. 1.1 Обоснование языка программирования 1.2 Введение в Visual Basic for Application 1.2.1 Об ... W o r k s h e e t s ( " Л и с т 1 " ) . R a n g e (" A l : C 3 " ) . C l e a r If Range("B1:C3")-Cells(i, j).Value > 0 Then |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
| Дифференциальные уравнения и описание непрерывных систем | ||
|
... университет Кафедра Автоматики и управления Реферат по математическим основам теории систем на тему Дифференциальные уравнения и описание ... Разделив это уравнение на J и обозначив b=-k/J, x(t)=m(t)/J, а также принимая j(t) за управляющее воздействие u(t), получаем Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение нелинейно, то элемент называется ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Математическое моделирование и расчет систем управления техническими ... | ||
|
Министерство образования Российской Федерации Санкт-Петербургский государственный горный институт им. Г.В.Плеханова (технический университет ... Пусть дано дифференциальное уравнение n-порядка звена или системы автоматического управления (2). Необходимо получить выражения для импульсной переходной функции (функции веса) w(t ... Простейший пример такой модели - нелинейный интегратор dy/dt = F(x) структурно изображается как последовательное соединение безынерционного НЭ и линейного интегрирующего звена (рис ... |
Раздел: Рефераты по мате соединение безынерционного НЭ и линейного интегрирующего звена (рис ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Анализ на чувствительность двойственных оценок | |
|
Введение Под термином "программирование" понимают выбор программных действий для решения задачи. Математическое программирование представляет собой ... Стандартной или симметричной задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1.1) при выполнении условий (1.2) и ... Form1.StringGrid3.Cells[1,j]:='P'+inttostr(trunc(bz[1,j]) |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... ... няются в группы по самым различным интересам, начиная от нейтронных сетей, дифференциальных уравнений в частных производных, сплайн-аппроксимации, статистики и размытых множеств до ... F (1:k, j) |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |