Контрольная работа: Экономико-математическая статистика
Задание 1
По
данным приложения 2 произведите аналитическую группировку результата Y, разбив совокупность на четыре
группы. Каждую группу охарактеризуйте числом единиц в подгруппе и средними
показателями (![]() ). Сделайте анализ результатов
группировки.
). Сделайте анализ результатов
группировки.
Вычислите парные коэффициенты корреляции и постройте матрицу парных коэффициентов корреляции. Сделайте выводы о тесноте связи между признаками.
Найдите
линейное уравнение связи ![]() совокупный коэффициент корреляции
и детерминации, b-коэффициенты,
коэффициенты эластичности. Сделайте подробные выводы.
совокупный коэффициент корреляции
и детерминации, b-коэффициенты,
коэффициенты эластичности. Сделайте подробные выводы.
| № п/п | Урожайность, ц/га | Качество почвы, балл | Количество осадков за период вегетации, мм |
|
|
|
|
|
| 1 | 7,1 | 49 | 170 |
| 2 | 7,3 | 50 | 129 |
| 3 | 26,0 | 95 | 248 |
| 4 | 9,0 | 60 | 163 |
| 5 | 9,5 | 65 | 180 |
| 6 | 8,9 | 60 | 173 |
| 7 | 11,5 | 70 | 228 |
| 8 | 11,9 | 74 | 235 |
| 9 | 19,1 | 88 | 287 |
| 10 | 15,9 | 80 | 269 |
| 11 | 16,8 | 82 | 215 |
| 12 | 21,7 | 90 | 277 |
| 13 | 18,9 | 87 | 322 |
| 14 | 17,3 | 89 | 275 |
| 15 | 19,1 | 90 | 248 |
| 16 | 20,4 | 9! | 392 |
| 17 | 11,3 | 76 | 221 |
| 18 | 11,0 | 70 | 178 |
| 19 | 10,8 | 77 | 128 |
| 20 | 15,8 | 68 | 288 |
Проведем статистическую
группировку по отдельному группировочному признаку. С этой целью определим
величину интервала группировки по формуле Стерджесса ![]() .
.
![]() .
.
Группировка полей по урожайности
|
Группы полей по урожайности |
Середина интервала | Число полей в группе | Урожайность, ц/га | Качество почвы, балл | Количество осадков за период вегетации, мм | |||
| Всего | на 1 поле | Всего | на 1 поле | Всего | на 1 поле | |||
| 7,1 - 11,8 | 9,5 | 9 | 86,4 | 9,6 | 577 | 64 | 1570 | 174 |
| 11,8 - 16,5 | 14,2 | 3 | 43,6 | 14,5 | 222 | 74 | 792 | 264 |
| 16,5 - 21,2 | 18,9 | 6 | 111,6 | 18,6 | 527 | 88 | 1739 | 290 |
| 21,2 - 26,0 | 23,6 | 2 | 47,7 | 23,9 | 185 | 93 | 525 | 263 |
| Итого: | 20 | 289,3 | 1511 | 4626 |
На основании проведенной статистической группировки можно сделать вывод, что чем выше качество почвы, тем выше урожайность культуры. Так при среднем качестве почвы в 64 балла урожайность составляет от 7,1-11,8 ц/га, тогда как при качестве почвы в 93 балла урожайность составляет 21,2-26 ц/га.
Среди изучаемой совокупности больше всего полей (9 ед.) с урожайностью от 7,1-11,8 ц/га, меньше всего полей (2 ед.) с урожайностью от 21,2-26,0 ц/га.
Для расчета парных коэффициентов корреляции воспользуемся линейной зависимостью:
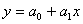 ,
,
где у – индивидуальное значение результативного признака (урожайности);
х - индивидуальное значение факторного признака (качество почвы);
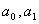 - параметры
уравнения прямой (уравнения регрессии).
- параметры
уравнения прямой (уравнения регрессии).
Параметры уравнения можно определить по следующим формулам:
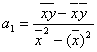 ;
; 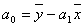
Для определения параметров уравнения регрессии построим расчетную таблицу (табл. 8.2).
Расчетная таблица для определения параметров уравнения регрессии
| № поля |
Качество почвы, балл
|
Урожайность, ц/га
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 49 | 7,1 | 347,9 | 2401 | 6,5 |
| 2 | 50 | 7,3 | 365 | 2500 | 6,8 |
| 3 | 95 | 26 | 2470 | 9025 | 20,5 |
| 4 | 60 | 9 | 540 | 3600 | 9,8 |
| 5 | 65 | 9,5 | 617,5 | 4225 | 11,4 |
Определяем параметры уравнения регрессии:
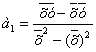 =
=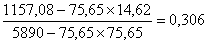 ;
;
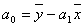 = 14,62 – 0,306
= 14,62 – 0,306 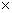 75,65 = -8,53
75,65 = -8,53
Уравнение корреляционной связи примет вид:
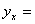 -28,53 + 0,306
-28,53 + 0,306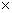 х
х
Для расчета коэффициента детерминации строим таблицу.
Расчетная таблица для определения коэффициента детерминации
|
№ поля |
Качество почвы, балл
|
Урожайность, ц/га
|
Yx |
|
|
|
( |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 49 | 7,1 | 6,5 | -8,12 | 65,93 | -7,52 | 56,55 |
| 2 | 50 | 7,3 | 6,8 | -7,82 | 61,15 | -7,32 | 53,58 |
| 3 | 95 | 26 | 20,5 | 5,88 | 34,57 | 11,38 | 129,50 |
| 4 | 60 | 9 | 9,8 | -4,82 | 23,23 | -5,62 | 31,58 |
| 5 | 65 | 9,5 | 11,7 | -2,92 | 8,53 | -5,12 | 26,21 |
| 6 | 60 | 8,9 | 9,8 | -4,82 | 23,23 | -5,72 | 32,72 |
| 7 | 70 | 11,5 | 12,9 | -1,72 | 2,96 | -3,12 | 9,73 |
| 8 | 74 | 11,9 | 14,1 | -0,52 | 0,27 | -2,72 | 7,40 |
| 9 | 88 | 19,1 | 18,4 | 3,78 | 14,29 | 4,48 | 20,07 |
| 10 | 80 | 15,9 | 16 | 1,38 | 1,90 | 1,28 | 1,64 |
| 11 | 82 | 16,8 | 16,6 | 1,98 | 3,92 | 2,18 | 4,75 |
| 12 | 90 | 21,7 | 19 | 4,38 | 19,18 | 7,08 | 50,13 |
| 13 | 87 | 18,9 | 18,1 | 3,48 | 12,11 | 4,28 | 18,32 |
| 14 | 89 | 17,3 | 18,7 | 4,08 | 16,65 | 2,68 | 7,18 |
| 15 | 90 | 19,1 | 19 | 4,38 | 19,18 | 4,48 | 20,07 |
| 16 | 91 | 20,4 | 19,3 | 4,68 | 21,90 | 5,78 | 33,41 |
| 17 | 76 | 11,3 | 14,7 | 0,08 | 0,01 | -3,32 | 11,02 |
| 18 | 70 | 11 | 12,9 | -1,72 | 2,96 | -3,62 | 13,10 |
| 19 | 77 | 10,8 | 15 | 0,38 | 0,14 | -3,82 | 14,59 |
| 20 | 68 | 15,8 | 12,5 | -2,12 | 4,49 | 1,18 | 1,39 |
| Итого | 1513 | 292,3 | 292,3 | 336,63 | 542,97 | ||
| В среднем | 75,65 | 14,62 |
Рассчитаем эмпирический коэффициент детерминации:

![]() -показывает долю вариации, то есть
62 % вариации урожайности объясняется фактором, включенным в модель (качеством
почвы), а 38% не включенными в модель факторами.
-показывает долю вариации, то есть
62 % вариации урожайности объясняется фактором, включенным в модель (качеством
почвы), а 38% не включенными в модель факторами.
Коэффициент корреляции равен:
![]()
Так как коффициент корреляции равен 0,79, это свидетельствует о том, что связь между изучаемыми факторами (урожайностью и качеством почвы) высокая.
Далее произведем расчет парных коэффициентов корреляции воспользовавшись линейной зависимостью:
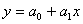 ,
,
коэффициент корреляция тренд уравнение
где у – индивидуальное значение результативного признака (урожайности);
х - индивидуальное значение факторного признака (количество осадков за период вегетации);
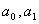 - параметры
уравнения прямой (уравнения регрессии).
- параметры
уравнения прямой (уравнения регрессии).
Параметры уравнения можно определить по следующим формулам:
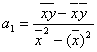 ;
; 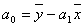
Для определения параметров уравнения регрессии построим расчетную таблицу (табл. 8.4).
Расчетная таблица для определения параметров уравнения регрессии
| № поля |
Количество осадков за период вегетации, мм
|
Урожайность, ц/га
|
|
|
|
| 1 | 170 | 7,1 | 1207 | 28900 | 11,4 |
| 2 | 129 | 7,3 | 941,7 | 16641 | 9,3 |
| 3 | 248 | 26 | 6448 | 61504 | 15,5 |
| 4 | 163 | 9 | 1467 | 26569 | 11,1 |
| 5 | 180 | 9,5 | 1710 | 32400 | 11,9 |
| 6 | 173 | 8,9 | 1539,7 | 29929 | 11,6 |
| 7 | 228 | 11,5 | 2622 | 51984 | 14,4 |
| 8 | 235 | 11,9 | 2796,5 | 55225 | 14,8 |
| 9 | 287 | 19,1 | 5481,7 | 82369 | 17,5 |
| 10 | 269 | 15,9 | 4277,1 | 72361 | 16,6 |
| 11 | 215 | 16,8 | 3612 | 46225 | 13,8 |
| 12 | 277 | 21,7 | 6010,9 | 76729 | 17,0 |
| 13 | 322 | 18,9 | 6085,8 | 103684 | 19,3 |
| 14 | 275 | 17,3 | 4757,5 | 75625 | 16,9 |
| 15 | 248 | 19,1 | 4736,8 | 61504 | 15,5 |
| 16 | 392 | 20,4 | 7996,8 | 153664 | 23,0 |
| 17 | 221 | 11,3 | 2497,3 | 48841 | 14,1 |
| 18 | 178 | 11 | 1958 | 31684 | 11,8 |
| 19 | 128 | 10,8 | 1382,4 | 16384 | 9,2 |
| 20 | 288 | 15,8 | 4550,4 | 82944 | 17,6 |
| Итого | 4628 | 292,3 | 72082,6 | 1155171 | 292,3 |
| В среднем | 231,4 | 14,62 | 3604,13 | 57758,55 |
Определяем параметры уравнения регрессии:
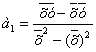 =
=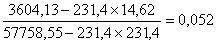 ;
;
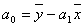 = 14,62 – 0,052
= 14,62 – 0,052  231,4 = 2,58
231,4 = 2,58
Уравнение корреляционной связи примет вид:
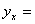 2,58 + 0,052
2,58 + 0,052 х
х
Для расчета коэффициента детерминации строим табл. 8.5.
По данным табл. 8.5 рассчитаем эмпирический коэффициент детерминации:

![]() -показывает долю вариации, то есть
43 % вариации урожайности объясняется количеством осадков за период вегетации,
а 57% факторами, не включенными в модель.
-показывает долю вариации, то есть
43 % вариации урожайности объясняется количеством осадков за период вегетации,
а 57% факторами, не включенными в модель.
Расчетная таблица для определения коэффициента детерминации
|
№ поля |
Количество осадков за период вегетации, мм |
Урожайность, ц/га |
Yx |
|
|
|
( |
| 1 | 170 | 7,1 | 11,4 | -3,22 | 10,37 | -7,52 | 56,55 |
| 2 | 129 | 7,3 | 9,3 | -5,32 | 28,30 | -7,32 | 53,58 |
| 3 | 248 | 26 | 15,5 | 0,88 | 0,77 | 11,38 | 129,50 |
| 4 | 163 | 9 | 11,1 | -3,52 | 12,39 | -5,62 | 31,58 |
| 5 | 180 | 9,5 | 11,9 | -2,72 | 7,40 | -5,12 | 26,21 |
| 6 | 173 | 8,9 | 11,6 | -3,02 | 9,12 | -5,72 | 32,72 |
| 7 | 228 | 11,5 | 14,4 | -0,22 | 0,05 | -3,12 | 9,73 |
| 8 | 235 | 11,9 | 14,8 | 0,18 | 0,03 | -2,72 | 7,40 |
| 9 | 287 | 19,1 | 17,5 | 2,88 | 8,29 | 4,48 | 20,07 |
| 10 | 269 | 15,9 | 16,6 | 1,98 | 3,92 | 1,28 | 1,64 |
| 11 | 215 | 16,8 | 13,8 | -0,82 | 0,67 | 2,18 | 4,75 |
| 12 | 277 | 21,7 | 17 | 2,38 | 5,66 | 7,08 | 50,13 |
| 13 | 322 | 18,9 | 19,3 | 4,68 | 21,90 | 4,28 | 18,32 |
| 14 | 275 | 17,3 | 16,9 | 2,28 | 5,20 | 2,68 | 7,18 |
| 15 | 248 | 19,1 | 15,5 | 0,88 | 0,77 | 4,48 | 20,07 |
| 16 | 392 | 20,4 | 23 | 8,38 | 70,22 | 5,78 | 33,41 |
| 17 | 221 | 11,3 | 14,1 | -0,52 | 0,27 | -3,32 | 11,02 |
Коэффициент корреляции равен:
![]()
Так как коффициент корреляции равен 0,66, это свидетельствует о том, что связь между изучаемыми факторами (урожайностью и количеством осадков за период вегетации) заметная.
Задание 2
По данным приложения 12 произведите аналитическое выравнивание ряда динамики методом наименьших квадратов и получите уравнение тренда. Найдите показатели вариации фактических уровней вокруг тренда. Вычислите средний уровень ряда, средний абсолютный прирост, средний темп роста и темп прироста. Оцените степень сезонных колебаний уровней ряда, используя индексы сезонности. Ряд динамики и тренд изобразите на графике. Осуществите точечный прогноз уровней на перспективу. По результатам расчетов сделайте выводы. .
Фонд заработной платы, млрд. руб.
| Месяцы | Годы | ||
| 1 | 2 | 3 | |
| I | 26,8 | 27,1 | 29,9 |
| II | 25,7 | 24,9 | 25,4 |
| III | 26,0 | 25,7 | 26,0 |
| IV | 25,5 | 26,3 | 27,2 |
| V | 25,5 | 25,9 | 26,0 |
| VI | 28,4 | 27,9 | 28,5 |
| VII | 29,3 | 29,9 | 30,1 |
| VIII | 27,9 | 30,1 | 31,3 |
| IX | 28,2 | 30,0 | 30,9 |
| X | 27,7 | 29,8 | 30,0 |
| XI | 26,7 | 27,1 | 31,2 |
| XII | 29,9 | 30,5 | 32,5 |
Рассмотрим аналитическое выравнивание ряда динамики по прямой, то есть уравнение вида:
![]()
где t – порядковый номер периодов или моментов времени.
Параметры
![]() прямой рассчитываются по методу
наименьших квадратов. Система нормальных уравнений в данном случае имеет вид:
прямой рассчитываются по методу
наименьших квадратов. Система нормальных уравнений в данном случае имеет вид:

Поиск
параметров можно упростить, если отсчет времени производить так, чтобы сумма
показателей времени изучаемого периода была равна нулю ![]() при этом условии система нормальных уравнений
преобразуется следующим образом:
при этом условии система нормальных уравнений
преобразуется следующим образом:
Решение системы уравнений позволяет получить выражение для параметров
![]() :
:
![]()
![]()
![]()
Откуда
 ;
; 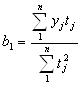 .
.
Эмпирические и выровненные уровни ряда
| Месяцы | Эмпирические уровни ряда(у) | Условные обозначения ряда (t) |
|
|
|
| 1 год | |||||
| I | 26,8 | -18 | 324 | -482,4 | 25,94 |
| II | 25,7 | -17 | 289 | -436,9 | 26,06 |
| III | 26,0 | -16 | 256 | -416 | 26,18 |
| IV | 25,5 | -15 | 225 | -382,5 | 26,3 |
| V | 25,5 | -14 | 196 | -357 | 26,42 |
| VI | 28,4 | -13 | 169 | -369,2 | 26,54 |
| VII | 29,3 | -12 | 144 | -351,6 | 26,66 |
| VIII | 27,9 | -11 | 121 | -306,9 | 26,78 |
| IX | 28,2 | -10 | 100 | -282 | 26,9 |
| X | 27,7 | -9 | 81 | -249,3 | 27,02 |
| XI | 26,7 | -8 | 64 | -213,6 | 27,14 |
| XII | 29,9 | -7 | 49 | -209,3 | 27,26 |
| 2 год | |||||
| I | 27,1 | -6 | 36 | 239,2 | 27,38 |
| II | 24,9 | -5 | 25 | 203,2 | 27,5 |
| III | 25,7 | -4 | 16 | 234 | 27,7 |
| IV | 26,3 | -3 | 9 | 272 | 27,74 |
| V | 25,9 | -2 | 4 | 286 | 27,86 |
| VI | 27,9 | -1 | 1 | 342 | 27,98 |
| VII | 29,9 | 1 | 1 | 391,3 | 28,34 |
| VIII | 30,1 | 2 | 4 | 438,2 | 28,34 |
| IX | 30,0 | 3 | 9 | 463,5 | 28,46 |
| X | 29,8 | 4 | 16 | 480 | 28,58 |
| XI | 27,1 | 5 | 25 | 530,4 | 28,7 |
| XII | 30,5 | 6 | 36 | 585 | 28,82 |
| 3 год | 239,2 | ||||
| I | 29,9 | 7 | 49 | 203,2 | 28,94 |
| II | 25,4 | 8 | 64 | 234 | 29,06 |
| III | 26,0 | 9 | 81 | 272 | 29,18 |
| IV | 27,2 | 10 | 100 | 286 | 29,3 |
| V | 26,0 | 11 | 121 | 342 | 29,42 |
| VI | 28,5 | 12 | 144 | 391,3 | 29,54 |
| VII | 30,1 | 13 | 169 | 438,2 | 43,836 |
| VIII | 31,3 | 14 | 196 | 463,5 | 29,78 |
| IX | 30,9 | 15 | 225 | 480 | 29,9 |
| X | 30,0 | 16 | 256 | 530,4 | 30,02 |
| XI | 31,2 | 17 | 289 | 585 | 30,04 |
| XII | 32,5 | 18 | 324 | 239,2 | 30,26 |
| Имтого | 1011,8 | 0 | 4218 | 504,5 | 1025,876 |
По итоговым данным таблицы 9.13.2. определяем параметры уравнения:
![]()
![]()
По рассчитанным параметрам записываем уравнение прямой ряда динамики, характеризующего уровень рентабельности продукции:
![]()
Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Экстраполируя при t =19-23найдем уровень для:
- I месяца четвертого года:
![]()
![]() млрд. руб.;
млрд. руб.;
- II месяца четвертого года:
![]()
![]() млрд. руб.;
млрд. руб.;
- III месяца четвертого года:
![]()
![]() млрд. руб.;
млрд. руб.;
- IV месяца четвертого года:
![]()
![]() млрд. руб.;
млрд. руб.;
- V месяца четвертого года:
![]()
![]() млрд. руб;
млрд. руб;
Таким образом, прогноз фонда заработной плате на I месяц четвертого года составляет 30,38 млрд.руб. г, на II месяц – 30,5 млрд.руб., на III месяц – 30,62 млрд.руб. на IV месяц – 547,2 г, на V месяц – 30,74 млрд.руб.
Глубину сезонных колебаний измеряют индексами сезонности, которые представляют собой отношение средних из фактических уровней одноименных месяцев (кварталов) за рассматриваемый период к средней из выравненных данных по тем же месяцам (кварталам), то есть:
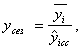
где ![]() средняя из фактических уровней i-го месяца (квартала) за весь рассматриваемый период;
средняя из фактических уровней i-го месяца (квартала) за весь рассматриваемый период;
![]() средний из выровненных уровней ряда i-го месяца (квартала).
средний из выровненных уровней ряда i-го месяца (квартала).
Для
получения значений ![]() произведем по способу средней
арифметической простой осреднение уровней одноименных периодов за 3 года.
произведем по способу средней
арифметической простой осреднение уровней одноименных периодов за 3 года.
Таблица 9.13.3 Исходные данные для расчета индекса сезонности
| Год | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | Итого |
| 1 | 26,8 | 25,7 | 26 | 25,5 | 25,5 | 28,4 | 29,3 | 27,9 | 28,2 | 27,7 | 26,7 | 29,9 | 327,6 |
| 2 | 27,1 | 24,9 | 25,7 | 26,3 | 25,9 | 27,9 | 29,9 | 30,1 | 30 | 29,8 | 27,1 | 30,5 | 335,2 |
| 3 | 29,9 | 25,4 | 26 | 27,2 | 26 | 28,5 | 30,1 | 31,3 | 30,9 | 30 | 31,2 | 32,5 | 349 |
| Итого за период | 83,8 | 76 | 77,7 | 79 | 77,4 | 84,8 | 89,3 | 89,3 | 89,1 | 87,5 | 85 | 92,9 | 1011,8 |
| Средний уровень за месяц | 27,934 | 25,3 | 25,9 | 26,3 | 25,8 | 28,267 | 29,767 | 29,767 | 29,7 | 29,166 | 28,3 | 30,967 | 337,168 |
| Абсолютное отклонение от общей средней величины | -0,16 | -2,8 | -2,2 | -1,8 | -2,3 | 0,167 | 1,167 | 1,167 | 1,6 | 1,066 | 0,2 | 2,867 | |
| Относительное отклонение от общей средней величины (в %) | -0,01 | 0,1 | -00,8 | -0,06 | -0,08 | 0,06 | 0,007 | 0,007 | 0, 056 | 0, 37 | 0,007 | 0,102 | |
| Индекс сезонности | 99,9 | 90 | 92,1 | 94 | 92 | 100,6 | 100,7 | 100,7 | 105,6 | 103,7 | 100,7 | 110,2 |
Для вычисления среднего уровня ряда воспользуемся средней арифметической простой:
![]() г
г
Средний абсолютный прирост составил:
![]() г
г
Средний темп роста:
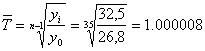 или 100,0001
млрд.руб.
или 100,0001
млрд.руб.
Средний темп прироста:
![]() млрд. руб.
млрд. руб.
Следовательно, фонд заработной платы за 3 года составила 28,1 млрд.руб., в среднем
R = 32,5 – 25,4= 7,1 млрд.руб.
Для определения среднего линейного отклонения и дисперсии произведем расчет необходимых показателей в следующей таблице.
Информация, необходимая для расчета дисперсии и среднего линейного отклонения
| Месяцы |
|
|
|
|
| 1 | 2 | 3 | 4 | |
| 1 год | ||||
| I | 26,8 | -1,3 | 1,69 | |
| II | 25,7 | -2,4 | 5,76 | |
| III | 26,0 | -2,1 | 4,41 | |
| IV | 25,5 | -2,6 | 6,76 | |
| V | 25,5 | -2,6 | 6,76 | |
| VI | 28,4 | 0,3 | 0,09 | |
| VII | 29,3 | 1,2 | 1,44 | |
| VIII | 27,9 | -0,2 | 0,04 | |
| IX | 28,2 | 0,1 | 0,01 | |
| X | 27,7 | -0,4 | 0,16 | |
| XI | 26,7 | -1,4 | 1,96 | |
| XII | 29,9 | 1,8 | 3,24 | |
| 2 год | ||||
| I | 27,1 | -1 | 1 | |
| II | 24,9 | -3,2 | 10,24 | |
| III | 25,7 | -2,4 | 5,76 | |
| IV | 26,3 | -1,8 | 3,24 | |
| V | 25,9 | -2,2 | 4,84 | |
| VI | 27,9 | -0,2 | 0,04 | |
| VII | 29,9 | 1,8 | 3,24 | |
| VIII | 30,1 | 2 | 4 | |
| IX | 30,0 | 1,9 | 3,61 | |
| X | 29,8 | 1,7 | 2,89 | |
| XI | 27,1 | -1 | 1 | |
| XII | 30,5 | 2,4 | 5,76 | |
| 3 год | ||||
| I | 29,9 | 1,8 | 3,24 | |
| II | 25,4 | -2,7 | 7,29 | |
| III | 26,0 | -2,1 | 4,41 | |
| IV | 27,2 | -0,9 | 0,81 | |
| V | 26,0 | -2,1 | 4,41 | |
| VI | 28,5 | 0,4 | 0,16 | |
| VII | 30,1 | 2 | 4 | |
| VIII | 31,3 | 3,2 | 10,24 | |
| IX | 30,9 | 2,8 | 7,84 | |
| X | 30,0 | 1,9 | 3,61 | |
| XI | 31,2 | -1,3 | 1,69 | |
| XII | 32,5 | -2,4 | 5,76 | |
| Итого | 1011,8 | -7,3 | 123,95 |
Дисперсию рассчитаем по следующей формуле:
![]() млрд.руб
млрд.руб
Среднее квадратическое отклонение найдем по формуле:
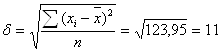 млрд.руб.
млрд.руб.
Коэффициент осцилляции рассчитывается с помощью формулы: Следовательно,
![]() %
%
Коэффициент вариации найдем по следующей формуле. Таким образом,
![]()
По результатам проведенных расчетов можно сделать следующие выводы: прирост заработной платы за 3 года за три года составил 28,1 млрд.руб. В среднем средний фонд заработной платы отклоняется от среднего уровня на 11 мллрд руб, так как коэффициент вариации больше 33%, то совокупность фонда оплаты труда является однородной.
Задача 3
Имеются данные по трем строительным организациям города:
| Строительные | Общая площадь, кв. м | Сметная стоимость 1 кв. м, д.ед. | ||
| организации | базисный | отчетный | базисный | отчетный |
| период | период | период | период | |
| 1 | 90 | 99 | 200 | 200 |
| 2 | 54 | 54 | 220 | 225 |
| 3 | 76 | 70 | 215 | 200 |
Определите:
1. Индивидуальные и общие индексы всей площади построенных домов, стоимости 1 кв. м. и стоимости площади построенных домов. Постройте соответствующие системы индексов.
2. Влияние на динамику стоимости площади построенных домов: а) объема площади, б) сметной стоимости 1 кв. м.
3. Найти соответствующие абсолютные показатели.
4. Проверить соответствие индексов и абсолютных показателей.
Сделайте выводы.
1. Индивидуальные индексы всей площади построенных домов, стоимости 1 кв. м. за 2 года вычислим по следующим формулам:
![]() ,
, ![]() ,
,
где ![]()
![]() площадь построенных
домов и сметная стоимость1 кв. м. в базисном и отчетном году соответственно.
площадь построенных
домов и сметная стоимость1 кв. м. в базисном и отчетном году соответственно.
Расчет индивидуальных индексов всей площади построенных домов и стоимости 1 кв. м. за 2 года
| Строительные организации | Сметная стоимость 1 кв. м, д.ед | Общая площадь, кв. м | Индивидуальные индексы | |||
|
базисный период |
отчетный период |
базисный период |
отчетный период |
сметной стоимости 1 кв. м |
площади построенных домов |
|
| 1 | 200 | 200 | 90 | 99 | 1,0000 | 1,1000 |
| 2 | 220 | 225 | 54 | 54 | 1,0227 | 1,0000 |
| 3 | 215 | 200 | 76 | 70 | 0,9302 | 0,9211 |
Как показывает анализ данных таблицы 10.1, в отчетном году по сравнению с базисным в наибольшей степени в относительном выражении выросла сметная стоимость 1 кв. м. во второй строительной организации (в 1,023 раза или на 102,3%), что касается общей площади построенных домов, то в отчетном году по сравнению с базисным выросла площадь построенных домов только по первой строительной организации (в 1,1 раза или на 10%), тогда как по второй строительной организации площадь построенных домов в отчетном году по сравнению с базисным не изменилась, а по третьей организации – сократилась на 7,9% (92,1-100).
2. Общий индекс стоимости площади построенных домов рассчитаем следующим образом:
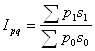 ,
,
где ![]() - стоимость площади
построенных домов в базисном периоде,
- стоимость площади
построенных домов в базисном периоде,
![]() - стоимость площади построенных
домов в отчетном периоде в фактических ценах.
- стоимость площади построенных
домов в отчетном периоде в фактических ценах.
![]() или 99,42%
или 99,42%
Общая стоимость площади построенных домов в отчетном периоде снизилась по сравнению с базисным на 0,58% (99,42-100). Общий индекс стоимости 1 кв. м. рассчитаем по формуле:
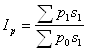 ,
,
![]()
![]() - стоимость построенных домов
отчетного периода в базисных ценах.
- стоимость построенных домов
отчетного периода в базисных ценах.
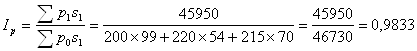 или 98,33%
или 98,33%
За счет снижения стоимости 1 кв. м. общая стоимость площади построенных домов отчетного периода снизилась по сравнению с базисным периодом на 1,67% (98,33-100). Общий индекс площади построенных домов рассчитаем следующим образом:
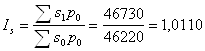 или 101,1%
или 101,1%
В результате роста площади построенных домов общая стоимость построенной площади в отчетном периоде выросла в 1,011 раза или на 1,1%.
Эти индексы взаимосвязаны между собой:
![]()
Чтобы найти абсолютное изменение показателей, надо из числителя соответствующего индекса вычесть его знаменатель. Абсолютный прирост выручки от реализации продукции равен:
![]() (ден. ед.)
(ден. ед.)
В том числе
1) за счет изменения стоимости 1 кв. м.:
![]()
![]() (ден. ед.)
(ден. ед.)
2) за счет изменения площади построенных домов:
![]() (ден. ед.)
(ден. ед.)
Таким образом, в отчетном периоде по сравнению с базисным стоимость построенных домов снизилась на 270 ден. ед. или 0,6%, в том числе за счет снижения стоимости 1 кв. м. - на 780 ден. ед. или 1,7%. В результате увеличения площади построенных домов их общая стоимость выросла на 510 ден. ед или на 1,1%.
Задача 4
| 2003 | 2004 | 2005 | 2006 | 2007 | |
|
Численность населения на начало года, тыс. чел. |
9898,6 | 9849,1 | 9800,1 | 9750,5 | 9714,5 |
| Естественный прирост (убыль) населения, тыс. чел. | -54,7 | 51,1 | -51,4 | 41,7 | - |
| Число родившихся, тыс. чел. | 88,5 | 88,9 | 90,5 | 96,7 | - |
| Умерло детей до года, чел. | 685 | 614 | 640 | 587 | - |
1. Рассчитайте за каждый год: численность умерших, относительные показатели естественного движения населения (коэффициенты рождаемости, смертности, естественного прироста (убыли), младенческой смертности).
2. Рассчитайте среднегодовые уровни и показатели динамики (абсолютное изменение, темп изменения, относительное изменение в процентах) по показателям: число родившихся и коэффициент рождаемости.
Решение:
1. Определим численность умерших (Чу) как разницу естественного прироста и численностью умерших детей до 1 года:
Чум03=54 700 - 685 = 54 015
Чум 04=51 100 - 614 = 50 486
Ч ум 05=51 400 - 640 = 50 760
Ч ум 06=41 700 - 587 = 41 113
2. Рассчитаем коэффициент рождаемости = Число родившихся / Численность населения:
Крожд03=88,9/9898,6=0,008981
Крожд04=88,5/9849,1=0,00898
Крожд05=90,7/9750,5=0,00923
Крожд06=96,5/9898,6=0,0093
3. Определим коэффициент смертности Число умерших/Численность населения
Крум03=54/9898,6=0,00547
Крожд04=50,5/9849,1=0,00512
Крожд05=50,7/9750,5=0,00515
Крожд06=41,1/9898,6=0,00416
Коэффициент естественного прироста = естественный прирост/численность населения
Кест03=-54,7/9898,6=-0,00552
Кеств04=51,1/9849,1=-0,00519
Кеств05=51,4/9750,5=-0,00527
Кеств06=41,7/9898,6=-0,00421
Коэффициент младенческой смертности = младенческая смертность/численность населения
Ксм млад03=0,685/9898,6=0,000069
Кеств04=0,614/9849,1=0,0000623
Кеств05=0,64/9750,5=0,0000656
Кеств06=0,587/9898,6=0,0000593
Рассчитайте среднегодовые уровни и показатели динамики (абсолютное изменение, темп изменения, относительное изменение в процентах) по показателям: число родившихся и коэффициент рождаемости.
Абсолютное изменение численности родившихся
ΔЧР=ЧР03-Чр04=88,9-88,5=0,5 тыс чел
ΔЧР=ЧР04-ЧР05=88,9-90,5=-1,6 тыс чел
ΔЧР=ЧР06-ЧР05=96,7-90,5=6,2 чел
Темп роста численности родившихся
ΔТ=ЧР03/ЧР04=88,9/88,5=100,45%
ΔТ=ЧР04/ЧР05=88,5/90,5=97,7%
ΔТ=ЧР05/ЧР06=90,5/96,7=93,5
Темп прироста численности родившихся
Т=ΔТ -100-ΔТ=104,5-100=4,5 %
Т=ΔТ -100-ΔТ=97,7-100=-2,3 %
Т=ΔТ -100-ΔТ=93,7-100=-6,3 %
Абсолютное изменение коэффициента рождаемости
ΔК рожд=Крож03-К рождр04=0,0547-0,00512==0,0035
ΔК рожд=Крож04-К рождр05=0,0512-0,00515=-0,003
ΔК рожд=Крож06-К рождр05=0,0515-0,00416==0,0099
Темп роста коэффициента рождаемости
ΔТ=К рожд03/К рожд04=0,00547/0,00512=106,8%
ΔТ=К рожд04/К рожд05=0,00512/0,00515=99,4%
ΔТ=К рожд05/К рожд05=0,00515/0,00416=123,8%
Темп прироста коэффициента рождаемости
Т=ΔТ -100=106,8-100=6,8 %
Т=ΔТ -100=99,4-100=-0,6 %
Т=ΔТ -100 =123,8-100=123 %
Список использованных источников
1. Гатаулин A.M. Система прикладных статистико-математических методов обработки экспериментальных данных в сельском хозяйстве: Ч.1,2 - М.: Изд-во МСХА, 2003.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. - М.: Финансы и статистика, 2006.
3. Маркова А.И. Курс лекций по сельскохозяйственной статистике с основами экономической статистики: Учеб. пособие. М.: Изд-во ОГАУ, 2007.