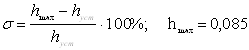Курсовая работа: Расчет структурно-алгоритмической схемы системы автоматического регулирования
Московский государственный текстильный университет им. А.Н. Косыгина
Кафедра автоматики и промышленной электроники
Курсовая работа
по дисциплине: «Теория автоматического управления»
на тему: «Расчет структурно-алгоритмической схемы системы автоматического регулирования»
Выполнил: студент гр. 14ВД-06
Кириллов М.В.
Принял: Ермолаев Ю.М.
Москва, 2011 г.
Перечень подлежащих разработке вопросов (содержание расчетно-пояснительной записки)
Математические модели, используемые при выполнении курсовой работы
1. По заданным математическим моделям получить структурно-алгоритмическую схему системы автоматического регулирования
2. Определить передаточные функции разомкнутой системы Y(p) / G(p), замкнутой системы Y(p) / G(p), Y(p) / F(p), E(p) / G(p), E(p) / F(p)
3. Для заданных исходных данных построить область устойчивости системы в плоскости параметров регулятора
4. Для заданной допустимой ошибки регулирования 5% определить значение Kp регулятора, при условии, что регулятор обеспечивает «П» - закон регулирования
5. Для значений параметров регулятора, выбранных произвольно из области устойчивости системы, построить кривые Михайлова и Найквиста
6. Повторить п. 5 задания для значений параметров регулятора, выбранных из области неустойчивой системы
7. Рассчитать настройки регулятора, обеспечивающие минимальное значение интегральной оценки качества
8. Построить переходные характеристики системы по задающему и возмущающему воздействию для значений параметров регулятора выбранных по пп. 5 и 7
9. Определить показания качества системы
Математические модели, используемые при выполнении курсовой работы
Исходные данные: K1 = 2; K2 = 0,7; T1 = 1; T2 = 0,5.
1. По заданным математическим моделям получить структурно-алгоритмическую схему системы автоматического регулирования
а) 
-
уравнение сумматора
б) 
-
уравнение регулятора
Применяя операторный метод Лапласа, получим:
;
в) 
-
апериодическое звено на выходе 
Применяя операторный метод Лапласа, получим:
;
г) 
-
апериодическое звено (инерционное) на выходе 
Применяя операторный метод Лапласа, получим:
Из данных нам математических моделей составим общую структурно-алгоритмическую схему системы автоматического регулирования:
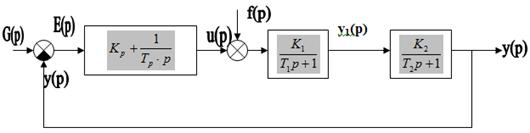
2. Определить передаточные функции разомкнутой системы Y(p) / G(p), замкнутой системы Y(p) / G(p), Y(p) / F(p), E(p) / G(p), E(p) / F(p)
Передаточная функция – это отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях.
Передаточная функция разомкнутой системы:
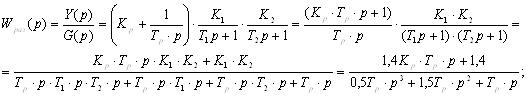
Передаточная функция для замкнутой системы:
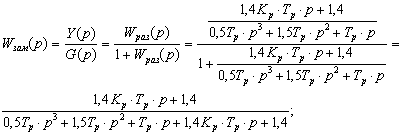
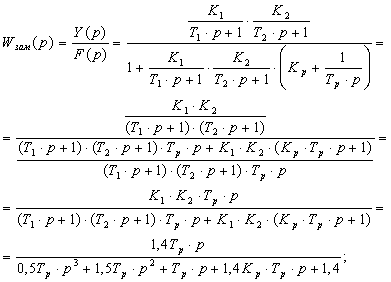
3. Для заданных исходных данных построить область устойчивости системы в плоскости параметров регулятора
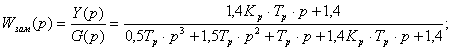
Чтобы получить характеристическое уравнение нашей системы, приравняем
знаменатель передаточной функции 
к нулю.
Система третьего порядка:
Представим:
a0 = 0,5Tp; a1 = 1,5Tp; a2 = Tp (1+1,4Kp); a3 = 1,4;
Используем критерии устойчивости Гурвица.
Необходимо и достаточно, чтобы выполнялись следующие условия:
1) 
(все
коэффициенты характеристического уравнения положительны);
2) 
>
при равенстве а1а2=а0а3 система находится на границе устойчивости.
Система будет устойчива, если:
Тр>0;
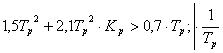
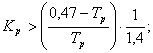
По найденному графику функции 
построим область устойчивости системы в плоскости
параметров регулятора.
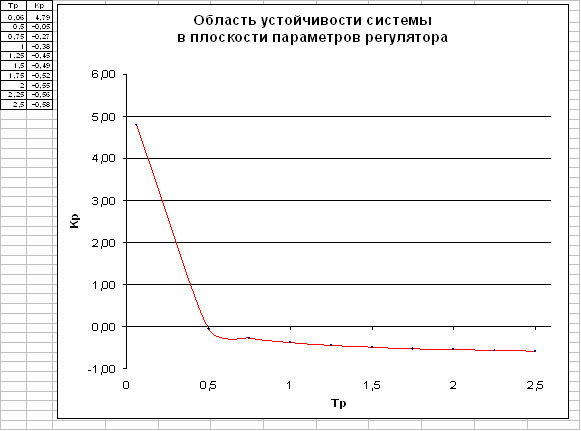
4. Для заданной допустимой ошибки регулирования 5% определить значение Кр регулятора, при условии, что регулятор обеспечивает «П» - закон регулирования
Структурная схема при использовании «П» - закона регулирования:
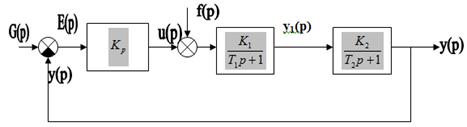
Еуст= 5 % = 0,05;
Wp = Kp;
G(p) = 1(t);
G(p) = g(t);
g(t) = A = 1;
G(p)=
;
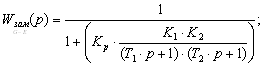
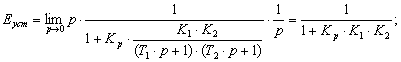
5. Для значений параметров регулятора, выбранных произвольно из области устойчивости системы, построить кривые Михайлова и Найквиста
Выберем произвольно из области устойчивости системы параметры:
Тр=0,25; Кр=1;
Построим кривую Михайлова и Найквиста.
Кривая Михайлова
Характеристическое уравнение нашей системы:
Заменим p на 
получим:
; 
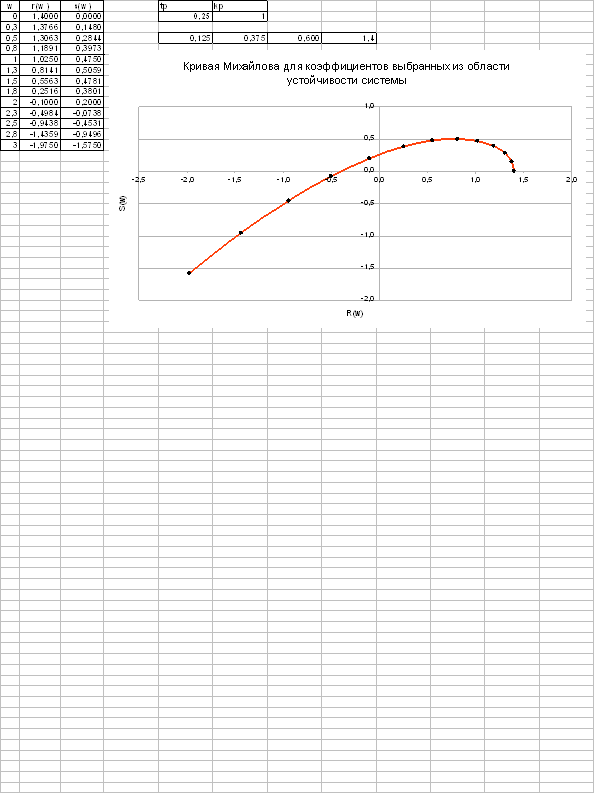
Кривая Найквиста
Строим при помощи MatLab 6.5;
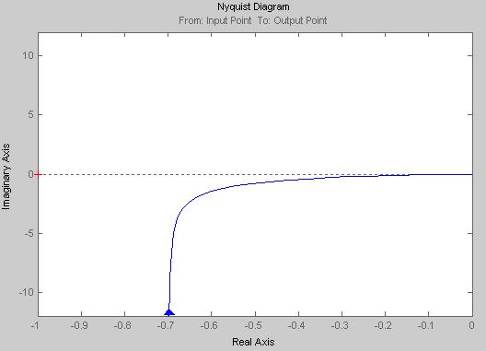
6. Повторить п. 5 задания для значений параметров регулятора, выбранных из области неустойчивой системы
Выберем произвольно из области неустойчивости системы параметры:
Тр=2; Кр=0,11;
Построим кривую Михайлова и Найквиста.
Кривая Михайлова
Характеристическое уравнение нашей системы:
Заменим p на получим:
; 
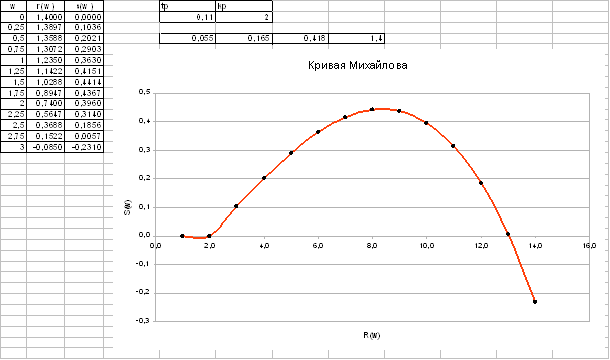
Кривая Найквиста
Строим при помощи MatLab 6.5;
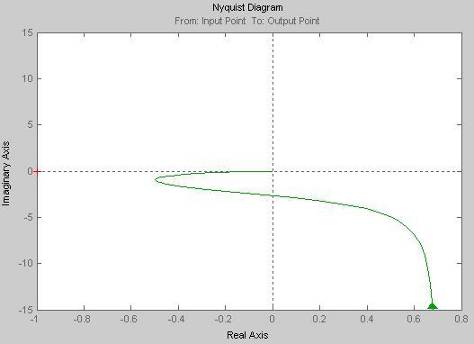
7. Рассчитать настройки регулятора, обеспечивающие минимальное значение интегральной оценки качества
Вычислим квадратичную интегральную оценку методом Мандельштама.
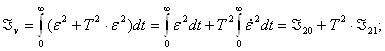
Для получения 
и 
вычислим квадратичную
интегральную оценку.
К1=2; К2=0,7; Т1=1; Т2=0,5; Кр=13,57;
(1)
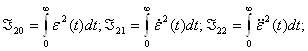
Запишем знаменатель выражения (1) в виде:
Обозначим: а0=0,5Тр; а1=1,5Тр; а2=20Тр; а3=1,4;
(2)
Обозначим: 
.
Умножаем поочередно уравнение (2) на 
.
(3)
(4)
(5)
2) Почленно интегрируем уравнения (3), (4) и (5).
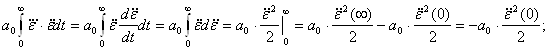
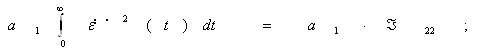
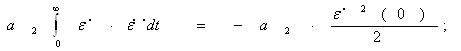
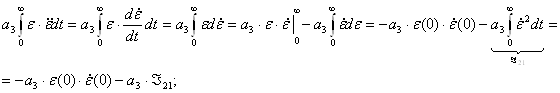
В итоге, интегрирование (3) уравнения дает:
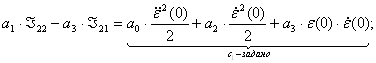
Уравнение (4):
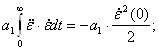
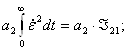
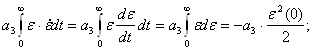
В итоге, интегрирование (4) уравнения дает:
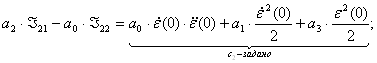
Уравнение (5):
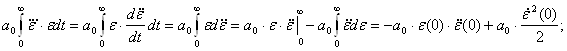
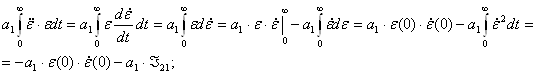
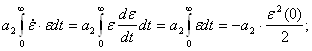
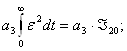
В итоге, интегрирование (5) уравнения дает:
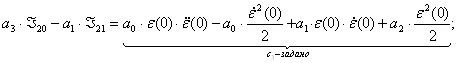
3) Получаем систему из трех уравнений относительно 3-х неизвестных:
Выразим и :
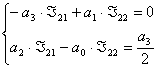
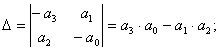
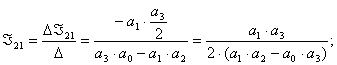
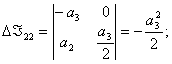
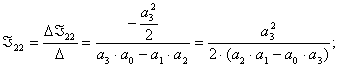
Выразим :
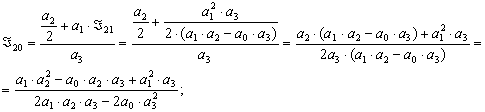
4) Берем производную по 
и приравниваем к нулю:
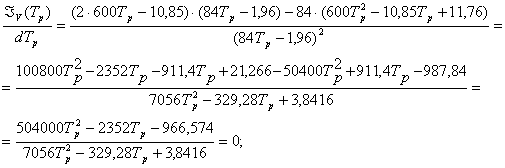
8. Построить переходные характеристики системы по задающему и возмущающему воздействию для значений параметров регулятора выбранных по пп. 5 и 7
Переходная характеристика по задающему воздействию для значений параметров регуляторов выбранных из пункта № 5.
Переходная характеристика по возмущающему воздействию для значений параметров регуляторов выбранных из пункта № 5.
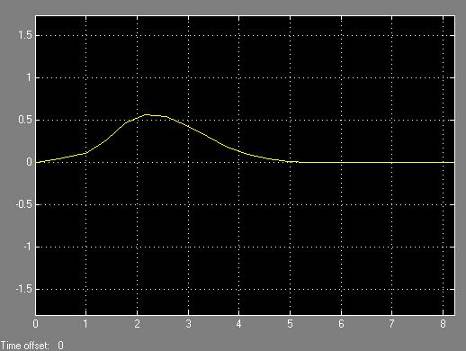
автоматический кривая михайлов найквист регулятор
Переходная характеристика по задающему воздействию для значений параметров регуляторов выбранных из пункта № 7.
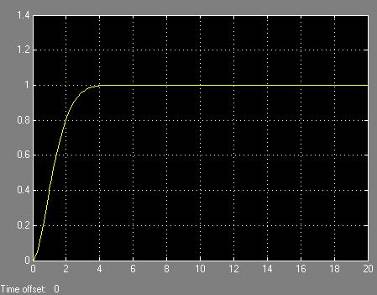
Переходная характеристика по возмущающему воздействию для значений параметров регуляторов выбранных из пункта № 7.
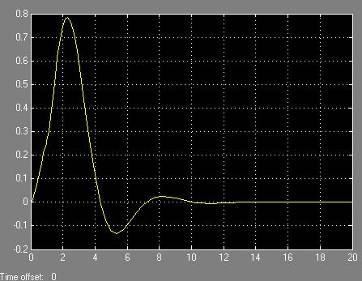
9. Определить показатели качества системы
Переходная характеристика по задающему воздействию для значений параметров регуляторов выбранных из пункта № 5.
Время регулирования
Теоретически время достижения выходной координаты до заданного значения равно бесконечности, поэтому вводится допустимая погрешность.
В момент, когда выходная координата попадает в область допустимых значений и больше из нее не выходит, считается окончанием процесса регулирования.
Статическая точность
Характеризует статический режим в системе и не зависит от динамики переходного процесса.
Величина перерегулирования
Перерегулирование – это максимальное превышение регулируемой величины над установившемся значением.
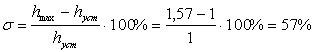
Колебательность
Система совершила за время регулирования 2 полных колебания.
По возмущающему воздействию:
tрег = 5,5 сек
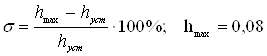
По пункту 7
По задающему воздействию:
tрег = 2,2 сек
1 полное колебание.
По возмущающему воздействию:
tрег = 18 сек
