–†–µ—Д–µ—А–∞—В: –Ф–≤–Њ–є–љ–Њ–µ –≤–µ–Ї—В–Њ—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
–Т—Л–њ–Њ–ї–љ–Є–ї–∞: –Ш–ї—М–µ–љ–Ї–Њ¬† –£–ї—М—П–љ–∞ –Ш–≥–Њ—А–µ–≤–љ–∞, —Б—В—Г–і–µ–љ—В–Ї–∞ 1 –Ї—Г—А—Б–∞, –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Д–∞–Ї—Г–ї—М—В–µ—В–∞
–Ч–∞–њ–Њ—А–Њ–ґ—Б–Ї–Є–є –љ–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В
–Ч–∞–њ–Њ—А–Њ–ґ—М–µ, 2006 –≥–Њ–і
–Ґ—А—С–Љ –≤–µ–Ї—В–Њ—А–∞–Љ a, b –Є c –Љ–Њ–ґ–љ–Њ –њ–Њ—Б—В–∞–≤–Є—В—М –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –≤–µ–Ї—В–Њ—А, —А–∞–≤–љ—Л–є a×(b×c). –≠—В–Њ—В –≤–µ–Ї—В–Њ—А –љ–∞–Ј—Л–≤–∞—О—В –і–≤–Њ–є–љ—Л–Љ –≤–µ–Ї—В–Њ—А–љ—Л–Љ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ –≤–µ–Ї—В–Њ—А–Њ–≤ a, b –Є c. –Ф–≤–Њ–є–љ–Њ–µ –≤–µ–Ї—В–Њ—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤—Б—В—А–µ—З–∞–µ—В—Б—П –≤ –Љ–µ—Е–∞–љ–Є–Ї–µ –Є —Д–Є–Ј–Є–Ї–µ.
–Ф–≤–Њ–є–љ–Њ–µ –≤–µ–Ї—В–Њ—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤—Л—А–∞–ґ–∞–µ—В—Б—П —З–µ—А–µ–Ј –ї–Є–љ–µ–є–љ—Г—О –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—О –і–≤—Г—Е –Є–ї–Є —В—А—С—Е —Б–≤–Њ–Є—Е —Б–Њ–Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
a×(b×c) = b(ac) - c(ab).
–Ф–Њ–Ї–∞–ґ–µ–Љ —Н—В–Њ. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј x —А–∞–Ј–љ–Њ—Б—В—М –ї–µ–≤–Њ–є –Є –њ—А–∞–≤–Њ–є —З–∞—Б—В–µ–є —Н—В–Њ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞
x = a×(b×c) - b(ac) + c(ab).
–Э–∞–Љ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ x = 0.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ –≤–µ–Ї—В–Њ—А—Л b –Є c –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л. –Х—Б–ї–Є –Њ–љ–Є –Њ–±–∞ –љ—Г–ї–µ–≤—Л–µ, —В–Њ –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є –і–ї—П –≤–µ–Ї—В–Њ—А–∞ x –≤—Б–µ —Б–ї–∞–≥–∞–µ–Љ—Л–µ —А–∞–≤–љ—Л –љ—Г–ї–µ–≤–Њ–Љ—Г –≤–µ–Ї—В–Њ—А—Г –Є –њ–Њ—Н—В–Њ–Љ—Г —А–∞–≤–µ–љ—Б—В–≤–Њ
x = 0 –≤—Л–њ–Њ–ї–љ–µ–љ–Њ. –Х—Б–ї–Є –ґ–µ –Њ–і–Є–љ –Є–Ј –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ b, c –љ–µ–љ—Г–ї–µ–≤–Њ–є, –љ–∞–њ—А–Є–Љ–µ—А c, —В–Њ –і–ї—П –і—А—Г–≥–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–∞ –њ—А–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–Љ α —Ф R –≤—Л–њ–Њ–ї–љ–µ–љ–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ b=αc. –Э–Њ —В–Њ–≥–і–∞
x=a×(αc×c)-αc(ac)+cα(ac)=0.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ —В–µ–њ–µ—А—М, —З—В–Њ –≤–µ–Ї—В–Њ—А—Л b –Є c –љ–µ–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л. –Ґ–Њ–≥–і–∞ –Є—Е –≤–µ–Ї—В–Њ—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –љ–µ —А–∞–≤–љ–Њ –љ—Г–ї–µ–≤–Њ–Љ—Г –≤–µ–Ї—В–Њ—А—Г –Є –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ –љ–µ–љ—Г–ї–µ–≤–Њ–Љ—Г –≤–µ–Ї—В–Њ—А—Г b. –Т–µ–Ї—В–Њ—А—Л
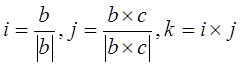
–Њ–±—А–∞–Ј—Г—О—В –њ—А–∞–≤—Л–є –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–є –±–∞–Ј–Є—Б –≤ V3 (—Н—В–Њ –Є –Њ—В—А–∞–ґ–∞–µ—В—Б—П –≤ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П—Е). –Т —Н—В–Њ–Љ –±–∞–Ј–Є—Б–µ —Б–њ—А–∞–≤–µ–і–ї–Є–≤—Л —Б–ї–µ–і—Г—О—Й–Є–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –≤–µ–Ї—В–Њ—А–Њ–≤:
b=|b|i , c = c1i+c2k , a = a1i + a2j + a3k ,
–Є –њ–Њ—Н—В–Њ–Љ—Г
b×c = - |b|c2j , a×(b×c) = - |b|c2(a1k вАУ a3i).
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ,
ac = a1c1 вАУ a3c2 , ab = a1|b|.
–Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –љ–∞—Е–Њ–і–Є–Љ, —З—В–Њ –Є –≤ —Б–ї—Г—З–∞–µ –љ–µ–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ b –Є c –≤—Л–њ–Њ–ї–љ–µ–љ–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ
x= -|b|c2(a1k вАУ a3i) вАУ (a1c1 вАУ a3c2)|b|i + a1|b|(c1i + c2k) = 0.
–Я—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ (a×b)×c –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ –≤–µ–Ї—В–Њ—А—Г a×b, —В–Њ –µ—Б—В—М –≤ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –≤–µ–Ї—В–Њ—А—Л a –Є b –љ–µ –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л, –ї–µ–ґ–Є—В –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –≤–µ–Ї—В–Њ—А–Њ–≤ a –Є b. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Њ–љ–Њ —А–∞–Ј–ї–∞–≥–∞–µ—В—Б—П –њ–Њ –≤–µ–Ї—В–Њ—А–∞–Љ a –Є b, —В–Њ –µ—Б—В—М —Б—Г—Й–µ—Б—В–≤—Г—О—В —В–∞–Ї–Є–µ –і–≤–∞ —З–Є—Б–ї–∞ x –Є y, —З—В–Њ
(a×b)×c=xa+yb.
–І—В–Њ–±—Л –љ–∞–є—В–Є —Н—В–Є —З–Є—Б–ї–∞, –Љ—Л –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –ї–µ–Љ–Љ–Њ–є, —Б–Њ–≥–ї–∞—Б–љ–Њ –Ї–Њ—В–Њ—А–Њ–є —Б—Г—Й–µ—Б—В–≤—Г—О—В –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ –Њ—А–Є–µ–љ—В–Є—А–Њ–≤–∞–љ–љ—Л–є –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–є –±–∞–Ј–Є—Б –µ1, –µ2, –µ3 ,—Б–≤—П–Ј–∞–љ–љ—Л–є —Б –≤–µ–Ї—В–Њ—А–∞–Љ–Є a, b –Є —Б —Д–Њ—А–Љ—Г–ї–∞–Љ–Є
a=a1e1
b=b1e1+b2e2,
c=c1e1+c2e2+c3e3.
–Т —Н—В–Њ–Љ –±–∞–Ј–Є—Б–µ –≤–µ–Ї—В–Њ—А a×b –Є–Љ–µ–µ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л (0,0, a1b2) , –Є –њ–Њ—В–Њ–Љ—Г –≤–µ–Ї—В–Њ—А (a×b)×c вАУ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л
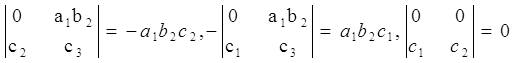
–Ґ–∞–Ї –Ї–∞–Ї –≤–µ–Ї—В–Њ—А xa+yb –Є–Љ–µ–µ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л (xa1+yb1, yb2, 0), —В–Њ, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Д–Њ—А–Љ—Г–ї–∞ (a×b)×c=xa+yb –±—Г–і–µ—В –Є–Љ–µ—В—М –Љ–µ—Б—В–Њ –њ—А–Є
x = -b1c1 вАУ b2c2 , y = a1c1.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г, —Б –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л, –∞1—Б1 = –∞—Б –Є b1c1+b2c2 = bc, —Н—В–Є–Љ –і–Њ–Ї–∞–Ј–∞–љ–Њ —Б–ї–µ–і—Г—О—Й–µ–µ –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є–µ:
–Я–†–Х–Ф–Ы–Ю–Ц–Х–Э–Ш–Х. –Ф–ї—П –ї—О–±—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ a, b, c –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ (a×b)×c=(ac)b-(bc)a.
–Ш–Ј —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї—Л –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ –≤—Л—В–µ–Ї–∞–µ—В —Б–ї–µ–і—Г—О—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –ѓ–Ї–Њ–±–Є:
(a×b)×c+(c×a)×b+(b×c)×a=0.
–Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, –≤ —Б–Є–ї—Г –Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ–Њ—Б—В–Є —Б–Ї–∞–ї—П—А–љ–Њ–≥–Њ —Г–Љ–љ–Њ–ґ–µ–љ–Є—П
(ac)b-(bc)a+(cb)a-(ab)c+(ba)c-(ca)b=0.
–° –њ–Њ–Љ–Њ—Й—М—О —Д–Њ—А–Љ—Г–ї—Л (a×b)×c=(ac)b-(bc)a –ї–µ–≥–Ї–Њ –≤—Л—З–Є—Б–ї—П–µ—В—Б—П —В–∞–Ї–ґ–µ —Б–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ (a×b)(x×y) –і–≤—Г—Е –≤–µ–Ї—В–Њ—А–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –њ–Њ–ї—М–Ј—Г—П—Б—М –∞–љ—В–Є–Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ–Њ—Б—В—М—О —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П, –Љ—Л –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ –њ–Њ–ї—Г—З–Є–Љ, —З—В–Њ
(a×b)(x×y)=((xa)y-(ya)x)b=(xa)(yb)-(ya)(xb),
—В–Њ –µ—Б—В—М
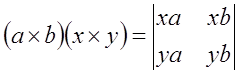
–Ю–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї—Л –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –≤–Ј–∞–Є–Љ–љ—Л–Љ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–Љ –У—А–∞–Љ–Љ–∞ –њ–∞—А –≤–µ–Ї—В–Њ—А–Њ–≤ a,b –Є x,y.
![]() –Я—А–Є a=x –Є b=y —Д–Њ—А–Љ—Г–ї–∞ –і–∞—С—В —Д–Њ—А–Љ—Г–ї—Г
–Я—А–Є a=x –Є b=y —Д–Њ—А–Љ—Г–ї–∞ –і–∞—С—В —Д–Њ—А–Љ—Г–ї—Г
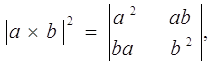
–Ї–Њ—В–Њ—А—Г—О –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —В–∞–Ї–ґ–µ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –Є–Ј—П—Й–љ–Њ–Љ –≤–Є–і–µ:
|a×b|2+|ab|2 = a2 b2.
–Ю–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –њ—А–µ–і—Л–і—Г—Й–µ–є —Д–Њ—А–Љ—Г–ї—Л –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–Љ –У—А–∞–Љ–Љ–∞ –њ–∞—А—Л –≤–µ–Ї—В–Њ—А–Њ–≤ a –Є b.
![]() –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г |a×b| —А–∞–≤–љ–Њ –њ–ї–Њ—Й–∞–і–Є S
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е a, b, —Д–Њ—А–Љ—Г–ї–∞
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г |a×b| —А–∞–≤–љ–Њ –њ–ї–Њ—Й–∞–і–Є S
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е a, b, —Д–Њ—А–Љ—Г–ї–∞
—А–∞–≤–љ–Њ—Б–Є–ї—М–љ–∞ —Д–Њ—А–Љ—Г–ї–µ
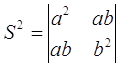
–≤ –Ї–Њ—В–Њ—А–Њ–є –≤–µ–Ї—В–Њ—А–љ—Л–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П —П–≤–љ–Њ –љ–µ —Г—З–∞—Б—В–≤—Г—О—В. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Љ—Л –≤–Є–і–Є–Љ, —З—В–Њ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –У—А–∞–Љ–∞ –њ–∞—А—Л –≤–µ–Ї—В–Њ—А–Њ–≤ —А–∞–≤–µ–љ –Ї–≤–∞–і—А–∞—В—Г –њ–ї–Њ—Й–∞–і–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ —Н—В–Є—Е –≤–µ–Ї—В–Њ—А–∞—Е.
–Т—Л—З–Є—Б–ї–Є–≤ —Б–Ї–∞–ї—П—А–љ—Л–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П —З–µ—А–µ–Ј –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Љ—Л –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ –њ–Њ–ї—Г—З–Є–Љ —Б–ї–µ–і—Г—О—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –Ы–∞–≥—А–∞–љ–ґ–∞ :
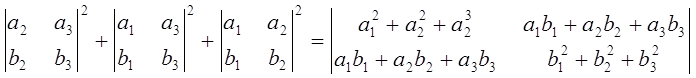 –Я—А–Є –∞3=0 , b3 = 0 (¬Ђ—Б–ї—Г—З–∞–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є¬ї)
—В–Њ–ґ–і–µ—Б—В–≤–Њ –Ы–∞–≥—А–∞–љ–ґ–∞ —А–∞–≤–љ–Њ—Б–Є–ї—М–љ–Њ —В–Њ–ґ–і–µ—Б—В–≤—Г
–Я—А–Є –∞3=0 , b3 = 0 (¬Ђ—Б–ї—Г—З–∞–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є¬ї)
—В–Њ–ґ–і–µ—Б—В–≤–Њ –Ы–∞–≥—А–∞–љ–ґ–∞ —А–∞–≤–љ–Њ—Б–Є–ї—М–љ–Њ —В–Њ–ґ–і–µ—Б—В–≤—Г
(a21+a22)(b21+b22) = (a1b1 + a2b2)2 + (a1b2 вАУ a2b1)2,
–Ш–Ј–≤–µ—Б—В–љ–Њ–Љ—Г –Є–Ј —В–µ–Њ—А–Є–Є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е —З–Є—Б–µ–ї (—В–Њ–ґ–і–µ—Б—В–≤–Њ –≤—Л—А–∞–ґ–∞–µ—В —В–Њ—В —Д–∞–Ї—В, —З—В–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Љ–Њ–і—Г–ї–µ–є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е —З–Є—Б–µ–ї a1+ia2 –Є b1+ib2 —А–∞–≤–љ–Њ –Љ–Њ–і—Г–ї—О –Є—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П).
–Р–љ–∞–ї–Њ–≥–Њ–Љ –≤—Л—И–µ–њ—А–Є–≤–µ–і—С–љ–љ—Л—Е —Д–Њ—А–Љ—Г–ї—Л –Є —В–Њ–ґ–і–µ—Б—В–≤–∞ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –Є –і–ї—П —В—А—С—Е –≤–µ–Ї—В–Њ—А–Њ–≤ a, b, c. –Т –љ—С–Љ —Г—З–∞—Б—В–≤—Г–µ—В –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М
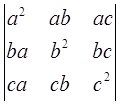
–љ–∞–Ј—Л–≤–∞–µ–Љ—Л–є –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–Љ –У—А–∞–Љ–Љ–∞ —В—А–Њ–є–Ї–Є –≤–µ–Ї—В–Њ—А–Њ–≤ a, b, c. –Т –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –±–∞–Ј–Є—Б–∞ e1, e2, e3 , –≤ –Ї–Њ—В–Њ—А–Њ–Љ –≤–µ–Ї—В–Њ—А—Л a, b, c –≤—Л—А–∞–ґ–∞—О—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–∞–Љ
a=a1e1
b=b1e1+b2e2,
c=c1e1+c2e2+c3e3 , —Н—В–Њ—В –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –Є–Љ–µ–µ—В –≤–Є–і
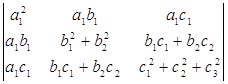
–Р–≤—В–Њ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –≤—Л—З–Є—Б–ї–µ–љ–Є–µ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –Њ–љ —А–∞–≤–µ–љ a21b22c23. –° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л, –Ї–∞–Ї –Љ—Л —Г–ґ–µ –Ј–љ–∞–µ–Љ, a1b2c3= abc. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
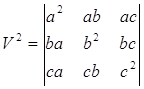
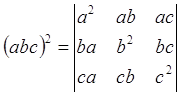
, —В–Њ –µ—Б—В—М
–≥–і–µ V вАУ –Њ–±—К—С–Љ –њ–∞—А–∞–ї–ї–µ–ї–µ–њ–Є–њ–µ–і–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е a, b, c.
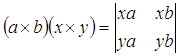
–Р–љ–∞–ї–Њ–≥ —Д–Њ—А–Љ—Г–ї—Л –Є–Љ–µ–µ—В –≤–Є–і
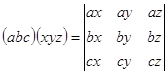
–≥–і–µ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М —Б–њ—А–∞–≤–∞ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –≤–Ј–∞–Є–Љ–љ—Л–Љ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–Љ –У—А–∞–Љ–∞ —В—А–Њ–µ–Ї a, b, c –Є x, y, z.
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л
–Ф–ї—П –њ–Њ–і–≥–Њ—В–Њ–≤–Ї–Є –і–∞–љ–љ–Њ–є —А–∞–±–Њ—В—Л –±—Л–ї–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ—Л –Љ–∞—В–µ—А–Є–∞–ї—Л —Б —Б–∞–є—В–∞ http://referat.ru/
| –®–њ–∞—А–≥–∞–ї–Ї–Є –њ–Њ –≥–µ–Њ–Љ–µ—В—А–Є–Є, –∞–ї–≥–µ–±—А–µ, –њ–µ–і–∞–≥–Њ–≥–Є–Ї–µ, –Љ–µ—В–Њ–і–Є–Ї–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є (–Ш–У–Я–Ш ... | |
|
–Ъ–Њ–ї—М—Ж–Њ–Љ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —З–Є—Б–ї. –Љ–љ–Њ–ґ. –Э–∞ –Ї–Њ—В–Њ—А–Њ–Љ –≤—Л–њ–Њ–ї–љ—П—О—В—Б—П —В—А–Є –Њ–њ–µ—А-–Є–Є: —Б–ї–Њ–ґ, —Г–Љ–љ–Њ–ґ, –≤—Л—З–Є—В. –Я–Њ–ї–µ–Љ –љ–∞–Ј. –І–Є—Б–ї –Љ–љ–Њ–ґ. –Э–∞ –Ї–Њ—В–Њ—А–Њ–Љ –≤—Л–њ–Њ–ї–љ—П—О—В—Б—П 4 –Њ–њ–µ—А–∞—Ж–Є–Є: —Б–ї–Њ–ґ ... –°–≤–Њ–є—Б—В–≤–∞ —Г–Љ–љ–Њ–ґ-—П: 1.(–Ф–ї—П –ї—О–±. –∞,bѭN) ab=ba 2. (–і–ї—П –ї—О–±. a,b,c ѭN) (ab)c=a(bc) 3.(a,b,cѭN) a(b+c)=ab+ac –Т–µ–Ї—В–Њ—А–љ—Л–Љ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ –≤–µ–Ї—В–Њ—А–Њ–≤ a" –Є b" –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —В—А–µ—В–Є–є –≤–µ–Ї—В–Њ—А c" –Ї–Њ—В–Њ—А—Л–є —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—Б–ї–Њ–≤–Є—П–Љ: |
–†–∞–Ј–і–µ–ї: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –Ґ–Є–њ: —А–µ—Д–µ—А–∞—В |
| –Я—А–Њ–≥—А–∞–Љ–Љ–∞ –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ–Њ–≥–Њ —Н–Ї–Ј–∞–Љ–µ–љ–∞ –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –і–ї—П —Б—В—Г–і–µ–љ—В–Њ–≤ ... | |
|
–Я—А–Њ–≥—А–∞–Љ–Љ–∞ –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ–Њ–≥–Њ —Н–Ї–Ј–∞–Љ–µ–љ–∞ –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –і–ї—П —Б—В—Г–і–µ–љ—В–Њ–≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Д–∞–Ї—Г–ї—М—В–µ—В–∞ –Ь–Њ—Б–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –≥–Њ—А–Њ–і—Б–Ї–Њ–≥–Њ –њ–µ–і–∞–≥–Њ–≥–Є—З–µ—Б–Ї–Њ–≥–Њ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ –Р–ї–≥–µ–±—А–∞ ... –Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ. –∞) –Ш–Ј –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є t(x) –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ —Б–ї–µ–і—Г–µ—В —Г–Ї–∞–Ј–∞–љ–љ–Њ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤ —Б–Є–ї—Г –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —В–Њ–ґ–і–µ—Б—В–≤–∞ –ї–µ–≥–Ї–Њ –њ–Њ–і—Б—З–Є—В–∞—В—М —З–Є—Б–ї–Њ —Б–ї–∞–≥–∞–µ–Љ—Л—Е, –Ї–∞–ґ–і–Њ–µ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е ... 1. –Ъ–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ kn –Є–Љ–µ–µ—В —Б—В–∞–љ–і–∞—А—В–љ—Л–є –±–∞–Ј–Є—Б –Є–Ј –µ–і–Є–љ–Є—З–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ ei := (0, . . . , 0, 1, 0, . . . , 0) ( –µ–і–Є–љ–Є—Ж–∞ –љ–∞—Е–Њ–і–Є—В—Б—П –љ–∞ –Љ–µ—Б—В–µ —Б –љ–Њ–Љ–µ—А–Њ–Љ i), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, dim kn ... |
–†–∞–Ј–і–µ–ї: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –Ґ–Є–њ: —А–µ—Д–µ—А–∞—В |
| –Ы–Є–љ–µ–є–љ–∞—П –Р–ї–≥–µ–±—А–∞. –Ґ–µ–Њ—А–Є—П –≥—А—Г–њ–њ | |
|
... –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Њ–є –Њ–њ–µ—А–∞—Ж–Є–Є –У–Њ–≤–Њ—А—П—В, —З—В–Њ –љ–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ S –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ (–±–Є–љ–∞—А–љ–∞—П) –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–∞—П –Њ–њ–µ—А–∞—Ж–Є—П (–Р–Ю) " *", –µ—Б–ї–Є –і–ї—П –≤—Б—П–Ї–Є—Е –і–≤—Г—Е –µ–≥–Њ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ x –Є y ... –У–Њ–≤–Њ—А—П—В, —З—В–Њ –љ–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ S –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ (–±–Є–љ–∞—А–љ–∞—П) –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–∞—П –Њ–њ–µ—А–∞—Ж–Є—П (–Р–Ю) " *", –µ—Б–ї–Є –і–ї—П –≤—Б—П–Ї–Є—Е –і–≤—Г—Е –µ–≥–Њ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ x –Є y –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ —Н–ї–µ–Љ–µ–љ—В z=x*y –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–є ... –≠—В–Њ –Љ–Њ–ґ–љ–Њ –њ—А–Њ–і–µ–ї–∞—В—М, –Є—Б–њ–Њ–ї—М–Ј—Г—П —В–Њ–ґ–і–µ—Б—В–≤–Њ: -3xyz= (x+y+z)( -xy-xz-yz)=(x+y+z)S. –Ф–Њ—Б—В–∞—В–Њ—З–љ–Њ –≤—Н—П—В—М x=d, y=e, z=f –Є –і–Њ–Љ–љ–Њ–ґ–Є—В—М —З–Є—Б–ї–Є—В–µ–ї—М –Є –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М –љ–∞ S. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, [Q() :Q]=3 –Є ... |
–†–∞–Ј–і–µ–ї: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –Ґ–Є–њ: —А–µ—Д–µ—А–∞—В |
| –Ы–Њ–≥–Є—З–µ—Б–Ї–Њ–µ –Є —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–µ –њ—А–Њ–≥—А–∞–Љ–Љ–Є—А–Њ–≤–∞–љ–Є–µ | |
|
–Ы–Ю–У–Ш–І–Х–°–Ъ–Ю–Х –Ш –§–£–Э–Ъ–¶–Ш–Ю–Э–Р–Ы–ђ–Э–Ю–Х –Я–†–Ю–У–†–Р–Ь–Ь–Ш–†–Ю–Т–Р–Э–Ш–Х –Т–≤–µ–і–µ–љ–Є–µ –¶–µ–ї—М—О –ї–Њ–≥–Є—З–µ—Б–Ї–Њ–≥–Њ –Є —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ –њ—А–Њ–≥—А–∞–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—П —П–≤–ї—П–µ—В—Б—П –≤—Л–≤–Њ–і —А–µ—И–µ–љ–Є–є –Є –Њ–љ–Є —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ—Л ... –Я—А–Є –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П (3) –±–∞–Ј–Є—Б–Њ–Љ –Є–љ–і—Г–Ї—Ж–Є–Є —П–≤–ї—П–µ—В—Б—П —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ U(a), –Є–љ–і—Г–Ї—Ж–Є–Њ–љ–љ—Л–Љ —И–∞–≥–Њ–Љ - —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ ("n:a$n<b)(U(n)°U(n+1)), –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ–Љ –Є–љ–і—Г–Ї—Ж–Є–Є U(k), –≥–і–µ k ... –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В–µ—А–Љ–∞–Љ–Є –±—Г–і—Г—В: a, b, c, f(a), g(f(x), y). |
–†–∞–Ј–і–µ–ї: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Є–љ—Д–Њ—А–Љ–∞—В–Є–Ї–µ, –њ—А–Њ–≥—А–∞–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—О –Ґ–Є–њ: —Г—З–µ–±–љ–Њ–µ –њ–Њ—Б–Њ–±–Є–µ |
| –Э–µ—З–µ—В–Ї–Є–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –≤ —Б–Є—Б—В–µ–Љ–∞—Е —Г–њ—А–∞–≤–ї–µ–љ–Є—П | |
|
–Т. –ѓ. –Я–Є–≤–Ї–Є–љ, –Х. –Я. –С–∞–Ї—Г–ї–Є–љ, –Ф. –Ш. –Ъ–Њ—А–µ–љ—М–Ї–Њ–≤ –Э–µ—З–µ—В–Ї–Є–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –≤ —Б–Є—Б—В–µ–Љ–∞—Е —Г–њ—А–∞–≤–ї–µ–љ–Є—П –Я–Њ–і —А–µ–і–∞–Ї—Ж–Є–µ–є –і–Њ–Ї—В–Њ—А–∞ —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –љ–∞—Г–Ї, –њ—А–Њ—Д–µ—Б—Б–Њ—А–∞ –Ѓ.–Э ... –Ф–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ —Б–≤–Њ–є—Б—В–≤–Њ –і–Є—Б—В—А–Є–±—Г—В–Є–≤–љ–Њ—Б—В–Є –љ–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П, —В.–µ. A (B C) (A B)(A C). –Ф–ї—П –ї–µ–≤–Њ–є —З–∞—Б—В–Є –Є–Љ–µ–µ–Љ: a(b+c-bc) = ab+ac-abc; –і–ї—П –њ—А–∞–≤–Њ–є: ab+ac-(ab)(ac) = ab+ac+a2bc. –° = –Р B C(z)=( A(x) B(y)) |
–†–∞–Ј–і–µ–ї: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –ї–Њ–≥–Є–Ї–µ –Ґ–Є–њ: —А–µ—Д–µ—А–∞—В |
Ї–µ
–Ґ–Є–њ: —А–µ—Д–µ—А–∞—В