Курсовая работа: Использование статистических функций в математическом пакете MathCAD
Министерство общего и профессионального образования
Свердловской области
Учебно-технический центр ООО «Омега-1»
КУРСОВАЯ РАБОТА
Использование статистических функций в математическом пакете MathCAD
Исполнитель: Молчанов Е.Е.
группа ВМ-311
Руководитель: Нечаева М.Г.
Екатеринбург 2010
Содержание
Введение
В MathCAD имеется ряд встроенных функций, задающих используемые в математической статистике законы распределения. Они вычисляют как значение плотности вероятности различных распределений по значению случайной величины х, так и некоторые сопутствующие функции. Все они, по сути, являются либо встроенными аналитическими зависимостями, либо специальными функциями. Большой интерес представляет наличие генераторов случайных чисел, создающих выборку псевдослучайных данных с соответствующим законом распределения, что является основой методов Монте-Карло.
Перед автором встала проблема, выяснения статистических функции в программе MathCAD.
Актуальность проблемы объясняется следующей причиной:
· Сейчас много людей работает с компьютерами, занимается программированием и работает в MathCAD, но для успешной работы некоторые не знают таких вещей как статистические функции, без них работа не будет такой успешной как хотелось бы.
Автор предложил гипотезу: зная статистические функции, можно успешно работать в MathCAD.
Объект исследования этой темы: MathCAD.
Предмет исследования этой темы: статистические функции.
Цель этой работы: выяснить какие бывают статистические функции в MathCAD.
В соответствии с целью сформулированы задачи работы:
· узнать что такое MathCAD
· узнать какие бывают статистические функции
Источником информации для этой работы является интернет.
Новизна этой работы субъективная, автор раньше этого не знал и не задумывался над этой темой.
1. MathCAD и основные принципы работы в MathCAD
MathCAD — программа для выполнения и документирования инженерных и научных расчётов.
Основные возможности:
· Решение дифференциальных уравнений различными численными методами
· Построение двух- и трёхмерных графиков функций
· Использование греческого алфавита, как в уравнениях, так и в тексте
· Выполнение вычислений в символьном режиме
· Выполнение операций с векторами и матрицами
· Символьное решение систем уравнений
· Аппроксимация кривых
· Выполнение подпрограмм
· Поиск корней многочленов и функций
· Проведение статистических расчётов и работа с распределением вероятностей
· Поиск собственных чисел и векторов
· Вычисления с единицами измерения
· Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
2. Типовые статистические функции в MathCADС помощью системы MathCAD можно проводить наиболее распространенные статистические расчеты с данными, представленными векторами их значений. Существует также ряд статистических функций для скалярного аргумента. С них и начнем.
Существуют следующие встроенные статистические функции скалярного аргумента x:
cnorm(x) - функция кумулятивного стандартного нормального распределения;
erf(x) - функция ошибок;
rnd(x) - функция генерации случайных чисел;
corr(VX,VY) - коэффициент корреляции двух векторов - VX и VY;
cvar(X,Y) - коэффициент ковариации X и Y.
Через функцию erf(x) легко вычисляется дополнительная функция ошибок:
erfc(x):= 1- erf(x)
Это одна из дополнительных и хорошо известных статистических функций, включенных в состав MathCAD.
Функция rnd(x) при каждом обращении к ней возвращает случайное число с равномерным распределением на отрезке [0, 1]. Эта функция широко применяется при статистическом моделировании различных физических процессов. Числа являются не строго случайными - в действительности это повторяющиеся последовательности из большого количества чисел, распределение которых близко к равномерному.
3. Статистические функции для векторов и матрицСледующая группа функций относится к вычислению основных статистических параметров одномерного массива данных - вектора:
mean(V) - возвращает среднее значение элементов вектора V;
median(V) - возвращает медиану элементов вектора V;
var(V) - возвращает дисперсию (вариацию) для элементов вектора V;
stdev(V) - задает стандартное отклонение элементов вектора V;
hist(int,V) - возвращает вектор частот попадания данных V в заданные интервалы int (служит для построения гистограмм).
В функции hist(int,V) вектор int должен содержать значения границ, в которых подсчитывается число попаданий данных из вектора V. Если строится гистограмма из N элементов, то вектор int должен содержать N + 1 элемент. Функция возвращает вектор из N элементов, числовые значения которых можно использовать для графического построения гистограмм.
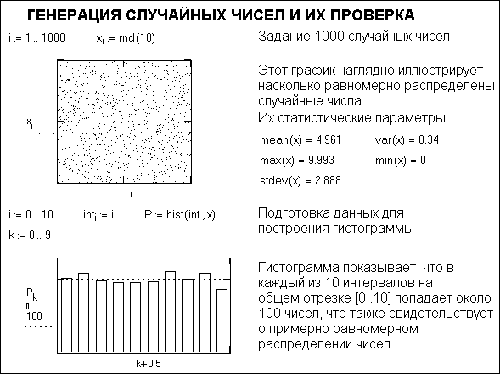
Рис. 1. Работа со случайными числами
На рис. 1. представлен фрагмент документа MathCAD, в котором организована генерация вектора X из 1000 случайных чисел, дано их распределение и вычислены основные статистические параметры массива случайных чисел - вектора X. Этот фрагмент иллюстрирует также применение функции hist.
При достаточно большом числе случайных чисел вид гистограммы приближенно говорит о законе их распределения. Так, если высоты столбцов примерно равны, то распределение будет равномерным.
Указанные функции могут использоваться и для обработки данных, представленных элементами (действительными и комплексными) матриц A размера m x n.
4. Функции вычисления плотности распределения вероятностиФункции вычисления плотности вероятности распределения представлены следующим набором:
· dbeta(x,s1,s2) - бета-распределение (s1, s2>0 - параметры формы, 0 dbinom(k,n,p) - биномиальное распределение (возвращает значение вероятности P(x = k), где n и k целые числа, причем 0ЈkЈn и 0ЈpЈ1);
· dcauchy(x,l,s) - распределение Коши (l - параметр разложения, s>0 - параметр масштаба);
· dchisq(x,d) - хи-квадрат-распределение (x, d>0, причем d - число степеней свободы);
· dexp(x,r) - экспоненциальное распределение (r,x>0);
· dF(x,d1,d2) - распределение Фишера (d1, d2>0 - числа степеней свободы, x>0);
· dgamma(x,s) - гамма-распределение (s>0 - параметр формы, xі0);
· dgeom(k,p) - геометрическое распределение (0<pЈ1 - вероятность успеха в отдельном испытании, k - целое неотрицательное число);
· dlnorm(x,m,s) - логарифмическое нормальное распределение (m - натуральный логарифм среднего значения, s>0 - натуральный логарифм среднеквадратичного отклонения, x>0);
· dlogis(x,l,s) - логистическое распределение (l - параметр разложения, s>0 - параметр масштаба);
· dnbinom(k,n,p) - отрицательное биномиальное распределение (n>0 и k>0 - целые числа, 0<pЈ1);
· dnorm(x,m,s) - нормальное распределение (m - среднее значение, s>0 - среднеквадратичное отклонение);
· dpois(k,l) - распределение Пуассона (l>0, k - целое неотрицательное число);
· dt(x,d) - распределение Стьюдента (d>0 - число степеней свободы, x - вещественное число);
· dunif(x,a,b) - равномерное распределение (a и b - граничные точки интервала, причем a<b и aЈxЈb);
· dweibull(x,s) - распределение Вейбулла (s>0 - параметр формы).
5. Функции распределенияФункции распределения дают вероятность того, что случайная величина будет иметь значения, меньшие или равные определенной величине. Они представлены ниже (смысл и значения параметров указаны ранее):
· pbeta(x,s1,s2) - значение в точке x функции бета-распределения;
· pbinom(k,n,p) - значение функции распределения биномиального закона для k успехов в серии из n испытаний;
· pcauchy(x,l,s) - значение в точке x функции распределения Коши со шкалой параметров l и s;
· pchisq(x,d) - значение в точке x кумулятивного хи-квадрат-распределения, в котором d - степень свободы;
· pexp(x,r) - значение в точке x функции экспоненциального распределения;
· pF(x,d1,d2) - значение в точке x функции распределения Фишера;
· pgamma(x, s) - значение в точке x функции гамма-распределения;
· pgeom(k,p) - значение в точке x функции геометрического распределения;
· plnorm(x,m,s) - значение в точке x функции логарифмического нормального распределения;
· plogis(x,l,s) - значение в точке x функции логистического распределения;
· pnorm(x,m,s) - значение в точке x функции нормального распределения;
· pnbinom(k,n,p) - значение в точке x функции отрицательного биномиального распределения;
· ppois(k,l) - значение для k функции распределения Пуассона;
· pt(x,d) - значение в точке x функции распределения Стьюдента;
· punif(x,a,b) - значение в точке x функции равномерного распределения;
· pweibull(x,s) - значение в точке x функции распределения Вейбулла.
6. Квантили распределенияСледующая группа задает обращения (квантили) функций распределения случайных величин. Они позволяют по заданной вероятности вычислить такое значение x, при котором вероятность равна или меньше заданного значения p:
· qbeta(p,s1,s2) - квантили обратного бета-распределения с параметрами формы s1 и s2;
· qbinom(p,n,q) - количество успешных определений при решении уравнения Бернулли, если число испытаний равно n, вероятность этого количества успешных определений равна p, а q - вероятность успеха при однократном испытании (0JqЈ1 и 0ЈpЈ1);
· qcauchy(p,l,q) - квантили обратного распределения Коши со шкалой параметров l и s (s>0 и 0<p<1);
· qchisq(p,d) - квантили обратного xи-квадрат-распределения;
· qexp(p,r) - квантили обратного экспоненциального распределения, при котором параметр r>0 определяет частоту (0Јp<1);
· qF(p,d1,d2) - квантили обратного распределения Фишера, в котором d1 и d2 - степени свободы;
· qgamma(p,s) - квантили обратного гамма-распределения;
· qgeom(p,q) - квантили обратного геометрического распределения;
· qlnorm(p,m,s) - квантили обратного логарифмического нормального распределения;
· qlogis(p,l,s) - квантили обратного логистического распределения;
· qnbinom(p,n,q) - квантили обратного отрицательного биномиального распределения с размером n и вероятностью ошибки q;
· qnorm(p,m,s) - квантили обратного нормального распределения со средним значением m и стандартным отклонением s;
· qpois(p,l) - квантили обратного распределения Пуассона;
· qt(p,d) - квантили обратного распределения Стьюдента (d определяет степени свободы, d>0 и 0 qunif(p,a,b) - квантили обратного равномерного распределения;
· qweibull(p,s) - квантили обратного распределения Вейбулла.
7. Функции создания векторов с различными законами распределенияПоследняя группа статистических функций служит для создания векторов с определенными законами распределения значений их элементов:
· rbeta(m,s1,s2) - бета-распределение;
· rbinom(m,n,p) - биномиальное распределение;
· rcauchy(m,l,s) - распределение Коши;
· rchisq(m,d) - хи-квадрат-распределение;
· rexp(m,r) - экспоненциальное распределение,
· rF(m,d1,d2) - распределение Фишера;
· rgamma(m,s) - гамма-распределение;
· rgeom(m,p) - геометрическое распределение;
· rlnorm(m,m,s) - логарифмическое нормальное распределение;
· rlogis(m,l,s) - логистическое распределение;
· rnbinom(m,n,p) - отрицательное биномиальное распределение;
· rnorm(m,m,s) - нормальное распределение;
· rpois(m,l) - распределение Пуассона;
· rt(m,d) - распределение Стьюдента;
· runif(m,a,b) - равномерное распределение;
· rweibull(m,s) - распределение Вейбулла.
На рис. 2. показан фрагмент документа MathCAD с примерами построения графиков различных статистических функций и задания наборов чисел с различным распределением.
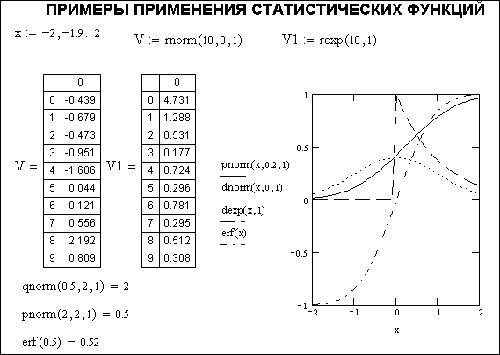
Рис. 2. Примеры применения статистических функций
Обилие статистических функций, включенных в систему MathCAD, позволяет с ее помощью выполнять достаточно сложные статистические расчеты. Однако все же надо отметить, что существуют более мощные специализированные пакеты для выполнения статистических расчетов, например Statistica или StatGraphics, которые заметно превосходят MathCAD в части многовариантности статистических вычислений.
1. Линейная регрессия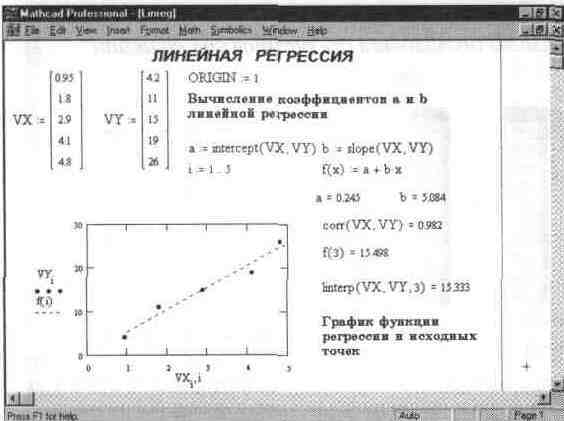
Рис.3. Линейная регрессия
Как видно на рис 3. прямая регрессии проходит в «облаке» исходных точек с максимальным среднеквадратичным приближением к ним. Чем ближе коэффициент корреляции к 1, тем точнее представленная исходными точками зависимость приближается к линейной.
2. Функции для линейной регрессииДругой широко распространенной задачей обработки данных является представление их совокупности некоторой функцией у(х). Задача регрессии заключается в получении параметров этой функции такими, чтобы функция приближала облако исходных точек (заданных векторами VX и VY) с наименьшей среднеквадратичной погрешностью. Чаще всего используется линейная регрессия, при которой функция у(х) имеет вид:
у(х) =а+ Ь*х
и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двухпараметрических зависимостях у(х).
Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций:
· corr(VX, VY) — возвращает скаляр — коэффициент корреляции Пирсона;
· intercept(VX, VY) — возвращает значение параметра а (смещение линии регрессии по вертикали);
· slope(VX, VY) — возвращает значение параметра b (наклона линии регрессии).
3. Линейная регрессия общего вида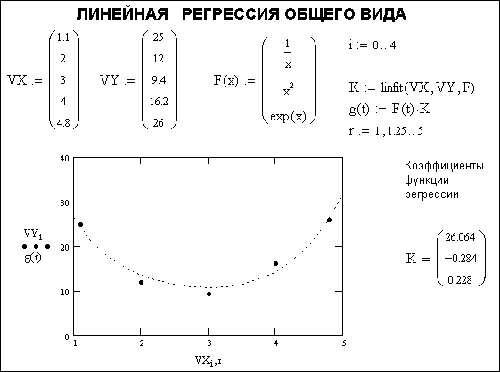
Рис. 4. Линейная регрессия общего вида
Расположение координат точек исходного массива может быть любым, но вектор VX должен содержать координаты, упорядоченные в порядке их возрастания, а вектор VY ординаты, соответствующие абсциссам в векторе VX.
8. Функция для линейной регрессии общего видаВ MathCAD реализована возможность выполнения линейной регрессии общего вида. При ней заданная совокупность точек приближается функцией вида:
F(x, К1 ,К2, ., Kn)= K1, F1(x)+K2 F2(x)+ +КnFn(x)
Таким образом, функция регрессии является линейной комбинацией функций F1(x), F2(x), ..., Fn(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.
Для реализации линейной регрессии общего вида используется функция linfit(VX,VY,F) Эта функция возвращает вектор коэффициентов линейной регрессии общего вида К, при котором среднеквадратичная погрешность приближения облака исходных точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной Вектор F должен содержать функции F1(x), F2(x), , Fn(x), записанные в символьном виде.
9.Полиномиальная регрессия
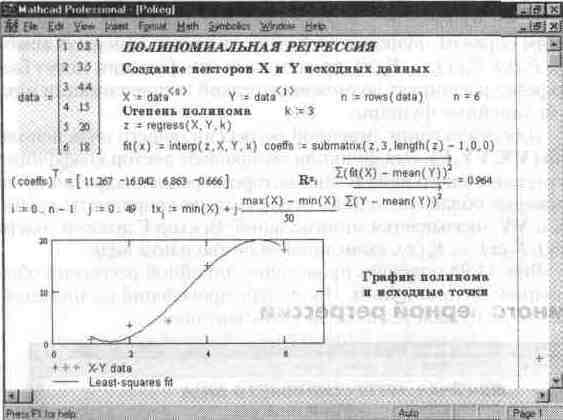
Рис. 5. Полиномиальная регрессия
На практике не рекомендуется делать степень аппроксимирующего поли нома выше четвертой — шестой, поскольку погрешности реализации регрессии сильно возрастают.
Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т е глобально. Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени, — loess(VX, VY, span). Эта функция возвращает используемый функцией interp(VS,VX,VY,x) вектор VS, дающий наилучшее приближение данных (с координатами точек в векторах VX и VY) отрезками полиномов второй степени Аргумент span>0 указывает размер локальной области приближаемых данных (рекомендуемое начальное значение — 0,75).
Чем больше span, тем сильнее сказывается сглаживание данных. При больших span эта функция приближается к regress(VX,VY,2).
На рис. 5. показан пример приближения сложной функции со случайным разбросом ее ординат с помощью совокупности отрезков полиномов второй степени (функция loess) для двух значений параметра span.
На рис. 5. нетрудно заметить, что при малом значении span, равном 0 05, отслеживаются характерные случайные колебания значений функции, тогда как уже при span=0,5 кривая регрессии становится практически гладкой. К сожалению, из-за отсутствия простого описания аппроксимирующей.
10. Функции для одномерной и многомерной полиномиальной регрессииВведена в новую версию MathCAD и функция для обеспечения полиномиальной регрессии при произвольной степени полинома регрессии
regress(VX,VY, n)
Она возвращает вектор VS, запрашиваемый функцией interp(VS,VX,VY,x), содержащий коэффициенты многочлена п-й степени, который наилучшим образом приближает «облако» точек с координатами, хранящимися в векторах VX и VY.
11. Практическая часть
Тема: Использование статистических функции в математическом пакете MathCAD.
Цель: Создать регрессию.
Программные средства: математический пакет MathCAD.
Ход работы:
1. Задаю вектора экспериментальных значений x и y.
2. Присваиваю значение к переменной z и ввожу функцию regress(x, y, n)
3. Вывожу результат переменной z
4. Создаю график, задаю нужные значения
5. Результат
Заключение
статистический функция регрессия распределение
В ходе работы были сделаны следующие выводы:
- автор узнал, что такое MathCAD, для чего он используется и узнал какие статистические функции бывают в MathCAD.
- так же автор узнал, по предложенным картинкам как выглядят те или иные функции.
Самооценка: автор считает, что он достиг поставленной цели и понятно изложил всю тему.
Значимость моей работы заключается в том что, я решил эту проблему, и теперь могу без проблем работать в MathCAD. Так же я узнал новое из этой работы, и те учащиеся, которые заинтересованы в этой теме тоже узнали нового. Конечно, возникла трудность с поиском литературы, материала для данной работы существует не так много.
Гипотеза автора подтвердилась, автор узнал, какие бывают статистические функции, и теперь он без проблем может работать в MathCAD.
Цель была достигнута, автор выяснил, какие бывают статистические функции.
Задачи этой работы были решены, автор узнал, что такое MathCAD и узнал какие бывают статистические функции/
Список литературы
1. http://www.sistemair.ru/dok/mathcad12/Glava_12/Index03.php
2. http://www.piter.com/attachment.php?barcode=978531800362&at=exc&n=0
3. http://ru.wikipedia.org/wiki/MathCad
| Нейрокомпьютерные системы | |
|
Введение. ПОЧЕМУ ИМЕННО ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ? После двух десятилетий почти полного забвения интерес к искусственным нейронным сетям быстро ... Таким образом, в течение данной фазы вектор S в точности дублирует вектор X. Далее для каждого нейрона в слое распознавания вычисляется свертка вектора его весов Вj и вектора С ... 1. Найден запомненный образ, сходство которого с вектором Х выше уровня параметра сходства, т.е. S>p. Если это происходит, проводится обучающий цикл, в процессе которого ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Теория вероятностей и математическая статистика | |
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования "Южный ... 56. Статистическая оценка коэффициентов линейной функции регрессии методом наименьших квадратов. Если и P вероятностная функция вектора, то частное распределение компоненты определяется равенством: , где B() |
Раздел: Рефераты по математике Тип: учебное пособие |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... е. преоб-е I это нейтр-й эл-т относ-о умнож-я преоб-я. Обратным преоб-м преобразованию S наз-ся преоб-е S-1 такое, что S*S-1=S-1*S=I. Подпрост-во L явл-ся инвариантным относ-о ... Пусть прямая задана направляющим вектором a"{m,n} и фикс. точкой M(x0,y0) Угловым кооф-ом прямой называется отношение второй координаты направляющего вектора к первой. k=n/m Если m ... |
Раздел: Рефераты по математике Тип: реферат |
| Технология и автоматизация производства РЭА | |
|
2КОМИТЕТ РФ ПО ВЫСШЕМУ ОБРАЗОВАНИЮ 2МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ 2(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) конспект лекций ... При синтезе эффективной ТС необходимо обеспечить min С(M,L,K,S,P). p 4i 0(y)=[1/(s- 7? 0(2 7p 0))]exp{[-y-f(x 4i 0) 52 0] /(2s 52 0)} (63). |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Статистический анализ числовых величин (непараметрическая статистика) | |
|
РЕФЕРАТ Статистический анализ числовых величин (непараметрическая статистика) В учебных курсах по теории вероятностей и математической статистике ... Простейшая вероятностно-статистическая модель такова [8]. При нулевой гипотезе H0 результаты наблюдения x1., x2.,., xn рассматриваются как реализация независимых одинаково ... Пример 3. Построим семейство пар функций распределения F(x) и G(x) таких, что их медианы различны, но для F(x) и G(x) выполнена гипотеза (6). Пусть распределения сосредоточены на ... |
Раздел: Рефераты по экономике Тип: реферат |