Курсовая работа: Напрямки розвитку волоконної оптики
Вступ
Одним з основних напрямків розвитку волоконної оптики в теперішній час є створення волоконних лазерів, що генерують в нових спектральних діапазонах. [4] Волоконні лазери були розроблені порівняно недавно, в 1980-х роках минулого сторіччя. З лазерів з напівпровідниковим накачуванням найбільш популярними є волоконні лазери.
У цей час відомі моделі волоконних технологічних лазерів потужністю до 20 кВт. Ці пристрої мають невисоку вартість, компактні, зручні для сполучення з магістральним волокном при мінімумі внесених втрат. Сьогодні ці пристрої досягли рівня характеристик, у першу чергу, потужності, надійності, що дозволяють із успіхом використовувати їх для розв’язку різних завдань лазерної обробки матеріалів. Вони являють собою практично ідеальні перетворювачі світлової енергії лазерних діодів накачування в лазерне випромінювання з рекордним ККД, у порівнянні, наприклад, із твердо тільними Nd:YAG-лазерами. [5]
Волоконні лазери володіють унікальним набором робочих характеристик і високими експлуатаційними якостями. У дослідницькій практиці отримана генерація в ближній інфрачервоній області спектра на великій кількості активних середовищ, реалізованих легуванням волоконних світловодів рідкоземельними елементами. [4]
Основним елементом волоконних лазерів є волоконний світловод з подвійною оболонкою, одномодова серцевина якого легована домішкою рідкоземельного елементу. Випромінювання накачування, зазнаючи повного внутрішнього відбивання на границі з зовнішньою полімерною оболонкою, розповсюджується по внутрішній оболонці з кварцевого скла. Перетинаючи серцевину, випромінювання накачування поглинається іонами рідкоземельного елементу, при цьому генерація виникає в одномодовій серцевині з характерним поперечним розміром 5-10 мкм. Таким чином, волоконний лазер з накачуванням в оболонку є приладом, який підвищує густину потужності випромінювання на 2-3 порядки. [6]
Найбільше поширення одержали неодимові, іттербієві, ербієві волоконні лазери [1]. Значний інтерес викликають лазери, генерація яких відбувається за допомогою вимушеного комбінаційного розсіяння (ВКР) у волокні. Внаслідок аморфності скла волоконних світловодів спектр ВКР-підсилення широкий і тому можлива генерація такого лазера на будь-якій довжині хвилі в діапазоні від 1 до 2 мікрон [2]. Застосування фосфосилікатних волоконних світловодів становить особливий інтерес, так як вони мають велику величину стоксового зсуву, що становить ~1300 см-1 [3]. [4]
Створення таких лазерів стало результатом багаторічного розвитку лазерної техніки. Останнім часом волоконні лазери активно витісняють традиційні лазери з таких областей застосування лазерної техніки, як, наприклад, лазерне різання й зварювання матеріалів, маркування й обробка поверхонь, поліграфія й швидкісне лазерне друкування. Їх використовують у лазерних далекомірах і тривимірних локаторах, апаратурі для телекомунікації, у медичних установках і інших сферах промислових і військових комплексів.[5]
Розділ 1. Тенденції розвитку волоконних лазерів. Використання волоконних лазерів у різних галузях
Лазерна техніка не стоїть на місці, розвивається, у тому числі відбувається й постійне вдосконалювання тих типів лазерів, які використовуються в лазерних системах для цифрової флексографії.
Говорячи про сьогоднішній день цифрової технології флексографії, слід зазначити, що зараз у лазерних системах запису зображень домінують лазери з так званим напівпровідниковим накачуванням. Їхні основні переваги, на відміну від лазерів з ламповим накачуванням у тому, що вони споживають значно менше електроенергії; не потрібні зовнішнє водяне охолодження, у конструкції цих лазерів відсутні змінні компоненти (у ламповій системі, наприклад, лампу накачування доводиться міняти кожні 500-1000 год. роботи). В лазерах з напівпровідниковим накачуванням «часи життя», що перевищують 10000 год. дозволяють будувати надійні й, разом з тим, зручні системи лазерного запису, експлуатувати які могли б оператори, що не є фахівцями в лазерній техніці, що надзвичайно важливо для поліграфічних підприємств. Інша істотна особливість таких систем полягає в тім, що за названий час лазерна система повністю відкуповує себе - це надзвичайно важливо при плануванні інвестицій.
З лазерів з напівпровідниковим накачуванням, у свою чергу, найбільш популярними стають волоконні лазери (Fiber Laser або Faser). Сьогодні ці пристрої досягли рівня характеристик, у першу чергу, потужності, надійності, що дозволяють із успіхом використовувати їх для розв’язання різних завдань лазерної обробки матеріалів. Дуже часто волоконні лазери заміняють у додатках лазери інших типів, наприклад, твердо тільні Nd:YAG-лазери. Вони являють собою практично ідеальні перетворювачі світлової енергії лазерних діодів накачування в лазерне випромінювання з рекордним ККД, у порівнянні, наприклад, з Nd:YAG-лазерами. Створення таких лазерів стало результатом багаторічного розвитку лазерної техніки.
Говорячи про технічну сторону справи, варто зупинитися на деяких конструкційно-технологічних і експлуатаційних перевагах систем з волоконними лазерами.
Спочатку зупинимося на технічних особливостях самих волоконних лазерів з напівпровідниковим накачуванням. Саме загальне подання про них давалося на сторінках журналу приблизно рік тому у загальному огляді лазерів, застосованих для технологій Computer-to-Plate. Нагадаємо деякі найбільш важливі особливості цих лазерів. На рис. 1.1 представлена схема роботи волоконного лазера з напівпровідниковим накачуванням і в загальному виді весь оптичний тракт аж до оброблюваного матеріалу.
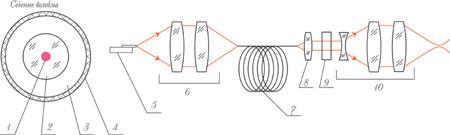
Рис. 1.1. Оптична система з волоконним лазером: 1 — серцевина, легована металом, діаметр 6–8 мкм; 2 — кварцове волокно, діаметр 400–600 мкм; 3 — полімерна оболонка; 4 — зовнішнє захисне покриття; 5 — лазерні діоди оптичного накачування; 6 — оптична система накачування; 7 — волокно (до 40 м); 8 — коліматор; 9 — модулятор світла; 10 — фокусуюча оптична система
Головна особливість цього лазера в тому, що випромінювання тут відбувається в тонкому, діаметром усього в 6-8 мкм, волокні (серцевині - наприклад, активне середовище іттербій), що фактично перебуває усередині кварцового волокна діаметром 400-600 мкм. Випромінювання лазерних діодів накачування вводиться у кварцове волокно й поширюється уздовж усього складного складеного волокна, що має довжину кілька десятків метрів. Це випромінювання «перетинає», тобто оптично накачує серцевину, саме в ній на атомах іттербія (Yb) відбуваються ті фізичні перетворення, що приводять до виникнення лазерного випромінювання. Поблизу кінців волокна на серцевині є два дифракційних дзеркала - у вигляді набору «насічок» на циліндричній поверхні серцевини (дифракційні решітки); у такий спосіб створюється резонатор волоконного лазера. Загальну довжину волокна й кількість лазерних діодів вибирають, виходячи з необхідної потужності, ефективності. На виході отримуємо ідеальний одномодовий лазерний пучок з досить рівномірним розподілом потужності, що дозволяє сфокусувати випромінювання в пляму малого розміру й мати більшу, ніж у випадку потужних твердо тільних Nd:YAG-лазерів, глибину різкості, а це надзвичайно важлива для лазерних систем властивість, особливо для багатопроменевих оптичних систем (рис. 1.2).
Також варто відзначити, що ряд властивостей випромінювання волоконних лазерів, наприклад, характер поляризації пучка, робить більш зручним і надійним керування цим випромінюванням за допомогою акустооптичних компонент, дозволяє реалізувати багатопроменеві схеми запису зображень. У цілому підвищується надійність усього оптичного тракту лазерної системи. Оскільки оптичне накачування йде по всій довжині волокна, відсутні, наприклад, властиві звичайним твердо тільним лазерам ефекти, як термолінза в кристалі, спотворення хвильового фронту внаслідок дефектів самого кристала, девіація променя з часом та ін. Ці ефекти завжди були перешкодою для досягнення максимальних можливостей твердо тільних систем. У волоконному ж лазері сам принцип його пристрою й роботи гарантує високі характеристики і робить такі лазери практично ідеальними перетворювачами світлового випромінювання в лазерне.

Рис. 1.2. Форма пучка різних лазерних джерел: а - волоконні лазери, одно модовий режим; б - Nd:YAG-лазери, багато модовий режим; в - випромінювання лазерних діодів
Цікава історія розвитку цих лазерів. Спочатку це були підсилювачі волоконних ліній зв'язку, у яких використовується такий же фізичний принцип підсилення сигналу, що й при генерації лазерного випромінювання. Такі підсилювачі широко використовуються в системах телекомунікації на базі оптичних волокон. Розвиток цих пристроїв привів до того, що потужність створеного ними оптичного випромінювання досягло декількох десятків ват, а це уможливило їхнє застосування в лазерній обробці матеріалів. Для одного з таких завдань - видалення тонкого чорного шару на цифровому фотополімері - ці лазери підходять найбільш оптимально, можна сказати, ідеально.

Рис. 1.3. Апарат Laser-Graver4003DS
Серед західних виробників додрукованих систем для цифрової технології флексографії, що використовують випромінювачі даного типу - фірми Hell, FlexoLaser, Cartomac. Фірма «Альфа», провідна російська компанія, що займається виготовленням цих систем і поставляє їх не тільки на вітчизняний, але й на західні ринки, також перейшла на даний тип лазерів. Восени 2001 р. «Альфа» зняла з виробництва машини LaserGraver, на базі Nd:YAG-лазерів з ламповим накачуванням. Рік тому кожна модель LaserGraver (рис. 1.3), мала чотири застосування: одно- або двопроменева (DualBeam) оптична система, з лазером з ламповим або з напівпровідниковим накачуванням. Тепер кожна машина із заданим форматом пропонується лише у двох модифікаціях - один або два промені, а як лазер завжди використовується волоконний лазер з напівпровідниковим накачуванням (активне середовище іттербій, ІЧ-випромінювання).
Перед прийняттям цього рішення був проаналізований досить тривалий досвід роботи систем LaserGraver з такими лазерами в умовах реальних виробництв флексографічних форм у деяких європейських клієнтів. Тому зараз вітчизняним користувачам фактично пропонується розв’язок, перевірений на заході, що, безумовно, представляє додатковий інтерес. Пропозиція вітчизняним поліграфістам цих сучасних лазерних систем, що відповідають прийнятим у даній області техніки світовим стандартам, стало можливим після того, як розвиток волоконних лазерів і розширення спектра їх застосування в промисловості дозволило знизити на них ціни. Тому з'явилася можливість створити доступні й вітчизняним флексографічним друкарям моделі устаткування.
На закінчення підсумуємо головні переваги лазерних систем запису зображень на цифровому фото полімері, побудованих на базі волоконного лазера з напівпровідниковим накачуванням:
· мале енергоспоживання, наприклад, системи LaserGraver являють собою практично офісну техніку, живлення якої здійснюється від звичайної розетки;
· ніякого водяного охолодження, для компонентів волоконного лазера досить повітряного охолодження;
· відсутність змінних елементів і профілактичних операцій з боку оператора;
· зручність для побудови багатопроменевих оптичних систем;
· висока надійність устаткування. [7]
Переваги:
· високий ККД до 40 % і більше;
· висока якість (мала розбіжність) випромінювання – до M2 ≈1.05 при вихідній потужності 100 Вт;
· можливість генерації як неперервного, так і коротких (до нс) імпульсів випромінювання з великою частотою (20 кГц і більше);
· рекордно великі потужності випромінювання - до 50 кВт ( в 2005 р.) і це не межа;
· ефективність генерації на багатьох довжинах хвиль (1.06 мкм (Nd, Yt), 1.56 мкм (Er), 1.75-2.0 мкм (Tu) і ін.) для обробки матеріалів (1.06 мкм), медицини (1.75-2.0 мкм) і зв'язку (1.56 мкм);
· зручність електричного керування тимчасовими й перемикальними характеристиками;
· електричне накачування (діодів) електроенергією з низькою напругою;
· природна волоконна доставка випромінювання;
· висока надійність і великий ресурс роботи більше 1 млн. годин;
· висока стабільність параметрів ± 2%, стійкість до механічних, теплових забруднень навколишнього середовища (пилу) та інших впливів;
· висока просторова й спектральна яскравість;
· малі масо габаритні розміри.
Потужні волоконні лазери на іттербії (λ = 1050 −1080 нм)
Основні характеристики:
Неперервний режим
· вихідна потужність - до 50 кВт;
· можлива модуляція вихідного випромінювання із частотою 5 кГц;
· ККД - 25 %;
· вихід - волокно 200 мкм;
· якість пучка — M2 = 2,5 − 6 мрад;
· термін служби - > 100 кілогодин;
· габарити - 86х81х150 см;
· вага - 100 кг при 10 кВт.
Імпульсний режим:
· середня вихідна потужність - до 200 Вт;
· тривалість імпульсу - 30-100 нс;
· енергія в імпульсі – 0,5-2 мДж;
· частота проходження імпульсів - 20-100 кГц
· волоконний вихід;
· зовнішнє цифрове керування;
· компактний з повітряним охолодженням;
· колімований вихідний пучок з M2 =1,4 − 5;
· термін служби - > 100 кілогодин;
· ККД - більше 10 %.
На рис. 1.4, 1.5 наведений зовнішній вигляд деяких типових вузлів волоконних лазерів.


Рис. 1.4.


Рис. 1.5.
Ведучий генератор (а), підсилювач (б) і вихідний коліматор волоконного лазера і загальний вид імпульсного лазера потужністю 200 Вт ( 1 - одномодове активне оптичне волокно, 2 – модуль напівпровідникового накачування). 700 Вт іттербієвий волоконний лазер неперервної дії (рис 1.4) і його робоча станція (рис 1.5). [8]


Потужні іттербієві лазери Лазерний обробний центр із 500 Вт, 1 кВт, 2 кВт. роботом для зварювання Al.
Таким чином, волоконні лазери з комплексу властивостей найбільш оптимальні для застосування в системах цифровий флексографії й у цьому, мабуть, головна причина знаходження ними все більшої популярності в цій області техніки. [7]
Розділ 2. Теоретичні основи волоконних лазерів
Оскільки активним елементом волоконного лазера є оптичне волокно, розглянемо механізми поширення оптичного випромінювання у волокні.
2.1 Поширення світла в оптичних волокнах
Принцип дії оптичного волокна базується на використанні відомих процесів відбивання i заломлення оптичної хвилі на межі розділу двох середовищ з різними оптичними властивостями. Оптичні властивості матеріалу залежать від показника заломлення. В однорідному середовищі електромагнітна хвиля розповсюджується прямолінійно, проте на межі зміни густини середовища її напрям i якісний склад змінюються. В спрощеному вapiaнтi розглянемо два середовища, що межують, з різною густиною. Розповсюджуючись в одному з них промінь може досягати поверхні іншого під деяким кутом а (до нормалі поверхні). При цьому хвиля частково відбивається в середовище з якого прийшла під кутом b i частково проникає в нове середовище в зміненому напрямі під кутом с. При падінні променя на межу розділу двох середовищ в загальному випадку з'являються заломлена i відбита хвилі.
|
|
Рис 2.1. Відбивання і заломлення променя на межі і заломлення відповідно розділу двох середовищ
Згідно закону Снелліуса кут падіння пов’язаний з кутами відбивання і заломлення наступним співвідношенням:
![]() (2.1)
(2.1)
де ![]() – показники заломлення двох
середовищ;
– показники заломлення двох
середовищ; ![]() - кути падіння
- кути падіння
Згідно фізичним законам поширення світла кут падіння променя рівний куту відбивання, тобто а= b .
У мipy збільшення кута падіння можна досягти такого стану, коли заломлений промінь починає ковзати по межі розділу середовищ без переходу в середовище з меншим показником заломлення. Кут падіння, при якому спостерігається такий ефект, називається граничним кутом повного внутрішнього відбивання, який можна знайти, виходячи з закону заломлення:
![]() (2.2)
(2.2)
Для всіх кутів падіння, які перевищують граничний, матиме місце тільки відбивання, а заломлена хвиля буде відсутня.
Це явище називається повним внутрішнім відбиванням, воно закладене в основу передачі оптичного випромінювання по волокну.
Оптичні волокна, звичайно, мають круглий поперечний пepepiз i складаються з двох концентричних шарів діелектрика. В центрі розташовується серцевина з оптично більш густого скла, яка оточена оболонкою з скла з меншою оптичною густиною. Показник заломлення оптичної оболонки менш ніж на 1% менший показника заломлення серцевини.

Рис. 2.2. Будова оптичного волокна
На межі розділу серцевини i оболонки відбувається відбивання світла, яке поширюється вздовж oci волокна. Таким чином, серцевина служить для передачі електромагнітної енергії, оболонка призначена в основному для покращення умов відбивання на межі розділу серцевина/оболонка i захисту від випромінювання енергії в оточуюче середовище. Волокно має додаткову захисну оболонку навколо оптичної оболонки. Захисна оболонка (один або декілька шарів полімеру) оберігає серцевину i оптичну оболонку від дій, які можуть вплинути на їx оптичні властивості i не впливає на процес розповсюдження світла по волокну. [13]
2.2 Профіль показника заломлення
Існують декілька видів профілів показника заломлення, серед яких часто використовуються два: ступінчастий i градієнтний. Волокно з ступінчастим профілем має серцевину з однорідним показником заломлення.
При цьому присутній різкий стрибок показника заломлення на межі між серцевиною i оптичною оболонкою. У ступінчастому оптичному волокні промені світла спрямовуються внаслідок явища повного внутрішнього відбивання на межі серцевина/оболонка. Якщо кут падіння променя на межу оболонка-серцевина менший ніж критичний кут, то промінь заломлюється в оболонку i виходить з волокна.

Рис. 2.3. Поширення світла в оптичному волокні
2.3 Просторові параметри випромінювання волоконного лазера
Просторові параметри волоконного лазера визначаються геометричними розмірами оптичного волокна, профілем показника заломлення серцевини оптичного волокна, співвідношенням показників заломлення серцевини i оболонки, а також довжиною хвилі випромінювання.
Волоконні світловоди, в яких може поширюватися лише одна мода, на даний час є найбільш перспективними для активних середовищ волоконних лазерів.
Електричний та магнітний вектори Е i Н модового поля волоконного світловоду з круговою симетрією поперечного січення можна записати у вигляді:
![]() , (2.3а)
, (2.3а)
![]() . (2.3б)
. (2.3б)
де ![]() - постійна поширення моди,
- постійна поширення моди, ![]() - полярні координати в площині
поперечного перерізу волокна, а
- полярні координати в площині
поперечного перерізу волокна, а ![]() - відстань по oci волокна. У
загальному випадку вектори Е i Н знаходять з розв’язку рівнянь Максвела. Проте,
оскільки оптичні волокна є слабо напрямлюючими (слабо каналізуючими), тобто відносна
різниця між максимальним та мінімальним значеннями профілю показника заломлення
- відстань по oci волокна. У
загальному випадку вектори Е i Н знаходять з розв’язку рівнянь Максвела. Проте,
оскільки оптичні волокна є слабо напрямлюючими (слабо каналізуючими), тобто відносна
різниця між максимальним та мінімальним значеннями профілю показника заломлення
![]() мала - зазвичай менше 1 %, вектори Е i
Н можна апроксимувати розв’язками скалярного хвильового рівняння.
мала - зазвичай менше 1 %, вектори Е i
Н можна апроксимувати розв’язками скалярного хвильового рівняння.
Постійна
поширення ![]() основної моди повинна знаходитися
в інтервалі між двома екстремумами, які визначаються значеннями
основної моди повинна знаходитися
в інтервалі між двома екстремумами, які визначаються значеннями ![]() для плоских хвиль, що поширюються у
напрямку z у нескінченно (однорідних) середовищах з показником заломлення, рівним
максимальному та мінімальному значенням профілю волокна
для плоских хвиль, що поширюються у
напрямку z у нескінченно (однорідних) середовищах з показником заломлення, рівним
максимальному та мінімальному значенням профілю волокна![]() .
.
Якщо ці значення
визначити як ![]() - максимальне значення показника
заломлення
- максимальне значення показника
заломлення ![]() ,
, ![]() - мінімальне значення показника
заломлення
- мінімальне значення показника
заломлення ![]() , то
, то ![]() буде обмежуватися інтервалом
буде обмежуватися інтервалом
![]() (2.4)
(2.4)
де ![]() - довжина хвилі у вакуумі. З
урахуванням слабкої каналізації світловодів, призначених для систем оптичного
зв'язку, тобто
- довжина хвилі у вакуумі. З
урахуванням слабкої каналізації світловодів, призначених для систем оптичного
зв'язку, тобто ![]() ,
,
з (2.4) випливає![]() , що співпадає з постійною поширення
плоскої хвилі у z - напрямку у безмежному середовищі з показником заломлення
, що співпадає з постійною поширення
плоскої хвилі у z - напрямку у безмежному середовищі з показником заломлення ![]() .
.
Таким чином, основна мода волоконного світловоду повинна бути квазіпоперечною електромагнітною (ТЕМ00) хвилею, у найпростішому випадку - це хвиля, одно рідно поляризована лише в одному напрямку. Позначивши напрямок поляризації через х, поле у світловоді можна записати у вигляді:
![]() (2.5)
(2.5)
Тут компоненти
поля Еу, Ez , H у , Hz не
враховуються, оскільки вони дуже малі, ![]() описує просторову фільтрацію у площині,
перпендикулярній oci світловода,
описує просторову фільтрацію у площині,
перпендикулярній oci світловода, ![]() - магнітна проникність середовища,
- магнітна проникність середовища,
![]() ,
,
де ![]() і
і![]() - діелектрична проникність вакууму.
- діелектрична проникність вакууму.
Оскільки ![]() , поляризаційні властивості волоконної
структури слабо впливають на поле у світловоді. Відмітимо, що якщо діелектричні
середовища мають приблизно однакові параметри, то відбивання плоскої хвилі від
межі їх розділення практично не реагує на поляризацію падаючої хвилі. Відповідно
й просторова варіація
, поляризаційні властивості волоконної
структури слабо впливають на поле у світловоді. Відмітимо, що якщо діелектричні
середовища мають приблизно однакові параметри, то відбивання плоскої хвилі від
межі їх розділення практично не реагує на поляризацію падаючої хвилі. Відповідно
й просторова варіація ![]() поля повинна бути нечутливою до поляризаційних
ефектів, тому
поля повинна бути нечутливою до поляризаційних
ефектів, тому ![]() - розв’язок скалярного хвильового рівняння,
тобто
- розв’язок скалярного хвильового рівняння,
тобто
![]() , (2.6)
, (2.6)
де ![]() визначається виразом
визначається виразом
![]() (2.7)
(2.7)
Основна мода
описується розв’язком рівняння (2.6), що відповідають найбільшому ![]() , не залежному від полярного кута
, не залежному від полярного кута ![]() .
.
Отже, основна
мода - це квазіпоперечна електромагнітна хвиля, що визначається формулою (2.6),
з просторовою залежністю![]() , що є розв’язком скалярного
хвильового рівняння.
, що є розв’язком скалярного
хвильового рівняння.
2.4 Оптичні волокна з гаусівським профілем показника заломлення
Числові методи
розв’язку рівняння (2.6) для ступінчастого профілю волокна показують, що форма ![]() приблизно гаусівська. У відповідності
з цим поле моди ТЕМ11 має вигляд:
приблизно гаусівська. У відповідності
з цим поле моди ТЕМ11 має вигляд:
![]() (2.8)
(2.8)
де ![]() - розмір плями. Цей вираз можна
представити у якості пробної функції для стаціонарного виразу постійної
поширення
- розмір плями. Цей вираз можна
представити у якості пробної функції для стаціонарного виразу постійної
поширення ![]() , крім того розмір плями вибирається з
умови забезпечення найбільшого
, крім того розмір плями вибирається з
умови забезпечення найбільшого ![]() . Основна мода відповідає максимальному
значенню
. Основна мода відповідає максимальному
значенню ![]() . Стаціонарний вираз для
. Стаціонарний вираз для ![]() має вигляд:
має вигляд:
 (2.9)
(2.9)
Таким чином,
розмір плями ![]() знаходиться безпосередньо. Підставляючи
наближений вираз (2.8) у (2.9) можна визначити
знаходиться безпосередньо. Підставляючи
наближений вираз (2.8) у (2.9) можна визначити ![]() з умови
з умови ![]() . Наближення для постійної поширення
. Наближення для постійної поширення ![]() отримується далі підстановкою
отримується далі підстановкою ![]() у вираз (2.9). Знаючи
у вираз (2.9). Знаючи ![]() та
та ![]() ми можемо повністю характеризувати
поле за допомогою формул (2.5) та (2.8).
ми можемо повністю характеризувати
поле за допомогою формул (2.5) та (2.8).
За допомогою
загального виразу для розподілу показника заломлення можна конкретизувати форму
профілю показника заломлення ![]() , який має узагальнений вигляд:
, який має узагальнений вигляд:
![]() (2.10)
(2.10)
![]() - різниця показників заломлення, що
визначається як
- різниця показників заломлення, що
визначається як
![]() (2.11)
(2.11)
причому ![]() характеризує довільну форму профіля
(
характеризує довільну форму профіля
(![]() при максимальній величині показника
заломлення), а
при максимальній величині показника
заломлення), а ![]() - радіус серцевини оптичного волокна.
- радіус серцевини оптичного волокна.
Спочатку ми
розглянемо профіль, форма якого ![]() представляється гаусівською
функцією:
представляється гаусівською
функцією:
![]() , (2.12)
, (2.12)
Рівняння (2.12)
визначає зв'язок радіуса серцевини волокна![]() , сталої розповсюдження світлової
хвилі
, сталої розповсюдження світлової
хвилі ![]() і відносної різниці показників
заломлення з радіусом світлової плями на виході оптичного волокна
і відносної різниці показників
заломлення з радіусом світлової плями на виході оптичного волокна ![]() :
:
![]() , (2.13)
, (2.13)
де![]() , а V - безрозмірний параметр
волокна, що визначається як
, а V - безрозмірний параметр
волокна, що визначається як
![]() . (2.14)
. (2.14)
Розмір плями ![]() , знаходиться з умови
, знаходиться з умови ![]() , що дає
, що дає
![]() , (2.15)
, (2.15)
Вираз (2.15) має
фізичний зміст лише при ![]() (
(![]() додатне). Проте, як буде показано
нижче, цей факт не заважає вичерпному описові співвідношення (2.15)
передавальних характеристик волоконних світловодів. Підставляючи
додатне). Проте, як буде показано
нижче, цей факт не заважає вичерпному описові співвідношення (2.15)
передавальних характеристик волоконних світловодів. Підставляючи ![]() у (2.8), отримуємо вираз для
у (2.8), отримуємо вираз для ![]()
![]() , (2.16)
, (2.16)
який придатний тільки
при V ![]() 0,5, так як з (2.4) випливає, що
0,5, так як з (2.4) випливає, що ![]() .
.
Розмір плями та
постійна поширення цілковито характеризують поле основної моди, а відповідно, й
передавальні властивості одномодових світловодів, що розглядаються нижче. Доцільність
введення параметра V випливає з того, що![]() залежить лише від V.
залежить лише від V.
2.5 Діапазон значень V для одномодового режиму
При збільшенні V
вище певного визначеного значення стає можливим поширення й інших мод; для світловодів
зi ступінчастим профілем це значення![]() , а для волокон з гаусівським профілем
, а для волокон з гаусівським профілем
![]() . Проте в реальних випадках волокна є
"ефективно одномодовими" i при великих значеннях V (наприклад при V
. Проте в реальних випадках волокна є
"ефективно одномодовими" i при великих значеннях V (наприклад при V![]() 3 для ступінчастого профілю), оскільки
моди вищих порядків мають великі втрати на випромінювання, викликані не регулярностями
волокон.
3 для ступінчастого профілю), оскільки
моди вищих порядків мають великі втрати на випромінювання, викликані не регулярностями
волокон.
Розподіл густини
потужності, або профіль інтенсивності![]() , представлений у табл. 2.1, має
вигляд
, представлений у табл. 2.1, має
вигляд
 ,
,
тобто зі збільшенням відстані від oci інтенсивність спадає експоненційно.
В табл. 2.1
наведені вирази для параметрів основної моди, які виражені через розмір плями ![]() для гаусівського i ступінчастого профілів.
для гаусівського i ступінчастого профілів.
Таблиця 2.1 Параметри основної моди
| Густина потужності у z-напрямку |
|
|
| Сумарна потужність |
|
|
|
Доля потужності у січенні від 0 до |
|
|
| Гаусівський профіль показника заломлення | Ступінчастий профіль показника заломлення | |
|
|
|
|
|
|
|
|
|
|
|
при |
При менших
значеннях V зниження відбувається повільніше, тому, чим менше V, тим менша
частина загальної потужності поширюється поблизу oci волокна. Цей ефект
безпосередньо ілюструється шляхом обчислення долі потужності![]() в інтервалі від 0 до
в інтервалі від 0 до![]() , як показано в табл. 2.1. 3
наведених даних зрозуміло, що у світловодах з малим V, випромінювання, що
поширюється, захоплює більшу частину поперечного перерізу, ніж у випадку V >2
[13].
, як показано в табл. 2.1. 3
наведених даних зрозуміло, що у світловодах з малим V, випромінювання, що
поширюється, захоплює більшу частину поперечного перерізу, ніж у випадку V >2
[13].
На виході волоконного лазера розбіжність випромінювання приблизно визначається числовою апертурою волокна. Для градієнтного волокна, яким є волокно з гаусівським профілем, використовується поняття локальної числової апертури, яка визначається наступним виразом:
![]() , (2.17)
, (2.17)
значення якої максимальне на oci і падає до нуля на границі розділу серцевини i оболонки. А відповідно розбіжність випромінювання визначається наступним чином [13]:
![]() (2.18)
(2.18)
2.6 Оптичні волокна зі ступінчастим профілем показника заломлення
Для волокна з ступінчастим профілем справедливими є наступні вирази для радіуса плями i сталої розповсюдження:
![]() , (2.19)
, (2.19)
які приводять до
інших значень параметрів у табл. 2.1(![]() )[13].
)[13].
Розбіжність випромінювання в даному волокні визначається показниками заломлення серцевини i оболонки [13]:
![]() (2.20)
(2.20)
волоконний лазер оптичний спектральний
2.7. Вимоги до матеріалів активних середовищ
Лазерне середовище волоконного лазера створюють легуванням серцевини волокна (основа) активаторами, що володіють заданою картиною енергетичних рівнів. Склоподібна основа (в нашому випадку кварц) повинна задовольняти деяким умовам.
• Оптична прозорість для випромінювання накачування i для випромінювання іонів активатора;
• Ефективний відвід тепла;
• Висока оптична однорідність (відсутність механічних напружень, мікровключень);
• Структура повинна допускати введення активатора в заданій концентрації.
Іони активатора вводяться в основу без порушення оптичної однорідності i механічної міцності, створюють збуджені метастабільні piвнi, час життя на яких повинен визначатись в основному випромінювальними оптичними переходами, володіють широкими смугами поглинання i сильними вузькими лініями люмінесценції. Для виготовлення таких волокон застосовують, зокрема, силікатні, фосфатні, боратні, германатні, теллуридні, фторофосфатні скла, які активовані такими рідкоземельними іонами, як Nd3+,Tb+, Но3+, Ег3+, Tm3+,Yb3+. 3 допомогою Yb3+ - волоконного лазера з домішками Tm3+ можна реалізувати волоконний лазер з пасивним переключенням добротності, при якому адсорбер інтегрований в підсилювальне волокно. Узгоджена адсорбція в цій системі базується на легуванні Tm3+.
У волоконних лазерах переважає неоднорідне розширення лінії випромінювання, механізм якого полягає в тому, що резонансні частоти окремих атомів розподіляються в деякій смузі частот (не співпадають) i, відповідно, лінія всієї системи є розширеною при відсутності розширення лінії окремих атомів. Рівні енергії, а отже i частоти переходів, залежать від найближчих сусідів кожного атома. Випадкові деформації, які завжди мають місце в оптичному волокні, змінюють це оточення від іона до ioнa, що приводить до розкиду частот переходів.
Волоконний лазер може генерувати як в неперервному, так i в імпульсному режимі, які будуть розглянуті нижче. Модовий режим роботи буде залежати від оптичного волокна, яке використовується.
2.8 Схема накачування волоконного лазера
Спектр випромінювання активатора може відповідати три- або чотири рівневі cxeмi. В своїй більшості іони рідкоземельних металів володіють набором енергетичних рівнів, що відповідають чотири рівневі системі.

Рис. 2.4. Схема розміщення енергетичних рівнів для Nd3+ в скляній матриці
|
|
|
|
|
| 1330 |
2,05 |
1,13 | 0,62 |
| 1059 |
2,7 |
1,48 | 0,62 |
| 956 |
1,9 |
1,04 | 0,62 |
Розглянемо чотирирівневу модель роботи волоконного лазера. При термодинамічній рівновазі майже вci атоми згідно статистики Больцмана знаходяться в основному стані (нульовий рівенъ). Під дією випромінювання лазерного діода (накачування) атоми переходить з рівня 0 на рівень 3. З цього рівня атоми будуть швидко релаксувати з переходом на більш низький метастабільний рівень 2. Якщо така релаксація проходить достатньо швидко, то рівень 3 залишається практично незаселеним. Оскільки рівень 1 спочатку був незаселеним, кожний атом, що знаходиться в збудженому стані буде давати вклад в інверсію заселеності між рівнями 2 i 1. Коли в лазері виникає генерація, атоми в процесі вимушеного випромінювання переходять з рівня 2 на рівень 1.

Рис. 2.5. Схема енергетичних рівнів чотирирівневого лазера
Якщо верхній рівень накачування пустий, то швидкість, з якою верхній лазерний рівень 2 буде заселятись з допомогою накачування можна записати у вигляді:
![]() , (2.21)
, (2.21)
тут ![]() - заселеність основного рівня, a Wp-
швидкість накачування. Для того щоб досягнути порогових умов, швидкість
накачування повинна перевищувати деяке порогове значення.
- заселеність основного рівня, a Wp-
швидкість накачування. Для того щоб досягнути порогових умов, швидкість
накачування повинна перевищувати деяке порогове значення.
2.9 Забезпечення додатного зворотного зв'язку в волоконному лазері
Напруженість електричного поля оптичних хвиль, які поширюються по волокну в прямому i зворотному напрямах:
![]() , (2.22)
, (2.22)
![]() , (2.23)
, (2.23)
де ![]() - амплітуда падаючої на гратку хвилі i
поширюється зліва направо;
- амплітуда падаючої на гратку хвилі i
поширюється зліва направо; ![]() - відбита від граток Брегга хвиля, що
поширюється справа наліво;
- відбита від граток Брегга хвиля, що
поширюється справа наліво; ![]() - стала розповсюдження по оптичному
волокну, її можна виразити таким чином:
- стала розповсюдження по оптичному
волокну, її можна виразити таким чином: ![]() ;
;![]() - середнє значення показника
заломлення оптичного волокна;
- середнє значення показника
заломлення оптичного волокна;![]() - функція, яка пропорційна
напруженості електричного поля впоперек волокна i є нормованою;
- функція, яка пропорційна
напруженості електричного поля впоперек волокна i є нормованою; ![]() - циклічна частота.
- циклічна частота.
Методом
зв'язаних хвиль при параболічному наближенні на основі хвильового рівняння для
одномодового оптичного волокна з гратками Брегга можна отримати систему
рівнянь, яка пов'язує між собою падаючу хвилю з амплітудою ![]() i відбиту хвилю з амплітудою
i відбиту хвилю з амплітудою ![]() (рис. 2.6), i які мають
(рис. 2.6), i які мають
наступний вигляд:
 (2.24)
(2.24)
де  - величина, що характеризує відхилення
від умов Брегга;
- величина, що характеризує відхилення
від умов Брегга; ![]() - період зміни показника заломлення
в оптичному волокні
- період зміни показника заломлення
в оптичному волокні
![]() (2.25)
(2.25)
![]() - коефіцієнт зв'язку між хвилями
- коефіцієнт зв'язку між хвилями ![]() , для волокна без втрат - дійсна
величина i для нашого випадку визначається співвідношенням:
, для волокна без втрат - дійсна
величина i для нашого випадку визначається співвідношенням:
![]() , (2.26)
, (2.26)
де![]() – хвильове число;
– хвильове число;![]() коефіцієнт модуляції показника заломлення
оптичного волокна за наявності граток
коефіцієнт модуляції показника заломлення
оптичного волокна за наявності граток ![]() , причому
, причому ![]() .
.
Система рівнянь (2.24) є лінійною iз змінними коефіцієнтами, яку шляхом заміни змінних:
![]()
з наступним
опусканиям штриха біля![]() , приведемо до лінійної системи з
постійними коефіцієнтами, яка остаточно матиме наступний вигляд:
, приведемо до лінійної системи з
постійними коефіцієнтами, яка остаточно матиме наступний вигляд:
 (2.27)
(2.27)
Цю систему рівнянь необхідно доповнити такими початковими умовами:
 (2.28)
(2.28)

Рис. 2.6.
Система чотирьох граток на серцевині оптичного волокна з відповідними
геометричними розмірами. ![]() - падаюча хвиля;
- падаюча хвиля; ![]() -відбита хвиля;
-відбита хвиля; ![]() - період гратки;
- період гратки; ![]() - довжини граток;
- довжини граток; ![]() - відстані між сусідніми гратками.
- відстані між сусідніми гратками.
Для знаходження
спектральної залежності коефіцієнтів пропускання ![]() i відбивання
i відбивання ![]() системи граток необхідно мати
розв’язок системи (2.25) за початкових умов (2.26) на інтервалі [0,
системи граток необхідно мати
розв’язок системи (2.25) за початкових умов (2.26) на інтервалі [0,![]() ]. Для
]. Для ![]() i
i ![]() є справедливими такі співвідношення:
є справедливими такі співвідношення:
![]() . (2.29)
. (2.29)
Згідно теорії лінійних
систем диференціальних рівнянь з постійними коефіцієнтами, амплітуди хвиль ![]() i
i ![]() на п - ній гратці зліва в матричній
формі можна записати так:
на п - ній гратці зліва в матричній
формі можна записати так:
 , (2.30)
, (2.30)
де матриці ![]() відповідно рівні:
відповідно рівні:
 , (2.31)
, (2.31)
 , (2.32)
, (2.32)
причому  .
.
Маючи співвідношення (2.28), (2.30), (2.31), (2.32), ми можемо виконати розрахунок спектральної залежності пропускання (відбивання) системи граток Брегга в оптичному волокні.
Розділ 3. Розрахунок одномодового волоконногоYAG: Nd 3+ лазера
Розрахунок лазера може проводитись по - різному в залежності від того, які параметри є заданими у технічному завданні на лазер. Як правило, в технічному завданні на лазер задаються такі основні параметри: робоча довжина хвилі, вихідна потужність, діаметр пучка та розбіжність на виході. При необхідності може вказуватись необхідна довжина когерентності, габарити резонатора та інше.
3.1 Розрахунок просторових параметрів випромінювання
До просторових параметрів випромінювання лазера належать розбіжність випромінювання i діаметр пучка на виході лазера i модовий склад випромінювання. Ці параметри залежать від будови волокна, а саме, від діаметру серцевини, i різниці показників заломлення оболонки i серцевини. В даній роботі були досліджені і розраховані просторові параметри випромінювання волоконного лазера при використанні в якості активного елемента одномодового оптичного волокна, серцевина якого легована неодимом, з гаусівським i ступінчастим профілем показника заломлення.
Проведені дослідження розбіжності випромінювання в залежності від відносної різниці показників заломлення серцевини i оболонки оптичного волокна. Розбіжність у волокні з ступінчастим профілем визначається як
![]() , (3.1)
, (3.1)
де ![]() i
i ![]() - показники заломлення серцевини і оболонки
відповідно. Для гаусівського волокна вираз для розбіжності випромінювання
- показники заломлення серцевини і оболонки
відповідно. Для гаусівського волокна вираз для розбіжності випромінювання
 . (3.2)
. (3.2)
На рис. 3.3 представлена залежність розбіжності випромінювання від відносної різниці показників заломлення, з якої видно, що розбіжність збільшується із збільшенням показника заломлення серцевини волокна i для однакових значень розбіжність у волокні з ступінчастим профілем більша. При цьому показник заломлення оболонки складав 1,45, а показник заломлення серцевини змінювався в межах, що відповідають значенням безрозмірного параметра V для забезпечення одномодового режиму.
Проведені теоретичні дослідження радіуса пучка випромінювання в залежності від радіуса серцевини волокна.
Для гаусівського профілю радіус пучка випромінювання визначається наступним чином:
 , де
, де ![]() (3.3)
(3.3)
де ![]() - радіус серцевини. Для
ступінчастого профілю вираз для радіуса пучка має вигляд:
- радіус серцевини. Для
ступінчастого профілю вираз для радіуса пучка має вигляд:
 (3.4)
(3.4)
На рис. 3.1 i 3.2
представлені залежності радіуса пучка випромінювання від радіуса серцевини
волокна для гаусівського i ступінчастого профілів відповідно при piзниx
значеннях![]() , з яких видно, що при сталому
значенні
, з яких видно, що при сталому
значенні ![]() радіус пучка буде більший у волокні
з меншим
радіус пучка буде більший у волокні
з меншим ![]() .
.
Вибір діаметра серцевини волокна проводимо довільно. Для одномодового режиму діаметр серцевини волокна повинен бути меншим ніж 10 мкм.
Визначаємо ![]() - різницю показників заломлення
- різницю показників заломлення
![]() . (3.5)
. (3.5)
З графіка на рис. 3.1
вибираємо радіус серцевини, що відповідає ![]() для гаусівського профілю волокна:
для гаусівського профілю волокна:![]()
При використанні оптичного волокна з гаусівським профілем показника заломлення для забезпечення заданого радіуса серцевини визначаємо радіус волокна з (3.3):


Знаючи показник заломлення кварцу, легованого неодимом (1,46) визначимо розбіжність неодимового волоконного лазера для гаусоподібного волокна з (3.2) :


Рис. 3.1. Графік залежності радіуса пучка
Рис. 3.2. Графік залежності радіуса пучка випромінювання на виході лазера від радіуса випромінювання на виході лазера від радіуса серцевини волокна для гаусівського профілю серцевини волокна для ступінчастого профілю показника заломлення показника заломлення

Рис. 3.3. Графік залежності розбіжності випромінювання на виході волоконного лазера від відносної різниці показників заломлення ступінчастого(а) і гаусівського(б) профілів показника заломлення серцевини
3.2 Розрахунок енергетичних параметрів випромінювання
Розрахунок волоконного лазера можна проводити по-різному, в залежності від того, які параметри є заданими у технічному завданні на даний лазер. В нашому випадку необхідно спроектувати неодимовий волоконний лазер з певною вихідною потужністю.
Для початку нам
необхідно обчислити підсилення активного середовища ![]() , яке залежить від січення переходу
, яке залежить від січення переходу ![]() (для неодиму
(для неодиму ![]() i стаціонарної різниці населеностей
рівнів.
i стаціонарної різниці населеностей
рівнів.
Інверсія
населеностей визначається самим активним середовищем (матеріалом), i залежить від
часу життя верхнього i нижнього лазерного рівнів, а також від ймовірностей
переходів з цих рівнів. Для кварцу, легованого неодимом вона складає 0,55![]() см-3. Загальна концентрація
неодиму в кварці - Nt=2,8
см-3. Загальна концентрація
неодиму в кварці - Nt=2,8![]() см-3 (молярна концентрація
1,5%) - є оптимальною, оскільки при більших концентраціях неодиму тривалість люмінесценції
зменшується, що зумовлено концентраційним гасінням. Показник підсилення для
даного матеріалу:
см-3 (молярна концентрація
1,5%) - є оптимальною, оскільки при більших концентраціях неодиму тривалість люмінесценції
зменшується, що зумовлено концентраційним гасінням. Показник підсилення для
даного матеріалу:
![]() (3.6)
(3.6)
![]() см-1
см-1
Основними джерелами втрат в резонаторі волоконного лазера є релеєвське розсіяння, поглинання інфрачервоного випромінювання деформацій при скручуванні волокна.
В кварцових волокнах коефіцієнт затухання, пов'язаний з розсіянням, визначається формулою:
![]() [дБ/км] (3.7)
[дБ/км] (3.7)
де KR-
коефіцієнт розсіяння, рівний для кварцу 0,8 мкм4 ![]() дБ/км,
дБ/км,
![]() см-1
см-1![]()
Оскільки інтенсивність розсіяння обернено-пропорційна довжині хвилі в четвертому степені, то вона швидко зменшується з ростом довжини хвилі.
Втрати на поглинання інфрачервоного випромінювання обчислюються наступним чином:
![]() (3.8)
(3.8)
де для кварцу ![]() м,
м, ![]() - постійні коефіцієнти,
- постійні коефіцієнти,
![]() см-1
см-1![]()
При згині волокна відбувається зміна кута падіння світлової хвилі в границю розділу серцевина/оболонка i, як наслідок цього, для частин променів кут падіння стає меншим кута повного внутрішнього відбивання.
Вираз коефіцієнта
затухання ![]() за рахунок втрат на випромінювання
при макрозгинах має наступний вигляд:
за рахунок втрат на випромінювання
при макрозгинах має наступний вигляд:
 (3.9)
(3.9)
де ![]() ; R3 - радіус кривизни
згину,
; R3 - радіус кривизни
згину, ![]() - радіус серцевини волокна;
- радіус серцевини волокна; ![]() - показники заломлення серцевини i
оболонки волокна. Радіус серцевини волокна рівний
- показники заломлення серцевини i
оболонки волокна. Радіус серцевини волокна рівний ![]() , радіус кривизни згину R3
приймаємо 8 см, тоді
, радіус кривизни згину R3
приймаємо 8 см, тоді ![]() , визначаємо втрати
, визначаємо втрати  0,023 Дб = 0,0023 см-1
0,023 Дб = 0,0023 см-1![]()
Знаючи підсилення i втрати в резонаторі ми можемо записати формулу для вихідної потужності: [9]
![]() , (3.10)
, (3.10)
де ![]() - довжина активного середовища;
- довжина активного середовища; ![]() - пропускання вихідного дзеркала;
- пропускання вихідного дзеркала; ![]() - площа поперечного січення пучка,
визначаємо за формулою:
- площа поперечного січення пучка,
визначаємо за формулою:
![]() ,
,![]() см2 (3.11)
см2 (3.11)
![]() - коефіцієнт відбивання глухого
дзеркала (задаємо, наприклад,99,98%); R2 - коефіцієнт відбивання
вихідного дзеркала (оскільки підсилення у волоконних лазерах велике i вони
можуть генерувати без вихідного дзеркала для початку можна задати, наприклад,
2%, а далі він буде перерахованим, як оптимальний);
- коефіцієнт відбивання глухого
дзеркала (задаємо, наприклад,99,98%); R2 - коефіцієнт відбивання
вихідного дзеркала (оскільки підсилення у волоконних лазерах велике i вони
можуть генерувати без вихідного дзеркала для початку можна задати, наприклад,
2%, а далі він буде перерахованим, як оптимальний); ![]() - параметр насичення (характеристика активного
середовища), який обернено-пропорційний до інтенсивності насичення:
- параметр насичення (характеристика активного
середовища), який обернено-пропорційний до інтенсивності насичення:

![]() мс – час життя верхнього лазерного
рівня; c=3
мс – час життя верхнього лазерного
рівня; c=3![]() см/с - швидкість світла; h=
см/с - швидкість світла; h=![]() - стала Планка. Формула (3.10) нам
необхідна для приблизного визначення довжини волокна, якщо в умові задачі є певні
обмеження щодо довжини волокна ми можемо приблизно визначити
- стала Планка. Формула (3.10) нам
необхідна для приблизного визначення довжини волокна, якщо в умові задачі є певні
обмеження щодо довжини волокна ми можемо приблизно визначити ![]() .
.
Розглянувши вci види втрат в резонаторі волоконного лазера,можна визначити, що домінуючими є втрати на деформації при скручування волокна. На рис. 3.4 представлена залежність вихідної потужності волоконного лазера від довжини активного елементу.
|
|
Рис. 3.4. Графік залежності вихідної потужності волоконного лазера від довжини оптичного волокна при різних радіусах скручування
Визначаємо довжину активного елементу волокна, яка б забезпечила вихідну потужність лазера.
![]() (3.12)
(3.12)
До отриманої довжини волокна додаємо 10 - 15 %.
Обчислимо
оптимальний коефіцієнт відбивання вихідного дзеркала, при якому на виході
лазера отримаємо максимальну потужність. Для цього необхідно визначити сумарні
шкідливі втрати ![]() :
:
![]() [см-1] (3.13)
[см-1] (3.13)
Оптимальний коефіцієнт відбивання вихідного дзеркала (вихідної гратки):
![]() (3.14)
(3.14)
З порогової умови генерації визначаємо пороговий показник підсилення:
![]() (3.16)
(3.16)
Добротність резонатора, яка характеризує резонансну систему i визначається втратами в резонаторі: [2]
![]() (3.17)
(3.17)
Ефективний переріз i об'єм лазерного середовища визначаються відповідно:
![]()
![]() (3.18)
(3.18)
Оскільки нам вже відомий пороговий показник підсилення (3.16), ми можемо визначити порогову інверсію населеностей, яка необхідна для генерації лазера:
![]() (3.19)
(3.19)
Порогова швидкість накачування лазера визначається критичною іверсією i загальною концентрацією неодиму в оптичному волокні:
![]() (3.20)
(3.20)
Накачування неодимового волоконного лазера здійснюється на довжині 0,85 мкм. Порогова потужність накачування визначається наступним чином:
![]() (3.21)
(3.21)
де ![]() - частота випромінювання лазера i
частота на якій здійснюється накачування;
- частота випромінювання лазера i
частота на якій здійснюється накачування; ![]() - ефективність накачування.
- ефективність накачування.
ККД накачування включає
в себе декілька складових: ![]() - випромінювальна ефективність діодного
лазера накачування (ККД лазера накачування), в нашому випадку
- випромінювальна ефективність діодного
лазера накачування (ККД лазера накачування), в нашому випадку![]() ;
; ![]() - ефективність вводу випромінювання,
яка залежить безпосередньо від конструкції волоконного лазера
- ефективність вводу випромінювання,
яка залежить безпосередньо від конструкції волоконного лазера ![]() ;
; ![]() — ефективність поглинання, тобто
частина світла, яке потрапило в оптичне волокно i дійсно поглинулася ним, для
неодимового лазера
— ефективність поглинання, тобто
частина світла, яке потрапило в оптичне волокно i дійсно поглинулася ним, для
неодимового лазера![]() ;
; ![]() - квантова ефективність лазера,
- квантова ефективність лазера,![]() . Загальний ККД накачування визначається
так:
. Загальний ККД накачування визначається
так:
![]() (3.22)
(3.22)
Потужність випромінювання
накачування змінюється вздовж оптичного волокна за експоненційним законом
Бугера-Ламберта. Показник поглинання кварцу, легованого нeoдимoм,![]() складає 0,048 см-1. Poзpaxyнoк
потужності накачування проводився з розрахунку, що на протилежному кінці
волокна потужність накачування повинна перевищувати порогову. Потужність
накачування неодимового лазера:
складає 0,048 см-1. Poзpaxyнoк
потужності накачування проводився з розрахунку, що на протилежному кінці
волокна потужність накачування повинна перевищувати порогову. Потужність
накачування неодимового лазера:
![]() (3.23)
(3.23)
Оскільки відомі потужність накачування i її порогова величина, можна визначити число перевищення порогу.
![]() (3.24)
(3.24)
Таким чином визначаємо інверсію населеностей i швидкість накачування лазера.
![]() (3.25)
(3.25)
![]() (3.26)
(3.26)
Вихідну потужність лазерного випромінювання визначаємо за формулою:
![]() (3.27)
(3.27)
де: ![]() (3.28)
(3.28)
![]()
ККД лазера визначається як:
![]()
де ![]() - ККД зв'язку на виході лазера;
- ККД зв'язку на виході лазера; ![]() – відношення площі перерізу активного
середовища до площі поперечного січення пучка,
– відношення площі перерізу активного
середовища до площі поперечного січення пучка, ![]()
3.3 Розрахунок спектральних характеристик неодимового волоконного лазера
Спектральні характеристики неодимового волоконного лазера визначаються високо селективними бреггівськими гратками показника заломлення, записаними голографічним методом на серцевині оптичного волокна. Бреггівські гратки створюють резонатор i забезпечують додатній зворотній зв'язок в лазері. Розрахована система бреггівських граток для даного лазера зображена на рис. 3.5.

Рис. 3.5 Схема забезпечення додатного зворотного зв'язку в лазері
Необхідно розрахувати спектральні характеристики лазера. Маючи співвідношення (2.6), (2.8), (2.9), (2.10), ми можемо виконати розрахунок спектральної залежності пропускання (відбивання) системи граток Брегга в оптичному волокні.
Вхідним дзеркалом служить одинарна бреггівська гратка. Вона є прозорою для випромінювання накачування i має максимальний коефіцієнт відбивання на довжині хвилі генерації лазера. Одно частотний режим роботи лазера досягається за рахунок системи двох вихідних граток, які розміщуються по принципу еталона Фабрі - Перо.
3.4 Конструкція волоконного лазера
Конструкція волоконного лазера повинна забезпечити високу ефективність введення випромінювання накачування в серцевину оптичного волокна (мінімальні втрати), простоту i зручність користування. В якості джерела накачування може використовуватись лазерний діод з вертикальним резонатором (VCSEL), випромінювання якого поширюється з поверхні, а не з торця, як у звичайних. В цьому лазері розбіжність випромінювання менша, у порівнянні зі звичайними лазерними діодами, i є однаковою у двох перпендикулярних напрямках, що полегшує введення випромінювання у волокно.
На рис. 3.6 представлена альтернативна конструкція волоконного лазера, в якій для фокусування світла в оптичне волокно використовується лінза, що розміщується із зовнішньої сторони оптичного вікна корпуса. Сам лазерний діод встановлений на міцному радіаторі

Рис. 3.6. Ескіз конструкції волоконного лазера з введенням випромінювання накачування в оптичне волокно з допомогою лінзи
Якщо необхідно використовувати більш потужні лазерні діоди тоді необхідно побудувати систему з 2 - 8 лазерних діодів розміщених в просторі певним чином для вводу випромінювання в оптичне волокно. Розбіжність оптичного волокна визначаємо з (3.5).
Оскільки нам відома апертура оптичного волокна можемо визначити кутове збільшення лінзи (фокусуюча система для введення випромінювання у волокно):
 (3.29)
(3.29)
В залежності від потужності накачки вибираємо лазерний діод з потрібними характеристиками:
| Лаз.діод VCT- | F85A41-OH | F85A1G-IS | F85A42-S | F85A3F-O | F85A45-IS | F85A3F-OH |
|
|
100 | 150 | 120 | 200 | 175 | 250 |
|
|
10 | 6 | 6 | 12 | 8 | 12 |

Рис. 3.7. Ескіз конструкції фокусуючої системи для введення випромінювання у волокно
Відповідно лінійне збільшення лінзи:
![]() (3.39)
(3.39)
Вибираємо відстань між діодом i лінзою а (2 - 10 см). Розраховуємо необхідну відстань між лінзою i оптичним волокном а0, а також фокусну віддаль лінзи f:
![]() (3.40)
(3.40)
![]() (3.41)
(3.41)
Товщина лінзи:
![]() (3.42)
(3.42)
де ![]() - радіус кривизни поверхонь лінзи (вибираємо
довільний, але d повинно бути в межах 0,5-2 см, оскільки розрахунок проводимо
для тонкої лінзи).
- радіус кривизни поверхонь лінзи (вибираємо
довільний, але d повинно бути в межах 0,5-2 см, оскільки розрахунок проводимо
для тонкої лінзи).
3.5 Розрахунок просторових параметрів випромінювання
При використанні оптичного волокна з гаусівським профілем показника заломлення для забезпечення діаметру визначаємо радіус серцевини волокна:
Знаючи радіус
серцевини розраховуємо параметр волокна V i відносну різницю показників
заломлення ![]() з (3.2) :
з (3.2) :
V<2,59, отже розрахунок для забезпечення одномодової генерації вірний.
Розрахунок енергетичних параметрів випромінювання
![]()
Список літератури
1. Буфетов И.А. и др. Волоконные Yb-, Er-Yb- и Nd-лазеры на световодах с многоэлементной первой оболочкой // Квантовая электроника, 2005, т. 35, № 4, с. 328-334.
2. Dianov E.М. et al. Raman fiber lasers emitting at a wavelength above 2μm // Quant. Electr., 2004, vol. 34, p. 695-697.
3. Dianov E.M., Grekov M.V., Bufetov I.A. et al., CW high power 1.24 μm and 1.48 μm Raman lasers based on low loss phosphosilicate fibre // El. Lett. 1997, vol. 33, N 18, p. 1542-1544.
4. Власов Александр Анатольевич «Волоконные брэгговские решётки для применений в перестраиваемых волоконных лазерах» Автореферат диссертации на соискание учёной степени кандидата физико-математических наук Новосибирск – 2009
5. Волоконные технологические лазеры и оценка эффективности их применения
6. Методичка
7. «Флексо Плюс» №2 (26), апрель 2002 г.
8. Вейко В.П. Опорный конспект лекций по курсу «Физико–технические основы лазерных технологий». Раздел: Технологические лазеры и лазерное излучение. – СПб: СПбГУ ИТМО, 2005. – 50 с.
9. Байбородин Ю. В. Основы лазерной техники, К.,1981.
10.О. Звелто. Принципы лазеров. М.,1999.
11. Десурвир «Световая связь: пятое поколение», В мире науки, №3, 1992 .
12. «Волоконно-оптическая техника», Технико-коммерческий сборник. М., АО ВОТ, N1, 1993.
13. А.В.Снайдер, Д. Лав, «Теория оптических волноводов»


