Курсовая работа: Методика формирования понятия массы в курсе физики средней школы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
"БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени А.С. Пушкина"
КУРСОВАЯ РАБОТА
по методике преподавания физики
Методика формирования понятия массы в курсе физики средней школы
Брест, 2011
Содержание
Введение
§1. Понятие массы в физической науке
§2. Введение понятия массы в курсе физики средней школы
§3. Вопросы и примеры задач на закрепление понятия массы
Заключение
Список литературы
Введение
Введение понятия масса очень важно. Этот вопрос волновал ученых с давних времен. Массу рассматривали как количество материи. С середины 19 века начинает обсуждаться вопрос об определении величины массы. Подвергается критике определение Ньютона, который определял ее как величину, пропорциональную объему тела и его плотности. Появляется ряд других определений.
Существовало много и методов введения понятия массы. Вопрос о том, как лучше определять или вводить понятие массы, обсуждали и в 19в., и в 20в., его обсуждают и в настоящее время.
Поэтому актуальность данной проблемы подтолкнула меня к изучению введения данного понятия.
Основная цель курсовой работы состояла в изучении и анализе методики формирования понятия массы в курсе физики средней школы. Объектом использования курсовой работы являлся процесс обучения физики в средней школе, а предметом исследования: методика формирования основных физических понятий. Для достижения основной цели работы потребовалось решение следующих задач:
1. Анализ научно-методической литературы по теме исследования.
2. Рассмотрение различных определений понятия массы.
3. Оценка подходов к введению понятия массы в 6, 9, 11 классах.
В ходе выполнения курсовой работы использовались следующие методы исследования:
· Теоретический анализ методической литературы по данной теме исследования.
· Анализ учебников физики и программы курса физики 6, 9 и 11 класса.
§1. Понятие массы в физической науке
урок физика масса энергия
Масса (от греческого μάζα) — одна из важнейших физических величин. Первоначально (XVII—XIX века) она характеризовала "количество вещества" в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями "энергия" и "импульс" (по современным представлениям — масса эквивалентна энергии покоя).


В Парижской палате мер и весов хранятся эталоны фундаментальных единиц измерения - массы (килограмм) и длины (метр). Эталон массы представляет собой гирьку из сплава платины и иридия и помещен в эту палату еще в 1889 году. Копии эталона хранятся также и в России, во ВНИИ метрологии им. Менделеева, который, собственно, и создал в 1893 году Главную палату мер и весов, предшественницу этого института.
Масса в ньютоновой механике.
Как хорошо известно, масса в ньютоновой механике обладает рядом важных свойств, и проявляется, так сказать, в нескольких обличиях:
1. Масса является мерой количества вещества, количества материи.
2. Масса составного тела равна сумме масс составляющих его тел.
3. Масса изолированной системы тел сохраняется, не меняется со временем.
4. Масса тела не меняется при переходе от одной системы отсчета к другой, в частности, она одинакова в различных инерциальных системах координат.
5. Масса тела является мерой его инертности (или инерции, или инерционности, как пишут некоторые авторы).
6. Массы тел являются источником их гравитационного притяжения друг к другу.
Обсудим более подробно два последних свойства массы.
Как мера инерции тела, масса тела выступает в формуле, связывающей импульс тела р и его скорость v:
p = mv. (1.1)
Масса входит также и в формулу для кинетической энергии тела Ек:
Eк = p2/2m = mv2/2. (1.2)
В силу однородности пространства времени импульс, и энергия свободного тела сохраняются в инерциальной системе координат. Импульс данного тела меняется со временем только под воздействием других тел:
dp/dt = F, (1.3)
где F - сила, действующая на тело. Если учесть, что по определению ускорения а
a = dv/dt, (1.4)
и учесть формулы (1.1) и (1.3), то получим
F = mа. (1.5)
В этом соотношении масса снова выступает как мера инерции. Таким образом, в ньютоновой механике масса как мера инерции определяется двумя соотношениями: (1.1) и (1.5). Одни авторы предпочитают определять меру инерции соотношениями (1.1), другие - соотношением (1.5). Для предмета нашей статьи важно лишь, что оба эти определения совместимы в ньютоновой механике.
Обратимся теперь к гравитации. Потенциальная энергия притяжения между двумя телами с массами М и m (например, Земли и камня), равна
Ug = - GMm/r, (1.6)
где G - 6,7×10-11 Н×м2кг-2 (напомним, что 1 Н = 1 кг×м×с2). Сила, с которой Земля притягивает камень, равна
Fg = - GMmr/r3, (1.7)
где радиус-вектор r, соединяющий центры масс тел, направлен от Земли к камню. (С такой же, но противоположно направленной силой камень притягивает Землю.)
Из формул (1.7) и (1.5) следует, что ускорение тела, свободно падающего в гравитационном поле, не зависит от его массы. Ускорение в поле Земли обычно обозначают g:
G = Fg/m = - GMr/r3. (1.8)
Как нетрудно оценить, подставив в формулу (1.8) значения массы и радиуса Земли (Мз " 6×1024 кг, Rз " 6,4×106 м), g " 9,8 м/с2.
Впервые универсальность величины g была установлена Галилеем, который пришел к выводу, что ускорение падающего шара не зависит ни от массы шара, ни от материала, из которого он сделан. С очень высокой степенью точности эта независимость была проверена в начале XX в. Этвешем и в ряде недавних экспериментов. Независимость гравитационного ускорения от массы ускоряемого тела в школьном курсе физики обычно характеризуют как равенство инертной и гравитационной массы, имея при этом в виду, что одна и та же величина m входит как в формулу (1.5), так и в формулы (1.6) и (1.7).
Мы не будем здесь обсуждать другие свойства массы, перечисленные в начале этого раздела, поскольку они кажутся самоочевидными с точки зрения здравого смысла. В частности, ни у кого не вызывает сомнения, что масса вазы равна сумме масс её осколков:
m = Smi (1.9)
Никто не сомневается также в том, что масса двух автомобилей равна сумме их масс независимо от того, стоят они или мчатся с предельной скоростью навстречу друг другу.
Соотношении Эйнштейна Е = mс2. Естественно задать вопрос, каким образом осуществляется в литературе и умах читателей мирное сосуществование взаимоисключающих формул:
Е0 = mс2 (1.10)
Е = mс2 (1.11)
Прежде чем искать ответ на этот вопрос, еще раз напомню, что согласно первой формуле массе покоящегося тела отвечает энергия покоя Е0, а согласно второй любое тело с энергией Е имеет массу Е/с2. Согласно первой масса тела не меняется при его движении. Согласно второй масса тела растет с ростом скорости тела. Согласно первой фотон без массы, согласно второй у фотона есть масса, равная Е/с2.
Чтобы ответить на поставленный вопрос о сосуществовании формул, нам придется обратиться к истории создания, интерпретации и признания специальной теории относительности.
Обычно рождение теории относительности связывают со статьей Эйнштейна 1905 г., в которой была четко сформулирована относительность одновременности. Но, разумеется, работа над созданием и интерпретацией теории началась задолго до 1905 г. и продолжалась долгое время после этого.
Если говорить об интерпретации, то процесс, по-видимому, происходит до сих пор. Иначе не было бы необходимости писать данную статью. Что касается признания, то можно сказать, что даже в конце 1922 г., когда Эйнштейну была присуждена Нобелевская премия, теория относительности не была общепризнанной.
Секретарь Шведской академии наук писал Эйнштейну, что Академия присудила ему Нобелевскую премию за открытие закона фотоэффекта, "но не учитывая ценность, которая будет признана за Вашими теориями относительности и гравитации, после того, как они в будущем будут подтверждены".
Формула Е = mс2 появилась в 1900 г., до создания теории относительности. Написал ее А. Пуанкаре, который исходил из того, что плоская световая волна, несущая энергию Е, несет импульс р, абсолютная величина которого, в соответствии с теоремой Пойнтинга, равна Е/с. Используя нерелятивистскую формулу Ньютона для импульса р = mv от и учитывая, что для света v = с, Пуанкаре пришел к выводу, что фотон должен обладать инертной массой m=Е/с2.
Еще за год до этого, в 1899 г., Лоренц впервые ввел понятие продольной и поперечной масс ионов, первая из которых растет с ростом скорости как g3, а вторая как g. К этому выводу он пришел, используя ньютонову связь между силой и ускорением F = mа.
Так на границе столетий из-за, как мы теперь понимаем, незаконного использования нерелятивистских формул для описания релятивистских объектов, возникло семейство "масс", растущих с энергией тела:
"релятивистская масса" m = Е\с2 (1.12)
"поперечная масса" mt = mg (1.13)
"продольная масса" ml = mg3 (1.14)
Заметим, что при m ¹ 0 релятивистская масса равна поперечной, но, в отличие от поперечной, она имеется и у безмассовых тел, у которых m = 0. Здесь букву m мы употребляем в обычном смысле, так как употребляли ее в первой части этой статьи. Но все физики в первые пять лет этого века, т.е. до создания теории относительности, а (многие и после создания теории относительности называли массой и обозначали буквой m релятивистскую массу, как это сделал Пуанкаре в работе 1900 г. И тогда с неизбежностью должен был возникнуть и возник еще один, четвертый термин: "масса покоя", которую стали обозначать m0. Термином "масса покоя" стали называть обычную массу, которую при последовательном изложении теории относительности обозначают m [6].
В современной физике понятие "количество вещества" имеет другой смысл, а под массой понимают два различных свойства физического объекта:
- Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.
- Инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
Гравитационная и инертная
масса равны друг другу (практически с гигантской точностью порядка ![]() ), а в большинстве
физических теорий — точно), поэтому в большинстве случаев просто говорят о
массе, не уточняя, какую из них имеют в виду.
), а в большинстве
физических теорий — точно), поэтому в большинстве случаев просто говорят о
массе, не уточняя, какую из них имеют в виду.
Масса тела не зависит от скорости тела и от того, какие внешние силы на это тело действуют. В классической механике масса системы тел равна сумме масс составляющих её тел, но в теории относительности показывается, что масса системы в общем случае не равна арифметической сумме масс компонентов, включая в себя энергию связи, а также энергию движения частиц друг относительно друга.
Понятие массы было введено в физику Ньютоном, до этого естествоиспытатели оперировали с понятием веса. Вес — сила воздействия тела на опору (или другой вид крепления в случае подвешенных тел), возникающая в поле сил тяжести. В труде "Математические начала натуральной философии" Ньютон сначала определил "количество материи" в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон вводит массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе.
Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения. Толкование её как меры "количества материи" — не более чем наглядная иллюстрация, и оно подверглось критике ещё в XIX веке как нефизическое и бессодержательное.
Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается [4].
§2. Введение понятия массы в курсе физики средней школы
На изучение темы "Масса тела. Единицы массы " отводится один урок и одна лабораторная работа "Изучение рычажных весов. Измерение массы". Повторение и систематизация учебного материала по теме "Основные понятия молекулярной теории строения вещества. Масса тела. Плотность вещества"; Контрольная работа 2 по теме "Основные понятия молекулярной теории строения вещества. Масса тела. Плотность вещества" [7].
В 6 классе вводится понятие массы как мера инертности. Перед этим проводят демонстрационный опыт. Берут две тележки, одну порожнюю другую груженную и приводят их в движение.
Затем задают вопрос: "Какую тележку (рис 2.1) легче привести в движение: порожнюю или груженую?" А затормозить? Почему? У них разная масса. Чем больше масса тела, тем труднее его вывести из состояния покоя и тем труднее его потом остановить. Иначе говоря, чем больше масса, тем в большей степени тело стремится сохранить свое состояние покоя или движения.

Рис 2.1
Свойство тела сохранять постоянным состояние покоя или состояние движения называют инерцией. Значит, масса — мера инерции (инертности). Все тела обладают инертностью, но разной.
В курсе физики масса обозначается буквой m.
Вы можете сами привести множество примеров, доказывающих, что массивное тело труднее разогнать, но и труднее остановить.
От чего зависит масса тела?
Сравните целое яблоко и половину яблока. Где вещества больше? Конечно же, в целом яблоке. Но и масса его в 2 раза больше, чем половины. Значит, чем больше данного вещества в теле, тем больше его масса.
Основной единицей массы в СИ является 1 килограмм (1 кг).
Есть еще кратные единицы массы — тонна (т) и центнер (ц):
1 т = 1000 кг = 1 • 103 кг;
1 ц = 100 кг = 1 • 102 кг;
и дольные единицы массы — грамм (г) и миллиграмм (мг):
1 г = 0,001 кг = 1 • 10-3 кг;
1 мг = 0,001 г = 0,000001 кг = 1 • 10-6 кг..
А если сравнить массы тел из разных веществ, количество молекул (атомов) в которых одинаково? Будут ли они равны?
Массой (т. е. инерцией) обладает каждая молекула (атом). Массу всего тела можно рассматривать как сумму масс всех его молекул. Но поскольку массы молекул (атомов) различных веществ неодинаковы, то при равном их числе в двух телах (например, в алюминиевой и чугунной деталях) массы этих тел будут сильно различаться. Масса чугунной детали будет больше массы алюминиевой.
Измеряют массу с помощью весов (рис 2.2).
После рассмотрения нового материала ученикам можно дать задание: рассмотреть свои весы, открыть коробочку разновесов, найти гирьки и разобрать пример взвешивания 2г 600мг. Все это делается для того, чтобы познакомить учащихся с правилами взвешивания.

Рис 2.2
В результате изучения материала темы учащиеся должны усвоить определение массы как меры инертности, ее символическое обозначение и основную единицу измерения. Уметь раскрыть своими словами сущность понятия "масса" и переводить основную единицу массы в дольные и кратные [1].
На изучение параграфа "Масса" в 9 классе отводится один урок. Обобщение и систематизация знаний по теме "Основы динамики" и контрольная работа по теме "Основы динамики".
Введение понятия массы трактуется как мера гравитационных свойств.
Все мы привыкли характеризовать определённые свойства тел словами тяжёлый и лёгкий, большой и маленький, гигантский и крохотный. Имеют ли они какое-либо отношение к слову масса? (Имеют). Наша с вами задача – выяснить, что же такое масса тела, и какое место это понятие занимает в физике. Не зря мы познакомились с понятием инерции раньше, чем с понятием массы.
Оказывается, что эти два понятия тесным образом связаны друг с другом. Давайте ещё раз вспомним, что же такое инерция.
Сравнить массы двух тел можно различными способами.
1.Сравнение масс тел путем взвешивания на весах
Имеются два типа весов: рычажные (рис. 2.3, а) и пружинные (рис. 2.3, б). Для всех весов определение массы производится путем сравнения двух сил: силы F — притяжения к Земле взвешиваемого тела и силы Fэт — притяжения к Земле эталона (гирь).


Рис. 2.3, а. Рис. 2.3, б.
На рычажных весах (см. рис. 12.3, а) при равенстве плеч силы притяжения к Земле взвешиваемого тела и набора гирь будут одинаковы и масса тела будет равна массе гирь (m= mэт)
При взвешивании на пружинных весах (рис. 2.3, б) их показания пропорциональны силе F, с которой Земля притягивает взвешиваемое тело. На Луне эти показания были бы меньше, чем на Земле (примерно в 6 раз). Чтобы по силе притяжения найти массу тела, следует провести "контрольное взвешивание": взвесить на тех же весах эталон массы. Поскольку модуль силы притяжения эталона — Fэт =gmэт, а тела — F =gm, то:
![]() =
=![]() (2.1)
(2.1)
Тогда и на рычажных, и на пружинных весах значение массы будет одним и тем же и на Земле, и на Луне. Для рычажных весов это очевидно: тело будет уравновешено таким же набором гирь. Дли пружинных весов модуль силы F на Луне будет меньше, чем на Земле, но во столько же раз меньше будет и модуль силы Fэт. В результате поучаемое из соотношения (2.1) значение массы
m=mэт![]() (2.2)
(2.2)
не изменяется.
А можно ли сравнить массы тел, не используй силы
2. Сравнение масс по инертности тел
Любое тело обладает свойством двигаться по инерции, сохраняя свою скорость неизменной, пока на это тело не подействуют силы. При этом одни тела легче разогнать (а разогнав, остановить), а другие — труднее. Для разгона или остановки груженой тележки на нее следует действовать гораздо большей силой (или гораздо дольше), чем на порожнюю. Груженая тележка более инертна.
Как определите, во сколько раз одно тело более инертно, чем другое?
Проведем опыт. Поставим на горизонтальную поверхность две тележки
разной массы (m![]() >m
>m![]() ) способные катиться почти без трения.
Сообщим тележкам одинаковые ускорения. Для этого на тележку 1 придется
подействовать силой, большей, чем на тележку 2 (рис. 2.4). Первая
тележка во столько раз инертнее второй, во сколько раз модуль силы F
) способные катиться почти без трения.
Сообщим тележкам одинаковые ускорения. Для этого на тележку 1 придется
подействовать силой, большей, чем на тележку 2 (рис. 2.4). Первая
тележка во столько раз инертнее второй, во сколько раз модуль силы F![]() больше, чем F
больше, чем F![]() .
.
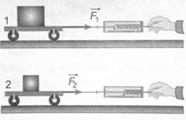
Рис. 2.4
Для массы как меры инертности получится такая же пропорция, как и при взвешивании:
![]() =
=![]() (2.3)
(2.3)
Подобный опыт можно использовать для сравнения масс любых тел в
любых условиях: на Земле, на Луне, на орбитальной станции. При этом F![]() следует понимать как модуль
результирующей всех сил, приложенных к первому телу, F
следует понимать как модуль
результирующей всех сил, приложенных к первому телу, F![]() — ко второму.
— ко второму.
Напомним еще о двух практически важных свойствах массы;
• общая масса m нескольких тел равна сумме их масс:
m=m1+m2+...; (2.4)
• масса однородного вещества, заключенного в объеме V пропорциональна этому объему:
m=ρV (2.5)
где ρ — плотность вещества.
Массу как меру инертности называют инертной массой, а массу, определяемую по силе притяжении тел друг к другу, — гравитационной массой.
Вывод:
- сила, с которой Земля притягивает тело, пропорционально его массе (Fт=gm);
- масса тела — мера его гравитационных свойств.
Для закрепления материала можно задать следующие вопросы:
1. Что такое масса?
2. Что такое инерция?
3. Изменится ли масса тела при его переносе с Земли на другую планету?
Решить некоторые задачи из упражнения после параграфа [2].
В 11 классе вводится понятие массы как мера энергии. На изучение параграфа "Закон взаимосвязи массы и энергии" отводится один урок и одно занятие на решение задач. Решение задач по теме "Основы специальной теории относительности" и обобщение, систематизация знаний по теме "Основы специальной теории относительности". Самостоятельная работа по теме "Основы специальной теории относительности" [7].
В релятивистской механике масса тела связана с энергией, "заключенной в теле". Так, в системе отсчета, в которой тело покоится (такая система отсчета называется собственной), его энергия (энергия покоя) определяется по формуле:
E0=mc![]() (2.6)
(2.6)
Таким образом, любое тело, благодаря факту своего существования, обладает энергией, которая пропорциональна массе покоя m. Эта энергия выделяется при уменьшении массы тела, и наоборот, при поглощении энергии релятивистская масса тела возрастает. Релятивистская энергия имеет колоссальные значения. Например, тело массой 1 г обладает энергией покоя
E0=10-3кг•(3•108)2![]() =9•1013Дж. (2.7)
=9•1013Дж. (2.7)
Эта энергия эквивалентна энергии, выделяющейся при сгорании 2000 т
бензина с удельной теплотой сгорания 4,5•10![]()
![]() .
.
Таким образом, увеличение энергии тела на ∆E связано увеличением его массы на ∆m, причем
∆m=![]() (2.8)
(2.8)
Это соотношение выражает закон взаимосвязи массы и энергии.
В окружающем нас мире изменение массы, связанное с изменением энергии тел, пренебрежимо мало. Так, например, при нагревании 1 л воды от 0 до 100 °С масса воды увеличивается только ∆m = 5•10-9 г.
Трудно переоценить практическое значение этой несложной формулы, поскольку именно она указала на взаимосвязь и взаимопревращение вещества в энергию и наоборот. В конечном итоге человечество узнало о возможности получения энергии из вещества.
Вывод: масса и энергия взаимопревращаемы. Соотношение E=mc![]() показывает, какую энергию E необходимо
израсходовать, чтобы создать массу m, и наоборот, какая энергия заключена в массе m.
показывает, какую энергию E необходимо
израсходовать, чтобы создать массу m, и наоборот, какая энергия заключена в массе m.
Для закрепления темы можно задать вопросы:
1. Каково соотношение между массой и собственной энергией тела?
2. Сформулируйте закон взаимосвязи массы и энергии?
В результате изучения материала темы учащиеся должны усвоить определение массы как меры энергии и закон взаимосвязи массы и энергии[3].
§3. Вопросы и примеры задач на закрепление понятия массы
Вопросы по изучению темы "Масса тела. Единицы массы " в 6 классе.
1. Предложите метод, который вам позволит оценить массу макового зернышка. В вашем распоряжении имеются весы с разновесами и пакетик маковых зерен.
(Ответ: Необходимо отсчитать достаточное количество зерен, а затем с помощью весов найти их массу. Далее, разделить значение массы на общее число зерен и получить искомую оценку).
2. При взвешивании тела на правой чашке уравновешенных весов оказались две гири по 200г, гиря 50г, 10г и две – по 100мг. Чему равна масса тела в граммах? В килограммах? (Ответ: m=200+50+10+2*0.1=260,2г. m=0,2602кг)
Вопрос и задача по изучению темы "Масса" в 9 классе.
1.Одинакова ли масса одного и того же тела на Земле и Луне? (Ответ: Да, одинакова. )
2.
Какова масса воды в аквариуме размером 1×1×1 м? Какова масса воздуха
в этом же объеме (при нормальных условиях)? Что больше: масса 1 м![]() олова или 1м
олова или 1м![]() алюминия?
алюминия?

Задачи по изучению темы "Закон взаимосвязи массы и энергии" в 11 классе.
1.Солнце
ежесекундно излучает в пространство примерно ∆Е=3,75*10![]() Дж энергии. На сколько
вследствие этого каждую секунду уменьшается масса Солнца?
Дж энергии. На сколько
вследствие этого каждую секунду уменьшается масса Солнца?

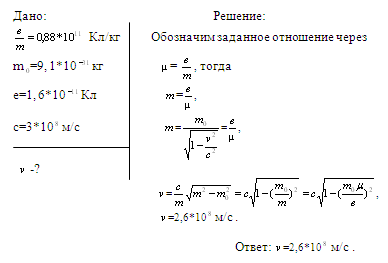
2.Отношение
заряда движущегося электрона к его массе ![]() Кл/кг. Определите скорость
Кл/кг. Определите скорость
![]() электрона, если его масса
покоя m
электрона, если его масса
покоя m![]() =9,1*10
=9,1*10![]() кг
, заряд e=1,6*10
кг
, заряд e=1,6*10![]() Кл, скорость света в
вакууме c=3*10
Кл, скорость света в
вакууме c=3*10![]() м/c
м/c
Заключение
Данная курсовая работа посвящена методика формирования понятия массы в курсе физики средней школы. Этот вопрос в преподавании физики не новый. Актуальность этой темы в том, что подход к изучению понятия массы вводится с разных точек зрения, нет единого трактата.
Цель данной курсовой работы достигнута. Мною были рассмотрены различные учебные пособия, изучено календарно-тематическое планирование по учебному предмету "Физика" на 2010/2011 учебный год.
Рассмотрел различные подходы к изучению видов массы. В разных классах дается свое определение массы:
-В 6 классе вводится понятие массы как мера инертности. Свойство тела сохранять постоянным состояние покоя или состояние движения называют инерцией. Значит, масса — мера инерции (инертности). Здесь учащиеся впервые сталкиваются с этим понятием. Инертная масса, которая характеризует меру инертности тел и фигурирует в старших классах во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
- В 9 классе вводится понятие массы как мера гравитационных свойств. Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.
- В
11 классе вводится понятие массы как мера энергии. Масса
и энергия взаимопревращаемы. Соотношение E=mc![]() показывает, какую энергию E необходимо
израсходовать, чтобы создать массу m, и наоборот, какая энергия заключена в массе m.
показывает, какую энергию E необходимо
израсходовать, чтобы создать массу m, и наоборот, какая энергия заключена в массе m.
Для закрепления этих подходов привел вопросы и задачи. Мной были рассмотренные различные примеры использования понятия массы на уроках физики, так как именно на практике можно наиболее ярко продемонстрировать важность данной физической величины.
Список литературы
1. Исаченкова, Л. А. Физика: учеб. пособие для 6 кл. общеобразоват. учреждений с рус. яз. обучения / Л. А. Исаченкова, И. Э. Слесарь. — Минск: Нар. асвета, 2010.
2. Исаченкова, Л. А. Физика: учебное пособие для 9 класса общеобразоват. учреждений с рус. Яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский / под ред. А. А. Сокольского. — Минск: Нар. асвета, 2010.
3. Жилко, В. В. Физика: учеб. пособие для 11 кл. общеобразоват. шк. с рус. яз. обучения / В. В.Жилко, Л. Г. Маркович. — Минск: Нар. асвета, 2009.
4. http://ru.wikipedia.org/wiki/Масса_покоя
5. М. Джеммер. Понятие массы в классической и современной физике. Издательство "Прогресс" - Москва 1961.
6. Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 1989
7. Примерное календарно-тематическое планирование по учебному предмету "Физика" на 2010/2011 учебный год