Доклад: Зависимость силы
Извечным было стремление определить лучшего из лучших в различных видах спорта. В тяжелой атлетике, где спортсмены разделены весовыми категориями, первая такая попытка относится к 1936 году, когда путем простого деления поднятых килограммов на собственный вес атлета сильнейшим был провозглашен египтянин Кхадр эль Тоуни. В дальнейшем к решению этой задачи подключилась спортивная наука и уже с конца семидесятых годов ИВФ пользуется системой, разработанной канадским профессором Синклером. Безусловно, она довольно близко приближается к определению истинной силы спортсменов с различным собственным весом, однако, на мой взгляд, не идеальна.
В середине восьмидесятых годов, заинтересовавшись этой проблемой, я попытался построить собственную систему. Была проанализирована динамика мировых рекордов в отдельных упражнениях с конца двадцатых - начала тридцатых годов и - по сегодняшний день. Просчитывались соотношения рекордных результатов между различными категориями. После суммирования многолетних значений была получена шкала (позднее была выведена и формула), которая несколько разошлась со шкалой Синклера.
Наиболее существенно расхождение в легких весовых категориях. Для проверки полученных результатов были сделаны опять-таки многочисленные сравнения по итогам самых различных соревнований, результатам лучших атлетов на протяжении многих лет. Одним из объективных показателей, характеризующих реальную силу спортсменов, может служить соотношение мировых рекордов в сумме двоеборья:
|
Таблица 1 |
|
||||
| Категория (кг) | Мировой рекорд (кг) | Коэфф. автора | Привед. рез-т | Коэфф. Синклера | Привед. рез-т |
| 52 | 272,5 | 1,746 | 475,7 | 1,7780 | 484,5 |
| 56 | 300 | 1,599 | 479,8 | 1,6394 | 491,8 |
| 60 | 342,5 | 1,487 | 509,4 | 1,5285 | 523,5 |
| 67,5 | 355 | 1,338 | 475,1 | 1,3732 | 487,5 |
| 75 | 382,5 | 1,240 | 474,2 | 1,2642 | 483,5 |
| 82,5 | 405 | 1,172 | 474,5 | 1,1858 | 480,2 |
| 90 | 422,5 | 1,123 | 474,5 | 1,1284 | 476,7 |
| 100 | 440 | 1,078 | 474,2 | 1,0749 | 473,0 |
| 110 | 445 | 1,047 | 476,2 | 1,0397 | 473,1 |
| +110 | 475 | 1,0 | 475,0 | 1,0 | 475,0 |
Но мировые рекорды иногда способны опережать время (как в случае с категорией до 60 кг), поэтому интересно и соотношение результатов пяти лучших атлетов, следующих за мировыми рекордсменами в каждой из весовых категорий:
|
Таблица 2 |
|
||||
| Категория (кг) | Средний рез-т 5 атлетов (кг) | Коэфф. автора | Привед. рез-т | Коэфф. Синклера | Привед. рез-т |
| 52 | 264,5 | 1,746 | 461,8 | 1,7780 | 470,3 |
| 56 | 293 | 1,599 | 468,5 | 1,6394 | 480,3 |
| 60 | 315,5 | 1,487 | 469,1 | 1,5285 | 482,2 |
| 67,5 | 348 | 1,388 | 465,6 | 1,3732 | 477,9 |
| 75 | 374,5 | 1,240 | 464,4 | 1,2642 | 473,4 |
| 82,5 | 396,5 | 1,172 | 464,7 | 1,1858 | 470,2 |
| 90 | 417,5 | 1,123 | 468,8 | 1,1284 | 471,1 |
| 100 | 432,5 | 1,078 | 466,2 | 1,0749 | 464,9 |
| 110 | 442,5 | 1,047 | 463,3 | 1,0397 | 460,1 |
| +110 | 466 | 1,0 | 466,0 | 1,0 | 466,0 |
Другим характерным показателем может быть соотношение высших результатов, показанных в каждой из категорий на каком-либо одном соревновании. По итогам различных турниров были подсчитаны результаты атлетов, занявших с 1-го по 6-ое места, и определены наиболее "весомые" из них:
|
Таблица 3 |
||||
| Категория (кг) | Турнир | Сумма рез-тов 6 атлетов | Уср. приведенный рез-т автора | Уср. приведенный рез-т Синклера |
| 52 | Олимпийские игры-88 | 1532,5 | 446,0 | 454,1 |
| 56 | Чемпионат мира-89 | 1672,5 | 445,7 | 457,0 |
| 60 | Чемпионат мира-87 | 1800 | 446,1 | 458,6 |
| 67,5 | Чемпионат мира-91 | 2022,5 | 451,0 | 462,9 |
| 75 | Чемпионат СНГ-92 | 2165 | 447,4 | 456,2 |
| 82,5 | Чемпионат мира-86 | 2312,5 | 451,7 | 457,0 |
| 90 | Чемпионат Европы-87 | 2377,5 | 445,0 | 447,1 |
| 100 | Чемпионат СССР-84 | 2487,5 | 446,9 | 445,6 |
| 110 | Олимпийские игры-88 | 2567,5 | 448,0 | 444,9 |
| +110 | Чемпионат мира-87 | 2700 | 450,0 | 450,0 |
Некоторый разброс полученных значений неизбежен, однако во всех рассмотренных примерах результаты в моей шкале достаточно близки, а у Синклера прослеживается значительное преимущество легких весов перед тяжелыми.
Этого-то как раз и не должно быть, если мы стремимся установить истинную зависимость между весом спортсмена и показанным им результатом. Такую возможность дает использование формулы:
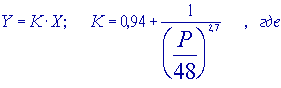
Y - приведенный результат;
X - результат, показанный тяжелоатлетом;
K - переходный коэффициент для атлета данного веса;
P - вес спортсмена.
Величина переходного коэффициента приходит в этой формуле к 1,0 для атлетов, имеющих собственный вес 136 кг, а для более тяжелых спортсменов становится уже понижающей. Подставив соответствующие значения собственного веса спортсмена и показанного им результата, мы легко можем сравнить достижения атлетов любых категорий.
Автор Андрей Важенин