Курсовая работа: Основы теории цепей
Министерство высшего и среднего специального образования Российской Федерации
Южноуральский Государственный Университет
Кафедра «цифровые радиотехнические системы»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКАК КУРСОВОМУ ПРОЕКТУ
по курсу:
ОСНОВЫ ТЕОРИИ ЦЕПЕЙЮУрГУ-К.200780.000 П3
Нормоконтролёр: РуководительКоровин В.М. Коровин В.М
«___»___________ 1999г. «___»___________ 1999г.
Автор проекта
Студент группы ПС-266
Суходоев Д.В.
«___»___________ 1999г.
Проект защищен с оценкой______________________
«___»___________ 1999г.
Челябинск
1999г.
Южноуральский Государственный Университет Факультет: ПСКафедра: ЦРТС
Заданиепо курсовой работе
студенту группы Суходоеву Дмитрию Владимировичу .
1) Тема работы: Анализ линейной динамической цепи .
2) Срок сдачи работы: _______________________________________
3) Исходные данные к работе: ________________________________
R = 1 кОм; Rн = 1 кОм; .
С1 = 1,5774·10-9 Ф; L1 = 0,6339·10-3 Гн; .
С2 = 2,3663·10-9 Ф; L1 = 0,4226·10-3 Гн; .
4) Содержание расчетно-пояснительной записки (перечень надлежащих разработке вопросов): 1) электрическая схема фильтра, система уравнений цепи; 2) комплексная функция передачи; 3) карта полюсов и нулей; 4) АЧХ, ФЧХ и импульсная характеристика .
5) Перечень графического материала: _________________________
________________________________________________________________________________________________________________
6) Консультанты по работе с указанием относящихся к ним разделов работы: _________________________________________
________________________________________________________________________________________________________________
7) Дата выдачи задания: _____________________________________
________________________________________________________
Руководитель: Коровин В.М. .
Задание принял к исполнению: ________________Подпись студента: ___________________________
АННОТАЦИЯ
Объем выполнения курсовой работы определен в учебном пособии [1].
Для выполнения работы был применен математический пакет MathCad v7.0 Pro © 1986-1997 by MathSoft, Inc, с его помощью было определено и построено: комплексная функция передачи цепи, карта полюсов и нулей, АЧХ, ФЧХ и импульсная характеристика.
СОДЕРЖАНИЕ
Введение……………………………………………………………..5
1. Электрическая схема фильтра
Система уравнений цепи………………………………………..…..6
2. Определение комплексной функции передачи…...…………….…8
3. Карта полюсов и нулей………………………………...………..…..9
4. Графики АЧХ и ФЧХ…………………………………………..…..11
5. Импульсная характеристика цепи……………………...…………13
Заключение…………………………………………………………14
Литература………………………………………………………….15
Приложение 1………………………………………………………16
Приложение 2………………………………………………………17
ВВЕДЕНИЕ
При выполнении курсовой работы необходимо отразить следующие
пункты: построить электрическую схему фильтра, составить систему уравнений цепи в обычной и матричной формах, определить комплексную функцию передачи цепи, перейти к операторной функции передачи и построить карту полюсов и нулей, также необходимо построить АЧХ, ФЧХ и импульсную характеристику, и в заключении курсового проекта необходимо отразить все аспекты выполнения тех или иных задач и написать список литературы, которой пользовались при выполнении работы.
1. ЭЛЕКТРИЧЕСКАЯ СХЕМА ФИЛЬТРА.
СИСТЕМА УРАВНЕНИЙ ЦЕПИ
На рис.1 дана принципиальная электрическая схема фильтра, элементы данной схемы занесены в таблицу 1.
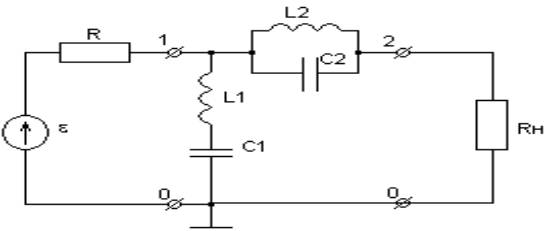
Рис.1 Электрическая схема фильтра.
Таблица 1.
| Наименование | Обозначение | Значение |
| Э.Д.С (источник) | e | - |
| Сопротивление | R | 1 кОм |
| Индуктивность | L1 | 0,6339·10-3 Гн |
| Конденсатор | С1 | 1,5774·10-9 Ф |
| Индуктивность | L2 | 0,4226·10-3 Гн |
| Конденсатор | С2 | 2,3663·10-9 Ф |
По имеющейся схеме составим систему уравнений цепи в обычной (скалярной) и матричной формах, применяя метод узловых напряжений. В качестве базисного узла взят узел «0»:
X1 = j(xL1-xC1); Y1 = 1/X1
© raVen design
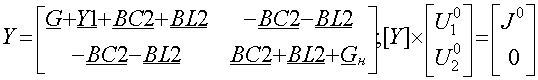
где:
G, Gн – активные проводимости;
Y, Y1, BC2, BL2, BC1, BL1 – реактивные комплексные проводимости;
U10, U20 – комплексные узловые напряжения соответствующих узлов;
J0 – комплексный ток задающего источника тока.
По матрице Y- проводимостей можно написать систему уравнений в скалярной форме:
U10(G + Y1 + BC2 + BL2) + U20( - BC2 – BL2) = J0
U20(BC2 + BL2 + Gн) + U10( - BC2 – BL2) = 0
2. ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОЙ ФУНКЦИИ ПЕРЕДАЧИ ЦЕПИ
Начертим схему цепи по которой можно определить коэффициент передачи и обозначим узлы:
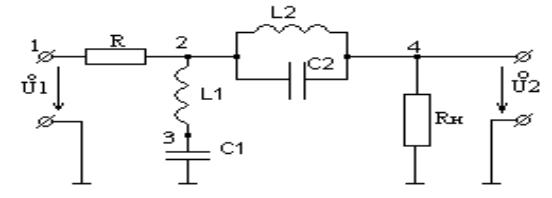
Рис.2 Схема фильтра.
Воспользуемся упрощенным вариантом определения функции передачи обратимой цепи, где за основу примем диагональную матрицу собственных проводимостей узлов, умножив для удобства все ее элементы на частоту p:
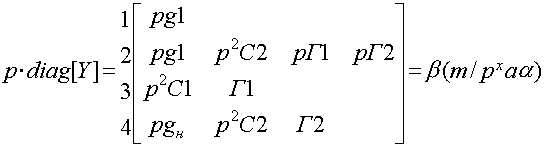
![]()
- звездное число.
![]()
Произведем нахождения дифференцируемой , это будет изоморфно диагональной матрице собственных проводимостей без первой строки.
© raVen design
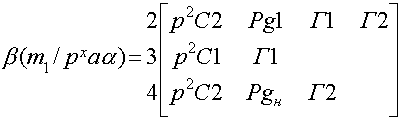
Теперь определим древесное число:
![]()
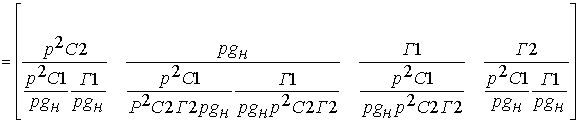
![]()
Произведя аналогичные вычисления определим
Только вместо первой строчки вычеркнем четвертую:
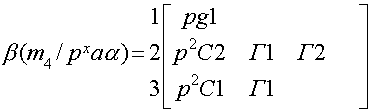
Древесное число:
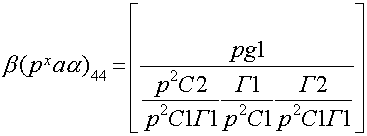
![]()
Теперь запишем H41(p):
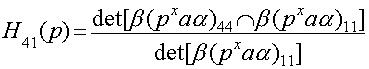
![]()
Сократим на p и получим следующее:
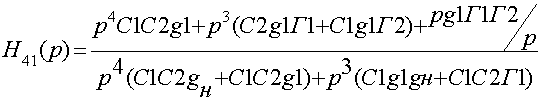
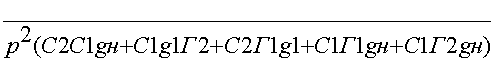
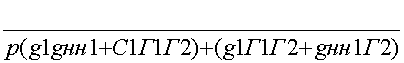
Учитывая, что
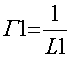
и
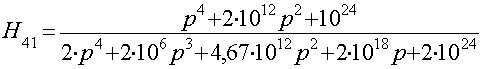 Подставим все значения элементов в формулу H41(p) получим выражение:
Подставим все значения элементов в формулу H41(p) получим выражение:
Теперь перейдем к нормированной частоте:
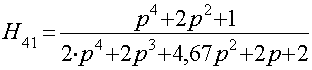
© raVen design
3. КАРТА ПОЛЮСОВ И НУЛЕЙ
По имеющейся формуле комплексной передачи цепи,
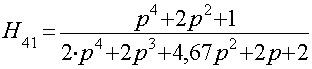
Найдем полюса и нули.
![]() Для нахождения нулей воспользуемся уравнением:
Для нахождения нулей воспользуемся уравнением:
![]()
Решая это уравнение с получим нули:
Для нахождения полюсов воспользуемся уравнением:
![]()
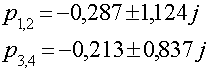 Решая это уравнение: получим полюса:
Решая это уравнение: получим полюса:
Теперь построим карту полюсов и нулей:
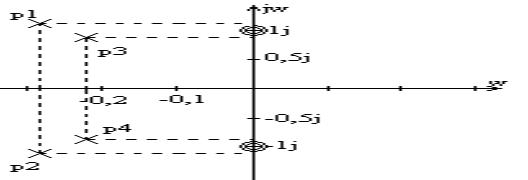
© raVen design
4. ГРАФИКИ АЧХ и ФЧХ
Формула, по которой строится график АЧХ:По АЧХ определяем крутизну спада в полосе задержания сигнала:
S = 73,6 дб/окт, что равноценно S = 210 дб/дек.
По ФЧХ определяем групповое время задержки сигнала, причем в разных частях графика оно будет различное, поэтому найдем его в двух местах:
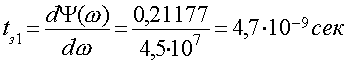
![]()
6. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА
Импульсная характеристика представлена в Приложении 2.
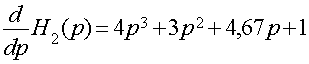
![]()
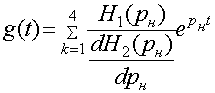
p к – полюса, которые были найдены ранее в главе 2.
Расчет и построение графика импульсной характеристики приведены в Приложении 2.
ЗАКЛЮЧЕНИЕ
При выполнении курсовой работы было выявлено много различных принципов и особенностей цепи, в итоге мы имеем фильтр, которые настроен на определенную частоту f=106 Гц.
Данный фильтр может найти широкое применение из-за высокой крутизны среза в полосе задержания.
Были построены АЧХ, ФЧХ и импульсная характеристика этой цепи, по которым можно судить о принципах работы фильтра.
Также была построена карта полюсов и нулей по которой можно очень легко построить импульсную характеристику.
В настоящее время данный фильтр возможно применять с усилительными элементами (например транзисторы) при котором можно получить схемы и которые также применяются в различной радиомеханике.
И в заключении можно сказать что данный расчет фильтра по своему объему уступает другим расчетам при проектировании более сложной радиотехнической аппаратуры.
ЛИТЕРАТУРА
1. Коровин В.М. Анализ линейных цепей с применением микрокалькуляторов: учебное пособие. - Челябинск: ЮурГУ, 1988. –37 с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи: Учебник для электротехнических и радиотехничесикх специальностей ВУЗов. – 3-у издание, переработанной и дополненное. – Москва: Высшая школа, 1990 – с.92-392.
3. Общие требования к оформлению учебной документации. / под общей редакцией А.В.Миних и др. – Челябинск: ЮУрГУ. 1992. – 60 с.
© raVen design
ПРИЛОЖЕНИЕ 1
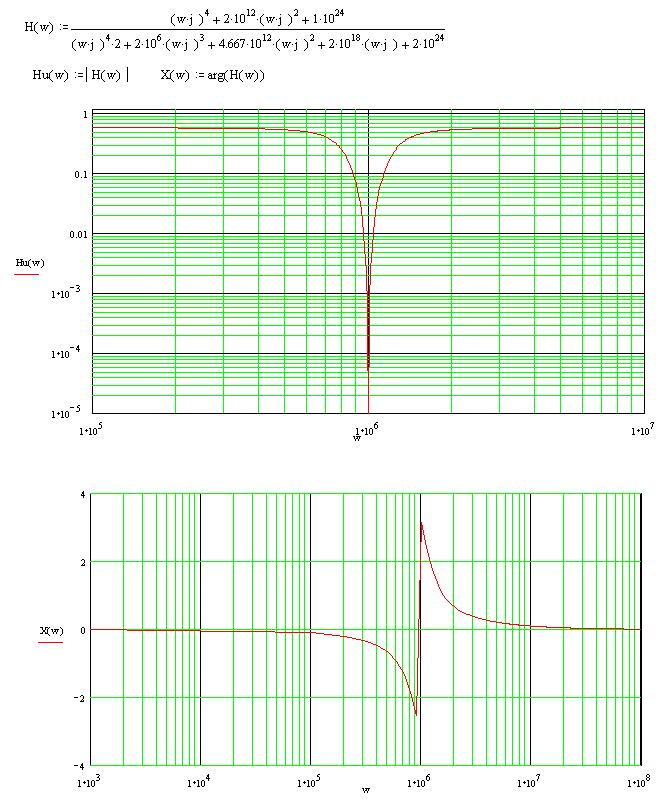
© raVen design
ПРИЛОЖЕНИЕ 2
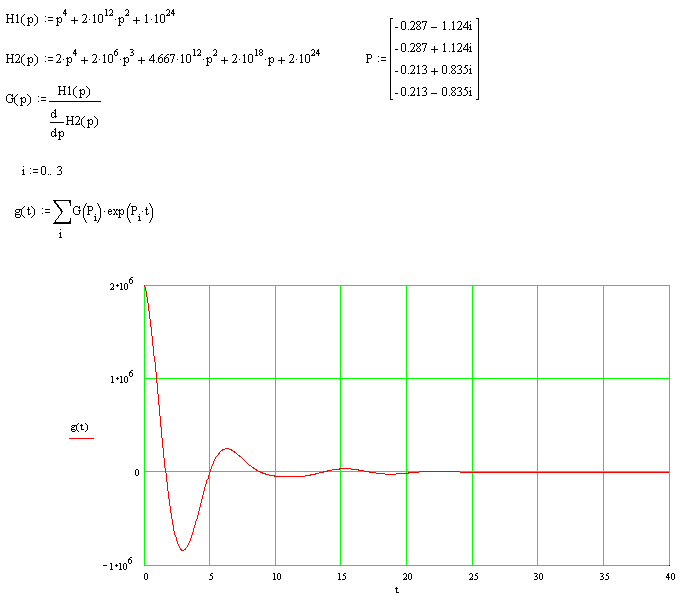
© raVen design
| Активный полосовой фильтр | |
|
Министерство образования Республики Беларусь БНТУ Приборостроительный факультет Кафедра "Информационно-измерительная техника и технологии" Гр. 113030 ... В этом случае фильтр является всеполюсным или полиномиальным, поскольку его передаточная функция обладает тем свойством, что все ее полюсы конечны, а конечных нулей не содержит. Очевидно, что коэффициент усиления фильтра Баттерворта, описываемого уравнением (9), равен К (значению передаточной функции при s=0). Если фильтр построен на основе каскадного ... |
Раздел: Рефераты по коммуникации и связи Тип: курсовая работа |
| Синтез частотно-избирательного фильтра | |
|
... Авиационный Институт имени СЕРГО ОРДЖОНИКИДЗЕ (технический университет) Кафедра 405 "Радиотехнические цепи и сигналы" Курсовая работа на тему После проведенного анализа данных с помощью справочника, были определены параметры: тип, порядок фильтра, полюсы и нули ФНЧ-прототипа, а также нормированные значения элементов цепи ... Теперь с помощью формулы 2.1, где , , а , по полученным полюсам и нулям построим АЧХ ППФ, причем АЧХ равно . |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Фильтр верхних частот Баттерворта | |
|
... национальный университет радиоэлектроники Кафедра РЭУ КУРСОВАЯ РАБОТА РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА ФИЛЬТР ВЕРХНИХ ЧАСТОТ БАТТЕРВОРТА Харьков 2008 Каждый тип АЧХ реализуют определенным количеством полюсов (RC-цепей) в соответствии с заданной крутизной спада АЧХ. Фильтр Баттерворта имеет максимально плоскую АЧХ, в полосе подавления наклон переходного участка равняется 6 дБ/окт на полюс, но он имеет нелинейную ФЧХ, входное импульсное ... |
Раздел: Рефераты по коммуникации и связи Тип: курсовая работа |
| Дискретные цепи | |
|
А. Т. Бизин Сибирская Государственная Академия телекоммуникаций и информатики Новосибирск 1998 г. Разностное уравнение и дискретная цепь Непрерывный ... Нули передаточной функции могут распологаться в любой точке плоскости Z. Если нули расположены в пределах единичного круга, то характеристики АЧХ и ФЧХ такой цепи связаны ... Импульсную характеристику можно определить непосредственно по схеме как реакцию цепи на d - функцию, или решением разностного уравнения цепи, полагая, x(nT) = d (t). |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Проектирование активных фильтров на интегральных операционных ... | |
|
Проектирование активных фильтров на интегральных операционных усилителях Реферат Целью данной курсовой работы является проектирование активного ... 3. Расчет АЧХ и ФЧХ фильтра на ЭВМ. С помощью средств ЭВМ произведен анализ полученной схемы, построены ее АЧХ и ФЧХ. |
Раздел: Рефераты по коммуникации и связи Тип: курсовая работа |