Реферат: Интеграл по комплексной переменной
Определение 1: Кривая Г называется гладкой ,если она имеет непрерывно изменяющуюся касательную.
Определение 2: Кривая называется кусочно-гладкой ,если она состоит из конечного числа гладких дуг.
Основные свойства : Пусть на комплексной плоскости Z задана кусочно-гладкая кривая С длиной l, используя параметрическое задание кривой С зададим h(t) и x (t), где h и x являются кусочно-гладкими кривыми от действительной переменной t. Пусть a t i.
Dz i =z i – z i-1. Составим интегрируемую функцию S = åf (z*)Dz i . (1)
где z*– производная точки этой дуги.
Если при стремлении max |Dz i |® 0 существует предел частных сумм не зависящий ни от способа разбиения кривой С на частичные дуги, ни от выбора точек z i , то этот предел называется интегралом от функции f (z ) по кривой С.
![]() (2)
(2)
f (zi* ) = u (Pi*) + iv (Pi*) (3)
где Dz i = Dx (t) + iDh(t) (x (t) и h(t) - действительные числа)
Подставив (3) в (1) получим :
![]()
(4)
Очевидно, что (4) состоит из суммы двух частных сумм, криволинейных интегралов действительной переменной. Переходя в (4) к пределу при Dx и Dh ® 0 и предполагая, что данные пределы существуют, получаем :
![]()
(5)
Заметим, что для существования криволинейного интегралов, входящих в (5), а тем самым и для существования интеграла (2) достаточно кусочной непрерывности функций u и v. Это означает, что (2) существует и в случае неаналитичности функции f (z ).
Сформулируем некоторые свойства интеграла от функции комплексной переменной. Из равенства (5) следуют свойства :
![]()
![]()
![]()
![]()
![]()
О ограниченности интеграла.
При этом z = j (z ).
7.) Пусть Cp – окружность радиуса r, с центром в точке Z0. Обход вокруг контура Cp осуществляется против часовой стрелки. Cp : z = Z0 + r×eij, 0 £ j £ 2p, dz = ir×eij dj .

Кусочно-гладкую замкнутую кривую будем называть
замкнутым контуром, а интеграл по замкнутому контуру – контурным интегралом.
ТЕОРЕМА КОШИ.
В качестве положительного обхода контура выберем направление при котором внутренняя область, ограниченная данным замкнутым контуром остается слева от направления движения :
![]()
Для действительной переменной имеют место
формулы Грина. Известно, что если функции P(x, y) и Q(x, y) являются непрерывными в некоторой заданной области G, ограниченны кусочно-гладкой кривой С, а их частные
производные 1-го порядка непрерывны в G, то имеет место формула Грина:
![]()
( 8 )
ТЕОРЕМА : Пусть в односвязной области G задана аналитическая функция f(Z), тогда интеграл от этой функции по замкнутому контуру Г целиком лежащему в G , равен нулю.
Доказательство : из формулы (5) следует:
![]()
Т.к. f(z ) аналитическая всюду, то U(x, y), V(x, y) - непрерывны в области, ограниченной этим контуром и
при этом выполняются условия Коши-Римана. Используя свойство криволинейных интегралов:
![]()
Аналогично :
По условию Коши-Римана в последних равенствах скобки равны нулю, а значит и оба криволинейных интеграла равны нулю. Отсюда :
![]()
ТЕОРЕМА 2 (Вторая формулировка теоремы Коши) : Если функция f(z) является аналитической в односвязной области G, ограниченной кусочно-гладким контуром C, и непрерывна в замкнутой области G, то интеграл от такой функции по границе С области G равен нулю.
TEOPEMA 3 (Расширение теоремы Коши на многосвязную область) :
 Пусть f (z) является аналитической функцией в
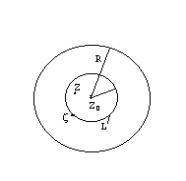
многосвязной области G, ограниченной извне контуром С0, а изнутри контурами С1, С2,
.. ,Сn (см. рис.). Пусть f (z) непрерывна в замкнутой области G, тогда :
Пусть f (z) является аналитической функцией в
многосвязной области G, ограниченной извне контуром С0, а изнутри контурами С1, С2,
.. ,Сn (см. рис.). Пусть f (z) непрерывна в замкнутой области G, тогда :
![]()
, где С – полная граница области G, состоящая из контуров С1, С2, .. , Сn. Причем обход кривой С осуществляется в положительном направлении.
Неопределенный интеграл.
Следствием формулы Коши является следующее положение : пусть f(Z) аналитична в односвязной области G, зафиксируем в этой области точку Z0 и обозначим:
интеграл по какой-либо кривой, целиком лежащей в области G, содержащей Z0 и Z, в силу теории Коши этот интеграл не зависит от выбора кривой интегрирования и является однозначной функцией Ф(Z). Аналитическая функция Ф(Z) называется первообразной от функции f(Z) в области G, если в этой области имеет место равенство : Ф¢ (Z) = f( Z).
Определение: Совокупность всех первообразных называется неопределенным интегралом от комплексной функции f(Z). Так же как и в случае с функцией действительного переменного имеет место равенство :
( 9)
Это аналог формулы Ньютона-Лейбница.
Интеграл Коши. Вывод формулы Коши.
 Ранее была сформулирована теорема Коши, которая
позволяет установить связь между значениями аналитической функции во внутренних точках области ее аналитичности и граничными значениями этой функции.
Ранее была сформулирована теорема Коши, которая
позволяет установить связь между значениями аналитической функции во внутренних точках области ее аналитичности и граничными значениями этой функции.
![]()
Пусть функция f(Z) – аналитическая функция в односвязной области G, ограниченной контуром С. Возьмем внутри этой области произвольную точку Z0 и в области G вокруг этой точки построим замкнутый контур Г. Рассмотрим вспомогательную функцию j (Z). Эта функция аналитична в области G всюду, кроме точки Z=Z0. Проведем контур g с достаточным радиусом, ограничивающий точку Z0, тогда функция будет аналитична в некоторой двусвязной области, заключенной между контурами Г и g. Согласно теореме Коши имеем :
По свойствам интегралов :
(2 )
![]() Так как левый интеграл в (2) не зависит от выбора
контура интегрирования, то и правый интеграл также не будет зависеть от выбора контура. Выберем в качестве g
окружность gr с радиусом r . Тогда:
Так как левый интеграл в (2) не зависит от выбора
контура интегрирования, то и правый интеграл также не будет зависеть от выбора контура. Выберем в качестве g
окружность gr с радиусом r . Тогда:
(3)
Уравнение окружности gr : z = Z0 + reij (4)
Подставив (4) в (3) получим :

( 5 )

( 6 )

(7)
 Устремим gr® 0, т.е. r® 0.
Устремим gr® 0, т.е. r® 0.
Тогда т.к. функция f(z) аналитична в точке Z=Z0 и всюду в области G, а следовательно и непрерывна в G, то для всех e>0 существует r>0, что для всех z из r–окрестности точки Z0 выполняется | f(z) – f(Z0) | < e.>
![]()

(8)
Подставив ( 7) в ( 6) с учетом ( 8) получаем :

Подставляя в ( 5) и выражая f(Z0) имеем :
(9)
![]() Это интеграл Коши.
Это интеграл Коши.
Интеграл, стоящий в (9) в правой части выражает значение аналитической функции f(z) в некоторой точке Z0 через ее значение на произвольном контуре g , лежащем в области аналитичности функции f(z) и содержащем точку Z0 внутри.
Очевидно, что если бы функция f(z) была аналитична и в точках контура С, то в качестве границы g в формуле (9) можно было использовать контур С.
Приведенные рассуждения остаются справедливыми и в случае многосвязной области G.
Следствие : Интеграл Коши, целиком принадлежащий аналитической области G имеет смысл для любого положения Z0 на комплексной плоскости при условии, что эта точка есть внутренней точкой области Г. При этом если Z0 принадлежит области с границей Г, то значение интеграла равно (9), а если т. Z0 принадлежит внешней области, то интеграл равен нулю :

При Z0 Î Г
указанный интеграл не существует.
Интегралы, зависящие от параметра.
Рассматривая интеграл Коши, видим, что подинтегральная функция зависит от 2-х комплексных переменных : переменной интегрирования z и Z0. Таким образом интеграл Коши может быть рассмотрен как интеграл, зависящий от параметра, в качестве которого выбираем точку Z0.
Пусть задана функция двух комплексных переменных j (Z, z ), причем Z= x + iy в точке, принадлежащей некоторой комплексной плоскости G. z= x+ ih Î С. (С - граница G).
Взаимное расположение области и кривой произвольно. Пусть функция j (Z, z ) удовлетворяет условиям : 1) Функция для всех значений z Î С является аналитической в области G. 2) Функция j (Z, z ) и ее производная ¶j/¶Z являются непрерывными функциями по совокупности переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях :
![]()
Интеграл существует и является функцией
комплексной переменной. Справедлива формула :
![]() (2)
(2)
Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру.
ТЕОРЕМА. Пусть f(Z) является аналитической функцией в области G и непрерывной в области G (G включая граничные точки ), тогда во внутренних точках области G существует производная любого порядка от функции f(Z) причем для ее вычисления имеет место формула :
![]()
(3)
С помощью формулы (3) можно получить производную любого порядка от аналитической функции f (Z) в любой точке Z области ее аналитичности. Для доказательства этой теоремы используется формула (2) и соответственные рассуждения, которые привели к ее выводу.
ТЕОРЕМА МОРЕРА. Пусть f(Z) непрерывна в односвязной области G и интеграл от этой функции по любому замкнутому контуру, целиком принадлежащему G равен 0. Тогда функция f (Z) является аналитической функцией в области G. Эта теорема обобщается и на случай многосвязной области G.
Разложение функции комплексного переменного в ряды.
Если функция f(x, y) определена и непрерывна вместе с частными производными (до n-го порядка ), то существует разложение этой функции в ряд Тейлора :
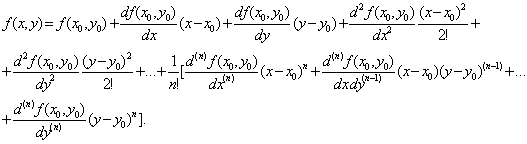
Итак, если задана функция f (z) комплексного переменного, причем f (z) непрерывная вместе с производными до n-го порядка, то:
![]() (2)
– разложение в ряд Тейлора.
(2)
– разложение в ряд Тейлора.
Формула (2) записана для всех Z принадлежащих некоторому кругу | Z-Z0 |
Функция f (z), которая может быть представлена в виде ряда (2) является аналитической функцией. Неаналитическая функция в ряд Тейлора не раскладывается.
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Причем | Z | < R, R ® ¥ .>
Формулы ЭЙЛЕРА.
Применим разложение (3) положив, что Z = ix и Z= - ix;
![]()
![]()
![]() (6)
(6)
Аналогично взяв Z = - ix получим :
![]() (7)
(7)
Из (6) и (7) можно выразить т.н. формулы Эйлера :
![]() (8)
(8)
В общем случае :
![]() (9)
(9)
Известно, что :
![]() (10)
(10)
Тогда из (9) и (10) вытекает связь между тригонометрическими и гиперболическими косинусами и синусами:
![]()
Ряд ЛОРАНА.
Пусть функция f(z) является аналитической функцией в некотором круге радиусом R, тогда ее можно разложить в ряд Тейлора (2). Получим тот же ряд другим путем.
ТЕОРЕМА 1.
Однозначная функция f(Z) аналитическая в круге радиусом |Z-Z0| < R раскладывается в сходящийся к ней степенной ряд по степеням Z-Z>0.
Опишем в круге радиусом R окружность r, принадлежащую кругу с радиусом R.
Возьмем в круге радиуса r точку Z, а на границе области точку z , тогда f(z) будет аналитична внутри круга с радиусом r и на его границе. Выполняется условие для существования интеграла Коши :
![]() (13)
(13)
 (11)
(11)
Поскольку
![]() , то выражение
, то выражение можно представить как сумму бесконечно убывающей геометрической прогрессии со знаменателем
, т.е. :
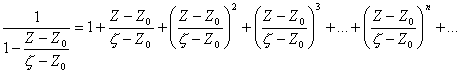
![]() (12)
(12)
Представим равномерно сходящимся рядом в круге радиуса r, умножая (12) на 1/(2pi) и интегрируя по L при фиксированном Z, получим : слева интеграл (13) который равен f (Z), а справа будет сумма интегралов :

Обозначая ![]() , получим :
, получим : (14)
Это разложение функции f (Z) в круге R в ряд Тейлора. Сравнивая (14) с рядом (2) находим, что (15)
ТЕОРЕМА 2.
Если однозначная функция f(Z) аналитична вне круга с радиусом r с центром в точке Z0 для всех Z выполняется неравенство r < |Z-Z>0 |, то она представляется рядом :
![]() (16)
(16)
где h - ориентированная против часовой стрелки окружность радиуса r (сколь угодно большое число). Если обозначить (17) , получим :
![]() (18)
(18)
ТЕОРЕМА 3.
Если однозначная функция f(Z) аналитическая в кольце Z< |Z-Z>0 |0 существует M>0 и S0³0 такие, что выполняется условие : |f(t)|S0t
Рассмотрим функцию f(t)×e-pt , где р – комплексное число р = ( а + i b).
![]() (1)
(1)
Применим к этому соотношению формулу Эйлера :
![]()
Проинтегрировав это равенство получим :
 (2)
(2)
Оценим левую часть равенства (2) :

А согласно свойству (3) |f(t)| < Me >S0t

В случае если a>S0 имеем :
![]()
Аналогично можно доказать, что существует и сходится второй интеграл в равенстве (2).
Таким образом при a>S0 интеграл, стоящий в левой части равенства (2) также существует и сходится. Этот интеграл определяет собой функцию от комплексного параметра р :
 (3)
(3)
Функция F(p) называется изображением функции f(t) по Лапласу, а функция f(t) по отношению к F(p) называется оригиналом.
f(t) Ü F(p), где F(p) – изображение функции f(t) по Лапласу.
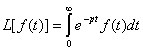 - это оператор Лапласа.
- это оператор Лапласа.
Смысл введения интегральных преобразований.
Этот смысл состоит в следующем : с помощью перехода в область изображения удается упростить решение многих задач, в частности свести задачу решения многих задач дифференциального, интегрального и интегро-дифференциального уравнения к решению алгебраических уравнений.
Теорема единственности: если две функции j( t) и Y(t) имеют одно и то же изображение F(p), то эти функции тождественно равны.
Смысл теоремы : если при решении задачи мы определим изображение искомой функции, а затем по изображению нашли оригинал, то на основании теоремы единственности можно утверждать, что найденная функция является решением в области оригинала и причем единственным.
Изображение функций s0(t), sin (t), cos (t).
Определение: ![]() называется единичной
функцией.
называется единичной
функцией.
Единичная функция удовлетворяет требованиям, которые должны быть наложены на функцию для существования изображения по Лапласу. Найдем это изображение :

Изображение единичной функции ![]()
Рассуждая аналогичным образом получим изображение для функции sin(t) :

интегрируя по частям получим :
![]() т.е.
т.е.
Аналогично можно доказать, что cos (t) переходит в функцию в области преобразований. Откуда :
Изображение функции с измененным масштабом независимого переменного.
 где а – константа.
где а – константа.
Таким образом : ![]()
![]() и
и
Свойства линейности изображения.
Теорема : изображение суммы нескольких функций умноженное на постоянные равны сумме изображений этих функций умноженных на те же постоянные.
![]()
Если ![]() , то
, то , где
![]()
Теорема смещения : если функция F(p) это изображение f(t), то F(a+p) является изображением функции e-at f(t) (4)
Доказательство :
Применим оператор Лапласа к левой части равенства (4)
![]()
Что и требовалось доказать.
Таблица основных изображений:
| F(p) | f(t) | F(p) | f(p) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изображение производных.
Теорема. Если ![]() , то справедливо выражение :
, то справедливо выражение :
![]() (1)
(1)
Доказательство :


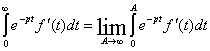 (2)
(2)
 (3)
(3)
Подставляя (3) в (2) и учитывая третье условие существования функции Лапласа имеем :
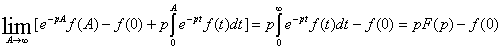
Что и требовалось доказать.
Пример: Решить дифференциальное уравнение :
![]() Если x(0)=0 и x’(0)=0
Если x(0)=0 и x’(0)=0
Предположим, что x(t) – решение в области оригиналов и , где
![]() - решение в области изображений.
- решение в области изображений.
![]()
![]()
![]()
Изображающее уравнение :
![]()
![]()
![]()
Теорема о интегрировании оригинала. Пусть находится в области оригиналов,
![]() , тогда
, тогда также оригинал, а его изображение
.
Таким образом операции интегрирования в области оригиналов соответствует операция деления в области изображений.
Теорема о интегрировании изображений : Пусть – функция оригинал, которая имеет изображение
и
![]() также оригинал, а
также оригинал, а - является сходящимся интегралом, тогда
.
Толкование теоремы : операция деления на аргумент в области оригиналов соответствует операции интегрирования в пределах от р до ¥ в области изображений.
Понятие о свертке функций. Теорема о свертке.
Пусть заданы две функции a(t) и b(t), удовлетворяющие условиям существования изображения по Лапласу, тогда сверткой таких функций называется следующая функция :
 (1)
(1)
Свертка обозначается следующим образом :
![]() (1’)
(1’)
Равенства (1) и (1’) идентичны.
Свертка функции подчиняется переместительному закону.
Доказательство:


Теорема о умножении изображений. Пусть ![]() и
и , тогда произведение изображений
![]() представляется
сверткой оригиналов
представляется
сверткой оригиналов ![]() .
.
Доказательство :
Пусть изображение свертки ![]()
 (1)
(1)
Интеграл (1) представляет собой повторный интеграл относительно переменных t и t . Изменим порядок интегрирования. Переменные t и t входят в выражение симметрично. Замена переменной производится эквивалентно.

Если в последнем интеграле сделать замену переменной, то после преобразований последний интеграл преобразуется в функцию F2(p).
Операция умножения двух функций в пространстве изображений соответствует операции свертки их оригиналов в области оригиналов. Обобщением теоремы о свертке есть теорема Эфроса.
Теорема Эфроса. Пусть функция ![]() находится в области
оригиналов,
находится в области
оригиналов, ![]() , а Ф(р) и q(р) – аналитические функции в области изображений,
такие, что
, а Ф(р) и q(р) – аналитические функции в области изображений,
такие, что ![]() , тогда
, тогда .
В практических вычислениях важную роль играет следствие из теоремы о свертке, наз. интеграл Дюамеля. Пусть все условия теоремы выполняются, тогда
 (2)
(2)
Соотношение (2) применяется при решении дифференциальных уравнений.
Обратное преобразование Лапласа.
 - Это прямое преобразование Лапласа.
- Это прямое преобразование Лапласа.
Обратное преобразование есть возможность получить функцию-оригинал через известную функцию-изображение :
 , где s – некоторая константа.
, где s – некоторая константа.
Пользоваться формулой для обратного преобразования можно при определенном виде функции F(p), либо для численного нахождения функции-оригинала по известному изображению.
Теоремы разложения.
Известная методика разложения дробно-рациональных функций на сумму элементарных дробей (1)-(4) может быть представлена в виде двух теорем разложения.
Первая теорема разложения. Пусть F(p) – изображение некоторой функции, тогда эта функция представляется в виде , k – постоянная, может быть сколь угодно большим числом,
, то возможен почленный переход в пространство оригиналов с помощью
формулы :
![]() .
.
Вторая теорема разложения. Если изображение представляется дробно-рациональной
функцией ![]() . Степень числа s меньше
степени знаменателя n, знаменатель имеет корни a1, a2, …, a n соответствующий кратности k1, k2, …, kn , при этом k1+ k2 +…+ kn = n. В этом случае оригинал функции определяется по
формуле :
. Степень числа s меньше
степени знаменателя n, знаменатель имеет корни a1, a2, …, a n соответствующий кратности k1, k2, …, kn , при этом k1+ k2 +…+ kn = n. В этом случае оригинал функции определяется по
формуле :

 (3)
(3)
Например :
![]()

Связь между преобразованиями Фурье и Лапласа.
Преобразование Лапласа имеет вид :
 (1)
(1)
На f(t) наложены условия :
1) f(t) определена и непрерывна на всем интервале: (-¥ ; ¥ )
2) f(t) º 0 , t Î (- ¥ ;0)
3) При M, S0 >0 , для всех t > 0 выполняется условие |f(t)|S0t
Если отказаться от условий 2 и 3, и считать, что f(t) принимает произвольное значение при t < 0, то вместо (1) можно рассмотреть следующий интеграл :>
![]() (2)
(2)
Формула (2) – двустороннее преобразование Лапласа.
Пусть в (1) и (2) p =a + in, где a и n – действительные числа.
Предположим, что Re(p) = a = 0, т.е.
 (4)
(4)
![]() (5)
(5)
(4) и (5) соответственно односторонние и двусторонние преобразования Фурье.
Для существования преобразования Фурье, функция должна удовлетворять условиям :
1) Должна быть определена на промежутке (-¥ ; ¥ ) , непрерывна всюду, за исключением конечного числа точек разрыва первого рода.
2) Любой конечный промежуток оси t можно разделить на конечное число промежутков, в каждом из которых функция либо кусочно-гладкая, либо кусочно-монотонная.
3) Функция абсолютно интегрируема : ![]() , это условие выполняется, если |f(t)|S0t
, это условие выполняется, если |f(t)|S0t
Из существования преобразования Лапласа не следует преобразование Фурье. Преобразования Фурье существуют для более узкого класса функций. Преобразования Фурье не существуют для постоянной и ограниченной функции : f(t) = C

Аналогично преобразования Фурье не существуют и для гармоничных функций :
![]() т.к.
т.к.
Если f(t) = 0 при t>0 и преобразование для этой функции существует, то оно может быть получено из таблицы оригиналов и изображений для преобразования Лапласа путем замены параметра t на iu, но при этом необходимо убедиться, что F(p) не обращается в число справа от мнимой оси.
Если f(t) ¹ 0, t
 (6)
(6)
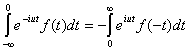
Обозначим 
Очевидно, что ![]() (6’)
(6’)
Функция (6) называется спектральной плотностью

В связи с изложенным можно указать два пути отыскания спектральной плотности :
1) Вычисление интеграла (5)
2) Использование преобразования Лапласа или Фурье.
Непосредственное вычисление спектральной плотности для абсолютно интегрируемой функции.
Функция F(iu) может быть представлена, как комплексная функция действительной переменной
![]() (7)
(7)
|F(iu)| - амплитудное значение спектральной плотности, y (u) – фазовый угол.
В алгебраической форме : F(iu) = a(u) +ib(u)
![]() (8)
(8)
![]() (9)
(9)
Для непосредственного вычисления спектральной плотности вычисляется интеграл (6), а затем по формулам (8) и (9) определяется амплитудное значение |F(iu)| и фазовый угол y (u).
Пример.
Найти спектральную плотность импульса :

откуда ![]() , далее
, далее
![]()
![]()
Отыскание спектральной плотности для неабсолютно интегрируемых функций.
Прямое преобразование Фурье для таких функций не существует, существует преобразование Лагранжа.
Прямое преобразование Фурье необходимо :
1) Для облегчения процесса решения дифференциальных и интегральных уравнений.
2) Для исследования амплитудной и частотной характеристик спектральной плотности, определенной всюду на числовой оси.
Введем следующее определение спектральной плотности для неабсолютно интегрируемых функций:
Если для заданной функции y=f(t) существует непрерывное изображение по Лапласу F(p), то спектральной плотностью функции называется изображение функции по Лапласу при p = iu.
Спектральной плотностью F1(iu) неабсолютно интегрируемой функции называется предел от спектральной плотности F2(iua) абсолютно интегрируемой функции.
![]()
![]()
| Дискретизация и квантование изображений | |
|
ИСТОРИЧЕСКИЙ ОЧЕРК. Еще с середины 40-ых годов , специалисты по радиоэлектроники начали задумываться над возможностью применения специализированных ... Эта теорема утверждает , что если сигнал f(t) имеет преобразование Фурье Sf(w) отличное от нуля при частотах меньших 2pFm . f(t)=тC(t)y(t-t)dt - Свертка -интеграл Дюамеля (прохождение |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... 3. Пусть H(z) будет Z-преобразованием импульсной реакции h. Пусть у будет реакцией при нулевом состоянии на входе U, прикладываемый в момент t=0. Z(f+g)=Z(f)+Z(g) =|Z|>max (Rf,Rg) |
Раздел: Рефераты по математике Тип: реферат |
| Исследование движения центра масс межпланетных космических аппаратов | |
|
2. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ 2.1. ВВЕДЕНИЕ В данной работе проводится исследование движения центра масс МКА под действием различных возмущающих ... e = f/mz, где f - вектор Лапласа m_f << x << '\t' << Fz << '\t' << Fs << '\t' << Fl << '\t' << Fa |
Раздел: Рефераты по астрономии Тип: реферат |
| Основные понятия математического анализа | |
|
1. Определение неопред. интеграла. Если ф-ия F(x) - первообр для ф-ии f(x) на промежутке [a,b], то мн-о ф-ий F(x)+C, где С =const, назыв неопред ... 9. Интеграл =[f(x)=g(x)]dx= =f(x)dx==g(x)dx -неопред интеграл от алгебраической суммы двух ф-ий равен алгебраической суммe интегр от этих Пусть F(x) и G(x) - первообразные для ф-ий f(x) и g(x): =[f(x)+g(x)]dx==(F"(x)+G"(x))dx==(F(x)+G(x))"dx==d(F(x)+G(x))= F(x)+G(x)+C= F(x)+G(x)+C1+C2=F(x)+C1+G(x)+C2 ==f(x)dx+=g(x)dx ... |
Раздел: Рефераты по математике Тип: шпаргалка |
| Ряды | |
|
Фун 2 числовых аргументов. Пусть имеется Е (х1;у1) - элементы принадлеж точке Е Сущ закон или правило по которому каж точке (xi;yi) ставится в соот-е ... Сущ закон или правило по которому каж точке (xi;yi) ставится в соот-е число Wi или любой точке (xi;yi) или паре чисел ставится в соот-е zi след-но zi=F(х;у), где Е-обл опред-я F(х ... Пусть точка М0(х0;у0) I обл опр-я фун-и f(х;у). Фун-я z=f(х;у) наз непрерывной в точке М0(х0;у0), если имеет место равенство limх°х0(у°у0)f(х;у)=f(х0;у0) или limDх°0(Dу°0)f(х0+Dх ... 3) Если фун z=j(m) непрерывна в точке m=х0;у0, а фун y=f(z) непрерывна в соот-й точке z0=j(х0;у0), то фун y=f(j(х;у)) непрер-а в точке (х0;у0). |
Раздел: Рефераты по математике Тип: шпаргалка |