Реферат: Нейросетевая реализация системы
автономного адаптивного управления
Принятые обозначения
- множество
неотрицательных целых чисел
- граф со
множеством вершин V и множеством ребер N
- ребро,
направленное из вершины i в вершину j
-
взаимнооднозначное отображение множества X на множество Y
- множество
конечных подмножеств множества X
R[a,b] – множество вещественных чисел на [a,b]
BN - пространство двоичных векторов размерности N
- пустое слово из
множества входных слов КА
0 – ложь в выражении трехзначной логики
1 – истина в выражении трехзначной логики
- неопределенность
в выражении трехзначной логики
- 
есть подвектор
(совокупность выбранных компонент) вектора 
- класс Y
является потомком класса X
Введение.
1.1. Введение и задачи работы.
При современном уровне развития техники, когда даже бытовая техника оснащается микропроцессорными устройствами, возникла потребность в интеллектуальных адаптивных системах управления, способных приспосабливаться к очень широкому диапазону внешних условий. Более того, возникла потребность в универсальной технологии создания таких систем. Научный опыт человечества свидетельствует о том, что в природе можно найти великое множество ценных идей для науки и техники. Человеческий мозг является самым удивительным и загадочным созданием природы. Способность живых организмов, наделенных высшей нервной системой, приспосабливаться к окружающей среде может служить призывом к подражанию природе или имитации при создании технических систем.
Среди имитационных подходов выделяется класс нейросетевых методов. Нейронные сети (НС) нашли широкое применение в областях искуственного интеллекта, в основном связанных с распознаванием образов и с теорией управления. Одним из основных принципов нейросетевого подхода является принцип коннективизма. Суть его выражается в том, что рассматриваются очень простые однотипные объекты, соединенные в большую и сложную сеть. Таким образом, НС является в первую очередь графом, с которым можно связать совокупность образов, представленных как численные значения, ассоциированные с вершинами графа, алгоритм для преобразования этих численных значений посредством передачи данных между соседними вершинами и простых операций над ними. Современный уровень развития микроэлектроники позволяет создавать нейрочипы, состоящие из очень большого числа простых элементов, способных выполнять только арифметические операции. Таким образом, нейросетевые методы поддерживается аппаратно.
Математически НС можно рассматривать как класс методов
статистического моделирования, который в свою очередь можно разделить на три
класса: оценка плотности вероятности, классификация и регрессия [NN]. В
частности, в [NN] показано, что с помощью сетей обратного распространения и
обобщенного 
- правила решается задача
оценки плотности вероятности методом смешивания гауссовских распределений.
В отделе имитационных систем Института Системного Программирования РАН разработан метод автономного адаптивного управления (ААУ). Предполагается, что система ААУ может быть полностью реализована на нейронной сети [Диссер, Жданов1-9]. В отличии от традиционного использования НС для решения только задач распознавания и формирования образов, в методе ААУ согласованно решаются задачи
распознавания и формирования образов
получения и хранения знаний (эмпирически найденных закономерных связей образов и воздействий на объект управления)
оценки качественных характеристик образов
принятия решений (выбора воздействий).
Особенностями метода ААУ являются:
Избыточность нейронов в сети, необходимая для адаптации системы управления (УС) к изменяющимся условиям существования объекта управления (ОУ). Вследствие этого для практической реализации УС необходимо создание больших НС (для сравнения человеческий мозг содержит ~1011 нейронов).
НС состоит из специфичных нейронов, являющимися более близкими аналогами биологического нейрона и приспособленными для решения задач ААУ (раздел 3.2)
Нейроны в сети соединяются специальным образом, также для решения задач ААУ.
Особенности метода ААУ делают непригодными или малопригодными существующие системы САПР и системы моделирования традиционных НС (например, BrainMaker) для создания прототипов УС ААУ. Ввиду этого обстоятельства задачами дипломной работы были:
Разработка инструмента СПИНС для моделирования и исследования нейросетевых реализаций прототипов УС ААУ.
Разработка общей схемы нейросетевой реализации прототипов УС ААУ.
1.2. Формальная модель нейрона и нейросети.
Понятие схемы было введено для формализации вычислений на параллельных компьютерах [Итоги91]. Мы используем это понятие для формального описания нейронных сетей, т.к. оно подходит для этих целей почти без изменений. Одним из следствий такой близости схем и НС является возможность хорошего распараллеливания вычислений в моделях НС.
Определение 1.2.1. Назовем схемой c
ориентированный ациклический ортграф (допустимы ребра с общими вершинами),
вершинами которого являются параметризованные операции, т.е. операции,
зависящие от некоторого параметра t. Аргументами операции являются все входные
вершины или входы, т.е. такие вершины, для которых есть ребра (входные
ребра), исходящие из них и направленные к данной вершине, 
- входная арность i-ой
вершины, т.е. число входных вершин, 
-выходная
арность i-ой вершины, т.е. число выходных вершин или выходов.
Определим размер схемы s(c) как общее число вершин схемы, глубину
схемы d(c) как максимальную длину ориентированного пути в графе c. Порядок
вершины определяется рекурсивно: для вершин у которых нет входов,
принадлежащих сети (истоки сети), порядок равен 0, для остальных порядок
есть максимум порядка входов плюс единица. Входами сети будем называть
некоторое подмножество множества истоков сети. Выходами сети будем
считать просто некоторое множество вершин сети.
Определение1.2.2. Здесь и далее под нейронной сетью будем понимать схему.
По сути схема является совокупностью композиций некоторых параметризованных операций. Глубина схемы есть максимальный уровень вложенности композиций. В методологии НС важно, что эти операции являются вычислительно простыми, наподобие взвешенной суммы или булевых конъюнкции и дизъюнкции, при этом выбирается большое количество аргументов и композиций. В этом суть коннективизма. Параметр t является по сути временным параметром. Заметим, что здесь и далее полагаем время дискретным, хотя для формализации НС это не принципиально. Перенумеровав вершины схемы, можно записать общий вид параметризованной операции:
,
где 
(t) - i-ая
параметризованная операция, 
-
входные вершины, 
- синаптическая
задержка на ребре 
. Конкретный вид
функции 
для предлагаемой модели
нейрона будет представлен в разделе “Аппарат ФРО”.
Пример 1.2.1. В качестве операции-вершины может быть любая операция трехзначной логики (разд. 1.5).
Определение1.2.3. Выходами подграфа G(V,
N), где V - множество ребер, N – множество вершин. сети будем
называть все ребра 
, входами все
ребра 
.
Определение1.2.4. Определим блок как связный подграф сети с одним выходом.
Определение1.2.5. Назовем блок 
шаблоном некоторого
блока 
если между этими
блоками существует изоморфное отображение, т.е. такая пара отображений 
Определение1.2.6. Разбиением сети на блоки с
шаблоном B будем называть совокупность непересекающихся блоков 
такую, что для всех этих
блоков B является шаблоном и объединение всех блоков и межблоковых ребер
(имеется ввиду два разных объединения: множеств вершин и множеств ребер) есть
вся сеть.
Определение1.3.7. Совокупность рекурсивных разбиений
сети 
, где 
есть разбиение шаблона 
будем называть конструкцией
сети, а множество 
шаблонами
конструктора.
Определение1.2.8. Таким образом, под формальной
моделью нейрона будем понимать шаблон 
разбиения
сети 
, у которого выход есть
булева операция. Под нейроном будем понимать собственно блок.
Например, на рис.1.2.1 представлена формальная модель
перспептрона, где все блоки 
имеют
один шаблон МакКаллока-Питтса [Маккалок].
Вообще говоря, состояние обученности нейрона для каждой формальной модели определяется по своему и, неформально выражаясь, это состояние, в котором считается, что нейрон уже “обучен” для решения своей задачи классификации. Отметим, что процесс обучения необратим.
Определение 1.2.9. Будем говорить, что сетью распознан образ i, если после предъявления сети некоторого входного сигнала на выходе i-ого нейрона появляется 1.
Распознавание образа есть по сути положительный ответ в решении задачи классификации для данного нейрона.
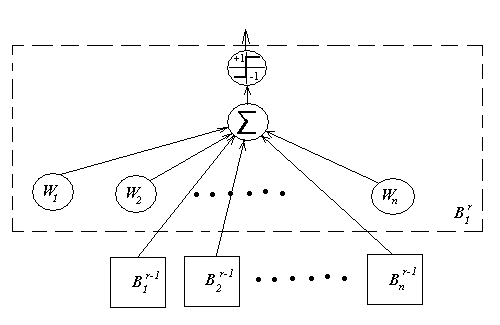
Рис.1.2.1.
1.3. Краткое описание метода автономного адаптивного управления.
Метод ААУ подробно описан в работах [Жданов3-9], поэтому представим только основные его стороны. Будем называть управляющей системой (УС) систему управления, имитирующую нервную систему в соответствии с методологией ААУ. Под объектом управления (ОУ) будем понимать организм, который несет в себе нервную систему, другими словами, ОУ - это объект, который должен управляться посредством УС, расположенной внутри ОУ и взаимодействующей со своим окружением посредством блока датчиков (БД) и исполнительных органов (ИО).
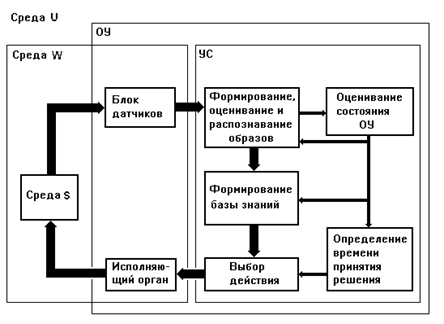
Рис. 1.3.1.
На рис. 1.3.1 представлена система, под которой будем понимать среду, в которую вложен ОУ, в свою очередь содержащий в себе УС. Как видно из рисунка, можно утверждать, что УС управляет не только ОУ, но всей системой. Под средой в системе можно понимать разные объединения объектов. Будем называть средой W совокупность объектов, лежащих вне УС; средой S - совокупность объектов, лежащих вне ОУ; средой U - всю систему.
Блок датчиков поставляет УС входную информацию в виде двоичного вектора. Этот блок необходим в реальных системах для сопряжения среды и УС, поэтому при моделировании УС на ЭВМ не использовался и мы не акцентируем внимание на нем в данной работе.
Работу блока формирования и распознавания образов (ФРО) можно представить следующим способом (подробное описание см. в работах [Жданов3, Жданов8]). В блоке ФРО на основании априорной информации о возможных функциональных свойствах среды заданы некоторые объекты, назовем их нейронами (например, нейроны специального вида, описанные в работе [Жданов8]), на которые отображаются некоторые классы пространственно-временных явлений, которые потенциально могут существовать в системе. Отображение задается топологией сети. В классе, отображаемом на нейрон, выделяется подкласс, который может восприниматься данным нейроном. Каждый нейрон может статистически анализировать воспринимаемый им подкласс. Накапливая статистическую информацию о воспринимаемом подклассе, нейрон может принять решение, является ли этот подкласс случайным или неслучайным явлением в системе. Если какой-либо нейрон принимает решение, что отображаемый на него подкласс является неслучайным событием, то он переходит в некоторое отличное от исходного ²обученное² состояние. Если нейрон обучен, то будем говорить также, что сформирован образ, этот образ идентифицируется номером данного нейрона. Подкласс явлений, воспринимаемый нейроном, и вызвавший его обучение, то есть пространственно-временные явления, статистически достоверно существующие в системе, называется прообразом данного образа. Сформированный образ может быть распознан блоком ФРО, когда прообраз данного образа наблюдается БД. Блок ФРО указывает, какие из сформированных образов распознаны в текущий момент. Одновременно с этим распознанные образы участвуют в формировании образов более высоких порядков, то есть имеет место агрегирование и абстрагирование образов.
Блок формирование базы знаний [Жданов4-6] (БЗ) предназначен для автоматического представления эмпирически найденных УС знаний о функциональных свойствах системы. Элементарной конструкцией базы знаний (БЗ) в методе ААУ является статистически достоверное сведение о том, как определенное действие Yj влияет на прообраз определенного сформированного образа. Действием Yj названо подмножество множества допустимых воздействий, элементы которого абсолютно идентичны для УС по их влиянию на сформированные образы. Непустое сведение может иметь одно из двух значений: либо действие Yj влечет распознавание образа Oi , либо действие Yj влечет вытеснение образа Oi. При помощи БЗ можно видеть, как конкретное действие влияет на всю совокупность сформированных образов.
Блок оценки состояния [Жданов7] (БОС) вырабатывает интегральную оценку качества состояния ОУ St. Оценка St используется для расчета оценки (веса) pi каждого из вновь сформированных образов некоторым статистическим способом. В свою очередь, St функционально зависит от оценок pi распознанных образов. Имеется некоторое множество изначально сформированных и оцененных образов. Оценка St используется также для расчета темпа принятия решений.
Блок выбор действия [Жданов4-6] или, в дальнейшем, блок принятия решений (БПР) реализует процедуру принятия решения, основанную на анализе текущей ситуации, целевых функций, содержимого БЗ, а также оценки текущего значения оценки St. Фактическая информация о текущей ситуации представлена множеством образов, распознанных в текущий момент блоком ФРО, а информация о качестве текущего состояния представлена оценкой St. Множество распознанных образов определяет в БЗ тот ее раздел, который адекватен текущей ситуации (те знания, которые истинны в текущих условиях). В соответствии с целевой функцией, предполагающей стремление УС к улучшению качества состояния ОУ, УС выбирает по БЗ то действие, которое имеет максимальную сумму оценок вызываемых и вытесняемых образов. Из множества выходных воздействий, соответствующего выбранному действию Yj, конкретное выходное воздействие выбирается случайным способом, что соответствует второй целевой функции, предусматривающей стремление к получению новых знаний.
Блок определение времени принятия решения определяет глубину просмотра БЗ в зависимости от текущей оценки St. Чем выше значение St, тем больше образов (в порядке убывания модуля их веса) может учесть УС при принятии решения, тем меньше темп принятия решений. При моделировании этот блок не использовался и в данной работе рассматриваться не будет.
В УС могут быть средства для априорного анализа последствий альтернативных выбираемых действий на несколько шагов вперед.
Таков в самых общих чертах алгоритм управления, реализуемый УС в методе ААУ. Основные свойства процесса управления состоят в том, что УС автоматически накапливает эмпирические знания о свойствах предъявленного ей объекта управления и принимает решения, опираясь на накопленные знания. Качество управления растет по мере увеличения объема накопленных знаний. Заметим также, что управление состоит не в том, что УС реагирует на входную информацию (в определенном смысле - отрицательная обратная связь), а в том, что УС постоянно активно ищет возможный в текущих условиях способ улучшить состояние ОУ (положительная обратная связь). Тем самым УС ААУ обладает внутренней активностью.
При создании приложений может быть целесообразным использование УС ААУ для управления только в тех областях пространства признаков, в которых ранее используемые методы неэффективны. Другими словами, полезно разделить признаковое пространство на две области: на область, для которой имеется априорная информация о свойствах ОУ, и в которой можно применить подходящую детерминированную систему управления, и на область, в которой нет априорной информации о свойствах ОУ, где требуется адаптация в реальном времени управления, в этой области целесообразно управление по методу ААУ.
1.4. Основные понятия и обозначения.
Каждый вход и выход блока среды U представляется в
математической модели, вообще говоря, случайным вектором, а совокупность
случайных векторов, параметризованных временем 
,
образуют процесс. Кроме того, выделим вторую категорию процессов, в которую
входят процессы, сформированные параметризованными СВ - выходами внутренних
элементов блоков УС. Например, для ФРО и, вообще, всех блоков, состоящих из
нейронов, это выходы всех нейронов. В полной математической модели среды U,
процесс, представляющий выходы всех нейронов УС и выходы внутренних блоков
среды W , назовем процессом среды U.
В дальнейшем мы будем пользоваться следующими обозначениями:
T – конечный временной интервал жизни системы;
- параметр
времени;
- начальный
момент времени работы УС;
– входной
процесс, входной процесс для ФРО, а значит и для УС;
– i – ая
компонента 
;
- реализация
входного процесса, или входной фильм, определенный на интервале времени 
;
– i – ая
компонента 
;
– процесс
среды, выход блока среды W;
– i – ая
компонента ;
– процесс ФРО,
совокупность выходов всех нейронов блока ФРО на интервале ;
– i - ая
компонента 
;
– процесс
управляющих воздействий на среду 
со
стороны УС, где
Y – множество допустимых воздействий на среду со стороны УС;
F – множество образов аппарата ФРО.
1.5. Алгебра образов.
В качестве алгебраических операций над образами мы будем
использовать операции трехзначной логики, которая является расширением обычной
логики с двумя значениями: истина и ложь, обозначаемые далее как
1 и 0 соответственно, и имеет третье значение: неопределенность или . Здесь приведены таблицы
для операций трехзначной логики. Первый столбец содержит значения первого
аргумента, первая строка – второго.
|
|
1 | 0 |
|
| 1 | 1 | 0 |
|
| 0 | 0 | 0 | 0 |
|
|
|
|
|
Таблица 1.5.1
|
|
1 | 0 |
|
| 1 | 1 | 1 | 1 |
| 0 | 1 | 0 |
|
|
|
|
|
|
Таблица 1.5.2
|
|
1 | 0 |
|
| 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
|
|
|
|
|
Таблица 1.5.3
Отрицание 
для
неопределенности дает неопределенность, для остальных значений – то же самое,
что и в двузначной логике. Для удобства мы полагаем, что результат операции в
момент 
есть неопределенность по
определению.
2. Моделирование среды.
Для экспериментальной проверки метода автономного адаптивного управления необходимо создать математическую модель среды, достаточную для имитации реакции и поведения реальной среды на некотором уровне, приемлемом для данной управляющей системы. Но проверка является не единственной задачей, решаемой с помощью модели среды. Во-первых, если на начальном этапе в базе знаний УС нет знаний, ее необходимо наполнить начальными данными. Возможны случаи, когда получение исходных знаний невозможно во время реальной работы УС, поскольку оно происходит методом проб и ошибок и существует реальная угроза гибели всей системы. Поэтому начальное обучение в таких случаях необходимо проводить “на стенде”, т.е. с моделью среды. Естественно, чем ближе модель к свойствам реальной среды, тем лучше обучится УС и тем выше вероятность выживания системы. Моделировать среду можно множеством способов. Например, сделать макет объекта управления, поместить его в условия, близкие к тем, где он предназначен работать и дать ему возможность обучаться, пока у экспериментаторов не будет уверенности в живучести аппарата и в способности к адаптации в том диапазоне внешних условий, где он предназначен работать. Но на пути создания реальной действующей системы возможно несколько промежуточных этапов. Представим, что система создается “с нуля” и известна только некоторая априорная информация о среде и, возможно, какие-то представления о законах управления. Создавать сразу действующий макет дорого, поскольку на данном этапе даже не известно, какие образы УС должна уметь распознавать, и, возможно, придется делать несколько эспериментальных прототипов. Для исследования данного вопроса предлагается смоделировать среду, например, с помощью ЭВМ.
Как одну из моделей среды для исследований свойств ААУ мы предлагаем взять конечный автомат [КА]. КА является широко известным, хорошо изученным, понятным и удобным при моделировании среды объектом по следующим соображениям: 1) различные состояния среды естественным образом отображаются в состояния КА; 2) переходы из одного состояния среды в другое под воздействием УС и других объектов естественным образом отображаются в переходы КА между состояниями при чтении входного слова. Отметим, что среди известных и распространенных КА наиболее подходящими для модели являются автоматы Мура и недетерминированные автоматы Рабина-Скотта или НРС-автоматы. Правда, модели, основанные на первых, нуждаются в дополнительном введении стохастических источников, а НРС-автоматы нуждаются в модификации, поскольку реальные среды являются недетерминированными объектами. Более того, недетерминированность модели среды необходима для обучения УС. В самом деле, если бы реакция среды была полностью детерминированной и зависела только от воздействий на нее УС, то УС, найдя первый закон управления, использовала бы только его при выборе управляющих воздействий, так как по критериям системы управления лучше использовать хоть какой-нибудь закон управления и получить относительно гарантированный результат, чем продолжать поиски методом проб и ошибок. Получился бы замкнутый порочный круг: система воздействует на среду только одним способом, среда детерминированно реагирует на это воздействие, УС видит только одну реакцию (которая может быть не самой лучшей) и пытается вызвать только эту реакцию. Избежать таких “зацикливаний” можно посредством моделирования недетеминированной реакции среды.
Приведем определение автоматов Мура [КА] и введем модифицированные НРС-автоматы.
Определение 2.1. (Конечный) автомат Мура есть
пятерка А = (Z, X, Y, f, h). Здесь Z
– множество состояний, X – множество входов, Y – множество
выходов, f – функция переходов, 
и
h –функция выходов, 
-
сюръективное отображение.
Автомат работает по следующему принципу. Если КА находится в
некотором состоянии 
, то выход
автомата определяется функцией выхода. Выход автомата интерпретируется в
данном случае как реакция среды, которая, возможно, с некоторыми
преобразованиями в блоке датчиков может быть подана на вход аппарата
формирования и распознавания образов как двоичный вектор. В каждый момент
времени автомат читает входное слово, которое интерпретируется как суммарное
воздействие со стороны УС и других внешних объектов. Множество входов может
быть шире чем множество допустимых воздействий на среду со стороны УС и
включать в себя слова или команды, которые могут подаваться со стохастических
источников, находящихся внутри среды. По прочитанному входному слову и
функции переходов определяется состояние в следующий момент времени.
Определение 2.2. (Конечный) модифицированный
недетерминированный автомат Рабина-Скотта (МНРС) есть семерка А = (Z,
X, T, S, F, h, p). Здесь Z и X
– конечные множества (состояний и входов соответственно; X называют
также входным алфавитом автомата А); 
(множества
начальных и финальных состояний соответственно); 
, где 
, 
(иначе говоря T –
многозначное отображение 
с
конечной областью определения); h – то же, что и для автомата Мура; p
– функция вероятности переходов, 
,
причем
. (2.1)
Отметим, что мы рассматриваем только неалфавитные
МНРС, т.е. КА, у которых нет переходов для пустого слова : 
, а, следовательно, нет и спонтанных
переходов. Отличительной особенностью МНРС является неоднозначность
переходов или возможность соответствия одной и той же паре состояние - входное
слово нескольких переходов и приписанной каждому переходу вероятности. Условие
(2.1) означает, что сумма вероятностей всех переходов из любого состояния есть
1.
Отличие принципа действия МНРС от автомата Мура состоит в том, что, когда автомат находится в некотором состоянии и прочел входное слово, то реализуется один из возможных из данного состояния и при данном входном слове переход, при этом вероятность реализации перехода определяется функцией p.
Приведенные две модели среды с двумя разными КА не являются эквивалентными и задают разные модели поведения. Очевидно, что любая модель с автоматом Мура может быть смоделирована моделью с МНРС, причем обратное утверждение для любой модели неверно. Автомат Мура проще в реализации и исследованиях, а с помощью МНРС можно построить более точную модель среды.
3. Аппарат формирования и распознавания образов.
3.1. Биологический нейрон.
На рис. 3.1.1, взятом из [Turchin] представлен в упрощенном виде биологический нейрон. Схематично его можно разделить на три части: тело клетки, содержащее ядро и клеточную протоплазму; дендриты – древовидные отростки, служащие входами нейрона; аксон, или нервное волокно, - единственный выход нейрона, представляющий собой длинный цилиндрический отросток, ветвящийся на конце. Для описания формальной модели нейрона выделим следующие факты:
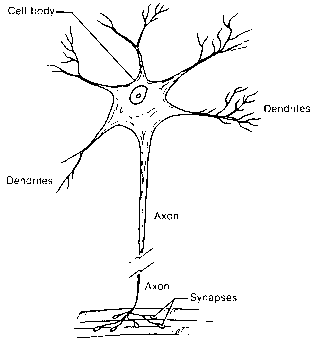
Рис. 3.1.1
В любой момент возможны лишь два состояния волокна: наличие импульса и его отсутствие, так называемый закон “все или ничего”.
Передача выходного сигнала с аксона предыдущего нейрона на дендриты или прямо на тело следующего нейрона осуществляется в специальных образованиях – синапсах. Входные сигналы суммируются с синаптическими задержками и в зависимости от суммарного потенциала генерируется либо нет выходной импульс – спайк.
3.2. Формальная модель нейрона.
Впервые формальная логическая модель нейрона была введена Маккалоком и Питтсом в 1948 году [Маккалок] и с тех пор было предложено огромное количество моделей. Но все они предназначены для решения в основном задач распознавания и классификации образов. Можно указать целый ряд основных отличий предлагаемой в данной работе модели и уже существующих. Во-первых, в классических моделях всегда присутствует “учитель” или “супервизор”, подстраивающий параметры сети по определенному алгоритму, предлагаемый же нейрон должен подстраиваться “сам” в зависимости от “увиденной” им последовательности входных векторов. Формально говоря, при работе нейрона должна использоваться только информация с его входов. Во-вторых, в предложенной модели нет вещественных весов и взвешенной суммации по этим весам, что является большим плюсом при создании нейрочипа и модельных вычислениях, поскольку целочисленная арифметика выполняется всегда быстрее, чем рациональная и проще в реализации. Главное же отличие предлагаемой модели состоит в цели применения. C помощью нее решаются все задачи управляющей системы: формирование и распознавание образов (ФРО), распознавание и запоминание закономерностей (БЗ), анализ информации БЗ и выбор действий (БПР), в отличии от классических моделей, где решается только первая задача.
Важной задачей ФРО для автономных систем также является не только распознавание образов, но и их хранение или запоминание. Это следует из автономности системы, т.к. для неавтономных систем распознанные образы могут храниться и использоваться вне системы. Вообще говоря, проблему запоминания можно решить множеством способов. Например, один из известных способов – организовать кольцо из нейронов, в котором сигнал мог бы прецессировать до бесконечности или в течении некоторого времени в случае затухания. В последнем случае система приобретает новое полезное свойство “забывчивости”, которое, как известно, присуще биологическим системам и позволяет более рационально и экономно использовать ресурсы, т.к. ненужная или малоиспользуемая информация просто “забывается”. Эксперименты проводились с формальной моделью без памяти, но очевидно, что она нужна. Нами предлагается ввести так называемую синаптическую память, т.е. способность запоминать входной сигнал в синаптическом блоке.
В данной работе мы используем нейрон из [Жданов2], который модифицирован в соответствии с [Братищев]. Мы приведем лишь краткое описание. На рис. 3.2.1 представлена блочная схема предлагаемой формальной модели нейрона. Входы нейрона xit подаются на блоки задержки Di для задержки сигнала на время Di , а затем на триггерные элементы Ti для удлинения сигнала на величину ti . Данные элементы обеспечивают некоторую неопределенность момента поступления входного сигнала по отношению к моменту генерации выходного спайка и образуют таким образом синаптическую память, поскольку входной сигнал запоминается в этих элементах на некоторое время.
С учетом задержек Di и ti получаем, что, если на выходе обученного нейрона в момент t появился единичный сигнал, то единичные импульсы на входы нейрона поступили в интервалы времени di = [ t - ti - Di ; t - Di -1]. Неопределенность моментов поступления входных импульсов будет тем меньше, чем меньше задержки ti.
Пример временной диаграммы работы обученного нейрона с двумя входами и с заданными задержками Di и ti иллюстрирует рис. 3.2.2. Вопросительными знаками показаны неопределенности моментов прихода входных импульсов, соответствующие интервалам di.
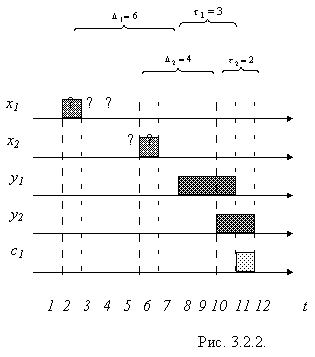
Различное отношение и расположение задержек Di и ti во времени наделяет нейрон возможностями формирования и распознавания образов следующих видов.
Если 
, то
имеем пространственный образ. Например, образ некоторой геометрической фигуры.
Если 
, то
имеем образ следования (важен порядок следования образующих, допустима
неопределенность в конкретных моментах прихода импульсов). Примером может быть
распознавание слов при чтении по буквам.
Если " ti = 1, то имеем пространственно-временной образ (ПВО), в этом случае однозначно определено, по каким входам и в какие моменты времени приходили сигналы. Примером может быть распознавание музыкального тона определенной высоты.
Элемент lw предназначен для набора статистики по данному пространственно-временному образу. Значение lw=1 указывает на то, что данный нейрон обучен.
Задержки Di и ti заданы изначально, т.е. являются константными параметрами нейрона. Если поступающая на данный нейрон последовательность сигналов содержит закономерность, описываемую такими временными параметрами, то нейрон сформирует образ такого пространственно-временного прообраза. Очевидно, что необходимое число нейронов такого типа в сети будет тем меньше, чем больше априорной информации о временных характеристиках прообразов известно на стадии синтеза сети.
Приведем формализм нейрона.
Owt+1 = cwt+1 & Swt+1 ;
cwt+1 = bwt+1 & lwt+1 ;
bwt+1 =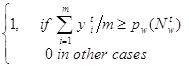 
yit = ù cwt & ait ;
ait = 
;
где 
= tï xit = 1 -
момент импульса на входе xi ;
lw t =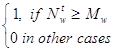 
;
Nw0 = 0;
Nwt = Nwt-1 + bwt ;
Rw(Nwt) - убывающая сигмоидальная функция.
3.3. Задача построения ФРО.
Для того, чтобы более правильно и экономно построить нейронную сеть ФРО, необходимо понять смысл или “концепцию” [Turchin] формируемых образов, т.е., более точно выражаясь, найти для данного образа множество обучающих входных фильмов или множество всех таких реализаций входных процессов, которые приводят к обучению данного нейрона или формированию данного образа. Введем понятие обучающего входного фильма.
Определение 3.3.1. Всякий входной фильм назовем обучающим
для нейрона 
, если 
- начальный момент времени
работы системы и 
, 
.
Таким образом, задачу построения НС ФРО можно сформулировать
следующим образом: для данной совокупности входных фильмов построить такую
сеть, в которой бы присутствовали нейроны, для которых данные входные фильмы
являются обучающими. Построенная таким образом сеть способна решать эталонную
задачу классификации, где в качестве эталонов используются данные входные
фильмы. Известно множество способов конструирования и настройки сетей для
классических формальных моделей нейронов, например, сети обратного распространения,
использующие обобщенное -правило.
Проблема предлагаемого подхода состоит в том, что 1) система должна быть
автономной, а значит отсутствует “учитель”; 2) вообще говоря, a priori не
известны все жизненно необходимые для системы образы. Но если мы обладаем
априорной информацией об условиях существования системы (что почти всегда
бывает), ее следует использовать при конструировании ФРО.
Можно иначе сформулировать задачу построения ФРО. Приведем
пример с системой “Пилот” [Диссер, Жданов9]. В математической модели спутника
используются величины углового положения спутника 
и
его производной 
, следовательно,
очевидно, что всевозможные сочетания возможных значений этих величин (т.е.
некоторая область на фазовой плоскости) необходимы для нахождения законов
управления системой. Действительно, допустим система в момент времени t
находится в состоянии 
и УС выбирает
некоторое управляющее воздействие 
(включение
одного из двигателей, например). Мы знаем, что в момент времени 
система окажется в
некотором состоянии, соответствующем точке на фазовой плоскости с некоторой
вероятностью 
, где 
- точка на фазовой
плоскости, таким образом, можно говорить о некотором вероятностном распределении
, заданном в фазовом
пространстве и характеризующем предсказание поведения системы через интервал 
при выборе воздействия в момент времени t.
Если бы параметров 
было недостаточно
для описания законов управления, то функция распределения зависела бы еще и от
других параметров, и при одних и тех же величинах 
принимала
бы другие значения в зависимости от значений неучтенных параметров.
Следовательно, УС не смогла бы найти никакого закона управления, поскольку
система ищет статистически достоверную корелляцию между наблюдаемым состоянием
ОУ, выбранным действием и состоянием ОУ через некоторый интервал времени.
Законом управления здесь мы назовем совокупность функций распределения для
каждого управляющего воздействия 
, где находится в некотором
диапазоне. Найденный УС закон управления отобразится в некотором внутреннем
формате в БЗ, причем он может быть получен в процессе обучения системы в
реальных условиях прямо во время работы, либо на тестовом стенде, “на земле”.
Следовательно, можно сказать, что задача построения ФРО состоит в
конструировании образов, соответствующих необходимому набору параметров,
описывающих состояние системы, и их комбинациям, необходимым для нахождения
закона управления. Нахождению таких образов может помочь математическая модель
объекта управления, если таковая имеется.
3.4. Распознавание пространственно-временных образов.
Определение 3.4.1. Всякую совокупность значений
реализации входного процесса в некоторые выбранные интервалы времени 
будем называть пространственно-временным
образом (ПВО).
Отметим, что один нейрон способен распознавать (т.е. способен обучиться выделять конкретный ПВО среди всех остальных) только те ПВО, у которых единичное значение сигнала для каждой выбранной компоненты входного процесса встречается не более одного раза (пример изображен на верхнем графике рис. 3.4.1). Сеть нейронов можно построить так, что в ней будут формироваться любые заданные ПВО (нижний график рис. 3.4.1).
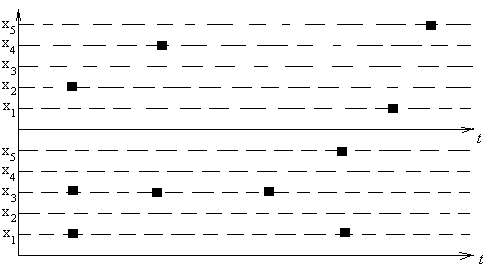
Рис 3.4.1.
4. База знаний.
Процесс накопления знаний БЗ в рамках методологии ААУ подробно рассмотрен в [Диссер], [Жданов4-8]. В данном разделе мы опишем лишь основные отличия от указанных источников.
Рассмотрим общий алгоритм формирования БЗ. Основная цель алгоритма состоит в накоплении статистической информации, помогающей установить связь между выбранными управляющей системой воздействиями на среду и реакцией среды на эти воздействия. Другая задача алгоритма состоит в приписывании оценок сформированным образам и их корректировки в соответствии с выходным сигналом блока оценки состояния.
Определение 4.1. Будем называть полным
отсоединением ФРО от среды следующее условие: процессы и являются независимыми.
Вообще говоря, в действующей системе, конечно же эти процессы зависимы,
например, в простом случае без блока датчиков 
,
но для введения некоторых понятий требуется мысленно “отсоединить” входной
процесс и процесс среды.
Определение 4.2. Назовем временем реакции среды на
воздействие число 
, где 
случайные величины 
и являются зависимыми при полном
отсоединении ФРО от среды. Закономерностью или реакцией среды
будем считать зависимость от .
Другими словами, время реакции среды это время, через которое проявляется, т.е. может быть распознана блоком ФРО, реакция на воздействие.
Пример 4.1. 
=
. Очевидно, что здесь 
.
Определение 4.3. Назовем минимальной 
и максимальной 
инертностью среды
минимальное и максимальное соответственно время реакции среды на воздействие для всех . Интервал 
будем называть интервалом
чувствительности среды.
Заметим, что 
.
Введем совокупность образов
. (4.1)
Параметр n > 0 назовем запасом на инертность
среды. Смысл 
состоит в том,
что если обучен, в текущий момент
времени распознан образ 
и УС
выберет воздействие то с некоторой
вероятностью через n шагов распознается образ 
. Аналогично введем образ
, (4.2)
смысл которого совпадает со смыслом , с тем лишь различием, что не распознается, а
вытеснится. Поскольку в конечном итоге способом управления УС является вызов
определенных образов и вытеснение других, то совокупность обученных образов 
является материалом,
способствующим достижению цели управления, то есть вызову или вытеснению
определенных образов посредством выбора воздействия из
множества возможных воздействий Y на каждом шаге t. Как
используется этот материал будет изложено в разделе “Блок принятия решений”.
Запас на инертность введен из следующих соображений.
Совершенно очевидно, что бесполезно пытаться уловить закономерность вида “был
распознан образ , применили и через m шагов
получили ”, где 
, так как среда будет просто
не успевать отреагировать. Таким образом, УС может уловить закономерности со
временем реакции среды не большим чем n. Аналогично, нет смысла выбирать
n слишком большим, т.е. гораздо большим, чем .
С другой стороны, используя синаптические задержки входных сигналов в нейроне,
мы можем отловить любую закономерность со временем реакции меньшим либо равным
запасу на инертность. Действительно, мы можем построить ФРО так, чтобы образы и формировались с нужными
задержками 
, где m – время
реакции среды. Заметим, что a priori нам неизвестно время реакции среды m,
поэтому имеет смысл лишь выбрать параметр n для всех образов одинаковым
и “наверняка” большим чем (для
этого необходимо воспользоваться априорной информацией о среде).
Теперь сопоставим каждому образу из ФРО некоторое число или оценку.
Пусть 
– выход блока оценки
состояния, а 
– оценка образа , получающаяся по следующему
алгоритму:
, 
,
где 
– некоторая
“усредняющая” функция, 
- множество
моментов времени, в которые образ был
распознан. В качестве обычно берется
просто среднее арифметическое
.
Теперь можно определить, что такое база знаний.
Определение 4.4. Назовем базой знаний
совокупность сформированных образов и
совокупность оценок для всех образов
ФРО.
Определение 4.5. Обозначим объединение множеств всех
образов (4.1) и (4.2) через 
, где F
– множество образов ФРО, Y – множество возможных воздействий. Назовем B пространством
образов БЗ.
5. Система построения и исследования нейронных сетей СПИНС.
5.1. Актуальность системы.
Для моделирования на ЭВМ компонентов УС, сконструированных из нейронов, была осознана необходимость в специальном инструменте, позволяющем с помощью удобного графического интерфейса создавать библиотеки шаблонов блоков, строить сети из блоков, построенных по шаблонам, и просчитывать сеть с возможностью просмотра промежуточных состояний сети, сбора и анализа статистики о работе сети в целях отладки. При создании (или выборе) инструмента использовались следующие критерии:
открытость, или спецификация и реализация (generic) интерфейса и (процедур обработки) форматов данных, позволяющие проводить модификацию и наращивание функциональности системы не затрагивая ядра системы и с минимальными затратами на модификацию связанных компонент, другими словами, минимизация связей между компонентами;
гибкость, возможности по конструированию как можно большего числа классов формальных моделей нейронов и сетей под самые различные приложения от моделей УС спутников и космических аппаратов до систем поддержки принятия решений и систем предсказания курса ценных бумаг;
многоплатформенность, максимальная независимость от операционной системы;
удобство и приспособленность к моделированию именно систем ААУ, простота в использовании и способность эффективно работать на относительно слабых ресурсах ЭВМ (класса персональных компьютеров), дешевизна.
Анализ имеющихся в наличии или доступных систем САПР и других систем (например, LabView или систем с классическими НС), тем или иным образом удовлетворяющих первым трем критериям, показал, что все они являются либо тяжеловесными, либо слишком дорогими, либо очень плохо приспособлены к моделированию систем ААУ и ОУ с формальной моделью нейрона, изложенной в разделе “Аппарат ФРО” или к работе с сетями, состоящими из тысяч нейронов. Таким образом, возникла необходимость в инструменте для научно-исследовательских целей, который бы позволял проверять идеи ААУ и создавать прототипы УС на НС.
5.2. Общая концепция системы.
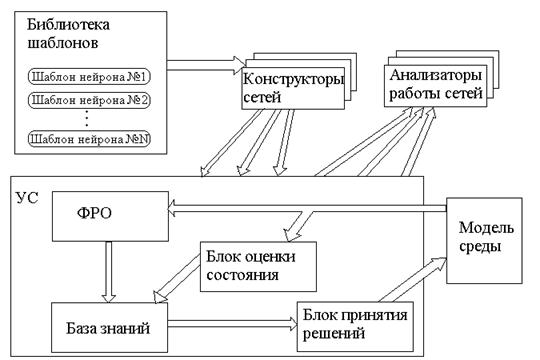
Рис. 5.1. Общая схема ядра СПИНС.
На приведенной схеме (рис 5.1) указаны основные классы объектов ядра системы и их взаимодействие. Стрелками показаны потоки данных при работе системы. Каждому из основных блоков УС соответствует свой блок в системе. Четыре блока: ФРО, БЗ, БОС и БПР составляют УС. Напомним, что в подразделе “Формализация НС” раздела 1 мы определили такие понятия как блок, выходная функция блока, шаблон, нейронная сеть и формальная модель нейрона. Из формальной модели НС следует, что блок – это иерархическая структура, в которой элементы одного уровня соединены в сеть и каждый из элементов уровня может быть сетью, состоящей из элементов более низкого уровня. Рассматривая выбранный элемент какого-нибудь уровня, можно считать его “черным ящиком”, т.е. абстрагироваться от его содержимого и внутреннего устройства. Например, можно на некотором промежуточном этапе конструирования УС абстрагироваться от нейро-сетевой реализации какого-либо блока верхнего уровня и попробовать различные реализации, причем необязательно нейросетевые. Система не накладывает ограничений на внутреннее устройство каждого блока, поэтому оно может не иметь внутренней иерархии, а просто представляться некоторой функцией выхода. Далее, в процессе развития УС, содержимое отдельных блоков может поменяться, возможно стать более сложным и иерархическим, при этом поведение системы не изменится, если новое содержимое обеспечивает функциональность старого в смысле эквивалентности выходных функций. Таким образом, облегчается разработка системы, т.к. появляется возможность конструирования “сверху вниз”, нет необходимости реализовывать блок сразу через НС, можно поставить временную “заглушку”, а в процессе развития системы усложнять, дополнять или заменять на совершенно иную внутреннюю конструкцию блоков.
Помимо указанных блоков, в систему входят еще два важных класса объектов: конструкторы сети и анализаторы работы сети. Первые, как видно из названия, предназначены для создания рабочих копий НС в памяти компьютера по различным источникам, например по спецификации сети из файла. Собственно, для каждого источника и создается свой объект. (Следует отличать данные объекты от конструкторов сетей, предназначенных для создания с помощью ГИП файлы спецификации сетей; эти конструкторы в ядро СПИНС не входят). Спецификация сети может ссылаться на шаблоны блоков из библиотеки, которые, таким образом, также могут являться источником для конструкции. Анализаторы нужны при отладке сетей. Дело в том, что сети могут содержать тысячи и десятки тысяч элементов (принципиальных ограничений нет,имеют место ограничения только по памяти и производительности компьютера), работу которых одновременно проследить просто невозможно, особенно если временной интервал работы составляет сотни и более тактов. Поэтому необходимо как-то обобщать информацию о состоянии сети (которое есть совокупность состояний каждого элемента) в каждый момент времени и выдавать пользователю суммарную информацию, возможно, с некоторой детализацией по усмотрению пользователя. Для такой задачи и нужны специальные объекты – анализаторы. Эти объекты могут сохранять историю состояний выбранных элементов в выбранные интервалы времени и впоследствии ее анализировать, т.е. определять статистического рода информацию. Каждый объект решает эту задачу по-своему и может быть выбран в зависимости от рода необходимой информации о работе сети.
Отметим здесь на наш взгляд очень полезную классификацию объектов на инструменты и материалы [СтатьяИнстрМатериалы]. Материалами называются объекты, являющиеся своего рода контейнерами информации и содержащие методы только для накопления и несложных преобразований этой информации. Инструментами называются объекты, предназначенные для обработки материалов, т.е. для более интеллектуальных и сложных преобразований той информации, которую хранят объекты - материалы. Таким образом, с точки зрения этой классификации, мы считаем нейронные сети (блоки) материалами, а конструкторы и анализаторы – инструментами. Следует не путать эти инструменты-объекты с инструментами–приложениями, являющимися надстройками над ядром.
В реализации программы мы существенно использовали идеи объектных шаблонов из [Gamma]. Далее, в описании реализации системы мы будем использовать русскоязычные аналоги терминов, введенных в [Gamma], поэтому, чтобы не возникло путаницы, отметим, что Фабрика соответствует Factory, объектные шаблоны – design patterns, Синглетон – Singleton, Chain of Responsibility – Цепочка Обработчиков. Названия классов объектов будут выделены курсивом и начинаться с заглавной буквы. Отметим, что идея шаблонов в программировании и computer science оказалась весьма плодотворной и слово “шаблон” здесь мы используем в трех различных смыслах: объектный шаблон (design pattern), просто шаблон (в смысле определения 1.x.5) и C++ - шаблон (template).
Мы опишем только реализацию ядра системы. Следование принципам открытости предполагает закладывание возможности развития системы через добавление надстроек над ядром (рис. 5.2). Мы, по возможности, старались следовать данному принципу. В частности, одним из направлений развития мы видим создание конструкторов библиотек шаблонов (а, следовательно, и сетей) с помощью ГИП. Предполагается, что выходным продуктом этих конструкторов будут файлы спецификации шаблонов, с которыми уже умеет работать ядро, из которых и будут формироваться библиотеки шаблонов. Далее, можно было бы создать трехмерный визуализатор БЗ (об этом далее), также мы считаем, понадобится отдельный инструмент для конструирования самих БЗ, а, возможно, при определенном уровне сложности блоков УС, и для каждого из них по отдельному инструменту, которые бы учитывали в полной мере специфику блоков УС.
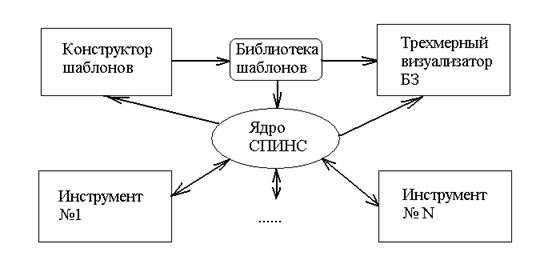
Рис. 5.2.
5.3. Конструкторы сетей. Библиотеки шаблонов.
Как уже было отмечено, конструкторы сетей ядра СПИНС предназначены для создания внутреннего представления сети в памяти компьютера по различным источникам. Здесь будет рассмотрен только один - конструктор по файлу-спецификации сети, но мы не исключаем возможности создания конструкторов, использующих другие источники.
Конструктор по сути своей является фабрикой объектов класса ЭлементСети.
Идея фабрики состоит в следующем. Поскольку конструирование сети состоит в
порождении огромного числа разнородных объектов ЭлементСети, то
необходим объект для регулировки процесса порождения и смерти этих объектов,
или фабрика элементов сети. То есть на Фабрику также возложены функции сборщика
мусора. Регулировка или управление процессом порождения состоит в
следующем. Мы имеем много разных потомков класса ЭлементаСети, например,
Нейрон, который, в свою очередь имеет несколько подклассов,
соотвествующих каждой из разновидностей формальных моделей, а также другие
элементы сети Блок, Источник, имеющий также несколько своих
подклассов и т.д. Предположим, мы модифицировали или создали новую версию
класса A из перечисленных классов - 
.
Тогда в каждом месте исходного текста мы должны заменить оператор порождения A
на оператор порождения . Более гибкой
является следующая схема. Фабрика1 умеет, или точнее выражаясь, имеет
методы для порождения объектов классов А, B, C и т.д. При
сообщении о порождении, например, объекта типа А, она порождает на самом
деле объект потомка А: , а Фабрика2
порождает в данном случае 
. Таким
образом, заменой только фабрик мы можем менять классы порождаемых объектов.
Отметим, что фабрика на языке C++ естественным образом реализуется через С++ -
шаблон (template) и параметризуется типом порождаемых объектов. Ссылка
на ФабрикуЭлементовСети, умеющую порождать каждый из конечных потомков ЭлементСети,
хранит объект Сеть. При инициализации КонструктораСети ему
сообщается ссылка на Сеть. Естественно, Сеть еще не содержит ЭлементовСети,
но уже должна иметь ссылку на ФабрикуЭлементовСети. При конструировании
сети по файлу спецификации КонструкторСетиПоФайлу (подкласс КонструктораСети)
использует методы порождения объектов ФабрикиЭлементовСети, ссылку на
которую он берет у Сети.
Отметим здесь, как решена была проблема передачи параметров конструктору (инициализатору, особому методу, вызывающемуся первым после размещения объекта в памяти) элемента сети и, вообще, конструктору любого объекта, порождение и удаление которого находится под управлением фабрики. Проблема состоит в унификации типа передаваемых параметров: они должны быть одни и те же для всех типов элементов сети. Был введен класс Атрибут и методу порождения объекта у фабрики и, соответственно, конструктору объекта передавался список Атрибутов. Каждый Атрибут имеет имя, и конструктор каждого элемента сети распознает только некоторое подмножество подклассов Атрибута, “свои атрибуты”, которые узнает по имени. Например, АтрибутВероятности является подклассом Атрибута, имеет свое поле рационального типа вероятность. Конструктор Нейрона2 распознает АтрибутВероятности в переданном списке атрибутов и использует значение его поля вероятность для инициализации Нейрона2. Для атрибутов также понадобилась ФабрикаАтрибутов.
При создании Фабрики был использован еще один объектный шаблон, так называемый Синглетон. Синглетон решает задачу обеспечения единственности экземпляра класса и управляет доступом к этому экземпляру.
Теперь о самой спецификации. При создании языка спецификации ставились следующие задачи:
Максимум широты спектра описываемых сетей, или максимальная гибкость языка
Относительная простота и удобочитаемость
Минимальная длина спецификаций
Возможность развития языка
В качестве элементарного примера смоделирована нейросеть из четырех нейронов, с помощью которых могут быть сформированы образы соответственно четырех состояний КА среды. Для данного примера спецификация имеет следующий вид:
[Meta]set for Neuron2 synonym Nset for Brancher synonym I[Inputs]I1,I2,I3,I4[Outputs]I1,I2,I3,I4,N1,N2,N3,N4
[Net Topology]
set for N default connection attribute delay=0
set for N default attribute study_counter=3
DecisionMaker(actions=0,1)
StochasticSource(probability=0.1,value=2)
Max[DecisionMaker,StochasticSource]
Env[or]
I1[Env(contact_number=0,delay=1)]
I2[Env(contact_number=1,delay=1)]
I3[Env(contact_number=2,delay=1)]
I4[Env(contact_number=3,delay=1)]
N1[I2,I3,I4]
N2[I1,I3,I4](study_counter=4)
N3[I1,I2,I4]
N4[I1,I2,I3]
Пример 5.3.1. Спецификация сети.
Спецификация состоит из секций. Секция начинается с указания имени секции в квадратных скобках и состоит из операторов спецификации. В Meta секции собраны операторы, область применения которых – вся спецификация, т.е. все секции. Здесь, например, можно задать имена–синонимы для шаблонов. Во многих секциях может появляться оператор set. Обычно, его синтаксис таков:
set for <имя-приемника> <что-установить> <значение>.
Например, set for Neuron2 synonym N устанавливает имя-синоним N для шаблона Neuron2. В секциях Inputs и Outputs просто перечисляются входы и выходы сети. Самая большая секция, обычно, Net Topology, где описывается топология сети. Ссылка на элемент сети в спецификации состоит из двух слитных слов: указания имени типа элемента сети (или его синонима) и его некоторого порядкового номера, причем нумерация для каждого типа своя. Описание топологии состоит из операторов описания топологии, в которых указывается некоторый элемент сети, его входы в квадратных скобках, причем в круглых скобках после указания каждого входа может стоять ассоциативный список (т.е. список пар имя-значение) атрибутов связи, и, дополнительно, после перечисления входов, может быть, в круглых скобках ассоциативный список атрибутов элемента. Каждая связь двух элементов сети может характеризоваться некоторым множеством атрибутов связи. Например, атрибутом связи может быть синаптическая задержка. Каждый элемент сети понимает свой набор атрибутов связи, некоторое множество атрибутов связи обрабатывается ядром системы, и, как мы уже упомянули, каждый элемент сети понимает свой набор атрибутов (элемента сети), значения которых могут передаваться в списке атрибутов элемента.
В примере спецификации 5.1 используются имена некоторых встроенных шаблонов, например, Neuron2 или Brancher. Вообще говоря, ядром поддерживается некоторое множество встроенных базовых шаблонов и в языке есть конструкция для определения новых шаблонов через уже определенные или встроенные. Информация об уже определенных шаблонах хранится в специальном объекте БиблиотекаШаблонов, являющемся Синглетоном и имеющем методы для получения идентификатора шаблона по его имени, извлечения информации о шаблоне по его идентификатору, а также добавления / удаления шаблонов. Если КонструкторСети при чтении спецификации встречает имя шаблона или конструкцию определения нового шаблона, то он обращается к БиблиотекеШаблонов для, соответственно, получения информации о шаблоне по имени или для добавления нового шаблона. Таким образом, пользователь может создавать библиотеки своих шаблонов, определения которых хранятся, например, в файлах и при их использовании просто включать соотвествующие файлы в своих спецификациях с помощью конструкции языка, аналогичной “#include” в языке C / C++. Отметим, что библиотечные файлы шаблонов могут создаваться специальным инструментом, конструктором шаблонов.
5.4. Организация вычислений в сети.
После создания внутреннего представления сети в памяти в виде совокупности связанных между собой элементов сети, сеть готова к вычислениям. Вычисления инициируются с некоторого выбранного подмножества элементов сети, называемых выходами сети. Каждый элемент имеет свой метод, реализующий операцию данной вершины сети и результат которого интерпретируется как значение выходного сигнала или значение выхода. Аргументами этого метода являются значения выходов у входов элемента в предыдущие моменты времени, и, возможно, в текущий момент. При этом, естественно, возможен бесконечный цикл в случае неправильной спецификации сети. На этот случай в систему предполагается добавить некоторый предварительный анализатор корректности топологии сети. Распараллеливание здесь возможно при вычислении значений выходов для элементов одного порядка, поскольку они являются независимыми.
Так как параметр времени в систему введен явно, существует
необходимость в сообщении каждому элементу о наступлении следующего такта
вычислений. При получении такого сообщения, каждый элемент выполняет завершительные
операции для данного такта либо может просто проигнорировать сообщение. В
реализации механизма передачи сообщений использован объектный шаблон Цепочка
Обработчиков [Gamma]. Суть его состоит в следующем. Предположим существует
некоторая иерархия классов или цепочка, где каждый предшествующий класс
является родительским для следующего, например ЭлементСети 
Нейрон Нейрон2. У ЭлементаСети
определен (виртуальный в терминах языка C++) метод обработки сообщения обработать_сообщение(Сообщение).
В этом методе у каждого класса при вызове определяется, может ли данный метод
обработать данное сообщение. Если да, то выполняется обработка. Затем в любом
случае вызывается метод обработки сообщения родительского класса, если он
существует. Например, метод обработки сообщений у ЭлементаСети
увеличивает счетчик тактов (счетчик времени) при получении сообщения СледующийТакт
(потомок класса Сообщение). Объект СредаСКонечнымАвтоматом,
являющийся потомком ЭлементаСети и КонечногоАвтомата при
получении данного сообщения выполняет чтение входного слова, и, естественно,
вызывает обработку сообщения для своих родительских классов.
5.5. Анализаторы работы сети.
Для отладки сетей часто необходимо знать разнообразную информацию о состояниии сети и отдельных ее элементов в некоторые моменты времени. Сети предполагаются гетерогенные, то есть состоящими из разных элементов-экземпляров классов-потомков ЭлементаСети, и состояние каждого элемента в некоторые моменты времени может характеризоваться, вообще говоря, некоторым своим набором параметров, помимо значения выходного и входного сигналов. Например, КА лучше охарактеризовать состоянием, в котором находится автомат. Поэтому схема была выбрана следующая: ЭлементСети является производным классом от Летописец, который имеет методы для записи объектов Событие в некоторую временную последовательность История, которую хранит каждый Летописец. В процессе работы сети каждый Летописец записывает в Историю один из своих или общих объектов подкласса Событие. Например, КА записывает помимо прочих событие СостояниеКА, в котором есть поле для указания состояния КА в данный момент времени. Каждый (потомок класса) АнализаторРаботыСети умеет обрабатывать Истории, извлекая оттуда необходимую информацию, и затем выдавая ее в удобном виде на экран. В примере 5.8.1 приведен результат работы программы, где изображена диаграмма выходных сигналов выбранных ЭлементовСети, имена которых выведены в первой строке диаграммы. Диаграмма получена как результат обработки Истории выбранных ЭлементовСети АнализаторомРаботыСети.
5.6. Реализация БОС.
Задача блока оценки состояния в конечном счете заключается в сопоставлении выходному вектору среды W некоторой оценки или числа. Фактически, речь идет о задании некоторого функционала над BN, где N - размерность выходного вектора среды W. Функционал задается как табличная функция, значения которой перечисляются в специальной секции файла спецификации. Здесь указываются типы аргумента и самой табличной функции, может быть указано значение по умолчанию, а затем перечисляются входные и соответствующие выходные значения.
[Evaluator]
set type for in BinaryVector
set type for out Integer
set default value for out=0
in=0111,out=15
in=1011,out=10
in=1101,out=5
in=1110,out=20
Пример 5.6.1. Спецификация табличной функции БОС.
Нейросетевая реализация этого блока нами не создавалась. Предполагается, что ее можно построить из двух простых подсетей, из которых одна представляет собой распознающую нейросеть, формирующую образы вектора in, а другая - комбинационную схему из нейронов, выдающую сигнал на выход с номером out в соответствии с заданным функционалом.
5.7. Реализация модели среды.
Представим среду с помощью КА Мура. Пусть КА имеет четыре состояния s1, s2, s3, s4 и представлен диаграммой Мура на рис. 5.7.1. Файл спецификации для модели среды содержит описание выходного сигнала в зависимости от состояния КА (первая часть в примере 5.7.1) и описание самого КА (вторая часть). Пятое дополнительное состояние КА initial является инициальным. Переходы указываются в виде (<исходное состояние>, <входное слово>) -> <конечное состояние>.
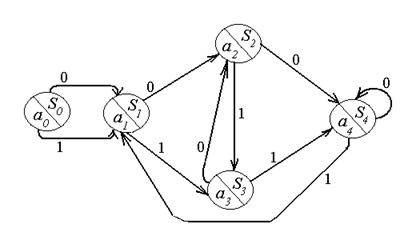
S0=initial, a0=0000, a1=0111, a2=1011, a3=1101, a4=1110
Рис. 5.7.1.
[Environment]
initial(output=1111)
s1(output=0111)
s2(output=1011)
s3(output=1101)
s4(output=1110)
[Finite State Automate]
set for word -1 synonym any
(initial,0)->s1
(initial,1)->s1
(s1,0)->s2
(s1,1)->s3
(s2,0)->s4
(s2,1)->s3
(s3,0)->s2
(s3,1)->s4
(s4,0)->s4
(s4,1)->s1
Пример 5.7.1. Спецификация модели среды.
Пример 5.8.1. Результат работы программы.
На диаграмме выведены выходные сигналы входных элементов (датчиков) I1, I2, I3, I4, нейронов N1, N2, N3, N4, БПР (DecisionMaker), БОС (Evaluator) и внутреннего элемента среды (Or), на который подаются сигналы от БПР и стохастического источника, а выход соединен с входом модели КА Мура. Множество возможных воздействий УС на среду состоит из двух элементов, обозначенных как 0 и 1. Из примеров 5.6.1 и 5.7.1 видно, что состоянием модели среды с наивысшей оценкой является s4. Из диаграммы 5.8.1 можно сделать вывод, что УС нашла закономерности управления, достаточные для удержания ОУ в состоянии s4 (t > 18), но в результате действия стохастического источника после некоторого времени пребывания в s4 ОУ перескакивает из этого состояния в s1, откуда УС снова переводит его в состояние s4.
Работу системы проиллюстрируем на рис. 5.8.1. В систему входят модель среды, состоящей из КА и Истока, и УС, состоящей из блоков ФРО, БОС, БЗ, БПР.
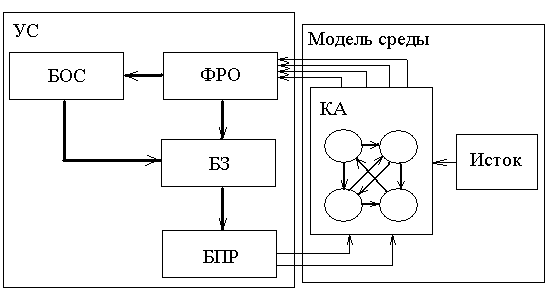
Рис. 5.8.1.
В конце примера выведена информация о состоянии БЗ, содержащей знания, эмпирически найденные УС к моменту окончания работы программы.
5.9. Перспективы развития СПИНС.
Кроме намеченных в разделе 5.1 направлений развития системы,
а именно создание конструктора сетей с графическим интерфейсом, расширение
языка спецификации сетей и др., необходима доработка и разработка нейросетевых
реализаций БЗ и БПР, разработка методов создания реальных приложений по
полученным с помощью СПИНС спецификациям сетей. Привлекательным является также
создание трехмерного визуализатора БЗ. Визуализация БЗ основана на введении
топологии в конечном пространстве образов базы знаний (определение 4.5)
посредством отображения F и Y в R, таким образом, области
в B отобразятся в области в 
.
Если образ 
, 
сформирован, то он
отображается точкой цвета, соответствующего сформировавшейся оценке образа 
. При этом в пространстве
обозначатся некоторые цветные области (рис. 5.9.1), иллюстрирующие закон
управления.
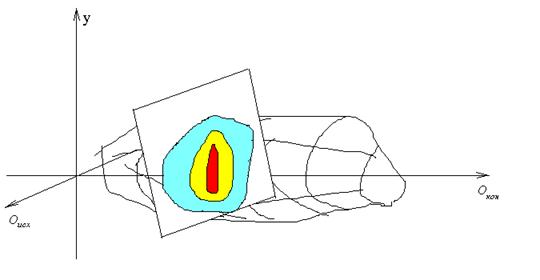
Рис. 5.9.1.
Заключение.
Основные результаты дипломной работы состоят в следующем:
Разработана концепция и реализовано ядро программной системы СПИНС для построения и исследования нейросетевой реализации прототипов управляющих систем, построенных по методу автономного адаптивного управления, созданного в отделе имитационных систем Института Системного Программирования РАН.
Доработаны аппарат формирования и распознавания образов, алгоритм заполнения базы знаний управляющей системы и алгоритм принятия решений.
Данные алгоритмы протестированы с помощью СПИНС на модельных примерах. Показано, что УС ААУ в рассмотренных примерах находит способ управления предъявленным объектом (средой) и осуществляет управление в соответствии с целевыми функциями.
Благодарности.
Автор выражает благодарность научному руководителю д. ф.-м. н. Александру Аркадьевичу Жданову за ценную поддержку и помощь в данной работе и член.-корр. РАН Виктору Петровичу Иванникову, под руководством которого были приобретены знания и опыт объектно-ориентированного программирования, в частности освоены объектные шаблоны (design patterns), использованные при разработке СПИНС.