Реферат: Автоматические устройства
Методические указания по выполнению курсовой работы
Составитель : Пономарев Б. Б. Иркутск, 1995 г.
Дана методика кинематического и динамического анализа механизмов с двумя степенями свободы. На основе примеров представлена последовательность составления дифференциальных уравнений движения механизмов, дан пример законов управления движением и определения управляющих моментов для реализации заданного движения. Предложена методика графоаналитической проверки правильности решения задач. Даны методики использования конечноразностной схемы Эйлера при решении дифференциальных уравнений на персональных компьютерах.
Предназначены для
студентов, выполняющих курсовую работу по “Механике автоматических устройств”
и обучающихся по специальностям: 2102 “Автоматизация производственных
процессов” (в машиностроении) и 2103 “Робототехнические системы”![]()
Библиогр.назв. 5. Ил. 5. Табл. 1.
Цель курсовой![]() работы - освоение методики
аналитического и графоаналитического исследования кинематики управляемого
движения автоматических устройств, приобретение опыта кинематического и
кинетостатического описания движения плоских механизмов, ознакомление с методикой
решения обратных задач динамики механических систем.
работы - освоение методики
аналитического и графоаналитического исследования кинематики управляемого
движения автоматических устройств, приобретение опыта кинематического и
кинетостатического описания движения плоских механизмов, ознакомление с методикой
решения обратных задач динамики механических систем.
Курсовая работа предусматривает решение трех самостоятельных задач :
1. Кинематика плоского механизма с двумя степенями свободы по заданному движению одной из точек.
2. Кинематика управляемого движения манипулятора.
3. Динамика механизма с двумя степенями свободы.
I. Кинематика плоского механизма. Описание задания.
У плоского механизма с
двумя степенями свободы (рис.1) движение точки М задано. Для одних вариантов
точка М движется по линии ав горизонтально со скоростью VMX=V1
sin (pt+a); VMY=0, для
других - вертикально со скоростью VMX=0; VMY=V1
sin (pt+a). Здесь p=![]() , t
, t![]() период.
период.
Исходные данные определяются
формулами (1), табл.1.![]()
![]()
V1=![]() , t1=0,23N, a=0,01N,
Dt=
, t1=0,23N, a=0,01N,
Dt=![]() ,
,
r1=r1T + 0,01n, ri =riT+0,01N (ri на рис.1) (1)
j1 (0)=j1T+0,01n, ji(0)= jiT+0,01N, i=(2,3),
где N - номер группы (присваевает преподаватель);
n - номер факультета (1 - для машиностроительного факультета, 2 - для заочного факультета);
T - индекс обозначает табличные значения.
Требуется:
1. Составить дифференциальные уравнения движения механизма.
2. Решить с помощью ЭВМ полученную систему уравнений на интервале времени t .
3. Построить графики w1Z(t), w2Z(t), w3Z(t).
4. Для момента времени t =(N + 1) Dt определить графоаналитическим методом угловые скорости звеньев и сравнить с результатами счета на ЭВМ.
Указания к составлению уравнений движения.
Выражения зависимостей неизвестных угловых скоростей w1z, w2z, w3z, w4z, или VC, от заданной скорости VМ точки М получаются из уравнений внешних связей,налогаемых на систему.Чтобы составить эти уравнения,надо выразить через wiz (i=1,2,3,4) скорости точек, в которых налагаются внешние связи, и приравнять их нулю. Выражения для скоростей получаются последовательным, от звена к звену, определением скоростей точек по формуле кинематики твердого тела
![]() (2)
(2)
Эта последовательность может быть различна и определяется графом. Из уравнений внешних связей определяют
w1z=w1z (j1, j2, j3,VM);
w2z=w2z (j1, j2, j3, VM); (3)
w3z=w3z (j1, j2, j3, VM);
w4z=w4z (j1, j2, j3, VM) или Vc=Vc (j1, j2, j3, VM)
Из уравнений (3) определяют угловые скорости звеньев для фиксированного момента времени при заданных в этот момент значениях j1, j2, j3. Изменение j1, j2, j3, а следовательно и w1z, w2z, w3z во времени определится,если дополнить систему (3) уравнениями:
![]() =w1z,
=w1z, ![]() =w2z,
=w2z, ![]() =w3z (4)
=w3z (4)
Уравнения (3), (4) образуют систему дифференциальных уравнений, интегрирование которой при заданных начальных значениях j1(0), j2(0), j3(0), решает кинематическую задачу о движении плоского механизма.
Система (3), (4) описывает движение механизма с двумя степенями свободы в избыточном наборе переменных. Поэтому начальные значения углов нельзя задавать произвольно. Значения их вычисляются предварительно и приводятся в (1) и табл. 1.
Исходные данные.
Таблица 1.
| Вариант |
r1т |
r2т |
r3т |
j1т |
j2т |
j3т |
Vkт |
xk(0) |
yk(0) |
d |
| 1 | 0,82 | 0,68 | 0,46 | 2,9 | 1,1 | 0,5 | 0,508 | -0,15 | 1,85 | 0,011 |
| 2 | 0,81 | 0,47 | 0,91 | 1,3 | 2,2 | 3,6 | 0,308 | -0,94 | 1,71 | 0,012 |
| 3 | 0,43 | 0,91 | 0,84 | 0,3 | 3,8 | 4,2 | 0,512 | -0,42 | 0,25 | 0,013 |
| 4 | 0,42 | 0,97 | 0,88 | 2,8 | 0,2 | 5,7 | 0,462 | -0,21 | 1,22 | 0,014 |
| 5 | 0,78 | 0,45 | 0,91 | 1,7 | 0,1 | 5,8 | 0,385 | 1,35 | 1,51 | 0,015 |
| 6 | 0,71 | 0,89 | 0,76 | 4,6 | 0,1 | 1,6 | 0,312 | 1,33 | -0,20 | 0,016 |
| 7 | 0,46 | 0,97 | 0,74 | 1,3 | 4,3 | 5,6 | 0,421 | -0,61 | -0,24 | 0,017 |
| 8 | 0,81 | 0,72 | 0,48 | 1,1 | 3,0 | 3,3 | 0,472 | -1,38 | 1,61 | 0,018 |
| 9 | 0,76 | 0,79 | 0,45 | 0,3 | 2,4 | 1,8 | 0,465 | 0,54 | 1,02 | 0.019 |
| 10 | 0,72 | 0,49 | 0,78 | 0,5 | 4,2 | 3,6 | 0,375 | 1,61 | -0,55 | 0,020 |
| 11 | 0,83 | 0,57 | 0,49 | 0,5 | 1,6 | 3,0 | 0,525 | -0,92 | 1,78 | 0,021 |
| 12 | 0,68 | 0,46 | 0,83 | 3,9 | 4,9 | 0,3 | 0,310 | 0,46 | -2,04 | 0,022 |
| 13 | 0,78 | 0,85 | 0,49 | 2,1 | 1,0 | 0,1 | 0,460 | 0,51 | 1,65 | 0,023 |
| 14 | 0,48 | 0,97 | 0,73 | 0,3 | 1,8 | 3,7 | 0,402 | -0,26 | 1,30 | 0,024 |
| 15 | 0,42 | 0,97 | 0,78 | 0,3 | 2,9 | 0,4 | 0,455 | 0,45 | 1,12 | 0,025 |
| 16 | 0,51 | 0,82 | 0,79 | 3,2 | 4,1 | 3,0 | 0,288 | -1,57 | 0,13 | 0,026 |
| 17 | 0,41 | 0,83 | 0,98 | 2,0 | 4,3 | 1,4 | 0,451 | -1,18 | 0,56 | 0,027 |
| 18 | 0,82 | 0,45 | 0,78 | 1,6 | 2,9 | 0,4 | 0,312 | -0,99 | 0,52 | 0,028 |
| 19 | 0,92 | 0,98 | 0,81 | 1,5 | 2,7 | 1,7 | 0,294 | -1,43 | 1,95 | 0,029 |
| 20 | 0,79 | 0,68 | 0,48 | 4,1 | 5,8 | 1,1 | 0,306 | 0,41 | -1,43 | 0,030 |
| 21 | 0,76 | 0,42 | 0,85 | 5,2 | 0,4 | 2,3 | 0,380 | 0,84 | 0,26 | 0,031 |
| 22 | 0,75 | 0,78 | 0,47 | 1,1 | 2,8 | 2,0 | 0,515 | -1,66 | 0,42 | 0,032 |
| 23 | 0,71 | 0,49 | 0,82 | 4,9 | 0,1 | 1,9 | 0,385 | 0,62 | 0,12 | 0,033 |
| 24 | 0,75 | 0,65 | 0,78 | 0,3 | 1,9 | 0,1 | 0,398 | 1,11 | 1,32 | 0,034 |
| 25 | 0,68 | 0,79 | 0,82 | 2,3 | 0,7 | 0,5 | 0,392 | 1,40 | 1,67 | 0,035 |
| 26 | 0,81 | 0,72 | 0,49 | 3,7 | 5,4 | 4,2 | 0,371 | 0,43 | -1,98 | 0,036 |
| 27 | 0,78 | 0,65 | 0,48 | 1,6 | 0,1 | 1,5 | 0,275 | 1,31 | 1,62 | 0,038 |
| 28 | 0,45 | 0,97 | 0,78 | 0,9 | 0,5 | 3,9 | 0,290 | 1,22 | 0,78 | 0,038 |
| 29 | 0,49 | 0,98 | 0,77 | 2,1 | 0,4 | 3,7 | 0,305 | 0,21 | 0,72 | 0,039 |
| 30 | 0,72 | 0,75 | 0,49 | 3,9 | 5,4 | 0,3 | 0,340 | 1,14 | -1,25 | 0,040 |
![]()
Зависимость от ji, wiz (i=1,2,3,4) для требуемой по условию скорости получается аналогично с помощью формул вида (2).
Указания к решению задачи.
Нелинейная система дифференциальных уравнений (3), (4) с заданными начальными условиями интегрируется в интервале времени [0, t1]. Запись выражений для w1z, w2z, w3z, w4z, Vcx, Vcy должна обеспечивать возможность присвоения последовательных значений этих переменных на каждом шаге интегрирования. В разных вариантах заданий наиболее компактная последовательность записи может быть различной,например w1z(ji, wkx), w2z(ji, w1z), w3z(ji, w1z, w2z), w4z(ji, w1z, w1z, w2z, w3z), Vcx(ji, w1z, w2z, w3z), Vсy(ji, w1z, w2z, w3z). На печать с шагом Dt=t/24 выводятся переменные t, j1, j2, j3, w1z, w2z, w3z, w4z или Vcx, Vcy.
Один из возможных вариантов решения задачи в котором уравнения (3), (4) интегрируются по конечноразностной схеме Эйлера, приведен в примере.
Контроль решения.
После решения задачи на ЭВМ проводится анализ таблицы результатов.Первая строка таблицы содержит найденные начальные значения w1z, w2z, w3z, w4z или Vcx, Vcy, и начальные значения j1, j2, j3. Последняя строка с некоторой погрешностью счета должна повторять первую.
Построенные по результатам счета графики не должны иметь разрывов.
Последняя проверка производится путем сравнения результатов счета на ЭВМ с результатами графоаналитического решения задания,для чего механизм изображается в масштабе 1:10 в момент времени t=(N+1) ´Dt ((N+2)-я строка таблицы счета). Для этого положения необходимо найти мгновенные центры скоростей звеньев, их угловые скорости, изобразить векторы скоростей точек, в которых соединяются звенья, указать направление вращения звеньев. Результаты этого решения должны быть близкими с результатами решения задачи на ЭВМ, содержащимися в строке таблицы счета.
Пример выполнения задания.
(вариант 31, n=1, N=2)
1. Постановка задачи. Рассматривается плоский механизм с двумя степенями свободы. Движение точки М задано: Vмx=0, Vмy=Vsin(pt+a).
Дано: a=4,35рад; DA=r1=0,953м; BC=r3=0,457м;
BM=2r3; AB=r2=0,847м; j1(0)=1,63рад; j2(0)=3,37рад;
j3(0)=2,87рад; CP=0,5r3; V1=4,5м/c; a=0,02рад;
t=0,48c; Dt=0.02c; p=13,08c-1.
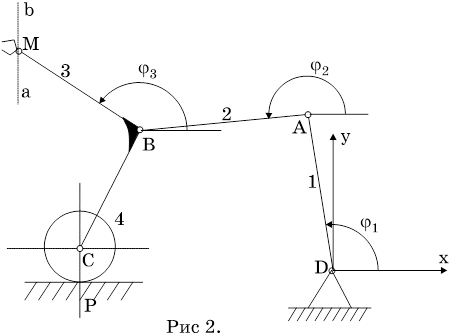
2. Составление уравнений движения. Составляются уравнения для четырех неизвестных угловых скоростей звеньев w1z, w2z, w3z, w4z. При заданном движении точки М они определяются из уравнений внешних связей, налагаемых на механизм. На данный механизм наложены связи: VDx=0, VDy=0, Vpx=0, Vpy=0, Vcy=0. (5)
При вычислении
скорости точки С последовательно определяются скорости точек в соответствии с
графом М![]() В
В![]() С,при
вычислении скорости точки Р - в соответствии с графом М
С,при
вычислении скорости точки Р - в соответствии с графом М![]() В
В![]() С
С![]() Р,при вычислении скорости
точки D4 - в соответствии с графом М
Р,при вычислении скорости
точки D4 - в соответствии с графом М![]() В
В![]() А
А![]() D
или Р
D
или Р![]() С
С![]() В
В![]() А
А![]() D
или С
D
или С![]() В
В![]() А
А![]() D.
D.
Составляются все возможные варианты векторных уравнений
![]()
![]()
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Проецируя обе части уравнений на оси координат X и Y с учетом (5) получим систему алгебраических уравнений для определения wiz(i=1,2,3,4). Уравнение (6) проецируется на ось Y, так как Vcy=0, то
![]() Vmy+w3z´2r3´cos(j3+p)+w3z´r3´сos(j3+
Vmy+w3z´2r3´cos(j3+p)+w3z´r3´сos(j3+![]() )=0 (11)
)=0 (11)
Уравнение (7) проецируется на оси X и Y, так как Vpx=0 и Vpy=0, то
0 - w3z´2r3´sin(j3+p) - w3z´r3´sin(j3+![]() ) - w4z´0,5r3´sin
) - w4z´0,5r3´sin![]() p=0 (12)
p=0 (12)
VMy + w3z´2r3´cos(j3+p) + w3z´r3´cos(j3+![]() ) + w4z´0,5r3´cos
) + w4z´0,5r3´cos![]() p=0 (13)
p=0 (13)
Уравнение (8) проецируется на оси X и Y, так как. VDx=0 и VDy=0, то
0 - w3z´2r3´sin(j3+p) - w2z´r2´sin(j2-p) - w1z´r1´sin(j1+p)=0 (14)
Vmy + w3z´2r3´cos(j3+p) + w2z´r2´cos(j2-p) + w1z´r1´cos(j1+p)=0 (15)
Уравнение (9) проецируется на оси X и Y, так как
VDx=0, VOy=0, VPx-0, VPy=0, то
-
w4z´0.5r3´sin![]() - w3z´r3´sin(j3
-
- w3z´r3´sin(j3
- ![]() ) - w2z´r2´sin(j2
- p)-w1z´r1´sin(j1+p)=0
) - w2z´r2´sin(j2
- p)-w1z´r1´sin(j1+p)=0
(16)
w4z´0.5r3´cos![]() +w3z´r3´cos(j3
-
+w3z´r3´cos(j3
- ![]() )+w2z´r2´cos(j2
- p)+w1z´r1´cos(j1+p)=0
)+w2z´r2´cos(j2
- p)+w1z´r1´cos(j1+p)=0
(17)
Уравнение (10) проецируется на ось Y, так как VDx=0, VDy=0 и VCy=0, то
w3z´r3´cos(j3
-![]() )+ w2z´r2´cos(j2
-p) + w1z´r1´cos(j1+p)=0 (18)
)+ w2z´r2´cos(j2
-p) + w1z´r1´cos(j1+p)=0 (18)
Из составленных
уравнений связей выбираем 4, позволяющих наиболее простым путем произвести
преобразования и выразить одни неизвестные через другие. В данном случае это
уравнения (11), (12), (16), (18), которые с учетом формул приведения запишутся
в следующем виде:
|
|
VMy - 2w3z´r3´cosj3 - w3z´r3´sinj3=0
2w3z´r3´sinj3 - w3z´r3´cosj3+0,5´w4z´r3=0 (19)
- 0,5´w4z´r3+w3z´r3´cosj3+w2z´r2´sinj2+w1z´r1´sinj1=0
w3z´r3´sinj3 - w2z´r2´cosj2 - w1z´r1´cosj1=0
Система уравнений (19) может быть разрешена относительно wiz:
|
|
![]()
![]()
|
|
w4z=2w3z(cosj3
- 2sinj3)
(20) ![]()
![]()
![]()
![]()
![]()
|
|
Дополним (20) уравнениями:
![]() ;
; ![]()
![]() (21)
(21)
Уравнения (20) и (21) образуют систему дифференциальных уравнений, интегрирование которой при заданных начальных значениях j1(0), j2(0), j3(0) решает задачу о движении механизма при заданном движении точки М.
3. Решение задачи и обработка результатов. Вычисления могут проводиться с использованием конечно-разностной схемы Эйлера, позволяющей связать значения углов и угловых скоростей в начале и конце k-го шага интегрирования :
j1(k+1)=j1(k)+w1z(k)´Dt;
j2(k+1)=j2(k)+w2z(k)´Dt; (22)
j3(k+1)=j3(k)+w3z(k)´Dt.
Программа счета составляется на любом языке программирования, результаты оформляются с помощью программы в виде таблицы. По результатам решения строятся графики w1z(t), w2z(t), w3z(t), w4z(t), которые не должны иметь разрыва и иметь явно выраженный синусоидальный характер.
4. Графическая проверка. Извлекаются из таблицы счета значения углов поворота звеньев из строки под номером (N+2). Механизм строится в масштабе 1:10, определяется положение мгновенных центров скоростей (рис. 3). Строятся векторы скоростей точек A, B, C, M и указываются дужками направления вращения звеньев. По известным значениям скоростей и расстояниям до мгновенных центров скоростей определяются значения угловых скоростей звеньев.
|
|

Результаты, полученные с помощью графических построений, должны быть близки к результатам рещения задачи на ЭВМ и не должны отличаться более чем на 5%.
II. Кинематика управляемого движения манипулятора.
Описание задания.
Манипулятор (рис.1), имеющий две системы свободы позволяет, при срабатывании приводов, захвату, точке М, осуществлять движение в плоскости по двум координатам и при определенных условиях совместить захват с двигающейся деталью,точкой К. Деталь К движется с постоянной скоростью Vк в указанном на рисунке направлении. Координаты точки К изменяются по закону:
XK=XK(0)+VKx´ t; YK=YK(0)+VKy´ t. (23)
Управление движением захвата М осуществляется по линейной комбинации рассогласований координат точек К и М, а также их производных. Рассогласование координат точек К и М в момент времени t=t2 должно составлять величину d от начальных рассогласований.
Исходные данные определяются формулами (24) и табл. 1
r1=r1T+0,001n, ri=riT+0,001N
j1(0)=j1T+0,001n, ji(0)=jiT+0,001N(i=2,3) (24)
VK=VKT - 0,003N, t2=1,2(1+0,02N)
Dt=![]() .
(24)
.
(24)
Требуется:
1. Выбрать управление, решающее поставленную задачу.
2. Исследовать движение манипулятора при выбранном управлении.
Конкретные пункты исследования приведены в примере.
Указания к составлению уравнений движения.
Предполагается, что координаты захвата М(XM,YM) в процессе движения известны, например, за счет прямых измерений;координаты детали К(XK,YK) заданы уравнениями (23). Тогда можно вычислить рассогласования:
DX=XK- XM; DY=YK- YM (25)
Управление движением захвата осуществляется по сигналам управления ux, uy, образованным линейной комбинацией рассогласований и их производных:
ux=DX+T*![]() DX; uy=DY+T*
DX; uy=DY+T*![]() DY, (26)
DY, (26)
где T* - множитьель размерности времени.
Сигналы (26) подаются на управление двигателями манипулятора с коэффициентом усиления k величина
kux, kuy (27)
В современных высокоточных механизмах коэффициэнты усиления k очень велики. Можно считать k®¥, при этом величины (27) остаются конечными,обеспечивающими требуемое движение манипулятора,поэтому можно предположить ux, uy®0.
Приближенные предельные уравнения
ux=0, uy=0 (28)
описывают движение манипулятора с погрешностью порядка 1/k.
Из (25), (26), (28) получим уравнения:
![]() =VKx+
=VKx+![]() (XK - XM)
(XK - XM)
![]() =VKy+
=VKy+![]() (YK - Y M) (29)
(YK - Y M) (29)
Манипулятор является механической системой с двумя степенями свободы, движение по двум координатам XM, YM, найденные по (29) однозначно определяет движение всех его звеньев. Кинематические уравнения, описывающие изменения углов поворота и угловых скоростей звеньев могут быть заимствованы из предыдущей задачи.
Указания к выбору коэффициэнта управления.
Уравнения (26), (28) в рассогласованиях DX и DY примут вид:
T*![]() DX +DX=0; T*
DX +DX=0; T*![]() DY +DY=0
DY +DY=0
Решение этих дифференциальных уравнений однотипно:
Dx=Dx(0)
е- ![]() ; Dy=Dy(0)
е-
; Dy=Dy(0)
е- ![]() (30)
(30)
По условию задания, к концу интервала времени t2 рассогласования DX, DY должны составлять величину d от начальных рассогласований.
Из (30) имеем : ![]() , откуда Т*=
, откуда Т*= ![]() .
.
Указания к выбору начальных условий. Если систему уравнений (29) и кинематических уравнений движения звеньев привести к форме Коши, то она будет иметь вид:
![]() M=VMx(XM,t);
M=VMx(XM,t); ![]() M=VMy(YM,t);
(31)
M=VMy(YM,t);
(31)
![]() i=wiz(ji,
Vmx, Vmy, t) (i=1,2,3)
i=wiz(ji,
Vmx, Vmy, t) (i=1,2,3)
Эти уравнения манипулятора,являющегося системой с двумя степенями свободы, записаны в избыточном наборе пяти переменных XM, YM, j1, j2, j3. Отсюда следует, что из начальных значений этих переменных независимо могут задаваться только два. В таблице 1 независимыми задаются величины j1(0), j2(0), значения j3(0) указанные в таблице,вычислены по j1(0), j2(0) для рассматриеваемой конструктивной схемы манипулятора. Значения XM(0), YM(0) следует находить по заданным j1(0), j2(0), j3(0).
Указания к решению задачи. Дифференциальные уравнения движения манипулятора с заданными начальными условиями интегрируются на интервале времени [ 0, t2 ] с шагом Dt. При решении задачи рекомендуется использовать конечноразностную схему Эйлера.
Контроль решения. Построенные по результатам счета графики не должны иметь разрывов. При t=t2 рассогласование между точками М и К должно быть величиной порядка d от начального. Результаты вычисления на ЭВМ для момента времени t=(N+1)´Dt угловых скоростей звеньев и скорости точки С должны совпадать с результатами графоаналитического решения для этого момента времени. Расхождения не должны превышать 5%.
Пример выполнения задания .
(вариант 31, n=1, N=2)
1. Постановка задачи. Управление манипулятором (рис.4) должно обеспечить за время t2 сближение захвата М с движущейся деталью К. Деталь движется прямолинейно с постоянной скоростью Vк в указанном на рисунке направлении. Начальное положение манипулятора задано углами поворота звеньев j1(0), j2(0), j3(0). К моменту времени t=t2 требуется относительная точность d совмещения точек М и К. Управление манипулятором осуществляется по линейной комбинации рассогласований и их производных.
Дано: Vk=0,304м/c; a=4,35рад; DA=r1=0,953м; BC=r3=0,457м; BM=2r3; AB=r2=0,847м; j1(0)=1.63рад; j2(0)=3,37рад; j3(0)=2,87рад; Xk(0)=-2,16м; Yk=1,18м; d=0,01; t2=1,37c; Dt=0,057c.

Требуется: 1. Составить уравнения управляемого движения точки М, уравнения углового движения звеньев манипулятора и уравнения для скорости точки С. 2. Выбрать параметры управления, обеспечивающего сближение точек М и К с заданной точностью. 3. Проинтегрировать с помощью ЭВМ уравнения движения на интервале времени [ 0, t2 ]. 4. Построить траектории сближения точек М и К и графики j1(t), w1z(t), Vcx(t). 5. Для момента времени t=(N+1)Dt=0,456c провести графоаналитическое решение задачи и сравнить с результатами счета.
2. Составление уравнений движения. Уравнения движения детали К имеют вид:
Xk=Xk(0)+Vkx´t; Vkx=Vkcosa= - 0,108м/c; (32)
Yk=Yk(0)+Vky´t; Vky=Vksina= - 0,284м/c.
Предполагая,что координаты захвата М известны в процессе движения,можно вычислить рассогласования координат точек К и М.
DX=Xk - XM; DY=Yk - YM (33)
Учитывая,что управление манипулятором осуществляется по линейной комбинации рассогласовании и их производных
ux=DX + T*![]() DX; uy=DY + T*
DX; uy=DY + T* ![]() DY (34)
DY (34)
При управлении с большими коэффициентами усиления k с погрешностью порядка 1/k выполняются соотношения:
ux=0, uy=0. (35)
Подставляя (35) в выражения (32), (33), (34) и приводя полученные уравнения к форме Коши получаем:
![]() =VMx; VMx=Vkx
+ [Xk(0) + Vkx´t - XM] / T*;
=VMx; VMx=Vkx
+ [Xk(0) + Vkx´t - XM] / T*;
![]() =VMy; VMy=Vky
+ [Yk(0) + Vky´t - YM]/T*. (36)
=VMy; VMy=Vky
+ [Yk(0) + Vky´t - YM]/T*. (36)
Угловое движение звеньев манипулятора и скорость точки С однозначно определяется движением точки М и внешними связями, налагаемыми в точках D и С. Составляются выражения для проекций скоростей точек С и М.
В соответствии с
графом С![]() В
В![]() М
запишем:
М
запишем:
VMx=Vcx
- w3z´r3´sin(j3 - ![]() )
- w3z´2r3´sinj3;
)
- w3z´2r3´sinj3;
Vmy=w3z´r3´cos(j3
- ![]() ) + w3z´2r3´cosj3;
(37)
) + w3z´2r3´cosj3;
(37)
В соответствии с графом D![]() A
A![]() B
B![]() C
C
Vcx= - w1z´r1´sinj1
- w2z´r2´sinj2 - w3z´r3´sin(j3
+ ![]() ); (38)
); (38)
Vcy= w1z´r1´cosj1
+ w2z´r2´cosj2 - w3z´r3´cos(j3
+ ![]() )=0.
)=0.
Из уравнений (37) , (38) получают:
w3z=VMy/[r3(2cosj3+sinj3)];
Vcx=VMx+w3z´r3(2sinj3 - cosj3); (39)
w1z= ;
;
w2z=![]() .
.
Уравнения (39) дополним дифференциальными соотношениями
![]() ;
; ![]() ;
; ![]() (40)
(40)
3. Определение параметра управления. Из (34) и (35) получим уравнение в рассогласованиях:
T*![]() Dx+Dx=0;
T*
Dx+Dx=0;
T*![]() Dy+Dy=0.
Dy+Dy=0.
Решение этих уравнений имеет вид:
Dx=Dx(0)
e- ![]() ,
Dy=Dy(0)
e-
,
Dy=Dy(0)
e- ![]() ,
,
По условию, при t=t2 должно выполняться соотношение
d = ![]() =0,01.
Отсюда
=0,01.
Отсюда
Т*
= ![]() =0,297 c.
=0,297 c.
4. Решение задачи и обработка результатов. Система уравнений (36), (39), (40) интегрируется с помощью ЭВМ на интервале [0; 1,37] с использованием конечноразностной схемы Эйлера. Шаг интегрирования Dt=0,057c.
Начальные условия по переменным j1, j2, j3 (рис.4) приведены в исходных данных, а по переменным XM, YM вычисляются по формулам :
XM=r1 ´cosj1+r2 ´cosj2+2r3 ´cosj3 (41)
YM=r1 ´sinj1+r2 ´sinj2+2r3 ´sinj3
Подставив в (41) числовые значения ri, ji(0), получают XM(0), YM(0). Последующие шаги интегрирования осуществляются с использованием зависимостей (22), с учетом, что
![]() =XM(k)+VMx(k)´Dt;
=XM(k)+VMx(k)´Dt;
![]() =YM(k)+VMy(k)´Dt,
(42)
=YM(k)+VMy(k)´Dt,
(42)
с использованием зависимостей (41)
Результаты счета по двум вариантам сравниваются.
Программа счета составляется на любом языке программирования,результаты оформляются в виде таблицы. По результатам решения строятся графики j1(t), w1z(t), Vcx(t) и траектории сближения точек М и К, которые не должны иметь разрывов,а координаты точек М и К в момент времени t должны быть достаточно близки.
Графоаналитическая проверка результатов счета производится аналогично проверке в первой задаче.
III. Динамика механизма с двумя степенями свободы.
Описание задания.
Манипулятор с двумя степенями свободы (рис.1) переносит точечный груз М массой m за время t3 под действием двигателей управления, расположенных в шарнирах B и D из точки d в точку е с заданной скоростью
VMx=0, VMy=V3 sinkt (43)
Элементы конструкции считаются абсолютно жесткими и безинерционными. Силы трения в шарнирах и ползунах отсутствуют. Катки относительно опорных поверхностей не проскальзывают.
Исходные данные определяются формулами (43), (44) и табл.1
r1=r1T+0,01n; ri=riT+0,01N(i=2,3,4);
V3=![]() ; t3=0,24N; k=
; t3=0,24N; k= ![]() .
(44)
.
(44)
ji(0)=jiT+0,01N , (i=1,2,3) m=10+N
Требуется исследовать с помощью ЭВМ движения манипулятора. Перечень пунктов исследования приведен в примере.
Указания к составлению уравнений кинетостатики для моментов и сил управления.
Система освобождается
от связей и разделяется на отдельные звенья или группы звеньев. Вводятся
реакции связей. Прикладываются активные силы: внешняя сила - вес точки М - и
внутренние моменты управления MBz, MDz или сила управления
Fcx, Fcy в вариантах 2, 3, 7, 9, 10, 12, 14, 17, 18, 20,
21, 23, 24, 26, 27, 28. При освобождении связей в точках В и D к смежным
звеньям прикладываются моменты противоположных знаков. Для определенности
положительный момент прилагается со стороны звена с большим индексом к звену c
меньшим индексом. По принципу Даламбера к точке М условно прикладывается сила
инерции ![]() =- m
=- m![]() м.
Она определяется для заданного движения (43) точки М .
м.
Она определяется для заданного движения (43) точки М .
Уравнения МBz, MDz или Fcx, Fcy получаются из уравнений кинетостатики для механической системы, включающей точку М и уравнений статики для механических систем, образованных из безинерционных звеньев. Из этих уравнений определяются
MBz=MBz(j1, j2, j3, t); MDz=MDz(j1, j2, j3, t); (45)
Fcx=Fcx(j1, j2, j3, t); Fcy=Fcy(j1, j2, j3, t).
В общем случае определяются моменты управления МBz и МDz, силы управления Fcz и Fcy определяются по указанию преподавателя при уточнении задания.
Указания к составлению кинематических уравнений движения.
Выражения для определения неизвестных угловых скоростей w1z, w2z, w3z, w4z и проекции скорости точки С Vcz или Vcy по известной скорости точки М получаются по аналогии с предыдущими заданиями или заимствованы полностью из этих заданий. Из этих уравнений:
w1z=w1z(j1, j2, j3, t); w2z=w2z(j1, j2, j3, t);
w3z=w3z(j1, j2, j3, t); w4z=w4z(j1, j2, j3, t); (46)
Vcx=Vcx(j1, j2, j3, t); Vcy=Vcy(j1, j2, j3, t).
Уравнения (46) позволяют определить угловые скорости звеньев и проекции скорости точки С для фиксированного момента времени при заданных в этот момент значениях j1, j2, j3. Изменение j1, j2, j3,а следовательно, и w1z, w2z, w3z, w4z, Vcx, Vcy во времени определяется,если дополнить систему (46) уравнениями:
![]() =
=![]() w1z,
w1z, ![]() =
w2z,
=
w2z, ![]() =w3z,
=w3z, ![]() =w4z,
=w4z, ![]() =Vcx;
=Vcx;
![]() =Vcy,
(47)
=Vcy,
(47)
Уравнения (46), (47) образуют систему дифференциальных уравнений, интегрированием которой при заданных начальных значениях j1(0), j2(0), j3(0) решается кинематическая задача о движении плоского механизма. Эти уравнения манипулятора, являющегося системой с двумя спепенями свободы записаны в избыточном наборе трех переменных j1, j2, j3. Поэтому начальные значения углов нельзя задавать произвольно. Они вычисляются предварительно для заданного начального положения точки М и приводятся в табл.1.
Указания к решению задачи.
Нелинейная система дифференциальных уравнений (46), (47) с заданными начальными условиями интегрируется на интервале времени [0,t] . Одновременно с вычислением ji по формулам (45) определяются МBz, MDz или Fcx, Fcy (по указанию преподавателя).
На печать с шагом Dt=![]() выводятся переменные t, w1z,
w2z, w3z, w4z,
j1, j2, j3,
MВz, Mdz, Vcx (или Vcy) или Fcx
(или Fcy).
выводятся переменные t, w1z,
w2z, w3z, w4z,
j1, j2, j3,
MВz, Mdz, Vcx (или Vcy) или Fcx
(или Fcy).
Решение задачи может производиться путем интегрирования с использованием конечноразностной схемы Эйлера или методом Рунге - Кутта.
Указания к вычислению мощности управляющих приводов.
Мощность, развиваемая приводами, вычисляется по формулам вида:
NB=MBzwiz + (- MBz) wjz, (48)
где i, j =i+1 - номер звеньев, соединяемых шарниром В. Если шарнир прикреплен к неподвижному основанию, формула (48) преобразуется в
NB=MBzwiz , ND=MDzwiz (49)
При движении ползуна в точке С в горизонтальном или вертикальном направлении мощность вычисляется соответственно по формулам вида:
Nc=Fcx´Vcx, Nc=Fcy´Vcy (50)
Контроль решения.
Построенные по результатам счета графики МBz (t), MDz (t) или Nc, j1(t), w1z(t), w2z(t), w3z(t),VM(t), Vcx(t), Vcy(t) не должны иметь разрывов. При t = 0 и t = t скорость груза М равна нулю, поэтому в правильно решенной задаче угловые скорости звеньев в начальный момент должны быть равны нулю, а при t = t отличие за счет погрешностей счета от нуля должно быть малым. Результаты вычисления на ЭВМ угловых скоростей звеньев должны близко совпадать с результатами графоаналитического решения для момента времени t=(N+1)Dt.
Пример выполнения задания.
(вариант 31, n=1, N=2)
1. Постановка задачи. Манипулятор (рис.5) перемещает точечный груз массы m за время t3 из точки d в точку е с заданной скоростью Vмс=0, Vмy=Vsin kt. Управляющие двигатели расположены в шарнирах B и D.
Дано: DA=r1=0,953м; BC=r3=0,457м; BM=2r3; AB=r2=0,847м; j1(0)=1,63рад; j2(0)=3,37рад; j3(0)=2,87рад; t3=1,68c; V=0,45м/c; k=1,87рад/c; m=17кг.
Массой элементов конструкции и приводов можно пренебречь.
Требуется: 1. Составить уравнения кинетостатики для определения управляющих моментов, реализующих заданное программное движение груза. 2. Составить кинематические уравнения, определяющие изменение во времени угловых скоростей, углов поворота звеньев и скорости точки С. 3. Решить полученные уравнения на ЭВМ на интервале времени [0,t3]. 4. Построить графики МBz, MDz, j1(t), w1z(t), w3z(t). 5. Для момента времени t=(N+1)Dt=0,56c определить с помощью графоаналитического метода угловые скорости звеньев, скорость точки С и сравнить с результатами счета на ЭВМ. 6. По данным счета найти мощность каждого двигателя при t=0,56c.
2. Составление уравнений кинетостатики для управляющих моментов.
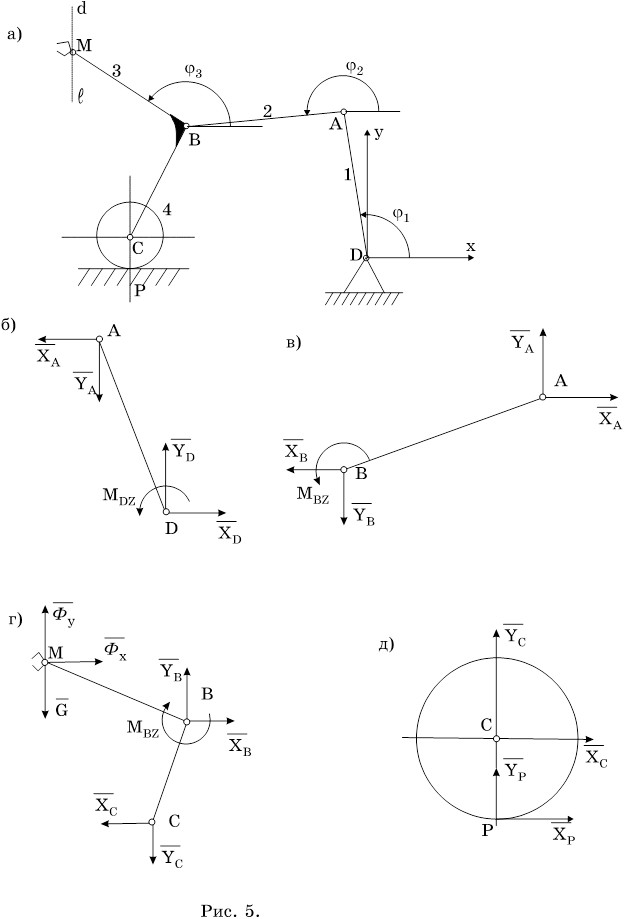
Для составления
уравнений кинетостатики система освобождается от связей. На рисунке
изображаются реакции связей, активные силы: сила ![]() -
точки М и внутренние моменты управления МBz, MDz. По
принципу Деламбера условно прикладываются к точке М силы инерции: сила
инерции
-
точки М и внутренние моменты управления МBz, MDz. По
принципу Деламбера условно прикладываются к точке М силы инерции: сила
инерции ![]() = - m
= - m![]() . Для заданного движения
эта сила в проекциях определяется так:
. Для заданного движения
эта сила в проекциях определяется так:
Фx=0
Фy=m´aмy=m![]() мy=m´V´p
cos pt (51)
мy=m´V´p
cos pt (51)
Составляются уравнения равновесия систем сил, указанных на рис. 4б, б, в, г, д.
Для звена 1 (рис 5б):
SXi=XD - XA=0
SYi=YD - YA=0 (52)
SMD=MD2+YA´r1´sin(j1
- ![]() )+XA´r1´cos(j1
-
)+XA´r1´cos(j1
- ![]() )=0
)=0
Для звена 2 (рис.5в):
SXi=XA - XB=0
SYi=YA - YB=0 (53)
SMB=MBz+XA´r2´sin(j2 -p)+YA´r2´cos(j2 -p)=0
Для звена 3 (рис.5г):
SXi=ФX + XB - XC=0
SYi=ФY - G+YB - YC=0 (54)
SMB= - MBz+(G - ФY)´2r3´sin(j3 - ![]() )
- Фx´2r2´cos(j3
-
)
- Фx´2r2´cos(j3
- ![]() ) -
) -
- Xc ´r3´sin(j3
- ![]() ) +Yc´r3´cos(j3
-
) +Yc´r3´cos(j3
- ![]() )=0
)=0
Для звена 4 (рис.5д):
SXi=XP + XC=0
SYi=YP + YC=0 (55)
Так как XP=0, то из (55) XC=0
Так как ФX=0 и XC=0, то из (54) XB=0, а из (53) и (52) XA=0 и XD=0. То есть
ФX=XP=Xc=XP=XD=XA=0 (56)
Из (52), (53) YA=YB=YD
Из (54) YB - YC=G - ФY (57)
Из уравнений (52), (53), (54)
MDz=YA´r1´cosj1
MBz=YA´r2´cosj2 (58)
MBz=(ФY - G)´2r3´cosj3+YC´r3´sinj3
Из уравнений (57), (58)
YC=YA - G+ФY
YA´r2´cosj2=(ФY- G)´2r3´cosj3+YA´r3´sinj + (ФY - G)´r3´sinj3
YA(r2 cosj2 - r3sinj3)=(ФY - G)(2r3 cosj3+r3sinj3)
![]() ,
,
MBz=![]() ,
,
MDz=![]() .
(59)
.
(59)
или из уравнений (58)
MDz=MBz![]() (60)
(60)
3. Составление кинематических уравнений.
Кинематические уравнения (39) заимствуются из ранее решенных задач и с учетом того,что VMx=0; VMy=V sin kt, запишутся:
w3z= ,
,
Vcx=w3z´r3(2sinj3 - cosj3), (61)
w1z= ,
,
w2z=![]() .
.
Дополним (61) уравнениями:
![]() =w1z;
=w1z; ![]() =w2z;
=w2z; ![]() =w3z, (62)
=w3z, (62)
4. Вычисление мощности двигателей управления.
NB=MBz(w2z - w3z) (63)
ND=MDz´w1z, (64)
5. Решение задачи и обработка результатов.
Вычисления в силу уравнений (59), (60), (61), (62) проводятся на ЭВМ. Для интегрирования уравнений (61), (62) используется конечноразностная схема Эйлера с шагом интегрирования, равным шагу печати Dt=0,07c.
По результатам решения задачи строятся графики j1(t), w1z(t), w2z(t), w3z(t), MBz(t), MDz(t).
Для вычисления мощности двигателей из таблицы счета выбираются значения угловых скоростей и моментов упрвления для t=0,56c. Эти значения подставляются в (63), (64).
6. Контроль решения.
Графики не должны иметь разрывов. При t=0 и t=t3 угловые скорости близки к нулю. Результаты графоаналитической проверки для момента времени t=0,56c близки результатам счета на ЭВМ.
Литература.
1. Красковский Е.Я., Дружинин Ю.А., Филатов Е.М., Расчет и конструирование механизмов приборов и вычислительных систем. Учебное пособие для приборостроительных специальностей вузов. -M; Высш.шк., 1991-480с.
2. Механика промышленных роботов; Учебное пособие для вузов: в 3 кн./Под ред. К. В. Фролова, Е. И. Воробьева, М. Высш.шк., 1988.
3. Бурдаков С.Ф. Проектирование манипуляторов промышленных роботов и роботизированных комплексов. Учебное пособие для студентов вузов, обучающихся по специальности: ” Робототехнические системы и комплексы ”/С. Ф. Бурдаков, В. А. Дьяченко, А. Н. Тимофеев М.: Высш.шк., 1988.
4. Камышный Н. М., Автоматизация загрузки станков - М.; Машиностроение, 1977.- 287c.
5. Красников В. Д., Промышленные роботы и манипуляторы: Учебное пособие Ростов-на-Дону: Институт с/x машиностроения, 1981 - 148c.
6. Новожилов И. В., Зацепин М. Ф. Типовые расчеты по теоретической механике на базе ЭВМ. Учебное пособие для вузов. - М.: Высш.шк., 1986 - 264 с.
