Реферат: Применение метода частотных диаграмм к исследованиям устойчивости систем с логическими алгоритмами управления
Московский Государственный Технический Университет им. Н.Э. Баумана
Курсовая работа по курсу “Нелинейные САУ”
на
тему:
Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.
Выполнил: ст-т гр. АК4-81
Смык В.Л.
Руководитель: профессор
Хабаров В.С.
Реутов 1997 г.
Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.
На ранней стадии развития теории автоматического регулирования требование устойчивости работы системы было первым и обычно единственным и содержание большинства теоретических исследований сводилось к иследованию устойчивости.
“Термин “устойчивость” настолько выразителен, что он сам за себя говорит”,-отмечают в начале изложения теории устойчивости Ж. Ла Салль и С. Лефшец [1]. Это вполне справедливо, но, несмотря на это, неточности и нелогичности можно встретить как раз не в математических, а в смысловых понятиях и терминах.
Устойчивостью любого явления в обиходе называю его способность достаточно длительно и с достаточной точностью сохронять те формы своего существования, при утрате которых явление перестает быть самим сабой. Однако не только в обиходе, но и в научной терминалогии устойчивым называют не явление, а систему, в корой оно наблюдается, хотя это не оправдывает логически. Устойчивы ли физические тела - шар или куб? Такой вопрос будет иметь смысл, если речь идет о материале, из которого они сделаны. (Металлический шар
устойчив, шар из дыма нет.) Теорию управления интересует, однако, не эта прочнасная устойчивость. Подразумевается, что система управления как инженерная конструкция заведома устойчива, и в теории изучается устойчивость не самой системы, а ее состояний и функционирования. В одной и той же системе одни состояния или движения могут быть устойчивыми, а другие не устойчивыми. Более того, одно и то же жвижение может быть устойчивым относительно одной переменной и неустойцивым относительно другой - это отмечал еще А.М. Ляпунов [2]. Вращение ротора турбины устойчиво по отношению к угловой скорости и неустойчиво относительно угла поворота вала. Движение ракеты устойчиво относительно траектории и неустойчиво по отношению к неподвижной системе координат. Поэтому нужно оговаривать, устойчивость какого состояния или движения в системе и относительно каких переменных изучается. Так же есть много методов для оценки самой устойчивости. Мы рассмотрим как можно оценить устойчивость системы с логическим алгоритмом управления методом круговых диаграмм.
Рассмотрим теоретическую часть и посмотрим что из себя представляет круговой критерий. Пусть дана система
.
x=Ax+bx, s=c’x, (1)
где
x
и s
- в общем случае
векторы (и,
следовательно,
b и с - прямоугольные
матрицы), а матрица
А не имеет
собственных
значений на
линейной оси.
Предположим
, что для некоторого
m,
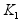 Ј
m
Ј
Ј
m
Ј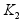
система (1), дополненая соотношением x=-ms, асимптотически усойчива.
Для
абсолютной
экпоненциальной
устойчивости
системы (1) в классе
М(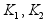 )
нелинейностей
x=j(s,t),
удовлетворяющих
условию
)
нелинейностей
x=j(s,t),
удовлетворяющих
условию
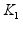 Ј
j(s,t)/s
Ј
Ј
j(s,t)/s
Ј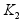 (2)
(2)
достаточно,
чтобы при всех
w,
-Ґ
Re{[1+
Круговой
критерий вытекает
из квадратичного
критерия для
формы F(x,s)=(
F(jw,x)=-Re{[1+
Из
этой формулы
после сокращения
на |x|
В (3)
Круговой
критерий представляет
собой распространение
линейных частотных
критериев
устойчивости
Найквиста,
Михайлова и
других на линейные
системы с одним
линейным или
нелинейным,
стационарным
или нестационарным
блоком. Он получается
из (3), если вместо
передаточной
матрицы использовать
частотную
характеристику
линейной части
W(jw).
Обозначая
комплексную
переменную
W(jw)=z,
рассмотрим
систему с одной
нелинейностью,
удовлетворяющей
одному из следующих
условий:
Re[(1+
Re[(1+
Re[z(1+
Пусть
С(
Круговой
критерий обеспечивает
также абсолютную
устойчивость
для системы
с любым блоком,
вход s
и выход x
которого
удовлетворяют
для всех t неравенству
(
Рисунок
1, а.
Рассмотрим
систему, приведенную
на рис. 2.
Рисунок
2.
Здесь
W
W
Алгоритм
регулятора
имеет вид:
y=Y
g=(
В форме
уравнений Коши
рассматриваемая
система имеет
вид:
k
где
-
k
g=c
Соответствие
записей системы
на рис. 2 достигается,
когда при
W
а при
W(p)=
Причем
для обоих случаев
(11) и (12) имеет место
соотношение
В
соответствии
с изложенным
одинаково
справедливо
рассматривать
в виде структурной
схемы на рис.
2 с известным
линейными
операторами
-
Дополнительно
отметим, что
структурная
интерпритация
рассматриваемой
системы на рис.
2 имеет еще одну
структурную
схему описания,
приведенную
на рис. 3.
Рисунок
3.
Это
означает, что
аналитической
записи (10) соответствуют
два структурных
представления
исследуемой
СПС, причем
второе позволяет
рассматривать
систему (10) как
релейную систему
с изменяемым
ограничение,
когда
Далее
перейдем к
анализу нашего
метода.
Согласно
частотной
теоремы (10), для
абсолютной
устойчивости
системы на рис.
3 лостаточно,
чтобы при всех
w,
изменяющихся
от -
Ґ
до + Ґ,
выполнялось
соотношение:
Re{[1+
а гадограф
mW(jw)+1
при
Для
исследуемой
системы условие
(3) удобнее записать
в виде
(4) и (5).
На
рис. 4 приведенны
возможные
нелинейные
характеристики
из класса М(
y=
“а”
“б”
“в”
“г”
Рисунок
4.
В
рассматриваемом
случае (10) при
W
W(p)=
W
годограф
W(jw)
системы на рис.
5.
W(jw)
w=Ґ
w=0
Рисунок
5.
В случае
(10) справедливы
графические
формы на рис.
4 в,г, т.е. исследуемая
система абсолютно
устойчива в
смысле кругового
критерия (3) или
(5) при
Интересно
заметить, что
достаточные
условия абсолютной
устойчивости
по Ляпунову
а
> 0 , y(t)
> 0
и
a
> c
для
рассматриваемого
случая совпадают
с достаточными
условиями
абсолютной
устойчивости,
полученными
для кругового
критерия (14), если
выполняется
требование
y(t)
> 0 (15)
поскольку,
согласно (11) и
(13) a=a
Докажем
это, используя
условия существования
скользящего
режима
-
т.е.
подставим сюда
вместо коэфициентов
а,с, и k их выражения
через
-
Согласно
рис. 5 и условия
(16) получаем:
1) при
2) при
3) при
что
и требовалось
доказать.
Теперь
рассмотрим
нашу систему
с логическим
алгоритмом
управления,
ее логическая
схема приведена
на рис. 6.
Рисунок
6.
В данном
случае считаем
что:
Рассмотрим
теперь саму
функцию:
W(p)=G(p)W
где
G(p) - функция корректора,
W
W
где
W(p)=
Теперь
заменяем p на
jw
и имеем вид:
Для
построения
гадогрофа
выведем формулы
для P(w),
jQ(w)
которые имеют
вид:
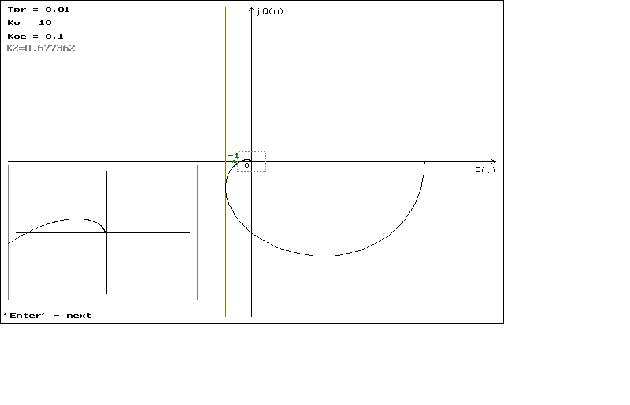
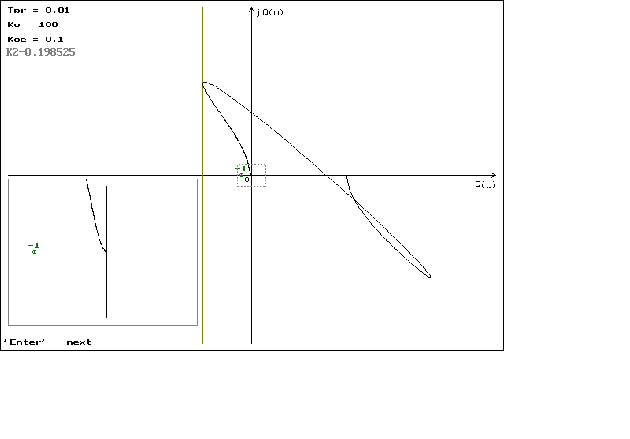
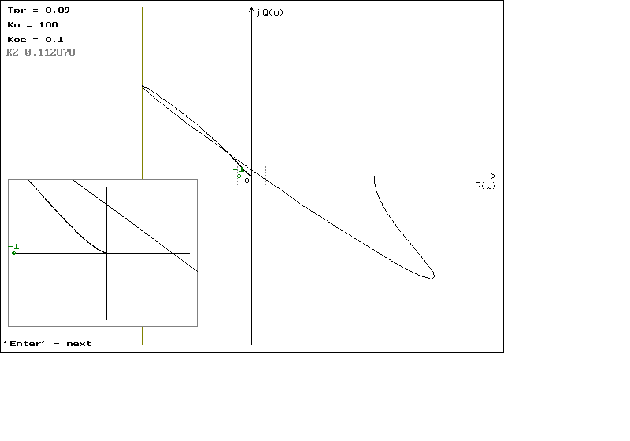
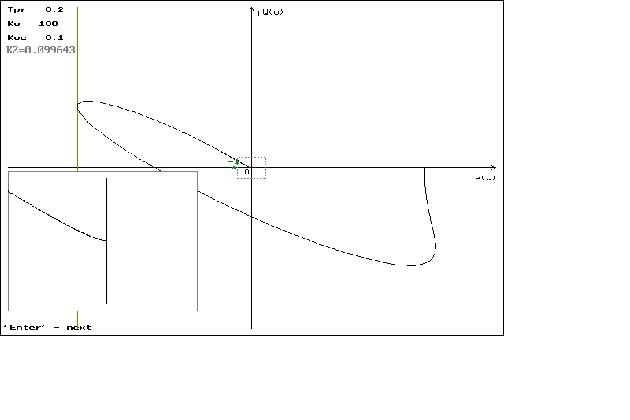
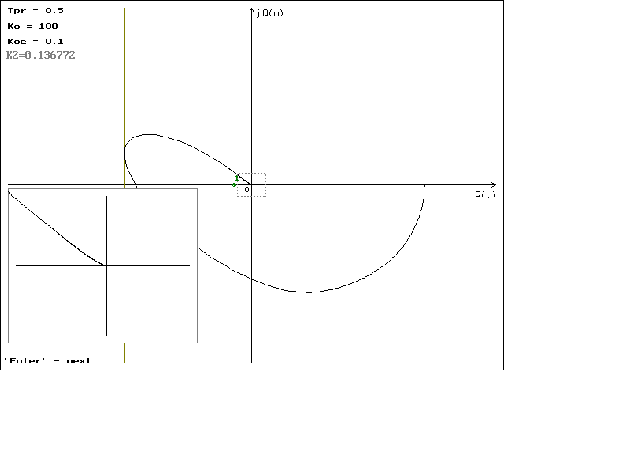
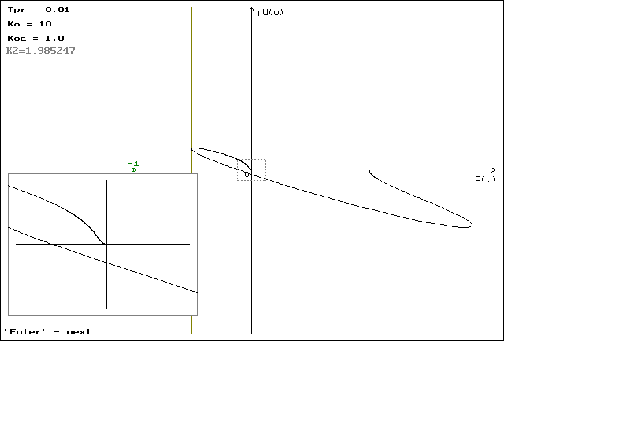
P(w)=
jQ(
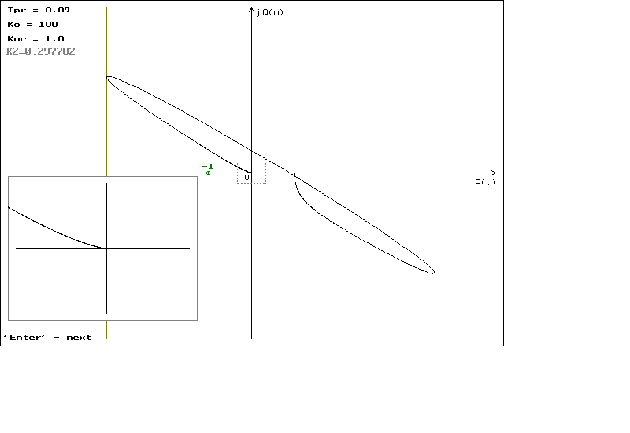
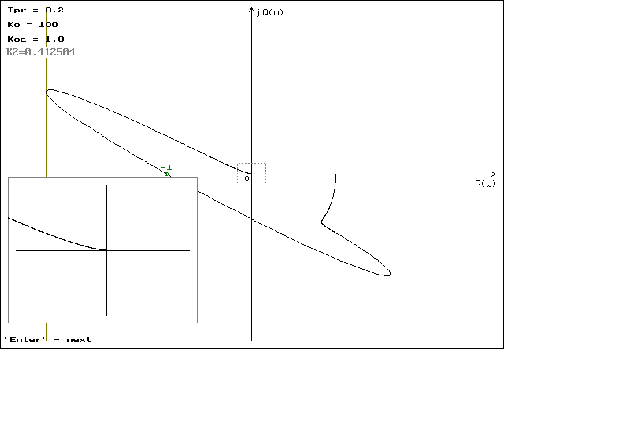
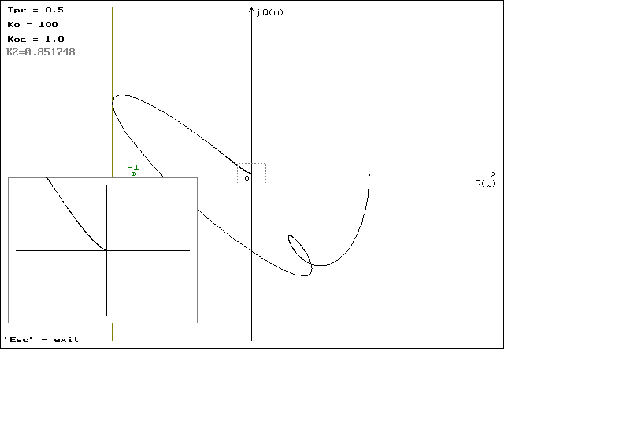
Графики
можно посмотреть
в приложении
N 2.
Учитывая
, что добротность
x
должна быть
і
0.5ё0.7
мы можем определить
добротность
нашей системы,
она примерно
равна 0.5. Отсюдо
видно, что из-за
увеличения
Но
это не подходит
по требованию
нашей задачи.
Так как
Минемальные
значения полки
нечуствительности
можно наблюдать
на графиках
1.9 - 1.12, особенно
при минемальном
значении
Приложение
N 1.
Программа
для построения
годографов
на языке программирования
СИ
++.
#include
#include
#include
#include
#include
#include
#include
#include
void Godograf(float Tpr,
float Ko, float Kos, int Color,
int Xc, int Yc, int x,
int y, int z, int err);
void Osi(int Xc, int Yc,
int kol);
int xmax, ymax;
float Kos[]={0.1,1.0},
Ko[] ={10.0,100.0},
Tpr[]={0.01,0.09,0.2,0.5};
void main(void)
{
float P_w, Q_w, w;
int driver, mode, err;
driver = DETECT;
initgraph(&driver,&mode,"");
err = graphresult();
if (err!=grOk)
{cout<<"\n\t"<
getch();}
else {
xmax = getmaxx();
ymax = getmaxy();
int Xc=(int)(xmax/2),
Yc=(int)(ymax/2);
for(int i=0;i<=1;i++)
for(int j=0;j<=1;j++) for(int k=0;k<=3;k++){
cleardevice();
setviewport(0,0,xmax,ymax,0);
Osi((int)(xmax/2),(int)(ymax/2),i+j+k);
Godograf(Tpr[k],Ko[j],Kos[i],15,(int)(xmax/2),(int)(ymax/2),k,j,i,1);
setcolor(7);
setlinestyle(1,0,1);
rectangle(Xc-18,Yc-15,Xc+18,Yc+15);
setlinestyle(0,0,1);
rectangle(10,Yc+5,250,Yc+205);
setcolor(15);
setviewport(10,(int)(ymax/2)+5,250,(int)(ymax/2)+205,1);
setfillstyle(1,0);
floodfill(5,5,7);
line(10,100,230,100);
line(125,10,125,190);
Godograf(Tpr[k],Ko[j],Kos[i],15,125,100,k,j,i,0);};
closegraph();
}
}
void Godograf(float Tpr,
float Ko, float Kos, int Color,
int Xc, int Yc, int x,
int y, int z, int err)
{
float P_w1=0.0,
Q_w1=0.0,
P_w, Q_w,
To=0.5, Tg=0.1,
P_w_min=0.0;
for(float
w=0;w<=100;w=w+0.05){
if(((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w))!=0){
P_w =
(Ko*w*Tg*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)+
(Kos*Ko*Ko-(To+Tpr)*Ko*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
Q_w =
(Tg*(Kos*Ko*Ko*w-(To+Tpr)*Ko*w*w)-
Ko*(w+Tpr*Kos*Ko*Ko*w-Ko*To*Tpr*w*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
if (abs(P_w)>abs(P_w1))
P_w1=P_w;
if (abs(Q_w)>abs(Q_w1))
Q_w1=Q_w;
if (P_w
if (P_w1==0)
P_w1=P_w1+0.01;
if (Q_w1==0)
Q_w1=Q_w1+0.01;
};
};
float KmasX
=(float)(xmax-Xc-100)/P_w1,
KmasY
=(float)(ymax-Yc-100)/Q_w1;
if (KmasX<0)
KmasX=-KmasX; if (KmasY<0) KmasY=-KmasY;
if (KmasX>=220)
KmasX=150;
if (KmasY>=140)
KmasY=100;
if (err==0)
{KmasX=KmasX*4; KmasY=KmasY*4;};
w = 0;
if(((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w))!=0){
P_w =
KmasX*(Ko*w*Tg*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)+
(Kos*Ko*Ko-(To+Tpr)*Ko*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
Q_w =
KmasY*(Tg*(Kos*Ko*Ko*w-(To+Tpr)*Ko*w*w)-
Ko*(w+Tpr*Kos*Ko*Ko*w-Ko*To*Tpr*w*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
moveto(Xc+P_w,Yc-Q_w); };
setcolor(Color);
setcolor(9);
line(Xc+P_w_min*KmasX,10,Xc+P_w_min*KmasX,ymax-10);
gotoxy(2,5);
printf("K2=");
printf("%f",(-1/P_w_min));
setcolor(15);
for(w=0;w<=700;w=w+0.05){
if(((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w))!=0){
P_w =
KmasX*(Ko*w*Tg*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)+
(Kos*Ko*Ko-(To+Tpr)*Ko*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
Q_w =
KmasY*(Tg*(Kos*Ko*Ko*w-(To+Tpr)*Ko*w*w)-
Ko*(w+Tpr*Kos*Ko*Ko*w-Ko*To*Tpr*w*w*w))/
((Kos*Ko-(To+Tpr)*w*w)*(Kos*Ko-(To+Tpr)*w*w)+
(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w)*(w+Tpr*Kos*Ko*w-To*Tpr*w*w*w));
lineto(Xc+P_w,Yc-Q_w);
};
};
setcolor(13);
circle(Xc-KmasX,Yc,2);
circle(Xc-KmasX,Yc,1);
putpixel(Xc-KmasX,Yc,13);
outtextxy(Xc-KmasX-7,Yc-12,"-1");
setcolor(15);
if (err==1){
if (x==0)
outtextxy(10,10,"Tpr = 0.01");
if (x==1)
outtextxy(10,10,"Tpr = 0.09");
if (x==2)
outtextxy(10,10,"Tpr = 0.2");
if (x==3)
outtextxy(10,10,"Tpr = 0.5");
if (y==0)
outtextxy(10,30,"Ko = 10");
if (y==1)
outtextxy(10,30,"Ko = 100");
if (z==0)
outtextxy(10,50,"Koc = 0.1");
if (z==1)
outtextxy(10,50,"Koc = 1.0");}
else {
char ch=' ';
while(ch!=27&&ch!=13)
if (kbhit()!=0)
ch=getch();};
};
void Osi(int Xc, int Yc,
int kol)
{
setcolor(15);
rectangle(0,0,xmax,ymax);
line(Xc,10,Xc,ymax-10);
line(10,Yc,xmax-10,Yc);
line((int)(xmax/2)-3,15,(int)(xmax/2),10);
line((int)(xmax/2),10,(int)(xmax/2)+3,15);
line(xmax-15,(int)(ymax/2)-3,xmax-10,(int)(ymax/2));
line(xmax-15,(int)(ymax/2)+3,xmax-10,(int)(ymax/2));
settextstyle(2,0,5);
outtextxy((int)(xmax/2)+7,10,"jQ(w)");
outtextxy(xmax-35,(int)(ymax/2)+7,"P(w)");
settextstyle(2,0,4);
outtextxy((int)(xmax/2)-8,(int)(ymax/2)+1,"0");
settextstyle(0,0,0);
if (kol==5)
outtextxy(5,ymax-15,"'Esc' - exit");
else
outtextxy(5,ymax-15,"'Enter' - next ");
setcolor(15);
};
Приложение
N 2.
Рисунок
N 1.1
Рисунок
N 1.2
Рисунок
1.3
Рисунок
1.4
Рисунок
1.5
Рисунок
1.6
Рисунок
1.7
Рисунок
1.8
Рисунок
1.9
Рисунок
1.10
Рисунок
1.11
Рисунок
1.12
Рисунок
1.13
Рисунок
1.14
Вставка
1.15
Рисунок
1.16
Литература:
1. Емильянов
С.В., Системы
автоматического
управления
с переменной
структурой.
- М.: Наука, 1967.
2. Воронов
А.А.,Устойчивость
управляемость
наблюдаемость,
Москва “Наука”,
1979.
3. Хабаров
В.С. Сранительная
оценка методов
исследования
абсолютной
устойчивости
СПС: Научн.-исслед.
работа.
4. Хабаров
В.С. Нелинейные
САУ: Курс лекций/
Записал В.Л.Смык,-1997.
Список
постраничных
ссылок:
1. Ла
Салль Ж., Лефшец
С. Исследование
устойчивости
прямым методом
Ляпунова.-М.:
Мир, 1964.-168 с.
2. Ляпунов
А.М. Общая задача
об устойчивости
движения. - Собр.
соч.- М.: Изд-во
АН СССР, 1956, т. 2, с.
7-271.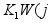 w)][1+
w)][1+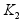 W(jw)]}>0.
(3)
W(jw)]}>0.
(3)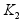 s-x)(x-
s-x)(x-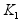 s).
Действительно,
как было показано
выше, форма
F(jw,x)
имеет вид
s).
Действительно,
как было показано
выше, форма
F(jw,x)
имеет вид
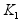 W(jw)][1+
W(jw)][1+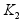 W(jw)]}|x|
W(jw)]}|x|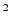
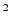 следует (3).
следует (3).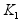 №-Ґ
,
№-Ґ
,
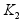 №+Ґ.
Случай, когда
либо
№+Ґ.
Случай, когда
либо
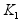 =-Ґ,
либо
=-Ґ,
либо
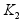 =+Ґ
рассматривается
аналогично.
=+Ґ
рассматривается
аналогично.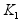 z)(1+
z)(1+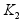 z
z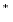 )]Ј0,
если
)]Ј0,
если
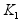 №-Ґ
,
№-Ґ
,
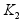 №+Ґ.
(4)
№+Ґ.
(4)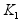 z)z
z)z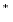 ]Ј0,
если
]Ј0,
если
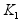 №-Ґ
,
№-Ґ
,
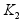 №+Ґ.
(5)
№+Ґ.
(5)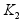 z
z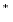 )]Ј0,
если
)]Ј0,
если
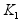 №-Ґ
,
№-Ґ
,
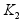 №+Ґ.
(6)
№+Ґ.
(6)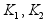 )
- облость комплексной
плоскости z,
определяемая
этими условиями.
Граница В(
)
- облость комплексной
плоскости z,
определяемая
этими условиями.
Граница В(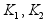 )
области определяемая
уравнениями
получаемыми
из (4)-(6) заменой
знаков неравенств
равенствами.
Для (4) получаем
окружность,
проходящую
через точки
-1/
)
области определяемая
уравнениями
получаемыми
из (4)-(6) заменой
знаков неравенств
равенствами.
Для (4) получаем
окружность,
проходящую
через точки
-1/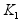 ,
-1/
,
-1/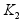 с
центром
на оси абсцисс,
причем область
С будет внутренностью
этой окружности,
если
с
центром
на оси абсцисс,
причем область
С будет внутренностью
этой окружности,
если
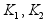 >0,
т.е. если нелинейные
характеристики
лежат в 1 и 3 квадрантах,
и ее внешностью,
если сектор
(
>0,
т.е. если нелинейные
характеристики
лежат в 1 и 3 квадрантах,
и ее внешностью,
если сектор
(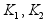 )
захватывает
два смежных
квадранта. Если
одна из границ
сектора совпадает
с осью абсцисс,
т.е. если
)
захватывает
два смежных
квадранта. Если
одна из границ
сектора совпадает
с осью абсцисс,
т.е. если
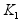 =0
или
=0
или
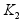 =0
, то область С
будет полуплоскостью,
а ее граница
- вертикальной
прямой, проходящей
соответственно
через -1/
=0
, то область С
будет полуплоскостью,
а ее граница
- вертикальной
прямой, проходящей
соответственно
через -1/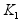 или -1/
или -1/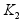 .
На
рисунке 1 показаны
границы в плоскости
z для различного
расположения
секторов (
.
На
рисунке 1 показаны
границы в плоскости
z для различного
расположения
секторов (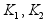 )
в плоскости
s,
x.
Там же изображены
кривые W(jw),
w>0
для неособого
случая, расположенные
так, что возможна
абсолютная
устойчивость.
Однако только
приемлимого
расположения
хаоактеристик
W(jw)
еще недостаточно
для суждения
об абсолютной
устойчивости
: кроме этого,
нужно еще
потребовать,
чтобы линейная
замкнутоя
система была
асимптотически
устойчивой.
)
в плоскости
s,
x.
Там же изображены
кривые W(jw),
w>0
для неособого
случая, расположенные
так, что возможна
абсолютная
устойчивость.
Однако только
приемлимого
расположения
хаоактеристик
W(jw)
еще недостаточно
для суждения
об абсолютной
устойчивости
: кроме этого,
нужно еще
потребовать,
чтобы линейная
замкнутоя
система была
асимптотически
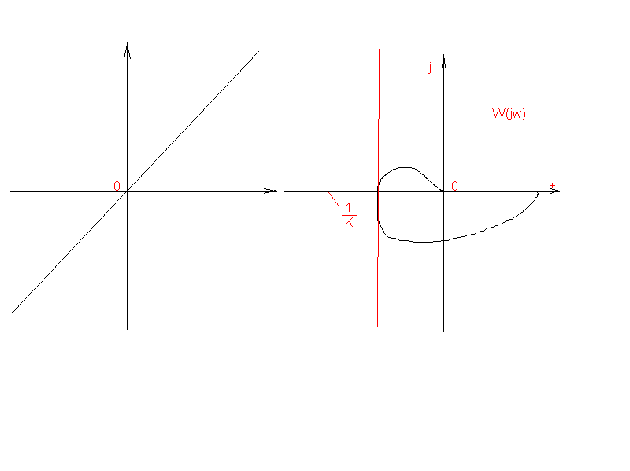
устойчивой.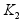 s-x)(x-
s-x)(x-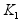 s)і0
(7)
s)і0
(7)







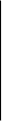


 А
Х Y
А
Х Y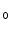 У
У
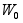 (P)
Z
(P)
Z (-)
(-)

 G(p)
g
G(p)
g
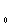 (p)
- оператор линейной
части системы,
которая может
иметь в общем
случае следущий
вид:
(p)
- оператор линейной
части системы,
которая может
иметь в общем
случае следущий
вид:
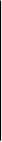
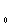 (p)=
(p)=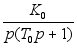 ;
;
 (8)
(8) W(p)=
W(p)=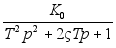 ;
;
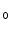 x,
x,



 при
gx>0
при
gx>0
 Y
Y =
(9)
=
(9) -
-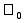 при gx<0,
при gx<0,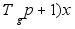

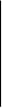
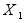 =
=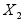 ,
,



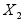 =-
=-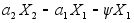 ,
(10)
,
(10)
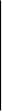


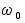 при g
при g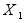 >0
>0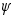 =
=
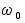 при g
при g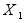 <0,
<0,
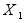 +
+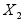 ;
;
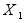 =
=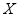 .
.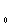 (p)=
(p)=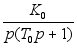 в уравнениях
(10) имеем:
в уравнениях
(10) имеем: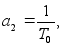
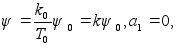 (11)
(11)
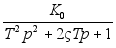 имеем:
имеем: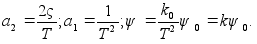 (12)
(12)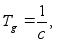 (13)
(13)
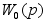 и G(p) или в виде
формы Коши
(10).
и G(p) или в виде
формы Коши
(10).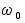 |x|=c
|x|=c











 l
g y z
l
g y z





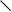
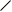
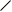
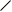
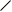

 (-) x
G(p) W(p)
(-) x
G(p) W(p)
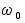 |x|
- var.
|x|
- var.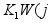 w)][1+
w)][1+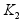 W(jw)]}>0,
W(jw)]}>0,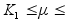
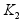 соответствовал
критерию Найквиста.
соответствовал
критерию Найквиста. )
и годографы
W(jw),
расположенные
таким образом,
что согласно
(4) и (5) возможна
абсолютная
устойчивость.
)
и годографы
W(jw),
расположенные
таким образом,
что согласно
(4) и (5) возможна
абсолютная
устойчивость.

 y ^
y ^
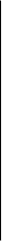
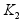 g
(
g
(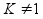 )
)

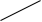
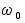 |x|
y=
|x|
y=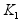 g
(при
g
(при
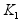 =0)
=0)
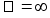


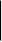
 >
>
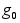 0
0






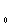 (p)=
(p)=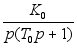 ,
когда
,
когда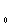 (p)G(p),
G(p)=
(p)G(p),
G(p)=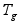 p+1,
p+1,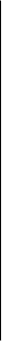 j
j

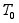 >
>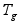
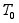
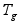
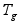 =
=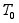
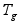 >
>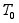 (14)
(14)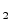 =
=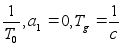 .
.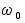 kЈy(t)=c
kЈy(t)=c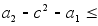
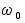 k
k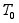 ,
,
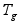 ,
,
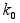 ,
тогда получим
,
тогда получим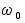
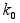 Ј
Ј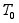 y(t)=
y(t)=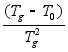 Ј
Ј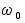
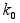 (16)
(16)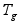 =
=
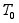 ,
y(t)=0
,
y(t)=0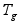 >
>
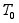 ,
y(t)>0
,
y(t)>0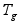
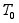 ,
y(t)<0,
,
y(t)<0,
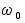 |x|=c
|x|=c















 l
g s
z
l
g s
z




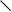
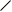
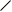
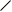




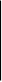
 (-) x
G(p)
(-) x
G(p)
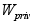 (p)
(p)
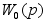



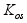

 - варьируемая
величина,
- варьируемая
величина,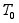 =0.5,
=0.5,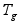 =0.1
(анализ поведения
системы при
изменении
данного параметра
исследуется
в работе ст-та
Новикова, мы
берем оптимальное
значение),
=0.1
(анализ поведения
системы при
изменении
данного параметра
исследуется
в работе ст-та
Новикова, мы
берем оптимальное
значение),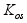 =0.1,1
(коэффициент
обратной связи),
=0.1,1
(коэффициент
обратной связи),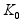 =10,100.
=10,100.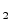 (p),
(p),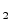 (p)=
(p)=
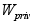 (p)W
(p)W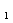 (p),
где
(p),
где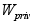 (p)=
(p)=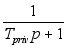 ,
а W
,
а W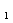 (p)
в свою очередь
будет:
(p)
в свою очередь
будет: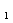 (p)=
(p)=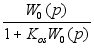 ,
,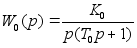 ,
соответственно
вся функция
имеет вид:
,
соответственно
вся функция
имеет вид: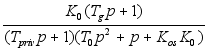 ;
;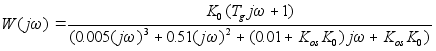 ;
;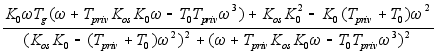 ;
;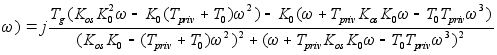 ;
;
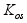 и
и
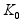 ,
x
уменьшается,
можно сделать
вывод, что
колебательность
звена увеличиться.
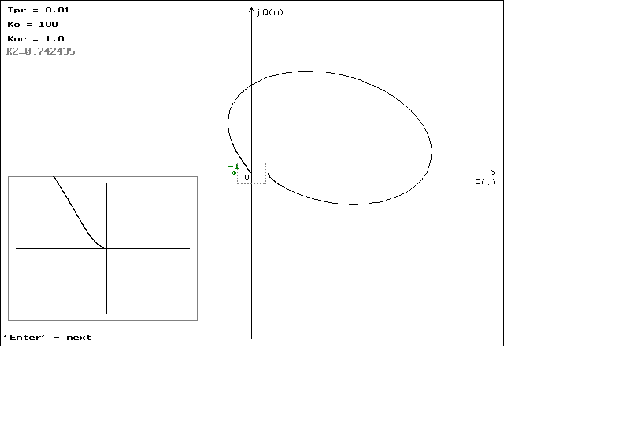
Это можно наблюдать
на графиках
1.13 - 1.16 в приложении
N 2.
,
x
уменьшается,
можно сделать
вывод, что
колебательность
звена увеличиться.
Это можно наблюдать
на графиках
1.13 - 1.16 в приложении
N 2.
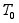
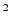 >
>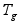 , то можно сделать
вывод, что коректор
будет влиять
только на высоких
частотах, а на
низких будет
преобладать
, то можно сделать
вывод, что коректор
будет влиять
только на высоких
частотах, а на
низких будет
преобладать
 ,
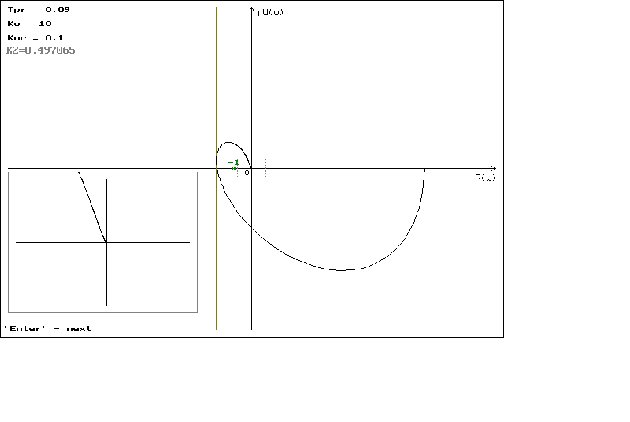
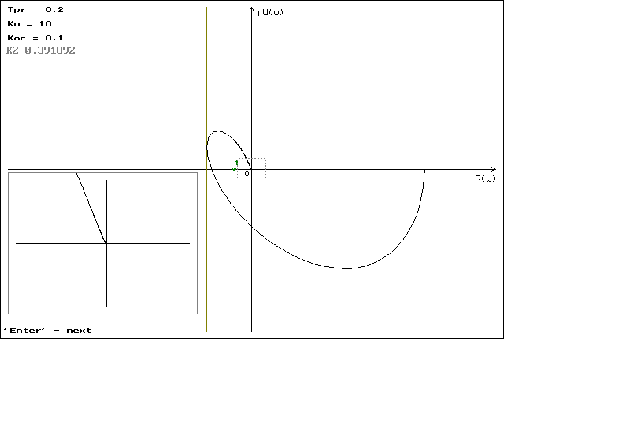
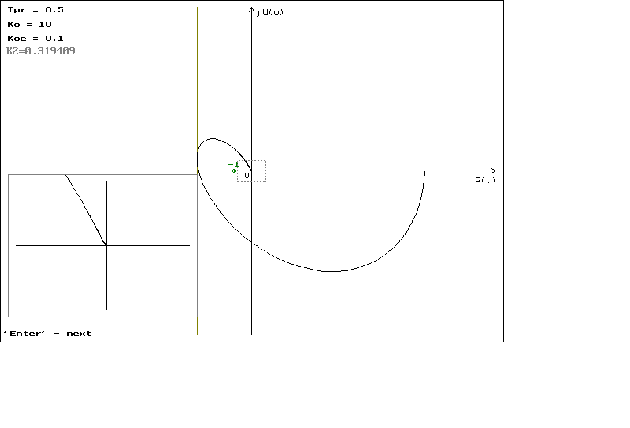
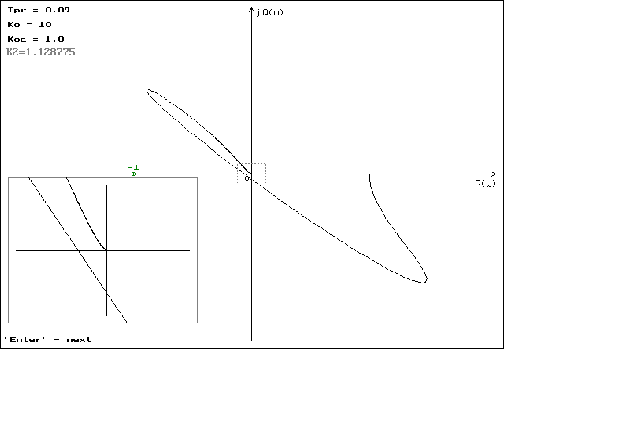
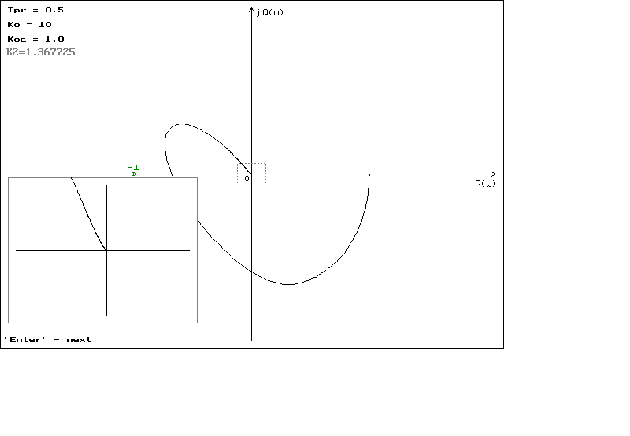
что можно наблюдать
на графиках
1.1 - 1.4. На графиках
1.5 - 1.8 можно наблюдать
минемальные
значения
,
что можно наблюдать
на графиках
1.1 - 1.4. На графиках
1.5 - 1.8 можно наблюдать
минемальные
значения
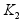 ,
это значит что,
при этих значениях
будет максимальные
значения полки
нечувствительности
релейного
элемента.
,
это значит что,
при этих значениях
будет максимальные
значения полки
нечувствительности
релейного
элемента.
 .
.