Реферат: Исследование статистических зависимостей для контактных систем типа W UMa
СОДЕРЖАНИЕ
ВВЕДЕНИЕ..................................................................................................3
§1 Классификация тесных двойных систем.............................................
§2 Алгоритм ZET.........................................................................................
§3 Применение метода ZET……………………………………………..
ВЫВОДЫ.......................................................................................................
ПРИЛОЖЕНИЕ.............................................................................................
ЛИТЕРАТУРА...............................................................................................
ВВЕДЕНИЕ.
Изучение фотометрических и абсолютных элементов тесных двойных систем, находящихся на разных стадиях эволюции, представляет большой интерес с точки зрения статистического исследования этих систем, изучения строения Галактики, а также теории происхождения и эволюции одиночных и двойных звезд. Одной из важных характеристик тесных двойных систем является отношение масс мене массивной компоненты к более массивной q=m2/m1 . Отношение масс позволяет уточнить эволюционный тип звезды, определить форму внутренней критической поверхности (т.н. полости Роша), а также положение первой точки Лагранжа. Для контактных систем, исследуемых в данной работе, у которых обе компоненты близки друг к другу и практически наполняют пределы полости Роша, отношение масс q, кроме всего прочего, определяет конфигурацию всей системы (зависящую от большой полуоси A, отношения масс q, угла наклона i).
Однако, отношение масс q известны точно для очень малого числа систем, имеющих данные спектроскопических наблюдений. Фотометрические же данные, полученные, как правило, с помощью метода синтеза кривых блеска, не являются надежными, так как этот метод позволяет получить точное решение лишь для симметричных кривых блеска. Так, например, у контактных систем, исследуемых в данной работе, вследствие близости компонент друг к другу, кривые блеска сильно искажены газовыми потоками, пятнами и околозвездными газовыми оболочками.
Для статистических исследований представляет значительный интерес хотя бы приближенная оценка относительных и абсолютных параметров тех затменных систем, для которых элементы спектроскопической орбиты неизвестны и прямое вычисление их абсолютных характеристик не представляется возможным.
М.А. Свечников и Э.Ф. Кузнецова в [2] для такой приближенной оценки использовали статистические соотношения (масса - радиус, масса - спектр, масса - светимость и др.) для компонент различных типов, а также ряд других статистических зависимостей. Из-за того, что использованные для определения элементов статистические зависимости носят приближенный характер, следует ожидать, что для многих систем найденные в [2] приближенные элементы окажутся неточными и даже ошибочными. Это обусловливает необходимость теоретических подходов к оценке параметров затменных переменных звезд. В изученной статье [1] отношение масс компонент q и спектральный класс главной компоненты Sp1 для звезд типа W UMa определяется с помощью статистического метода ZET, разработанного в Международной лаборатории интеллектуальных систем (Новосибирск) Н.Г. Загоруйко. Метод ZET применялся для восстановления глубины вторичных минимумов звездных систем типа РГП (ошибка прогноза составила 5-8%), спектров звезд этого типа, спектров класса главной компоненты контактных систем типа KW и отношения масс. Точность восстановления доходила до 10% и только для q этот результат был завышен. Была составлена таблица, в которую включены q, полученные разными авторами, для некоторых отдельных систем значения q имеют очень большие расхождения. Поэтому цель данной работы улучшить качества восстановления q методом ZET.
§1. Классификация тесных двойных систем.
В 1967-69 гг. М.А.Свечниковым была разработана классификация тесных двойных систем, сочетающая достоинства классификации Копала(1955), учитывающей геометрические свойства этих систем (размеры компонент по отношению к размерам соответствующих внутренних критических поверхностей (ВКП) Роша) и классификации Крата(1944, 1962 гг.), основанной на физических характеристиках компонентов, входящих в данную систему. Эта классификация удобна при статистических исследованиях тесных двойных звезд, и, будучи проведена по геометрическим и физическим характеристикам компонентов затменных систем (отношению размеров компонентов к размерам соответствующих ВКП, спектральным классам и классам светимости компонентов), оказывается в то же время связанной с эволюционными стадиями затменных систем, определяемыми их возрастом, начальными массами компонентов и начальными параметрами орбиты системы.
Как было показано в работе М.А.Свечникова (1969), подавляющее большинство изученных затменных переменных звезд (т.е. тех систем, для которых определены фотометрические и спектроскопические элементы) принадлежит к одному из следующих основных типов:
1. Разделенные системы главной последовательности (РГП), где оба компонента системы являются звездами главной последовательности, не заполняющими соответствующие ВКП, обычно не приближающиеся к ним ближе по размерам чем ¾
2. Полу разделенные системы (ПР), где более массивный компонент является звездой главной последовательности, обычно далекой от своего предела Роша, а менее массивный спутник является субгигантом, обладающим избытком светимости и радиуса и близким по размерам к соответствующей ВКП.
3. Разделенные системы с субгигантом (РС), у которых, в отличии от ПР-систем, спутник-субгигант, несмотря на большой избыток радиуса, не заполняет свою ВКП, а имеет размеры, значительно меньшие, чем последняя.
4. "Контактные" системы, в которых компоненты близки по своим размерам к соответствующим ВКП (хотя и не обязательно в точности их заполняют). Эти системы подразделяются на два разных подтипа:
а) Контактные системы типа W UMa (KW), имеющие, в большинстве случаев, спектры главных компонентов более поздние, чем F0. Главные (более массивные) компоненты у этих систем не уклоняются значительно от зависимостей масса-светимость и масса-радиус для звезд главной последовательности в то время, как спутники обладают значительным избытком светимости (подобно субгигантам в ПР и РС-системах), но не обладают избытком радиуса (вследствие чего они располагаются на диаграмме спектр-светимость левее главной начальной последовательности, примерно параллельно ей);
б) Контактные системы ранних спектральных классов (КР) (F0 и более ранние), где оба компонента, близкие по размерам к своим ВКП, тем не менее, в большинстве случаев не уклоняются значительно от зависимостей масса-светимость и масса-радиус для звезд главной последовательности.
5. Системы, имеющие хотя бы один компонент, являющийся либо сверхгигантом, либо гигантом позднего спектрального класса (С-Г). Такие системы сравнительно многочисленны среди изученных затменных переменных вследствие их высокой светимости и необычных физических характеристик, но в действительности они, по-видимому, должны составлять лишь небольшую долю от общего числа тесных двойных систем.
6. Системы, у которых, по крайней мере, один компонент лежит ниже главной последовательности и является горячим субкарликом или белым карликом (С-К). Сюда же были отнесены и системы, один из компонентов, которых является нейтронной звездой или "черной дырой", а также системы с WR-компонентами.
Подобная классификация была выполнена ранее М.А.Свечниковым (1969) для 197 затменных систем с известными абсолютными элементами. Она могла быть более или менее уверенно проведена также для затменных переменных с известными фотометрическими элементами, у которых можно каким-либо образом оценить и отношение масс компонентов q=m2/m1 и тем самым определить относительные размеры соответствующих ВКП. Так, из примерно 500 затменных систем с известными фотометрическими элементами, имеющихся в карточном каталоге М.А.Свечникова, надежную классификацию можно было провести для 367 систем. В остальных случаях при отнесении системы к тому или иному типу имеется некоторая степень неуверенности, обычно из-за отсутствия или ненадежности имеющихся данных о величине q.
§2 Алгоритм ZET.
Алгоритм ZET предназначен для прогнозирования и редактирования (проверки) значений в таблицах "объект-свойство". В таких таблицах строки соответствуют рассматриваемым объектам, а столбцы есть значения характеристик, описывающих эти объекты. Таким образом, на пересечение строки с номером "i" и столбца с номером "j", будет находиться значение j-ой характеристики для i-го объекта. Клетку таблицы, расположенную на пересечение i-ой строки и j-го столбца, обозначим символом Aij. Пусть значения Aij неизвестно. Можно достаточно уверенно предсказать это значение, если использовать имеющиеся в таблице закономерности. В реальных таблицах многие столбцы связаны друг с другом. Есть в таблицах и строки, похожие друг на друга по значениям своих характеристик. В алгоритме ZET выявляются такие связи, и на их основе выполняется предсказание искомого значения. Предсказание осуществляется на основе принципа локальной линейности. Это одна из основных идей, позволившая построить эффективный метод и получать хорошие результаты. Она заключается в том, что предсказание выполняется не на всей информации, имеющейся в таблице, а только на той ее части, которая наиболее тесно связана со строкой и столбцом, в которых этот пробел находится. Другими словами, в алгоритме ZET, в отличии от многих других алгоритмов заполнение пробелов, реализуется "локальный" подход к предсказанию каждого пропущенного значения. Для вычисления этого значения строится своя "предсказывающая подматрица", содержащая только имеющую отношение к делу информацию. В подматрицу отбираются в порядке убывания сходства строки, т.е. строки, самые похожие на строку, содержащую интересующий нас пробел, а затем для выбранных строк отбираются также в порядке убывания сходства столбцы "самые похожие" на столбец, содержащий этот пробел.
1 . . . k j . . . n
-
1
:
i
l
:
m
Фaik Aaij Aalk Aalj
Предсказание элемента Aij по k-му столбцу Aij(k) делается на основание гипотезы о линейной зависимости между столбцами, при этом сначала вычисляются коэффициенты линейной регрессии Вjk и Сjk ,и по ним находится элемент Aij(k):
Aij(k)=Bjk*Aik+Cjk.
После того, как будут сделаны предсказания Аij(k) по всем р столбцам, не имеющим пропуска в i-ой строке, вычисляется средневзвешенная величина элемента:
Aij(стб)=(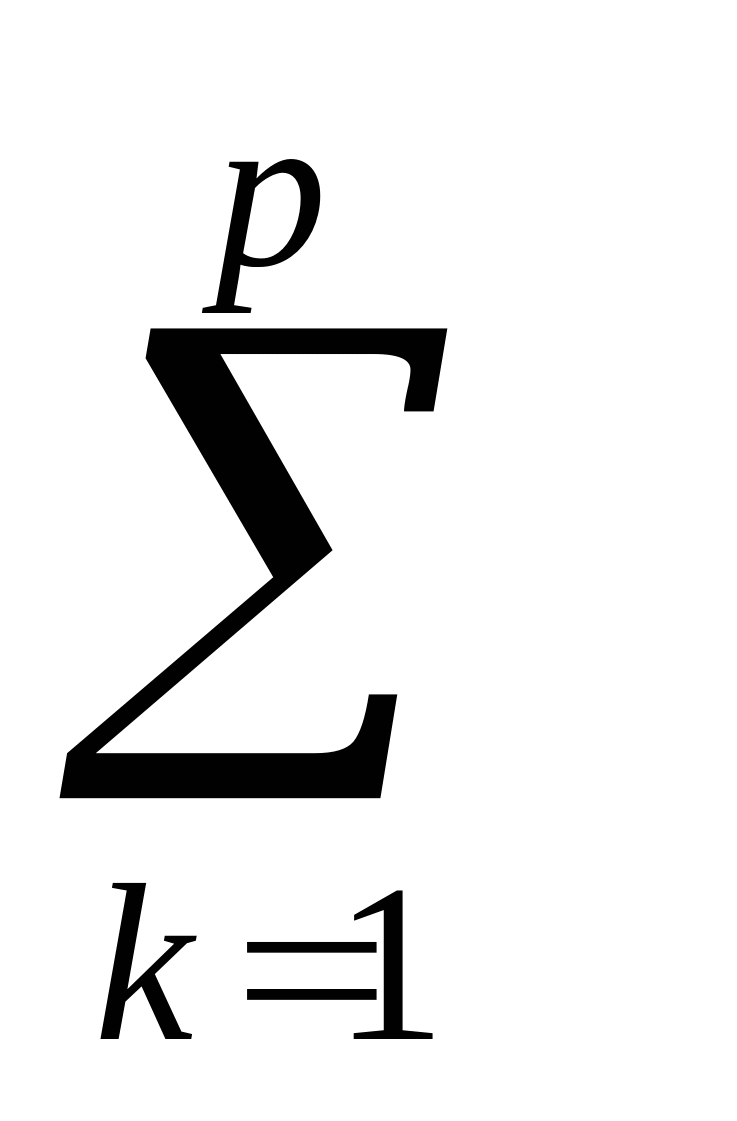 Aij(k)*Qkj)/(
Aij(k)*Qkj)/(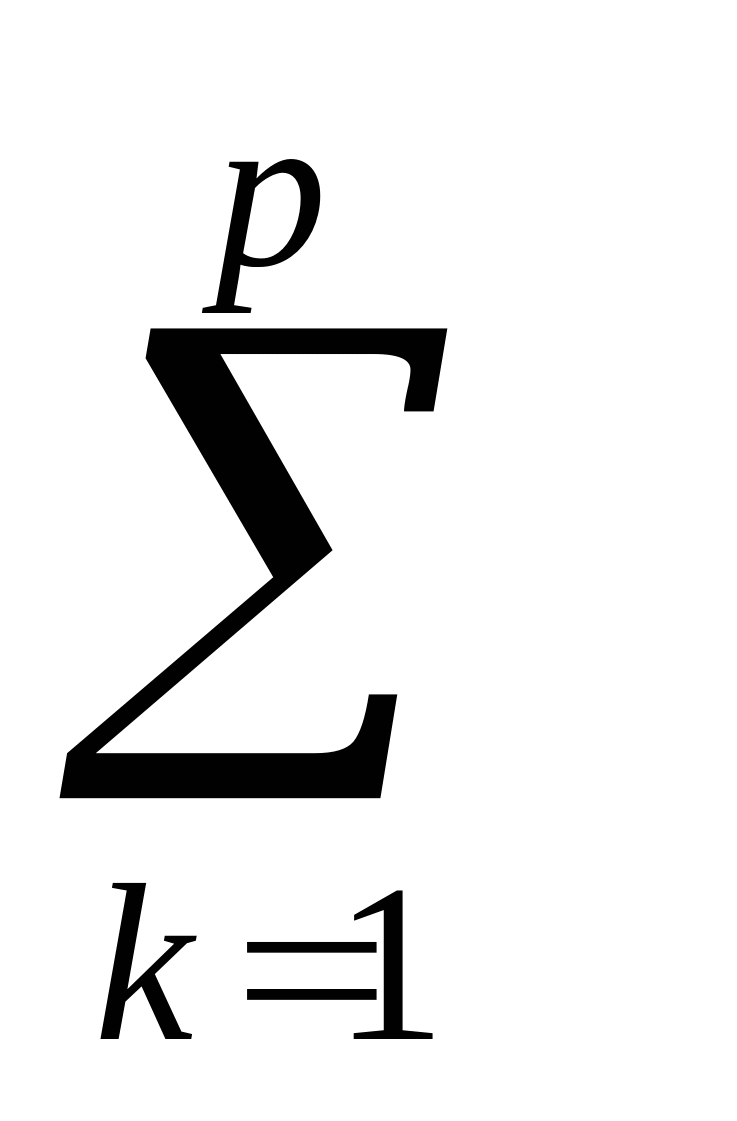 Qkj)
Qkj)
Вклад каждого столбца (строки) в результат предсказания зависит от их "компетентности" Q, являющейся функцией двух аргументов: "близости" между j-м и k-м столбцами (i-ой и l-ой строками) и "взаимной заполненность" этих столбцов (строк). "Близость" представляет собой степенную функцию модуля коэффициента линейной корреляции (Rkj)а (или (Ril)а). "Взаимная заполненность" k-го и j-го столбцов (Lkj) равна числу непустых пар элементов этих столбцов Alk и Alj для всех l от 1 до m. Отсюда:
Qil=(Ril)a*Lil
Qkj=(Rkj)a*Lkj .
Выбор показателя
степени а
осуществляется
следующим
образом, при
каждом из
последовательных
значений а (из
некоторого
заданного
диапазона
amin
Аналогичная
процедура
построения
формулы и оценки
точности вычисления
всех элементов
i-ой строки
выполняется
для проверки
возможности
предсказания
Aij как элемента
строки.
Aij(стр)=(
Данные в
матрице A(i,j)
предварительно
нормированы
так, чтобы элементы
каждого столбца
изменялись
в пределах от
0 до 1. После получения
оценок предсказания
по строкам и
столбцам сравнивается
точность, с
которой удалось
предсказать
известные
элементы i-ой
строки di и j-го
столбца dj. Окончательно
для предсказания
выбирается
либо Aij(стб), либо
Aij(стр), в зависимости
от того, где
точность d
оказалась выше.
Эта точность
рассматривается
в качестве
ожидаемой
ошибки предсказания
Aij.
Итак, в алгоритме
ZET можно выделить
основные этапы:
1. Проводится
нормировка
столбцов таблицы
исходных данных
по дисперсиям.
2. Выбирается
пробел Aij, находящийся
на пересечение
i-ой строки и
j-го столбца.
3. При определение
сходства столбцов
производится
их предварительная
нормировка
к интервалу
[0,1], и для строк
и для столбцов
степень сходства
определяется
на основе евклидова
расстояния
rев=[
где
Xj, Yj - соответственно
значения j-го
свойства объектов
X и Y. Использование
такой меры
сходства и
обуславливает
применимость
алгоритма к
таблицам данных,
представленных
в сильных шкалах,
для которых
операции,
использованные
в формуле, являются
допустимыми
преобразованиями.
По расстоянию
rев
выбирается
заданное число
объектов-аналогов,
а для них-
свойств-аналогов.
4. В матрице,
состоящей из
отобранных
строк, столбцы
нормируются
к интервалу
[0,1] и выбирается
заданное количество
столбцов, наиболее
сильно связанных
с j-м.
5. По исходной
таблице формируется
"предсказывающая"
подматрица,
составленная
из элементов,
находящихся
на пересечении
i-ой и ближайшей
к ней строк с
j-м и ближайших
к нему столбцами.
6. Столбцы
полученной
подматрицы
нормируются
к интервалу
[0,1].
7. Из уравнений
линейной регрессии
для k-го элемента
Aij вычисляются
"подсказки"
Aij от строк и (или)
столбцов
"предсказывающей"
подматрицы.
8. Находится
коэффициент
а, определяющий
степень учета
взаимного
сходства столбцов
(строк) подматрицы
при вычислении
итогового
значения
прогнозируемого
элемента Aij.
9. Процедура
2-8 повторяется
для каждого
пробела.
10. Значения,
вычисленные
в режимах заполнения
в зависимости
от входных
условий, заносятся
в таблицу сразу
же после вычисления
каждого из них
или только
после окончания
прогнозирования
значений для
всех пробелов
таблицы.
11. Пункты 1-10
повторяются.
Количество
повторений
задается во
входных условиях.
Когда сформирована
группа объектов-аналогов
и найдены в
этой группе
наиболее
информативные
свойства для
интересующего
нас объекта,
т.е. сформирована
"предсказывающая"
подматрица,
алгоритм переходит
к этапу построения
формулы для
прогнозирования.
Иначе говоря,
алгоритм ZET можно
разбить на две
части:
1. Выбор из
исходной таблицы
наиболее связанной
с интересующим
нас объектом
Aij информации-построения
"предсказывающей"
подматрицы.
2. Определения
параметров
формулы для
возможно лучшего
предсказания
значения
рассматриваемого
элемента Aij с
одновременной
оценкой ожидаемой
точности прогноза.
В алгоритме
ZET, как было отмечено
выше, предусмотрен
"персональный"
подход к прогнозированию
каждого интересующего
нас элемента
таблицы. Для
каждого элемента
Aij подбирается
своя предсказывающая
подматрица,
в которой содержатся
только строки,
наиболее похожие
на i-ую и столбцы,
наиболее связанные
с j-м и по этой
"персональной"
информации
подбирается
персональная
формула для
прогнозирования
элемента Aij. Для
того, чтобы при
определении
сходства объектов
(строк) "вклад"
каждого показателя
(свойства) не
зависел от
единиц измерения
и был сопоставим
с вкладами
других показателей,
производится
нормировка
каждого столбца
относительно
его дисперсии.
Если есть
необходимость
учесть неравнозначность
вкладов свойств
в меру сходства,
т.е. если из
каких-либо
соображений
известны
значимости,
"веса" свойств,
то их можно
учесть, умножив
отнормированные
данные на эти
веса.
Если пробелов
в данных много,
вряд ли можно
надеяться
заполнить их
все сразу с
хорошей точностью.
Поэтому организуется
многоступенчатая
процедура
заполнения.
Она состоит
в том, чтобы на
первом этапе
заполнить при
минимальном
размере подматриц
наиболее надежные
элементы, т.е.
те, которые
удается предсказать
с заданной
точностью.
Затем поставить
эти значения
в таблицу и,
уже считая их
известными,
вновь обратиться
к программе
с теми же условиями
на требуемую
точность и
размер подматриц.
Добавленная
в таблицу информация
может дать
возможность
предсказать
еще ряд значений.
Процесс
повторяется
при одних и тех
же условиях
до тех пор, пока
не прекратится
предсказание
новых элементов.
Тогда можно
повторять цикл
заполнения.
§ 3
Применение
метода ZET для
восстановления
физических
параметров
контактных
систем.
Для того,
чтобы правильно
спрогнозировать
неизвестные
элементы, необходимо
решить ряд
существенных
вопросов:
1. Какие характеристики
звезд могут
быть наиболее
информативны
с точки зрения
предсказания
отношения масс
q;
2. Можно ли
ожидать достаточно
хороших результатов;
3. Если да, то
как организовать
решение, чтобы
заполнить
больше пробелов
с приемлемой
точностью;
4. Можно ли
доподлинно
проверить
"качество"
вычисленных
значений.
Для решения
первой проблемы
- отбора наиболее
информативных
для предсказания
q характеристик
звезд было
выполнено
редактирование
всех известных
значений первого
столбца, содержащего
отношение масс
q контрольной
таблицы размерностью
15х14, куда вошли
15 систем типа
W UMa и 14 их параметров
из [3] (известных
абсолютно
точно), на предсказывающих
подматрицах
6х6, 5х5, 4х4. Объектами
в данной таблице
были контактные
системы типа
W UMa, а в качестве
свойств были
взяты следующие
параметры:
отношение масс
компонент q,
спектральный
класс главной
компоненты
Sp1, масса главной
компоненты
m1, абсолютная
болометрическая
величина более
массивной
компоненты
M1bol, большая полуось
орбиты в долях
радиуса Солнца
A, угол наклона
орбиты i, период
затменной
системы P, средний
радиус главной
компоненты
в долях большой
полуоси орбиты
r1, средний радиус
второстепенной
компоненты
в долях большой
полуоси орбиты
r2, относительный
блеск более
массивной
компоненты
L1, отношение
поверхностных
яркостей более
массивной
компоненты
к менее массивной
J1/J2, радиус главной
компоненты
в долях радиуса
Солнца R1, радиус
второстепенной
компоненты
в долях радиуса
Солнца R2, абсолютная
болометрическая
величина менее
массивной
компоненты
M2bol.
По результатам
редактирования
была составлена
таблица, где
показано участие
отдельных
параметров
в предсказании
отношения масс
компонентов
q. Из таблицы
видно, что параметры
P, r1, L1, J1/J2, R1 и M2bol плохо
(т.е. редко) участвуют
в предсказании
и вклад их
достаточно
мал, поэтому
их можно отбросить.
Так как параметры
r2 и R2 связаны с
q эмпирическими
формулами:
r~rкрит(q) и lg(m)=-0.153+1.56*lg(R),
то их также
представляется
целесообразным
отбросить.
Таким образом,
остается таблица
15х6, в которую
входят 15 объектов
и 6 параметров:
q, Sp1, M1bol, m1, A, i. На этой
таблице было
выполнено
редактирование
первого столбца,
содержащего
отношение масс
q и второго столбца,
содержащего
спектральные
классы главных
компонент Sp1.
Получены средние
ошибки редактирования
соответственно
d=13.555% и d=6.6791%. Поскольку
средние ошибки
редактирования
малы, то можно
сделать вывод,
что отобранные
параметры
позволяют с
достаточно
высокой степенью
точности восстановить
неизвестные
значения q.
Далее, из
[2] были взяты
295 систем типа
KW, для которых
выписаны указанные
выше 6 параметров,
и составлена
рабочая таблица
295х6 , где на месте
предсказываемых
элементов стоят
пробелы. В качестве
известных
значений q были
взяты значения
из [3 - 16]. Всего
получилось
72 известных
значения q, опираясь
на которые
программа
будет предсказывать
остальные
значения.
Для оценки
целесообразности
применения
метода ZET при
прогнозировании
недостающих
значений q на
рабочей таблице
295х6 было выполнено
редактирование
1-го столбца
при предсказывающей
подматрице
5х5. Средняя ошибка
редактирования
d=11.837%. Таким образом,
осталось 70 известных
значений q при
225 неизвестных.
Как видно из
результатов
редактирования
значения q могут
быть восстановлены
по имеющимся
в таблице данным
с достаточно
высокой степенью
точности.
Для дополнительной
проверки
эффективности
метода было
проведено
сравнение 72
известных
значений отношений
масс со значениями,
вычисленными
методом ZET. В
процессе вычисления
использовался
режим редактирования,
так как предполагалось,
что наблюденные
данные 72 звезд
получены с
достаточной
степенью надежности.
Было выполнено
редактирование
72 известных
элементов на
предсказывающих
подматрицах
4х4, 5х5, 6х6 и составлена
промежуточная
таблица полученных
ZET-методом q и
соответствующих
ошибок редактирования.
Получив данные
редактирования,
мы перешли
непосредственно
к предсказанию
неизвестных
значений q.
Предсказание
велось при
границах изменения
от 4 до 6 ближайших
строк и столбцов
при формирования
предсказывающих
подматриц, т.
е. для каждого
предсказываемого
значения программа
перебирает
все варианты
предсказывающих
подматриц от
4 до 6 (4х4, 4х5, и т.д. до
6х6) и выбирает
значение с
наименьшей
ожидаемой
ошибкой прогнозирования.
Было установлено,
что режим ZM1
занижает ошибку
предсказания
примерно в два
раза. Для этого
мы сравнили
прогнозируемую
и фактическую
ошибки (~8% и ~18%
соответственно).
Аналогично
установили,
что режим ZM3
несколько
завышает ошибку
предсказания
(~20% и ~22%). В режиме
ZM3 ожидаемое
отклонение
(min, при различных
a, средняя величина
отклонения
предсказанного
значения от
истинного всех
элементов
строки (столбца),
связанных с
прогнозируемым
элементом) не
является реальной
ошибкой предсказания,
исходя из этого
мы предложили
свой метод
определения
ошибки, разделив
ожидаемое
отклонение
на предсказанное
значение и
умножив на
100%. Как показало
редактирование,
режим ZM1 производит
более точное
предсказание,
чем режим ZM3 (хотя
значения предсказаний
довольно близки:
фактическая
ошибка в ZM1 ~17%, в
ZM3 ~20%), поэтому
предсказание
велось параллельно
в режимах ZM1 и
ZM3 для контроля
над ошибкой.
Получили
следующие
результаты
прогнозирования:
из 225 восстановленных
систем типа
W UMa 218 получены
с ошибкой
5%,
710%.
По сравнению
с данными наблюдения
реальная ошибка
превышает
полученную
методом в 3 раза.
Следовательно,
метод занижает
ошибку прогноза.
Часть полученных
значений q
приблизительно
совпадает, а
для некоторых
имеются существенные
отличия. Это
связано: 1) с
недостатком
наблюдательных
данных; 2) с ненадежностью
исходных данных;
3) с неполнотой
выборки; 4) с
некорректностью
подсчета ошибки
данным методом.
ЛИТЕРАТУРА:
1. Svirskaya E.M., Shmelev A.Yu. “Astronomical
and astrophysical transactions”
2. Свечников
М.А., Кузнецова
Э.Ф. “Каталог
приближенных
фотометрических
и абсолютных
элементов
затменных
переменных
звезд”, Свердловск,
Изд-во Уральского
Университета,
1990.
3. Свечников
М.А. ”Каталог
орбитальных
элементов,
масс и светимостей
тесных
двойных звезд”,
Иркутск, Изд-во
Иркутского
Университета
, 1986
.
Загоруйко
Н.Г. “Эмпирическое
предсказание”,
Новосибирск
, Изд-во Наука,
1979.
Загоруйко
Н.Г., Елкина В.Н.,
Лбов Г.С., “Алгоритмы
обнаружения
эмпирических
закономерностей”,
Новосибирск,
Изд-во Наука,
1985.
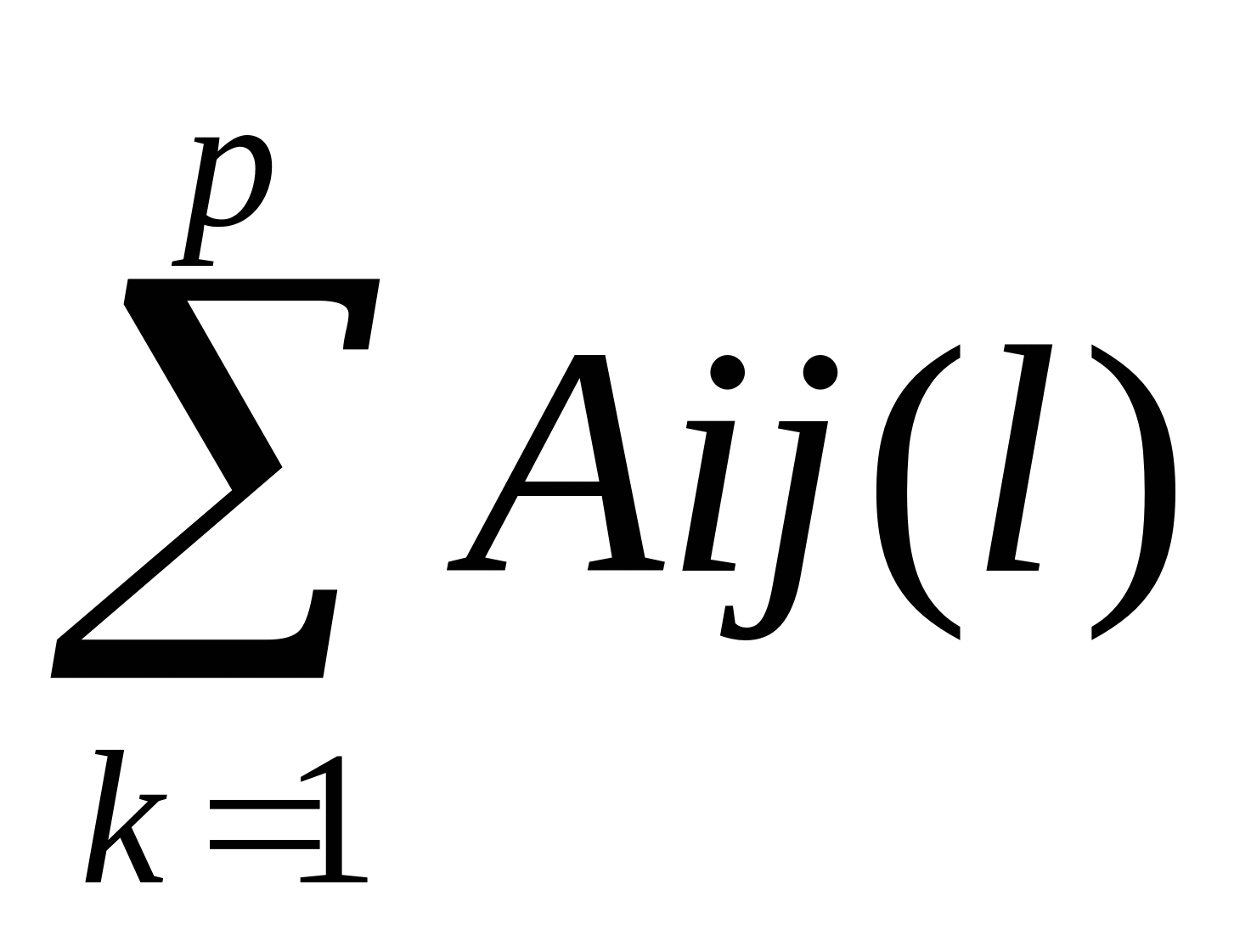 *Qil)/(
*Qil)/( )
)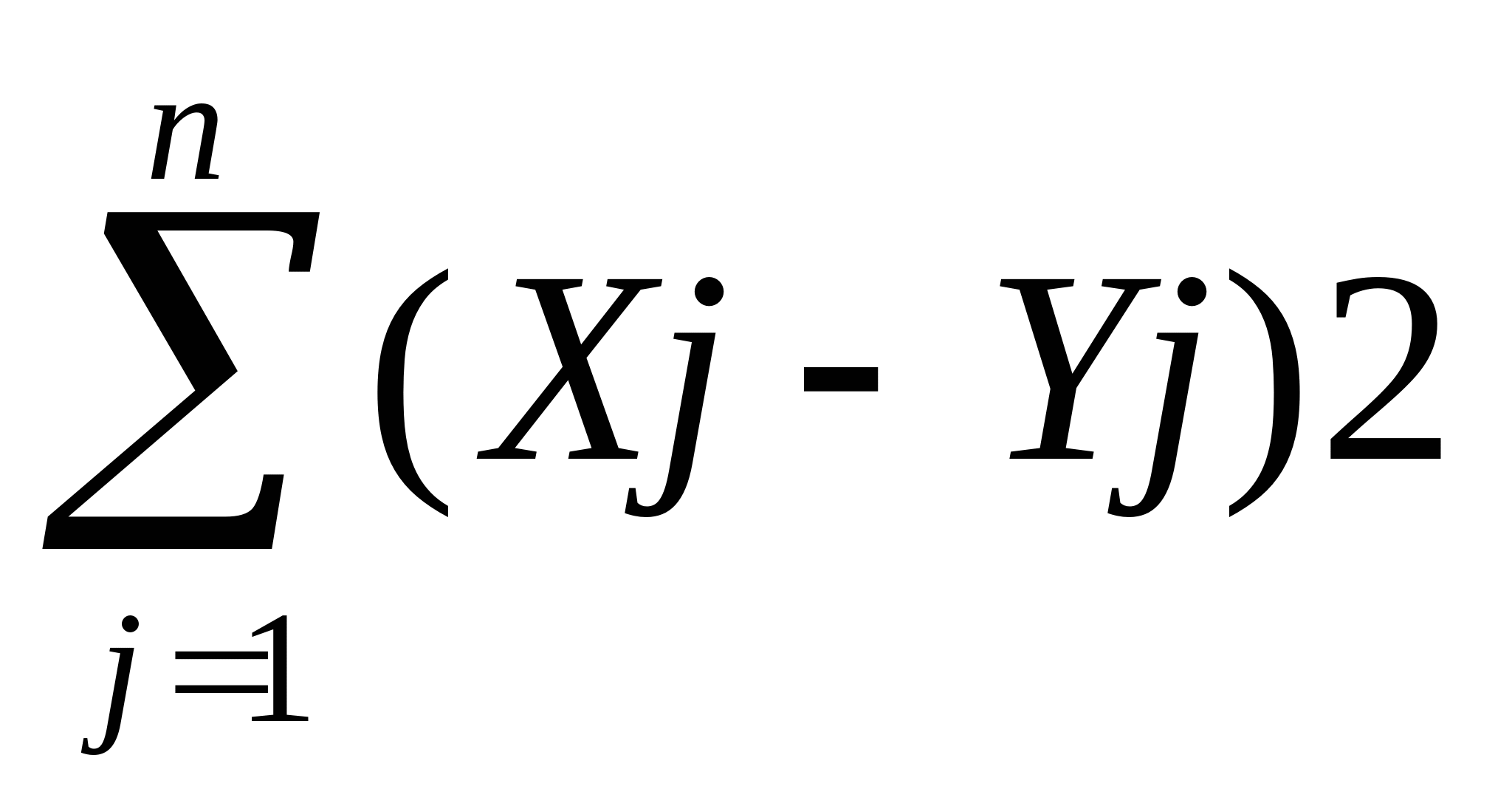 ]1/2
,
]1/2
,