Реферат: Геодезические опорные сети. Упрощенное уравнивание центральной системы
редисловие от автора.
В течении всего срока обучения мной было сделано несколько работ (курсовиков, лабораторных, практических), и сколько я не искал в инете, я ничего подходящего так и не нашел, и вот решил немного помочь следующим поколениям студентов землеустроителей.
Эта дипломная работа была написана студентом Пензенского Аграрного техникума Чижовым Олегом в 2002-03 году. В ней были использованы материалы:
Дипломная работа Зайцевой О.В.
Практика на тему гео-сети Шампарова В.В.
Диплом был защищен мной на оценку 4.
Работа почти готова к сдачи, только нужно в некоторых местах вписать несколько формул, нарисовать теодолит.
Желаю всем удачи.
По всем вопросам писать сюда: chizh@sura.ru
Министерство сельского хозяйства РФ
Пензенский Аграрный Техникум
Землеустроительное отделение
Пояснительная записка
К дипломному проекту
На тему
«Геодезические опорные сети»
Упрощенное уравнивание центральной системы.
Руководитель
Дипломного проекта: Кувардина Н. В.
Рецензент: Савичева Т. Ф.
Дипломник: Чижов О. Д.
Пенза 2003
Содержание
Раздел I Схема построения и классификация государственных
геодезических сетей.--------------------------------------------------------2
1. Понятие о геодезических опорных сетях-------------------------------------3
2. Построение геодезических опорных сетей.----------------------------------5
3. Измерение горизонтальных углов опорных сетей.-------------------------5
Радел II Инструменты применяемые для измерения углов и длин линий.—8
1. Устройство теодолита 2Т30П.---------------------------------------------------9
2. общие сведения о линейных измерениях.------------------------------------12
3. Измерение длины линии базиса мерной лентой.---------------------------12
Раздел III Камеральная обработка сетей сгущения.------------------------------14
1. Измерение длин сторон и накопление ошибок в триангуляции.--------15
2. Сущность способа наименьших квадратов.----------------------------------16
3. Виды условий уравнений в триангуляции.-----------------------------------19
4. Упрощенное уравнивание центральной системы.--------------------------22
Раздел IV Охрана труда в землеустройстве.----------------------------------------26
Раздел V Список использованной литературы.------------------------------------29
Приложения.--------------------------------------------------------------------------------31
ВВЕДЕНИЕ
Геодезия занимается изучением Земли в геометрическом отношении. Название геодезия произошло от греческих слов: гео-земля и дазаман-делю, т. е. Земле разделение. Отсюда видно, что геодезия очень близка к геометрии- науке об измерении. Обе эти науки зародились в глубокой древности. С развитием человеческого общества геометрия стала заниматься изучением пространственных форм, а практическая часть в приложении к вопросам измерения на земле получила название геодезия.
Геодезия в свою очередь тесно связана с картографией- наукой о составлении карт. Геодезические материалы служат основой для составления карт.
Задачей геодезии является изучение деталей земной поверхности. В результате изучения получают планы, карты и числовые характеристики, относящиеся к Земле в целом и отдельным участкам, линиям и точкам на ней.
В геодезии изучаются способы и инструменты, применяемые при измерении углов и длин линий.
Материалы геодезических работ в виде планов, карт и числовых величин (координат и высот) точек земной поверхности имеют большое применение в различных отраслях народного хозяйства. Всякое сооружение проектируют с учетом имеющихся на местности контуров сооружений, дорог, водных источников, почвы, грунта. Поэтому для проектирования необходим план местности с подробным отображением всех деталей. Проектирование и строительство сел, городов, железных и шоссейных дорог нельзя выполнять без геодезических материалов.
Геодезические работы по содержанию и характеру подразделяются на две стадии:
1. полевые измерительные работы с применением современной геодезической техники.
2. вычислительная обработка результатов измерений, графическое составление и оформление планов и карт.
Исключительно большое значение планова-картографический материал имеет в сельском хозяйстве. Землеустроительные органы занимаются проблемой рационального использования земли.
Перед сельским хозяйством стоят задачи орошение, осушение земельных участков, поведение мероприятий по борьбе с эрозией почв и др. все эти вопросы можно решить только с использованием геодезии. Для решения многих вопросов необходимы планы, карты, отображающие рельеф, границы видов почв, растительности, водоемов и др.
Методы изучения Земли в целом, как планеты значительно отличаются от методов изучения отдельных участков поверхности. Земля представляет собой сферическое тело, следовательно, исследуя ее в целом или больших ее участков необходимо учитывать сферичность, что и изучает наука высшая геодезия.
РАЗДЕЛ I
Схема построения и классификация государственных геодезических опорных сетей
Понятие о геодезических опорных сетях.
Основными материалами при проведении большого комплекса различных землеустроительных мероприятий являются планы и карты местности, создаваемые в результате проведения топографо-геодезических работ.
Создание планов и карт на большой территории требует предварительного построения на всю эту территорию плановых и высотных опорных геодезических сетей. Под этими сетями понимают совокупность пунктов на земной поверхности, положение которых определено координатами в принятой системе координат и высотами над уровнем моря или другой принятой уровневой поверхности. При этом пункты могут быть только плановые или только высотные. Эти пункты располагают согласно заранее составленному проекту и отмечают на местности соответствующими знаками.
Построение опорных геодезических сетей производится от общего к частному. Это значит, что первоначально на обширной территории строятся сети с редкими пунктами, но измерения проводят с высокой точностью. Затем от этих пунктов уже при меньшей точности, переходя постоянно к пунктам служащим непосредственным обоснованием съемки. Планово геодезические сети строятся методами триангуляции, трилатерации и полигонометрии или их сочетаний и видоизменений в зависимости от требуемой точности. Высотные сети создаются методами геометрического и тригонометрического, а иногда и барометрического нивелирования.
Метод триангуляции заключается в том, что на местности строят систему примыкающих один к другому треугольников, в которых измеряют все углы и обычно две стороны.
Метод трилатерации, подобно триангуляции представляет собой систему примыкающих друг к другу треугольников, в которых измеряют все стороны.
Полигонометрия состоит из одного или нескольких ходов, в которых измеряют с высокой точностью все углы и стороны. Этим методом обычно строят опору в равнинных закрытых районах, т. е. в залесенных местах и населенных пунктах.
Построение геодезических опорных сетей выполняют в три этапа: прежде всего строят государственную сеть, затем - сети местного значения, и наконец, съемочные сети. При съемках в масштабе 1:10000 и мельче сети местного значения не строят.
Государственная геодезическая сеть является главной геодезической основой съемок всех масштабов. Они подразделяются на: а) сети триангуляции, полигонометрии и трилатерации I, II, III и IV классов и б) нивелирные сети I, II, III и IV классов, различающиеся по точности измерений и по последовательности выполнения, чтобы сеть младшего класса строилась на основе сети старшего класса.
Триангуляция I класса строится в виде рядов, расположенных преимущественно вдоль меридианов и параллелей и образующих полигоны периметром около 800-1000 км. Звеня, составляющие полигоны должны иметь длину не более 200 км, причем звенья триангуляции I класса при необходимости могут быть заменены полигонометрией того же класса. Эту сеть еще называют астрономо-геодезической. Она служит для решения научных задач по определению формы и размеров Земли.
Триангуляция II класса строится в виде сетей треугольников, сплошь покрывающих площади полигонов триангуляции I класса. В отдельных случаях сети триангуляции могут быть заменены сетями ходов полигонометрии II класса. Внутри сетей триангуляции, примерно в середине полигона, измеряют не менее одной базисной стороны (ab), на концах которой также определяют широту, долготу и азимут.
На основе пунктов I и II классов по мере надобности строится триангуляция III класса в виде отельных систем, состоящих из нескольких пунктов. Триангуляция IV класса строится также в виде систем или отдельных пунктов на основе пунктов старшего класса.
В таком же порядке строят геодезические сети III и IV классов методом полигонометрии.
В районах, где сети I и II классов не построены, для обеспечения съемок в масштабах 1:5000 и 1:2000 на небольших участках разрешается строить самостоятельные сети триангуляции III и IV классов, в которых должно быть измерено не менее двух базисных сторон. Полигонометрические сети строят в этом случае полигонами с периметром для III класса - не более 60 км и для IV класса - не более 35 км.
Построение геодезических сетей методом триангуляции производится по программе, разрабатываемой в каждом отдельном случае в зависимости от фиизико-географических и других условий района работ.
Пункты государственной геодезической сети закрепляют на местности подземными сооружениями, призванными обеспечить их неизменное положение и долговременную сохранность. Для измерения углов и линий над центрами пунктов сооружают деревянные или металлические наружные знаки, конструкция которых зависит от физико-географических условий - рельефа, залесенности района, а также от расстояний между пунктами.
Построение геодезических опорных сетей сгущения.
Геодезические опорные сети сгущения разделяются на два разряда. Сети создаваемые методом триангуляции, образуют типовые фигуры: центральную систему, цепь треугольников и геодезический четырехугольник. Каждая такая фигура опирается на пункты геодезической опоры высшего класса.
Сети сгущения являются опорой для создания съемочного обоснования при крупномасштабных съемках. Густота пунктов местного значения зависит от масштаба топографической съемки. Например, для съемки в масштабе 1:10000 при расстояниях между пунктами 2-3 км количество пунктов на трапеции должно быть не менее 4-5. Пункты закрепляются бетонными центрами и наружными знаками в виде пирамид или вех. Все пункты сети сгущения 1 и 2 разряда должны иметь линейные координаты на плоскости и отметки центров, определяемые техническим нивелированием.
При создании опорных сетей сгущения на большой площади составляется предварительный проект ее построения. Проект содержит:
1. Изложение целей и задач создания опоры для съемки заданных
масштабов.
2. Сведение о наличии опорных пунктов государственной сети высших классов с координатами, высотами и территориальное размещение на заданной площади.
3. мелкомасштабный план со схематически нанесенными границами трапеций съемочных планшетов аналитической сети. При этом показываются типовые фигуры цепи треугольников, центральных систем, четырехугольников и др. В закрытой местности целесообразно проектировать полигонометрические ходы. Схема размещения пунктов должна обеспечивать опору каждого планшета для развития съемочного обоснования.
4. Сведения о характере закладке центров и знаков.
После составления проекта исполнитель выезжает в поле для осуществления проекта. Рекогносцировка состоит в уточнении проекта по размещению по размещению опорных пунктов и окончательном выборе местоположения пунктов. Пункты выбираются на командных высотах местности с учетом построения съемочной сети. При рекогносцировке иногда производятся небольшие изменения проекта в соответствии с местными условиями. После рекогносцировки производится построение центров и знаков, а затем измерение углов и линий.
3. измерение горизонтальных углов опорных сетей.
Измерение
направлений способом круговых приемов. Для измерения направлений из точки М на
пункты A, B, C, D в т. М устанавливают теодолит, алидаду скрепляют с
лимбом на отсчете 1-2’ и поворотом лимба направляют трубу на т. А. 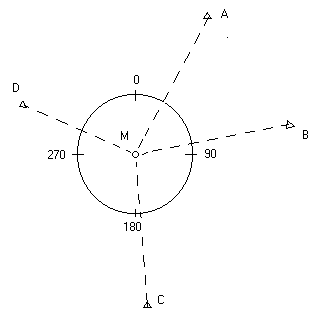
При этом положении инструмента берем отсчет по лимбу и записываем его в журнал полевых измерений. Затем лимб оставляют закрепленным, а алидаду поворачивают по направлению хода часовой стрелки и наводят трубу последовательно на точки B, C, D и снова на А, беря на каждой из них отчет и записывая в журнал. Повторный отсчет на тачку А контролирует постоянство положения лимба и уточняет наблюдение. Произведенный перечень наблюдений составляет один полуприем. Второй полуприем отличается от первого тем, что трубу переводим через зенит и берем отчеты против часовой стрелки, т. е. в последовательности A. D. C. B. A. Оба эти полуприема составляют один полный прием.
Измерение горизонтальных углов способом повторений.
Способ повторений позволяет измерять каждый угол в отдельности несколькими повторениями. При измерении этим способом алидаду ставят на отсчет по лимбу равный 1-2 ‘, поворотом лимба наводят трубу на левый пункт А, закрепляют лимб и берут отсчет, затем открепляют алидаду и наводят на правый пункт B измеряемого угла AMB, закрепляют алидаду и берут контрольный отсчет для вычисления приближенного значения угла. После этого открепляют лимб и поворачивают его с закрепленной алидадой, трубу наводят на точку А. После закрепления лимба открепляют алидаду и наводят трубу на т. В – это будет второе отложение на лимбе угла AMB. Поступая аналогично предыдущим действиям можно на лимбе повторить несколько отложений. Последний отсчет bn на т. В позволит вычислить n-кратный угол åb=bn-a.
Однократное значение угла будет равно:
b=(b+k*360°-a)/n
где k- число, показывающее сколько раз нуль алидады перешел через нуль лимба. Так измеряются углы одним полуприемом. Аналогично этому можно измерить угол при другом положении вертикального круга, оба измерения дают один полный прием. Таких приемов может быть несколько. Так измеряют все углы в точке М, и их сумма в теории должна быть равна 360°, но обычно бывают невязка, которая, при измерении 30-секундным теодолитом не должна превышать 15”Ön, где n- число измеренных углов.
РАЗДЕЛ II
Инструменты, применяемые
для измерения углов и длин
линий.
1. устройство теодолита 2Т30П
1. кремальера
2. закрепительный винт трубы
3. визир
4. колонка
5. закрепительный винт горизонтального круга
6. гильза
7. юстировочный винт
8. закрепительный винт алидады
9. уровень при алидаде
Теодолит основные особенности:
Система вертикальной оси повторительная;
Отсчет производится по одной стороне лимба с помощью шкалового микроскопа;
Малые масса и размеры защищенность основных узлов от пыли и воды.
Возможность центрирования над точкой с помощью зрительной трубы;
Возможность выполнить нивелирования с помощью уровня на трубе.
Возможность ориентирования с помощью ориентир-буссоли и определения магнитных азимутов;
Дно футляров одновременно является основанием подставки теодолита, что позволяет упаковать его не снимая со штатива;
Зрительная труба обоими концами переводится через зенит, фокусирование ее происходит вращением кремальеры, вращением диоптрического кольца окуляр устанавливают по глазу до резкой видимости изображения сетки нитей. Два горизонтальных коротких штриха сетки нитей выше и ниже перекрестия относятся к нитяному дальномеру.
Корпус зрительной трубы представляет единое целое с горизонтальной осью, установленной в пазах колонки.
Каллиматорный визир предназначен для грубой наводки на цель. При пользовании визиром, глаз должен быть на расстоянии 25-39 см от него.
Точное наведение зрительной трубы на предмет в горизонтальной плоскости осуществляется наводящим винтом, после закрепления алидады винтом в вертикальной плоскости- наводящим винтом 10, после закрепления винтом 2.
Вращение теодолита вместе с горизонтальным кругом производят винтом 1. для поворота алидады с (горизонтальным) кругом производят винтом 5, его открепляют, а винт 8 закрепляют.
Горизонтальный и вертикальный круги градуированы с ценой деления 1°. Горизонтальный круг имеет круговую оцифровку от 0 до 359, а вертикальный- секторную от 0 до 75 и от –0 до –75.
Изображений штрихов и цифр обоих кругов передаются в поле зрения микроскопа окуляра 2, резкость изображения которого устанавливают по глазу путем вращения диоптрийного кольца. Отчет по кругам производят по соответствующим шкалам микроскопа. Поворотом и наклоном зеркала 3 достигают оптимального освещения поля зрения.
Теодолит горизонтируют по уровню, вращением подъемных винтов подставки. Резьбовая часть винта защищена втулкой. Подставка соединена с основанием тремя винтами.
Вертикальная ось теодолита полая, а основание в центре имеет отверстие, что позволяет центрировать теодолит над точкой местности с помощью зрительной трубы, установленной в надир. При транспортировании отверстие в основании закрывают крышкой.
Уровень при трубе служит для установки визирной оси зрительной трубы в горизонтальное положение при выполнении нивелирования.
Штатив: служит для установки теодолита над точкой местности- вершиной измеряемого угла. Ножки штатива шарнирно соединены с головкой. Болтами регулируется их вращение в шарнирах. Высоту штатива изменяют выдвижением ножек, после чего их закрепляют винтами. Наконечники ножек углубляют в грунт, нажимают ногой на их упоры.
Теодолит устанавливают на плоскость головки и закрепляют становым винтом. На крючок внутри винта подвешивают нитяной отвес.
При транспортировки ножки задвигают до упора, закрепляют винтами и стягивают ремнем. Регулируемый ремень служит для переноса штатива на плече или за спиной. На одно из ножек имеется пенал с крышкой для нитяного отвеса и гаечного ключа.
Окулярные насадки. Применяются для удобства наблюдения предметов, расположенных под углами более 45° к горизонту, и центрирования теодолита над точкой с помощью зрительной трубы. Они надеваются на окуляры зрительной трубы и отсчетного микроскопа.
Окулярная насадка представляет собой призму, изменяющую направление визирной оси на 80°. Призма заключена в оправу, свободно вращающуюся в обойме. Насадка на зрительную трубу снабжена откидным светофильтром для визирования на солнце.
Ориентир-буссоль. Служит для измерения магнитных азимутов. При работе ее устанавливают в паз и закрепляют винтом. Положение магнитной стрелки наблюдают в зеркале, которому придают нужный наклон. Северный конец стрелки окрашен в темный цвет. Для уравновешивания стрелки на южном ее конце установлен передвижной груз.
Футляр. Теодолит закрывают колпаком, этом плоские пружины опираясь на колонку теодолита, фиксируют положение алидадной части. Поворотом рукояток замков, колпак закрепляют с основанием.
В гнезде внутри колпака закрепляют ориентир-буссоль.
Ремень на крышке колпака служит для переноски теодолита.
2. общие сведения о линейных измерениях.
Для создания опоры методом триангуляции измеряются длины исходных сторон или базисов. Линейные измерения по точности делятся на три группы:
1. Точные измерения обеспечивают относительные ошибки 1:10000-1:1000000. эти измерения выполняются базисным прибором с подвесными инварными проволоками или светодальномерами.
2. Линейные измерения повышенной точности обеспеччивают точность с ошибкой 1:5000-1:25000. выполняются измерения также базисными приборами с подвешенными проволоками (лентами) и светодальномерами. Этот тип измерений применяется для создания сетей сгущения.
3. Линейные измерения технической точности с ошибкой 1:2000-1:3000 выполняются мерной лентой или дальномерами двойного изобтажения.
Измерения длины линии мерной лентой.
При измерении линий мерными лентами их укладывают по земле на ровной местности. При вешении линии с створе в землю забивают толщиной 4-6 см с интервалами, равными длине ленты. На торцах кольев наносят штрих крестик. Ленту укладывают на землю и берут отсчеты З и П. Длина пролета
t=t0+П-З
Производят навелирование кольев и измеряют температуру. Общую длину линии также, как и проволокой
D=t0n+S(П-З)+at0S(t-t0)-S(n2/2t0)
Штриховой лентой линию измеряют следующим образом. Провешивают линию теодолитом и в створе ставят вехи, примерно через 200 м. В створе забивают колья толщиной 6-8 см с интервалами, равными длине ленты. Ленту прикладывают к кольям и концы (штрихи) на концах отмечают штрихами ножом или корандашом. Остаток в линии измеряется металической рулеткой. Для приведения длины линии в горизонтальное положение нивелиром или теодолитом определяют превышение. Если местность ровная, то с одной станции определяют превышение нескольких пролетов. Длину линии определяют по формуле:
Процесс компарирования представляет собой определение длины мерного прибора путем сравнения в лабораторных условиях с эталлоном. В начале определяют точную длину компаратора, затем его длину измеряют проверяемым прибором (лентой, проволокой). Разность полученых результатов дает поправку при измеряемой температуре. Учитывая коэффициент расширения, определяют длину проволоки при t-20°. Длина проволоки используется для вычисления длины измеряемой линии в поле.
РАЗДЕЛ III
Камеральная обработка
сети сгущения.
1. Определение длин сторон и накопление ошибок в триангуляции.
Триангуляция, представляющая систему треугольников, образует цепи треугольников, центральные системы или четырехугольники. После измерения горизонтальных углов и исходных длин линий или базисов производится камеральная обработка. В измеренные горизонтальные углы b вводятся поправки за центрировку редукцию. Для этого производится предварительное решенение треугольников по теореме синусов.
Ошибки вычисленных сторон треугольников зависят от ошибок измеренных величин. Хорактер накопления ошибок сторон можно вычислить по известной стороне и горизонтальным углам первого треугольника. Длина стороны:
a1=(d0sinx1)/siny1
Углы, обозначенные буквами g1 g2……gn и противоположные им стороны в треугольниках называются промежуточными, формула для вычисления длины стороны a1, показывает, что ошибка ее зависит от связующих углов x, y, и ошибки исходной стороны a0.
Dlg a1=lg a0+lg siny1
Ошибку логорифма вычисляемой стороны можно представить в виде:
Dlg a1=Dlg a0+Dlg sin x1-D lg sin y1=Dlg a0+u ctg x1(Dx1/r’)-uctg y1(Dy1/r”)
где (u/r”)ctg x1=dx; (u/r”)ctg y1=dy
выражают перемены логаривмов синусов углов при изменении углов на одну секунду.
Dlg a1=Dlg a0+dxDx1=dyDy1
где Dx, Dy истинные ошибки увязанных углов.
Сущность способа наименьших квадратов.
В камеральных вычислениях государственных опорных сетей большое место занимает уравновешивание, т. е. распределение невязок в целях получения лучших результатов и выполнение геометрических условий. Способ наименьших квадратов является точным методом распределения невязок и нередко требует больших вычислительных действий. Значение и сущность способа наименьших квадратов можно пояснить на свойстве на свойстве арифметической середины.
Пусть имеется ряд равноточных измерений l1, l2…..ln одной и той же и требуется из этого ряда результатов найти значение x от результатов отдельных измерений, т. е.
(l1-x)2+(l2-x)2+……+(ln-x)2=min
известно, что для отыскания минимума функции надо взять первую производную и приравнять ее к нулю, откуда
x=[l]/n
эта формула показывает, что искомая величина x, найденная под условием минимума суммы квадратов уклонений от отдельных результатов измерений, есть арифметическая середина. Из этого следует, что величина, найденная по принцыпу наименьших квадратов, обладает свойством вероятнейшиго значения. Принципы наименьших квадратов можно применять для решения условных уравнений и отыскания вероятнейшего значения поправок. Допустим, что теодолитном полигоне с n углами невязку f надо распределить так, что-бы сумма квадратов найденных поправок была минимальной. Условное уравнение поправок углов полигона выражается формулой
(1)+(2)+(3)+….+(n)+f=0
где цифры в скобках- искомые поправки к углам полигона, а f-невязка.
Для отыскания неизвестных поправок по способу наименьших квадратов надо к этому условному уравнению добавить уравнение минимума суммы квадратов. Тогда будет получено два уравнения:
(1) +(2)+(3)+….+(n)+f=0
(1)2 +(2)2+(3)2+….+(n)2=0
Для решения двух уравнений со многими неизвестными надо первое уравнение умножить на (-2k) и сложить со вторым уравнением.
(1)2 +(2)2+(3)2+….+(n)2-2k(1)-2k(2)-2k(3)-…-2k(n)-2kf=min
Коэффийиент k носит название корреллаты. Для отыскания минимума надо брать производные по каждому неизвестному и приравнивать их к нулю:
Откуда
(1)=k, (2)=k=….=(n)
Подставляя эти значения в первое уравнение, полуыим
nk+f=0
откуда
k=-f/n=(1)=(2)…(N)
Из этого следует, что искомые поправки равны между собой -f/n, где n- число углов.
Так решается по способу наименьших квадратов одно уравнение с несколькими неизвестными и коэффициентами при них, равными единицы. Такой вид уравнений имеют условия фигур и горизонта.
При уравновешивании геодезических сетей может возникать несколько условий, выражаемых математическими формулами. В общем виде эти формулы можно выразить уравнениями:
a1(1)+a2(2)+…..+an(n)+f1=0
b1(1)+b2(2)+…..+bcn(n)+f1=0
c1(1)+c2(2)+…..+cn(n)+f1=0
где (1), (2),…(т)- искомые неизвестные поправки к углам: a1 ,a2…an ; b1 ,b2…bn ; c1 ,c2…cn – коэффициенты, f1 , f2 , f3 – свободные члены (невязки).
Для уравнений по способу наименьших квадратов надо уравнение умножить на удвоенные коррелаты с минусом (-2k1 ,-2k2 , -2k3 ) и сложить с условием минимума суммы квадратов поправок (1)2+(2)2+….+(n)2=min.
Общий вид уравнения:
a1(1)+a2(2)+….+an(n)+f=0
Здесь a1 , a2 ,…an – коэффициенты при искомых поправках (1), (2), (3), (n);
f – невязка. Это уравнение надо решать под условием, чтобы сумма квадратов поправок равнялась минимуму.
Вычисление искомых поправок по способу наименьших квадратов выполняется следующим образом:
1. вычисляют коэффициент k – кореллату по формуле
k=-(f/åa2)
т.е. невязка с обратным знаком делится на сумму квадратов коэффициентов при поправках уравнения.
2. поправки решаемого уравнения вычисляют по формулам:
(1)=a1k; (2)=a2k; (n)=ank
В уравнениях поправок фигур треугольников, горизонта и азимутов при искомых поправках коэффициенты равны a=1. Поэтому a2=1. В уравнении поправок треугольников åa=3 и k=-(f/3).
Поправки равны, т. е. (1)=(2)=(3)=-(f/3)
В уравнениях поправок горизонта и азимута коэффициенты a=1 и åa2=n, где n-число поправок уравнения поровну распределяется с обратным знаком на углы. В уравнении поправок синусов и сторон коэффициенты ai – изменении логарифмов синусов не равных единицы, åa2 имеет большое значение.
3. Виды условных уравнений в триангуляции.
Задачи уравновешивания тригонометрической сети состоит в отыскании поправок в измеренные углы, которые наилучшим образом удовлетворили бы теоретические условия сети, а измеренные величины после введения в них поправок получили бы вероятнейшее значение. Треугольники триангуляции образуют центральные системы, которые должны удовлетворять теоретические условия геометрии.
1. Условия уравнивания фигур.
1. Условное уравнение фигур.
Сущность: Сумма углов 1,2,3 каждого треугольника должна быть равна 180 градусам, но на практике бывают невязки которые вычисляют по формуле:
![]()
 2
2
а.¦=1+2+3-180°
3
![]()
![]()
![]() поправка равна: ¦/3
поправка равна: ¦/3
1
б. 1+(1)+2+(2)+3+(3)-180=0
После вычитания формулы а. из формулы б. получим условное уравнение поправок треугольников
(1)+(2)+(3)+¦=0
Предельная невязка углов треугольников определяется формулой:
¦пред=2.5mbÖ3
где mb- средняя квадратическая ошибка углов.
Таких уравнений в сети возникает столько сколько треугольников с измеряемыми углами.
2. Условие уравнивания горизонта.
Сущность: в центральной системе при точке ТО сумма углов g должна быть равна 360°. Но практически будет невязка:
g4
![]() g5
g5

![]()
![]() g3
g3
 g1
g1
g2
![]()
а. g1+g2+g3+g4+g5-360°=¦g
поправка будет равна: ¦g/5
б. g1+(g1)+g2+(g2)+g3+(g3)+g4+(g4)+g5+(g5)-360° =0
Уравнение горизонта мы получим после вычитания формулы а. из б.
(g1)+(g2)+(g3)+(g4)+(g5)+¦g=0
Предельная невязка углов ¦ определяется формулой:
¦пред=2.5mbÖn
где n – количество углов при цетре.
3. Условное уравнение полюса:
Сущность: в каждом треугольнике должно быть выполнено условие пропорциональности сторон и противолежащих углов
bca/abc=1 это условие полюса в точке O для центральной системы.
Заменяя отношение сторон синусом противоположных углов, исправленных поправками. После логарифмирования и разложения функции в ряд мы получим:
W=lg(sin1sin3sin5/sin2sin4sin6)
Окончотельный вид полюсного условного уравнения будет выглядеть так:
d1(1)+d3(3)+d5(5)-d2(2)-d4(4)-d6(6)+W=0
Величина невязки зависит от ошибок в связующих углах
Wпред=2.5*mb*Ö(d)
4. Условное уравнивание сторон.
Условие сторон возникает в цепи треугольников расположенной между двумя сторонами исходной цепи. Геометрический смысл состоит в том, что при последовательном решении треугольников от начальной стороны должна быть получена конечная сторона.
d1(x1)+d2(x2)+d3(x3)+d4(x4)-b1(y1)-b2(y2)-b3(y3)-b4(y4)+WD=0
Wdпред=2.5*mb*Ö2mb+m2(d2+b2)
5. Условное уравнение координат
Условие координат возникает в сети, если в ней может быть выделен ход, заключенный между двумя твердыми точками.
Это условие заключается в том, чтобы сумма приращений по каждой координатной оси была равна разности координат конечной и начальной точек.
Невязки вычисляются по формуле:
¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн)
сумма поправок приращений должна равнятся нулю.
dxBC+dxCD+dXDE+¦x=0
dyBC+dyCD+dyDE+¦=0
4. Упрощенное уравнивание центральной системы.
В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур равно числу треугольников:
(x1)+(y1)+f1=0
(x2)+(y2)+f2=0
(x3)+(y3)+f3=0
(x4)+(y4)+f4=0
(x5)+(y5)+f5=0
Одно условное уравнение горизонта имеет вид:
(g1)+(g2)+(g3)+(g4)+(g5)=fg=0
Условное уравнение полюса согласно формуле имеет вид:
d1(x1)+d2(x2)+d3(x3)+d4(x4)+d5(x5)- d1(y1)-d2(y2)-d3(y3)-d4(y4)-d5(y5)+W=0
Таким образом в этой центральной системе возникает семь условных уравнений. При этом распределение невязок и отыскание поправок по способу наименьших квадратов все уравнения надо решать совместно – это требует больших вычислений, поэтому в сетях сгущения уравновешивание выполняется упрощенным способом. Упрощение состоит в том, что система всех уравнений разделяется на однотипные группы. Для наиболее простого способа уравновешивания к первой группе относят условные уравнения фигур и решают их по способу наименьших квадратов. В этой группе уравнений каждоя неизвестная искомая поправка в уравнения входит один раз, т.е. каждое уравнение имеет три искомых неизвестных, не входящих в другие уравнения. Следовательно, каждое уравнение можна решать отдельно по способу наименьших квадратов. Решение такого уравнения с коэффициентами при неизвестных, равными единици, было описано.
Согласно формуле искомые поправки равны между собой и равны f/n, где f- невязки, а n- число углов.
Поэтому в условном уравнении фигуры треугольника n=3 поправки в углы треугольников выражаются формулами:
(x1)’=(y1)’=(g1)’=-f1 /3
(x2)’=(y2)’=(g2)’=-f2 /3
(x3)’=(y3)’=(g3)’=-f3 /3
(x4)’=(y4)’=(g4)’=-f4 /3
(x5)’=(y5)’=(g5)’=-f5 /3
Решение первой группы уравнений дает первичные поправки, обозначенные одним штрихом. Затем приступают к решению второй группы условных уравнений, т.е. уравнение горизонта. При упрощенном уравновешивании получают вторые поправки к углам.
Условное уравнение примет вид:
(g1)”+ (g2)”+ (g3)”+ (g4)”+(g5)”+fg=0
Здесь невязка вычисляется по первично исправленным углам, т.е.
fg=[g1+(g1)’]+ [g2+(g2)’]+ [g3+(g3)’]+ [g4+(g4)’]+ [g5+(g5)’]-360°
Условное уравнение горизонта имеет коэффициенты при неизвестном, равные единице, поэтому решение уравнения по способу наименьших квадратов выполняются так же, как и условие фигур, невязка распределяется поровну на все углы и поправка равна -fg /n, следовательно, вторичные поправки к углу g будут:
(g1)”= (g2)”= (g3)”= (g4)”= (g5)”-fg” /n
Чтобы не нарушать условие фигур, выполненные введением первых поправок, надо и в связующие углы x, y каждого треугольника ввести вторичные поправки, которые должны быть равны половине второй поправки к углу g с обратным знаком:
(x1)”=(y1)”=-(g1)”/2
(x2)”=(y2)”=-(g2)”/2
Результаты этих поправок записаны в таблице. После решения условных уравнений фигур и горизонта приступают к решению полюсного условного уравнения, что дает третьи поправки к углам, но при условии, чтобы условия фигур и горизонта не были нарушены. Условное уравнение полюса примет вид:
d1(x1)”’+d2(x2)”’+d3(x3)”’+d4(x4)”’+d5(x5)”’-d1(x1)”’- d1(x1)”’-d1(x1)”’-d1(x1)”’ --d1(x1)”’+W=0
здесь d1, d2, …d5 – перемена логарифмов синусов углов x, входящие в числитель свободного члена W, а b1, b2…b5 – перемены логарифмов синусов углов y, входящие в знаменатель свободного члена. Невязка, т.е. свободный член уравнения, выражается формулой:
Здесь связующие углы x, y каждого треугольника представляют углы, исправленные предыдущими двумя поправками. Чтобы решением полюсного уравнения не нарушить условие фигур и горизонта, надо ввести дополнительное условие, согласно которому в каждом треугольнике связующие углы должны иметь равные поправки, но с разными знаками, т.е. (xi)”’=-(yi)”’. Тогда полюсное уравнения примет вид.
a1(x1)”’+ a2(x2)”’+ a3(x3)”’+ a4(x4)”’+ a5(x5)”’+W=0
a1=(d1+b1), …
для решения этого уравнения по способу наименьших квадратов надо добавить условие: (x1)”’2+(x2)”’2+(x3)”’2+(x4)”’2+(x5)”’2=min
для нахождения минимума функции возьмем производные и прировняем их к нулю.
f’x1=2(x1)”’-2ka1=0
f’x2=2(x2)”’-2ka2=0
………………………
f’xi=2(xi)”’-2kai=0
откуда поправки:
(x1)”’=a1k
(x2)”’=a2k
…………………….
(xi)”’=aik
подставляем полученные (x) в формулу
a1a1k+ a2a2k+ a3a3k+ a4a4k+ a5a5k+W=0
или
[aa]k+W=0
откуда
k=-W/[aa]
после обработанной замены коэффициента ai=dI+bi формула кореллатты k примет вид:
k=-W/å (d+b)2
Значение k начисляют по записям. После подстановки значения k в формулу поправок получим:
Эти поправки записывают в таблицу. После исправления углов третьими поправками решают треугольники на основе исходной стороны, т.е. находят длины сторон, затем вычисляют дирекционные углы сторон от дирекционного угла начальной линии. После вычисления дирекционных углов и длин линий вычислений приращения. В сомкнутом полигоне центральной системы будут невязки приращений fx , fy , которые распределяют пропорционально длинам линий. Так как в треугольниках сети сгущения длины сторон не очень отличаются между собой, то невязки приращений можно распределять поровну. После исправления приращений вычисляют координаты пунктов.
РАЗДЕЛ IV
Охрана труду в землеустройстве.
Техника безопасности при выполнении работ по землеустройству
Землеустройство включает проектно- изыскательские, съемочные и обследовательские работы.
Поскольку работу выполняют под открытым небом, возможен перегрев и переохлаждение организма, а следовательно, возможны солнечные удары, простудные и ревматические заболевания.
При съемочных и обследовательских работах возможны укусы насекомых и змей.
К работе по землеустройству допускаются лица, прошедшие медосмотр и получившие вводный инструктаж на рабочем месте по технике безопасности. В нужных случаях назначаемые на выполнение полевых работ проходят вакцинацию и обеспечиваются соответствующими средствами безопасности и защиты: спецодеждой, спец обувью, очками и т. д.
Рабочий обязан следить за исправленностью и чистотой спецодежды и других средств защиты. Запрещается стирать спецодежду в легковоспламеняющихся жидкостях.
Все работники должны строго соблюдать трудовую и производственную дисциплину. Запрещается без разрешения руководителя работ отлучаться с места работы и из полевого лагеря.
При организации полевого лагеря, палатки нужно устанавливать вне пределов возможного затопления и падения сухостойных деревьев, камней, осыпей. Территорию лагеря очищают устраняя мешающие проходу предметы.
При движении по лесу следуют поддерживать зрительную и голосовую связь в движущиеся группы.
Во избежании травмирования ветками необходимо между идущими выдерживать расстояние не менее 3 м.
Когда работы проводят в безводных местах, люди должны знать, где расположены колодцы и водоемы, иметь термос с кипяченой водой.
В случае обследования земель в заболоченной местности передвигаются по целине болот нужно « след в след » с интервалами между идущими 2 – 3 м с применением шестов, веревок.
Кочковатые болота безопаснее переходить по кочкам со страховочным шестом.
Переезды на транспортных средствах разрешаются, если эти средства приспособлены для перевозки людей.
Во время выполнения работ необходимо строго подходить к питанию и к поддержанию питьевого режима.
Продукты следует хранить в упаковке.
Питьевая вода должна быть чистой, кипяченой.
Купаться можно в предварительно проверенных местах. Запрещается выходить на полевые работы без карты, компаса, медицинской аптечки, лопаты и топора.
РАЗДЕЛ V
ТЭР.
РАЗДЕЛ VI
Список литературы.
ПРИЛОЖЕНИЕ
| Основы геодезических измерений | |
|
Содержание Введение 1. Устройство геодезических сетей при съемке больших территорий. 1.1 Государственные геодезические сети. 1.2 Геодезические сети ... Метод триангуляции состоит в том, что строят сеть треугольников, в которой измеряют все углы треугольников и как минимум две стороны на разных концах сети (вторую сторону измеряют ... Способы уравнения разделяются на строгие, когда уравнение производится под условием минимума суммы произведение квадратов поправок в измерение величины, и нестрогие (раздельные ... |
Раздел: Рефераты по геологии Тип: курсовая работа |
| Измерения геометрических величин в курсе геометрии 7-9 классов | |
|
Оглавление Введение Глава 1. Психолого-педагогические и научно-методические основы изучения измерений геометрических величин в школе §1. Практическая ... Итак, определения длины отрезка, градусной меры угла, площади, реализуемые в учебнике являются описательными [8], то есть перечисляются лишь основные свойства нового понятия [6 ... Учащиеся измеряют длины сторон а и b и длины высот, проведенных к стороне a, а также угол g. И вычисляют площадь треугольника по уже известной формуле. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Методические особенности изучения темы "Подобные треугольники ... | |
|
... Государственный Педагогический Университет Факультет Математики и Информатики Методические особенности изучения темы "Подобные треугольники" в средней Отношение площадей подобных треугольников равно квадрату коэффициента подобия", доказательство основано на применение теоремы об отношении площадей треугольника, имеющих по равному ... Изучая тему "Подобные треугольники", можно подробно остановиться на примерах из реального мира, необходимо рассказать об истории возникновения и развития подобия, подробно ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Решение задач с помощью ортогонального проектирования | |
|
Тема: "Решение задач с помощью ортогонального проектирования". Ученицы 11 "Б" класса Средней школы №46 Заиц Ю. А. Руководитель: Шелгинских В. А ... Если отрезок AB образует с плоскостью проекций угол ѭ, то, проведя AB*°A" B" (рис.2), получим из прямоугольного треугольника AB*B, что AB*=AB cos ѭ или A" B"= AB cos ѭ. 14, б), равного квадрату (С1)0C0D0(D1)0 , построенному на рисунке 14, а, строим отрезок (С1)0(S1)0 , который будет принят за сторону треугольника (С1)0Q0(S1)0 , подобно оригиналу ... |
Раздел: Рефераты по математике Тип: реферат |
| Планирование и промер глубин в прибрежной зоне судовыми средствами | |
|
БАЛТИЙСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ РЫБОПРОМЫСЛОВОГО ФЛОТА СУДОВОДИТЕЛЬСКИЙ ФАКУЛЬТЕТ КАФЕДРА СУДОВОЖДЕНИЯ ДИПЛОМНАЯ РАБОТА НА ТЕМУ: Планирование и ... Определение места выполняется одновременным измерением двух углов секстанами между опорными пунктами. Когда определение места производится на значительном удалении от опорных пунктов, секстаны должны быть особенно тщательно выверены, а углы следует измерять с использованием ... |
Раздел: Рефераты по транспорту Тип: реферат |