Реферат: Симметрия в неживой природе

     ВВЕДЕНИЕ........................................ 2

1. ЗАГЛЯНЕМ В СЛОВАРЬ.............................. 4

     2. ВИДЫ СИММЕТРИЙ................................. 5

3. АСИММЕТРИЯ ВНУТРИ СИММЕТРИИ.................. 7

     4. СИММЕТРИЯ В ГЕОЛОГИИ........................... 9

       4.1. ЛЕГЕНДЫ РУДОКОПОВ............................. 9

       4.2.СИММЕТРИЯ ПОМОГАЕТ ОТКРЫВАТЬ МЕСТОРОЖДЕНИЯ 11

     5. СИММЕТРИЯ ЗЕМЛИ КАК ПЛАНЕТЫ.................. 15

ЗАКЛЮЧЕНИЕ.................................... 25

ЛИТЕРАТУРА..................................... 26

«...быть прекрасным значит быть симметричным  и  соразмерным.»

Платон

Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений". «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мери и уверенностью человека в большей пригодности для практики правильных форм". Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика  А. В. Шубникова (1887—1970). - Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о «соразмерности», что и означает в переводе с греческого слово «симметрия», с течением времени приобрело универсальный характер и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360° : 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — поворотной, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Благодаря последней симметрии все физические приборы (в том числе и будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, какая бы царила на Земле неразбериха, если бы эта симметрия была нарушена!

 Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. «Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности»,— писал Вернадский. Действительно, еще Платон мыслил атомы четырех стихий — земли, воды, огня и воздуха — геометрически симметричными в виде правильных многогранников. И хотя сегодня «атомная физика» Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим принципом современной физики атома. За это время наука прошла путь от осознания симметрии геометрических тел к пониманию симметрии физических явлений.

Итак, в современном понимании симметрия — это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям. Математическим аппаратом изучения симметрии сегодня является теория групп и теория инвариантов.

«Принцип симметрии в XX веке охватывает все новые области. Из области кристаллографии, физики  твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона и ему подчинены будут явления квантов».

Этими словами академика В. И. Вернадского и хочется начать короткий разговор о принципах симметрии в неживой природе.

Во всех случаях, когда отрезки прямой, плоские фигуры или пространственные тела были подобными, но без дополнительных действий совместить их было нельзя, «практически» нельзя, мы встречались с явлением симметрии. Эти элементы соответствовали друг другу, как картина и ее зеркальное отражение. Как левая и правая рука. Если мы возьмем на себя труд заглянуть в «Современный словарь иностранных слов», то обнаружим, что под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра... такое расположение точек относительно точки (центра симметрии), прямой (оси симметрии) или плоскости (плоскости симметрии), при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии...»

И это еще не все, как часто бывает с иностранными словами, значений у слова «симметрия» существует множество. В том-то и состоит преимущество подобных выражений, что их можно использовать в случае, когда не хотят дать однозначное определение или просто не знают четкого различия между двумя предметами.

Термин «соразмерный» мы применяем по отношению к человеку, картине или какому-либо предмету, когда мелкие несоответствия не позволяют употребить слово «симметричный».

Давайте также заглянем в Энциклопедический словарь . Мы обнаружим здесь шесть статей, начинающихся со слова «симметрия». Кроме того, это слово встречается во множестве других статей.

В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения. Важную роль играет симметрия в кристаллографии. Интересно интерпретируется понятие симметрии в биологии. Там описывается шесть различных видов симметрии. Мы узнаем, например, что гребневики дисимметричны, а цветки львиного зева отличаются билатеральной симметрией. Мы обнаружим, что симметрия существует в музыке и хореографии (в танце). Она зависит здесь от чередования тактов. Оказывается, многие народные песни и танцы построены симметрично.

Можно увидеть, что это кажущаяся простота уведет нас далеко в мир науки и техники и позволит время от времени подвергать испытанию способности нашего мозга (так как именно он запрограммирован на симметрию).

2. ВИДЫ СИММЕТРИЙ

В отличие от искусства или техники, красота в природе не создаётся, а лишь фиксируется, выражается. Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. К числу таких образов относятся некоторые кристаллы, многие растения.

В конформной (круговой) симметрии главным преобразованием является инверсия относительно сферы. Для простоты возьмём круг радиуса R с центром в точке O. Инверсия этого круга определяется как такое преобразование симметрии, которое любую точку P переводит в точку P', лежащую на продолжении радиуса, проходящего через точку P на расстоянии от центра:

OP'=R² / OP

Конформная симметрия обладает большой общностью. Все известные преобразования симметрии: зеркальные отражения, повороты, параллельные сдвиги представляют собой лишь частные случаи конформной симметрии.

Главная особенность конформного преобразования состоит в том, что оно всегда сохраняет углы фигуры и сферу и всегда переходит в сферу другого радиуса.

Известно, что кристаллы какого-либо вещества могут иметь самый разный вид, но углы между гранями всегда постоянны.

Порассуждаем о зеркальной симметрии. Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична. Сначала представляется, что параллельно одной из его сторон могла бы проходить ось симметрии. Но стоит мысленно попробовать воспользоваться ею, как сразу убеждаешься, что это не так. Несимметрична и спираль.

В то время как симметричные фигуры полностью соответствуют своему отражению, несимметричные отличны от него: из спирали, закручивающейся справа налево, в зеркале получится спираль, закручивающаяся слева направо.

Если вы поместите буквы перед зеркалом, расположив его параллельно строке, то заметите, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».

Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф означает именно истинную середину.

В архитектуре оси симметрии используются как средства выражения архитектурного замысла. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля.

Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.

А что такое кристалл? Твердое тело, имеющие естественную форму многогранника. Характерная особенность того или иного вещества состоит в постоянстве углов между соответственными гранями и ребрами для всех образов кристаллов одного и того же вещества.

Что же касается формы граней ,числа граней и ребер и величины кристалла, то для одного и того же вещества они могут значительно отличаться друг от друга.

Для каждого данного вещества существует своя, присущая только ему идеальная форма его кристалла. Эта форма обладает свойством симметрии т.е. свойством кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов. Среди элементов симметрии различаются оси симметрии, плоскости симметрии, центр симметрии, зеркальные оси.

Внутреннее устройство кристалла представляется в виде пространственной решётки, в одинаковых ячейках которой, имеющих форму параллелепипедов, размещены по законам симметрии одинаковые мельчайшие частицы - молекулы, атомы, ионы и их группы. Многие, если не все, кристаллы более или менее легко раскалываются по некоторым строго определённым плоскостям. Это явление называется спайностью и свидетельствует о том, что механические свойства кристаллов анизотропны т. е. не одинаковы по разным направлениям.

Симметрия внешней формы кристалла является следствием его внутренней симметрии - упорядоченного взаимного расположения в пространстве атомов ( молекул).

Винтовая симметрия.  В пространстве существуют тела, обладающие винтовой симметрией, т.е. совмещаемые со своим первоначальным положением после поворота на какой-либо угол вокруг оси, дополненного сдвигом вдоль той же оси. Если данный угол поделить на 360 градусов - рациональное число, то поворотная ось оказывается также осью переноса.

Собственно говоря, симметрия и асимметрия должны бы взаимно исключать одна другую — как черное и белое или как день и ночь. Так оно и происходит на самом деле, пока симметрия или ее антипод рассматриваются по отношению к одному и тому же телу.

Тот факт, что растворы оптически активных веществ вращают плоскость поляризации в точности так же, как кристаллы, однозначно доказывает, что само кристаллическое состояние не может служить причиной этого явления. Ведь в растворе кристаллов нет. Но как в оптически активном кристалле, так и в растворах, обладающих этим свойством, присутствуют молекулы. Кристаллы, построенные — подобно металлам — из одних только атомов, оптически неактивны (кроме того, они непрозрачны!) Высокоупорядоченный кристалл, состоящий из ионов Na+CI- ,тоже не действует на проходящий свет. Однако кварц имеет более сложное строение, чем хлорид натрия. Кварц — это диоксид кремния, химическая формула которого Si02. Кремний, как и углерод, находится в четвертой группе периодической системы. А углерод постоянно изображают со связями:

=С=

Кремний, принадлежащий к той же группе, что и углерод, также четырехвалентен. Химия кремния, подобно химии углерода, весьма сложна. Кристаллическая структура кварца представляет собой трехмерный каркас из длинных цепей, построенных в форме винтовых лестниц. Разумеется, винтовые лестницы полностью асимметричны. Однако они бывают лево- и правосторонними, как изображение и его зеркальное отражение. Связанные между собой асимметричные цепи образуют либо левый, либо правый кристалл. Соответственно они оказывают оптическое влияние на свет.

У водо-растворимых кристаллов органических соединений зеркальная симметрия молекул прослеживается как в твердом, так и в растворенном состоянии. Известный пример — винная кислота. Она встречается в виде левых и правых кристаллов. Соответственно ведет себя и ее раствор. Под правым направлением здесь всегда понимается направление по часовой стрелке. Таким образом, левая винная кислота вращает плоскость поляризации против часовой стрелки. Нидерландский физико -химик Якоб Хендрик Вант-Гофф (1852—1911) объяснил такое поведение винной кислоты, исходя из строения ее молекулы. При одном и том же химическом составе можно написать три разные структурные формулы винной кислоты. Каждый из двух центральных атомов углерода в любом случае связан с группой СООН. В органической химии эта группа — отличительный признак кислоты. Проглотив таблетку аспирина или попробовав на язык уксус, вы ощущаете кисловатый вкус, он обусловлен именно присутствием группы СООН. Для нас, однако, важнее правая и левая связи атомов углерода. Они связывают либо атом водорода, либо группу ОН. Именно здесь кроется возможность возникновения двух зеркально-симметричных вариантов их взаимного расположения и, помимо того, третьего варианта, который симметричен сам по себе.

В книгах по химии часто можно встретить обозначения L- и D- кислота, производные от латинских слов laevus — левый и dexter — правый. Теперь нам уже нетрудно сообразить, ч то вещество, носящее название «декстро-энерген», должно быть оптически активным и притом правовращающим. В молекуле виноградного сахара (торговое наименование которого и есть «декстро-энерген » ) присутствует цепочка из атомов углерода, «подвески» которой могут быть синтезированы право- или лево- стор онн ими.

Вант-Гофф, впрочем, не пользовался такой простой плоскост н ой моделью, как мы. Он сразу рисовал ее в объемном изображении, что больше отвечает действительности. Каждый из 4-ёх углеродных атомов винной кислоты расположен в вершине тетраэдра. К этим угловым атомам углерода и привязаны прочие атомы, кислородные и водородные. Вследствие этого из одного совершенного платонова т ела (каким является тетраэдр) возникают две различные, зеркально-симметричные формы.

Когда Вант-Гофф опубликовал свою теорию о правых и левых молекулах, она была встречена в штыки. Многие из его современников никак не хотели согласиться с тем, что атомы в молекуле должны располагаться именно так, как их поместил Вант-Гофф. Однако теория нидерландского профессора давала единственно удовлетворительное объяснение вращению поляризованного света, поэтому она все же получила признание. Тем временем химики разработали методы прямого определения формы молекул. И мы теперь знаем, что Вант-Гофф был прав.

4. СИММЕТРИЯ В ГЕОЛОГИИ

4.1. ЛЕГЕНДЫ РУДОКОПОВ

В старину рудокопы были людьми сугубо практическими. Они не забивали себе голову названиями всевозможных горных пород, которые встречали в штольне, а просто делили эти породы и минералы на полезные и бесполезные, ненужные. Нужные они извлекали из недр, из них плавили медь, свинец, серебро и другие металлы, а ненужные сваливали в отвалы.

Для полезных (на их взгляд) минералов они подыскивали наглядные и запоминающиеся имена. Можно никогда не видеть копьевидного колчедана, но без особого труда представить его себе по названию. Не сложнее по названию отличить красный железняк от бурого железняка.

Для бесполезных камней (как уже было сказано — на их взгляд) горняки нередко находили названия в преданиях и легендах. Так, например, произошло название руды кобальтовый блеск. Кобальтовые руды похожи на серебряные и при добыче иногда принимались за них. Когда из такой руды не удавалось выплавить серебро, считалось, что она заколдована горными духами — кобольдами.

Когда же минералогия превратилась в науку, было открыто великое множество пород и минералов. И при этом все чаще возникали трудности с изобретением для них наименований. Новые минералы часто называли по месту находки (ильменит — в Ильменских горах) или в честь знаменитого человека (гетит — в честь Гете) или же давали ему греческое или латинское название.

Музеи пополнялись грандиозными коллекциями камней, которые становились уже необозримыми. Не слишком помогали и химические анализы, потому что многие вещества одного и того же состава образуют подчас кристаллы совершенно различного облика. Достаточно вспомнить хотя бы снежинки.

В 1850 г. французский физик Опост Браве (1811—1863) выдвинул геометрический принцип классификации кристаллов, основанный на их внутреннем строении. По мнению Браве, мельчайший, бесконечно повторяющийся мотив узора и есть определяющий, решающий признак для классификации кристаллических веществ. Браве представлял себе в основе кристаллического вещества крошечную элементарную частицу кристалла. Сегодня со школьной скамьи мы знаем, что мир состоит из мельчайших частиц — атомов и молекул. Но Браве оперировал в своих представлениях крошечным «кирпичиком» кристалла и исследовал, каковы могли быть у него углы между ребрами и в каких соотношениях его стороны могли находиться между собой.

В кубе три ребра расположены всегда под углом 90° друг к Другу. Все стороны имеют равную длину. У кирпича углы тоже составляют 90°. Но его стороны различной длины. У снежинок, наоборот, мы не найдем угла 90°, а только 60 или 120°.

Браве установил, что существуют 7 комбинаций ячеек с одинаковыми или разными сторонами (осями) и углами. Для углов он принял только два варианта: равный 90° и не равный 90°. Только один угол во всей его системе в порядке исключения имеет 120°. В самом скверном случае все три оси и все углы ячейки различны по величине, при этом в ней нет углов ни в 90, ни в 120°. Все в ней косо и криво, и, можно подумать, в мире кристаллов таким не должно быть места. Между тем к ним относится, например, сульфат меди (медный купорос), голубые кристаллы которого обычно всем так нравятся.

В некоторых из этих 7 пространственных решеток элементарные «кирпичики» можно упаковать по-разному. Для нас, знающих сегодня о строении атома, это нетрудно представить и продемонстрировать с помощью шариков для пинг-понга. Но 125 лет назад гениальная идея Браве была новаторской и открывала новые пути в науке. Весьма вероятно, что и Браве исходил из узоров кафеля или мотивов шахматной доски.

Если мы разделим квадратные поля диагоналями, то возникает новый рисунок из квадратов, стоящих на углах. В трехмерном пространстве это соответствует кубу, разложенному на шесть пирамид. Каждая такая пирамида составляет половину октаэдра.

Те, кто когда-нибудь выращивал кристаллы поваренной соли, знают, что соль может кристаллизоваться в кубах, а может — в октаэдрах. Иными словами, экспериментальные наблюдения совпадают с теоретическими соображениями.

Испробовав возможные варианты упаковки для всех семи осевых систем, Браве вывел 14 решеток.

Рассматривая решетки Браве внимательней и пробуя мысленно построить из них кристаллы, мы, вероятно, увидим, как можно провести в них плоскости и оси симметрии. Эти возможности сразу расширятся, если мы в одной из элементарных ячеек образуем новые грани. Возьмем куб, поставим его на угол и обрежем (все так же мысленно) все углы, тогда у него образуются совершенно новые треугольные грани. А из квадратных граней возникнут восьмиугольники: тем самым появятся новые мотивы симметрии.

Анализ элементов симметрии в каждой из осевых систем кристаллических решеток приводит к возникновению 32 классов симметрии. Все многообразие минералов в природе подразделяется на основе 32 классов симметрии. Вооруженные этими знаниями, задумаемся о классификации пяти тел Платона. То, что куб, с его тремя равными осями и тремя прямыми углами, относится к кубической осевой системе (сингонии), не нуждается в доказательстве. В рамках более детального подразделения он принадлежит пентагон - тетраэдрическому классу симметрии. Не стану здесь приводить названий других классов из-за их сложности. Однако стоит обратить внимание на термин «тетраэдрический», так как тетраэдр — одно из платоновых тел.

Тетраэдр можно образовать из куба. Остальные платоновы тела также относятся к кубической системе. Древние греки, надо думать, ужасно расстроились бы, знай они, что такой прозаический минерал, как серный колчедан, имеет ту же симметрию, что и их «совершенные» тела.

4.2. СИММЕТРИЯ ПОМОГАЕТ ОТКРЫВАТЬ МЕСТОРОЖДЕНИЯ

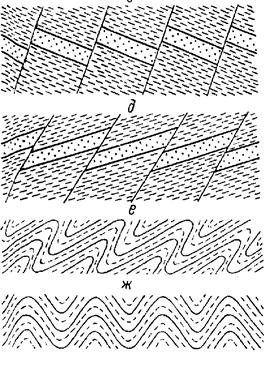Можно обнаружить широкое распространение проявлений симметрии в строении геологических тел самых различных размеров и происхождения, входящих в состав земной коры. Среди этих проявлений симметрии значительную часть составляют разнообразные симметричные структуры, образование которых связано с разрядкой механических напряжений, возникающих в геологических телах по разным причинам (тектонические движения, сокращение объема при охлаждении или дегидратации и т. д.). Обращение к симметрии этих структур, к закономерной повторяемости их элементов (структурных форм) позволяет подойти к рассмотрению механизмов образования таких структур с принципиально новых позиций.

До сих пор говорилось лишь об элементах симметрии и их сочетаниях, т. е. об общих закономерностях повторяемости фигур и их частей. В кристаллографии, как известно, этим дело не ограничивается, а, исходя из тех же законов симметрии, выводятся формы кристаллических фигур.

Рис. 1. Примеры симметричного распределения геологических структурных форм. б — "лестничные" жилы;  д — ступенчатый  сброс;    е — наклонные складки; ж — прямые складки.

Вспомним, что простыми гранными формами называются совокупности граней, связанных друг с другом элементами симметрии. По-видимому, в некоторых случаях целесообразно воспользоваться этими понятиями геометрической кристаллографии и применить их для характеристики геологических объектов.

В качестве примера рассмотрим простейшие формы блоков пород, изображенные на рис. 2. Так, например, купола, конусовидные вулканы, кольцевые дайки, штоки и некоторые  другие структуры обладают вертикальной осью симметрии бесконечного  (полная их симметрия — симметрия конуса L  P —  т). Из других осей симметрии в геология чаще всего встречаются оси второго порядка. Например, симметрия сундучных складок L2 2P — 2mm (рис. 2).

Вспомнив кристаллографические модели простых форм и их комбинаций, мы без труда найдем  здесь пинакоиды, различные призмы и кубы. Конусообразную форму вулкана можно уподобить п-гональной пирамиде, а горные хребты — комбинациям диэдров.

Рис. 2. Простые геологические структуры: а)  куполообразная; б)  сундучная.

Нам могут возразить, что приведенные здесь и далее примеры являются сугубо идеализированными. Однако вспомним, что и кристаллографические модели являются обобщенными идеализациями реальных форм. Идеализация с помощью статистических данных широко используется кристаллографами. Очевидно, аналогичные приемы могут быть рекомендованы и для геометризации геологических объектов.

Возникает вопрос: почему геометрические закономерности в распределении структурных форм сравнительно редко отмечались до сих  пор в геологической литературе.

По-видимому, имеется ряд причин, затрудняющих их выявление. Выше уже говорилось о необходимости обобщать и статистически идеализировать такие явления. Неоднородность строения геологических тел и их масштабы затрудняют подобные исследования. Следует иметь в виду также и то, что зачастую мы имеем дело со случайными срезами, неблагоприятными для выявления закономерностей симметрии. Кроме того, сами закономерности симметрии могут быть. достаточно сложными (например, в случае наличия плоскостей скользящего отражения или винтовых осей) и не бросаются в глаза при случайном взгляде на случайный срез структуры. Наконец, играют роль и некоторая сложность понятийного аппарата симметрии и недостаточная устремленность геологов пользоваться им.

Вместе с тем еще и еще раз следует подчеркнуть, что симметрия геологических образований подчиняется в общем тем же законам симметрии, которые хорошо известны в геометрии и кристаллографии. Анализ сетчатых систем трещин с особой убедительностью иллюстрирует сказанное. Во всех разобранных выше примерах не встречалось ни одного элемента симметрии и ни одной их совокупности, которые не были бы известны кристаллографам (оси бесконечного порядка, невозможные для кристаллических полиэдров, широко используются при характеристике оптических индикатрис). Пространственные группы Е. С. Федорова, сетки и решетки О. Браве, симметрия лент, бордюров и стержней — все это широко реализуется в геологических структурах.

Подводя некоторый итог, следует особо подчеркнуть всеобъемлющее значение строго математических законов симметрии пронизывающих все естествознание, а тем самым охватывающих и все без исключения объекты геолого-минералогических наук.

Исключительную роль в этом отношении играет вытекающий из принципа П. Кюри закон формирования природных тел в поле земного тяготения:

«Все что растет или движется по вертикали приобретает симметрию Ln nP — пт, все, что растет или движется по горизонтали, получает симметрию Р — т (или — —1)».

Невольно напрашивается идея о широком использовании этого закона для выявления процессов формирования геологических объектов.

При рассмотрении разнородных геологических образований нам пришлось помимо классической использовать новые понятия расширенной симметрии, учения об антисимметрии и динамической симметрии. Все эти понятия образуют единый методологический комплекс. Учение о симметрии в геологи, формирующееся на границе геометрической кристаллографии и наук геологического цикла, является сейчас новым научным направлением, требующим всемерного углубления и дальнейшего развития. Объектом этой новой дисциплины являются геометрические закономерности как всей планеты в целом, так и отдельных ее составляющих на различных уровнях организации вещества.

Кроме отмеченного выше существенного теоретического значения широкое распространение проявлений симметрии в геологических структурах имеет важное практическое значение. Понимание законов симметрии, проявляющихся в той или иной конкретной геологической структуре, может оказать весьма существенную помощь в деятельности геологов по поискам месторождений полезных ископаемых и отдельных рудных тел в пределах известных рудных полей.

Реальные примеры проявления в геологических структурах (в том числе и в структурах рудных полей) симметрии таких типов достаточно многочисленны и многократно описаны в геологической литературе.

Разумеется, используя представление о симметрии размещения рудных тел и месторождений, при поисках необходимо учитывать существование различных факторов, ограничивающих или затрудняющих применение этих представлений. Прежде всего необходимо помнить, что в частных случаях число рудных тел в симметричной серии может быть любым. Поэтому наличие одного или нескольких рудных тел не гарантирует наличия других рудных тел, связанных с известными телами законами симметрии. Далее, следует иметь в. виду, что достаточно строгие проявления симметрии в размещении структурных форм и рудных тел возможны лишь в достаточно однородной (в том масштабе, в котором ведется исследование) среде. Различного рода неоднородности среды, в которой размещены рудные тела, могут обусловливать в различной степени существенные отклонения от строгой симметрии.

Однако практически достаточно знать глубины выклинивания известных рудных тел, чтобы определить места возможного нахождения «слепых» рудных тел, принадлежащих этим симметричным сериям. Очевидно, что поиск рудных тел таким методом будет в этих случаях во много раз эффективнее, чем поиск путем разбуривания рудного поля по сетке, не увязанной с симметрией его структура.

Учтя такую возможность, мы сможем в этом случае выявить все рудные тела с минимальной затратой сил и средств.

Выявление симметрии размещения и внутреннего строения тектонических структур и других геологических образований, контролирующих размещение полезных ископаемых, помимо теоретического интереса, имеет и огромное прикладное значение и поэтому должно считаться одной из первоочередных задач геологической науки на современном этапе ее развития.

5. СИММЕТРИЯ ЗЕМЛИ КАК ПЛАНЕТЫ

Обзор законов симметрии, проявляющихся на конкретных теологических объектах, следует начать с рассмотрения вопроса о симметрии Земли как планеты в целом. Ведь именно Земля как планета является наиболее высокой таксономической категорией в существующей классификации морфологических геотекстур земного рельефа.

Форма Земли, отождествлявшаяся прежде с идеальным шаром (отсюда и название «земного шара»), позднее уподоблялась эллипсоиду вращения, трехосному эллипсоиду, геоиду. Наблюдения с помощью искусственных спутников установили ее принадлежность к кардиоиду или кардиоидальному эллипсоиду, в котором южное полушарие более сжато, чем северное.

Однако, как увидим далее, ряд характерных явлений, наблюдающихся на поверхности Земли, обусловлен ее близостью к шару и эллипсоиду. Поэтому приступая к выявлению симметрии зашей планеты в целом, нам придется учесть и симметрию идеального шара, и симметрию эллипсоида вращения и трехосного эллипсоида, и симметрию более сложных фигур.

Как согласовать между собой эти различные виды симметрии, относящиеся к одному и тому же объекту — фигуре Земли?

Упоминаемые далее различные виды симметрии фигуры Земли отражают различные степени приближения к объективной реальности. Вместе с тем важно заметить, что каждая из этих степеней приближения имеет вполне определенный физический смысл а сопоставление их позволяет проанализировать динамику формирования фигуры Земли, т. е. природу формирующих ее сил.

Приближение фигуры Земли к сферической форме обусловлено гравитационным полем Земли, т. е. притяжением всех составляющих ее материальных частиц друг к другу. Если бы было возможно изолировать Землю от влияния всех внешних факторов, в том числе и  гравитационного воздействия всех других космических тел, и остановить все ее движения, то под воздействием собственного гравитационного поля Земля рано или поздно приняла бы форму идеального шара. Таким образом, приближение фигуры Земли к сферической форме отражает действие собственного гравитационного поля Земли.

Приближение фигуры Земли к форме эллипсоида вращения обусловлено вращением Земли вокруг ее географической оси. Возникающие при вращении центробежные силы растягивают Землю в экваториальной плоскости. Если бы на Землю воздействовало только ее собственное гравитационное поле и единственным ее движением было вращение вокруг оси, то она имела бы форму идеального эллипсоида вращения. Таким образом, приближение фигуры Земли к форме эллипсоида вращения отражает взаимодействие собственного гравитационного поля Земли с центробежными силами, вызываемыми ее вращением.

Количественное выражение отклонения земного эллипсоида от сферической формы, определяемое отношением разности экваториального и полярного радиусов Земли к экваториальному радиусу, составляющее около 1/297, выражает также относительное значение роли центробежных сил и собственного гравитационного поля Земля в формировании ее фигуры. Небольшая по отношению к среднему радиусу разность экваториального и полярного радиусов довольно значительна в ее абсолютном значении (около 21 км).

Рассматривая отклонения фигуры Земли от идеального эллипсоида вращения, мы должны учесть, что гравитационное поле, воздействующее на любую материальную точку Земли и играющее, наиболее существенную роль в формировании этой фигуры включает в себя кроме собственного гравитационного поля Земли гравитационные воздействия всех других космических тел, причем наиболее значительны воздействия Солнца и Луны.

Следует помнить и о вращение Земли вокруг собственной оси.

Рассмотрим взаимодействие гравитационных и центробежных сил  воздействующих на Землю, движущуюся по ее околосолнечной орбиты (рис. 3).

В системе Солнце — Земля действуют те же гравитационные и центробежные силы, с которыми мы имели дело, рассматривая взаимодействие собственного гравитационного поля Земли и центробежных сел, связанных с ее вращением. На рис. 3. Земля может рассматриваться как часть вращающегося диска, совпадающего с плоскостью эклиптики, испытывающая растяжение под влиянием противоположно ориентированных центробежных (инерционных) и центростремительных (гравитационных) сил. И те и другие имеют максимальное значение на линии, проходящей через центры Солнца и Земли. В то же время величины их одинаковы, чем и обусловливается устойчивое нахождение Земли на орбите. Поэтому их взаимодействие направлено на придание земной сфере формы эллипсоида, удлиненного вдоль оси системы Солнце — Земля, а земному эллипсоиду — формы трехосного эллипсоида.

Аналогичное воздействие на форму Земли оказывают гравитационные и инерционные силы, проявляющиеся в системе Земля -Луна.

Вхождение Земли в системы Солнце — Земля и Земля - Луна обусловливает воздействие на нее гравитацнонно-инерционных силовых полей, обладающих симметрией эллипсоидов вращения, удлиненных вдоль осей вращения, совпадающих соответственно с осями этих систем

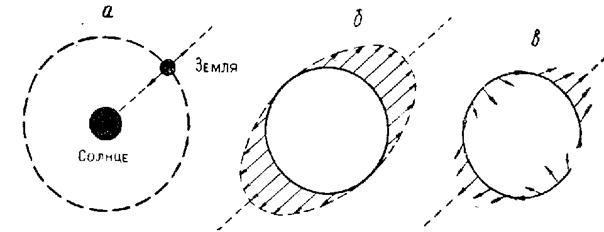
Рис. 3. Схемы гравитационно-ннерционного растяжения Земли вдоль оси Солнце — Земля (а), распределения приливообразующих сил на сферической недеформируемой Земле (б) и перемещении материальных точек поверхности Земли под действием приливообразующих сил (в).

Полные величины сил, растягивающих Землю вдоль осей Солнце— Земля и Земля — Луна, равны величинам центробежных л, действующих в соответствующих системах и уравновешиваемых гравитационными взаимодействиями. Они могут быть определены по формуле гравитационного взаимодействия

F = G m₁* m₂ / R²

Соответствен растягивающая сила, действующая на Землю вдоль оси Солнце Земля составляет около 3,5-10²⁷, вдоль оси Земля — Луна — 2*1²⁵ дин.

В предыдущем рассуждении мы пренебрегли изменениями расстояний от Солнца и Луны до Земли, выраженными, в частности, в эллиптичности земной и лунной орбит. Эти изменения должны рассматриваться как свойственные любым механическим системам колебания около положения равновесия. Эллиптичность орбит соответствует основным тонам этих колебаний. Обертоны выражаются наложением на эллиптические орбиты синусоидальных отклонении различных порядков. Рассмотрение симметрии всех этих колебаний несложно, и мы здесь на нем не останавливаемся.

До сих пор рассматривая силы, определяющие фигуру Земли, мы принимали во внимание только гравитационные и инерционные силы, так или иначе Бездействующие на Землю. При этом мы не учитывали действия в веществе Земли электромагнитных сил взаимодействия материальных частиц, соединяющих в твердые, жидкие и газообразные тела, отдельные атомы, ионы и молекулы и обеспечивающих устойчивость атомов, связывая электронные оболочки с ядром.

В предшествующем обзоре этими силами можно было пренебречь, поскольку нас интересовал лишь характер симметрии фигуры Земли, но не ее размеры, и поскольку постоянный характер собственного гравитационного поля Земли и ее собственного вращения позволял нам молчаливо допускать бесконечную длительность формирования фигуры Земли. Если бы не эти обстоятельства, то нам уже раньше пришлось бы отметить, что размеры фигуры Земли отражают взаимодействие между гравитационным полем, сжимающим Землю, и полем электромагнитных сил упругости, противодействующих сжатию.

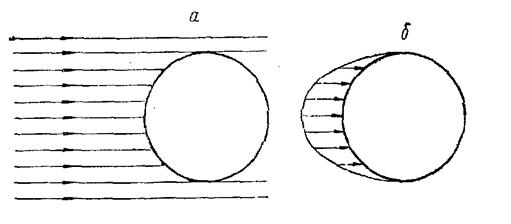
Рис. 16. Поле солнечной радиации в окрестностях Земли — симметрия цилиндра (а) и распределение солнечной радиации, поглощаемой поверхностью Земли, — симметрия конуса (б).

Во взаимодействии друг с другом атомов, ионов и молекул, не учтены также появляющиеся внутри атомных ядер ядерные силы и так называемые слабые взаимодействия, но их мы не будем касаться и в дальнейшем, поскольку их влияние на фигуру Земли незначительно и проявляется через электромагнитные силы.

Образующих все геологические тела, гравитационные силы имеют количественные значения во много порядков меньше, чем электромагнитные, и сами по себе не смогли бы произвести необходимо перераспределение вещества Земли. Реально осуществляющееся перераспределение (процессы денудации — аккумуляции на поверхности и миграция подвижных фаз внутри твердого тела Земли) протекает сравнительно быстро, благодаря тому, что помимо собственного гравитационного поля, задающего сферичность Земли, на последнюю воздействуют другие силовые поля, разрушающие или перестраивающие электромагнитные связи в твердых телах и тем самым способствующие перераспределению вещества Земли под воздействие гравитационного поля.

В частности, контролируемые гравитационным полем процессы денудации — аккумуляции на поверхности Земли не могли бы иметь сколько-нибудь существенные скорости без переменного воздействия солнечной радиации. Это воздействие, обусловливающее перестройку электромагнитных связей в атмосфере, гидросфере и на поверхности твердого тела Земли, обеспечивает энергией инсоляцию, дефляцию, эрозию и т. д. и вызывает перемещение огромных масс в атмосфере и гидросфере.

Симметрия воздействующего на Землю поля солнечной радиации соответствует, очевидно, симметрии конуса, ось которого совпадает с осью Солнце — Земля (рис. 16). Симметрия солнечной радиации, поглощаемой  Землей,  также  соответствует  симметрии конуса. Благодаря сферичности поверхности Земли плотность солнечной энергии, падающей на нее, распределяется по синусоидальному закону:

Е = Ео sin f;

где: Е — солнечная энергия, падающая на единицу площади поверхности Земли, Ео—тоже при вертикальном падении солнечных лучей; (f — угол между солнечными лучами и поверхностью Земли.

Величина поглощаемой Землей части солнечной анергии также зависит от (f):

Еа = КЕ sin f = КЕо sin2 f,

где: Еа, — солнечная энергия, аккумулируемая единицей площади, К — коэффициент аккумуляции (поглощения).

Следовательно, образующие конусов солнечной радиации, падающей на Землю и поглощаемой ею, имеют синусоидальный характер.

Собственно гравитационное поле Земли и поле центробежных сил, обусловленных ее вращением, жестко связаны с веществом Земли (с достаточной для данного рассмотрения точностью можно считать, что векторы этих полей в каждой материальной точке Земли постоянны и по направлению и по величине). В то же время силовые поля, обусловленные вхождением Земли в системы Солнце — Земля и Земля — Луна, не имеют такой связи. Вследствие «собственного» вращения Земли оси этих полей проскальзывают по ее телу, отражаясь на поверхности в виде пробегающих по ней волн лунно-солнечных приливов. В фиксированных точках поверхности Земли такое проскальзывание предстает в виде приливно-отливных движений, повторяющихся с определенной периодичностью. В силу значительной разницы в подвижности литосферы и гидросферы человечество с незапамятных времен знакомо с приливно-отливными движениями вод Океана. В настоящее время специальными геофизическими исследованиями установлено, что эти движения испытывает и литосфера, причем амплитуды их достигают нескольких дециметров. Имеются достоверные данные о приливно-отливных движениях подземных вод. Интенсивно исследуются приливно-отливные движения атмосферы .

Аналогично гравитационно-инерционным силовым полям, обусловливающим приливно-отливные движения в веществе Земли, проскальзывает по телу Земли и поле солнечной радиации. В настоящее время установлены связанные с этим проскальзыванием приливные движения в атмосфере — «температурные приливы». Можно предполагать, что в дальнейшем из состава приливных движений гидросферы будет выделена часть, аналогичная температурным приливай атмосферы.

Изменения фигуры Земли, связанные с воздействием силовых полей, проскальзывающих по ее телу, означают перестройку электромагнитных связей в веществе Земли, а всякая такая перестройка сопровождается возникновением в веществе звуковых, в частности сейсмических волн. Сами приливно-отливные движения вещества Земли являются, в сущности, вынужденными звуковыми колебаниями Земли, частоты и скорости распространения которых заданы скоростями ее вращения относительно осей систем Солнце — Земля и Земля — Луна.

Периоды приливных колебаний (23 ч для солнечных приливов и 14,5 - для лунных) более чем в 10 раз превышают период основного тона собственных колебаний Земли, составляющего несколько менее 1ч.  Поэтому приливы не вызывают резонансных явлений и не могут разорвать Землю. Вместе с тем они представляют собой непрерывно протекающую гигантскую деформацию всей Земли, и поглощение веществом Земли даже незначительной части энергии, обеспечивающей эту деформацию, может приводить к накоплению веществом энергии, достаточной для реализации разнообразных  геологических явлений. По-видимому, они являются одним из существеннейших энергетических источников для этих явлений.

Связанные с приливно-отливными движениями изменения напряженного состояния вещества Земли вызывают возникновение звуковых  волн (волн напряжении), соответствующих собственным частотам Земли в целом и ее оболочек. Эти волны распространяются во все стороны от осей симметрии приливов со скоростями, соответствующими скоростям звука в средах, по которым распространяются волны. Энергии этих волн незначительны. Возможно, что эти волны Исходят отражение в составе микросейсм, фиксирующихся в качестве фона при любых сейсмических наблюдениях. Однако постоянно пронизывая все тело Земли и в силу ограниченности Земли, интерферируя внутри нее и на ее поверхности, они могут обусловить формирование правильных (симметричных) сеток планетарной трещиноватости, привлекающих внимание многих исследователей

В связи с несовпадением экваториальной плоскости 3емли с плоскостью эклиптики оси симметрии силовых полей приливов и солнечной радиации, проскальзывая по телу Земли, совпадают в экваториальной плоскостью только 2 раза в год, совершая в течение года колебания относительно нее с амплитудой в 47°.

С наклоном земной оси к плоскости эклиптики связана антисимметрия распределения времен года на Земле. Благодаря упоряченному обращению Земли вокруг Солнца распределение климатических зон оказывается симметричным относительно экваториальной плоскости.

Исходя из вышесказанного, остановимся прежде всего на обобщенной симметрии внешней формы нашей планеты. К числу формообразующих факторов земного тепа следует отнести силу земного тяготения, воздействие космического гравитационного поля, одиннадцать различных видов движений Земли, деформации земной коры, связанные с перетеканием подкорового вещества и др.

Из перечисленных два фактора сыграли и продолжают играть доминирующую роль в деле формирования земного геоида — это сила земного тяготения и центробежная, обусловленная вращением Земли вокруг своей оси. Под влиянием первой силы Земля стремится принять шаровую форму. Вторая сила придает ей форму несколько сплющенного вдоль оси вращения одноосного эллипсоида (сфероида).

Суммарное воздействие силы земного тяготения можно идеализированно изобразить в виде пучка бесчисленного множества одинаковых стрелок (векторов), направленных к одной общей точке — центру Земли. Симметрия такого пучка, так же как и симметрия идеального и неподвижного шара отвечает бесчисленному множеству осей симметрии бесконечного порядка (осей вращения) и бесчисленному множеству плоскостей симметрии, пересекающихся в одной точке — центре шара.

Проявляется ли реально указанная симметрия на земном шаре и если проявляется, то в чем?

Прежде всего мы видим ее проявление в общей форме Земли, весьма близкой к шару. Кроме того, влияние этой симметрии ярко сказывается на внешней форме всех объектов, находящихся на поверхности Земли и испытывающих воздействие земного тяготения (внутри твердых тел электромагнитные силы несоизмеримо больше гравитационных).

Классифицируя эти явления, мы опять находим в них проявление общего закона Кюри, повсеместно проявляющегося в природе:

все то, что растет или движется по вертикали, т. е. вверх или вниз относительно земной поверхности, имеет симметрию типа Ln nP — пт и л и соответствующих подгрупп Ln —n, P—m —1.

Все то, что растет и движется горизонтально или косо по отношению к земной поверхности, характеризуется симметрией Р— n или т—1.

В чем же кроется объяснение столь широкого распространения двух типов симметрии.

Все вокруг нас находится в поле земного тяготения и, следовательно, должно неминуемо нести на себе отпечаток его воздействия. Примем какую-либо точку земной поверхности за исходную и изобразим действие на нее земного тяготения в виде вертикальной стрелки, направленной острием вниз.

Вокруг исходной точки находится бесчисленное множество Других точек земной поверхности, на которые такие действует сила земного тяготения. Следовательно, изображенную стрелку следует окружить бесконечным множеством аналогичных стрелок, направленных к центру земного шара и образующих в совокупность конус. Ясно, что симметрия стрелки над исходной точкой с учетом всех окружающих стрелок отвечает симметрии конуса L¥  ¥  P. Такая симметрия строго согласована с шаровой симметрией Земли: ось симметрии бесконечного порядка L¥  конуса совпадает с одним на диаметров шара, также являющимся осью симметрии бесконечного порядка, а бесчисленные плоскости симметрии конуса совмещаются с бесчисленными плоскостями симметрии шара, пересекающимися в одной из точек на его поверхности.

Итак, любая точка земной поверхности под влиянием силы земного тяготения получает «симметрию конуса», которая и налагает свой отпечаток на симметрию каждого тела, находящегося в данной точке.

Так объясняется универсальный закон симметрии, царящий на земной поверхности и обусловленный шаровой симметрией сил земного тяготения. Отметим, что этому всеобщему закону подчиняется не только органический мир, но и каменный природный материал, а именно кристаллы, главная ось которых ориентирована во время роста вертикально или косо относительно горизонтальной плоскости.

Перейдем к рассмотрению воздействия силы вращения Земли вокруг своей оси на симметрию формы и поверхности нашей планеты. Как известно, эта сила придает ей форму эллипсоида вращения.

Симметрия неподвижного конуса,  где ось бесконечного порядка (ось вращения) совпадает с осью конуса, плоскости симметрии направлены вдоль этой оси. Как показал А.Е Шубников, вращение конуса вокруг его оси аннулирует все плоскости симметрии. Следовательно, симметрия вращающегося конуса, аналогичным образом вращение земного сфероида, приводит к тому, что все плоскости симметрии, совпадающие с плоскостями меридианов, должны исчезнуть; остается лишь одна плоскость симметрии, перпендикулярная оси вращения и совпадающая экваториальной плоскостью. В результате получаем симметрию, которая отвечает одновременно вращающемуся одноосному эллипсоиду и вращающемуся вокруг одного из своих диаметров шару.

Этой симметрии подчиняются, помимо общей формы геоида, климатическая и почвенная зональности земного шара. Большую роль в деле возникновения именно такой симметрии играет воздействие подвижных оболочек (гидросферы и атмосферы) на литосферу в условиях вращения Земли.

Отсутствие меридиональных плоскостей симметрии наглядно иллюстрируется асимметричным развитием континентальных очертаний по широтным направлениям, а также законом Бэра для берегов рек, текущих вдоль меридианов. Подчеркнем, что в отношении распределения климатических и почвенных поясов симметрия земной поверхности хорошо согласуется с симметрией эллипсоида вращения. Сказанное можно пояснить словами В. И. Вернадского: «На всей поверхности планеты в общих основных чертах, идя к экватору от северного или южного полюса, мы наблюдаем единообразное повторение процессов природных вод.

Скопления льда и снега повторяются у южного и северного полюсов; области тундр и болот, лесов холодных и умеренных широт, степей и пустынь, подтропических богатых водными осадками областей могут быть отмечены по обе стороны от экватора, в обоих полушариях, в одинаковой последовательности». Как видим, ни о какой антиподальности или асимметрии южного и северного полушарий здесь не может быть и речи. Симметрия климатических поясов обладает центром инверсии и плоскостью симметрии, совпадающей с плоскостью экватора.

Как было показано выше, наиболее податливые элементы структуры земного шара—климатические и почвенные пояса—уже и сейчас почти всецело подчиняются симметрии. Конечно, и здесь приходится прибегать к некоторой идеализации. Отклонения от строгой закономерности вызываются, по-видимому, «блужданием оси» вращения в теле Земли.

Согласно исследованиям Г. Н. Каттерфельда, подкоровый субстрат, стремясь занять правильную форму эллипсоида вращения, перетекает от плоскости меридиана наибольшей оси в плоскость меридиана наименьшей оси. С этим явлением связаны тектонические опускания, а со вторым— по 90°  поднятия.

Мы рассмотрели целый ряд различных характеристик земного шара в отношении его симметрии. Противоречат ли друг другу эти характеристики? Напомним еще раз, что одно и то же реальное тело может получить различную симметрию в зависимости от тех свойств или явлений, которые принимаются во внимание. Поэтому приведенные выше различные группы симметрии имеют вполне реальное значение и не зачеркивают друг друга.

Можно сделать вывод. Земной шар, так же как и любое реальное тело, характеризуется различной симметрией в зависимости от изучаемых свойств и явлений.

Общее действие земного тяготения обусловливает геометрию большинства природных явлений на земной поверхности подчиняющихся симметрий неподвижного шара.  Климатическая и почвенная зональности характеризуются симметрией неподвижного эллипсоида вращения, а точнее — симметрией вращающегося шара или одноосного эллипсоида .

Идеализированной моделью распределения суши и воды на земном шаре может служить черно-белый «октаэдр» (комбинация двух тетраэдров) с антисимметрией.

Большинство этих видов симметрии является, быть может, переходными ступенями на пути к идеальной симметрии вращающегося одноосного эллипсоида или шара.

Конечно мы ограничились рассмотрением самых обобщенных схемам, трактующих симметрию Земли в наиболее упрощенном и сугубо идеализированном виде. Многое из вышесказанного является общеизвестным, однако, некоторые стороны вопроса еще недостаточно изучены и представляют несомненный интерес для науки.

Сейчас проблема уточнения и детализации симметрийных особенностей земного кардиоида привлекает внимание многочисленных исследователей, активно выступающих с новыми выводами и гипотетическими построениями.

ЗАКЛЮЧЕНИЕ

 Симметрия, проявляясь в самых различных объектах материального мира, несомненно, отражает наиболее общие, наиболее фундаментальные его свойства. Поэтому исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.

Например исследование симметрии Земли как планеты в цепом позволяет систематически и с соответствующей детальностью проанализировать динамику формирования фигуры Земли, т. е. рассмотреть качественную и количественную роль различных силовых полей, воздействие которых определяет эту фигуру. К сожалению, этот вопрос мы смогли представить лишь в самом обобщенном виде.

Наблюдающиеся проявления симметрии тектонических структур -наглядно свидетельствуют о наличии весьма общих закономерностей организации (структурирования) вещества, отраженных в самых разнообразных проявлениях природной симметрии: от симметрии свойств элементарных частиц до симметрии строения живых организмов и от симметрии кристаллических структур до симметрии геологических образований.

Применение законов и методики симметрии к исследованию тектонических и других геологических структур может помочь выявлению и систематизации закономерностей размещения этих структур. Оно облегчит также понимание физической природы выявленных закономерностей и механизма формирования структур, т. е., в конечном счете, теоретическое истолкование структурного материала.

Заканчивая реферат, я надеюсь, что смогла хоть немного приоткрыть всю сложность и многообразие проявлений симметрии в природе на примере понятий о симметрии в теории геологических дисциплин и о симметрии Земли как планеты в целом.

ЛИТЕРАТУРА

1.  Современный словарь иностранных слов.  М.: Русский язык, 1993г.Советский энциклопедический словарь  М.: Советская энциклопедия, 1980г.

2.  Урманцев Ю.А. Симметрия природы и природа симметрии  М.: Мысль, 1974г.

3.  Пидоу Дэн  Геометрия и искусство  М.: Мир, 1979г.

4.  Шафрановский И.И. Симметрия в  геологии Л.: Недра, 1975г.

5.  Трофимов В. Введение в геометрическом многообразии с симметриями М.: МГУ 1989г.