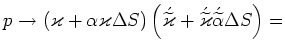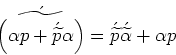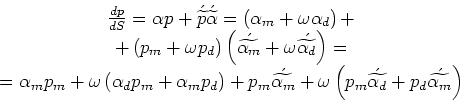Реферат: Полуточка: модель скорости

Каратаев Евгений Анатольевич

Настоящая статья строит модель скорости в рамках модели полуточки и приводит две простых иллюстрации, демонстрирующие и иллюстрирующие модель скорости в общеизвестных случаях поступательной и вращательной скорости. В статье приводится в основном модель скорости, и разбор отдельных случаев скорости и её видов представляется либо темой отдельной статьи, либо большой работы о кинематике, выраженной на языке гиперкомплексных чисел.

Для понимания предлагаемой модели скорости частично повторим основные положения модели полуточки и модели миров.

Точка пространства испытывает изменение при переходе от одной системы отсчёта к другой:

$\begin{displaymath}p \rightarrow \varkappa p \acute{\widetilde{\varkappa}}\end{displaymath}$

(1)

Считается, что точка принадлежит миру с временем :

$\begin{displaymath}S = \ln{\left(\left\vert p\right\vert\right)} = Re\left(\ln{\left( p \right)}\right)\end{displaymath}$

(2)

В этой статье понятия системы координат и системы отсчёта полагаются совпадающими. Полагается, что положение точки и её состояние измеряются в некоторой идеальной системе, выбираемой наблюдателем по его усмотрению.

Состояния точки в два различных момента времени могут быть определены относительно одной и той же системы координат. Будем полагать, что из первого состояния во второе можно попасть, совершив преобразование системы координат:

$\begin{displaymath}p \rightarrow e^{\alpha \Delta S} p \acute{\widetilde{ e^{\alpha \Delta S} }}\end{displaymath}$

(3)

Здесь величина $e^{\alpha \Delta S}$ определяет преобразование, которое следует совершить для такого перехода. При этом $\Delta S$ есть разность времён этих двух миров:

$\begin{displaymath}S \rightarrow S + \Delta S\end{displaymath}$

(4)

Также будем полагать, что эти два состояния разделены друг от друга бесконечно малым расстоянием во времени:

$\begin{displaymath}\lim\Delta S = 0\end{displaymath}$

(5)

Под скоростью будем понимать величину, определенную классическим способом: Если величина зависит от величины , и с течением величина испытывает изменение, то скоростью называется предел отношения приращений величин и :

$\begin{displaymath}v = \dot{x} = \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\end{displaymath}$

(6)

Ещё одно небольшое отступление нужно сделать для описания и выбора точной модели преобразования Пуанкаре. Дело в том, что пока рассматриваются лишь пространственно-временные преобразования, им в действительности удовлетворяет два различных преобразования:

$\begin{displaymath}p \rightarrow \varkappa p \acute{\widetilde{\varkappa}}\end{displaymath}$

(7)

$\begin{displaymath}p \rightarrow \varkappa p \acute{\overline{\varkappa}}\end{displaymath}$

(8)

Здесь в первом случае используется скалярно-векторное сопряжение, во втором - скалярно-алгебраическое. Для того, чтобы выявить, в чем они различаются с точки зрения группы Пуанкаре, распишем их операторное представление:

$\begin{displaymath} \varkappa = e^{\varphi} = exp\left(\dot{i}i \varphi_1 + \do... ...t{i}\varphi_4 + i \varphi_5 + j \varphi_6 + k \varphi_7\right) \end{displaymath}$	(9)
$\begin{displaymath} \acute{\widetilde{\varkappa}} = exp\left(\dot{i}i \varphi_1... ...t{i}\varphi_4 - i \varphi_5 - j \varphi_6 - k \varphi_7\right) \end{displaymath}$	(10)
$\begin{displaymath} \overline{\acute{\varkappa}} = exp\left(\dot{i}i \varphi_1 ... ...t{i}\varphi_4 - i \varphi_5 - j \varphi_6 - k \varphi_7\right) \end{displaymath}$	(11)

Видно, что эти два оператора отличаются псевдоскалярной частью параметра. В силу того, что её можно вынести из оператора преобразования, оба варианта могут быть представлены как:

$\begin{displaymath} p \rightarrow \varkappa_n e^{\dot{i}\varphi_4} p \acute{\wi... ...{i}\varphi_4} = \varkappa_n p \acute{\widetilde{\varkappa_n}} \end{displaymath}$	(12)
$\begin{displaymath} p \rightarrow \varkappa_n e^{\dot{i}\varphi_4} p \acute{\wi... ...kappa_n p \acute{\widetilde{\varkappa_n}}e^{2\dot{i}\varphi_4} \end{displaymath}$	(13)

где через $\varkappa_n$ обозначен оператор $\varkappa$ с вынесенной псевдоскалярной составляющей из его параметров:

$\begin{displaymath}\varkappa_n = exp\left(\dot{i}i \varphi_1 + \dot{i}j \varph......i}k \varphi_3 + i \varphi_5 + j \varphi_6 + k \varphi_7\right)\end{displaymath}$

(14)

Таким образом, предстоит сделать выбор между двумя вариантами преобразований: 1) использовать скалярно-векторное сопряжение или 2) использовать скалярно-алгебраическое сопряжение. Выберем вариант 1 с отбрасыванием рассмотрения псевдоскалярной составляющей параметра преобразований в силу того, что пока в наши цели не входит рассмотрение псевдоскалярных преобразований и в силу того, что векторное сопряжение удобнее в силу его линейности.

А именно:

$\begin{displaymath} \widetilde{\left(e^q\right)} = e^{\widetilde{q}} \end{displaymath}$	(15)
$\begin{displaymath} \acute{\left(e^q\right)} = e^{\acute{q}} \end{displaymath}$	(16)

Поэтому мы можем выполнить дальнейший вывод более наглядно.

В силу того, что величина и её приращение являются скалярами, имеем:

$\begin{displaymath}\acute{\widetilde{\left(e^{\alpha \Delta S}\right)}} = e^{\acute{\widetilde{\alpha}} \Delta S}\end{displaymath}$

(17)

И в случае когда $\Delta S$ мало, имеем:

$\begin{displaymath} e^{\alpha \Delta S} \approx 1 + \alpha \Delta S \end{displaymath}$	(18)
$\begin{displaymath} x \rightarrow e^{\alpha \Delta S} \varkappa \approx \varkappa + \alpha \varkappa \Delta S \end{displaymath}$	(19)

Используя это соотношение для преобразования полуточки, распишем выражение для преобразования точки:

$\displaystyle p \rightarrow \left(\varkappa + \alpha\varkappa\Delta S\right) \l... ...pa}} + \acute{\widetilde{\varkappa}}\acute{\widetilde{\alpha}}\Delta S\right) =$
$\displaystyle = \varkappa\acute{\widetilde{\varkappa}} + \alpha\varkappa\acute{... ...alpha\varkappa\acute{\widetilde{\varkappa}}\acute{\widetilde{\alpha}}\Delta S^2$			(20)

Оставив члены первого порядка малости по $\Delta S$ :

$\begin{displaymath}p \rightarrow \varkappa\acute{\widetilde{\varkappa}} + \alp......acute{\widetilde{\varkappa}}\acute{\widetilde{\alpha}}\Delta S\end{displaymath}$

(21)

Используя определение полуточки

$\begin{displaymath}p = \varkappa\acute{\widetilde{\varkappa}}\end{displaymath}$

получим:

$\begin{displaymath}p \rightarrow p + \left(\alpha{p} + \acute{\widetilde{p}}\acute{\widetilde{\alpha}}\right)\Delta{S}\end{displaymath}$

(22)

Положив точку функцией величины и сравнив с разложением её в ряд Тейлора в окрестности , получим:

$\begin{displaymath}\frac{dp}{dS} = \alpha{p} + \acute{\widetilde{p}}\acute{\widetilde{\alpha}}\end{displaymath}$

(23)

Это выражение и является определением скорости точки , если она движется во времени , испытывая в каждый его момент преобразование Пуанкаре:

$\begin{displaymath}p \rightarrow e^{\alpha\Delta{S}}p\acute{\widetilde{e^{\alpha\Delta{S}}}}\end{displaymath}$

(24)

Выражение (23) является скалярно-векторно сопряжённым самому себе:

$\begin{displaymath}\acute{\widetilde{\left(\alpha p +\acute{\widetilde{p}}\alp...... = \acute{\widetilde{p}}\acute{\widetilde{\alpha}} +\alpha p\end{displaymath}$

(25)

То есть абсолютное приращение точки выполняется несмотря на произвольность величины $\alpha$ так, что точка остается сама себе скалярно-векторно сопряжённой.

Отметим также, что в силу свойства точки $p = \acute{\widetilde{p}}$ верно равенство:

$\begin{displaymath}\frac{dp}{dS} = \alpha{p} + \acute{\widetilde{p}}\acute{\widetilde{\alpha}} = \alpha p + p \acute{\widetilde{\alpha}}\end{displaymath}$

(26)

Далее...

Придерживаясь модели полной группы Пуанкере, мы должны считать величины и $\alpha$ дуальными бикватернионами, имеющими 16 компонент. В силу требования скалярно-векторной сопряжённости самой себе точка часть компонентов имеет нулевыми.

Для понимания дальнейшего вывода представим величины и $\alpha$ в виде, явно содержащем разделение на главную и дуальную части:

$\displaystyle p = p_m + \omega p_d$
$\displaystyle \alpha = \alpha_m + \omega \alpha_d$			(27)

Здесь индексом обозначены главные части, а индексом - дуальные. Пользуясь введенным обозначением, распишем выражение скорости:

$\begin{displaymath}\begin{array}{c}\frac{dp}{dS} = \alpha{p} + \acute{\widet...... p_d \acute{\widetilde{\alpha_m}}\right) \nonumber\end{array}\end{displaymath}$

Сгруппировав главные и дуальные части, получим:

$\begin{displaymath}\frac{dp}{dS} = \alpha_m p_m + p_m\acute{\widetilde{\alpha_......a_d}} + \alpha_m p_d + p_d \acute{\widetilde{\alpha_m}}\right)\end{displaymath}$

(28)

Используя это разложение в главных и дуальных частях и задавая различные частные случаи величин , , $\alpha_m$ и $\alpha_d$ , оценим характер вклада в скорость точки отдельных величин $\alpha_m$ и $\alpha_d$ . А также найдём их сопоставление отдельным общеизвестным скоростям.

Случай 1.

Зададим точку как дуальный вектор с единичной главной частью:

$\begin{displaymath}p = 1 + \omega p_d \ \ \ \ (p_m = 1)\end{displaymath}$

(29)

а величину $\alpha$ как дуальный вектор с нулевой главной частью:

$\begin{displaymath}\alpha = \omega\alpha_d \ \ \ \ (\alpha_m = 0)\end{displaymath}$

(30)

Тогда, используя разложение (29), найдем скорость точки при таком преобразовании:

$\begin{displaymath}\frac{dp}{dS} = \alpha_m + \acute{\widetilde{\alpha_m}} + \......a_d}}+ \alpha_m p_d + p_d\acute{\widetilde{\alpha_m}}\right)\end{displaymath}$

(31)

В силу того, что выбрано условие $\alpha_m=0$ , имеем:

$\begin{displaymath}\frac{dp}{dS} = \omega\left(\alpha_d + \acute{\widetilde{\alpha_d}}\right)\end{displaymath}$

(32)

Таким образом, в приведённых выше условиях величина $\alpha_d + \acute{\widetilde{\alpha_d}}$ является линейной скоростью приращения дуальной части . В силу того, что в состав величины $\alpha_d$ входит как полярная, так и дуальная части, то есть:

$\begin{displaymath}\alpha_d = Pol\left(\alpha_d\right) + Ax\left(\alpha_d\right)\end{displaymath}$

(33)

то в силу свойств функций и , определённых как

$\begin{displaymath} Pol(q) = \dot{i}i q_1 + \dot{i}j q_2 + \dot{i}k q_3 + \omega \dot{i}i q_9 + \omega \dot{i}j q_{10} + \omega \dot{i}k q_{11} \end{displaymath}$	(34)
$\begin{displaymath} Ax(q) = i q_5 + j q_6 + k q_7 + \omega i q_{13} + \omega j q_{14} + \omega k q_{15} \end{displaymath}$	(35)

И имеющих свойства сопрягаться:

$\begin{displaymath} \acute{\widetilde{Pol(q)}} = Pol(q) \end{displaymath}$	(36)
$\begin{displaymath} \acute{\widetilde{Ax(q)}} = - Ax(q) \end{displaymath}$	(37)

Имеем равенство для первого случая:

$\begin{displaymath}\frac{dp}{dS} = 2\omega Pol\left(\alpha_d\right)\end{displaymath}$

(38)

Или: величина $2Pol\left(\alpha_d\right)$ является линейной скоростью изменения вектора .

Случай 2. Выберем величины и $\alpha$ такими, что выполняются следующие условия:

$\begin{displaymath}p_m = 1, \ \ \alpha_d = 0, \ \ Pol\left(\alpha_m\right)=0\end{displaymath}$

<527.png" alt="$2Ax(\alpha_m)$">является угловой скоростью вращения вектора

Таким образом, величины $2Pol(\alpha_d)$ и $2Ax(\alpha_m)$ имеют всем хорошо известные механические кинематические интерпретации.

Целью настоящей работы было дать модель скорости и её иллюстрация в частных случаях. Поэтому полный разбор сочетаний $\alpha$ и здесь не рассматривается и автор полагает, что такое рассмотрение должно стать темой отдельной работы, посвящённой именно этому вопросу.

К будущим исследованиям могут быть отнесены: величины $Pol(\alpha_m)$ и $Ax(\alpha_d)$ , а также отдельное исследование главной части точки . В данной работе рассматривалась лишь её дуальная составляющая. Но общая модель преобразования Пуанкаре потребовала объединения в одну величину дуальной и главной частей вектора , существенно увеличив его размерность. Автор полагает, что будущие исследования покажут оправданность такого объединения. Кроме того, остаётся совершенно нерассмотренной возможность замены скалярно-векторного сопряжения на скалярно-алгебраическое в преобразовании Пуанкаре и следствия такой замены.

Список литературы

5rik.ru

Материалы для учебы и работы

Реферат: Полуточка: модель скорости