Реферат: Контрольная работа

№385. Вычислить несобственные интегралы или установить их расходимость.

По определению несобственного интеграла имеем:

Интеграл сходится.

№301. Найти неопределенный интеграл.

Представим подинтегральную функцию в виде слагаемых

№522. Даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.

Понизим порядок дифференциального уравнения, т.е. введем новую функцию , тогда

и получаем уравнение

Это линейное уравнение первого порядка.

Введем новые функции u=u(x) и v=v(x).

Пусть , тогда , т.е.

(1)

Предположим, что функция такова, что она обращает в тождественный нуль выражение, стоящее в круглых скобках уравнения (1) т.е., что она является решением дифференциального уравнения.

это уравнение с разделяющимися переменными

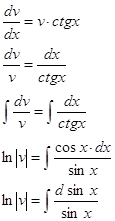
Здесь

Подставляем значение v в уравнение (1), получаем

Следовательно,

а т.к. , то

решим отдельно интеграл

, тогда

общее решение данного дифференциального уравнения.

Найдем частное решение при заданных условиях

Т.к. , то

- частное решение при заданных условиях.

№543. Даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.