Реферат: Контрольная работа по линейной алгебре

Министерство образования РФ

Московский государственный университет сервиса

Региональный институт сервиса

Контрольная работа

по математике

Выполнил студент 1 курса

спец. 060400 «Финансы и кредит»

сокр. форма обучения

группа__39-1_________

Самойлов Владислав Валерьевич

Ф. И. О.

Шифр:__Д/3001-525

Научный руководитель:

________Белов Борис Алексеевич

Дубна 2001 год
 


№ Оглавление Страница
1 Задание № 1 (а); (б) (выполнить действия) 3
2 Задание № 2 (а); (б) (вычислить определитель) 3
3 Задание № 3 (решить систему методом Гаусса) 4
4 Задание № 4 (а) (найти обратную матрицу) 4
5 Задание № 4 (б) 5
6 Задание № 5 (задача баланса) (а); (б) 6
7 Задание № 5 (в) 7
8 Задание № 6 (вычислить пределы) (а); (б) 7
9 Задание № 6 (в) 8
10 Задание № 7 (найти производную) (а) 8
11 Задание № 7 (задача на максимум) (б) 9

Задание № 1

Выполнить действия:

а)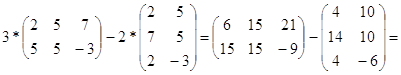

=

б)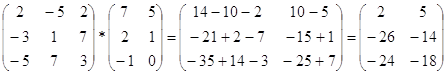

 Задание № 2

Вычислить определитель двумя способами:

а) способом Крамера D =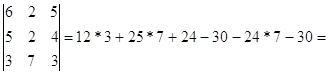

б) разложением по строке D=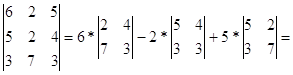

Задание № 3

Решить систему методом Гаусса:

 

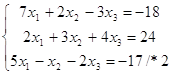
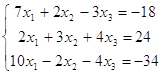
сложу третью строку с первой строкой системы и получу:

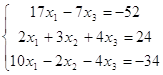
 сложу третью строку системы со второй и получу:

   

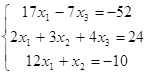
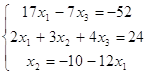
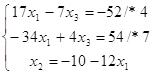
получим 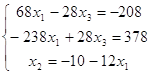 сложим первую и вторую строку и избавимся от переменной x3, затем получим: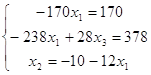  

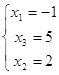
проверка: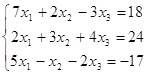    

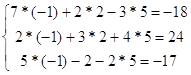
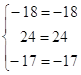
Задание № 4

Найти обратную матрицу и проверить результат:

а) А= найдем оределитель матрицы D=, определитель матрицы не равен нулю, следовательно матрица невырожденная

А11=1  А12=5

А21=-1  А22=3 

 

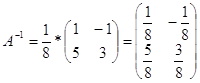
Проверка

А*А-1=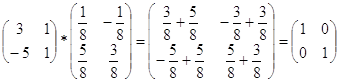

 б)А=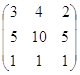 D=

определитель матрицы не равен нулю, следовательно данная матрица невырожденная

А= 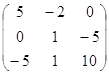 по формуле , следовательно

 А-1=1/5*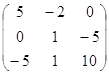

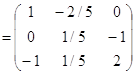
проверка

А-1*А=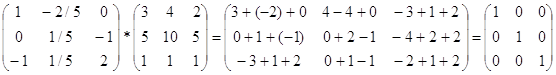

Задание № 5

Задача баланса: договор о взаимных услугах трех фирм

Производство услуг Потребление услуг Конечный продукт

Ф1

Ф2

Ф3

Ф1

 - 32% - 68

Ф2

 15% 20% 20% 38

Ф3

 40% 30% 20% 38

а) требуется составить систему уравнений баланса;

б) найти валовые обороты x1, x2, x3;

в) составить балансовую таблицу

Решение

а)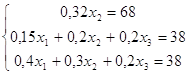

б)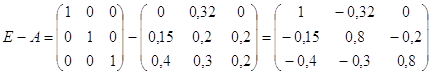

 

 

 

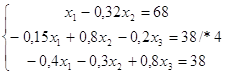
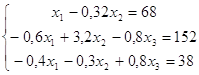
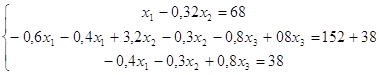
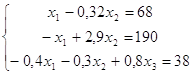
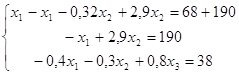
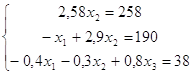
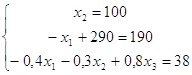
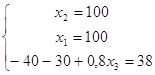
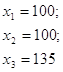
в)

Производство услуг Потребление услуг

Yi

Xi

Ф1

Ф2

Ф3

Ф1

 0 32 0 68 100

Ф2

 15 20 27 38 100

Ф3

 40 30 27 38 135
Остаток 45 18 81 144
Xj 100 100 135

Задание № 6

Вычислить пределы:

а)

= =  =

   =

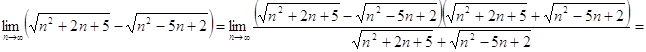
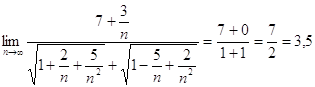
б)

   

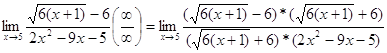
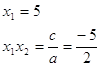
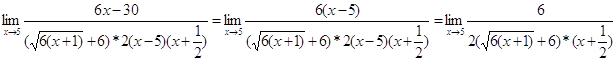
при x=5

в)

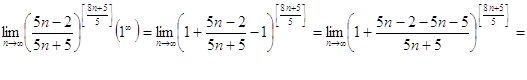
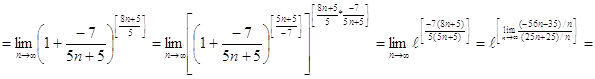
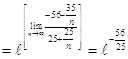
Задание № 7

Найти производную:

а)

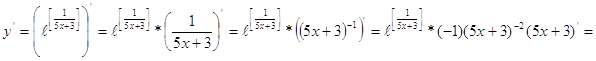
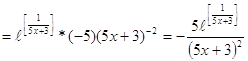
б) Из квадратного листа со стороной 5 изготавливается коробка без верха. Найти наибольший объем коробки и соответствующие ему размеры.


V=(5-2x)2x

 

0<x<21/2

Решение

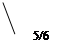
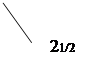
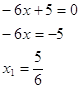
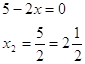
- сторона основания коробки

- высота коробки