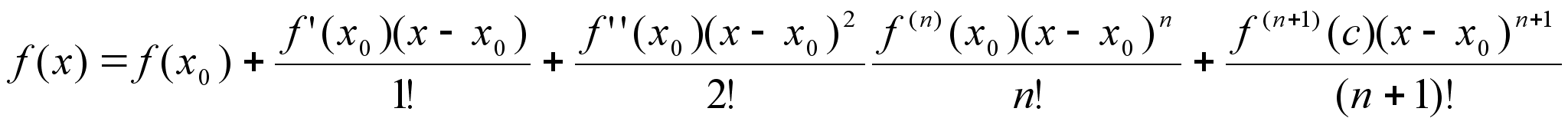Реферат: Лекции (1-18) по мат. анализу 1 семестр
По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик
van_mo_mail@mtu-net.ru или на сотовый:
8-901-7271056 спросить Ваню
екция №1Ведущая: Голубева Зоя Николаевна
Дата: вторник, 5 сентября 2000 г.
Тема: Введение
Условные обозначения:
: - так, что def – по определению
– включает ’’’ – [dnf(x)]/dxn=(d/dx)([dn-1f(x)]/dxn)
- следует, выполняется
- тогда и только тогда
- любой
- существует
] – пусть
! – единственный
[x] – целая часть
~ - эквивалентно
о - малое
Все R представляют десятичной дробью.
Все Q представляют конечной дробью, либо периодичной дробью.
Все иррациональные числа представляют бесконечной десятичной дробью ( не периодичной).
Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.
x
0 – отвечает за ноль.
Отрезок [0;1] отвечает за единицу
Единица за единицу.
Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков [0;x] из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны.
Каждому R отвечает точка на числовой прямой и наоборот, каждой точке отвечает R.
Основные числовые множества.
x
 Отрезок:
[/////////] x
Отрезок:
[/////////] x
a b
Обозначается [a;b] ab
Частный случай отрезка точка
Или axb – в виде неравенства.
х
 Интервал:
(/////////) x
– множество
точек на числовой
прямой.
Интервал:
(/////////) x
– множество
точек на числовой
прямой.
a b
Обозначается
(a;b)
или в виде
неравенства
a
x
a b
x a
b
Обозначается:
[a;b) axb (a;b]
a Всё
это числовые
промежутки. Замечание:
один из концов
( а или b)
может быть
символом . x b
x b
Вся
числовая прямая
– R=(-;+) Окрестности. Определение:
ε
–окрестностью
числа а
называется
множество чисел
х удовлетворяющие
неравенству ε>0
а-ε
а
а+ε Оε(а)={xR:x-a<ε} Проколотая
ε
окрестность
– Оε(а)
это множество
таких чисел
включающих
R,
и отстаёт от
точки на ε
и не принадлежит
а. Оε(а)={xR:0<x-a<ε} а-ε
а
а+ε Правая
ε поло окрестность
точки а:
О+ε(а)={xR:ax a
a+ε Проколотая
правая ε поло
окрестность
точки а:
Оε(а)={xR:a Левая
ε поло окрестность
точки а:
O-ε(a)={xR:a-ε a-ε
a Проколотая,
левая ε поло
окрестность
точки а:
О-ε(а)={xR:a-ε Модуль
и основные
неравенства. х=
0; x=0 -x;
x<0 |x| h>0
x<-h а,b
R:
|ab|a|+|b| а,b
R:
|a-b|||a|-|b|| Можно
рассматривать
окрестности
бесконечности: О ε>0
ε О ε>0
-ε
0 О x>ε;x<-ε
-ε
ε Функция.
Монотонность.
Ограниченность. х
– называется
независимой
переменной. у
– зависимой. Функцию
можно задавать
равенством
(у=х2) Таблицей Х1 Х2 Х3 Х4 У1 У2 У3 У4 Графиком,
то есть множеством
точек с координатами
(x,f(x))
на плоскости: Определение
f(x)
монотонности:
Пусть Х принадлежит
области определение
D
( ]xD) Пусть
Х подмножество
в области определения
в f(x). Функция
у=f(x)
называется: Возрастающая
на Х, если
для любого
х1;х2
принадлежащие
Х: х1 Убывающий
на Х, если для
любого х1;х2
принадлежащие
Х: х1 3)
Не убывающий
на Х, если для
любого х1;х2
принадлежащие
Х: х1 Не
возрастающая
на Х, если для
любого х1;х2
принадлежащие
Х: х1 Определение: Ограниченность.
Пусть Х включает
D
y=f(x)
называется: Ограниченной
сверху на Х
если существует
В, так что для
любого х
принадлежащего
Х выполняется
xR Ограниченной
снизу на Х если
существует
А, так что для
любого х
принадлежащего
Х выполняется
Ах Ограниченной
и сверху и снизу
на Х если существует
А,В, так что для
любого х
принадлежащего
Х выполняется
АхВ,
или существует
С, так что для
любого х
принадлежащего
Х выполняется
хС Лекция
№2 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 12 сентября
2000 г. Тема:
Функции
Определение
(сложная функция): Пусть
задано D,E,G,C,R На
D:
y=f(x)
с областью
значения E На
E:
z=g(y)
с областью
значения G Тогда
на множестве
D
определена
сложная функция
z=g(f(x))
с областью
значения G.
Тогда говорят,
что g(f(x))
есть суперпозиция
функций g,f. Пример:
Пример z=sin
ex
w=arctgcos
exx-ln
x y=ex=f(x) z=sin y=g(y) D=R E=R+ G=[-1;1] Определение
(обратной функции): Пусть
существует
D,E,C,R На
D:
y=f(x)
с областью
значений Е.
Если для каждого
у из
y=f(x)
найдётся единственный
х, то
говорят, что
на множестве
Е задана функция
обратная к
функции f(x),
с областью
значений D.
Иными словами
две функции
y=f(x)
и x=g(y)
являются взаимно
обратными если
выполняется
тождества: y=f(g(y)),
yE
y=f(g(y)),
для любого уЕ
x=g(f(x)),
xD
x=g(f(x)),
для любого хD П 1)y=x3
x=3y
D=R E=R 2 D=R+
{0}=[0;+) E=[0;+) D=R-
{0}=(-;0] E=[0;)
x=-y 3 D=[-/2;/2] E=[-1;1] x=arcsiny y[-1;1];
x[-/2;/2] Пусть
y=f(x) D=[a;b] E=[A;B] Определение:
y=f(x),
nN a1=f(1) a2=f(2) an=f(n) {an}
– множество
значений силовой
последовательности
nN
или аn { аn=1/n {аn}={sin1;sin2;sinn} аn=sinn аn=(-1)n/n
{(-1)n}={-1;1;-1;1;-1;1…}
Ограниченные
последовательности. Ограниченная
сверху, то есть
существует
В так что аnВ,
для любого nN Ограниченная
снизу, то есть
существует
А так что Аbn,
для любого nN Ограниченная,
то есть существует
А,В так что АаnВ,
для любого nN
существует
С>0 так что аnС,
для любого
nN. возрастающая
an убывающая
an>an+1,
nN не
возрастающая
anan+1,
nN не
убывающая
anan+1,
nN Пределы
последовательности.
Определение:
числа а
, называется
пределом числовой
последовательности
аn,
если для любого
сколь угодно
малого числа
ε>0,
найдётся натуральный
номер N
такой, что для
всех чисел nN
выполняется
модуль разности
an-a<ε
ε>0
N :
nN
an-a<ε. Lim
an=0 n Примеры:
Доказать, что
ln(-1)2/n=0 Зададим
любое ε>0,
хотим чтобы
(-1)n-0<ε,
начиная с некоторого
номера N,
1/n<ε
n>1/ε
N=[1/ε]+1 ε=0.01 N=[1/0.01]+1=101
|an|<0.01,
если
n101 *
* * an=1-1/n2 lim(1-1/n2)=1 n+ Для
любого ε>0
(1-1/n2)-1<ε -1/n2<ε
1/n2<ε
n2>1/ε
n>1/ε
N=[1/ε]+1 Лекция
№3 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 13 сентября
2000 г. Тема:
Последовательности Последовательность
аn
называется
бесконечно
малой , это
означает, что
предел этой
последовательности
после равен
0. an
– бесконечно
малая
lim
an=0
то есть для
любого ε>0
существует
N,
такое что для
любого n>N
выполняется
n+ an<ε Важные
примеры бесконечно
малой последовательности: 1)n=1/n
Докажем, что
для любого ε>0
1/n<ε
1/n<ε
n>1/ε
N[1/ε]+1 Докажем,
что lim1/n=0 n+ 2)
n=
sin(1/n). Докажем,
что для любого
ε>0
sin(1/n)<ε,
заметим, что
1/n принадлежит
первой четверти,
следовательно
1sin(1/n)>0,
следовательно
sin(1/n)<ε Следовательно
1/n 3)
n=ln(1+1/n)
n0;
1/n;
1+1/n1 lim ln(1+1/n)=0 n+ Докажем
ln(1+1/n)<ε
ln(1+1/n)<ε
1+1/n 1/n n>1/eε-1
N=[1/eε-1]+1 n=1-cos(1/n) lim(1-cos(1/n))=0 n+ Докажем
ε>0
1-cos(1/n)<ε 1/n
первой четверти
cos
первой четверти
положительный
0 cos(1/n)>1-ε
(считаем, что
0<ε<1) 1/n N=[1/arcos(1-ε)]+1 Свойства
бесконечно
малой последовательности. Теорема.
Сумма
бесконечно
малой есть
бесконечно
малое. nnбесконечно
малое
n+n
– бесконечно
малое. Доказательство. Дано: n-
бесконечно
малое
ε>0
N1:n>N1
n<ε n-
бесконечно
малое
ε>0
N2:n>N2
n<ε Положим
N=max{N1,N2},
тогда для любого
n>N
одновременно
выполняется
оба неравенства: n<ε
n+nn+n<ε+ε=2ε=ε1n>N n<ε Зададим
ε1>0,
положим ε=ε1/2.
Тогда для любого
ε1>0
N=maxN1N2
:
n>N
n+n<ε1
lim(n+n)=0,
то
n есть
n+n
– бесконечно
малое. Теорема
Произведение
бесконечно
малого есть
бесконечно
малое. n,n
– бесконечно
малое
nn
– бесконечно
малое. Докозательство: Зададим
ε1>0,
положим ε=ε1,
так как n
и n
– бесконечно
малое для этого
ε>0,
то найдётся
N1:
n>N
n<ε Возьмем
N=max {N1;N2},
тогда
n>N
= n<ε n<ε nn=nn<ε2=ε1 ε1>0
N:n>N
nn<ε2=ε1 lim
nn=0
nn
– бесконечно
малое, что и
требовалось
доказать. n Теорема
Произведение
ограниченной
последовательности
на бесконечно
малую последовательность
есть бесконечно
малая последовательность аn
– ограниченная
последовательность n
–бесконечно
малая последовательность
ann
– бесконечно
малая последовательность. Доказательство:
Так как аn
– ограниченная
С>0:
nN
anC Зададим
ε1>0;
положим ε=ε1/C;
так как n
– бесконечно
малая, то ε>0
N:n>N
n<ε
ann=ann ε1>0
N:
n>N
ann=Cε=ε1
lim ann=0
ann
– бесконечно
малое
n Замечание:
в качестве
ограниченной
последовательности
можно рассматривать
const
произведение
постоянно. Теорема
о представление
последовательности
имеющий конечный
предел. lim
an=a
an=a+n n+ Последовательность
an
имеет конечный
предел а
тогда и только
тогда, когда
она представлена
в виде an=a+n где
n
– бесконечно
малая. Доказательство: lim
an
ε>0
N:n>N
an-a<ε.
Положим an-a=n
n<ε,
n>N,
то есть n
- бесконечно
малая
n+ an=a+n
что и требовалось
доказать Доказательство
(обратное):
пусть an=a+n,
n
– бесконечно
малая, то есть
n=an-a
ε>0
N:
n>N
n=an-a<ε,
то
есть
lim an-а
n+ Теоремы
о пределах
числовых
последовательностей. Теорема
о пределе суммы:
Пусть
lim an=a
lim bn=b
lim an+n=a+b
n+
n+
n+ Докозательство:
an=a+n
bn=b+n
Сложим
an+bn=a+b+n+n=a+b+n
lim
an+bn=a+b
n+ 2)
Теорема
о произведение
пределов: Пусть
lim an=a
lim bn=b
lim anbn=ab
n+
n+
n+
Доказательство:
an=a+n
bn=b+n
anbn=(a+n)(b+n)
anbn=ab+an+bn+nn=ab+n
lim anbn=ab
что
и
n+
требовалось
доказать. Теорема
о пределе частного Пусть
lim an=a
lim bn=b
b0
lim an/bn=a/b
n+
n+
n+
Доказательство:
an=a+n
bn=b+n
так как b0,
то N1:
n>N1bn0 bn an/bn=an/bn-a/b+a/b=a/b+(ban-abn)/bbn=a/b+[b(a+n)-a(b+n)]/b(b+n)=a/b+n/b(1+bn/b) lim
an/bn=a/b
n+
Лекция
№4 Ведущая:
Голубева Зоя
Николаевна Дата:
понедельник,
19 сентября 2000 г. Тема:
Бесконечно
большие последовательности
. аn=(-1)n
– не имеет
предел. {bn}={1,1…} {an}={-1;1;-1;1…}
– предел не
существует. Бесконечно
большие последовательности. an=2n N:n>N
an>ε bn=(-1)n2n N:n>N
bn>ε cn=-2n N:n>N
cn<-ε Определение
(бесконечно
большие последовательности) 1) lim
an=+,
если ε>0N:n>N
an>ε
где ε-
сколь угодно
малое. n 2)lim
an=-,
если
ε>0
N:n>N
an<-ε n+ 3)
lim an=
ε>0
N:n>N
an>ε n+ Последовательностью
имеющий конечный
предел
называют
сходящимися.
В противном
случае последовательность
называют
расходящимися.
Среди них есть
последовательности,
которые расходятся
в бесконечность.
О них мы говорим,
что они имеют
бесконечный
предел. Доказательство: an=2n Берём
ε>0;
хотим 2n>ε n>log2ε N=[log2ε]+1 Правило
формирования
обратного
утверждения:
нужно поменять
местами значки
и ,
а знак неравенства
на дополнительный. Пример: Утверждение
lim an=a<
aR
ε>0
NN:n>N
an-a<ε n Обратное
утверждение
aR
ε>0
NN:
n>N
an-a<ε Всякая
бесконечно
большая не
ограниченная.
Обратное утверждение
неверно. bn{2;0;2n;0;23;0….} Теорема
(об
ограниченной
сходящейся
последовательности) Пусть
lim
an=a<
an
- ограниченная n+ Доказательство: Дано: ε>0N:n>N
an-a<ε Раз
ε>0
возьмем
ε=1
N:n>N
an-a<1 a-1 Этому
неравенству
может быть не
удовлетворять
только первые
N
члены последовательности. N1=max{a1;a2;…an;1+a;a-1} anc,
n>N Теорема
(о
единстве предела
сходящейся
последовательности). Если
lim
an=a
<,
то а- единственное. n+ Доказательство:(от
противного) Предположим,
что
b: lim an=b
и ba
ε=b-a/2>0
для определенности
пусть b>a
N1:n>N1
an-a<ε
n+ N2:n>N2
an-b<ε
N=max{N1;N2},
тогда оба неравенства
выполняются
одновременно
-(b-a)/2 -(b-a)/2 an-a<(b-a)/2 - b-a 0<0 –
противоречие
предположение,
что b>a
неверно. Аналогично
доказывается,
что b
Связь
между бесконечно
большими и
бесконечно
малыми величинами. Теорема: 1)an-
бесконечно
большая
1/an
– бесконечно
малая 2)т
– бесконечно
малая, n0
(n>N0)
1/n
– бесконечно
большая Доказательство: 1)an-
бесконечно
большая
lim
an=
для достаточно
больших номеров
n
an0.
Зададим любое
сколько
n+ угодно
малое ε>0,
положим ε=1/ε>0 Для
ε
N1:n>N1
an>ε,
то есть an>1/ε
N=max{N1;N0} Тогда
n>N
1/an<ε,
то есть lim
1/an=0,
то есть 1/an
– бесконечно
малое
n+ 2)n
– бесконечно
малое
lim
n=0
n+ Дано:
n0,
n>N0
зададим ε>0
положим ε=1/ε>0 N1:n>N1
n<ε=1/ε N=max{N0;N1}:
n>N
1/n=,
то есть 1/n
– бесконечно
большая. Основные
теоремы о
существование
предела последовательности. Теорема
Вейрштрасса: Пусть
an-
ограниченная
и моннатонна.
Тогда
lim
an=а<
n+ Лемма.
Среднее арифметическое
чисел больше
среднего
геометрического.
Равенство
достигается
только если
все числа равны. Л
По всем
вопросам и по
дальнейшему
пополнению
лекций обращаться
на ящик van_mo_mail@mtu-net.ru
или на сотовый: 8-901-7271056 спросить
Ваню Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 25 сентября
2000 г. Тема:
Бесконечно
большие последовательности Теорема:
lim(1-1/n)n=1/e
e=2,7183 n+ 0an=1-1/n1
nN,
то есть an=(1-1/n)n-
ограниченна. n+1an=n+1(1-1/n)n1=n+1(1-1/n)(1-1/n)…(1-1/n)1<[1+(1-1/n)+…+(1-1/n)]/n+1=(n+1-n1/n)/n+1=n/n+1=1-1/n+1 n+1(1-1/n)n<1-1/n+1 (1-1/n)n<(1-1/n+1)n+1 an (1-1/n)n
– имеет конечный
предел lim(1-1/n)n=1/e
n+ lim(1+1/n)n=e
n+ lim1/(1+1/n)n=(n/n+1)n=[1-1/(n+1)]n+1/
[1-1/(n+1)]=(1/e)/1=1/e n+ lim[1/(1+1/n)n]=1/e n+ lim(1+1/n)n=e n+ Пусть
дана an
зададим произвольный
набор натуральных
чисел таких,
что n1 an1,an2,…,ank,… Полученная
последовательность
называется
под последовательностью
и сходной
последовательности. an=(-1)n {an}={-1;1;-1;1….} n1=2;n2=4,….,nk=2k {ank}={1,1,1,1…} Пусть
последовательность
an
сходится, тогда
последовательности lim
an=a
{ank}
– гас
и
lim n+ lim
ank=0 n+ Доказательство
так как
an
– сходиться,
то ε>0
N:
n>N
an-a<ε ank;
nk>N
то есть
ank-a<ε an=(-1)n
– не имеет предела {a2n}={1,…,1,…,} {a2n-1}={-1,….,-1,…} имели
бы тот же самый
предел. Предел
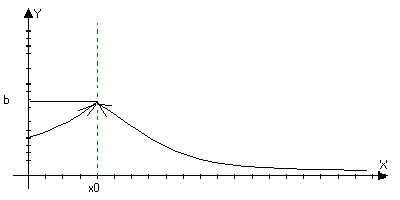
функции. Пусть
y=f(x)
определена
в O(x0).
Мы говорим, что
функция f(x)
имеет предел
в при хх0
если ε>0
>0 x:0<x-x0<
f(x)-b<ε lim f(x)=b xx Через
окрестности
это определение
записывается
следующим
образом ε>0
>0
x0(x0)f(x)0ε(b) Если
lim
f(x)=0,
то f(x)
наз бесконечно
малой при xx0. xx Замечание.
Необходимо
указать в каком
именно процессе
f(x)
бесконечно
малое. Надо
указать к какому
числу
а. f(x)=x-1 1.x1
lim(x-1)=0,
то есть y=x-1
бесконечно
малое при x1 x1 2 x1 Пример f(x)=2x+1
x1 Докажем
lim(2x+1)=3 x1
ε>0
>0
x:0<x-1<
(2x+1)-3<ε (2x+1)-3<ε |x-1<ε/2 x1 Положим
=ε/2 Теорема
о
бесконечно
малом 1)(x);(x)
– бесконечно
малое xx0
(x)+(x)
– бесконечно
малое при xx0 2)(x);(x)
– бесконечно
малое при xx0 3)Если
f(x)
– ограниченна
в O(x0)
и (x)
– бесконечно
малое при xx0,
то f(x);(x)
– бесконечно
малое при xx0 Доказательство
(3) Так
как f(x)
– ограниченна
в O(x0),
то
С>0: xO(x0)|f(x)C; Так
как (x)
– бесконечно
малое при хх0,
то ε>0
>0
x:
0<x-x0<
(x)<ε
ε1>0 Положим
ε=ε1/c >0
x:
0<x-x0|<
f(x)(x)=f(x)a(x)
xx Лекция
№6 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 26 сентября
2000 г. Тема:
Замечательные
пределы f(x)>g(x)
в O(x0)
и
lim
(f(x))=b
и
lim
(g(x))=c.
Тогда bc
xx
xx
Доказательство: Рассмотрим
функцию (x)=f(x)-g(x)>0
в O(x0)
lim
((x))=
lim
(f(x))
- lim
(g(x))=
b-c
и в силу предыдущей
xx
xx
xx теоремы
b-c0,
то есть b0
что и требовалось
доказать. Теорема f(x)(x)g(x)
xO(x0)
и
lim
(f(x))=b
и
lim
(g
(x))=b.
lim (
(x))=b
xx
xx
xx Доказательство: f(x)=b+(x) g(x)=b+(x) где
(x)
и (x)
– бесконечно
малые при хх0 b+(x)(x)b+(x) Так
как (х)
и (х)
– бесконечно
малые то ε>0
1>0:
xO1(x0)
(x)<ε
2>0:
xO2(x0)
(x)<ε Положим
=min{1;2} Т
(x)<ε -ε<(x)<ε -ε<(x)<ε b-ε -ε<(x)-b<ε (x)-b<ε
xO(x0) ε>0
=min{1;2}
(x)-b<ε
xO(x0)
то
есть
lim (
(x))=b
xx Терема
lim
(sin(x)/x)=1
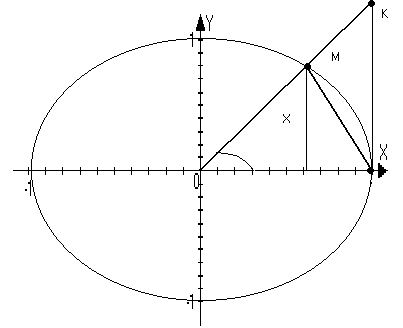
x0 Д S∆OMN=1/2
sin(x) SсекOMN=1/2(x) S∆OKN=1/2
tg(x) S∆OMN 1/2sin(x)<1/2(x) sin(x) 1 lim (1-cos(1/n))=0 n+ lim
(1-cos(x))=0
lim (cos(x))=1 x0
x0 lim (x/sin(x))=0 x0 x>0 lim (x/sin(x))=1 x0 lim(1/(x/sin(x)))=
lim(sin(x)/x)=1
что и требовалось
доказать x0
x0 Определение
бесконечного
предела и пределов
при х+. lim
(f (x))=+
ε>0
>0:
xO(x0)f(x)Oε(+) xx (x):
0<x-x0< ε lim (f
(x))=-
ε>0
>0:
xO(x0)f(x)Oε(-) xx (x):
0<x-x0< lim (f
(x))=
ε>0
>0:
xO(x0)f(x)Oε() xx f(x)>ε lim (f
(x))=b
ε>0
∆>0:
xO∆(+)f(x)Oε(b) x+ x:
x>∆
f(x)-b
<ε lim (f
(x))=b
ε>0
∆>0:
xO∆(-)f(x)Oε(b) x- x:
x<-∆
f(x)-b
<ε О f(x)
определена
в O+(x0) lim (f
(x))=b
ε>0
>0:
xO+(x0)f(x)Oε(b)
x0 xx+0 f(x)
определена
в O-(x0) lim (f
(x))=b
ε>0
>0:
xO-(x0)f(x)Oε(b)
x0- xx-0 Теорема
Пусть f(x)
определена
в O(x0)
Для того чтобы
существо- вал
предел
lim(f(x))=b
lim(f(x))=lim(f(x))=b xx
xx+0
xx-0 Пусть
lim(f(x))=b,
то есть ε>0
>0:
xO(x0)f(x)Oε(b)
f(x)O(b)
для
xO+(x0)
и для
xO- xx
xO-(x0)
lim(f(x));lim(f(x))=b
что и требовалось
доказать.
xx+0
xx-0 Второй
замечательный
предел. Теорема
lim(1+1/x)x=e x+ Доказательство:
Пусть n
– целая часть
х – n=[x]
nx [1+1/(n+1)]n(1+1/x)x(1+1/n)n+1 Если
x+,
то n+ [1+1/(n+1)]n+11/[1+1/(n+1)](1+1/x)x(1+1/n)n(1+1/n)
lim(1+1/x)x=e
x+ Лекция
№7 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 3 октября
2000 г. Тема:
Сравнение
бесконечно
больших и бесконечно
малых. Определение. Пусть
(x)
и (x)
– бесконечно
малые при хх0
() (x)
~ (x)
при хх0
()
если lim
(x)/(x)=1
xx0
()
(x)
и (x)
одинакового
порядка при
хх0
()
если lim
(x)/(x)=с0
xx0
()
(x)
бесконечно
малое более
высокого порядка
малости чем
(x)
при хх0
()
если lim
(x)/(x)=0
xx0
()
Определение. Пусть
f(x)
и g(x)
– бесконечно
большое при
хх0
() 1)
f(x)
~ g(x)
при хх0
()
если lim
f(x)/g(x)=1
xx0
()
2)f
(x)
и g
(x)
бесконечно
большие одинакового
порядка роста,
если при хх0
()
если limf(x)/g(x)=с
xx0
()
< В
частности, если
с=1, то они эквивалентны f
(x)
бесконечно
большое более
низкого порядка
роста чем g
(x)
или иначе g(x)
бесконечно
большое более
высокого порядка
роста чем g(x)
при хх0
()
если lim
f
(x)/g
(x)=0
xx0
()
Примеры: s x
при хх0
– бесконечно
малое Сравним
их lim
sin(x)/x=1
sin(x)~x
x0 при
х0 1n(1+x)
– бесконечно
малое х
при х0
– бесконечно
малое Сравним
их lim
ln(1+x)/x=
lim
ln(1+x)1/x
=1
x0
x0 ln(1+x)
~ x,
при х0 x2
– бесконечно
большие 2х2+1,
при х+
– бесконечно
большие Сравним
lim
x2/(2x2+1)
= lim
x2/x2(2+1/x2)=1/2 x+ x+ то есть
функция является
бесконечно
большой и одинакового
порядка. Замечание:
если одну из функций
одинакового
порядка роста
домножить на
одинаковую
const,
то они станут
эквивалентны.
Определение: пусть
(х)=о(х)
– бесконечно
малое при хх0().
То мы говорим,
что (х)
и (х)
при хх0
(),
если (х)=(х)(х),
бесконечно
малое при хх0
().
Другими словами
- (х)
– бесконечно
малое более
высокого порядка,
чем (х)
така как (х)/(х)=(х)
– бесконечно
малое, то есть
lim
(x)/(x)=0
x0
() пусть
f(х)=оg(х)
– бесконечно
большое при
хх0().
То мы говорим,
что f(х)
и g
(х) при хх0
(),
если f
(х)=(х)g
(х). Другими словами
- f
(х) – бесконечно
большое более
низкого порядка,
чем g(х)
так как f(х)/g
(х)=(х)
– бесконечно
малое, то есть
lim
f
(x)/g
(x)=0
x0
() Шкала
бесконечности. Степенные
бесконечности. xn=o(xm),
0 Докажем: xn=xm(xn/xm)=xm(1/x(m-n))=xm(x)
m-n>0
xm(x)o(xm) ах=о(bх),
1 Докажам ax=ax(bx/bx)=ax(a/b)x=bx(xo(bx)
(0
l ln(x) lim
ln(x)/x=lim
[(ln(x)/(x/2x/2))((/2)/(/2))]= x0
x0 lim
[(ln(x)/x/2)(2/(x/2)] x0 Произведение
бесконечно
малых на ограниченную
равно
бесконечно
малой. lim
(ln(x)/x)=0
(lim(x))/x=(x)
ln=x(x)ox, x0 x+ Показательная
и степенная. Xk=o(ax),
k>0,a>1 x+
lim(xk)/(ax)=0
x+ Теорема:
Пусть (x)
~ 1(x)
при xx0
()
(x)
~ 1(x)
при xx0
() Тогда
lim (x)/(x)=lim
1(x)/1(x) xx0
()
xx0
() Доказательство: lim(x)/(x)=lim[(x)1(x)1(x)]/[1(x)1(x)(x)]=lim((x)/(x))lim(1(x)/(x))lim(1(x)/1(x))=lim
1(x)/1(x)
что
x0
x0 x0
x0
x0
x0 и требовалось
доказать. Замечание:
аналогичное
утверждение
справедливо
для двух бесконечно
больших. Пример: lim sin(x)/3x=limx/3x=1/3 x0
x0 Определение:
(главного слагаемого) 1(x)+2(x)+…+n(x),
при xx0
() Главным
слагаемым в
этой сумме
называется
то слагаемое
по сравнению
с которым остальные
слагаемые
являются бесконечно
малыми более
высокого порядка
малости или
бесконечно
большие более
низкого порядка
роста. 1(x)
– главное слагаемое,
если 2(х)=о(1(х)),…,n(x)=o(1(x))
при xx0
() Конечная
сумма бесконечно
малых эквивалентна
своему главному
слагаемому:
1(x)+2(x)+…+n(x)
~ 1(x)
, при xx0
()
если 1(х)
– главное слагаемое. Доказательство: lim
[1(x)+2(x)+…+n(x)]/1(x)=lim[1(x)+1(x)(x)+…+1(x)(x)]/1(x)=lim[1(x)(1+1(x)+…+n(x))]/1(x)=1
xx0
()
xx0
()
xx0
() Пример: lim
(ex+3x100+ln3x)/(2x+1000x3+10000=lim
ex/2x=lim
ex/(ex(x))=+ x+
x+
x+ 2x=o(ex)ex(x) Основные
эквивалентности. ex-1
– бесконечно
малое при х0.
lim
(ex-1)/x=1,
то есть ex-1
~ x
при x0 x0 1-cosx
– бесконечно
малое при х0.
lim
(1-cos
x)/(x2/2)=lim{2sin(2x/2)]/[x2/2]=lim
[2(x/2)2]/[x2/2]=1, то есть
1-cos(x)
~ x2/2
при х0
и (1+x)p-1
~ px
при х0 Лекция
№8 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 10 октября
2000 г. Тема:
«Асимптотические
формулы» Формулы
содержащие
символ о
- называются
асимптотические. 1) lim
[sin(x)/x]=1
(по определению
конечного
предела sin(x)/x=1+(x),
где (х)
– бесконечно
малое при х0
x0 sin(x)=x+(x)x,
где (х)
– бесконечно
малое при х0
sin(x)=x+ox,
при х0;
sin(x)~x,
при х0 2) lim
[ln(1+x)/x]=1
(по определению
конечного
предела ln(1+x)/x=1+(x),
где (х)
– бесконечно
малое при
x0 х0
ln(1+x)=x+(x)x,
где (х)
– бесконечно
малое при х0
ln(1+x)=x+ox,
при х0;
ln(1+x)~x,
при х0 3) lim
[(ex-1)/x]=1
(по определению
конечного
предела (ex-1)/x=1+(x),
где (х)
– бесконечно
малое при х0
x0 (ex-1)=x+(x)x,
где (х)
– бесконечно
малое при х0
(ex-1)=x+ox,
при х0;
(ex-1)~x,
при х0;
ex=1+x+o(x),
при x0
4) lim
[(1-cos(x)/(x2/2)]=1
(по определению
конечного
предела
(1-cos(x)/(x2/2)=1+(x),
где (х)
– бесконечно
x0 малое
при х0
1-cos(x)=(x2/2)+(x)x2/2,
где (х)
– бесконечно
малое при х0
1- cos(x)=(x2/2)+ox2;
при х0;
1- cos(x)~x2/2,
при х0;
cos=1-x2/2+o(x2),
при x0
1) lim
[((1+x)p-1)/px]=1
(по определению
конечного
предела ((1+x)p-1)/px
=1+(x),
где (х)
– бесконечно
x0 малое
при х0
(1+x)p-1=px
+(x)-p,
где (х)
– бесконечно
малое при х0
(1+x)p-1=px+ox,
при х0;
(1+x)p-1~px,
при х0;(1+x)p=1+p(x)+o(x),
при x0 Если
f(x)~g(x), при хх0
(),
то lim[f(x)/g(x)]=1
f(x)/g(x)=1+(x),
где (х)–бесконечно
малое при хх0
() хх0
() f(x)=g(x)+(x)g(x)
f(x)=g(x)+og(x)
при хх0
() Замечание:
не всякие бесконечно
малые, бесконечно
большие можно
сравнить. Пример: (x)=xsin(1/x),
при х0 (х)=ф=х,
при х0 (x)/(x)=sin(1/x) lim[(x)/(x)]=lim[sin(1/x)]
– который в
свою очередь
не существует. x0
x0 Эти бесконечно
малые несравнимы. Для
удобства формул
полагают по
определению,
что о(1)=(х),
при хх0
() а01
n!=123….n
o! Определение:
Пусть y=f(x)
определена
в О(х0)
и
lim
f(x)=f(x0):
y=f(x)
при хх0
называется
непрерывной
в
хх точке
х0 (то
есть
ε>0
>0:
xO(x0)
f(x)Oε(f(x0)) Непосредственно
из определения
предела следуют
следуемые
теоремы о непрерывных
функциях. Теорема:
Пусть f(x),
g(x)
– непрерывны
в точки х0,
тогда f(x)+g(x)
– непрерывна
в точки х0 Доказательство:1)
f(x),
g(x)
определена
в О(х0)
f(x)+g(x)
определена
в О(х0) 2)
lim
(f(x)+g(x))=limf(x)+limg(x)=f(x)+g(x)
что и требовалось
доказать
хх
хх
хх Теорема:
Пусть f(x),
g(x)
– непрерывны
в точки х0,
тогда f(x)g(x)
– непрерывна
в точки х0 Доказательство:1)
f(x),
g(x)
определена
в О(х0)
f(x)g(x)
определена
в О(х0) 2)
lim
(f(x)g(x))=limf(x)limg(x)=f(x)g(x)
что и требовалось
доказать
хх
хх
хх Теорема:
Пусть f(x),
g(x)
– непрерывны
в точки х0,
тогда f(x)/g(x)
– непрерывна
в точки х0 Доказательство:1)
f(x),
g(x)
определена
в О(х0)
f(x)/g(x)
определена
в О(х0) 2)
lim
(f(x)/g(x))=limf(x)/limg(x)=f(x)/g(x)
что и требовалось
доказать
хх
хх
хх Теорема(об
ограниченности
непрерывной
функции в окрестности
точки).
Пусть y=f(x)
непрерывна
в точки х0,
тогда она ограниченна
в некоторой
окрестность
этой точки. Доказательство:
limf(x)=f(x0),
то есть
ε>0
>0
x:
x-x0<
f(x)-f(x0)<ε
. Предполагается,
что
выбрано так,
что f(x)
определена
в соответствующих
точках. О(х0)О(х0).
Так как это
справедливо
для любого ε>0,
то возьмем ε=1
>0
-1 xO(x0)O(x0) Теорема:(о
непрерывности
сложной функции)
Пусть y=f(x)
непрерывна
в точки х0,
а z=g(y)
непрерывна
в точки y0=f(x0),
тогда сложная
функция имеет
вид z=g(f(x0))
– непрерывна
в точки х0. Доказательство:
Зададим
ε>0
в силу непрерывности
z=g(y)
в точки у0
б>0x:
y-y0|<б
g(y)-g(x0)<ε По
найденному
б>0 в силу непрерывности
функции f(x)
в точки х0
>0
x:
x-x0<
f(x)-f(x0)<б ε>0
>0
x:x-x0<
y-y0<б
g(y)-g(y0)<ε
g(f(x))-g(f(x0))
то есть lim
g(f(x))=g(f(x0))
xx Замечание:
можно переходить
к пределу под
знаком непрерывной
функции limf(x)=limg(y)
limf(x)=f(x0)=y0
xx
xx
xx Непрерывность
некоторых
функций. 1) y=c
(постоянная)
непрерывна
в х0
R
lim
c=c.
Зададим ε>0
рассмотрим
разность
f(x)-f(x0)=c-c=0<ε
xx x:
x-x0<
(>0)! 2) y=x
непрерывна
в
x0R,
то есть lim
x=x0.
Зададим
ε>0
рассмотрим
разность
f(x)-f(x0)=x-x0<ε
xx x:
x-x0<
(>0)!
=ε! Следствие. Многочлен
p(x)=anxn+
an-1xn-1+…+a1x+a0 (an,an-1…a1,a0
– зададим
число) n=0,1,2,3….
непрерывен
в любой точки
х0 оси
как сумма
произведения
непрерывной
функции. Рациональная
функция: R(x)=p(x)/q(x).
Частная двух
многочленов
непрерывна
в любой точки
х0 в
которой q(x)0 Лекция
№9 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 11 октября
2000 г. Тема:
«Точки разрыва» 1)
Доказать, что
lim
[((1+x)p-1)/px]=1
x0
lim
[((1+x)p-1)/px]=
x0
y0
=lim ([ln(1+x)]/x)([(1+x)p-1]/[pln(1+x)]=lim
([ln(1+x)]/x)
x0
(1+x)p=y+1
x0
x0 p[ln(1+x)]=ln(y+1)
lim([(1+x)p-1]/[pln(1+x)]=lim
y/[ln(y+1)]=1
что и требовалось
доказать
(1+x)p-1~px
при x0 x0
y0
(1+x)p=1+px+o(x)
при х0 2)
Доказать, что
lim
(ex-1)/x=1
x0
lim
(ex-1)/x=
x0
y0
=lim
y/[ln(y+1)]=1
что и требовалось
доказать x0
ex=y+1
y0
x=ln(y+1)
ex-1~x
при x0 ex=1+x+o(x)
при х0 Определение:
Пусть y=f(x)
определена
в О(х0),
а в самой точке
х0 может
быть как и
определена,
так и неопределенна. 1) Точка
х0
называется
точкой разрыва
1ого
рода функции,
если
а)
Существует
lim
f(x)’=lim
f(x)’’
, но либо функция
неопределенна
в точки х0
либо f(x0)b.
Тогда точка
х0
xx+0
xx-0 точка
устранимого
разрыва. Y=(x-1)/(x-1)=
Не ,
x=1 б)
f(x)=cb
Можно
доопределить
или переопределить
в точке х0,
так что она
станет непрерывной. lim
f(x)=b; lim f(x)=c, но
bc xx+0
xx-0 Может
быть и определена
f(x0)=b Или
f(x0)=d 2 y=sin(1/x) Основные
теоремы о непрерывных
функциях. Теорема:
Все основные
элементы функции
непрерывны
в любой точки
своей области
определения. Определение:
(функции непрерывной
на отрезке) y=f(x)
– называется
непрерывной
на отрезке
[a,b],
если она непрерывна
в любой точке
х(a,b).
В точке х=а функция
непрерывна
справа, то есть
lim
f(x)=f(a),
а в точке х=b
функция непрерывна
слева lim
f(x)=f(b).
xx+0
xx-0 Функция
непрерывна
на множестве
D
если она непрерывна
в этой точке. Теорема:
(о сохранение
знака непрерывной
функции) Пусть
y=f(x)
непрерывна
в точке х0
и f(x0)>0
(f(x0)<0),
тогда f(x)>0
f(x)<0
непрерывна
в некоторой
точки О(х0) Доказательство:
lim
f(x)=f(x0)
ε>0
>0
x:
x-x0<
f(x)-f(x0)|<ε.
xx Пусть
f(x0)>0,
выберем ε=f(x0)
f(x)-f(x0) -f(x0) Теорема
Коши:
( о нуле непрерывной
функции) Пусть
f(x)
непрерывна
на [a,b]
и на концах его
принимает
значение разных
знаков f(a)
f(b)
<0, тогда
x0(a,b):
f(x0)=0 Доказательство: f(b)>0
f(a)<0 Разделим
отрезок [a,b]
пополам. Если
в середине
отрезка f(x)=0,
то всё доказано,
если нет, то
выберем ту
половину отрезка,
на концах которой
функция принимает
значение разных
знаков. Выбранной
отрезок поделим
пополам. Если
в середине
нового отрезка
f(x)=0,
то всё доказано,
если нет, то
выберем ту
половину от
той половины,
на концах которой
функция принимает
значение разных
знаков и т.д. [a,b][a1,b1][a2,b2] Последовательность
левых концов
удовлетворяет
отношению
a
bb1b2…bn…>a
{
x+
[anbn]=(b-a)/2n
0
при
n {bn}-ограниченная
не возрастающая
lim
bn= f(b)>0
f(bn)>0
n
x+ В
силу непрерывности
функции lim
f(an)=f
(lim
bn)=f()0
lim
(bn-an)=-=
lim
(b-a)/2n=0= f()0
f()=0
x0= f()=f()0 Условие
непрерывности
функции нельзя
отбросить:
f(b)>0;
f(a)<0 Теоремы
Вейштрасса. 1) Теорема:
Пусть функция
y=f(x)
непрерывна
на отрезке
[a,b].
Тогда она ограниченна
на нём.
Неограниченна
сверху
неограниченна б)
Нельзя заменить
отрезок на
интервал или
полуинтервал.
Непрерывна
на (0;1] 2) Теорема:
Пусть функция
y=f(x)
непрерывна
на отрезке
[a,b].
Среди её значений
есть наибольшее
и наименьшее. Замечание:
а) Множество
[0;1] наибольшее
значение 1М
наименьшее
значение 0
М нет
наименьшего
в) Множество
[0;1)=M
нет наибольшего
наименьшее
значение 0
М г)
Множество
(0;1)=М нет ни того
не другого. Условие
отрезка нельзя
заменить на
интервал или
полуинтервал. x(0;1]
непрерывна
на (0;1] нет наибольшего
значения Л
По всем
вопросам и по
дальнейшему
пополнению
лекций обращаться
на ящик van_mo_mail@mtu-net.ru
или на сотовый: 8-901-7271056 спросить
Ваню Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 17 октября
2000 г. Тема:
«Коши, производные» Теорема:
(Коши о промежуточных
значениях) Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b]
и на концах
принимает
значение разные
значения. f(a)=A
f(b)=B
AB.
Тогда С
лежащею между
А и В,
х0(a,b):
f(x0)=C.
Другими словами
нет точек которые
не являются
значением
отрезка. Д Эта
функция непрерывна
на отрезке
[a,b] (a)=f(a)-c=A-C<0
по теореме
Коши №11
x0(a,b):(x0),
то естьf(x0)-C=0
f(x0)=c (b)=f(b)-c=B-C>0 Замечание:
Условие непрерывности
нельзя отбросить [c,d][A,B] [c,d)E(f) Теорема:
(о существование
и непрерывности
обратной функции)
«Без доказательства» П П ∆ Х Х Разность
значений функций. ∆y=∆f(x0)=f(x)-f(x0)=f(x0+∆x)-f(x0)
– называется
приращением
функции в точки
х0. Через
эти обозначения
можно определить
непрерывность
функций: f(x)
– неопределенна
в точки х0,
если она определена
в O(x0)
и lim
∆y=0
∆
x0 lim[f(x)-f(x0)]=lim[f(x)-f(x0)]0
lim[f(x)]=f(x0)] x-x0
xx
xx Определение
непрерывной
функции в точки
приращения:
f(x)
– неопределенна
в точки х0,
если она определена
в O(x0)
и lim
∆y=0
∆
x0 Определение:
(производной
функции) Пусть
y=f(x)
определена
в О(х0)
и
lim[∆y/∆x]<,
тогда этот
предел называется
производной
функции f(x)
в
∆х0 точке
х0. f’(x0),
y’(x0),
dy/dx,
df(x0)/dx=df(x)/d(x) То
есть f’(x0)
по определению
=
lim[f(x)-f(x0)]/(x-x0)lim∆y/∆xdy/dx
∆x0
∆x0 Физический
смысл производной. Рассмотрим
прямолинейное
движение материальной
точки: x x0
x t0
t s(t)x(t);
∆s=∆x(t)=x(t)-x(t0) ∆ тогда
vcpvмнг lim
∆s/∆t=lim[x(t)-x(t0)]/[t-t0]=vмнг ∆t0
tt Геометрический
смысл производной. ∆х0 ∆y=y(x0+∆x)-y(x0) y’(x0)=tgкас
где кас
– угол наклона
в точке (х0;y(x0))
к оси Основные
теоремы о
производной. Теорема:
Пусть
f’(x)
и g’(x),
тогда
[f(x)+g(x)]’=
f’(x)+g’(x) Доказательство:
следует непосредственно
из определения
производной
и свойств предела
суммы. Теорема:
(связи между
непрерывностью
функции и
существование
производной) Пусть
f’(x)
функция f(x)
– непрерывна. Доказательство:
Пусть f(x)
определена
в О(х0)
и lim[f(x)-f(x0)]/(x-x0)=f’(x0)<
[f(x)-f(x0)]/(x-x0)=f(x0)+(x-x0)2
∆xx
[f(x)-f(x0)]=f’(x0)(x-x0)+(x-x0)(x-x0)
при хх0 lin[f(x)-f(x0)]=limf’(x0)(x-x0)+lim(x-x0)(x-x0)=0+0=0linf(x)=f(x0)
то есть f(x)
непрерывна
в точки х0 xx
xx
xx
xx Замечание:
обратное
утверждение
неверно, из-за
непрерывности
функции в точке
х0 не
следует существование
функции в этой
точки. y Н limx,
x0 x+0 lim|x|= =0 lim(-x),
x<0 x-0 y(0)=0 limy(x)=limy(x)=y(0)=0
limy(x)=y(0)=0
функция
непрерывна x+0 x-0
x0 lim∆y/∆x-не
существует,
действительно
х+0y(x)=x x0 lim[y(x)-y(0)]/x=lim(x-0)/x=1 x+0 x+0 x-0y(x)=-x lim[y(0)-y(x)]/x=lim(0-x)/x=-1
то есть lim∆y/∆x
– не существует x-0 x-0
х0 Теорема:
Пусть
u’(x)
и v’(x),
тогда (uv)’=u’v+v’u Доказательство:
Зададим приращение
∆х
в точки х.
Рассмотрим:
lim[∆(uv)]/∆x=
∆x0
lim[1/∆x][u(x+∆x)v(x+∆x)-u(x)v(x)]=lim[1/∆x][
u(x+∆x)v(x+∆x)-u(x)v(x+∆x)+u(x)v(x+∆x)-u(x)v(x)= ∆x0
∆x0 lim[(v(x+∆x))(u(x+∆x)-u(x))]/∆x+lim[(u(x))(v(x+∆x)-v(x))]/∆x=v(x)u’(x)+u(x)v’(x) ∆x0 ∆x0 Теорема:
(о произведение
частного) Пусть
u’(x)
и v’(x),
v’(x)0
в О(х), тогда
(u/v)’=[u’v-v’u]/v2 Доказательство:
(u/v)’=[u(1/v)]’=[u’(1/v)]+[(1/v)’u].
Функция u(x)
и v(x)
–непрерывны
в точки х0. lim[∆(1/v)/∆x]=lim[1/∆x][1/(v(x+∆x))-1/v(x)]=lim[[v(x)-v(x-∆x)]/[∆xv(x)x(x+∆x)]]-[v’(x)/v2(x)] ∆x0
∆x0
∆x0 (u/v)’=u’(1/v)-(uv)’/v2=[u’v-uv’]/v2
что и требовалось
доказать y=sinx (sinx)’=lim[sin(x+∆x)-sinx]/∆x=lim[2sin(∆x/2)cos((2x+∆x)/2)]/∆x=lim[2(∆x/2)cos(x+(∆x/2))]/∆x=cosx ∆x0 ∆x0 (sinx)’=cosx г y=cos(x) (cos(x))’=lim[cos(x+∆x)-cos(x)]/∆x=lim[-2sin(∆x/2)sin((2x+∆x)/2)]/∆x=lim[-2(∆x/2)sin(x+(∆x/2))]/∆x=-sinx
∆x0
∆x0
∆x0 (cos(x))’=-sinx г y=tg(x) (tg(x))’=(sin(x)/cos(x))’=[(sin(x))’cos(x)-(cos(x))’sin(x)]/cos2x=[cos2x+sin2x]/cos2x=1/cos2x (tg(x))’=1/cos2x г Лекция
№11 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 24 октября
2000 г. Тема:
«Производные,
дифференциал» y=xn y’(x)=lim[(x+∆x)n-xn]/∆x=1=lim[xn(1+(∆x/x))-1]/∆x=/∆x/x0,∆x0\=lim[xn(∆x/x)n]/∆x=nxn-1 ∆x0
∆x0
∆x0 ( Рассмотрим
когда х=0
y’(0)=lim(∆x)n/∆x=lim(∆x)n-1=/n>1\=0
если
n=1/0,n>1;1,n=1\
∆x0 ∆x0 Дифференциал
функции. Определение:
Пусть y=f(x)
определена
в некоторой
О(х0)
– она называется
дифференцируемой
в точке х0,
если её приращение
в этой точки
представимо
в виде: ∆y=∆f(x0)=A∆x+(∆x)∆x)1 (0)=0
A=const Определение:
линейная
∆х
часть приращение
дифференцируемой
функции называется
дифференциалом
функции в точке
х0: dy=df(x0)A∆x Теорема:
Если функция
дифференцируема
в точке х0
то A=f’(x0),
то она имеет
производную
в этой точке,
то A=f’(x0);
наоборот если
функция имеет
производную
в этой точке,
то она дифференцируема
в этой точке
– называется
дифференциалом. Доказательство:
Пусть y=f(x)
дифференцируема
в точке х0,
то есть в некоторой
О(х0)
справедливо
равенство
∆f(x0)=A∆x+(∆x)∆x1;
(0)=0.
Поделим обе
части этого
равенства на
∆х
и приведём к
пределу при
∆х0: lim(∆f(x0))/∆x=lim(A+(x))=A.
Этот предел
существует,
меньше ,
тогда по определению
этот предел
есть ∆x0
∆x0 производная. Доказательство:
(в обратную
сторону) Пусть
в точке х0
f’(x0)(<)
– это означает,
что f(x)
определена
в некоторой
О(х0)
и
lim(∆f(x0))/∆x=f’(x0)
по определению
предела следует,
что в некоторой
О(х0)
∆x0
(∆f(x0))/∆x=(∆х)+f’(x0)
при ∆х0
∆f(x0)=f’(x0)+(∆x)∆x,
так как lim(∆x)=0,
то в точке х0
y
(∆x)
может
∆х0 быть лишь
устранимым
разрывом . Устраним
его, определим
и доопределим: (0)=0,
тогда ∆f(x0)=f’(x0)∆x+(∆x)∆x
A=f’(x0)
из установленного
соответствия
получим выражения
для дифференцируемой
функции df(x0)=f’(x0)∆x Следствие:
по определению
полагают дифференциал
независимой
переменной
равной её приращению dx=∆x
(х - независимая
переменная) df(x)=f’(x)dx f(x)=x
– вычислим
дифференциал
f’(x)=1 df(x)=dx=f(x)∆x=1∆x Замечание:
дифференциал
функции зависит
от двух переменных
– от самой точки
х и от ей приращения y=cosx
x0=/2
∆x=/180 y’=-sinx
y’(/2)=-sin(/2)=-1 dy(/2)=-1∆x=-1/180=-/180 Теорема:
Пусть y=f(x)
дифференцируема
в точке х0,
а z=g(y)
дифференцируема
в точке у0=f(x0),
тогда сложная
функция z=g(f(x)
- дифференцируема
в точке х0
и z’(x0)=g’(f)f’(x) Доказательство:
(1) ∆z=g’(y0)∆y+(∆y)∆y (2)
∆y=f(x0)∆x+(∆x)∆x
(0)=0
(0)=0 Подставим
в первое равенство
второе: ∆z=g’(y0)f(x0)∆x+g’(y0)(∆x)∆x+[f’(x0)+(∆x)∆x][f’(x0)∆x+(∆x0∆x] lim∆z/∆x=limg’(x0)f’(x0)+limg’(x0)(∆x)+lim
(f’(x0)+(∆x)∆x)[f’(x0)+∆x]
z’(x0)=g’(y0)f’(x0)
что и требовалось ∆x0
∆x0 ∆x0
∆x0 доказать.
Теорема:
Пусть
функция y=f(x)
возрастает
(убывает) в О(х0)
и дифференцируема
в точке х0.
Тогда обратная
у ней функция
x=g(y)
дифференцируема
в точки y0=f(x0),
причём g’(y0)=1/f(x0) Д ∆у0 монотонности
функции и обратной
= к
ней следует
∆х0
∆y0
∆y0
∆у0,
то ∆х0
и наоборот
∆x0
∆x0 y=ax y’(x)=lim[ax+∆x-ax]/∆x=lim[ax(a∆x-1)]/∆x=lim[ax(e∆xlna-1)]/∆x=/∆x0,
то ∆xlna0\=lim[ax∆xlna]/∆x=axlna ∆x0
∆x0
∆x0
∆x0 y y=lnx y’=lim[ln(x+∆x)-lnx]/∆x=lim[ln((x+∆x)/x)]/∆x=lim[ln(1+∆x/x)]/∆x=/∆x/x0
при
∆x0\=lim(∆x/x)/∆x=1/x ∆x0 ∆x0
∆x0
∆x0 ( y y=arcsinx
обратная функция
x=siny
x[-1;1]
y[-/2;/2] (arcsinx)’x=x0=1/(siny)’y0=y=1/cosyy0=y= y[-/2;/2],
cosy0
cosy>0,
если y[-/2;/2]
то есть x1 =1/(1-sin2y)y=y0=1/(1-(sinarccosx)2)x=x0=1/(1-x02) (arcsinx)’=1/(1-x2) y=acrcosx,
обратная
x=cosy x[-1;1]
y[0;] (arcosx)’=1/(cosy)’y=y0=1/-sinyy=y0=-1/(1-cos2y)y=y0=-1/(1-(cosarccosy)2)x=x0=-1/(1-x02) (arcosx)’=-1/(1-x2) y=arctgx
обратная функция
x=tgy
y(-/2;/2) (arctgy)’=1/(tgy)’=cos2y=
/ 1+tg2y=1/cos2y
\ =1/(1+x2) (arctgy)’=1/(1+x2) ( Гиперболические
функции. chx=(ex+e-x)/2 shx=(ex-e-x)/2 chx2-shx2=1 chx2+shx2=ch2x ch(-x)=chx sh(-x)=-shx
chx shx c t (chx)’=sh(x) (shx)’=ch(x) (thx)=1 Лекция
№12 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 25 октября
2000 г. Тема:
«Линеаризация» Геометрический
смысл дифференциала
функции и уравнение
касательной. f’(x0)=tg уравнение
прямой : Y=kx+b y0=f(x0)=kx0+b k-угловой
коэффициент
прямой k=tg=f’(x0) Y=f(x0)+f(x0)-f’(x0)x0 b=f(x0)-kx0 Y=f(x)+f’(x0)(x-x0) ∆f(x0)=f’(x0)∆x+(∆x)∆x
при ∆х0
в некоторой O(x0)
f(x0)=f’(x0)+f’(x0)∆x+(∆x)∆x
при ∆х0 Y1=f(x0)+f’(x0)(x-x0)a=f’(x0)+f’(x0)∆x df(x0)=f’(x0)∆x Геометрический
смысл дифференциала: df(x0)
– это приращение
ординаты при
движение по
касательной
проведённой
к графику функции
в точки (х0;f(x0). Замечание:
Часто
говорят о касательной
проведённой
в точке х0. Линеаризация
функции. Определение:
Замена
функции в окрестности
данной точки
линейной функции
называется
линеаризацией
функции, точнее
в О(х0)
заменяется
отрезком касательной
в точке х0. ( Если
в равенстве
(*) отбросить
правую часть,
то мы получим
приближённое
равенство: f(x)f(x0)+f’(x0)(x-x0),
xx0
Y=f(x0)+f’(x0)(x-x0)
– уравнение
касательной
в точке х0 Формула
получена из
определения
дифференциала
в точке х0
функции f(x)=f(x0)+f(x0)∆x+o∆x
при ∆х0
– называется
критерием
дифференциальности
функции в точке
х0. Приближенные
вычисления
и оценка погрешности
вычисления.
Можно
приближенно
вычислять
значение функции
в точках близких
к заданной
точки. 38,001=1 х0=8 х=8,000 f(x)=3x f(x0)=f(8)=2 Проведём
линеаризацию
выбранного
корня. f’(x)х=8=(3x)’x=8=1/3x-2/3x=8=1/12 3x2+1/12(x-8),
x8 3x2+0,001/12 Yкас=2+1/12(x-8) 3x=2+1/12(x-8)+o(x-8)
при х8 Погрешности
вычисления. f(x)-f(x0)=df(x0)+o(x-x0)
при хх0 ∆f(x0)df(x0),
xx0 ∆1=∆f(x0)df(x0) f(x)=10x
в точке х0=4,
если ∆х=0,001
х=40,001 104∆=10423 f’(x)=10xln10;
f’(4)=104ln10=23000;
ln102,2 ∆230000,001=23 Изучение
поведения
функции при
помощи первой
производной.
Слева
от М0
tg
>0;
Справа от М0
tg
<0 tg
f’(x)>0
слева от М0 tg
f’(x)<0
справа от М0 Теорема:
Пусть y=f(x)
дифференцируема
x(a,b)
и f’(x)>0
(f’(x)<0),
тогда f(x)
возрастает
(убывает) на
(а,b) x1,x2(a,b)
x1 Надо
доказать: f(x1) Применим
теорему Лангранджа
на отрезке
(х1,x2)Теорема. f(x2)-f(x1)=f’(c)(x2-x1)
где c(x1,x2) f(x2)-f(x1)>0
f(x2)>f(x1) Экстремумы
функции. М f(x) f(x)>f(x1)
b и О2(х1).
Значенгие
функции в точке
М1, М3
и М5 – max;
M2
и М4
– min –
такие точки
назавыются
точкками
экстремума
или точками
локального
max и min. Определение:
(точки экстремума)
Пусть
функия f(x)
определена
в некоторой
О(х0)
и f(x)>f(x0)
в О(х0)
или f(x) З f(x)f(x1)
в О1(х1) f(x)f(x2)
в О2(х2) говорят,
что точки х1
и х2 точки
не строгого
локального
экстремума. Теорема:
(Ферма) (о необходимости
условия экстремума
дифференцируемой
функции) Пусть
y=f(x)
дифференцируема
в точки х0
и точка х0
– точка экстремума,
тогда f(x0)=0 Доказательсто:
Заметим, что
х0
точка экстремума,
то в её окрестности
f(x)
– f(x0)
сохраняет знак.
Запишем условие
∆f(x0)=f(x)-f(x0)(x-x0)+o(x-x0) f(x)-f(x0)=(x-x0)[f(x0)+(x-x0)]
то при х – достаточно
близких к х0
знак выражения
стоящего в
квадратных
скобках совпадает
со знаком f’(x0)0
(x-x0)
– меняет знак
при переходе
черех точку
х0
f’(x0)=0 Лекция
№13 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 31 октября
2000 г. Тема:
«Экстремумы» Замечание: О y=(x-1)3 y’=3(x-1)2 y’(1)=0 x0=1 xO-(1)f(x)<0 xO+(1)f(x)<0 x=1 –
не точка экстремума.
Теорема
(Ролля): Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b]
и дифференцируема
на (a,b).
Кроме того на
концах интервала
она принемает
равные значения
f(a)=f(b),
тогда
с(a,b):
f(c)=0 Доказательство:
Така как функция
непрерывна
на отрезке
[a,b],
то по второй
теореме Вейштрасса
есть наибольшее
и наименьшее
значение (m,M), если
m=M,
то f(x)const
(x[a,b])
(const)’=0. Пусть
m Замечание:
условие
дифференцируемсти
нельзя отбросить. непрерывна
на отрезке
[a,b] Геометрический
смысл. f’(x)=0,
то касательная
оси х. Теорема
не утверждает,
что это единственная
точка. Теорема
Лангранджа: Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b] и
дифференцируема
на отрезке
(а,b), то
с(a,b):
f(b)-f(a)=f(c)(b-a) Доказательство: F(x)=f(x)+x
где -
пока неизвестное
число. F(x)
– непрерывна
на отрезке
[a,b] как
сумма непрерывной
функции f(x)
– дифференцируема
на отрезке
[a,b] как
сумма дифференцируемой
функции. Выберем
число ,
так чтобы на
отрезке [a,b]
F(x) принимало
равное значение. F(a)=f(a)+a
F(b)=f(b)+b F(a)=F(b)
f(a)-f(b)=(a-b)
=[f(b)-f(a)]/[b-a] F(x)
– удовлетворяет
условию теоремы
Роллера на
отрезке [a,b]
c(a,b):F’(c)=0,
то есть F’(x)=f’(x)+ 0 То есть
на кривой которая
наклонена к оси х
под таким же
углом как и
секущая [f(b)-f(a)]/[b-a]=tg=f(x)
c(a,b) Замечание: Часто
точку с можно
представить
в
нужном
виде: с=х0+∆х 0<(c-x0)/(x-x0)=
<1 c-x0=(x-x0) c=x0+(x-x0)1 f(x)-f(x0)=f’(x0+∆x)(x-x0) 0<<1 ∆f(x0)=f’(x0+∆x)∆x Теорема:
(о необходимых
и достаточных
условиях экстремума
по первой
производной) Пусть
y=f(x)
непрерывна
на отрезке
[a,b] и
дифференцируема
в О(х0).
Если f’(x)
меняет знак
при переходе
через точку
х0, то точка
х0 – точка
экстремума.
Если меняет
знак: с + на – то
это точка максимума с – на + то
это точка минимума
Доказательство:
х1
О-(х0)
на [x1,x0];
c1(x1,x0)
f(x0)-f(x1)=f’(c1)(x0-x1)
f(x0)>f(x1)
x1O-(x0) х2
О+(х0)
на [x0,x2];
c2(x0,x2)
f(x2)-f(x0)=f’(c2)(x2-x0)
f(x2) f(x0)>f(x)
xO(x0)
точка х точка
максимума. Если в
точке х0 существует
производная
то она обязательно
равна 0 в силе
теоремы Ферма.
Но могут быть
точки в которых
f(x) существует,
а f’(x)
не существует. Принцип
решения подобных
задач:
Условие:
найти наибольшее
и наименьшее
значение функции
не отрезке
[a,b]. Ход решения: Находим
точки в которых
производная
либо равна 0
либо не существует
f’(x)=0
или f’(x)
Вычисляем
знак функции
на концах отрезка
и в этих точках
f(a), f(b),
f(x1)….f(xn) Выбираем
наибольшее
и наименьшее
mf(x) Определение:
точки в которых
функция определена,
а производная
либо равняется
нулю, либо не
существует
называют критическими
точками. Производная
функции высшего
порядка. Существует
f’(x)
x(a,b),
тогда эта производная
сама является
функцией х
(х)=f’(x)
и можно ставить
о дифференцируемости
этой функции. Существует
’(x)
x(a,b),
то мы называем
её второй производной
’(x)f’’(x) Лекция
№14 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 8 ноября
2000 г. Тема:
Производная
функции высшего
порядка. f(n)=def=(f(n-1)(x))’ ’’’ –
[dnf(x)]/dxn=(d/dx)([dn-1f(x)]/dxn) Теорема:
(Коши – обобщение
теоремы Лангранджа1) Пусть
функция f(x)
и g(x)
непрерывны
на отрезке
[a,b],
дифференцируема
на интервале
(a,b) и
g’(x)0,
x(a,b),
тогда
с (a,b)
такая, что
[f(b)-f(a)]/[g(b)-g(a)]=f’’(c)/g’(c) Доказательство:
Отметим прежде
всего, что g(b)g(a),
так как по теореме
Лангранджа1
для функции
g(x)
g(b)-g(a)=g’(c1)II
(b-a)III0
(c1(a,b))
Рассмотрим
вспомогательную
функцию
F(x)=f(x)-g(X)
где
-неизвестное
число F(x)
– непрерывна
на отрезке
[a,b] и
дифференцируема
на интервале
(a,b) Потребуем
F(a)=f(b) F(b)=f(b)-g(b) --- F(a)=f(a)-g(a) ___________________ 0=f(b)-f(a)-(g(b)-g(a))
=[f(b)-f(a)]/[g(b)-g(a)].
Получим, что
F(x)
удовлетворяет
условию теоремы
Ролля4
с(a,b):F’(c)=0,
то есть F’(c)=f’(c)-g’(c)
=f’(c)/g’(c)=[f(b)-f(a)]/[g(b)-g(a)],
что и требовалось
доказать. Правила
Лопиталя. Это правило
в случае дифференцируемости
функции позволяет
избавляться
от неопределённостей
типа 0/0 или /
при вычисление
пределов. Теорема:
Пусть функции
f(x) и g(x)
дифференцируемы
в О(х0), g’(x0)0
в О(х0),
f(x0)=g(x0)=0
и
lim
f’(x)/g’(x)=k
(конечный или
бесконечный
предел), тогда
lim
f(x)/g(x)=lim
f’(x)/g’(x)=k xx
xx
xx Доказательство:
lim f(x)/g(x)=lim
[f(x)-f(x0)]/g(x)-g(x0)=lim
f’(c(x))/g’(c(x))=
c=c(x)
лежащая между
х их0 если
xx
xx
xx хх0
то сх0=lim
f’(x)/g’(x)=k
xx Замечание(1):
f(x0)=g(x0)=0
требование
можно заменить
требованием
lim f(x)=0,
lim g(x)=0,
то есть в т х0
f(x) и
xx
xx g(x)
могут иметь
устранимый
разрыв, действительно
достаточно
переопределить
или доопределить
f(x) и g(x)
по непрерывности,
так чтобы
f(x0)=g(x0)=0 Замечание(2):
Если
f’(x0)
и g’(x0),
g’(x0)0,
то утверждение
теоремы будет: lim
f(x)/g(x)=lim
f’(x)/g’(x)=lim
[(x-x0)(f’(x0)+(x-x0))]/
[(x-x0)(g’(x0)+
(x-x0))]=f’(x0)/g’(x0) xx
xx
xx Теорема:
(/)
Пусть функции
f(x) и g(x)
непрерывны
в О(х0),
g'(x)0 и О(х0),
дифференцируемы
в О(х0)
и lim
f(x)=lim
g(x)=;
lim
f’(x)/g’(x)=k.
Тогда lim
f(x)/g(x)=lim
f’(x)/g’(x)=k xx
xx
xx
xx
xx
Без
доказательства! Замечание:
Если функции
f’(x) и
g’(x) сами
удовлетворяют
условия теоремы
то правило
Лопиталя можно
применить
повторно: f(x)=ex
g(x)=xn
x lim ex/xn=
lim ex/1!=
nN
lim ex/xn=
lim ex/nxn-1=
lim ex/[n(n-1)xn-2]=lim
ex/n!=+ x f(x)=lnx x+ g(x)=xn lim lnx/xn=
lim (1/x)/nxn-1=
lim 1/nxn=0 x+
x+
x+
Формулы
Тейлора. Определение:
(многочлена
Тейлора) Пусть
функция y=f(x)
– n – раз
дифференцируема
в точке х0
многочлен
(полином) вида Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)]/n!
называется
многочлен
Тейлора с центром
в точке х0 или
многочленом
по степеням
(х-х0) Свойства
многочлена
Тейлора. Теорема:
(основное свойство
многочлена
Тейлора) Пусть
функция y=f(x)
– n – раз
дифференцируема
в точке х0
f(x)=Tn(x0);
f’(x0)=Tn’(x0),…,f(n)(x0)=Tn(n)(x0) Доказательство;
(подстановкой)
Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)]/n!
, подставим х0
получим Tn(x0)=f(x0).
Продифференцируем
многочлен
Тейлора
Tn’(x)=f’(x0)/1!+[f’’(x0)2(x-x0)]/2!+
[f’’’(x0)3(x-x0)2]/3!+
[fn(x0)n(x-x0)n-1]/n!,
подставим
вместо х х0 Tn(x0)=f(x0) Tn’’(x)=f’’(x0)/1!+[f’’’(x0)32(x-x0)]/3!+…+
[f(n)(x0)n(n-1)(x-x0)n-2]/n! Tn’’(x)=f’’(x0) Формула
Тейлора с остаточным
членом пеано. Теорема:
Пусть функция
y=f(x)
– n – раз
дифференцируема
в точке х0,
тогда в О(х0)
f(x)=Tn(x)+o((x-x0)n),
xx0 f(x)=
f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)n]/n!+0((x-x0)n)(x-x0)1
lim[f(x)-Tn(x)]/(x-x0)n=(0/0)=lim
[f’(x)-Tn’(x)]/n(x-x0)n-1=(0/0)=….=lim
[f(n)(x)-Tn(n)(x)]/n!=0
функция
xx
xx
xx [f(x)-Tn(x)]/(x-x0)n=(х-х0)ii
f(x)-Tn(x)=(x-x0)n(x-x0)=0((x-x0)n)
при хх0
что и требовалось
доказать. Замечание:
в случае если
х0=0 формула
Тейлора называется
Маклорена
f(x)=f(0)+[f’(0)x]/1!+
[f’’(0)x2]/2!+
[fn(0)xn]/n!+0xn
при х0 1
На концах отрезка
[a,b] и на
концах принимает
значение разных
знаков 2
(x-x0)-бесконечно
малое при хх0 1
x0 1
(∆x)
– бесконечно
малое при ∆х0,
а (∆x)∆х
– есть о∆х 1
Y – ордината
касательной a
– x-x0
=∆x 1
∆-погрешность
вычисления. Теорема
–Если f(x)
непрерывна
на [a,b]
дифференцируема
на отрезке
(а,b), то
с(a,b):
f(b)-f(a)=f(c)(b-a) 1
(x-x0)=∆x 1
Теорема – Если
f(x) непрерывна
на [a,b]
дифференцируема
на отрезке
(а,b), то
с(a,b):
f(b)-f(a)=f(c)(b-a) II
– g’(c1)=0
по условия
теоремы III
– (b-a)=0 4
- Теорема
(Ролля): Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b]
и дифференцируема
на (a,b).
Кроме того на
концах интервала
она принемает
равные значения
f(a)=f(b),
тогда
с(a,b):
f(c)=0 1
0((x-x0)n)(x-x0)
– остаточный
член в форме
пеано ii
(х-х0)
– бесконечно
малое при хх0 Л
По всем
вопросам и по
дальнейшему
пополнению
лекций обращаться
на ящик van_mo_mail@mtu-net.ru
или на сотовый: 8-901-7271056 спросить
Ваню Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 14 ноября
2000 г. Тема:
Пять основных
разложений 1)y=ex,
x0=0 y y’(0)=ex|x=0=1 y’’(0)=ex|x=0=1 y(n)(0)=ex|x=0=1 n=1
ex=1+x+o(x),xx0 2) y=sinx, x0=0 y y’(0)=cos|x=0=1 y’’(0)=-sinx|x=0=0 y’’’(0)=-cosx|x=0=-1 y’’’’(0)=sinx|x=0=0 если
n – чётное,
то y(n)(0)=0;
n=2k+1 – нечётное
y(n)(0)=(-1)k 3) y=cosx, x0=0 y y’(0)=-sinx|x=0=0 * y’’(0)=-cosx|x=0=-1 y’’’(0)=sinx|x=0=0 y’’’’(0)=cosx|x=0=1 если
n=2k – чётное,
то y(n)(0)=(-1)k;
n=2k+1 – нечётное
y(n)(0)=0 4) y=ln(1+x), x0=0 y(0)=ln1=0 y’(0)=1/(1+x)|x=0=1 y’’(0)=1(-1)/(x+1)2x=0=-1 y’’’(0)=(-1)(-2)/(x+1)3x=0=(-1)(-2) y’’’’(0)=
(-1)(-2)(-3)/(x+1)4x=0=(-1)(-2)(-3) y(n)=[(-1)(-2)(-3)…(-n+1)]/(1+x)nx=0=(-1)n-1123…(n-1)=(-1)n-1(n-1)! 5) y=(1+x)p,
x0=0 y(0)=1 y’(0)=p(1+x)p-1|x=0=p y’’(0)=
p(p-1)(1+x)p-2x=0=p(p-1) y’’’(0)=
p(p-1)(p-2)(1+x)p-3x=0=p(p-1)(p-2) y(n)=p(p-1)(p-2)…(p-n+1)(1+x)p-nx=0=p(p-1)(p-2)…(p-n+1) Если р
– натуральное,
то y(n)(0)=0
np+1 (либо n Формула
Тейлора с остаточным
членом в форме
Лангранджа. Теорема:
Пусть функция
y=f(x)
– n+1 раз
дифференцируема
в О(х0), тогда
в некоторой
Оε(х0) где с лежит
между х и xn Доказательство:
Применим теорему
Коши о двух
функциях к
следующим
функциям (x)=f(x)-Tn(x)$
g(x)=(x-x0)n+1 (x0)=0;
’(x0)=0,…,(n)(x0)=0;
(n+1)(x)=f(n+1)(x) g’(x0)=(n+1)(x-x0)nx=0=0;
g(n+1)(x)=(n+1)! [a,b](x);(a,b)g(x);g’(x)0 Лекция
№16 Ведущая:
Голубева Зоя
Николаевна Дата:
вторник, 21 ноября
2000 г. Тема:
Применение
формулы Тейлора
с остаточным
членом в форме
Лангранджа,
Выпуклость,
Вогнутость. Применение
формулы Тейлора
с остаточным
членом в форме
Лангранджа. Пусть
функция f(x)
– два раза
дифференцируема
в О(х0),
тогда f уравнение
касательной Если
f’’(x)M
xO(x0) f(x)-n+1
– дифференцируема
в О(х0) f(x)=Tn(x)+Rn(x)
в О(х0) n=1 T n=2 - график
парабола
f(x)-T1(x)=f’(x0)x-x0 f(x)-T2(x)=[f’’(x0)x-x02]/2 T3(x)=ax3+bx2+cx+d
– график кубическая
парабола В Определение:
Пусть функция
f(x) –
дифференцируема
в точке
х0, то она называется
выпуклой (вогнутой)
в верх
в точке
х0, если f(x)-yкас<0
в О(х0)
Определение:
Пусть функция
f(x) –
дифференцируема
в точке
х0, то она называется
выпуклой (вогнутой)
вниз в
точке
х0, если f(x)-yкас>0
в О(х0)
Определение:
Пусть функция
f(x) –
дифференцируема
в точке
х0, то она называется
выпуклой (вогнутой)
в верх
(вниз)
на интервале
(a,b), если
она выпукла
в верх (вниз) в каждой
точке этого
интервала.
Определение:
(точки перегиба)
Пусть функция
f(x) диф- ференцируема
в О(х0)
и непрерывна
в О(х0). Точка
х0 – называется
точкой перегиба
графика f(x),
если при пере- ходе
через точку
меняется знак
выпуклости. Теорема:
(о достаточном
условии выпуклости
функции). Пусть
функция f(x)
дважды дифференцируема
в точке х0 и
f’’(x0)<0
(f’’(x0)>0),
тогда f(x)
– выпукла вверх
(вниз) в тоске
х0. Доказательство:
Напишем формулу
Тейлора с остаточным
членом в форме
пеано: Если
х близко к х0,
то знак квадрата
скобки определяется
знаком f(x0).
Если f’’(x0)<0,
то f(x)-yкас>0
в О(х0). Если
f’’(x0)>0,
то f(x)-yкас>0
в О(х0) Теорема:
Путь функция
f(x) непрерывна
в О(х0) и дважды
дифференцируема
в О(х0),
причём f’(x)
меняет знак
при переходе
через точку
х0, тогда точка
х0 – точка
перегиба. Доказательство: f’’(x)
- + x0 f’’(x)<0
в O-(x0)
f(x) –
выпукла вверх
в О-(х0) f’’(x)>0
в O+(x0)
f(x) –
выпукла вниз
в О+(х0) Следствие:
Если f(x)
дважды дифференцируемы
в точке х0. Если
точке х0 точка
перегиба, то
f’’(x0)=0 Путь
точка х0 точка
перегиба и
существует
f’’(x0)>0,
тогда
то есть
при переходе
через точку
х0 левая часть
равенства
f(x)-yкас
не меняет знак.
Аналогично
получаем для
f(x)>0
f’’(x0)=0 Замечание:
Условие равенства
f’’(x0)=0
необходимо,
но недостаточно. Теорема:
(о достаточном
условие экстремума
по второй
производной) Пусть
функция f(x)
дважды дифференцируема
в точке х0,
тогда точка
х0 точка максимума
если f’’<0,
точка х0 точка
минимума если
f’’(x0)>0. Доказательство:
При
х достаточно
большим и х0
знак в квадратных
скобках совпадает
со знаком f’’(x0)
f(x)-f(x0)>0
в О(х0),
если f’’(x0)>0
то есть f(x)>f(x0)
в О(х0)
х0
точка минимума,
если f(x)-f(x0)<0
в О(х0),
и если f’’(x0)<0
то есть f(x) Замечание:
Если f’(x0)=0
и f’’(x0)=0,
то нужны дополнительные
исследования. Лекция
№17 Ведущая:
Голубева Зоя
Николаевна Дата:
среда, 22 ноября
2000 г. Тема:
Асимптоты.
Полное исследование
функции. Асимптоты. Вертикальные Пусть
функция f(x)
определена
в
Наклонные
асимптоты
2.1 Пусть функция
f(x) определена
в
2.2 Пусть функция
f(x) определена
в
Необходимые
и достаточные
условия существования
наклонной
асимптоты.
Пусть функция
f(x) определена
в О(+) и
тогда
прямая y=kx+b
правая наклонная
асимптота Замечание:
если условие
1) не выполнено,
то нужно посчитать
предел lim(f(x)),
чтобы выяснить
поведение
х+ функции
на бесконечности. Полное
исследование
функции. Область
определения Симметрия
и периодичность Вертикальные
асимптоты Наклонные
асимптоты Критические
точки, если
есть, то находим
точки экстремума
и промежутки
возрастания
и убывания
функции f'(x)=0 или
f’(x) не
существует,
а f(x)
существует Возможные
точки перегиба
f’’(x)=0,
либо f’’(x)
не существует,
но f’(x)
существует
следовательно
промежутки
выпуклости
и вогнутости Точки
пересечения
с осями координат
и промежутки
знака постоянства
(если можно) Пример: Область
определения
D: x№3 Функция
не симметрична
и не периодична
Ю
х=3 правая и левая
вертикальная
асимптота 4)
Ю
y=0 правая
и левая горизонтальная
асимптота 5) критическая
точка х1=-3/2 f(-3/2)=4/243 6) критическая
точка х2=-3 f(-3)=1/72 7)x=0 y=0 Приближенные
методы решения
уравнения
f(x)=0 1) Метод
хорд
а)
f(x), f’(x),
f’’(x)
– непрерывны
на отрезке
[a,b]
б)
f(a)f(b)<0 в)
f’(x) и
f’’(x)
– сохраняют
знаки на отрезке
[a,b] f()=0;A(a;(f(a)),B(b;f(b)) Лекция
№18 Ведущая:
Голубева Зоя
Николаевна Оценка
скорости сходимости. 2)
Метод касательных
(метод Ньютона) f(x)=0 1)f(x),f’(x),f’’(x)-непрерывна
на [a,b] 2)f(a), f(b) <0 3)f’(x),f’’(x)
– сохраняет
знак на [a,b] точка
пересечения
х1 –
это точка пересечения
касательной
с осью Ох Yкас=0,
x=x1 0=f(b)+f’(b)(x1-b) f’(b)b-f(b)=f’(b)x1 Формула
Тейлора с остаточным
членом в форме
Лангранджа
в точке xn c
– лежит между
х и хn Положим
x=;
f()=0 M>0:|f”(x)|M x[a,b]
m>0:|f’(x)|m;x[a,b] Надо
выбирать отрезок
так b-a<1 |f”(x)|M Вектор
функция. Параметрическая
производная. По
закону (1) ставиться
в соответствие
вектор r(t).
(x(t),y(t)
– заданные
числовые функции r(t)
– вектор функция.
Кривая описываемая
концом вектора
– называется
годографом. Видим,
что кривые на
плоскости можно
задать в виде: x2+y2=r2 Остроида x2/3+y2/3=a2/3 Циклоида Лекция
№19 Ведущая:
Голубева Зоя
Николаевна Параметрическая
производная. *
o’1
x2n+2=xx2n+1=o(x2n+1) #
$
-Tn(x)
– многочлен
Тейлора
Rn(x)-остаточный
член в форме
Лангранджа Полуинтервал:
(/////////] x
Полуинтервал:
(/////////] x [/////////)
x
[/////////)
x ///////////////]
x
(-;b]
или -
///////////////]
x
(-;b]
или - ///////////////)
x
(-;b)
или -
///////////////)
x
(-;b)
или - a-ε
a-ε (////////)
x
(////////)
x
 ///////)
x
///////)
x (////////
x
(////////
x x;
x>0
x;
x>0
 ε(+)={xR:x>ε}
(//////////
x
ε(+)={xR:x>ε}
(//////////
x ε(-)={xR:x<-ε}
///////////)
x
ε(-)={xR:x<-ε}
///////////)
x ε()={xR:x>ε}
\\\\\\)
(////// x
ε()={xR:x>ε}
\\\\\\)
(////// x
Х
У
 римеры:
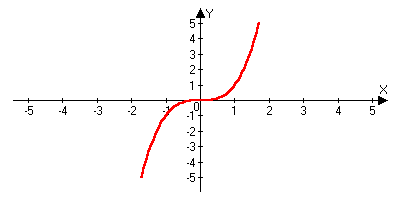
римеры: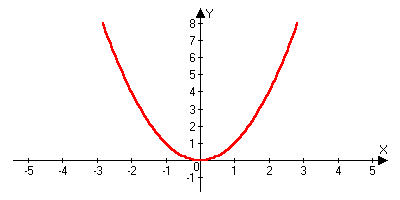 )y=x2
x=y
)y=x2
x=y
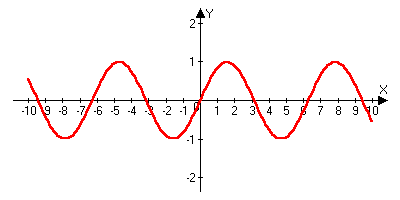 )y=sinx
)y=sinx
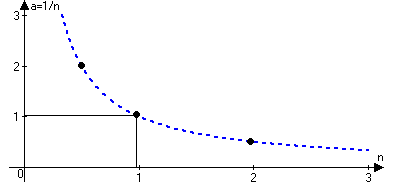 аn}={1,1/2,1/3,…,1/n,…}
аn}={1,1/2,1/3,…,1/n,…}
Монотонные
последовательности
 Начиная
с этого номера
N
все числа этой
последовательности
попадают в ε
окрестность
числа а.
Другими словами
начиная с номера
N
вне интервала
а-ε;а+ε
может находиться
не более конечного
числа членов
последовательности.
Начиная
с этого номера
N
все числа этой
последовательности
попадают в ε
окрестность
числа а.
Другими словами
начиная с номера
N
вне интервала
а-ε;а+ε
может находиться
не более конечного
числа членов
последовательности.Бесконечно
малые последовательности
 n+
n+
 N2:
n>N2
n<ε
N2:
n>N2
n<ε
 0
(////////b/////////)
x
0
(////////b/////////)
x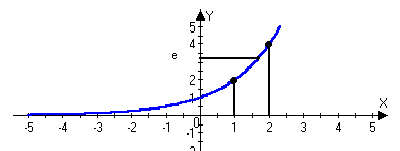

 an-b>-(b-a)/2
an-b>-(b-a)/2
Следствие
Определение
под последовательности
Теорема
Пример
Определение
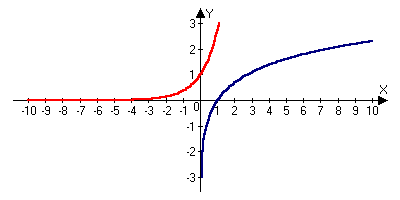
 .x2
lim(x-1)=1,
то есть y=x-1
не является
бесконечно
малой при x2
.x2
lim(x-1)=1,
то есть y=x-1
не является
бесконечно
малой при x2Теорема
 огда
xO(x0)
(x)<ε
огда
xO(x0)
(x)<εПервый
замечательные
пределы.
 оказательство:
оказательство:
 (//////////
x
(//////////
x
 дносторонние
пределы.
дносторонние
пределы.Определение
Определение
 in(x)
– бесконечно
малое
in(x)
– бесконечно
малое 
Показательные
бесконечности.
Логарифмическая
бесконечность
 n(x)=o(x),
>0.
Логарифмическая
бесконечность
слабее любой
степенной
бесконечности.
n(x)=o(x),
>0.
Логарифмическая
бесконечность
слабее любой
степенной
бесконечности.
 y=(1+x)p-1
y=(1+x)p-1
 y=ex-1
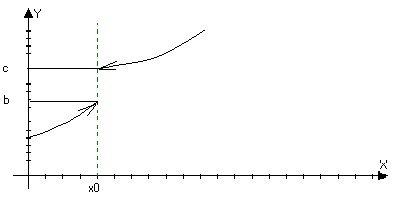
y=ex-1Классификация
точек разрыва
функции.
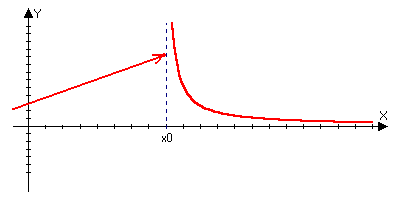
 1,x=1
1,x=1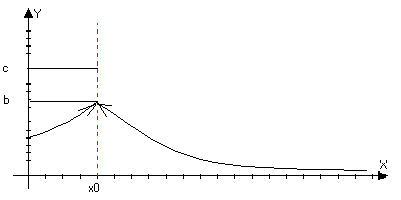
 )Точка
х0
называется
точкой разрыва
2ого
рода функции
если она не
является точкой
разрыва 1ого
порядка, то
есть если хотя
бы один из
односторонних
пределов не
существует
или равен
бесконечности.
)Точка
х0
называется
точкой разрыва
2ого
рода функции
если она не
является точкой
разрыва 1ого
порядка, то
есть если хотя
бы один из
односторонних
пределов не
существует
или равен
бесконечности.
 an}-ограниченная
не убывающая
lim
an=b f(a)<0
f(an)<0
n
an}-ограниченная
не убывающая
lim
an=b f(a)<0
f(an)<0
n
 x+
x+
x+
x+
x+
x+
x+
x+ 
 Замечание:
а) Условие
непрерывности
нельзя отбросить
Замечание:
а) Условие
непрерывности
нельзя отбросить
 б) Множество
(0;1]=М наибольшее
значение 1М
б) Множество
(0;1]=М наибольшее
значение 1М
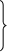 оказательство:
A
оказательство:
A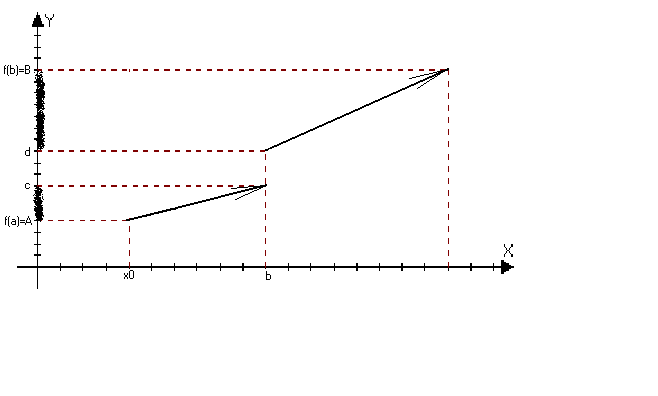
 усть
на множестве
D
задана непрерывная
возрастающая
или убывающая
функция y=f(x).
Тогда на множестве
её значений
Е определена
обратная ей
функция x=g(y),
которая непрерывна
и возрастает
или убывает
на множестве
Е.
усть
на множестве
D
задана непрерывная
возрастающая
или убывающая
функция y=f(x).
Тогда на множестве
её значений
Е определена
обратная ей
функция x=g(y),
которая непрерывна
и возрастает
или убывает
на множестве
Е. Производная
функции.
∆Х
Производная
функции.
∆Х
 усть
y=f(x)
определена
в O(x0)
усть
y=f(x)
определена
в O(x0)
 x=x-x0
– называется
приращением
аргумента в
т х0
Х
x=x-x0
– называется
приращением
аргумента в
т х0
ХОбозначения:

 S
S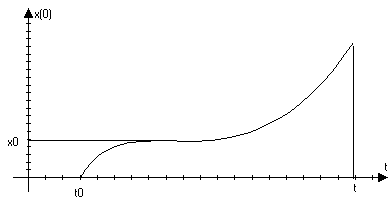 s/∆t=[x(t)-x(t0)]/[t-t0]=vcp.
Если ∆t0
s/∆t=[x(t)-x(t0)]/[t-t0]=vcp.
Если ∆t0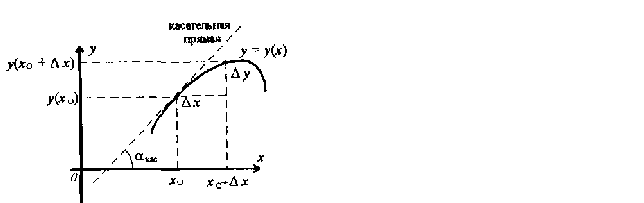 y’(x0)=lim∆y/∆x
– производная
функции у(х) и
в точке х0.
y’(x0)=lim∆y/∆x
– производная
функции у(х) и
в точке х0. =х
=х
 епрерывна
в точки х0=0
епрерывна
в точки х0=0Таблица
производных
 де sin(x)
де sin(x) (sin(x))’=cos(x)
(sin(x))’=cos(x)
 де cosx
де cosx (cos(x))’=-sin(x)
(cos(x))’=-sin(x)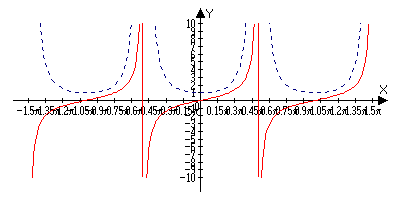
 де tg(x)
де tg(x) (tg(x))’=1/cos2x
(tg(x))’=1/cos2x
 xn)’=nxn-1
xn)’=nxn-1 y=x^3
y=x^3 y’=3x^2
y’=3x^2
 оказательство:
из дифференцируемой
функции f(x)
в точке х0
и из монотонности
следует существование
обратной функции
в точке х0
и её непрерывность
lim[∆y(y0)]/∆y=
∆y0,
то ∆у0
в силу строгой
оказательство:
из дифференцируемой
функции f(x)
в точке х0
и из монотонности
следует существование
обратной функции
в точке х0
и её непрерывность
lim[∆y(y0)]/∆y=
∆y0,
то ∆у0
в силу строгой
 =lim∆x/∆y=lim1 /(∆y/∆x)=
в силу непрерывности
следует
=1/[lim∆y/∆x]=1/[lim∆f(x0)/∆x]=1/f(x0)
f(x0)0
=lim∆x/∆y=lim1 /(∆y/∆x)=
в силу непрерывности
следует
=1/[lim∆y/∆x]=1/[lim∆f(x0)/∆x]=1/f(x0)
f(x0)0 ’=axlna,
частный случай
y=ex
(ex)’=ex
’=axlna,
частный случай
y=ex
(ex)’=ex y=x^2
y=x^2 y’=x^2
lnx
y’=x^2
lnx lnx)’=1/x
lnx)’=1/x y=lnx
y=lnx y’=1/x
y’=1/x =logax=lnx/lna
(logax)’=1/xlna
=logax=lnx/lna
(logax)’=1/xlna y=lgx
y=lgx y’=1/xln10
y’=1/xln10
 y=arcsinx
y=arcsinx y’=1/(1-x^2)
y’=1/(1-x^2)
 y=arccosx
y=arccosx y’=--1/(1-x^2)
y’=--1/(1-x^2) arcctgy)’=-1/(1+x2)
arcctgy)’=-1/(1+x2) y=arctgsx
y=arctgsx y’=-1/
(1+x^2)
y’=-1/
(1+x^2) y=arcctgx
y=arcctgx y’=--1/
(1+x^2)
y’=--1/
(1+x^2)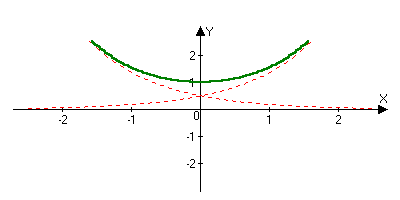
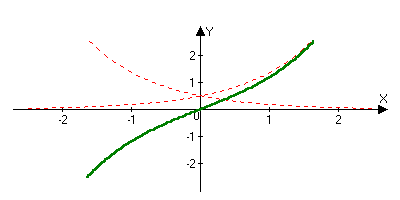
 thx=chx/shx
thx=chx/shx hx=shx/chx
hx=shx/chx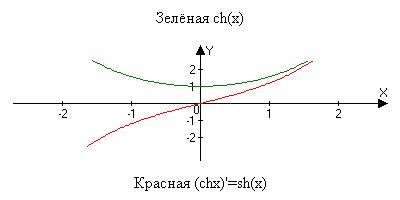
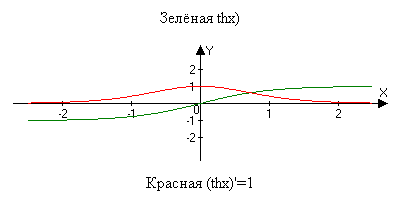
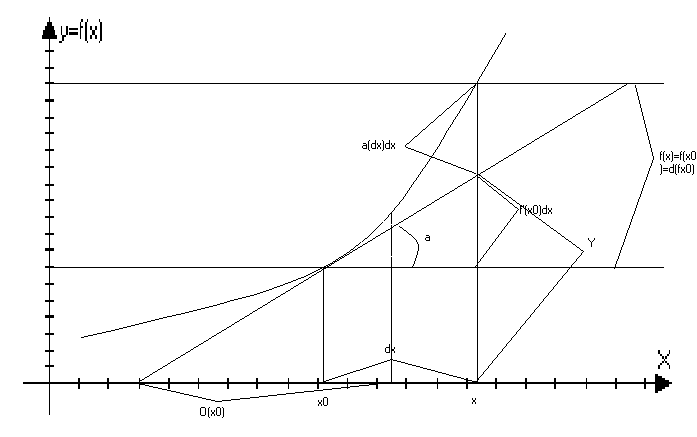
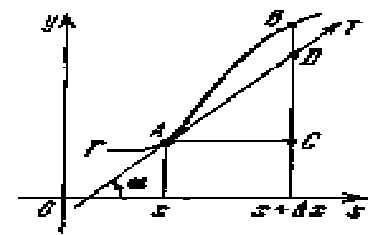
 *)
f(x)-Y=(∆x)∆x-o(∆x)
*)
f(x)-Y=(∆x)∆x-o(∆x)
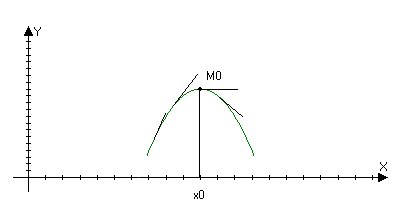
 a(
|x1
|x2
)b
a(
|x1
|x2
)b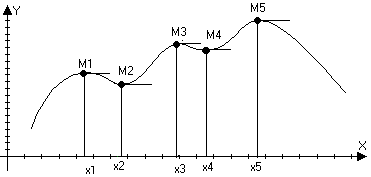 ожно
указать О(х1)
в которой все
значения функции
ожно
указать О(х1)
в которой все
значения функции
 амечание:
амечание:
 братное
утверждение
неверно. Из-за
того, что произведение
в данной точки
равно нулю, не
следует, что
это экстремум.
братное
утверждение
неверно. Из-за
того, что произведение
в данной точки
равно нулю, не
следует, что
это экстремум.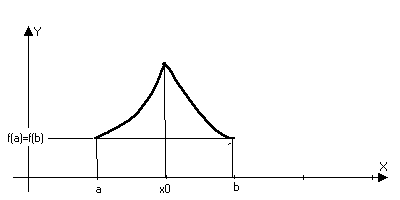
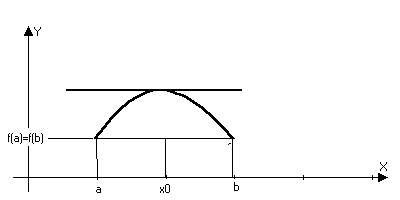
 =f’(c)+
f’(c)=-=[f(b)-f(a)]/[b-a]
=f’(c)+
f’(c)=-=[f(b)-f(a)]/[b-a]
x1,
xn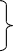 +
x+
x+
x+
x+
x+
+
x+
x+
x+
x+
x+
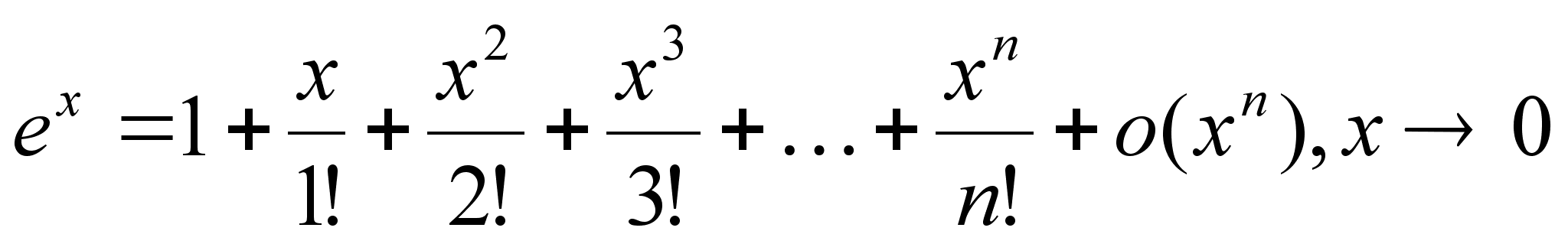 (0)=1
(0)=1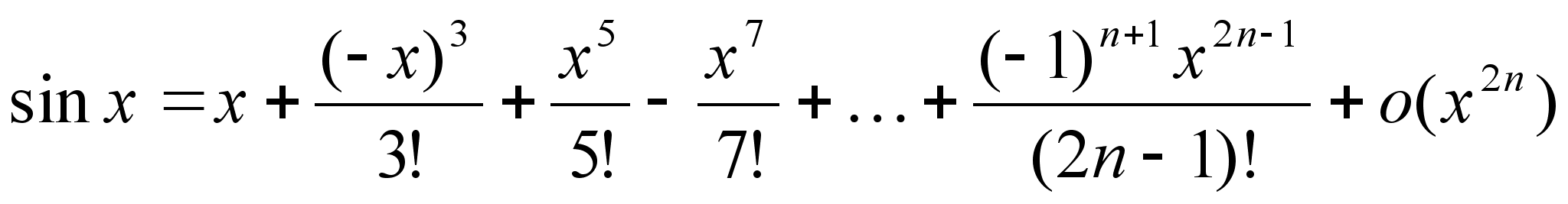 (0)=0
(0)=0 (0)=1
(0)=1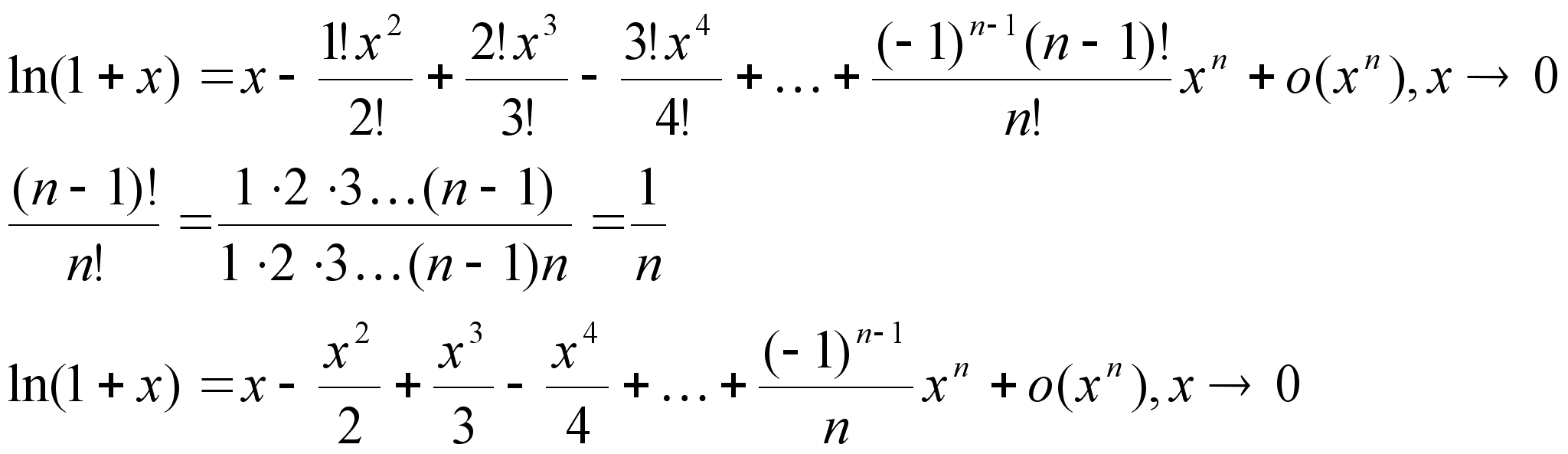
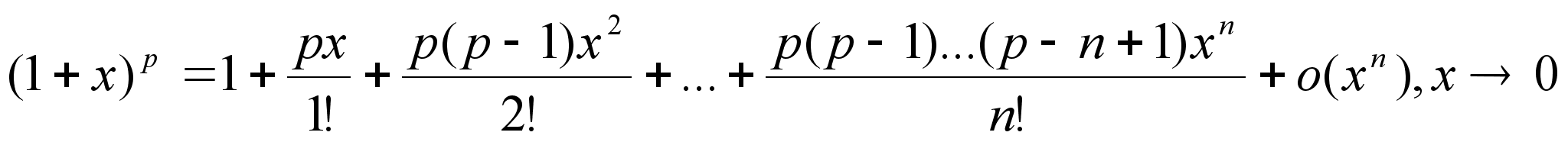
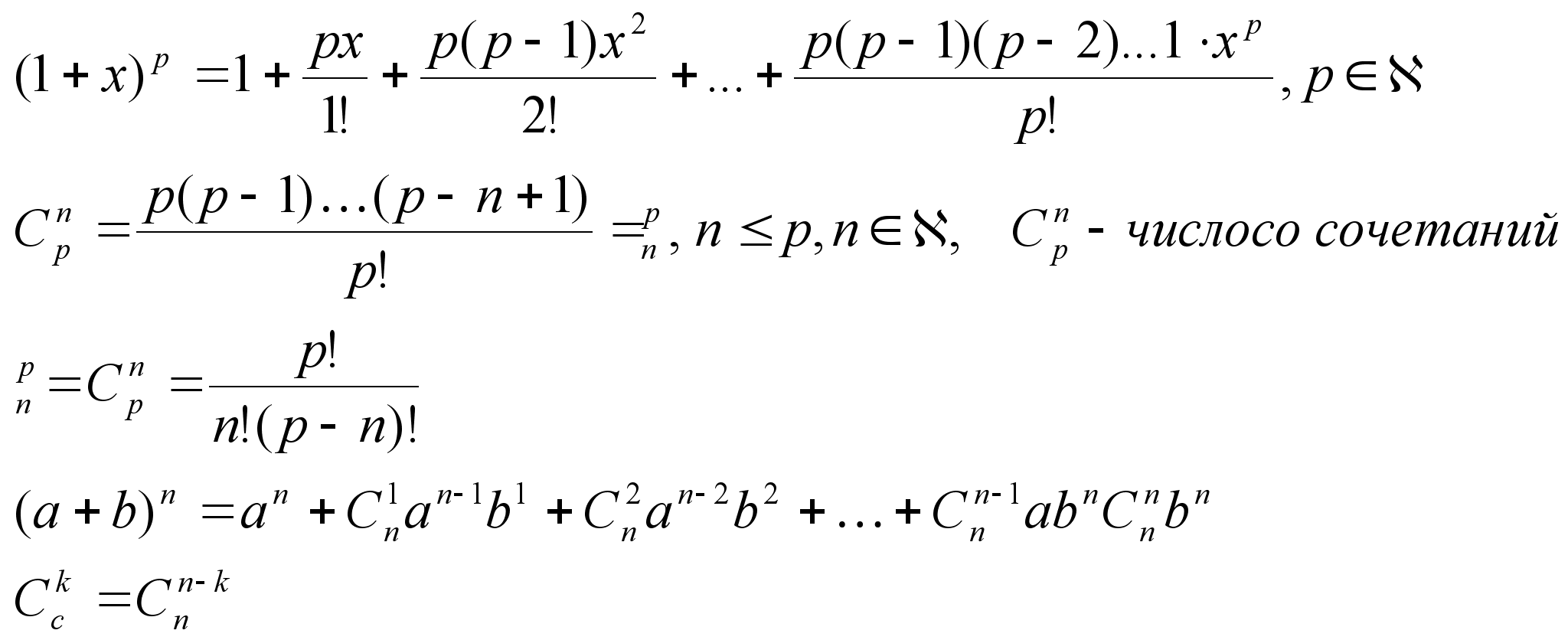
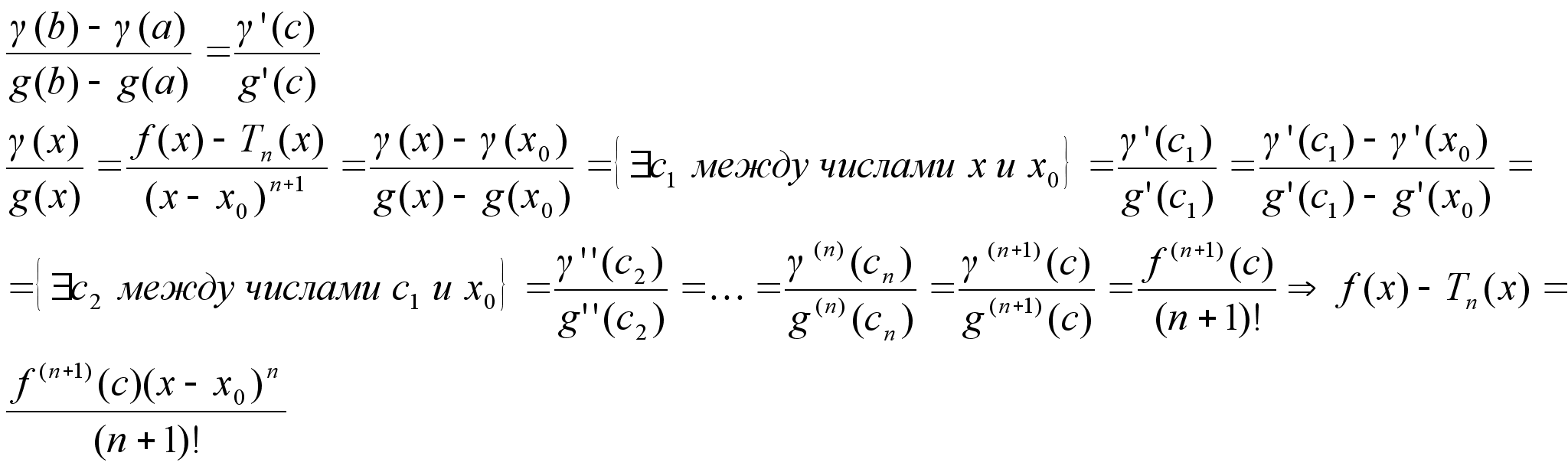
 (x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2
где с лежит
между х и х0
(x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2
где с лежит
между х и х0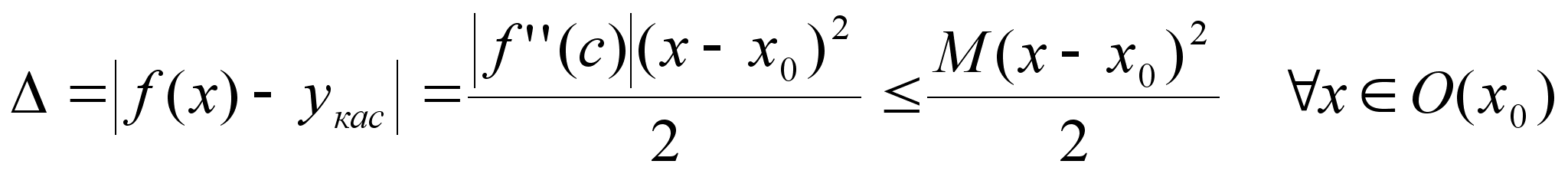
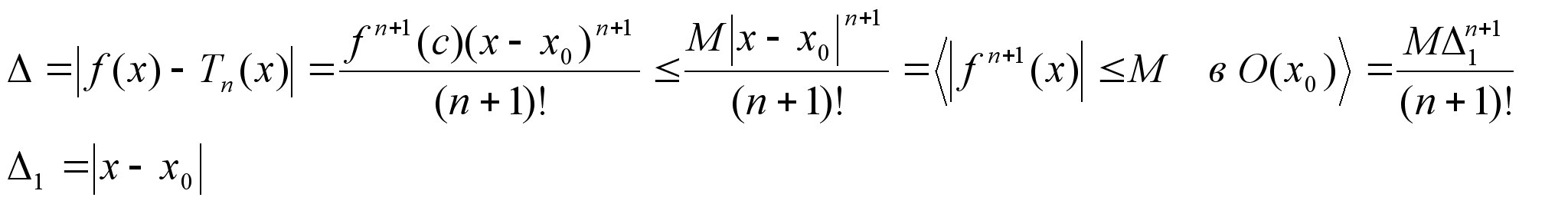
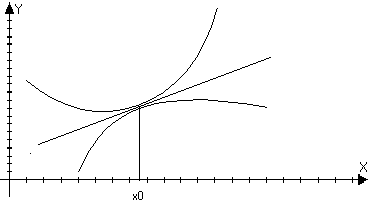 1(x)
– линейная
функция
1(x)
– линейная
функция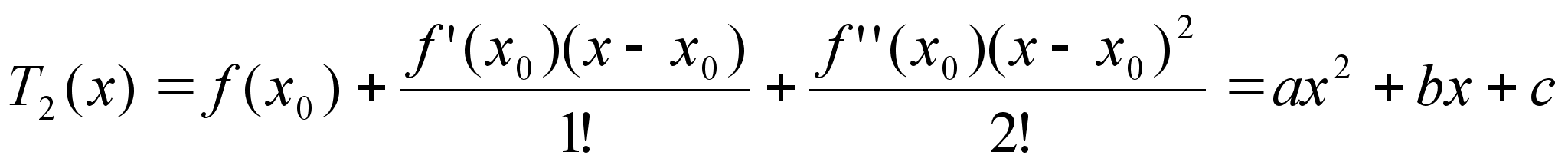
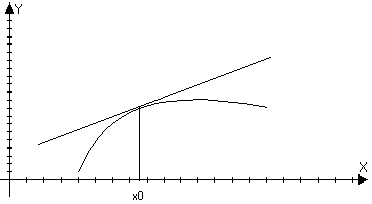 ыпуклость
и вогнутость.
ыпуклость
и вогнутость.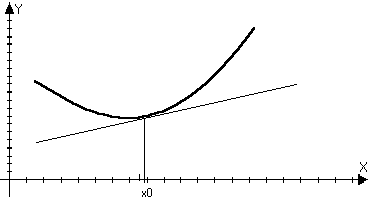
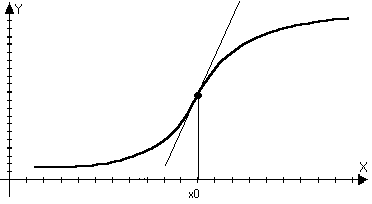
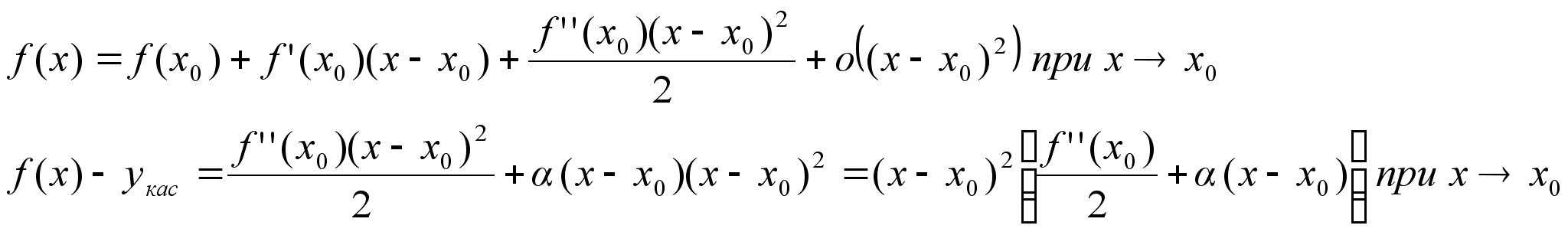
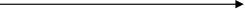 (
) x
(
) x 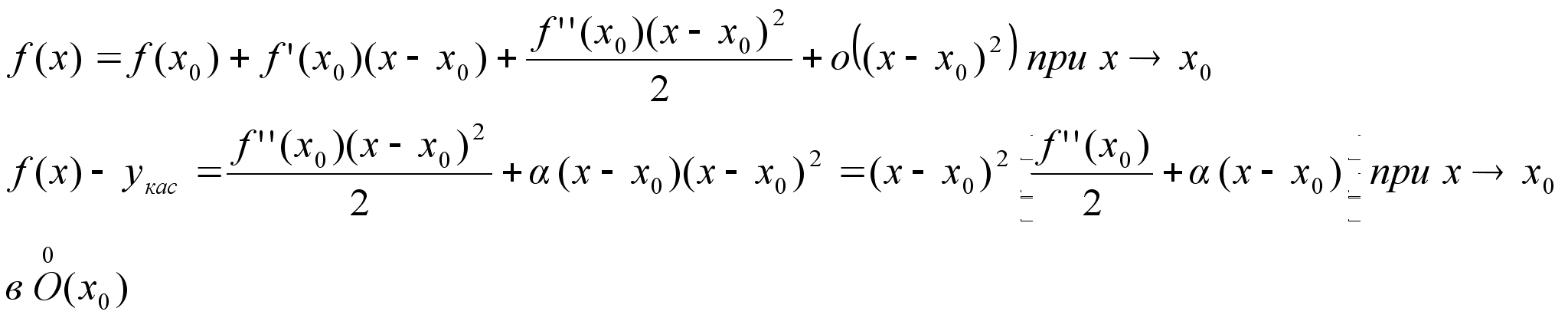
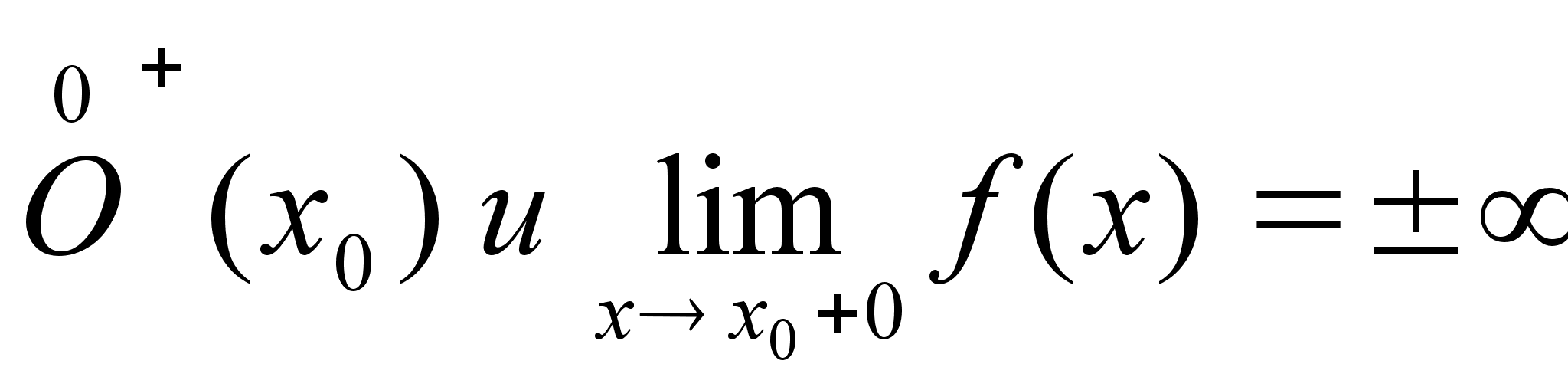 ,
тогда прямая
х=х0 называется
правой вертикальной
асимптотой
для функции
f(x)
,
тогда прямая
х=х0 называется
правой вертикальной
асимптотой
для функции
f(x) 
 Пусть
функция f(x)
определена
в
Пусть
функция f(x)
определена
в
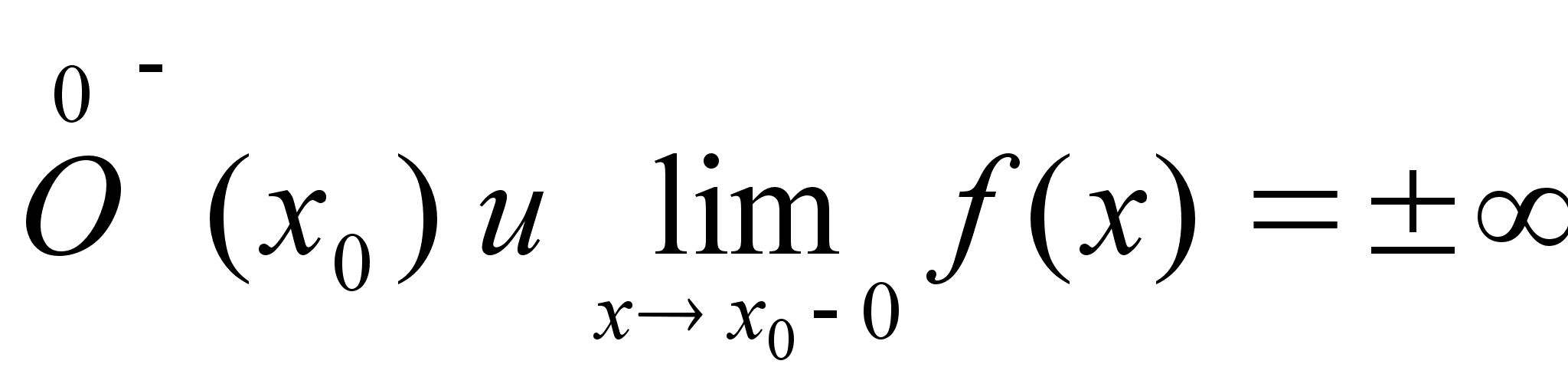 ,
тогда прямая
х=х0 называется
левой вертикальной
асимптотой
для функции
f(x)
,
тогда прямая
х=х0 называется
левой вертикальной
асимптотой
для функции
f(x) 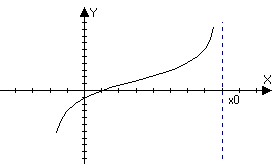
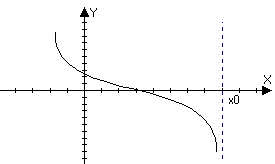
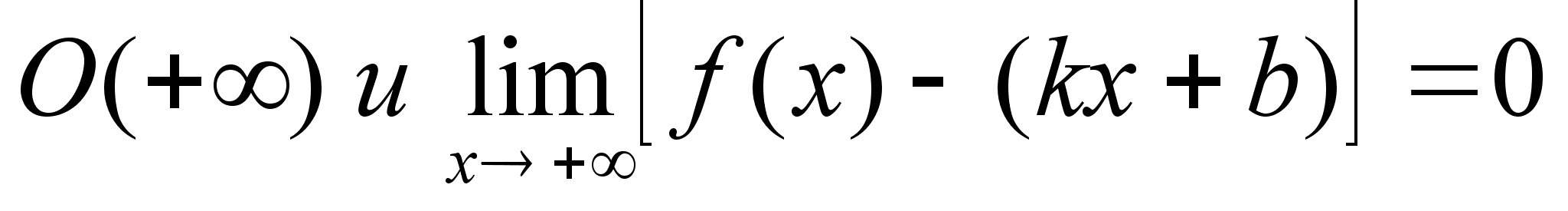 ,
тогда прямая
y=kx+b
называется
правой наклонной
асимптотой
для функции
f(x). (Если
k=0, то говорят,
что y=b
– горизонтальная
асимптота).
,
тогда прямая
y=kx+b
называется
правой наклонной
асимптотой
для функции
f(x). (Если
k=0, то говорят,
что y=b
– горизонтальная
асимптота). 
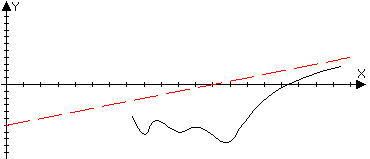
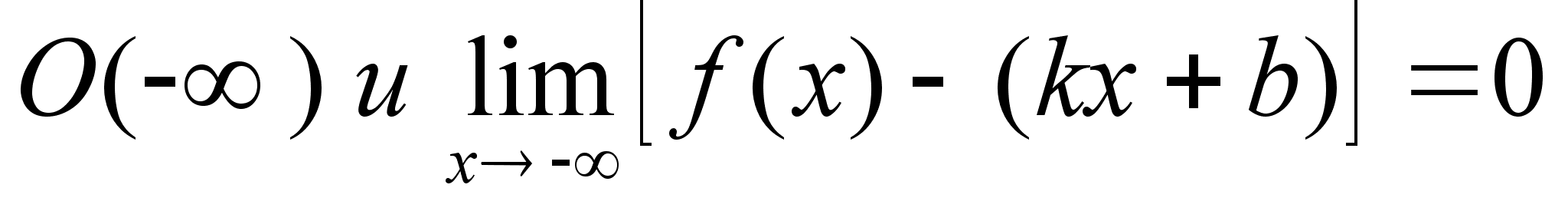 ,
тогда прямая
y=kx+b
называется
левой наклонной
асимптотой
для функции
f(x).
,
тогда прямая
y=kx+b
называется
левой наклонной
асимптотой
для функции
f(x).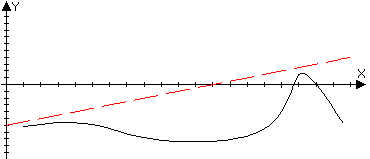
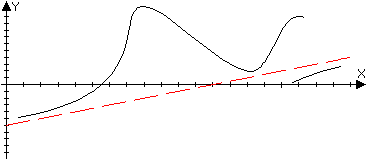
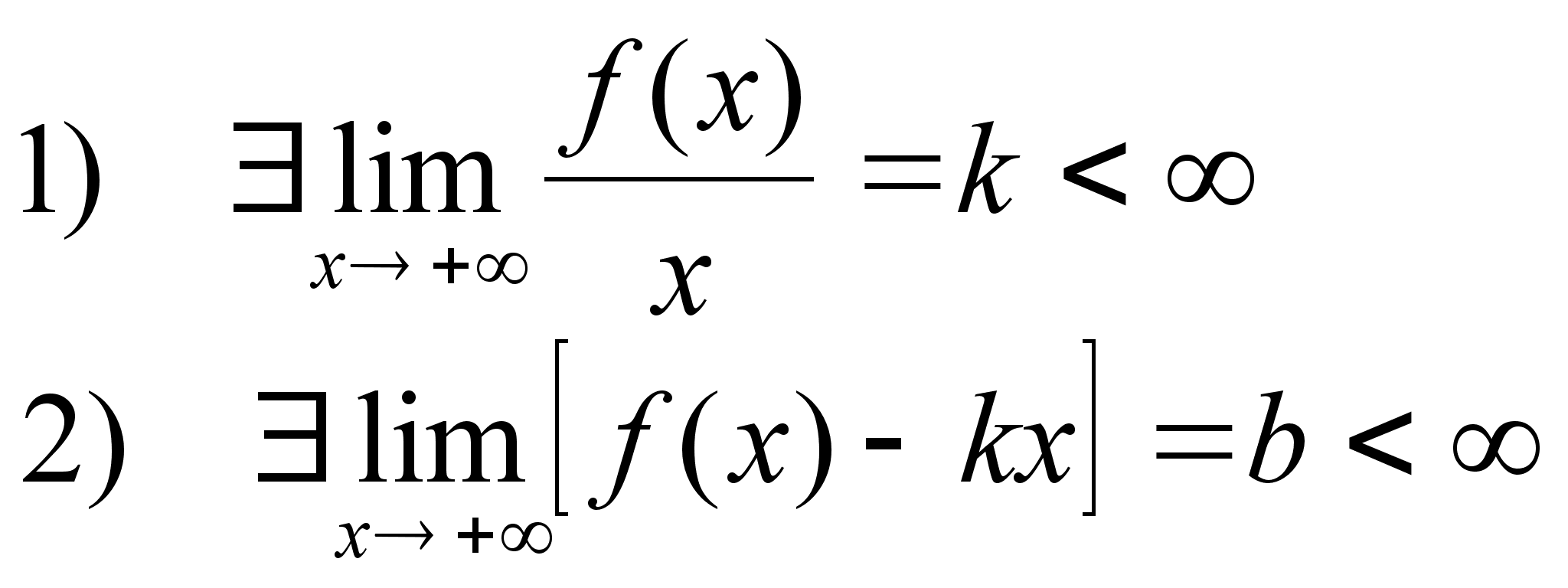
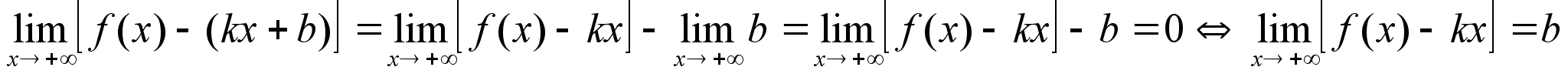
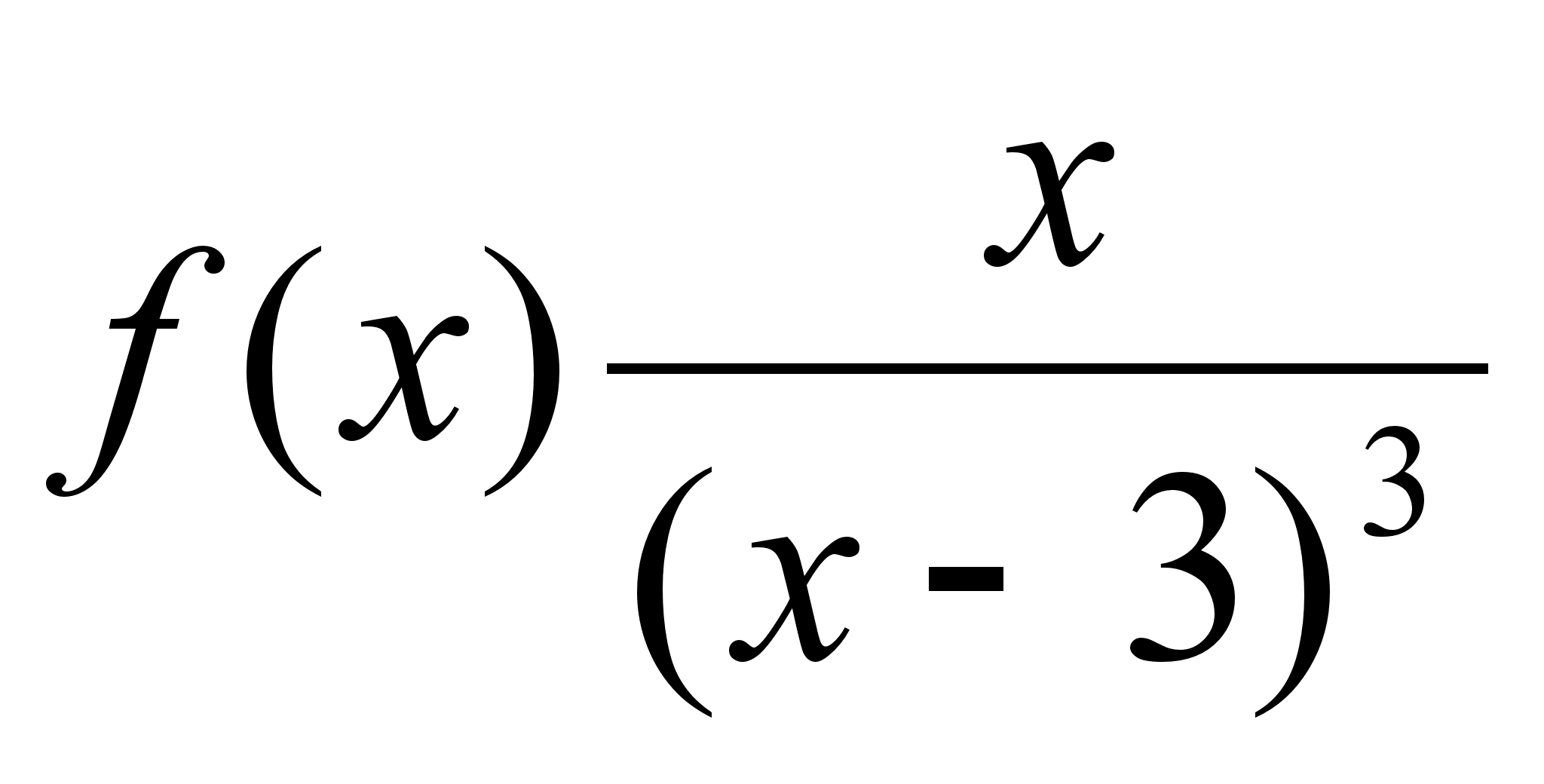
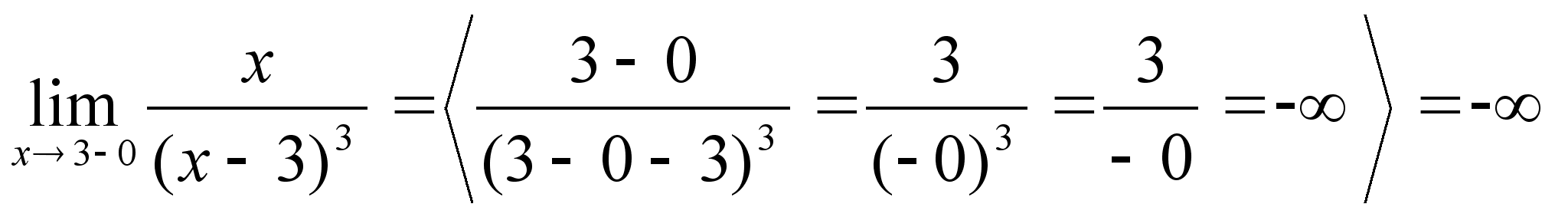
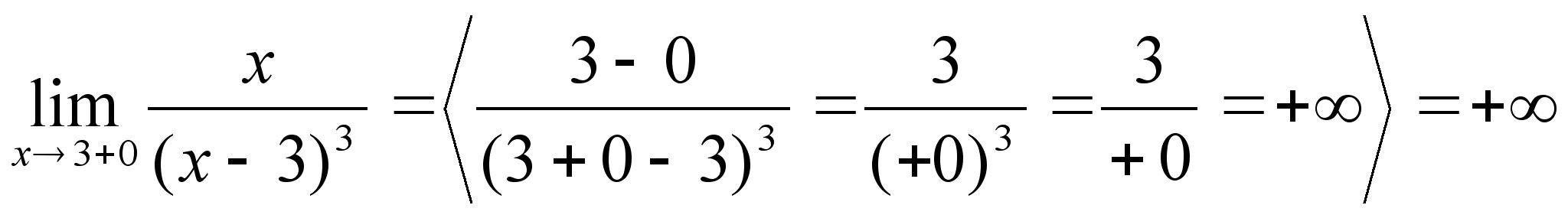
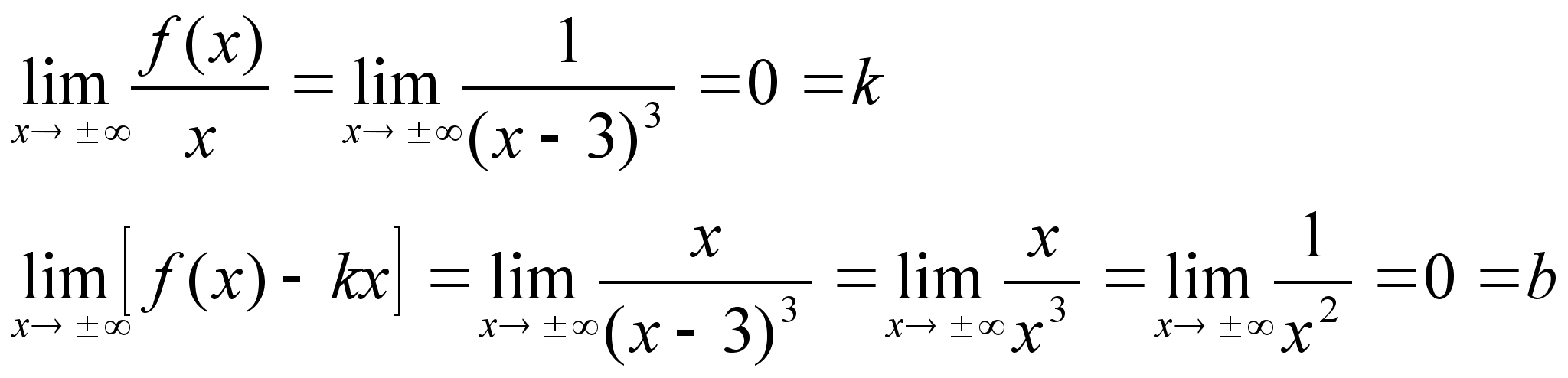
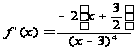

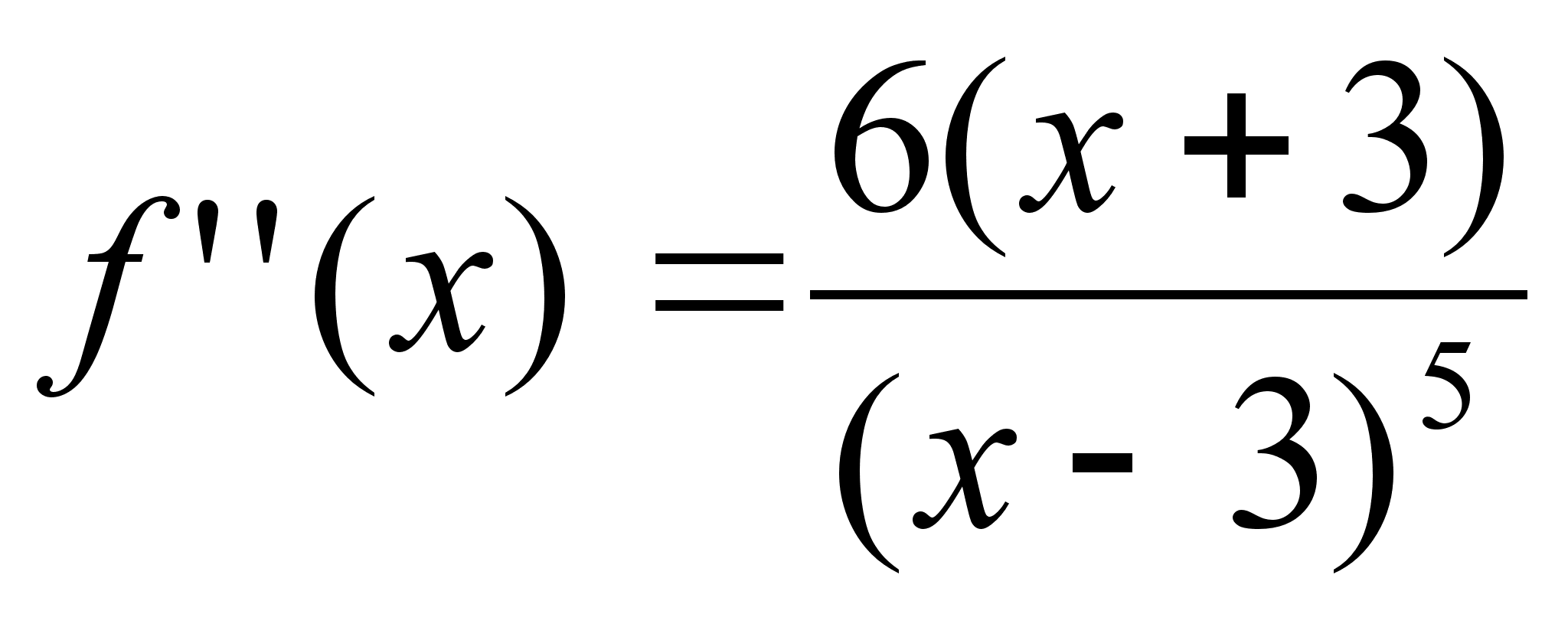
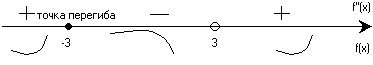
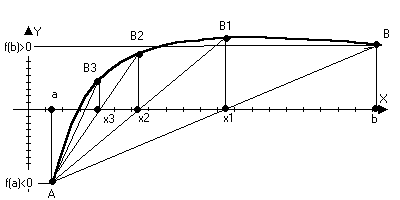
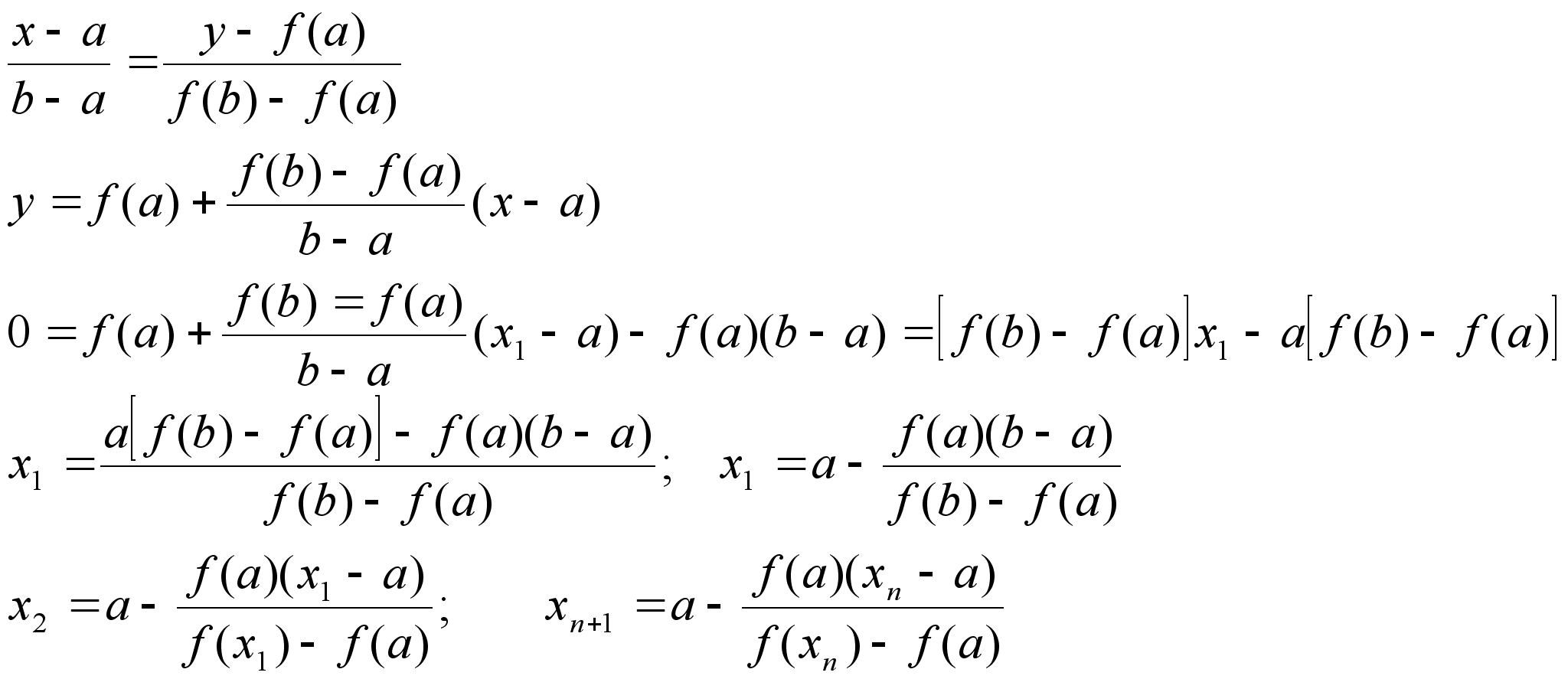
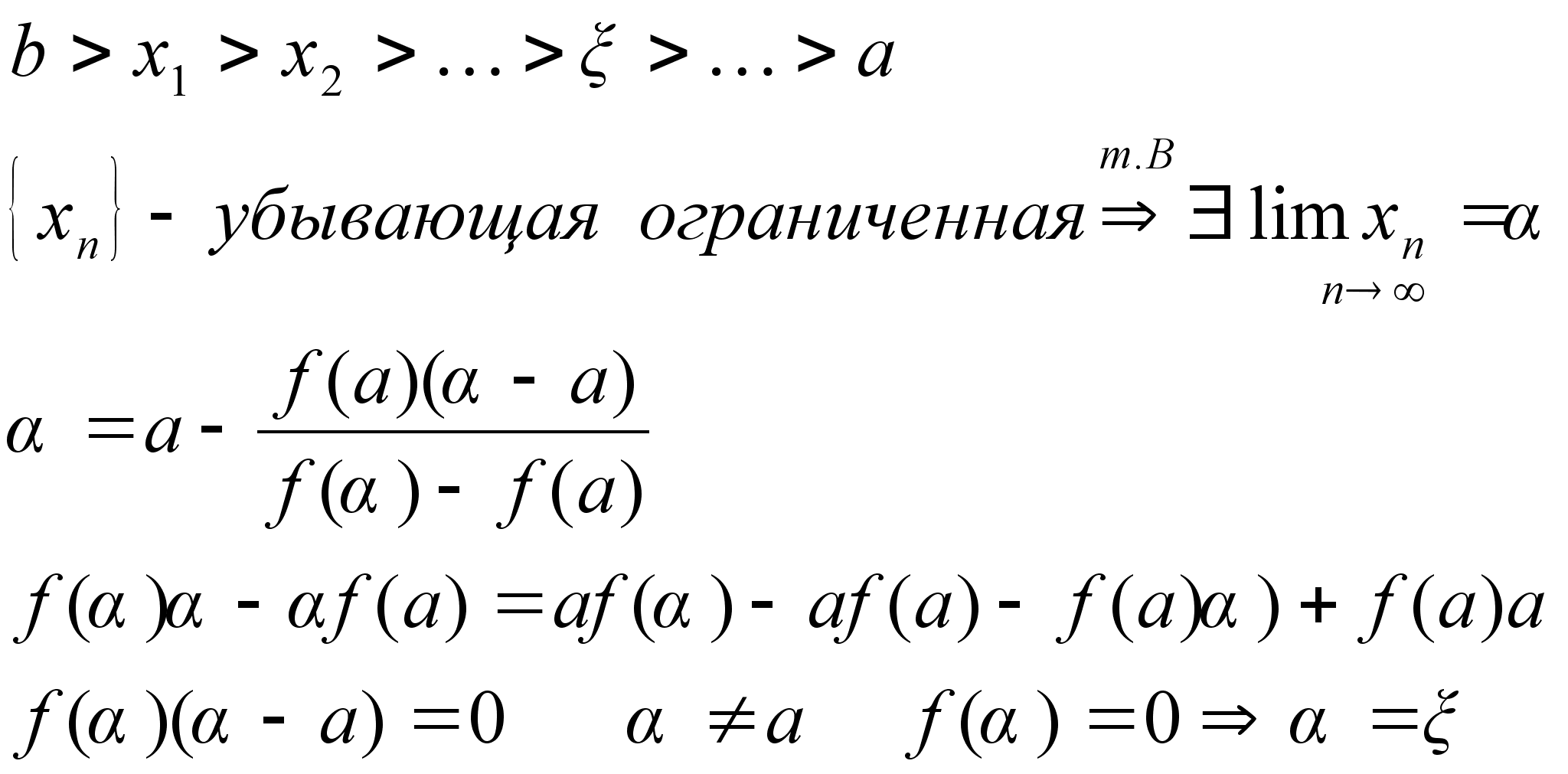
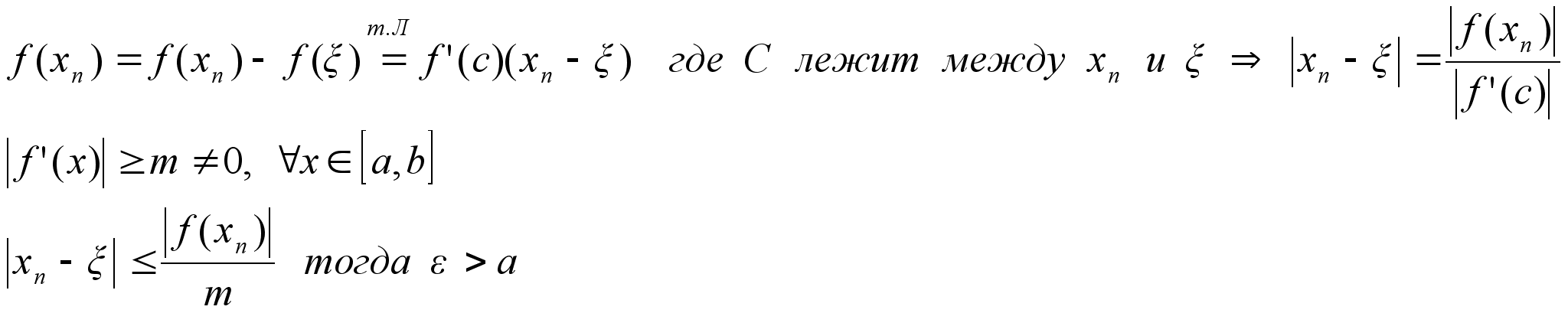 2
2
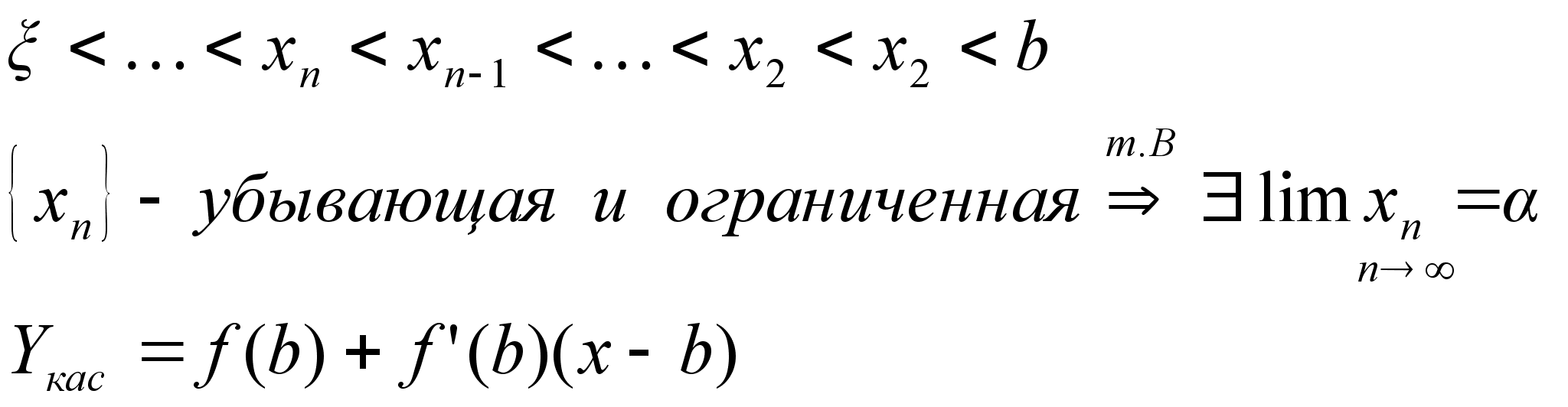
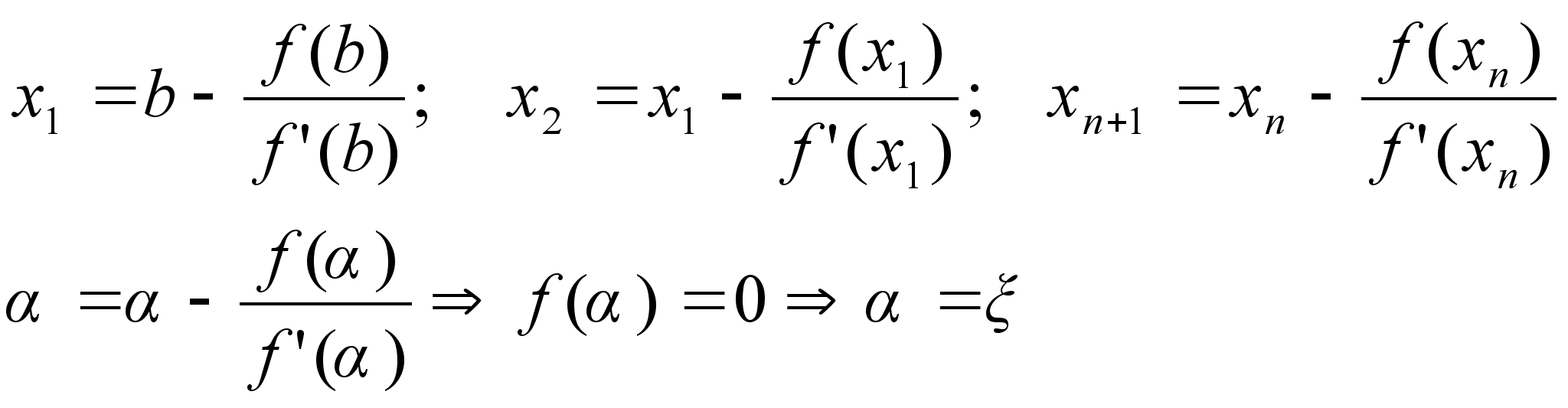
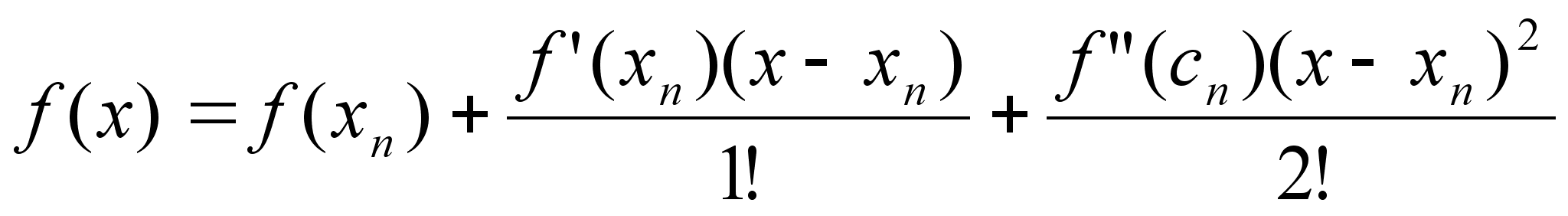
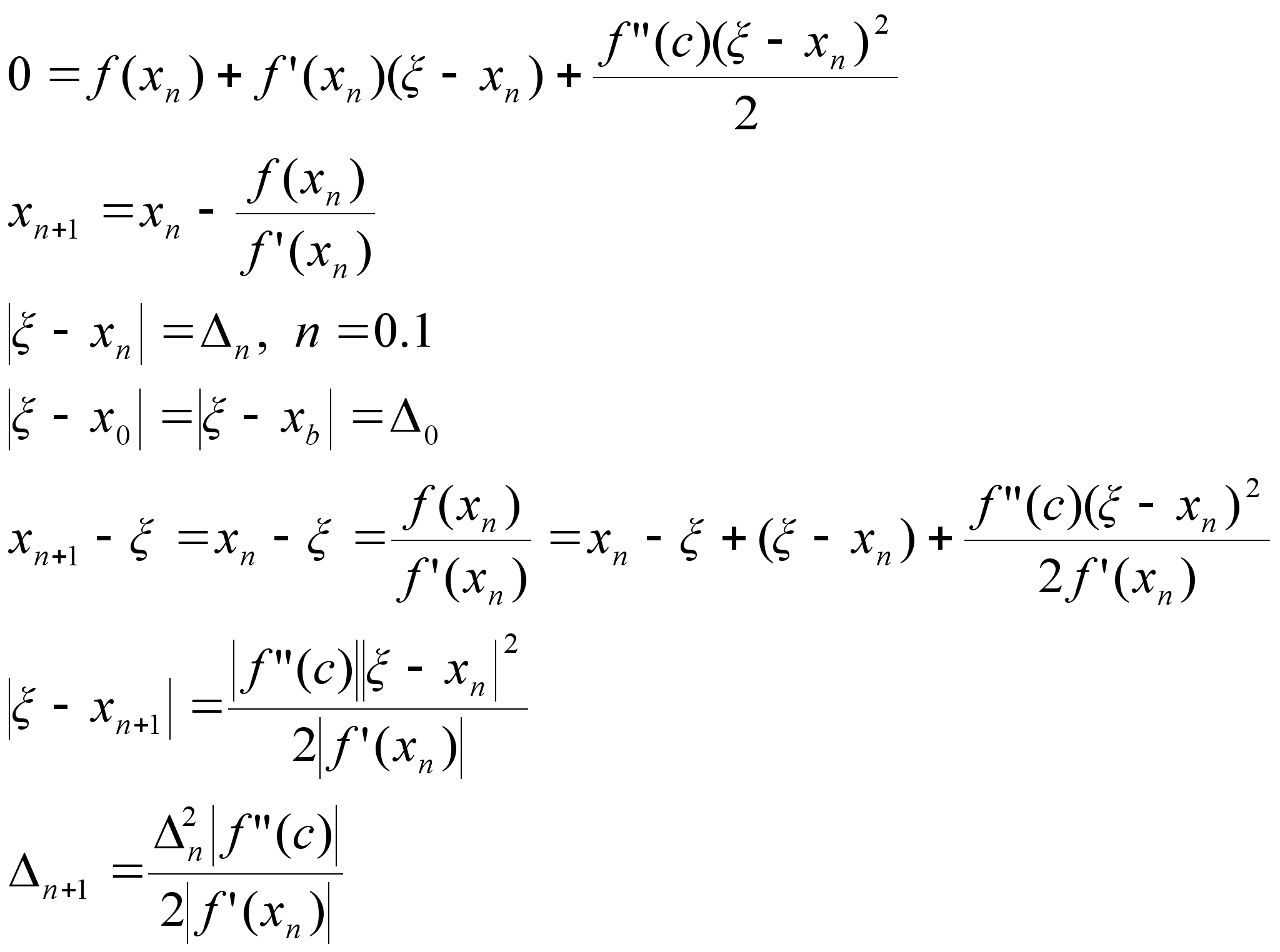
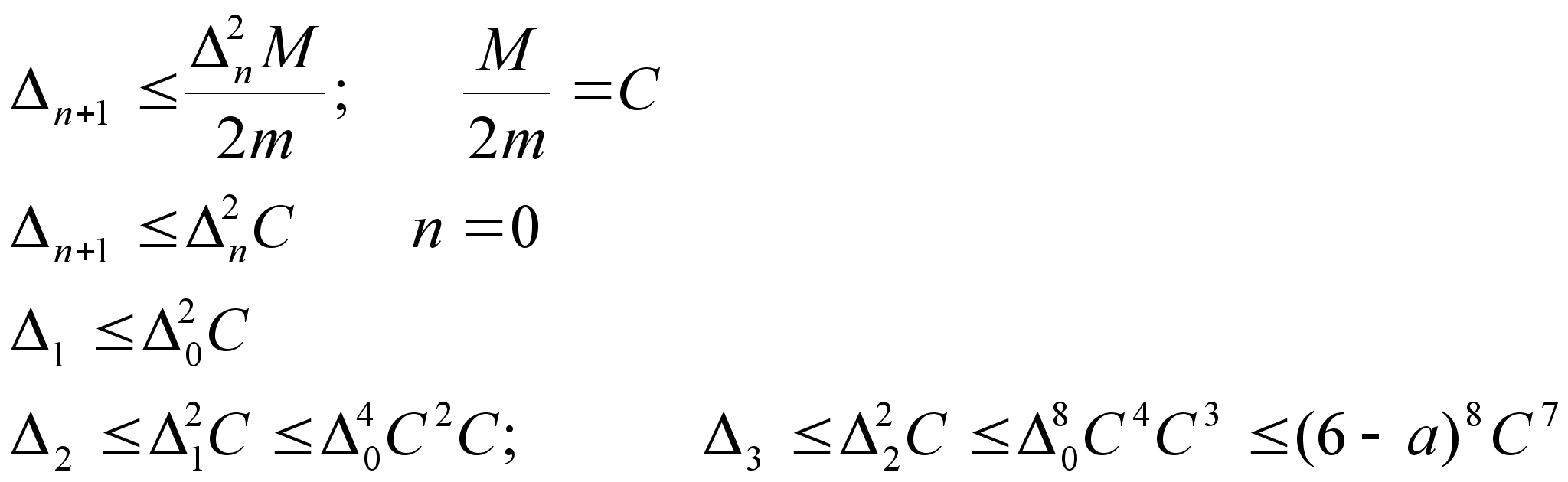
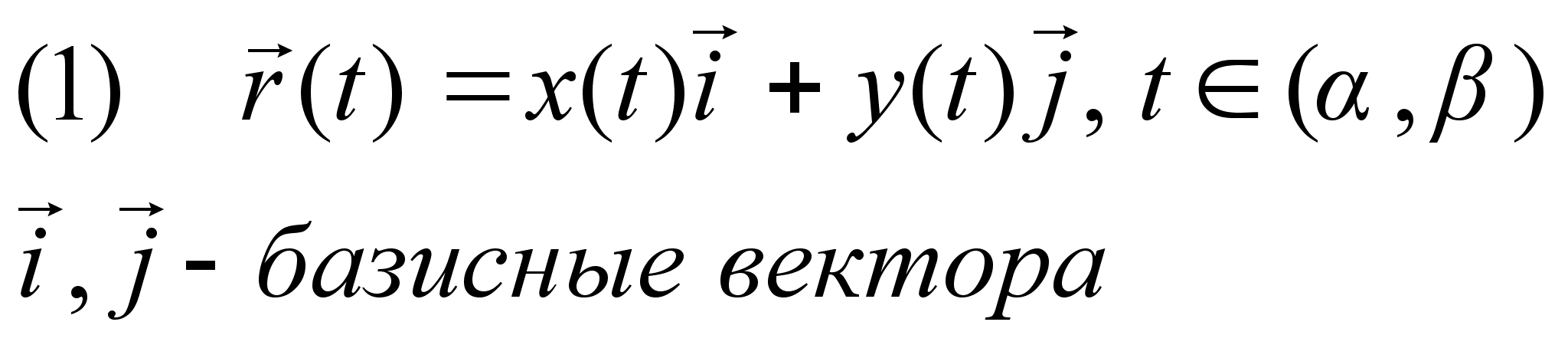
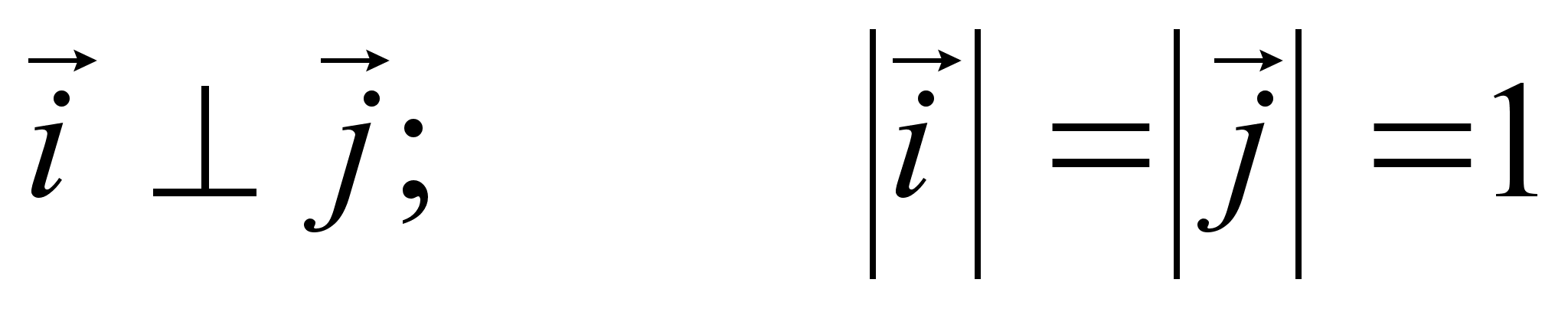
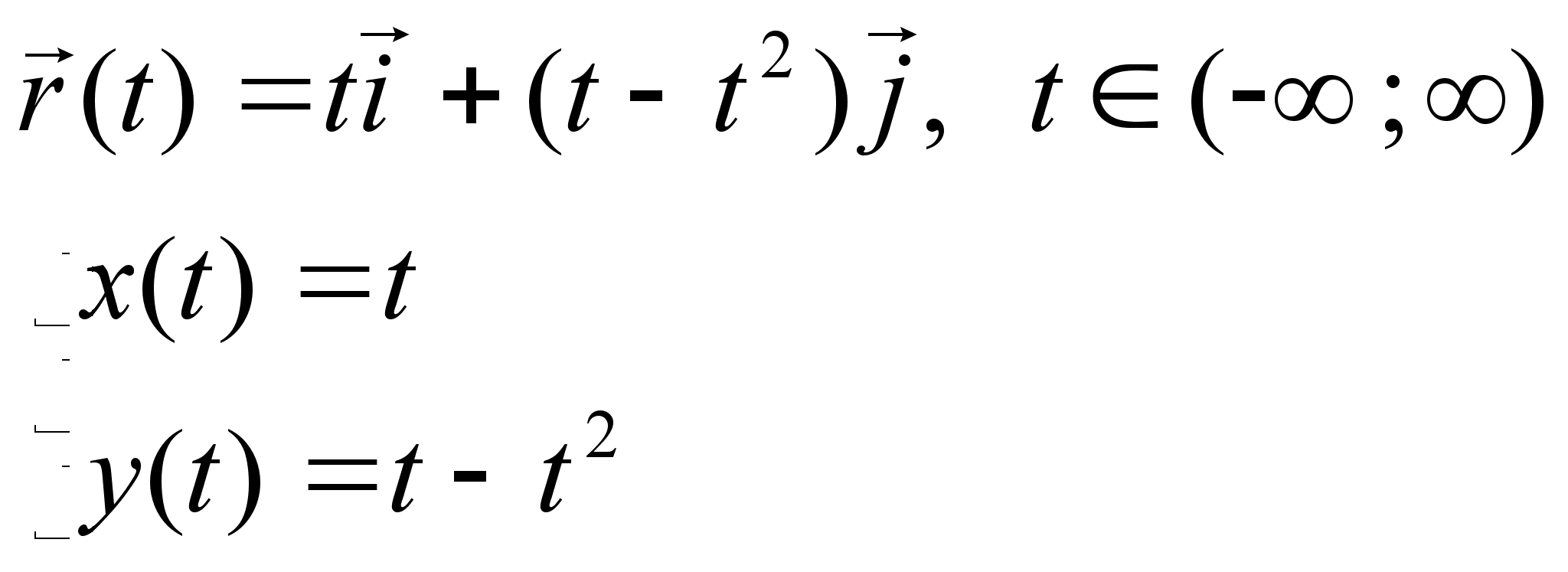
t
0
1
-1
2
3
Ѕ
x(t)
0
1
-1
2
3
Ѕ
y(t)
0
0
-2
-2
-6
1/4
r(t)
0
i
-i-2j
2i-2j
3j-6j
1/2i+1/4j
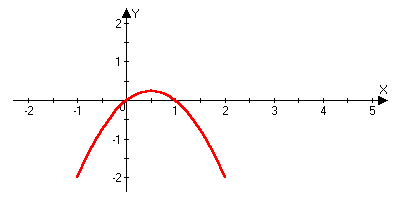
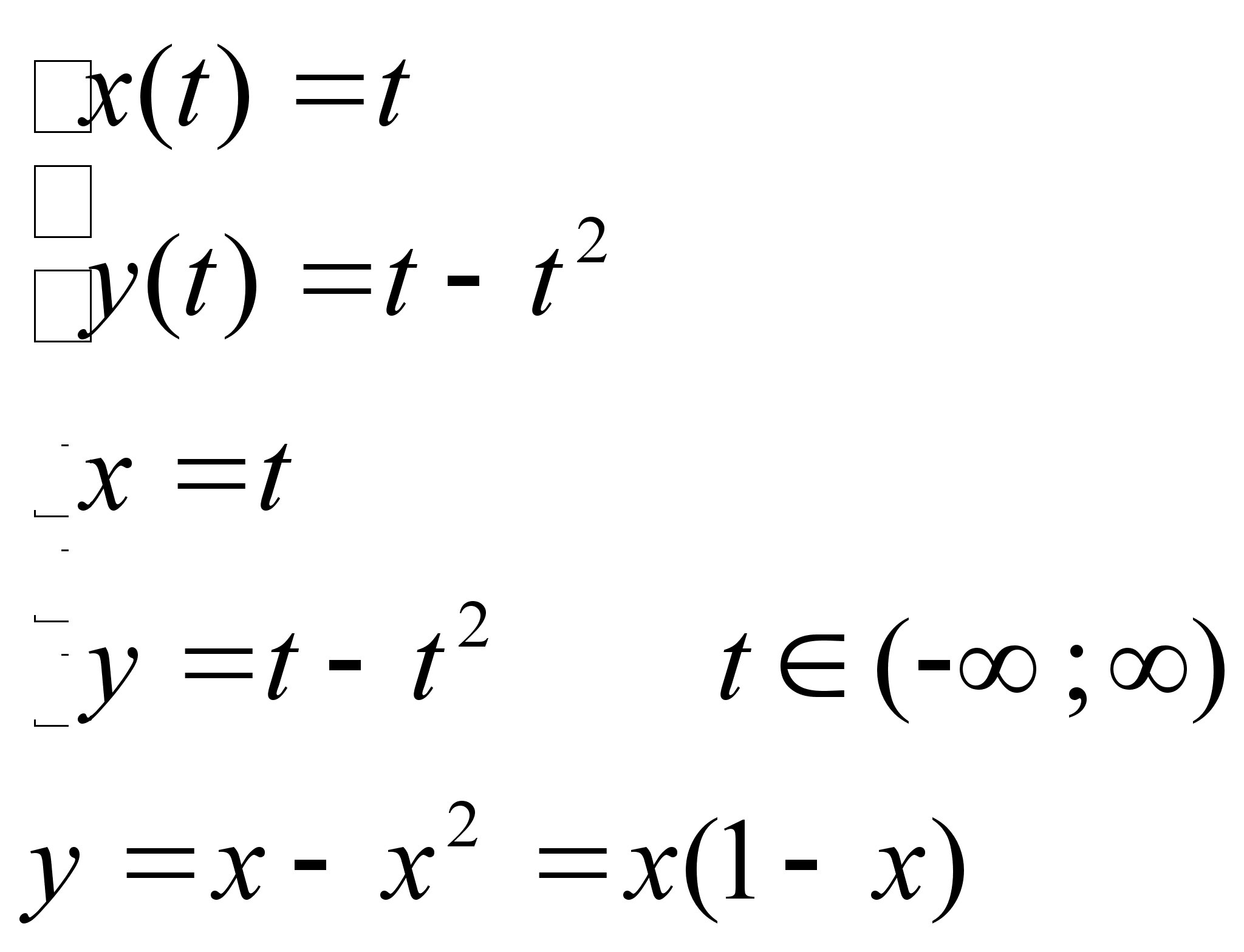
 Называется
параметрическое
задание кривой,
где t
–параметр
Называется
параметрическое
задание кривой,
где t
–параметр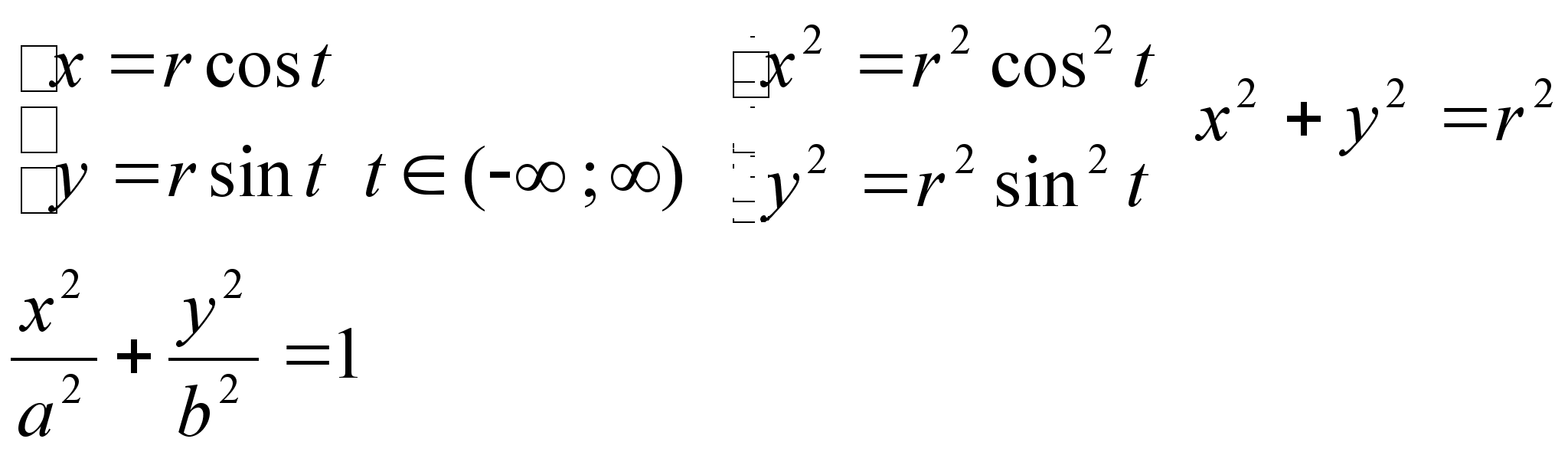
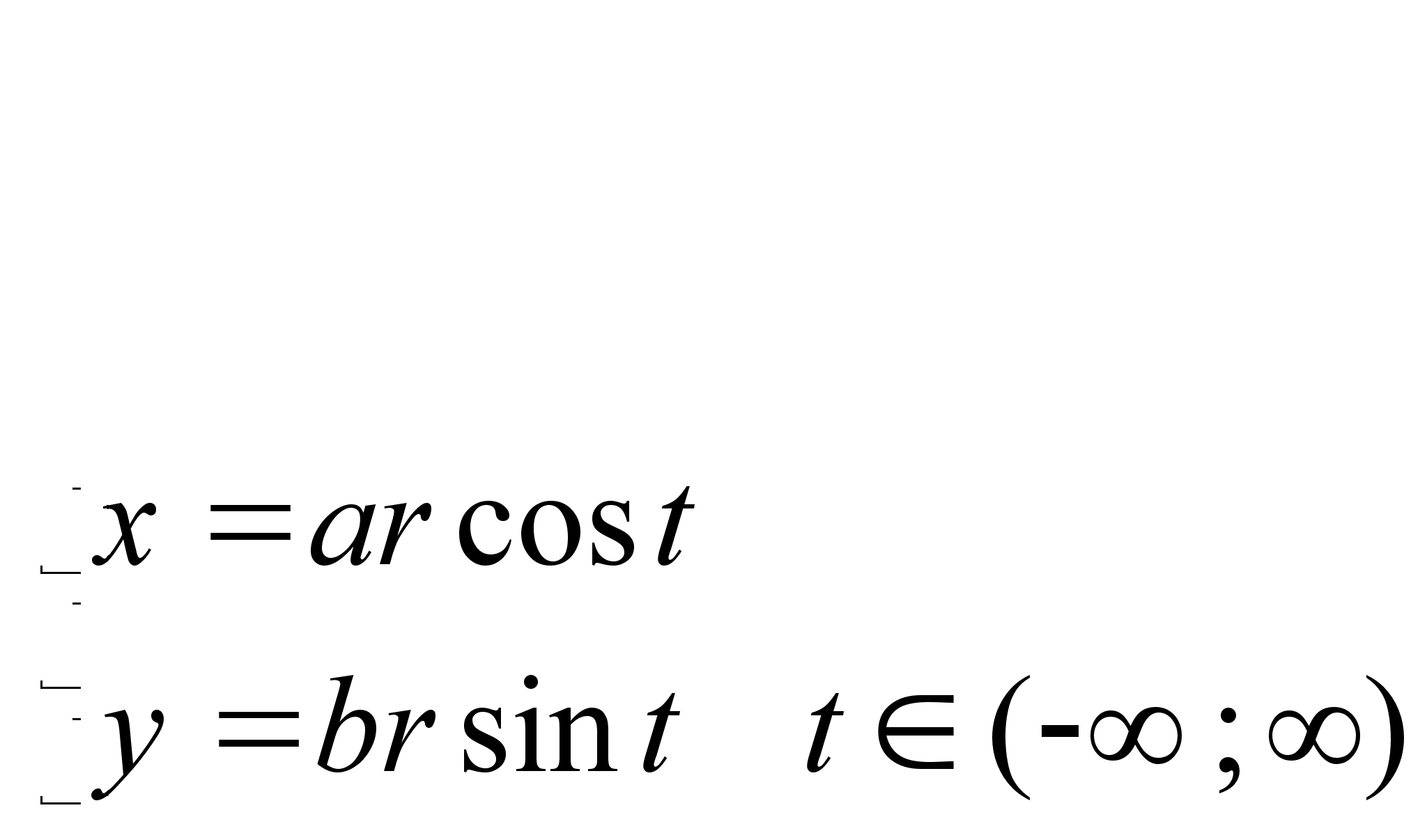
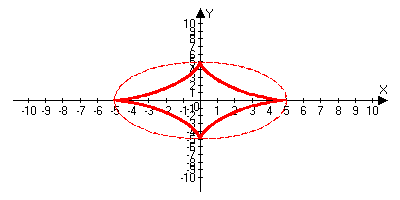
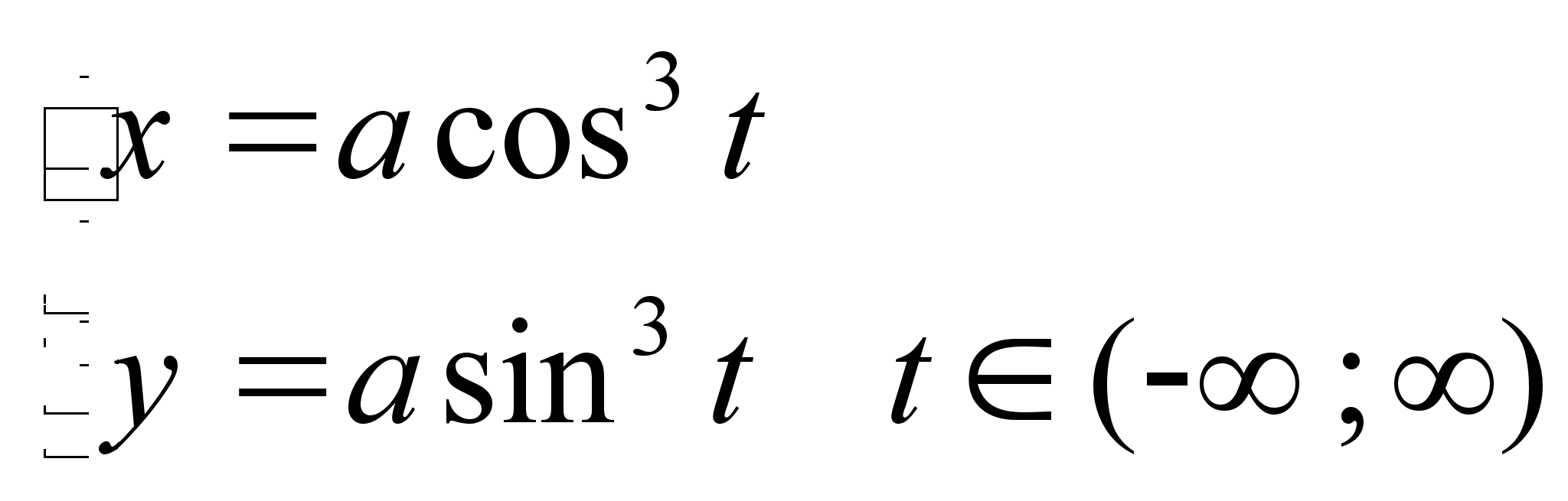
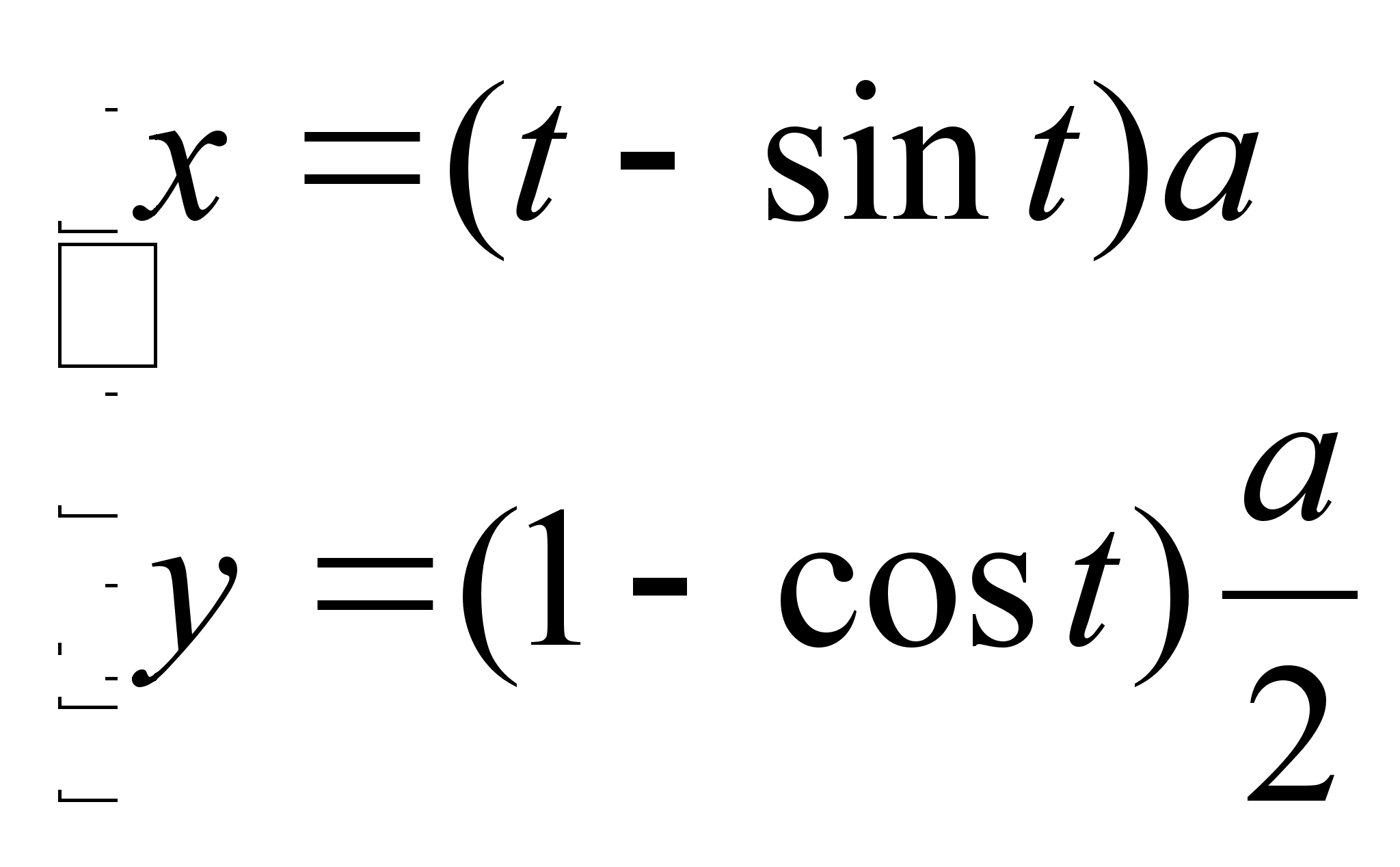
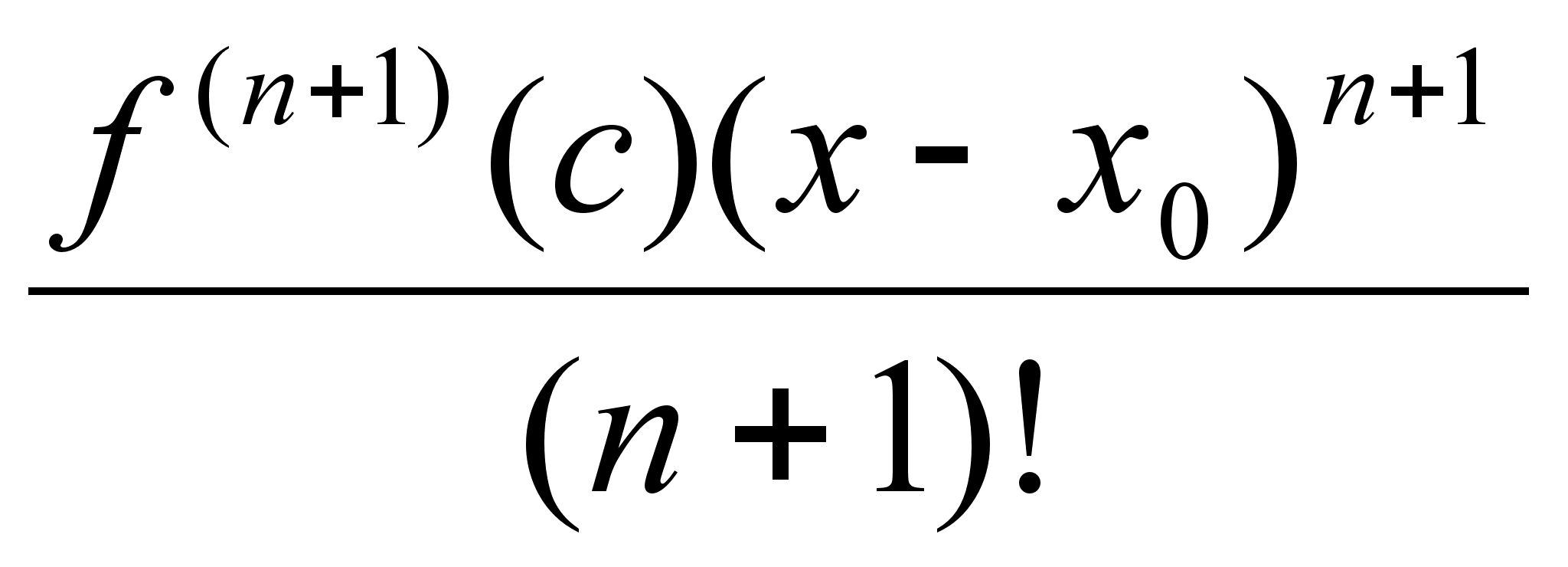 -
остаточный
член в форме
Лангранджа
-
остаточный
член в форме
Лангранджа