Реферат: Математика 1 часть
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СКАЛЯРНЫХ И ВЕКТОРНЫХ ВЕЛИЧИН.
ВЕКТОР
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
КОЛЛИНЕАРНЫЕ И КОМПЛАНАРНЫЕ ВЕКТОРЫ
Величины называют скалярными (скалярами), если они после выбора единиц измерения полностью характеризуются одним числом.
Если некоторая скалярная величина полностью определяется одним числом, не зависящим от выбора осей отсчета, то тогда говорят о чистой скалярной величине или об истинном скаляре.
Если некоторая скалярная величина определяется одним числом, абсолютная величина которого не зависит от выбора осей отсчета, а ее знак зависит от выбора положительного направления на осях координат, то тогда говорят о псевдоскалярной величине
Величина называется вектором (векторной), если она определяется двумя элементами различной природы: алгебраическим элементом - числом, показывающим длину вектора и являющимся скаляром, и геометрическим элементом, указывающим направление вектора.
Геометрически
принято изображать
вектор направленным
отрезком. Зная
координаты
начала и конца
вектора
 и
и
 ,
можно найти
координаты
вектора, определяемого
этими точками
,
можно найти
координаты
вектора, определяемого
этими точками
 ,
т.е. от координат
конца вычитают
координаты
начала вектора.
,
т.е. от координат
конца вычитают
координаты
начала вектора.
Сложение и вычитание
 Сложение
и вычитание
векторов
производят
геометрически
(рис. 7).
Этот способ
называют правилом
треугольника.
Сложение
и вычитание
векторов
производят
геометрически
(рис. 7).
Этот способ
называют правилом
треугольника.
Математически
сложение
записывают
 или
или
 ,
если речь идет
о вычитании
векторов (рис.
7).
,
если речь идет
о вычитании
векторов (рис.
7).
Если
в пространстве
задано несколько
векторов, число
которых больше
двух, то операцию
сложения
(вычитания)
записывают
как
 Геометрически
этот способ
называют правилом
многоугольника.
Геометрически
этот способ
называют правилом
многоугольника.
Умножение
вектора на
скалярную
величину.
При умножении
вектора
 на
скаляр
получают новый
вектор
на
скаляр
получают новый
вектор
 ,
совпадающий
по своему типу
с исходным,
длина (модуль)
которого
изменяется
в
раз, а направление
совпадает с
направлением
исходного
вектора
,
совпадающий
по своему типу
с исходным,
длина (модуль)
которого
изменяется
в
раз, а направление
совпадает с
направлением
исходного
вектора
 ,
если
0, или
противоположно
исходному
вектору, если
< 0.
В
координатной
форме, если
,
если
0, или
противоположно
исходному
вектору, если
< 0.
В
координатной
форме, если
 ,
то
,
то
 .
.
 Два
одинаково
направленных
и параллельных
вектора называют
коллинеарными.
Коллинеарные
векторы могут
быть разной
длины
Два
одинаково
направленных
и параллельных
вектора называют
коллинеарными.
Коллинеарные
векторы могут
быть разной
длины
Два
вектора
 и
и
 называют
коллинеарными,
если существуют
такие два числа
и ,
не равные нулю
одновременно,
что выполняется
равенство
называют
коллинеарными,
если существуют
такие два числа
и ,
не равные нулю
одновременно,
что выполняется
равенство
Три
вектора
 ,
, и
и
 назовем
компланарными,
если существуют
такие три числа
,
и ,
не равные
одновременно
нулю, что выполняется
равенство
назовем
компланарными,
если существуют
такие три числа
,
и ,
не равные
одновременно
нулю, что выполняется
равенство

ТЕМА 2. Действия над векторами
|
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ РАЗЛОЖЕНИЕ ВЕКТОРА ПО КООРДИНАТНЫМ ОРТАМ. СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ |
Скалярным
произведением
двух векторов
В этом
случае результат
представляет
собой проекцию
вектора
Если
скалярное
произведение
двух векторов
равно нулю,
то эти векторы
ортогональны.
Действительно,
если ни один
из векторов
не нулевой,
то, по определению
скалярного
произведения,
последнее
может быть
равно нулю
только тогда,
когда
Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:
где
где ,
и
- углы, которые
составляет
вектор
Если
скалярное
произведение
двух векторов
равно нулю,
то эти векторы
ортогональны.
Действительно,
если ни один
из векторов
не нулевой,
то, по определению
скалярного
произведения,
последнее
может быть
равно нулю
только тогда,
когда
Скалярное произведение векторов в координатной форме
|
ТЕМА 3. Векторное произведение векторов. Смешанное произведение трех
векторов.
|
ПРАВАЯ И ЛЕВАЯ ТРОЙКИ ВЕКТОРОВ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ |
Линейно
независимые
векторы
Три единичных вектора i, j, k, попарно ортогональные друг другу и образующие правую тройку векторов, называют прямоугольной декартовой системой координат.
Углом
между
векторами
Векторное
произведение
обозначают:
. Смешанным
произведением
векторов
Очевидно,
что если
Из определения смешанного произведения следует интересный факт, что произведение не зависит от порядка следования векторов в смешанном произведении, так как объем параллелепипеда (положительный или отрицательный) зависит только от расположения этих векторов в пространстве (левая или правая тройка) потому, что является псевдоскаляром. Следовательно, можно записать
Это свойство смешанного произведения служит обоснованием упрощения записи смешанного произведения:
|
ТЕМА 4. Прямая линия на плоскости.
|
УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ УРАВНЕНИЕ ПРЯМОЙ С ЗАДАННОЙ ТОЧКОЙ И НАПРАВЛЯЮЩИМ ВЕКТОРОМ УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ ТОЧКАМ |
На плоскости, заметим, могут быть заданы только двухмерные, или плоские преобразования.
Уравнение
По определению линия — это есть соотношение, связывающее координаты точек некоторой области пространства, и, причем только эти координаты. Уравнение представляет собой аналитическую запись уравнения любой плоской линии.
Если вместо
Известно, что уравнение прямой имеет вид:
По условию задачи k задан. Точка M (x0 ,y0) должна также принадлежать искомой прямой и, по определению линии, обращать уравнение прямой в тождество. Воспользуемся этим и подставим значения x0 и y0 в уравнение, получим :
В последнем уравнении неизвестно b. Элементарным преобразованием из последнего уравнения получим
Найденное b подставим в уравнение и окончательно
Уравнение является уравнением прямой, проходящей через данную точку в заданном направлении.
Неизвестен
k -
угловой коэффициент
наклона линии
по отношению
к положительному
направлению
0X.
Однако, зная
общий вид
уравнения
прямой (
где
Подставим найденное k в любое из уравнений и определим b
Подставим найденные k и b в уравнение прямой
Преобразуем последнее уравнение
и окончательно
Данное уравнение называется уравнением прямой, проходящей через две точки. |
ТЕМА 5. Прямая и плоскость в пространстве.
|
ПРЯМАЯ КАК ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ |
Любая поверхность есть геометрическое место точек, ее составляющих, определенное уравнением
Иными словами, все точки, которые удовлетворяют этому уравнению, будут принадлежать поверхности. Пусть в пространстве XYZ задана плоскость и к ней в точке K проведем
вектор нормали
ориентирована произвольно в пространстве,
то вектор
Выберем
на плоскости
точку
M, не совпадающую
с K и свяжем
с этой точкой
вектор
Получаем
нормальное
уравнение
плоскости:
Однако, если
представим
вектор
Зная, что для любой точки, принадлежащей плоскости, с координатами (A,B.C) можно вычислить направляющие косинусы
с учетом которых можно уравнение преобразовать
которое известно, как уравнение плоскости.
Прямой линией
назовем пересечение
двух плоскостей
в пространстве.
Определение
можно записать
математически
как
Пусть плоскости и (рис. 6) заданы уравнениями:
и
где
система из этих уравнений:
пространстве, записанными в векторной форме. |
ТЕМА 6Матрицы и определители.
|
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ ОПРЕДЕЛИТЕЛИ ИХ СВОЙСТВА СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ. |
Матрицей
A называется
любая прямоугольная
таблица, составленная
из чисел
Суммой
двух матриц
Произведением
матрицы
матрица C = (cij), у которой (cij) = (kaij).
Если матрица
A не нулевая,
т.е. существует
хотя бы один
Определителем
n-го порядка
называется
число
Количество строк (или столбцов) в определителе называется порядком определителя Решением системы называется совокупность из n чисел (с1, с2, ..., сn), которые, будучи подставленными в систему на место неизвестных x1, x2, ..., xn, обращают все уравнения системы в истинные равенства Систему уравнений, имеющую хотя бы одно решение, называют совместной, систему, не имеющую решений, - несовместной.
Решения
Если совместная система имеет единственное решение, то она называется определнной; если совместная система имеет по крайней мере два различных решения, то она называется неопределенной.
Формулы
Крамера
Метод Гаусса. Пусть А - невырожденная матрица, то есть det A 0, и, следовательно, она имеет обратную матрицу А-1. Умножив обе части на А-1 слева, получаем: А-1 (А Х) = А-1 В (А-1 А)Х = А-1 В Е Х = А-1 В, то есть Х = А-1 В и есть искомое решение системы (14). Действительно, подставив (16) в (14), получим А (А-1 В) = (А-1 А)В = Е В = В. |
ТЕМА 7. Предел функции.
|
ПОНЯТИЕ ФУНКЦИИ. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ |
Если
некоторому
множеству
значений
Если
некоторому
множеству
значений
Для того
чтобы обозначить,
что
Если
невозможно
выразить
Если
надо выделить
некоторое
частное значение
функции, соответствующее
какому-либо
конкретному
значению
Если каждому
натуральному
n по
какому-либо
известному
правилу поставлено
в соответствие
некоторое
число
Последовательность
Последовательность
ТЕОРЕМА: Для
того чтобы
последовательность Эта теорема дает связь между пределом сходящейся последовательности и бесконечно малыми.
Функции
Функция
|
ТЕМА 8. Производная.
|
ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ |
Если отношение
производной
функции
значении
Производная
функции
Из определения
ясно - в случае
убывающей
функции производная
отрицательна.
Это объясняется
тем, что
Производная
алгебраической
суммы равна
алгебраической
сумме производных.
Производная
произведения
равна
Если функция
Если
Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д.
Пример 1.
Пример 2.
Пример 3.
Пример
4.
|
ТЕМА 9. Экстремум функции.
|
ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ ЭКСТРЕМУМ ФУНКЦИИ ПРАВИЛО ЛОПИТАЛЯ |
Функция
называется
возрастающей
на некотором
промежутке
Функция
называется
убывающей
на некотором
промежутке
Если
функция определима
и непрерывна
на некотором
отрезке
Функция
Функция
Правило поиска экстремальных точек
1. Находим область
определения
функции
2. Находим производную
функции
3. Определяем
критические
точки
4. Исследуем
5. Если слева
от точки
6. Если слева
от точки
7. Если
Если функции
Теорема Коши.
Если при соблюдении
предположений
относительно
функций
Эта
теорема позволяет
формулировать
правило Лопиталя.
При раскрытии
неопределенности
вида
|
ТЕМА 10
ТЕМА 11
ТЕМА 12
ТЕМА 13
ТЕМА 14
ТЕМА 15
 ).
Эта операция
обозначается
).
Эта операция
обозначается
 .В
частности,
скалярный
квадрат вектора
равен квадрату
его длины, т.е.
.В
частности,
скалярный
квадрат вектора
равен квадрату
его длины, т.е.
 .
Если один из
перемножаемых
векторов
единичный,
то:
.
Если один из
перемножаемых
векторов
единичный,
то: .
. .
Следовательно,
любой вектор
можно представить
как
.
Следовательно,
любой вектор
можно представить
как
 ,
где
,
где
 - проекции вектора
- проекции вектора
 ,
т.е.
,
т.е.
 .
. Если
вектор представлен
через проекции
на базисные
векторы, то
говорят о
разложении
вектора
Если
вектор представлен
через проекции
на базисные
векторы, то
говорят о
разложении
вектора
 .
.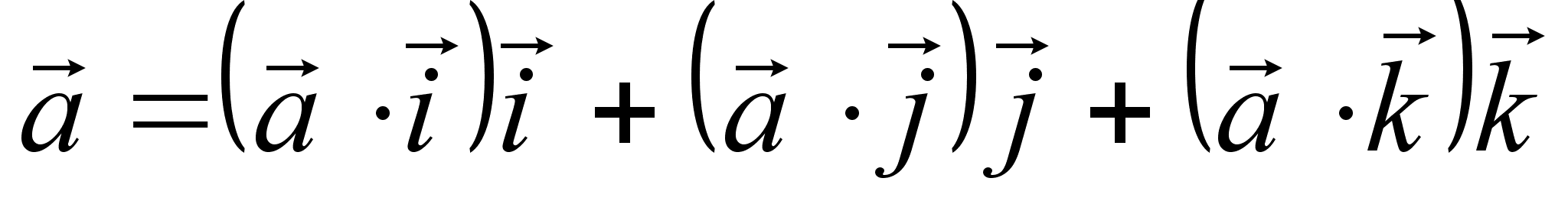 ,
, ,
,
 и
и
 есть
скалярное
произведение
вектора
есть
скалярное
произведение
вектора


 .
. Под
векторным
произведением
векторов
Под
векторным
произведением
векторов
 ,
имеющий длину
и направленный
перпендикулярно
к плоскости
,
имеющий длину
и направленный
перпендикулярно
к плоскости
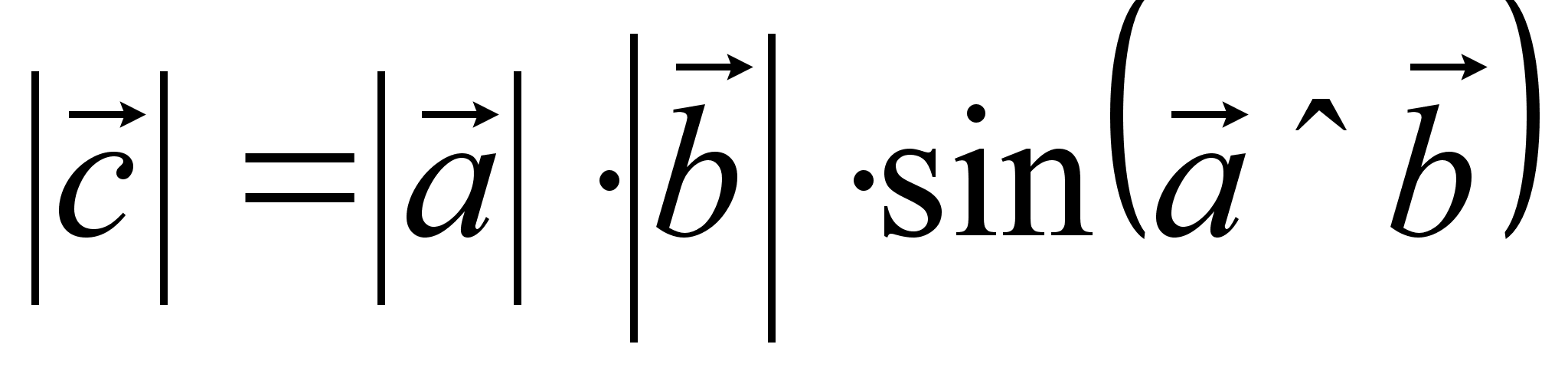 ,определяемой
векторами
,определяемой
векторами
 или
или
 .
Очевидно, что
.
Очевидно, что
 (из определения
векторного
произведения).
(из определения
векторного
произведения).
 .
Векторное
произведение
подчиняется
только распределительному
закону:
.
Векторное
произведение
подчиняется
только распределительному
закону: .
. назовем
число К, равное
объему
параллелепипеда,
построенного
на этих векторах
(рис.
10)
и вычисляемое
как:
назовем
число К, равное
объему
параллелепипеда,
построенного
на этих векторах
(рис.
10)
и вычисляемое
как:
 =0.
=0. или
или
 .
. .
. ,
связывающее
две переменные
x и y называется
уравнением
линии L в выбранной
плоской системе
координат,
если координаты
любой точки
этой линии L
удовлетворяют
уравнению, а
любые другие
координаты
точек, не принадлежащих
лини L, не удовлетворяют
указанному
уравнению.
,
связывающее
две переменные
x и y называется
уравнением
линии L в выбранной
плоской системе
координат,
если координаты
любой точки
этой линии L
удовлетворяют
уравнению, а
любые другие
координаты
точек, не принадлежащих
лини L, не удовлетворяют
указанному
уравнению.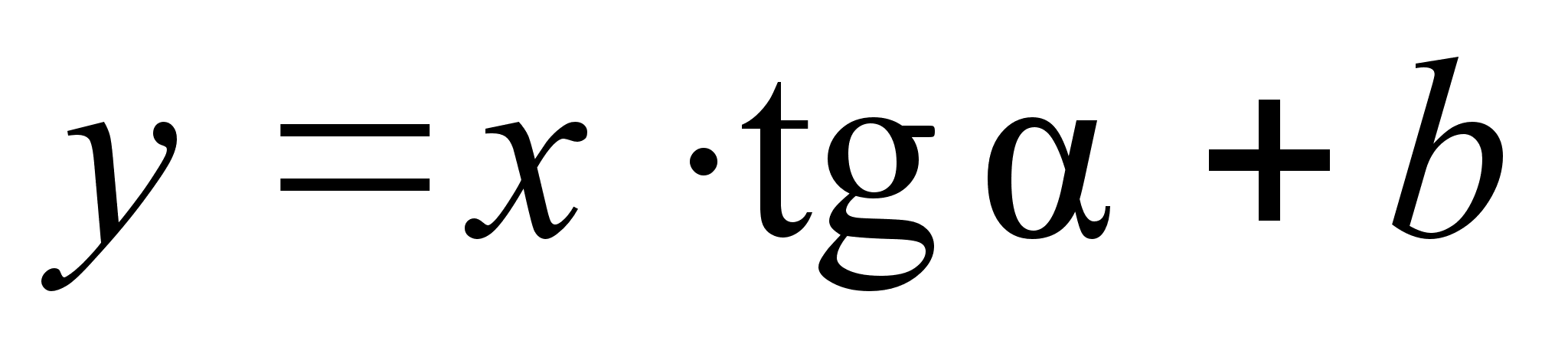 .
. подставить
его численное
значение, от
получим известное
уравнение
прямой
подставить
его численное
значение, от
получим известное
уравнение
прямой
 .
. .
. .
. .
. ) и учитывая,
что обе точки
расположены
на искомой
линии, можно
составить
следующую
систему:
) и учитывая,
что обе точки
расположены
на искомой
линии, можно
составить
следующую
систему: ,
, – координаты
точек M1
и M2 соответственно,
(известны),
а k и b – искомые
неизвестные.
Вычитая из
первого уравнения
второе, выразим
k,
– координаты
точек M1
и M2 соответственно,
(известны),
а k и b – искомые
неизвестные.
Вычитая из
первого уравнения
второе, выразим
k,
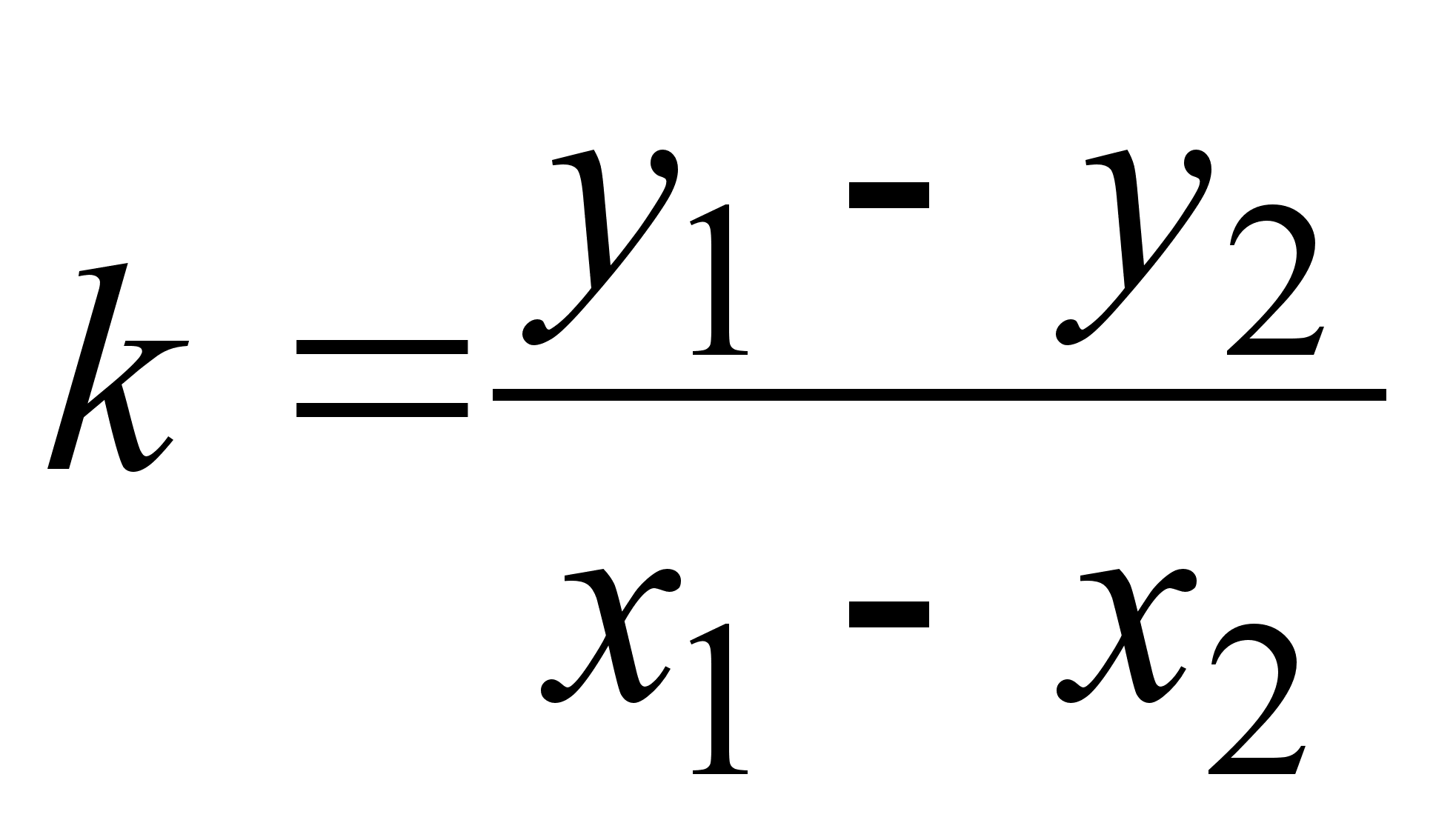 .
. .
. .
.
 .
.
 УРАВНЕНИЕ
ПЛОСКОСТИ.
УРАВНЕНИЕ
ПЛОСКОСТИ.
 .
Так как плоскость
.
Так как плоскость
 .
Очевидно,
что
.
Очевидно,
что
 ,
где
,
где  ,
из уравнения
получаем
,
из уравнения
получаем
 .
. .
. как
как
 ,
а вектор
,
а вектор

 ,
тогда подставив
полученные
выражения,
получаем
,
тогда подставив
полученные
выражения,
получаем


 ,
, .
.
 ,
, ;
;
 ,
,

 Уравнения
называются
общими уравнениями
прямой в
Уравнения
называются
общими уравнениями
прямой в
 ,
которые называют
элементами
матрицы и
обозначается
,
которые называют
элементами
матрицы и
обозначается Если
в выражении
(1)
Если
в выражении
(1)
 ,
то говорят о
квадратной
матрице, а если
,
то говорят о
квадратной
матрице, а если
 ,
то о прямоугольной.
,
то о прямоугольной. и
и
 называется
матрица C,
у которой
называется
матрица C,
у которой
 ,
и записывают
,
и записывают
 .
. на
число
на
число
 называется
такая
называется
такая
 такое,
что 1) у матрицы
A имеется минор
такое,
что 1) у матрицы
A имеется минор
 го
порядка
го
порядка
 ;
2) всякий минор
матрицы A порядка
;
2) всякий минор
матрицы A порядка
 и выше равен
нулю, тогда
число
и выше равен
нулю, тогда
число
 .
Из определения
вытекает, что
1) ранг любой
прямоугольной
матрицы не
должен быть
больше, чем
минимальный
размер матрицы.
Если матрица
квадратная,
то ранг не может
быть больше,
чем размер
матрицы. Математически
это можно выразить
так
.
Из определения
вытекает, что
1) ранг любой
прямоугольной
матрицы не
должен быть
больше, чем
минимальный
размер матрицы.
Если матрица
квадратная,
то ранг не может
быть больше,
чем размер
матрицы. Математически
это можно выразить
так
 2) если все элементы
матрицы A равны
нулю, т. е.
2) если все элементы
матрицы A равны
нулю, т. е.
 ,то ранг этой
матрицы тоже
будет равен
нулю
,то ранг этой
матрицы тоже
будет равен
нулю
 .
. равное алгебраической
сумме
равное алгебраической
сумме
 ,
где
,
где
 есть алгебраические
дополнения
элемента
есть алгебраические
дополнения
элемента
 ,
а
,
а
 -
есть соответствующие
миноры, т.е.
определители
(n-1)-го порядка,
получающиеся
из исходного
определителя
вычеркиванием
первой строки
и n-го столбца,
на пересечение
которых находится
элемент
-
есть соответствующие
миноры, т.е.
определители
(n-1)-го порядка,
получающиеся
из исходного
определителя
вычеркиванием
первой строки
и n-го столбца,
на пересечение
которых находится
элемент
 и
и
 считают различными,
если хотя бы
одно из чисел
считают различными,
если хотя бы
одно из чисел
 не совпадает
с соответствующим
числом
не совпадает
с соответствующим
числом

 .
. поставлено
по определенному
правилу F
во взаимнооднозначное
соответствие
некоторое
множество
поставлено
по определенному
правилу F
во взаимнооднозначное
соответствие
некоторое
множество
 ,
то тогда говорят,
что на множестве
,
то тогда говорят,
что на множестве
 есть
функция от
есть
функция от ,
используют
следующие
виды записи:
,
используют
следующие
виды записи:
 ;
;  ;
;  и т.д.
и т.д. ;
;  ;
;  и т.д.
и т.д. ,
тогда записывают:
,
тогда записывают:
 .
. ,
тогда говорят,
что задана
последовательность
,
тогда говорят,
что задана
последовательность
 ,
которая
обозначается
как
,
которая
обозначается
как
 Правило, по
которому
формируется
последовательность
Правило, по
которому
формируется
последовательность
 ,
обозначается
как
,
обозначается
как
 и называется
общим числом
последовательности.
Число
и называется
общим числом
последовательности.
Число
 назовем пределом
последовательности
назовем пределом
последовательности при
при
 значений функции
значений функции
 и это записывают
как
и это записывают
как
 .
. называется
бесконечно
большой, если
для любого
числа
называется
бесконечно
большой, если
для любого
числа
 найдется номер
N, такой
что для всех
найдется номер
N, такой
что для всех
 выполняется
неравенство
выполняется
неравенство
 .
Геометрически
это обозначает,
что какой бы
большой номер
числа последовательности
мы ни взяли,
то всегда найдется
число, принадлежащее
этой последовательности,
и лежащее правее
выбранного,
если последовательность
составлена
из положительных
чисел, или левее,
если последовательность
составлена
из отрицательных.
Это записывают
.
Геометрически
это обозначает,
что какой бы
большой номер
числа последовательности
мы ни взяли,
то всегда найдется
число, принадлежащее
этой последовательности,
и лежащее правее
выбранного,
если последовательность
составлена
из положительных
чисел, или левее,
если последовательность
составлена
из отрицательных.
Это записывают
 ,
или
,
или
 .
.
 ,
где
,
где
 .
. или
в точке
или
в точке
 .А
так как функция
при этом должна
быть непрерывной
в точке
.А
так как функция
при этом должна
быть непрерывной
в точке
 .
. называется
непрерывной
в точке
называется
непрерывной
в точке
 ,
если для всех
положительных,
сколь угодно
малых
,
если для всех
положительных,
сколь угодно
малых  ,
для которого
выполняется
неравенство
,
для которого
выполняется
неравенство
 для всех
для всех
 .
. ПРОИЗВОДНАЯ,
ЕЁ СВОЙСТВА
И ГЕОМЕТРИЧЕС-КИЙ
СМЫСЛ.
ПРОИЗВОДНАЯ,
ЕЁ СВОЙСТВА
И ГЕОМЕТРИЧЕС-КИЙ
СМЫСЛ. имеет предел
при
имеет предел
при
 этот предел
называют
этот предел
называют .
.
 ,
если
,
если будет
отрицательным.
На этом свойстве
производной
основано
исследование
поведения
функции на
возрастание
(убывание) на
заданном отрезке.
будет
отрицательным.
На этом свойстве
производной
основано
исследование
поведения
функции на
возрастание
(убывание) на
заданном отрезке. .
. .
. и функция
и функция
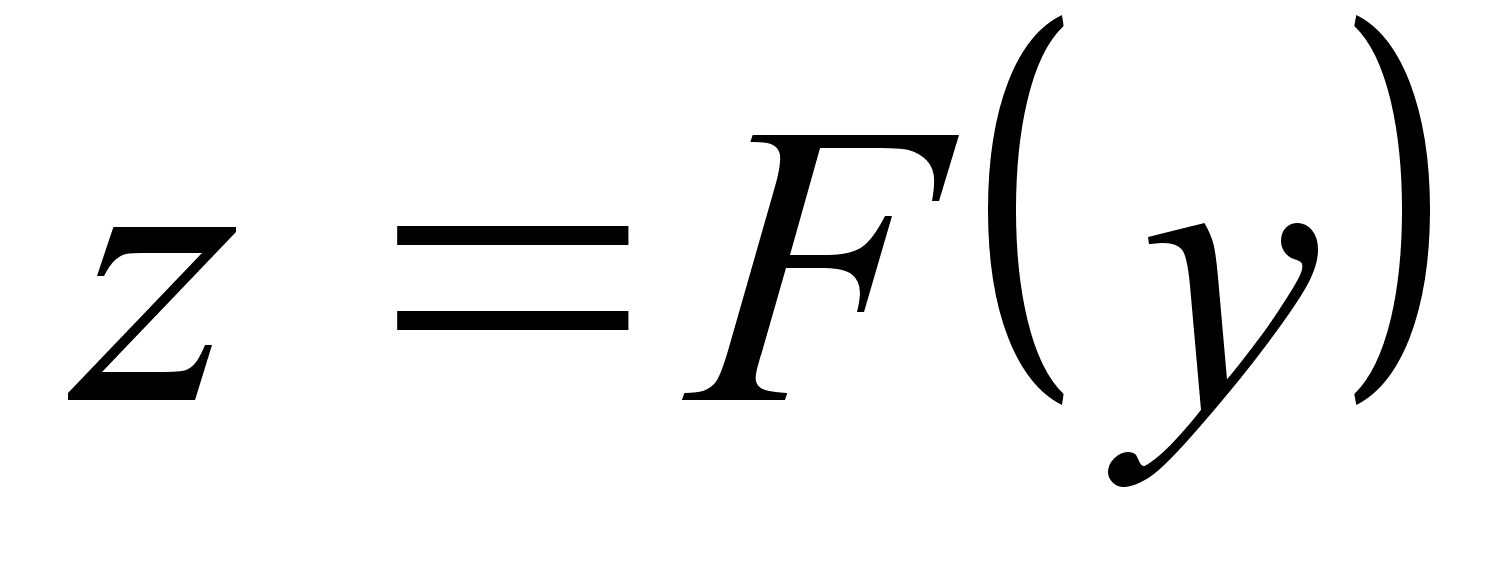 имеет в точке
имеет в точке
 ,
тогда сложная
функция
,
тогда сложная
функция
 имеет в точке
имеет в точке
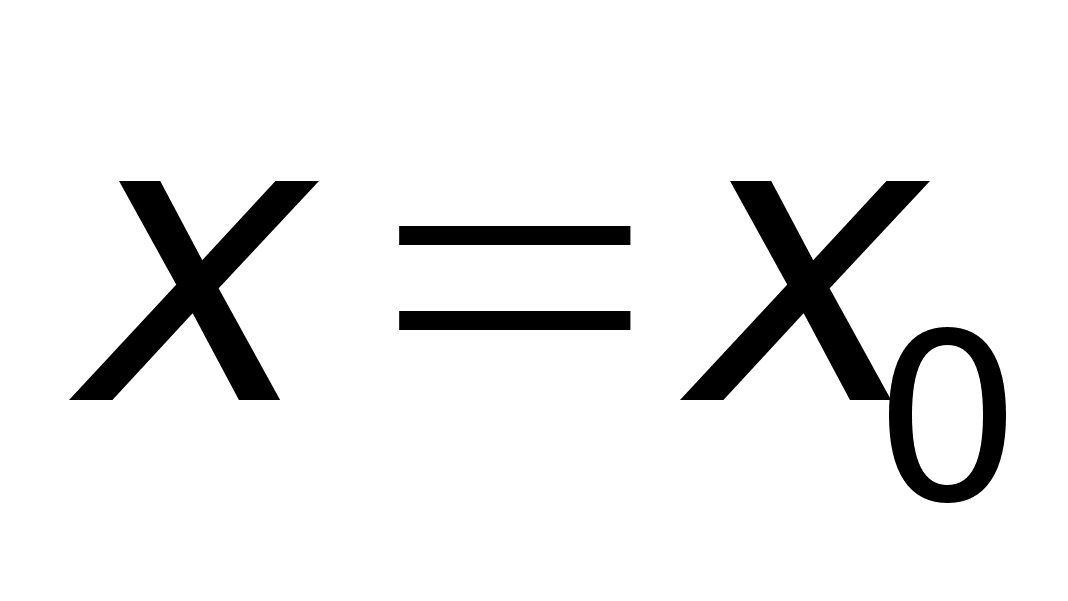 производную,
равную
производную,
равную

 также имеет
производную
и имеет место
соотношение
также имеет
производную
и имеет место
соотношение
 .
. ;
;
 ;
;
 ;
...;
;
...;
 ;
;
 .
. ;
;
 ;
;
 ;
;
 ;
;
 .
Так как
.
Так как
 ,
то можно предположить,
что в данном
случае функцию
можно дифференцировать
бесконечное
количество
раз.
,
то можно предположить,
что в данном
случае функцию
можно дифференцировать
бесконечное
количество
раз.
 .
.
 .
Как и во втором
примере, эта
функция дифференцируема
бесконечное
количество
раз.
.
Как и во втором
примере, эта
функция дифференцируема
бесконечное
количество
раз.
 .
.
 ;
;
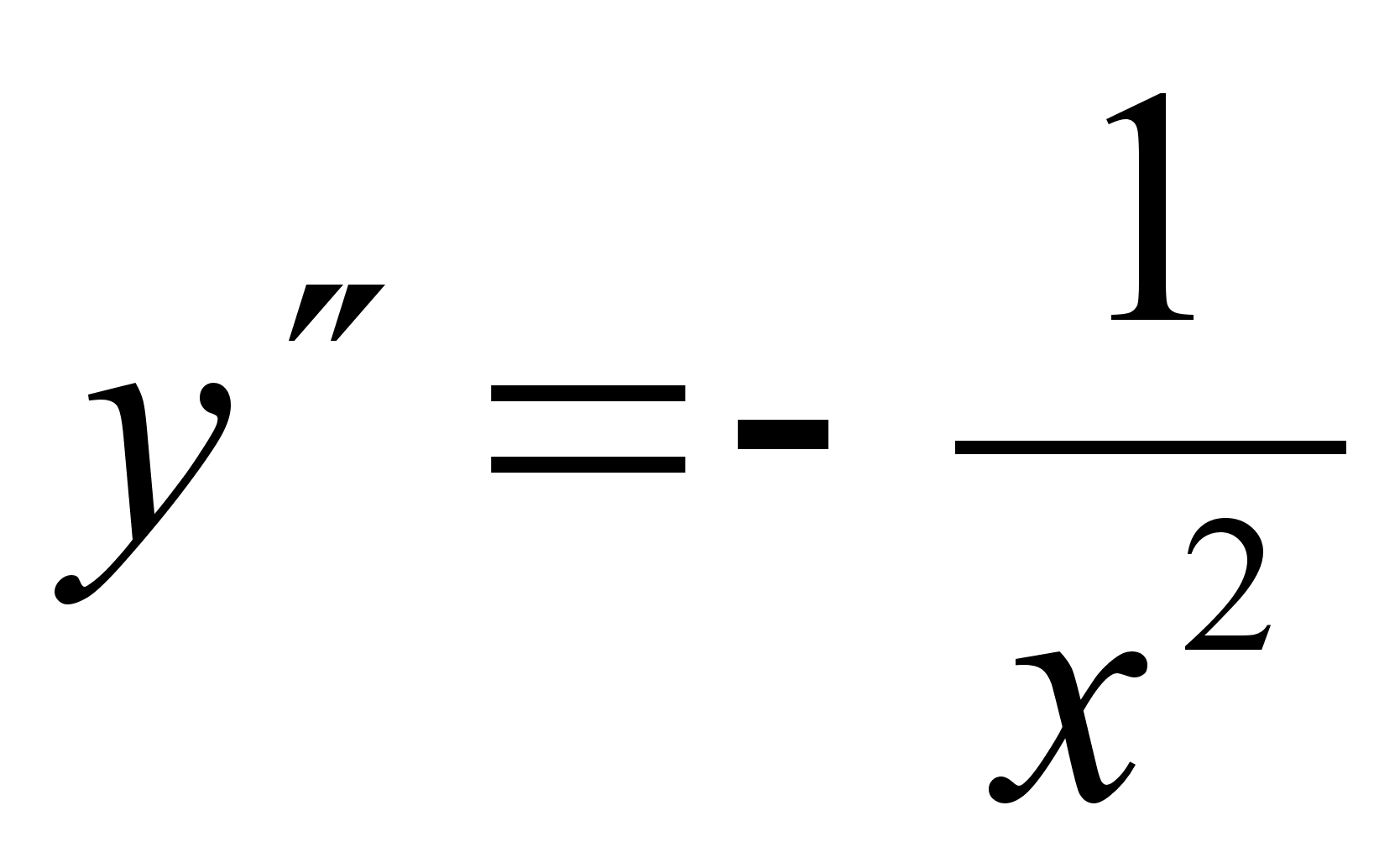 ;
;
 ;
…
;
…
 ;
...Как следует
из приведенных
примеров, разные
функции ведут
себя по-разному
при многократном
дифференцировании.
Одни имеют
конечное
количество
производных
высших порядков,
другие – переходят
сами в себя,
а третьи, хотя
и дифференцируемы
бесконечное
количество
раз, но порождают
новые функции,
отличные от
исходной. Однако
все сформулированные
теоремы о
производных
первых порядков
выполняются
для производных
высших порядков.
;
...Как следует
из приведенных
примеров, разные
функции ведут
себя по-разному
при многократном
дифференцировании.
Одни имеют
конечное
количество
производных
высших порядков,
другие – переходят
сами в себя,
а третьи, хотя
и дифференцируемы
бесконечное
количество
раз, но порождают
новые функции,
отличные от
исходной. Однако
все сформулированные
теоремы о
производных
первых порядков
выполняются
для производных
высших порядков. ,
если на этом
промежутке
большему значению
независимой
переменной
соответствует
большее значение
функции, т.е.
если
,
если на этом
промежутке
большему значению
независимой
переменной
соответствует
большее значение
функции, т.е.
если
 и
и

 ,
то выполняется
,
то выполняется
 .
. .
. и на концах
отрезка имеет
знак, то на
указанном
отрезке эта
функция имеет
по крайне мере
хотя бы одну
точку, в которой
и на концах
отрезка имеет
знак, то на
указанном
отрезке эта
функция имеет
по крайне мере
хотя бы одну
точку, в которой
 .
. достигает
своего максимума
в точке
достигает
своего максимума
в точке
 ,
если ее значение
в окрестности
этой точки
меньше, чем
значение функции
в этой же точке
,
если ее значение
в окрестности
этой точки
меньше, чем
значение функции
в этой же точке
 .
. .
. .
. ,
а справа
,
а справа
 ,
то тогда говорят,
что точка
,
то тогда говорят,
что точка
 является точкой
максимума.
является точкой
максимума. ,
а справа
,
а справа
 ,
то тогда говорят,
что точка
,
то тогда говорят,
что точка
 является точкой
минимума.
является точкой
минимума. слева и справа
от критической
точки не меняет
знак, то говорят,
что
слева и справа
от критической
точки не меняет
знак, то говорят,
что
 является точкой
перегиба функции.
является точкой
перегиба функции. и
и
 непрерывны
при
непрерывны
при
 ,
где
,
где
 не обращается
в нуль при
вычитании
указанных
условий, тогда
можно сформулировать
следующую
теорему.
не обращается
в нуль при
вычитании
указанных
условий, тогда
можно сформулировать
следующую
теорему. стремится к
некоторому
числу при
стремится к
некоторому
числу при
 ,
то тогда к такому
же числу будет
стремиться
отношение
функций
,
то тогда к такому
же числу будет
стремиться
отношение
функций
 .
. можно функцию
числителя
можно функцию
числителя
 ,
соответственно,
и рассматривать
предел
,
соответственно,
и рассматривать
предел
 вместо
вместо
 в указанной
точке.
в указанной
точке.