Реферат: Математическая Логика
Конспекты лекций по математической логике.
1. Теория алгоритмов
1.1 Различные подходы к определению алгоритма:
10. Неформальное понятие алгоритма (последовательность инструкций для выполнения действия).
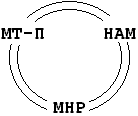
20. Машина с неограниченными регистрами (МНР).
30 Машина Тьюринга – Поста (МТ-П).
40 Нормальные алгоритмы Маркова (НАМ).
1.1.1 Машина с неограниченными регистрами (МНР).
![]() Имеется некое устройство, в котором счетное число
ячеек памяти (регистров), в которых хранятся целые числа.
Имеется некое устройство, в котором счетное число
ячеек памяти (регистров), в которых хранятся целые числа.
Допустимые команды:
Z(n) - обнуление регистра Rn.
S(n) - увеличение числа в регистре Rn на 1.
T(m,n) - копирует содержимое Rm в регистор Rn.
I(p,q,n) - если содержимое Rp = Rq то выполняется команда с номером n , если нет
следующая.
Программа для МНР должна быть последовательностью команд Z, S, T, I с определенным порядком, выполняемые последовательно.
Тезис Черча (Churcha): Первое и второе определение алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть представлен в программе для МНР.
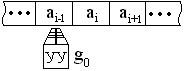 1.1.2 Машина Тьюринга - Поста.
1.1.2 Машина Тьюринга - Поста.
Имеется
устройство просматривающее бесконечную ленту, где есть ячейки содержащие
элементы алфавита: ![]() , где
, где ![]() - пустой символ (пустое
слово), который может принадлежать и не принадлежать А. Также
существует управляющая головка (устройство) (УУ)/(УГ), которая в
начальный момент расположена в определенном месте, в состоянии
- пустой символ (пустое
слово), который может принадлежать и не принадлежать А. Также
существует управляющая головка (устройство) (УУ)/(УГ), которая в
начальный момент расположена в определенном месте, в состоянии ![]() . Также существуют внутренние состояния машины:
. Также существуют внутренние состояния машины: ![]()
Слово в данном алфавите - любая конечная упорядоченная последовательность букв данного алфавита, притом длина слова это количество букв в нем (у пустого слова длина 0).
Допустимые команды:
|
1) 2) |
Последовательность команд называется программой, если в этой последовательности не встречается команд с одинаковыми левыми частями. Машина останавливается если она не находит команды с левой частью подобной текущей. |
1.1.3 Нормальные алгоритмы Маркова.
Тип
машины перерабатывающий слова, в которой существует некий алфавит ![]() , для которого W -
множество всех слов.
, для которого W -
множество всех слов.
Допустимые команды: (Для машин этого типа важна последовательность команд.)
|
|
Пример: Программа:
|
1.1.4 Реализация
функции натурального переменного. ![]()
![]() но
мы допускаем не всюду определенную функцию.
но
мы допускаем не всюду определенную функцию.
![]()
![]()
![]() то это означает, что
то это означает, что ![]()
притом
![]() , если f не определена,
то и программа не должна ничего выдавать.
, если f не определена,
то и программа не должна ничего выдавать.
![]()
![]()
![]()
![]()
![]()
![]()
притом
![]() , если f не определена,
то и программа не должна ничего выдавать.
, если f не определена,
то и программа не должна ничего выдавать.
(![]() , а числа представляются в виде
, а числа представляются в виде ![]() ,например
,например ![]() .)
.)
1.2 Эквивалентность трех подходов к понятию алгоритм.
1.2.1 Теорема об эквивалентности понятия вычислимой функции.
![]() вычислима: (
вычислима: (![]() )
)
1) Если существует программа МНР, которая вычисляет эту функцию.
2) Если существует программа МТ-П, которая вычисляет эту функцию.
3) Если существует программа НАМ, которая вычисляет эту функцию.
Использование
НАМ: ![]()
![]()
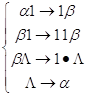
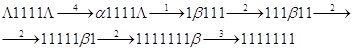
 Теор.:
Классы функций вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Теор.:
Классы функций вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Пусть
![]() которая вычисляется на
МТ-П, вычислим её на НАМ.
которая вычисляется на
МТ-П, вычислим её на НАМ.
МТ-П: 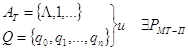
НАМ: ![]()
Команда
МТП: ![]() преобразуется по правилам:
преобразуется по правилам:
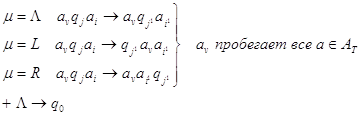
Команда
МТП: ![]()
![]()
![]()
2. Булевы функции.
2.1 Основные определения
2.1.1 Декартово произведение
![]() -
мн-во всевозможных упорядоченных пар элементов из А и В.
-
мн-во всевозможных упорядоченных пар элементов из А и В.
Пример: ![]()
![]()
![]()
![]()
2.1.2 Декартова степень произвольного множества.
Опр: ![]() -
множество всевозможных упорядоченных наборов длины n , элементов
множества А.
-
множество всевозможных упорядоченных наборов длины n , элементов
множества А. ![]()
2.1.3 Определение булевой функции от n переменных.
Любое
отображение ![]() - называется булевой функцией от n
переменных, притом множество
- называется булевой функцией от n
переменных, притом множество ![]()
![]()
2.1.4 Примеры булевой функции.
1)
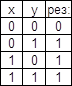
![]() логическая
сумма (дизъюнкция).
логическая
сумма (дизъюнкция).
2)
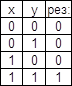
![]() логическое
умножение (конъюнкция).
логическое
умножение (конъюнкция).
3)
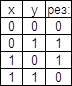
![]() сложение
по модулю два.
сложение
по модулю два.
4)
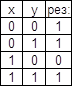
![]() логическое
следствие (импликация).
логическое
следствие (импликация).
5)
![]()
![]() отрицание.
отрицание.
2.1.5 Основные булевы тождества.
1)
![]() (ассоциативность)
(ассоциативность)
2)
![]() (коммутативность)
(коммутативность)
3)
![]() (свойство
нуля)
(свойство
нуля)
4)
![]() (закон поглощения для 1)
(закон поглощения для 1)
5)
![]() (ассоциативность)
(ассоциативность)
6)
![]() (коммутативность)
(коммутативность)
7)
![]() (свойство нуля по умножению)
(свойство нуля по умножению)
8)
![]() (свойство нейтральности 1 по умножению)
(свойство нейтральности 1 по умножению)
9)
![]() (дистрибутивность)
(дистрибутивность)
10) ![]() (дистрибутивность
2)
(дистрибутивность
2)
11) ![]() (закон
поглощения)
(закон
поглощения)
12) ![]() (
Законы
(
Законы
13) ![]() де
Моргана)
де
Моргана)
14) ![]() (закон
снятия двойного отрицания)
(закон
снятия двойного отрицания)
15) ![]() (tertium non datur – третьего не дано)
(tertium non datur – третьего не дано)
16) ![]() (ассоциативность)
(ассоциативность)
17) ![]()
18) ![]()
19) ![]()
20) ![]()
21) ![]() (Свойства
(Свойства
22) ![]() идемпотентности)
идемпотентности)
2.2 Дизъюнктивные нормальные формы.
2.2.1 Основные определения.
![]() -
конечный алфавит из переменных.
-
конечный алфавит из переменных.
Рассмотрим
слово: ![]()
Экспоненциальные
обозначения: ![]()
![]() -
элемент конъюнкции.
-
элемент конъюнкции.
S – длина элемента конъюнкции.
ДНФ – дизъюнкция нескольких различных элементарных конъюнкций.
![]()
Любая булева функция может быть представлена как ДНФ
2.2.2 Теорема о совершенной ДНФ.
Любая
булева функция ![]() тождественно не
равная 0 может быть разложена в ДНФ следующего вида:
тождественно не
равная 0 может быть разложена в ДНФ следующего вида:
![]()
Опр: Носитель булевой функции ![]()
![]() .
.
Лемма: ![]()
1)
![]() это элементарно
это элементарно ![]()
2)
![]() возьмем набор
возьмем набор ![]()
а)
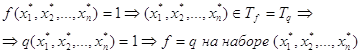
б)
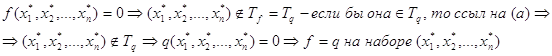
Доказательство:
![]() , будем доказывать, что
, будем доказывать, что![]() .
.
1)
Докажем, что ![]() . Возьмем
. Возьмем ![]() он попадает в число
суммируемых наборов и по нему будет проводиться сумирование.
он попадает в число
суммируемых наборов и по нему будет проводиться сумирование.
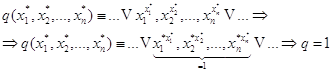
2)
Докажем, что ![]() . Возьмем другой набор из
. Возьмем другой набор из ![]()
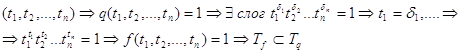
Следовательно
![]()
2.2.3 Некоторые другие виды ДНФ.
Опр:
![]() - называется минимальной
ДНФ, если она имеет
- называется минимальной
ДНФ, если она имеет ![]() - наименьшую
возможную длину из всех ДНФ данной функции.
- наименьшую
возможную длину из всех ДНФ данной функции.
Опр:
![]() - называется тупиковой
ДНФ, если из неё нельзя выбросить ни одного слагаемого с сохранением
булевой функции.
- называется тупиковой
ДНФ, если из неё нельзя выбросить ни одного слагаемого с сохранением
булевой функции.
(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не верно.)
Опр:
К-мерной гранью называется такое подмножество ![]() , которая является носителем
некоторой элементарной конъюнкции длины: n-k.
, которая является носителем
некоторой элементарной конъюнкции длины: n-k.
Опр:
Предположим дана функция ![]() и есть
и есть ![]() . Грань называется отмеченной,
если она целиком содержится в носителе Т.
. Грань называется отмеченной,
если она целиком содержится в носителе Т.
Опр: Максимальная грань – это такая грань, которая не содержится ни в какой грани более высокой размерности.
Предложение: Любую отмеченную грань можно вложить в максимальную грань.
Предложение:
![]()
(Носитель любой функции можно разложить в объединение нескольких граней разной размерностей)
Предложение:
Носитель любой функции разлагается в объединение всех своих максимальных
граней. ![]()
Опр: Элементарная конъюнкция называется минимальной, если её носитель является максимальной гранью. Следовательно всякая булева функция разлагается в дизъюнкцию всех своих элементарных конъюнкций.
Опр: Сокращенная ДНФ – разложение данной булевой функции в соответствующие ДНФ, которые соответствуют объединению её максимальных граней.
Теор: Минимальная ДНФ может быть получена из сокращенной отбрасыванием некоторого количества слагаемых, возможно пустого.
3 Логические Исчисления.
3.1 Исчисления высказывания (ИВ).
3.1.1 Определения.
![]()
![]()
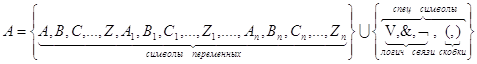
Опр: V – словом в алфавите А, называется любая конечная упорядоченная последовательность его букв.
Опр:
Формативная последовательность слов – конечная последовательность
слов и высказываний ![]() , если они имеют
формат вида:
, если они имеют
формат вида:
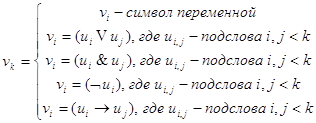
Опр: F – формулой ИВ, называется любое слово, входящее в какую-нибудь формативную последовательность.
Пример:
![]()
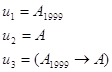
![]()
Опр:
Аксиомы – специально выделенное подмножество формул. ![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
Reg – правила вывода ИВ (некоторые правила преобразования первого слова в другое).
a
– символ переменной ![]()
![]() - произвольное
слово ИВ (формула)
- произвольное
слово ИВ (формула)
Отображение
![]() действует так, что на место
каждого вхождения символа а , пишется слово
действует так, что на место
каждого вхождения символа а , пишется слово ![]() .
.
Пример:
![]()
Правило modus
ponens: ![]()
![]()
3.1.2 Формальный вывод.(простейшая модель доказательства теоремы)
Опр: Последовательность формул ИВ, называется формальным выводом, если каждая формула этой последовательности имеет следующий вид:
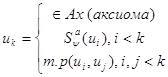
Опр:
Выводимый формулой (теоремой) ИВ называется любая формула входящая в
какой-нибудь формальный вывод. ![]() -
выводимая формула ИВ.
-
выводимая формула ИВ.
Пример:
![]()
| 1) |
|
|
| 2) |
|
|
| 3) |
|
|
| 4) |
|
|
| 5) |
|
|
| 6) |
|
|
Правило одновременной подстановки.
Замечание: Если формула ![]() выводима,
то выводима и
выводима,
то выводима и ![]()
Возьмем
формативную последовательность вывода ![]()
![]() и добавим в неё
и добавим в неё ![]() , получившаяся
последовательность является формальным выводом.
, получившаяся
последовательность является формальным выводом.
(Если
выводима ![]() то если
то если ![]() , то выводима
, то выводима ![]() )
)
Теор:
Если выводимая формула ![]() , то
, то ![]() (
(![]() - различные символы
переменных) выводима
- различные символы
переменных) выводима
Выберем
![]() - символы переменных
которые различны между собой и не входят не в одну из формул
- символы переменных
которые различны между собой и не входят не в одну из формул ![]() , сделаем подстановку
, сделаем подстановку ![]() и последовательно применим
и последовательно применим ![]() и в новом слове делаем
последовательную подстановку:
и в новом слове делаем
последовательную подстановку: ![]() , где
, где ![]() - является формальным
выводом.
- является формальным
выводом.
3.1.3 Формальный вывод из гипотез.
Опр:
Формальным выводом из гипотез ![]() (формулы),
называется такая последовательность слов
(формулы),
называется такая последовательность слов ![]() ,
каждая из которых удовлетворяет условию:
,
каждая из которых удовлетворяет условию:
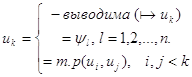
![]() если
формулу
если
формулу ![]() можно включить в некоторый
формальный вывод из гипотез
можно включить в некоторый
формальный вывод из гипотез ![]() .
.
Лемма: ![]() ;
; ![]() : то тогда
: то тогда ![]()
Напишем список:
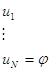
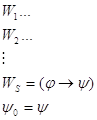
![]()
Лемма:![]()
Док: 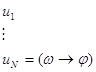

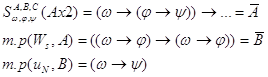
3.1.4 Теорема Дедукции.
Если из
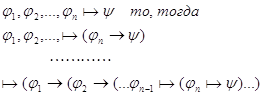
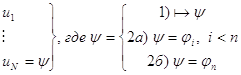
1)
и 2а) ![]() , где
, где
![]()
![]() по
правилу m.p.
по
правилу m.p. ![]() ,
ч.т.д.
,
ч.т.д.
2б)
![]() - уже выводили
- уже выводили ![]() , ч.т.д.
, ч.т.д.
Базис
индукции: N=1 ![]() - формальный вывод из длинного списка
- формальный вывод из длинного списка ![]()
![]() (только
что доказано), осуществим переход по индукции:
(только
что доказано), осуществим переход по индукции:
![]()
![]() по
индукции
по
индукции
![]() и
по лемме 2
и
по лемме 2
![]()
Пример:
![]()
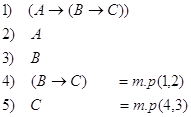 по
теореме дедукции
по
теореме дедукции 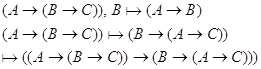
3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
![]() -
тавтология
-
тавтология
при любой интерпретации алфавита (символов переменных)
![]()
3.2.2 Понятие интерпретации.
![]()
символ
переменной ![]()
![]() переменную
поставим в соответствие.
переменную
поставим в соответствие.
![]() ,
где
,
где ![]() - проекция на
- проекция на ![]() .
.

![]()
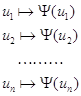 ;
; ![]() -
только символ
-
только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где:
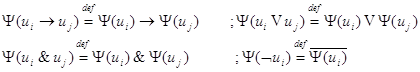
3.2.3 Доказательство теоремы.
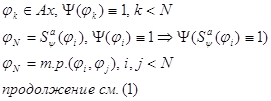
![]()
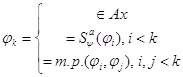 формальный
формальный
вывод
![]()
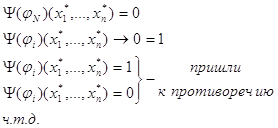
(1)
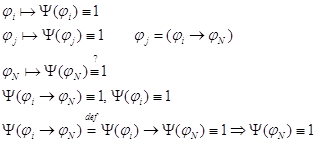
3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1)
ИВ противоречиво,
если формула А выводима в нем. ![]() .
.
2)
![]() формула выводима в ИВ)
формула выводима в ИВ)![]() ИВ
противоречиво.
ИВ
противоречиво.
3)
![]() ИВ противоречиво.
ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к любому из трех определений.
Док-во: (1) Если ![]() , то соответствующая ей
булева функция будет тождественно равна 1.
, то соответствующая ей
булева функция будет тождественно равна 1. ![]()
(2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3)
Пусть ![]() и
и ![]()
![]() -
булева функция
-
булева функция
![]() - противоречие.
- противоречие.
3.4 Формальные исчисления.
Алфавит – конечное или счетное множество символов, возможно, разбитых на группы. Алфавит должен быть упорядоченным множеством.
Слово – конечная упорядоченная последовательность символов алфавита, в т.ч. пустое слово.
V – множество всех слов.
Вычислимая
функция от нескольких натуральных переменных ![]()
( f – может быть не всюду определенной )
f – называется вычислимой,
если ![]() такая машина Тьюринга,
которая её вычисляет.
такая машина Тьюринга,
которая её вычисляет.
![]() -
разрешимое множество, если характеристическая функция
-
разрешимое множество, если характеристическая функция
![]() -
является вычислимой.
-
является вычислимой.
Множество
![]() называется перечислимым,
если
называется перечислимым,
если ![]() такая вычислимая функция
такая вычислимая функция
![]()
М - разрешимо ![]() М
и N \M перечислимы.
М
и N \M перечислимы.
М – перечислимо ![]() М
– область определения некоторой вычислимой функции.
М
– область определения некоторой вычислимой функции.
Множество всех формул F – некоторое разрешимое подмножество V.
Т – счетное множество, если ![]() его
биективное отображение на V.
его
биективное отображение на V.
![]() - обозначение
счетного множества. (
- обозначение
счетного множества. (![]() - алеф-нуль)
- алеф-нуль)
Если
![]() и зафиксировано биективное
и вычислимое отображение
и зафиксировано биективное
и вычислимое отображение ![]() (вычис.),
(вычис.),
то L – ансамбль.
V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение: В произвольном формальном исчислении: ![]() - множество
всех аксиом – разрешимое подмножество множества всех формул.
- множество
всех аксиом – разрешимое подмножество множества всех формул.
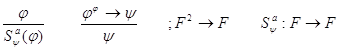
Правило вывода:
![]() ,при
,при ![]() разрешимо. Для ИВ N=2.
разрешимо. Для ИВ N=2.
Пример:
![]()
![]() (пустое слово) ,
(пустое слово) , ![]()
![]()
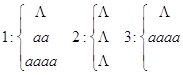 1 и
2 – формальные выводы.
1 и
2 – формальные выводы.
3 – не является формальным выводом.
4 Предикаты и кванторы.
4.1 Определение предиката.
![]()
![]() -
высказывание, содержащее переменную.
-
высказывание, содержащее переменную.
![]() -
предметная область предиката.
-
предметная область предиката.
![]()
Пусть А – множество объектов произвольной природы (предметная область предиката).
![]() -местный предикат – произвольное отображение
-местный предикат – произвольное отображение ![]()
![]()
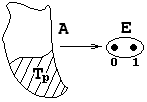 Множество истинности данного предиката
Множество истинности данного предиката ![]()
![]() -
-
- характеристическая
функция от x на множестве
А - совпадает
с предикатами
![]()
![]()
![]()
4.2 Понятие квантора.
![]() k –
связанная переменная
k –
связанная переменная
n – свободная переменная
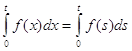 t – свободная, x –
связанная.
t – свободная, x –
связанная.
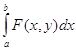 ,
a,b,y – свободные переменные, x – связанная.
,
a,b,y – свободные переменные, x – связанная.
![]()
![]()
![]()
![]()
![]()
![]()
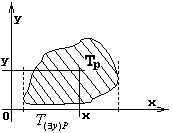
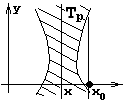
4.3 Геометрическая интерпретация навешивания кванторов.
|
|
|
|
Пронесение отрицания через кванторы
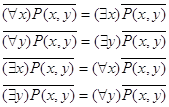
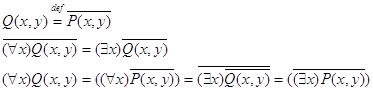
Геометрическое 'доказательство':
![]() не
обладает свойством, что прямая
не
обладает свойством, что прямая ![]() целиком
лежит в
целиком
лежит в ![]()
![]()
![]()
![]() ч.т.д.
ч.т.д.
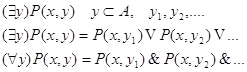
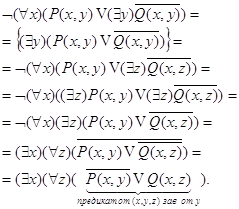
| Элементы теории множеств | |
|
Курсовая работа Выполнил студент 3 курса 4 группы физико-математического факультета Данилюк Ярослав Борисович Мозырский государственный педагогический ... Множества обозначаются прописными буквами латинского или готического алфавита: Современная теория множеств строится на системе аксиом - утверждений, принимаемых без доказательства, из которых выводятся все теоремы и утверждения теории множеств. |
Раздел: Рефераты по математике Тип: курсовая работа |
| Булевы функции | |
|
1.Основные понятия булевой алгебры Технические вопросы, связанные с составлением логических схем ЭВМ, можно решить с помощью математического аппарата ... Функция f, зависящая от n переменных x1,x2,...,xn, называется булевой, или переключательной, если функция f и любой из ее аргументов принимают значения только из множества {0,1 ... Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом ... |
Раздел: Рефераты по математике Тип: контрольная работа |
| Дискретная математика | |
|
Министерство образования и науки Российской Федерации Российский химико-технологический университет им. Д.И. Менделеева Новомосковский институт ... В силу теоремы Поста функция х | у образует полную систему, т. е. с помощью штриха Шеффера можно получить любую булеву функцию. ... в том или ином виде автомату отображения "вход-выход", осуществляемого этим автоматом; часто такое отображение можно интерпретировать как вычисление предиката, и поскольку каждый ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Теория искусственного интеллекта | |
|
Создание высокоавтоматизированных производств предполагает автоматизацию не только физического, но и умственного труда человека. В последние ... Начиная с 1960 г., был разработан ряд программ, способных находить доказательства теорем в исчислении предикатов (лог. - пропозициональная функция, т.е. выражение с неопределенными ... Эта программа за 3 минуты работы IBM-704 вывела 220 относительно простых лемм и теорем из фундаментальной математической монографии, а затем за 8.5 мин выдала доказательства еще ... |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Элементы теории множеств | |
|
Федеральное агентство по образованию ФГОУ ВПО Чувашский государственный университет им. И.Н. Ульянова Алатырский филиал Факультет управления и ... Обычно множества обозначают прописными буквами латинского алфавита, а элементы множеств - строчными буквами. Более формально: множество X является счётным, если существует биекция , где обозначает множество всех натуральных чисел. |
Раздел: Рефераты по математике Тип: курсовая работа |
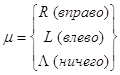 .
.