Реферат: Математический анализ
1.Счетные и несчетные множества. Счетность множества рациональных чисел.
Множество - совокупность некоторых объектов
Элементы множества - объекты составляющие множество
Числовые множества - множества элементами которых являются числа.
Задать множество значит указать все его элементы:
1 Способ: А={а: Р(а)} эти записи Читать- множество тех а таких что...
A={а-Р(а)} равноценны
Р(а) - предикат = высказывание об элементе, бывает ложно или истинно по отношению к кокретному элементу. Множество А состоит из тех а для которых предикат истина.
2 Способ: Конструирование из других множеств:
AB = {c: cA cB}, AB = {c: cA cB}, A\ B = {c: cA сB}
U - универсальное множество (фиксированное)
UA; U \ A = A’ = cA (A’ - дополнение множества A)
Свойства:
1. A(BC)=(AB)C - ассоциативность; AB=BA - коммутативность; A=A; AU=U
2. A (BC)=(AB)(AC) & A (BC)=(AB)(AC) - дистрибутивность; А=А
A” =A - закон исключающий третьего (AB)’=A’B’; (AB)’=A’B’; AA’=
Иллюстрация свойств: Диаграммы Эйлера-Венна.
"=>" c(AB)’ => cAB => cA & cB => c A’ & cB’ => cA’B’
"<=" cA’B’ => cA’ & cB’ => cA & cB => cAB => cAB)’
Отображение множеств:
f:Aна множестве А задано отображение f со значением множества B
aA; b=> b - образ элемента а при отображении f; a - прообраз элемента b при отображении f
Так как для каждого элемента из А ставится в соответствие элемент из В, значит А - область определения (Dom f=А), а область значенийB (Im f B)
Для отображения задают: 1) способ 2) Dom 3) Im
Отображение f инъективно если f(x)=f(x’) => x=x’(разные переходят в разные)
Отображение f сурьективно если Im f =B(каждый переходит в каждый)
Если же отображение инъективно+сурьективно, то множества равномощны(содержат одинаковое кол-во элементов), а отображение биективно - взаимооднозначно.
Счетные множества - множества равномощные множеству натуральных чисел (N)
Теорема: Множество Q счетно.
Докозательство:
Q=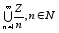
Лемма 1: nN Z/n - счетно.
Каждому элементу из N надо взаимноднозначно сопоставить элемент Z/n:
10/n 5-2/n
2/n 63/n
3-1/n 7-3/n
42/n ...
Лемма 2: Объединение счетного или конечного(не более чем счетного) числа счетных множеств - счетно.
А1={а11, а12, а13,...}
А2={а21, а22, а23,...}
А3={а31, а32, а33,...}
...
Применяем диагональную нумерацию (а11 - 1; а21 - 2; а12 - 3; а31 - 4; а22 - 5...) и таким образом взаимнооднозначно сопоставляем каждому элементу из таблицы его номер, значит объединение счетного или конечного числа счетных множеств - счетно.
Часть может быть равномощна целому: (-1,1) равномощен R (через полуокружность и лучи)
Из Леммы1 и Леммы 2 получаем: Множество рациональных чисел счетно
2. Определение действительного числа бесконечной десятичной дробью. Плотность Q в R.
Действительные числа - множество чисел вида [a0],а1 a2 а3... где а0Z а1,а2,а3,...{0,1,...,9}
Действительное число представляется в виде суммы целой и дробной части:
[ао],а1 а2 а3...ак (0) = ао + а1/10 + а2/100 + ... +ак/10k = [ао],а1 а2 а3...а’к (9), где а’к=ак-1
х=[хо],х1 х2 х3...хк...
у=[уо],у1 у2 у3...ук...
х’к - катое приближение икса с недостатком = [хо],х1 х2 х3...хк
у”к - катое приближение игрека с избытком = [уо],у1 у2 у3...ук + 1/10k
х’к+1 > х’к (х’к - монотонно растет)
у”к+1 у”k (у”k - не возрастает), т.к. у”к=[уо],у1 у2 у3...ук + 1/10к
у”к+1 = [уо],у1 у2 у3...ук ук+1 + 1/10к+1
у”к - у”к+1 = 1/10к - ук+1 + 1/10к+1 0
10 - ук+1 - 1 / 10к+1 0
9 ук+1
Определение: 1) х > у <=> к: х’к > у”к
2) х = у <=> х’к не> у”к & у”к не> х’к
По определению получаем, что [1],(0)=[0],(9)
Свойства: 1)х, у либо х<у, либо х>у, либо х=у
2) х>у & у>z => х>z
3) х не> х
Док-во (2): х>у у>z
х’к>у”к у’m>z”m
n=max{k;m}
х’nх’к>у”ку”n у’n у’m>z”mz”n
у”n>у’n => х’n>z”n
Определение: Если АR и х,уR аА: х<а<у, то А плотно в R
Теорема: Q плотно в R.
Доказательство: х > у х’к > у”к х х’к у”к у
х х’к / 2 + х’к / 2 > х’к / 2 + у”к / 2 > у”к / 2 + у”к / 2 > у
Видим: х > х’к / 2 + у”к / 2 > у, где (х’к / 2 + у”к / 2)Q
3.Несчетность множества действительных чисел.
Теорема: R несчетно.
Доказательство от противного:
1х1=[х1], х11 х12 х13... |
2х2=[х2], х21 х22 х23... | Пусть здесь нет девяток в периоде
3х3=[х3], х31 х32 х33... |
... | (*)
кхк=[хк ], хк1 хк2 хк3... |
... |
Найдем число которого нет в таблице:
с=[с], с1 с2 с3...
[с][х1] => сх1
с1 {9;х21} => сх2
с2 {9;х32} => сх3
...
ск {9;хк+1к} => схк
Таким образом С - число которое отсутствует в таблице (*)
5.Теорема Дедекинда о полноте R
Пусть
1) 0АR;
2)
aA,
b:
а
Замечания: 1) для Q и I не выполняется (между двумя иррациональными всегда одно рациональное следует из теоремы о плотности Q в R)
2) А называют нижним множеством сечения (нижний класс), В называют верхним множеством сечения (верхний класс)
Доказательство:
aA, b: а A ограничено сверху => SupA=m => b: bm => B ограничено снизу => InfB=n, mn
Докажем, что m = n:
Пусть
m
следует, что m=n если обозначим m=n через c, то получим асb
Докажем, что с единственное(от противного):
Пусть с’с,с’>с
(с’<с), так как
c=n=InfB=m=SupA=>по опр-нию.
с’>с
(с’<с) найдется
такое b(a), что b
8.Лемма о зажатой последовательности (Лемма о двух милиционерах)
Если n0:n>n0 xNyNzN и Lim xN=x, Lim zN=z, причем x=z, то Lim yN=y => x=y=z.
Доказательство: n>n0 xNyNzN
Возьмем произвольно Е>0, тогда n’: n>n’ xN(х-Е,х+Е) & n”: n>n” zN(х-Е,х+Е) => n>max{n0,n’,n”} yN(x-E,x+E)
4. Верхние и нижние грани числовых множеств.
Определение: АR mR, m - верхняя (нижняя) грань А, если аА аm (аm).
Определение: Множество A ограничено сверху (снизу), если существует такое m, что аА, выполняется аm (аm).
Определение: SupA=m, если 1) m - верхняя грань A
2) m’:
m’
InfA = n, если 1) n - нижняя грань A
2) n’: n’>n => n’ не нижняя грань A
Определение: SupA=m называется число, такое что: 1) aA am
2) >0 aA, такое, что aa-
InfA = nназывается число, такое что: 1) 1) aA an
2) >0 aA, такое, что aEa+
Теорема: Любое, непустое ограниченное сверху множество АR, имееет точную верхнюю грань, причем единственную.
Доказательство:
Построим на числовой прямой число m и докажем что это точная верхняя грань А.
[m]=max{[a]:aA} [[m],[m]+1]A=>[m]+1 - верхняя грань A
Отрезок [[m],[m]+1] - разбиваем на 10 частей
m1=max[10*{a-[m]:aA}]
m2=max[100*{a-[m],m1:aA}]
...
mк=max[10K*{a-[m],m1...mK-1:aA}]
[[m],m1...mK, [m],m1...mK + 1/10K]A=>[m],m1...mK + 1/10K - верхняя грань A
Докажем, что m=[m],m1...mK - точная верхняя грань и что она единственная:
к:
[m’K,m”K)Aк
аА:
а
Единственность(от противного):
аА, пусть а>m”K => к: а’K>m”K => аа’K>m”K - это противоречит ограниченности => am
Точная верхняя грань:
Пусть
l
Теорема: Любое, непустое ограниченное снизу множество АR, имееет точную нижнюю грань, причем единственную.
Рассмотрим множество B{-а: аА}, оно ограничено сверху и не пусто => -SupB=InfA
6.Бесконечно малые и бесконечно большие последовательности. Их свойства.
Определение: Последовательность аN называется бесконечно малой (бм) если ее предел равен нулю (Е>0 n0: n>n0 |аN|<Е)
Теорема: Сумма (разность) бм последовательностей является бм последовательностью.
Доказательство:
Пусть Lim aN=Lim
bN=0, cN=aN+bN,
dN=aN-bN.
Так как вне
любой эпсилон-окрестности
точки 0
(в частности
окрестности
Е/2) лежит конечное
число членов
последовательности
aN,
т.е.
n’: n>n’:
|aN|<Е/2.
Аналогично
n”: n>n”:
|bN|<Е/2.
При n>max{n’,n”} выполнены
оба неравен
ства |aN|<Е/2
& |bN|<Е/2
=> при любом n>
max{n’,n”} имеем:
|cN|=|aN+bN||aN|+|bN| Теорема:
Произведение
бм и ограниченной
последовательности
- бм последовательность. Доказательство:
Пусть aN
- бм посл-ть, bN
- ограниченная
посл-ть zN=aN*bN. Т.к.
bN - ограниченная
посл-ть, значит
такое с: |bN|с0 Т.к.
aN - бм
посл-ть, значит
вне любой
Е-окрестности
точки 0 (в частности
Е/с)лежит конечное
число членов
посл-ти aN,
т.е.
n0: n>n0
|aN|<Е/с.Таким
образом n>n0:
|zN|=|aN*bN|=|aN|*|bN|<Е/с
* с=Е Следствие:
произведение
бм посл-тей -
тоже бм посл-ть Теорема:
Пусть aN
- бм. Еслиn’:
n>n’
последовательностьть
|bN|aN
=> bN - бм Доказательство:
aN - бм
=>
n”: n>n”:
|aN|<Е.
Для n>=max{n’,n”} |bN||aN|<Е Определение:
Последовательность
аN
называется
бесконечно
большой (бб)
если Е>0
n0: n>n0
|аN|>Е) Теорема:
Если aN
- бм, то 1/aN
- бб последовательностьть,
обратное тоже
верно. Доказательство:
"=>"
aN-бм=>вне
любой эпсилон-окрестности
точки 0 (в частности
1/Е) находится
конечное число
членов посл-ти,
т.е. n0:
n>n0
|aN|<1/E
=>1/|aN|>Е. "<="
1/|aN| - бб
последовательность
=> Е>0
n0: n>n0
1/|aN|>1/Е
=> |aN|<Е Теорема:
Пусть aN
- бб. Если
n’: n>n’
последовательность
bN|aN|
=> bN - бб.
Доказательство:
aN - бб
=>
n”: n>n”
|aN|>Е.
Для n>max{n’,n”} bN|aN|>Е
7.Арифметика
пределов Предложение:
Число а
является пределом
последовательности
aN
если разность
aN-a
является бм
(обратное тоже
верно) Докозательство:
Т.к. Lim aN=a,
то |aN-a|<Е.
Пусть N=aN-a.
|N|=|aN-a|<Е Обратное:
Пусть N=aN-a,
т.к. N
- бм => |N|Е.
|N|=|aN-a|<Е Теорема:
Если Lim xN=x,
Lim yN=y, то:
Lim (xN+yN)
и Lim (xN+yN)=х+у
Lim (xN*yN)
и Lim (xN*yN)=х*у n
yN0
& y0
=>
Lim (xN/yN)
и Lim(xN/yN)=х/у Доказательство: Пусть
xN=х+N,
N
- бм; yN=у+N,
N
- бм 1)
(xN+yN)-(х+у)=N+N
(По теореме
о сумме бм: N+N
- бм => (xN+yn)-(х+у)-бм,
дальше по
предложению) 2)
xN*yN
- х*у = х*N+у*N+N*N
(По теоремам
о сумме бм посл-тей
и * бм посл-тей
на огр. посл-ти
получаем: xN*yN
- х*у - бм, дальше
по предл-нию) 3)
xN/yN
- х/у = (у*N-х*N)
/ (у*(у+N))=
(у*N-х*N)
* 1/у * 1/уN
доказательство
сводится к
доказательству
утверждения:
если уn
- сходящаяся
не к 0 посл-ть,
то 1/уN
тоже сходящаяся
последовательность:
Lim уN=y =>
по определению
предела получаем
n0: n>n0
|уn-у|<у/2 (Е=y/2),
что равносильно
неравенству:
у-у/2<уN<у/2+у,
откуда получаем:
|уN|уN>у/2.|уN|>у/2=>1/|уN|<2/у
=> n:
1/|уN|max{2/у,
1/у1,
1/у2,...1/уno} Теорема:
Если хN
сходится к х,
yN сходится
к у и
n0: n>n0
последовательность
хNуN,
то ху Доказательство(от
противного):
Пусть х>у. Из
опр. предела
E>0
(в частности
Е<(у-х)/2): n’:
n>n’
|xN-x|
(х-Е,х+Е)(у-Е,у+Е)=.
И т.к мы предположили,
что х>у, то
n>max{n’,n”}:
хN>уN
- противоречие
с условием =>
ху. 5.
Определение
предела последовательности
и его единственность. Определение:
Пусть даны два
множества Х
и У. Если каждому
элементу хХ
сопоставлен
по определенному
правилу некоторый
элемент уУ,
то говорят,
что на множестве
Х определена
функция f и пишут
f:ХУ
или х
(f(х)| хХ). Определение:
Последовательность-это
ф-ция определенная
на мн-ве N, со
значениями
во мн-ве R f:NR.
Значение такой
ф-ции в (.) nN
обозначают
аN. Способы
задания: 1)
Аналитический:
Формула общего
члена 2)
Рекуррентный:
(возвратная)
формула: Любой
член последовательности
начиная с некоторого
выражаетс
через предидущие.
При этом способе
задани обычно
указывают
первый член
(или нсколько
начальных
членов) и формулу,
позволющкю
определить
любой член
последовательности
через предидущие.
Пример: а1=а;
аN+1=аN
+ а 3)
Словесный:
задание последовательности
описанием:
Пример: аN
= n-ый десятичный
знак числа Пи Определение:
Число а
называется
пределом
последовательности
аN,
если
n0:
n>n0
выполняется
неравенство
|аN-a|<.
Обозначение
Lim aN=a. Если
не существует
числа а,
являющегося
пределом посл-ти,
то говорят что
последовательность
расходится,
если существует,
то сходится
(к числу а). Геометрически
существование
предела последовательности
означает, что
любой интервал
вида (а-,а+),
называемый
эпсилон-окрестностью
точки а,
содержит все
члены последовательности
аN
начиная с некоторого
номера, или
что то же самое,
вне любой
эпсилон-окрестности
точки а
находится ко
нечное число
членов последовательности
аN. Определение:
Число а
назывется
пределом посл-ти
аN
если вне всякой
окрестности
точки а
содержится
конечное число
членов последова
тельности. Теорема:
Сходящаяся
последовательность
имеет только
один предел. Доказательство(от
противного):
Пусть
последовательность
аN
имеет предел
а и
предел с,
причем ас.
Выберем такой
эпсилон, чтобы
пересечение
эпсилон-окрестностей
точек а
и с бы
ло пусто. Очевидно
достаточно
взять эпсилон
меньше |а-с|/2.
Вне окрестности
точки а содержится
конечное число
членов последовательности
=> в ок рестности
точки с содержится
конечное число
членов последовательности
- противоречие
с условием
того, что с - предел
последовательности. Теорема:
Сходящаяся
последовательность
ограничена. Доказательство:
Пусть
последовательность
аN
сходится к
числу а.
Возьмем какое-либо
эпсилон, вне
эпсилон-окрестности
точки а лежит
конечное число
членов последо
вательности,
значит всегда
можно раздвинуть
окрестность
так, чтобы все
члены последовательности
в нее попали,
а это и означает
что последователь
ность ограничена. Замечания:
1) Обратное не
верно (аn=(-1)N,
ограничена
но не сходится)
2) Если существует
предел последовательности
аN,
то при отбрасывании
или добавлении
конечного
числа членов
предел не меняется. Порядковые
свойства пределов: Теорема
о предельном
переходе:
Если Lim xN=x,
Lim yN=y, n0:
n>n0
хNyN,
тогда xy Доказательство(от
противного):
Пусть
х>у => по определению
предела
n0’: n>n0’
|хN-х| Теорема:
Если n0:n>n0
aNbNcN
и Lim
aN=a, Lim
cN=c, причем
a=c, то Lim
bN=b => a=b=c. Доказательство:
Возьмем произвольно
Е>0, тогда
n’: n>n’
=> cN<(a+E)
&
n”: n>n”
=> (a-E) 9.
Предел монотонной
последовательности Определение:
Последовательность
называется
монотонно
возрастающей
(убывающей)
если n1>n2
(n1 Замечание:
Если xN1
строго больше
(меньше) xN2,
тогда посл-ть
называется
строго монотонно
возрастающая
(убывающая) в
случае нестрогости
неравенства
последовательность
называется
нестрого
возрастающей
(убывающей). Теорема:
Всякая ограниченная
монотонная
последовательность
сходится. Доказательство:
Пусть хN
ограниченная
монотонно
возрастающая
последовательность.
Х={xN: nN} По
теореме о
существовании
точной верхней
грани у ограниченного
множества
имеем:
SupX=x, Е>0
xE:
(х-Е)<хE
=>
n0 xNo>(х-E).
Из монотон
ности имеем:
n>n0
xNxNo>(x-E),
получили xNx=SupX,
значит n>n0
xN(x-E,х]<(x-E,x+E) 10.Лемма
о вложенных
промежутках Определение:
Пусть а,bR
и а 1)
Mножество хR:
ахb
(а<х 2)
Mножество хR:
ахb)
- открытый справа
(слева) промежуток
3)
Mножество хR:
а<х & x
4)
Mножество хR:
ах
& хb
- числовой луч 5)
Mножество хR
- числовая прямая Определение:
Число b и а (если
они существуют)
называются
правым и левым
концами отрезка
(далее промежутка),
и его длина
равна b-a Лемма:
Пусть aN
монотонно
возрастает,
bN монотонно
убывает, n
aNbN
и (bN-aN)-бм,
тогда !
с: n
c[aN,bN]
(с[aN,bN]) Доказательство: aNbNb1
aN монтонно
возрастает
& aNb1
=> Lim
aN=a a1aNbN
bN монтонно
убывает & a1bN
=>
Lim bN=b aNa
bbN
aNbN
=> ab Lim
(bN-aN)=b-a=0(по
условию)=>a=b Пусть
c=a=b, тогда aNcbN Пусть
с не единственное:
aNc’bN,
с’с aNcbN=>-bN-c-aN
=> aN-bNc’-cbN-aN
=> (По теореме
о предельном
переходе) =>
Lim(aN-bN)Lim(c’-c)Lim(bN-aN)
=> (a-b)Lim(c`-c)b-a)
=>
0lim(c`-c)0
=> 0(c`-c)0
=> c’=c => c - единственное. Перефразировка
Леммы: Пусть
имеется бесконечнаz
посл-ть вложенных
друг в друга
промежутков
(промежуток
1 вложен в промежуток
2 если все точки
промежутка
1 принадлежат
промежутку
2: [a1,b1],[a2,b2],...,[an,bn]..., так что
каждый последующий
содержится
в предыдущем,
причем длины
этих промежутков
стремятся к
0 при n
lim(bN-aN)=0,
тогда концы
промежутков
aN и bN
стремятся к
общему пределу
с (с разных сторон). 42.Локальный
экстремум.
Теорема Ферма
и ее приложение
к нахождению
наибольших
и наименьших
значений. Определение:
Пусть задан
промежуток
I=(a;b), точка x0a;bТочка
x0, называется
точкой локалниого
min(max), если для всех
xa;bвыполняется f(x0) Лемма:
Пусть функция
f(x) имеет конечную
производную
в точке x0.
Если эта производная
f‘(x0)>0(f‘(x0)<0),
то для значений
х, достаточно
близких к x0
справа, будет
f(x)>f(x0)
(f(x) Доказательство:
По определению
производной, Если
f‘(x0)>0,
то найдется
такая окрестность
(x0-,x0+)
точки x0,
в которой (при
хx0)
(f(x)-f(x0))/(x-x0)>0.
Пусть x0 Теорема
Ферма: Пусть
функция f(x) определена
в некотором
промежутке
I=(a;b) и во внутренней
точке x0
этого промежутка
принимает
наибольшее
(наименьшее)
значение. Если
функция f(x)
дифференцируема
в точке x0,
то необходимо
f‘(x0)=0. Доказательство:
Пусть для
определенности
f(x) принимает
наибольшее
значение в
точке x0.
Предположение,
что f‘(x0)0,
приводит к
противоречию:
либо f‘(x0)>0,
и тогда (по лемме)
f(x)>f(x0),
если x>x0
и достаточно
близко к x0,
либо f‘(x0)<0,
и тогда f(x)>f(x0),
если x Следствие:
Если существует
наибольшее
(наименьшее)
значение функции
на [a;b] то оно
достигается
либо на концах
промежутка,
либо в точках,
где производной
нет, либо она
равна нулю. 43.Теоремы
Ролля, Лагранжа,
Коши (о среднем
значении). Теорема
Ролля
Пусть
1) f(x) определена
и непрерывна
в замкнутом
промежутке
[a;b]
2) сущестует
конечная производная
f’(x), по крайней
мере в отткрытом
промежутке
(a;b)
3) на концах
промежутка
функция принимает
равные значения:
f(a)=f(b)
Тогда
между a и
b найдется
такая точка
c(a Доказательство:
f(x) непрерывна
в замкнутом
промежутке
[a;b] и потому, по
второй теореме
Вейерштрасса
(Если f(x), определена
и непрерывна
в замкну том
промежутке
[a;b], то она достигает
в этом промежутке
своих точных
верхней и нижней
границ), принимает
в этом промежутке
как свое наибольшее
значение M, так
и свое наименьшее
значение m. Рассмотрим
два случая: 1)
M=m. Тогда f(x) в промежутке
[a;b] сохраняет
постоянное
значение:
неравенство
mf(x)M
в этом случае
x
дает f(x)=M => f’(x)=0 во
всем промежутке,
так что в качестве
с можно
взять любую
точку из (a;b). 2)
M>m. По второй
теореме Вейерштрасса
оба эти значения
функцией
достигаются,
но, так как
f(a)=f(b), то хоть одно
из них достигается
в некоторой
точ ке с
между a и
b. В таком
случае из теоремы
Ферма (Пусть
функция f(x) определена
в некотором
промежутке
I=(a;b) и во внутренней
точке x0
этого промежутка
принимает
наибольшее
(наименьшее)
значение. Если
функция f(x)
дифференцируема
в точке x0,
то необходимо
f‘(x0)=0)
следует, что
произ водная
f’(с) в этой точке
обращается
в нуль. Теорема
Коши: Пусть
1) f(x) и g(x) непрерывны
в замкнутом
промежутке
[a;b] & g(b)g(a)
2) сущестуют
конечные производные
f’(x) и g’(x), по крайней
мере в отткрытом
промежутке
(a;b)
3) g’(x)в
отткрытом
промежутке
(a;b) Тогда
между a и
b найдется
такая точка
c(a Доказательство:
Рассмотрим
вспомогательную
функцию h(x)=[f(x) - f(a)
- Эта
функция удовлетворяет
всем условиям
теоремы Ролля:
1)
h(x) непрерывна
на [a;b], как комбинация
непрерывных
функций
2)
сущестует
конечная производная
h’(x) в (a;b), которая
равна h’(x)=f’(x) - 3)
прямой подстановкой
убеждаемся
h(a)=h(b)=0 Вследствие
этого в промежутке
(a;b) существует
такая точка
с, что
h’(x)=0 => f’(c) - Разделив
обе части равенства
на g’(x) (g’(x)0)
получаем требуемое
равенство. Теорема
Лагранжа: Пусть
1) f(x) определена
и непрерывна
в замкнутом
промежутке
[a;b]
2) сущестует
конечная производная
f’(x), по крайней
мере в отткрытом
промежутке
(a;b) Тогда
между a и
b найдется
такая точка
c(a Доказательство:
По теореме
Коши, полагая
g(x)=x, имеем:
Промежуточное
значение с
удобно записывать
в виде с=а+b-a,
где (0;1).
Тогда принимая
x0=a, (b-a)=h, мы
получаем следующее
следствие:
Следствие:
Пусть f(x)
дифференцируема
в интервале
I=(a;b), x0
x0+hтогда
0;1f(x0+h)-f(x0)=f’(x0+h)*h
([x0;x0+h]
h>0, [x0+h;x0]
h<0) 11.
Подпоследовательности.
Теорема
Больцано-Вейерштрасса. Определение:
Пусть аN
некоторая
числовая посл-ть
и kN-строго
возрастающая
посл-ть N чисел.
В результате
композиции
ф-ций naN
и nkN
получа ем посл-ть
aKn-которая
наз. подпосл-тью
посл-ти aN=>подпосл-сть
- это либо сама
посл-ть либо
исходная посл-ть,
из которой
выбросили
часть членов. Теорема:
Если Lim аN=а,
то и Lim аKn=а. Доказательство:
Вне любой
Е-окрестности
точки а
лежит конечное
число членов
последовательности
аn и в частности
последовательности. Доказательство:
Пусть для заданного
Е нашлось n0:
n>n0
|аN-а|<Е,
ввиду того что
kNсуществует
и такое n’, что
при всех n>n’
kN>n0
тогда при тех
же значениях
n будет верно
|аKn-а|<Е Теорема
Больцано-Вейерштрасса:
Из всякой
ограниченной
последовательности
можно выделить
сходящуюся
подпоследовательность. Доказательство:
хN -
ограничена
=> n:
ахNb.
Поделим промежуток
[a,b] пополам, хотя
бы в одной его
половине содержится
бесконечное
множество
членов посл-ти
хN (в
противном
случае и во
всем промежутке
содержится
конечное число
членов посл-ти,
что невозможно).
Пусть [а1,b1]
- та половиа,
которая содержит
бесконечное
число членов
посл-ти. Аналогично
выделим на
промежутке
[а1,b1]
промежуток
[а2,b2]
также содержащий
бесконечное
число членов
посл-ти хN.
Продолжая
процесс до
бесконечности
на к-том
шаге выделим
промежуток
[аK,bK]-также
содержащий
содержащий
бесконеч ное
число членов
посл-ти хN.
Длина к-того
промежутка
равна bK-аK
= (b-a)/2K, кроме
того она стремится
к 0 при к
и аKаK+1
& bKbK+1.
Отсюда по лемме
о вложенных
промежутках
!
с: n
аNcbN. Теперь
построим
подпоследовательность: хN1
[а1,b1] хN2
[а2,b2]
n2>n1 .
. . хNK[аK,bK]
nK>nK-1 ахNkb.
(Lim aK=LimbK=c
из леммы о вложенных
промежутках) Отсюда
по лемме о зажатой
последовательности
Lim хNk=c -
ч.т.д. 12.Верхний
и нижний пределы
последовательности. xN
- ограниченная
последовательность
=>n
аNхNbN хNKх,
так как
хNK-подпоследовательность
=> n
ахNb
=>ахb х
- частичный
предел последовательности
хN Пусть
М - множество
всех частичных
пределов. Множество
М ограничено
(аМb)
=>
SupM &
InfM
Верхним
пределом посл-ти
xN называют
SupMSup{xN}:
пишут Lim xN Нижним
предел ом посл-ти
xn называют
InfMnf{xN}:
пишут lim
xN Cуществование
нижнего и верхнего
пределов вытекает
из определения. Достижимость: Теорема:
Если хN
ограничена
сверху (снизу),
то
подпосл-ть
хNK: предел
которой равен
верхнему (нижнему)
пределу хN. Доказательство:
Пусть х=SupM=верхний
предел хN
х’М:
х-1/к<х’ (следует
из того что х
- SupМ), т.к. х’М
=>
подпоследовательность
хNSх’
=> Е>0
(в частности
Е=1/к)
s0: s>s0
=>
х’-1/к<хNS<х’+1/к х
-1/к-1/к<х’-1/к<хNS<х’+1/к<х+1/к
(т.к.х-1/к<х’ и
х’<х=SupМ) х-2/к<хNS<х+1/к Берем
к=1: х-2<хNS<х+1,
т.е
s0: s>s0
это неравенство
выполняется
берем член
посл-ти хNS
с номером больше
s0 и
нумеруем его
хN1 k=1:
х-2/1<хN1<х+1/1 k=2:
х-2/2<хN2<х+1/2
n1
... k=k:
х-2/к<хNK<х+1/к
nK-1 При
к
хNKх 13.Фундаментальные
последовательности. Определение:
Последовательность
{аN} -
называется
фундаментальной,
если Е>0
n0: n>n0
и любого рN
выполнено
неравенство
|аN+р-аN|<Е.
Геометрически
это означает
что Е>0
n0, такой
что расстояние
между любыми
двумя членами
посл-ти, с большими
чем n0
номерами, меньше
Е. Критерий
Коши сходимости
посл-ти:
Для того, чтобы
данная посл-ть
сходилась
необходимо
и достаточно,
чтобы она являлась
фундаментальной. Доказательство: Необходимость:
Пусть Lim xN=x,
тогда Е>0
n0: n>n0
|хN-х|<Е/2.
n>n0, n’>n0
|хN-хN’|=|хN-х+х-хN’|<|хN-х|+|х-хN’|<Е/2+Е/2<Е Достаточность:
Пусть хN
- фундаментальная 1)
Докажем что
хN
ограничена:
Е1=1998
n0: |хN-хN’|<Е,
n>n0, n’>n0 n>n0
|хN-хN0|<Е1
х
N0-1998<хN<х
N0+1998 => хN
- ограничена 2)
По теореме
Больцано-Вейерштрасса
подпосл-ть
хNKх.
Можно выбрать
к настолько
большим, чтобы
|хNK-х|<Е/2
и одновременно
nк>n0.
Следовательно
(из фунд-ти)
|хN-хNK|<Е/2
=> |хNK-х|<Е/2
=> х-Е/2<хNK<х+Е/2
=> |хN-хNK|<Е/2
=> хNK-Е/2<хN<хNK+Е/2
=> х-Е<хN<х+Е
=> |хN-х|<Е 14.Бином
Ньютона для
натурального
показателя.Треугольник
Паскаля. Формула
Ньютона для
бинома:
...
*:
Доказательство(по
индукции): 1)
n=0 - верно (1+х)0=1
=> 2)
Пусть верно
для n: докажем
что это верно
и для n+1: 16.Последовательности
1)
Lim 2)
Lim xN= n=(1+xN)n n= xN2<2/(n-1) 16.Последовательность
(1+1/n)n
и ее предел. xN= xN
монотонно
возрастает:
докажем: xN=(1+1/n)n=1+
n/1!*1/n + n*(n-1)/2!*1/n2
+... < 1 + 1/1! + 1/2!+...+1/n! = yN =>
yN Воспользуемся
неравенством
Бернулли
(1+x)n1+nx,
x>-1) (доказывается
по индукции): x=1/n
=> (1+1/n)n1+n/n=2 Получили:
2
xN<3 => xN
- ограничена,
учитывая что
xN - монотонно
возрастает
=> xN -
сходится и ее
пределом является
число е. 17.
Последовательности
1)
Lim a)
a1: xN= xN+1=xN
* xN=xN+1
* xN=xN+1*xN*(n+1) Lim
xN=Lim
(xN+1*xN*(n+1))
=> x = x*x => x = 1 б)
0 Lim 2)
Lim
xN= xN+1=xN* Lim
xN+1 = Lim xN* Докажем,
что если xN1
=> (xN)1: a)
n:
xN1
и 0 (xN)
[](xN)<(xN)[]+1
=> по лемме
о зажатой посл-ти,
учитывая что
Lim (xN)[]=Lim
(xN)[]+1=1
(по теореме о
Lim произведения)
получаем Lim
(xN)=1 б)
n:
0 yN=1/xN
=> yn>1 Lim yN=lim1/xN=1/1=1
=> (по (а)) Lim (yN)
=1 => lim 1/(xN)=1
=> Lim (xN)
=1 Объединим
(а) и (б): xN1
>0 xN1,xN2,...>1
(1) xM1,xM2,...<1
(2) Вне
любой окрестности
точки 1 лежит
конечное число
точек (1) и конечное
число точек
(2) => конечное
число точек
xN. в)
<0 (xN)
=1/(xN)
<0
=> ->0
=> по доказанному
для >0
получаем, Lim
1/(xN)
= 1 => Lim (xN) 15.
Доказательство
формулы e=... yN= 1)
yN монотонно
растет 2)
yN 3)
zN-yN0 4)
zN монотонно
убывает Доказателство: zN-zN+1
= yN + 2=y1 e
= Lim yN =
Lim zN - по
лемме о вложенных
промежутках
имеем: yN<e Если
через
обозначить
отношение
разности e
- yN к
числу 1/(n*n!), то можно
записать e
- yN =/(n*n!),
заменяя yN
его развернутым
выражением
получаем e
= yN + /(n*n!),
(0,1) Число
e иррационально: Доказательство(от
противного):
Пусть e=m/n,
mZ,
nN m/n
= e = yN
+ /(n*n!) m*(n-1)!=
yN*n! + /n,
где (m*(n-1)! & yN*n!)Z,
(/n)Z
=> противоречие 23.
Определения
предела функции
по Коши и по
Гейне. Их эквивалентность. Определение
по Коши:
f(x) сходится к
числу А при
хх0
если Е>0
>0:
0<|х-х0|<
& хDf
=> |f(x)-А|<Е Определение
по Гейне:
f(x) сходится к
числу А при
хх0
если
последовательности
хNх0,
хNх0
f(xN)А Теорема:
Два определения
эквивалентны: Д-во:
Для эквивалентности
определений
достаточно
доказать, что
из сходимости
по Коши следует
сходимость
по Гейне и из
сходимости
по Гейне следует
сходимость
по Коши. 1)
(К)=>(Г) Е>0
>0:
0<|х-х0|<
& хDf
=> |f(x)-А|<Е - определение
Коши хNх0,
хNх0,
т.к. хNх0
=>
n0: n>n0
0<|xN-x0|<Е
(Е=)
=> 0<|xN-x0|<
=> по определению
Коши |f(xN)-А|<Е 2)
(Г)=>(К) Воспользуемся
законом логики:
Если из отрицания
B следует отрицание
А, то из А следует
В: Таким
образом нам
надо доказать
что из отрицания
(К) => отрицание
(Г) Отрицание
(К):
Е>0:
>0 x:
0<|x-x0|<
=> |f(x)-A|E Отрицание
(Г):
хNх0,
хNх0:
|f(xN)-A|E
хNх0,
хNх0
=>
n0: n>n0
0<|xN-x0|<Е
(Е=)
=> по отрицанию
определения
Коши |f(xN)-А|Е Для
ф-ции хf(х)
определенной
на интервале
(а,+),
определяется
предел при
хN
следующим
образом: limf(х) при
хN
= Limf(1/t) t+0 (если
последний
существует).
Таким же образом
определяются
Lim f(х) при хN
= Lim f(1/t) t0
и хN
= lim f(1/t) t0 24.
Односторонние
пределы. Классификация
разрывов.
Определение
непрерывности. Lim(х0|h|)
при h0
- называется
односторонним
правым (левым
пределом) ф-ции
f(x) в точке х0 Теорема:
Пусть интервал
(x0-,x0+)\{x0}
принадлежит
области определения
ф-ции для некоторго
>0.
Тогда Lim f(x) в точке
х0
существует
<=> когда cуществуют
правый и левый
предел f(x) в точке
х0 и
они равны между
собой. Необходимость:
Пусть предел
f(х) существует
и равен А => Е>0
>0: -<х-х0<
=> |f(х)-А|<Е, т.е.
такое,
что как только
х попадает в
-окрестность
точки x0
сразу f(х) попадает
в интервал
(f(х)-А,f(х)+А). Если
х попадает в
интервал (0, x0+)
=> x попадает в
интервал (x0-,x0+)
=> f(х) попадает
в интервал
(f(х)-А,f(х)+А) => правый
предел существует
и он равен А.
Если х попадает
в интервал
(x0-,0)
=> x попадает в
интервал (x0-,x0+)
=> f(х) попадает
в интер вал
(f(х)-А,f(х)+А) => левый
предел существует
и он равен А. Достаточность:
Lim (х0|h|)
при h0:
Lim(х0+|h|)
= Lim(х0-|h|)=А Е>0
’
>0: 0<х-х0<’
=> |f(х)-А|<Е Е>0
”
>0: -”<х-х0<0
=> |f(х)-А|<Е Получили
Е>0
0<=min{’,”}:
-
<х-хо<
=> |f(х)-А|<Е Определение:
Функция f(x) называется
непрерывной
в точке х0
если при хх0
Lim f(х)=f(х0).
Заменяя в
определениях
предела фнкции
по Коши и по
Гейне А на f(х0)
получаем определения
по Коши и по
Гейне непрерывности
ф-ции f(x) в точке
х0. Поскольку
в опр-нии по
Коши нер-во
|f(х)-f(х0)|<Е
выполнено и
при х=х0 =>
в определении
можно снять
ограничение
хх0
=> получим второе
равносильное
определение: Определение
2: Функция
f(x) называется
непрерывной
в точке х0,
если Е>0
>0:
-
<х-хо<
=> |f(х)-f(а)|<Е Аналогично
сняв ограничение
хх0
- получим определение
по Гейне: Определение
3: Функция
f(x) называется
непрерывной
в точке х0,
если
посл-ти хNх0,
f(xN)f(a) Если
при хх0
limf(х)f(х0),
то говорят что
функция f(x) имеет
разрыв в точке
х0. Это
происходит
если:
а)
f(х) неопределена
в точке х0
б)
Предел f(х) в точке
х0 не
существует в)
f(х) определена
в х0
и limf(х) в точке х0
существует
но равенство
Дшь f(х)=f(а) не
выполняется Различают:
1)
точки разрыва
I рода, для которых
существуют
конечные
односторонние
пределы (либо
они неравны
друг другу
либо равны, но
неравны f(х0) 2)
точки разрыва
II рода - не существует
хотя бы один
односторонний
предел.
Если
правый и левый
предел в х0
совпадают, то
х0 называют
устранимой
точкой разрыва.
Если
хотя бы один
из односторонних
пределов равен
бесконечности,
то х0
- точка бесконечного
разрыва.
Пусть
x0 - точка
разрыва, x0
называется
изолированной,
если в некоторой
окрестности
этой точки
других точек
разрыва нет. Если
значение правого
(левого) предела
в точке х0
совпадает со
значением
f(x0), то
f(x) называется
непрерывной
справа (слева). Если
предел f(x) справа
(слева) в точке
х0 не
существует,
а предел слева
(справа) существует
и равен значению
f(х0), то
говорят что
функция f(x) имеет
в точке х0
разрыв справа
(слева). Такие
разрывы называют
односторонними
разрывами f(x)
в точке х0. Функция
хf(x)
называется
непрерывной
на множестве
Х если она
непрерывна
в каждой точке
х этого множества. 26.
Арифметика
пределов функций.
Порядковые
свойства пределов. Теорема:
Все пределы
в точке х0:
Пусть ф-ции
f:ХR
и g:ХR
(ХR)
таковы, что
Lim f(x)=F, Lim g(x)=G, тогда
Lim
f(x) Lim
g(x) = FG Lim
f(x)*Lim g(x) = F*G Если
G0
и g(x)0
Limf (x) / Lim g(x) = F/G Доказательство: 1)
Е>0(в
частности Е/2)
’>0:
-’<х-х0<’
=> |f(х)-F|<Е & ”>0:
-”<х-х0<”
=> |g(х)-G|<Е
Получили
Е>0
0<=min{’,”}:
-<х-х0<
=>-Е/2 - Е/2 2)
Пусть посл-ть
хNх0
(хNх0,
xNX),
тогда в силу
определения
предела по
Гейне имеем:
при n
Lim f(xN)=F &
Lim g(xN)=G по
теореме об
арифметике
пределов посл-тей
получаем: при
n
Lim f(xN)*g(xN)=Lim
f(xN)*Lim g(xN)=
F*G => по определению
предела по
Гейне при хх0
Lim f(x)*Lim g(x)=F*G 3)
Пусть посл-ть
хNх0
(хNх0,
xNX),
тогда в силу
определения
предела по
Гейне имеем:
при n
Lim f(xN)=F &
Lim g(xN)=G по
теореме об
арифметике
пределов посл-тей
получаем: при
n
Lim f(xN)/g(xN)=Lim
f(xN)/Lim
g(xN)=F/G =>
по определению
предела по
Гейне при хх0
Lim f(x)/Lim g(x)=F/G, G0
и g(x)0. Порядковые
свойства пределов: Теорема:
Если
хX:
f(x)g(x),
при хх0
A=Lim f(x), B=Lim g(x), то AB Доказательство(от
противного):
Пусть
A>B => из определения
предела следует
(берем 0<Е<|A-B|/2):
’>0:
|х-х0|<’
=> |f(x)-A| Получили,
что 0<=min{’;”}:
|х-х0|<
=> |f(x)-A|<|A-B|/2 & |g(х)-B|<|A-B|/2, учитывая
что А>В и что
(А-Е,А+Е)(В-Е,В+Е)=
получаем что
для
х(х0-,
х0+)
f(x)>g(x) - противоречие
с условием. Теорема:
Если
хX:
f(x)g(x)h(x)
и при хх0
Lim f(x)=А=Lim h(x), то Lim g(x)=А Доказательство:
Е>0
’>0:
|х-х0|<’
=> A-E Получили,
что 0<=min{’;”}:
|х-х0|<
=> A-E 27.
Непрерывность
тригонометрических
функций. Предел
(Sin x)/x при х 1)
Sin x: Lim
Sin x = Sin x0
(при хх0) |Sin
x-Sin x0|=2*|Sin((x-x0)/2)|*|Cos((x+x0)/2)|
< 2*|(x-x0)/2|=|x-x0|
=> -|x-x0| 2)
Cos x: Lim
Cos x = Cos x0
(при хх0) Cos
x = Sin (П/2 - x) = Sin y; Cos x0
= Sin (П/2 - x0)
= Sin y0 |Sin
y-Sin y0|=2*|Sin((y-y0)/2)|*|Cos((y+y0)/2)|
< 2*|(y-y0)/2|=|y-y0|
=> -|y-y0| 3)
Tg x - непрерывная
ф-ция исключая
точки х = П/2 +2Пк,
кZ 4)
Ctg x - непрерывная
ф-ция исключая
точки х = Пк, кZ Теорема:
Lim (Sin x)/x=1 (при х0),
0 Доказательство:
Составляем
нер-во для площадей
двух треугольников
и одного сектора
(Sсект=х*R2)
откуда и получаем
Sinx 28.Теорема
о промежуточном
значении непрерывной
функции. Определение:
Пусть а,bR
и а 1)
Mножество хR:
ахb
(а<х 2)
Mножество хR:
ахb)
- открытый справа
(слева) промежуток
3)
Mножество хR:
а<х & x
4)
Mножество хR:
ах
& хb
- числовой луч 5)
Mножество хR
- числовая прямая Теорема:
Пусть f(x) непрерывна
на [a,b] и с - произвольное
число лежащее
между f(а) и f(b), тогда
существует
х0[a,b]:
f(х0)=c. Доказательство:
g(х)=f(х)-с (g(x) - непрерывна).
g(а)*g(b)<0 Поделим
промежуток
[a,b] пополам, если
в точке деления
g((а+b)/2)=0, то полагая
х0=(а+b)/2
видим что теорема
доказана
(g(х0)=f(х0)-с=0
=> f(х0)=с).
Пусть в точке
деления функция
g(x) в ноль не обращается,
тогда выбираем
из двух полученных
промежутков
тот, для которого
g(а1)*g(b1)<0,
делим его пополам
если в точке
деления функция
g(x) обращается
в ноль => теорема
доказана. Пусть
в точке деления
функция g(x) в ноль
не обращается,
тогда выбираем
из двух полученных
промежутков
тот для которого
g(а2)*g(b2)<0...
продолжая
процесс до
бесконечности
мы либо получим
на каком-либо
шаге что ф-ция
g(x) обращается
в ноль, что означает
что теорема
доказана, либо
получим бесконечное
число вложенных
друг в друга
промежутков.
Для n-го
промежутка
[aN,bN]
будем иметь:
g(aN)<0,
g(bN)>0,
причем длина
его равна
bN-aN=(b-a)/2n0
при n.
Построенная
посл-ть промежутков
удов летворяет
условию Леммы
о вложенных
промежутках
=>
точка x0
из промежутка
[a,b], для которой
Lim aN=Lim bN=
x0. Покажем,
что x0-удовлетворяет
требованию
теоремы: g(aN)<0,
g(bN)>0 =>
переходим к
пределам: Lim
g(aN)0,
Lim g(bN)0,
используем
условие непрерывности:
g(x0)0
g(x0)0
=> g(x0)=0 =>
f(х0)-c=0
=> f(х0)=c Следствие:
Если функция
f(x) непрерывна
на промежутке
Х, то множество
У=f(Х)={f(х):хХ}
также является
промежутком
(Непрерывная
ф-ция перево
дит промежуток
в промежуток.) Доказательство:
Пусть у1,у2У;
у1уу2,
тогда существуют
х1,х2Х:
у1=f(х1),
у2=f(х2).
Применяя теорему
к отрезку [х1,х2]Х
(если х1<х2)
и к отрезку [х2,х1]Х
(если х2<х1)
получаем, что
у=f(с) при некотором
с => У - удовлетворяет
определению
промежутка. 29.
Предел суперпозиции
функций. Непрерывность
суперпозиции
непрерывных
функций
Определение:
Суперпозицией
(композицией)
двух функций
f и g называется
функция f(g(x)) -
определенная
для всех х
принадлежащих
области опреде
ления ф-ции g
таких что значения
ф-ции g(x) лежат
в области
определения
ф-ции f. Теорема:
Если Lim g(x)=b (при xa)
и f - непрерывна
в точке b, то Lim
f(g(x))=f(b) (при xa) Доказательство:
Пусть
xN: xNa
- произвольная
посл-ть из области
определения
ф-ции хf(g(x)),
сходящаяся
к а, тогда
последовательность
yN: yN=g(xN)
сходится к b в
силу опр. по
Гейне. Но тогда
Lim f(yN)=f(b)
(n)
в силу опр.
непрерывности
ф-ции f по Гейне.
Т.о. Lim f(g(xN))=Lim
f(yN)=f(b) (n).
Заметим что
в посл-ти yN
- некоторые (и
даже все члены)
могут оказаться
равными b. Тем
не менее в силу
нашего замечания
о снятии ограничения
yNb
в определении
непрерывности
по Гейне мы
получаем f(yN)f(b) Следствие:
Пусть функция
g непрерывна
в точке x0,
а функция f
непрерывна
в точке у0=g(x0),
тогда ф-ция
f(g(x)) непрерывна
в точке х0. 30.
Обращение
непрерывной
монотонной
функции. Определение:
Функция f обратима
на множестве
Х если уравнение
f(х)=у однозначно
разрешимо
относительно
уf(Х). Определение:
Если функция
f обратима на
множестве Х.
То функция
однозначно
сопоставляющая
каждому уо
такое х0
что f(х0)=у0
- называется
обратной к
функции f. Теорема:
Пусть строго
возрастающая
(строго убывающая)
ф-ция f определена
и непрерывна
в промежутке
Х. Тогда существует
обратная функция
f’,
определенная
в промежутке
Y=f(Х), также строго
возрастающая
(строго убывающая)
и непрерывная
на Y. Доказательство:
Пусть f строго
монотонно
возрастает.
Из непрерывности
по следствию
из Теоремы о
промежуточном
значении следует,
что значения
непрерывной
функции заполняют
сплошь некоторый
промежуток
Y, так что для
каждого значения
у0 из
этого промежутка
найдется хоть
одно такое
значение х0Х,
что f(х0)=у0.
Из строгой
монотонности
следует что
такое заначение
может найтись
только одно:
если х1>
или <х0,
то соответственно
и f(х1)>
или было
х’>х”, тогда
из возрастания
f следует что
у’>у” - противоречие
с условием,
если х’=х”, то
у’=у” - тоже
противоречие
с условием.
Докажем
что f` непрерывна:
достаточно
доказать, что
Lim f`(у)=(у0)
при уу0.
Пусть f`(у0)=х0.
Возьмем произвольно
Е>0. Имеем уУ:
|f`(у)-f`(у0)|<Е
<=> х0-Е полагая
=min{’,”}
имеем: как только
|у-у0|<
=> -’<у-у0<”
<=> |f`(у)-f`(у0)|<Е Непрерывность
степенной
функции с
рациональным
показателем: Определение:
Степенной
функцией с Q
показателем
называется
функция хM/N
- где mZ,
nN.
Очевидно степенная
функция явл-ся
cуперпозицией
непре рывных
строго монотонно
возрастающих
ф-ций хM
и х1/M
=> ф-ция хM/N
- непрерывна
при х>0. Если
х=0, то хM/N
= 1, а следовательно
непрерывна.
Рассмотрим
ф-цию хN,
nN:
она непрерывна
так как равна
произведению
непрерывных
функций у=х. n=0:
хN
тождественно
равно константе
=> хN -
непрерывна
х-N=1/хN,
учитывая что:
1)
1/х - непрерывная
функция при
х0
2)
хN (nN)
- тоже непрерывная
функция
3)
х-N=1/хN
- суперпозиция
ф-ий 1/х и хN
при х0 По
теореме о
непрерывности
суперпозиции
ф-ций получаем:
х-N -
непрерывная
при х0,
т.о. получили
что хMmZ
- непрерывная
ф-ция при х0.
При х>0ф-ция
хN nN
строго монотонно
возрастает
и ф-ция хNнепрерывна=>функция
обратная данной,
которая также
строго монотонно
возрастает
(при m>0), очевидно
этой функцией
будет функция
х1/N Тригонометрические
функции на
определенных
(для каждой)
промежутках
обратимы и
строго монотонны
=>имеют непрерывные
обратные функции
=> обратные
тригонометрические
функции - непрерывны 31.
Свойства
показательной
функции на
множестве
рациональных
чисел. Определение:
Показательная
функция на
множестве
рациональных
чисел: Функция
вида аX,
а>0, а1
xQ. Свойства:
для mZ
nN 1)
(аM)1/N
= (а1/N)M (аM)1/N=(((а1/N)N)M)1/N
= ((а1/N)N*M)1/N
= (((а1/N)M)N)1/N
= (а1/N)M 2)
(аM)1/N=b
<=> аM=bN 3)
(аM*K)1/N*K=(аM)1/N (аM*K)1/N*K=b
<=> аM*K=bN*K
<=> аM=bN
<=> (аM)1/N=b Из
свойств для
целого показателя
вытекают св-ва
для рационального
если обозначить:
aM/N=(аM)1/N=(а1/N)M,a-M/N=1/aM/N,
а0=1 Св-ва:
x,yQ 1)
aX * aY
= aX+Y
aX
* aY
=b; x=m/n, y=-k/n => aM/N
* 1/aK/N
= b => aM/N
= b * aK/N
=> aM
= bN
* aK
=> aM-K
= bN
=> a(M-K)/N =
b => aX+Y
= b 2)
aX/aY
= aX-Y 3)
(aX)Y=aX*Y (aX)Y=b;
x=m/n, y=k/s => (aM/N)K/S=b
=> (aM/N)K=bS
=> (a1/N)M*K=bS
=> (aM*K)1/N=bS
=> aM*K=bS*N
=> a(M*K)/(S*N)=b
=> aX*Y=b 4)
x z=y-x>0;
aY=aZ+X
=> aY-aX=aZ+X-aX=aX*aZ-aX=aX*(aZ-1)
=> если aZ>1
при z>0, то aX z=m/n
=> aZ=(a1/N)M
=> a1/N>1
=> (a1/N)M>1
=> aX*(aZ-1)>1,
(a>1 n>0) 5)
при x0
aX1
(xR) Т.к.
Lim a1/N=1 (n),
очевидно, что
и Lim a-1/N=Lim1/a1/N=1
(n).
Поэтому Е>0
n0:
n>n0
1-E a-1/N 32.Определение
и свойства
показательной
функции на
множестве
действительных
чисел. Определение:
Показательная
функция на
множестве
действительных
чисел: Функция
вида аX,
а>0, а1
xR. Свойства:
x,yR. 1)
aX * aY
= aX+Y xNx,
yNy
=> aXn
* aYn
= aXn+Yn
=> Lim aXn
* aYn
= Lim aXn+Yn
=> Lim aXn
* lim aYn
= Lim aXn+Yn
=> aX
* aY
= aX+Y 2)
aX / aY
= aX-Y 3)
(aX)Y=aX*Y xNx,
yKy
=>
(aXn)Yk
=
aXn*Yk
=>
(n)
(aX)Yk=aX*Yk
=>(k)
(aX)Y=aX*Y 4)
x x x-x`>q>0
=> aX-X’
aQ>1
=>
aX-X’1
=> aX 5)
при x n0
aX 1 Т.к.
Lim a1/N=1 (n),
очевидно, что
и Lim a-1/N=Lim1/a1/N=1
(n).
Поэтому Е>0
n0:
n>n0
1-E a-1/N 6)
aX - непрерывна Lim
aX=1 (n
из (5) - это означает
непрерывность
aX в точке
0 => aX-aXo=
aXo(aX-Xo
- 1) при хx0
x-x0 n0
=> aX-x0
n1
=> при хx0
lim(aX - aXo)=
Lim
aXo*Lim(aX-Xo
- 1) = x0 * 0 = 0
=> aX -
непрерывна 33.Предел
функции (1+x)1/X
при x0
и связанные
с ним пределы. 1)
Lim (1+x)1/X = e
при x0 У
нас есть Lim (1+1/n)n
= e при n Лемма:
Пусть nK
nKN
Тогда (1+1/nK)Nke Доказательство: E>0
k0:
n>n0
0 Lim
(1+xK)1/Xk
при x0+: 1/xK=zK+yK,
zKN
=> 0yK<1
=> (1+1/zK+1)Zk<(1+xK)1/Xk
<
(1+1/zK)Zk+1=(1+1/zK)Zk*(1+1/zK)=>(1+1/zK+1)Zk=(1+1/zK+1)Zk+1)/(1+1/zK+1)
=> (1+1/zK+1)Zk+1/(1+1/zK+1)
< (1+xK)1/Xk
< (1+1/zK)Zk*(1+1/zK)
kучитывая,
что: (1+1/zK)1
(1+1/zK+1)1
=> получаем: eLim
(1+xK)1/Xke
=> Lim (1+xK)1/Xk=e
=> Lim (1+x)1/X=e
при x0+ Lim
(1+xK)1/Xk
при x0-: yK=-xK0+
=> доказываем
аналогично
предыдущему
=> получаем Lim
(1+x)1/X=e при
x0- Видим
что правый и
левый пределы
совпадают =>
Lim (1+x)1/X=e
при x0 2)
n
lim (1+x/n)N =
(lim (1+x/n)N/X)X
= eX 3)
xx
R
- непрерывна x=(eLn
x)=e*Ln
x непр
непр непр
непр xLn
x*Ln*Ln
x => xe*Ln
x 4)
x0
Lim (Ln (1+x))/x = Lim Ln (1+x)1/X
= Ln e = 1 4’)
x0
Lim LogA(1+x)1/X
= 1/Ln a 5)
x0
Lim (eX-1)/x =
{eX-1=t} = Lim
t/Ln(1+t) => (4) = 1/1 = 1 5’)
x0
Lim (aX-1)/x = Ln
a 6)
x0
Lim ((1+x)-1)/x
= Lim ([e*Ln
(1+x) -1/[Ln(1+x)]Ln
(1+x)]/x = 11= 34.Теорема
Вейрштрасса
об ограниченности
непрерывной
функции на
отрезке. Функция
хf(x)
называется
непрерывной
на множестве
Х если она
непрерывна
в каждой точке
х этого множества. Теорема:
Функция непрерывная
на отрезке
[a,b], является
ограниченной
на этом отрезке
(1 теорема Вейрштрасса)
и имеет на нем
наибольшее
и наимень шее
значение (2 теорема
Вейрштрасса). Доказательство:
Пусть m=Sup{f(x):x[a,b]}.
Если f не ограничена
сверху на [a,b], то
m=,
иначе mR.
Выберем произвольную
возрастающую
посл-ть (сN),
такую что Lim cN=m.
Т.к. nN:
cN Для
mR
- по теореме о
том, что предел
произвольной
подпосл-ти
равен пределу
посл-ти получаем
cKnm.
Для
m=+
- по Лемме о том
что всякая
подпосл-ть бб
посл-ти явл-ся
бб посл-тью
получаем cKnm.
Переходя к
пределу в нер-вах
cKn Lim
f(xKn)=b n
но в силу непрерывности
ф-ции f имеем
Lim f(xKn)=f()
=> f()=m
- что и означает
что функция
f ограничена
сверху и достигает
верхней граница
в точке .
Существование
точки =Inf{f(x):x[a,b]}
доказывается
аналогично. 35.
Равномерная
непрерывность.
Ее характеризация
в терминах
колебаний. Определение:
Е>0
>0:
х’,х”:
|х’-х”|<
=> |f(x’)-f(x”)|<Е => функция
называется
равномерно
непрерывной Отличие
от непрерывности
состоит в том,
что там
зависит от Е
и от х”, то здесь
не зависит от
х”. Определение:
Ф-ция f - не равномерно
непрерывна,
если Е>0
>0: х’,х”:
|х’-х”|<
=> |f(x’)-f(x”)|Е>0 Рассмотрим
множество
{|f(x’)-f(x”)|:|x’-x”|<,
x’,x”I},
IDf. Верхняя
точная граница
этого множества
обозначаемое
Wf()
называется
колебанием
функции f на
множестве I
вызванное
колебаниями
аргумента:
1/х
- Wf()
= +Sin
x - Wf()
= 1 Таким
образом равномерно
непрерывную
функцию можно
определить
по другому:
Е>0
>0:
Wf()Е
Lim Wf()=0
0 36.Теорема
Кантора о
равномерной
непрерывности
непрерывной
функции на
отрезке. Теорема:
Если f непрерывна
на [a,b], то она
равномерно
непрерывна
на [a,b]. Доказательство(от
противного): Пусть
f не равномерно
непрерывна
на [a,b]=>Е>0
>0
х’,х”:
|х’-х”|<=>|f(x’)-f(x”)|Е.
Возьмем
=1/к, кN
хK,
х’K[a,b]:
|хK-х’K|<1/к
|f(xK)-f(x’K)|E Т.к
хK -
ограничена
=> из нее по теореме
Больцано-Вейерштрасса
можно выделить
подпосл-ть xKs
сходящуюся
к х0.
Получаем:
|хKs-х’Ks|<1/к
хKs-1/k<х’Ks<хKs-1/k
по Лемме о зажатой
посл-ти х’Ksх0
kS
|f(xKs)-f(x’Ks)|E
кS0E
- противоречие
с условием. 37.Определение
производной
и дифференциала. Касательная
в точке x0
к функции xf(x):
возьмем еще
одну точку х
соединим x0
и х - получим
секущую. Касательной
назовем предельное
положение
секущей при
хx0,
если это предельное
положение
существует.
Т.к. касательная
должна пройти
ч/з точку (x0,f(x0)
=> уравнение
этой касательной
(если она не
вертикальна)
имеет вид
y=k*(x-x0)+f(x0).
Необходимо
только опр-ть
наклон k
касательной.
Возьмем произвольное
число х0
так, чтобы x0+хХ.
Рассмотрим
секущую МОМ,
МО(x0,f(x0)),
М(x0+х,f(x0+х)).
Уравнение
секущей имеет
вид: у=к(х)(х-x0)+f(x0),
где k=f((x0+х)-f(x0))/х
- наклон секущей.
Если существует
Lim к(х)
при х0,
то в качестве
искомого наклона
k возьмем
это предел.
Если Lim к(х)=при
х0,
то перепишем
уравнение секу
щей в виде
x=(1/k(х))*(y-f(x0))+x0
перейдя к пределам
при х0,
получим x=x0
(Lim x=Lim x0
х0
=> x = Lim x0) Определение:
Производным
значением
функции f в точке
х0
называется
число f’(х0)=Lim
(f(x0+х)-f(x0))/х
xx0,
если этот предел
существует. Геометрически
f’(х0)
- это наклон
невертикальной
касательной
в точке (x0,f(x0)).
Уравнение
касательной
y=f’(x0)*(x-x0)+f(x0).
Если Lim (f(x0+х)-f(x0))/х=
х0,
то пишут f`(x0)=
касательная
в этом случае
вертикальна
и задается
уравнением
х=x0.
f`(x0)=lim(f(x0+х)-f(x0))/х
xx0=>(f(x0+х)-f(x0))/х=f’(x0)+(x),
(x)0
при xx0.
f(x0+х)-f(x0)=f`(x0)*х+(x)*х
учитывая, что
x0+х=x
и обозначая
(x)*х
через o(x-x0)
получим
f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0).
Необхо димо
заметить, что
o(x-x0)
уменьшается
быстрее чем
(x-x0) при
xx0
(т.к. o(x-x0)/(x-x0)0
при xx0) Определение:
Ф-ция f называется
дифференцируемой
в точке x0
если сR:
в некоторой
окрестности
точки x0
f(x)=С(x-x0)+f(x0)+o(x-x0) Теорема:
Функция диффференцируема
в точке x0
<=>
f’(x0) Доказательство: <=:
f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0)
=> f`(x0)=C =>:
f(x)=C(x-x0)+f(x0)+o(x-x0)
=> (f(x)-f(x0))/(x-x0)=C+o(x-x0)/(x-x0)=C+(x),
(x)0
при xx0. Переходим
к пределу при
xx0
=> Lim (f(x)-f(x0))/(x-x0)=C+0=C
=> Слева записано
производное
значение ф-ции
f => по определению
C=f`(x0) Определение:
Если функция
хf(x)
дифференцируема
в точке x0,
то линейная
функция хf’(x0)*х
называется
дифференциалом
функции f в точке
x0 и обозначается
df(x0). (диф-ал
ф-ции хх
обозначают
dx). Т.о. df(x0):хf`(x0)*х
и dх:хх.
Отсюда df(x0)=f’(x0)*dх
=> df(x0)/dх:
хf`(x0)*х/х=f’(x0)
при х0.
В силу этого
пишут также
f’(x0)=df(x0)/dх
- обозначение
Лейбница. График
диф-ла получается
из графика
касательной
переносом
начала коор
динат в точку
касания. Теорема:
Если ф-ция f диф-ма
в точке x0,
то f непрерывна
в точке x0. Докозательство:
f(x)=f(x0)+f’(x0)*(x-x0)+o(x-x0)f(x0)
при xx0
=> f непрерывна
в точке x0. Определение:
Нормаль к ф-ции
f в точке x0:
это прямая
перпендикулярная
касательной
к ф-ции f в точке
x0. Учитывая
что тангенс
угла наклона
нормали равен
tg(90+угол наклона
касательной)=
-Ctg(наклона касательной),
получаем уравнение
нормали:
y=-1/f’(x0)*(x-x0)+f(x0) 38.
Арифметика
диф-цирования.
Производные
тригонометрических
функций. Теорема:
Пусть ф-ции f
и g дифференцируемы
в точке x0,
тогда ф-ции
f+g, f*g и f/g (при g(x0)0)
дифференцируемы
в точке x0
и: 1)
(f+g)’(x0)=f’(x0)+g’(x0) 2)
(f*g)’(x0)=f’(x0)*g(x0)+f(x0)*g’(x0) 3)
(f/g)’(x0)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x0)2 Доказательство: 1)
f(x0)=f(x0+x)-f(x0)
g(x0)=g(x0+x)-g(x0)
(f+g)(x0)=f(x0)+g(x0)=f(x0+x)-f(x0)+g(x0+x)-g(x0)
(f+g)(x0)/x=(f(x0+x)-f(x0)+g(x0+x)-g(x0))/x=(f(x0+x)-f(x0))/x+(g(x0+x)-g(x0))/xf’(x0)+g’(x0)
при x0 2)(f*g)(x0)=f(x0+x)*g(x0+x)-f(x0)*g(x0)=(f(x0)+f(x0))*(g(x0)+(x0))-f(x0)*g(x0)=g(x0)*f(x0)+f(x0)*g(x0)+f(x0)*g(x0)
(f*g)(x0)/x=g(x0)*(f(x0)/x)+f(x0)*(g(x0)/x)+(f(x0)/x)*(g(x0)/x)*xf’(x0)*g(x0)+f(x0)*g’(x0)
при x0 3)
Ф-ция g - дифференцируема
в точке x0
=> Ф-ция g - непрерывна
в точке x0
=> Е>0
(Е=|g(x0)|/2)
>0:
|x|<=>
|g(x0+x)-g(x0)|<|g(x0)|/2. g(x0)-|g(x0)|/2 Рассмотрим
разность
(1/g(x0+x)-1/g(x0))/x
= -(g(x0+x)-g(x0))/x*g(x0+x)*g(x0)
-g’(x0)/g(x0)2
при x0 (f/g)’(x0)=(f*1/g)’(x0)
=> (2) =
f’(x0)*1/g(x0)+f(x0)*(1/g)’(x0)=f`(x0)*1/g(x0)+f(x0)*(-g’(x0)/g(x0)2)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x0)2 Теорема:
Пусть
f=Sin(x), g=Cos(x) 1)
Sin’(x0) =
Cos (x0) 2)
Cos’(x0) =
-Sin (x0) Доказательство: 1)f/x=(Sin(x0+x)-Sin(x0))/x
= Sin(x/2)/(x/2)
* Cos(x0+x/2)
Сos
x0 при
x0 2)
g/x=(Cos(x0+x)-cos(x0))/x=Sin(x/2)/(x/2)*-Sin(x0+x/2)
-Sin
x0 при
x0 Производные
Tg и Ctg выводятся
непосредственно
из производных
для Sin и Cos по формулам
дифференцирования. 39.
Производная
суперпозиции.Производные
степенной,
показательной
и логарифмической
функции. Теорема:
Пусть функция
g диф-ма в точке
x0, а ф-ция
f диф-ма в точке
y0=g(x0),
тогда ф-ция
h(х)=f(g(х)) диф-ма в
точке x0
и h’(x0)=f`(y0)*g’(x0) Доказательство: y=y-y0,
x=x-x0,
f(y0)=f’(y0)*y+o(y),
g(xo)=g’(xo)*x+o(x),
y=g(x0+x) h(x0)=f(g(x0+x))-f(g(x0))=f(y)-f(y0)=f’(y0)*y+o(y)=f’(y0)*(g(x0+x)-g(x0))+o(g)==f’(y0)*(g’(x0)*x+o(x))+o(y)=
f’(y0)*g’(x0)*x+f’(y0)*o(x)+o(y) h(x0)/x=f’(y0)*g’(x0)+r,
r=f`(y0)*o(x)/x+o(y)/x r=f`(y0)*o(x)/x+o(y)/x=f`(y0)*((x)*x)/x+(’(x)*y)/x=f’(y0)*(x)+’(x)*y/xf’(y0)*0
+ 0*g’(y0)
при x0
((x)0
’(x)0) Производная: 1)
x=*x-1 Lim
(y/x)=lim((x+x)-x)/x
= Lim x*
((1+x/x))/x/x.
Используя
замечательный
предел x0
Lim ((1+x)-1)/x=,
получим x0
Lim
x*Lim((1+x/x))/x/x
= x 2)
(aX)’=aX*Ln
a (xaX)’=(xeX*Ln
a)’
xeX*Ln
a - композиция
функций xеX
и xx*Ln
a обе непрерывны
на R => (xaX)’=(xе
X*Ln a)’=(xеX*Ln
a)’*(xx*Ln
a)’=aX*Ln a Д-во
: (eX)’=eX Lim(y/x)=Lim(eX+X-eX)/x=LimeX*(eX-1)/x,
используя
зам-ный предел
при x0
Lim(eX-1)/x=1,
получим при
x0
Lim(y/x)=eX 3)
(LogA(x))’=1/x*Ln
a Lim(y/x)
= Lim (LogA(x+x)
- LogA(x))/x
= Lim 1/x*LogA(1+x/x)/x/x,
используя
замечательный
предел при x0
Lim LogA(1+x)/x=1/Ln
a, получим Lim
(y/x)
= Lim 1/x*Lim LogA(1+x/x)/x/x=1/x*Ln
a 40.
Производная
обратной функции.
Производные
обратных
тригонометрических
функций. Предложение:
Если производная
обратной функции
g для ф-ции f существует
в точке y0,
то g’(y0)=1/f’(x0),
где y0=f(x0) Доказательство:
g(f(x))=x g’(f(x))=1 g’(f(x0))=g’(f(x0))*f’(x0)=1,
g’(f(x0))=g(y0)=1/f’(x0) Теорема:
Пусть ф-ция f
строго монотонно
и непрерывно
отображает
()
в (а,b) тогда
обратная ей
ф-ция g, которая
строго монотонно
и непрерывно
отображает
(а,b) в ().
Если f диф-ма
в точке x0()
и f’(x0)0,
то g диф-ма в точке
y0=f(x0)
и g’(y0)=1/f’(x0)
Доказательство:
Возьмем
произвольную
последовательность
сходящуюся
к y0:
yNy0,
yNy0
=>
посл-ть xN:
xN=g(yN),
f(xN)=yN g(yN)-g(y0)/yN-yO
= xN-xO/f(yN)-f(yO)
= 1/f(yN)-f(yO)/xN-xO
1/f’(xo) при nполучили
при xNxO
g(yN)-g(yO)/yN-yO1/f’(xO)
=> g’(уO)=1/f’(xO) Производные: 1)
xrcsin
x по теореме
имеем Arcsin’x=1/Sin’y,
где Sin y=x при условии,
что Sin’y<0, получаем
(используя
производную
синуса): Arcsin’x=1/Cos y,
т.к. rcsin:
[-1,1][-П/2,П/2]
и Cos:[-П/2,П/2][0,1],
то Cos y0
и, значит Arcsin’x =
1/Cos y = 1/(1-Sin2y)1/2
= 1/(1-x2)1/2 2)
xArccos’x
= -1/(1-x2)1/2 3)
xArctg’x
= 1/1+x2 4)
xArcctg’x=
-1/1+x2 41.Производные
и дифференциалы
высших порядков. Определение:
Если ф-ция f диф-ма
в некоторой
окрестности
точки xO,
то ф-ция f’(x):xf’(x)
в свою очередь
может оказаться
диф-мой в точке
xO или
даже в некоторой
ее окрестности.
Производная
ф-ции f’(x) - называется
второй производной
(или производной
порядка 2) ф-ции
f в точке xO
и обознача
ется f”(x). Аналогично
определяется
третья и четвертая
производная
и так далее.
Для единообразия
обозначаем
через fN(xO)
- производную
порядка n функции
f в точке xO
и при n=0 считаем
f0(xO)=f(xO). Замечание:
Cуществование
производной
порядка n требует
того чтобы
существовала
производная
пордка (n-1) уже
в некоторой
окрестности
точки xO
(следует из
теоремы о связи
диф-ти и непрерывности),
в таком случае
функция xfN-1(x)
непрерывна
в точке xO,
а при n2
все производные
порядка не
выше (n-2) непрерывны
в некоторой
окрестности
точки xO. Определение:
Дифференциалом
ф-ции f порядка
n в точке xO
называют функцию
dхfN(x)*dх
и обозначают
dNf(x). Таким
образом
dNf(x):dхfN(x)dxN. Так
как fN(x)dхN:dхfN(x)dxN,
то dNf(x)=fN(x)dхN.
В силу этого
соотношения
производную
fN(x) обозначают
также dNf(x)/dхN Инвариантность: Пусть
функции у=f(х)
и х=g(t) таковы, что
из них можно
составить
сложную функцию
у=f(g(t)). Если существуют
производные
у’(х) и х’(t) то
cуществует
производная
у’(t)=у’(х)*х’(t). Если
х считать
независимой
переменной,
то диф-ал dy=y’(х)dx.
Перейдем к
независимой
переменной
t, учитывая что
у’(t)=у’(х)*х’(t):
dy=y’(t)dt=y’(x)*х’(t)dt. x’(t)dt=dх
=> dy=y’(t)dt=у’(х)*х’(t)*dt=у’(x)dх
- видим что при
переходе к
новой независимой
переменной
форма дифференциала
может быть
сохранена -
это свойство
называют
инвариантностью
формы первого
дифференциала. Пусть
функции у=f(х)
и х=g(t) таковы, что
из них можно
составить
сложную функцию
у=f(g(t)) Если существуют
производные
у’(х) и х’(t) то
существует
производная
у’(t)=у’(х)*х’(t) и
по доказанному
ее первый диф-ал
по t можно написать
в форме dy=y’(х)dх,
где dх=x’(t)dt. Вычисляем
второй диф-ал
по t: d2y=d(y’(x)dx)=dy’(x)dx+y’(x)d(dx).
Снова пользуясь
инвариантностью
первого диф-ла
dy’(x)=у”(х2)dx
=> d2y=у”(х2)dx2x+y’(x)*d2x,
в то время как
при независимой
переменной
х второй диф-ал
имел вид д2y=у’(х2)*dx2x
=> неинвариантность
формы второго
диф-ла. Формула
Лейбница: f(x)=u(x)*v(x)
Доказательство
по индукции. 1)
n=0 верно 2)
Предположим
для n - верно =>
докажем для
(n+1) Если
для u и v n+1)
производные,
то можно еще
раз продифференцировать
по х - получим: Объединим
теперь слагаемые
обеих последних
сумм, содержащие
одинаковые
произведения
производных
функций u и v (сумма
порядков производ
ных в таком
произведении,
как легко видеть,
равна всегда
(n+1)). Произведение
u0*vN+1
входит только
во вторую сумму
с коэффициентом
С0N=1.
Произведение
uN+1*v0
входит только
в первую сумму
с коэффициентом
СNN=1.
Все остальные
произведения
входящие в эти
суммы имеют
вид uK*vN+1-K.
Каждое такое
произведение
встречается
в первой сумме
с номером k = i-1, а
во второй i=k. Сумма
соотв. коэффициентов
будет
получаем
fN+1(x)=u0*vN+1+ 44.
Нахождение
промежутков
постоянства
монотонности
функции и ее
экстремумов. Теорема:
Пусть f(x)
непрерывна
в замкнутом
промежутке
[a;b] и диф-ма в открытом
промежутке
(a;b), если f’(x)=0 в (a;b), то
f(x)-const в [a;b]. Докозательство:
Пусть
xb,
тогда в замкнутом
промежутке
в [a;x] по теореме
Лагранжа имеем:
f(x)-f(a)=f’(a+(x-a))(x-a)
0<т.к.
по условию
f’(x)=0 в (a;b), то f’(a+(x-a))=0
=> f(x)=f(a)=Const для все
х(a;b). Теорема:
Пусть f(x)
непрерывна
в замкнутом
промежутке
[a;b] и диф-ма в открытом
промежутке
(a;b), тогда: 1)
f монотонно
возрастает(убывает)
в нестрогом
смысле в (a;b) <=>
f’(x)0(f’(x)0)
в (a;b). 2)
Если f’(x)>0(f’(x)<0) в
(a;b) и f непрерывна
в [a;b], то f строго
возрастает(убывает)
в [a;b]. Доказательство: 1)
Пусть f непрерывна
на [x’,x”] x’, x”(a;b),
тогда по теореме
Лагранжа
(f(x”)-f(x’))/(x”-x’)=f’(c),
с(x’,x”).
По условию
имеем f’(x)f’(x)в
(a;b) => f’(c)f’(c)f(x”)f(x’)(
f(x”)f(x’))
=> f(x) возрастает(убывает)
в нестрогом
смысле в (a;b). 2)
Используя
аналогичные
(1) рассуждения,
но заменяя
неравенства
на строгие
получим (2).
Следствие:
Если xO-критическая
точка непрерывной
ф-ции f. f’(x) в достаточно
малой -окр-ти
точки xO
имеет разные
знаки, то xO-экстремальная
точка.
Достаточное
условие экстремума:
(+)xO(-)
=> локальный
min, (-)xO(+)
=> локальный
max 46.
Выпуклые множества
Rn. Условие Иенсена.
Выпуклые
функции.Неравенство
Йенсена. Определение:
Множество М
выпукло <=> если
А,ВМ
[А,В]М [А,В]М
=> [А,В]={А+t(В-А):t[0,1]}
=> А(1-t)+tВМ [А,В]М
=> А,ВМ;
1=1-t,
2=t
=> 1+2=1
1,20
=> 1А+2ВМ Рассмотрим
точки: А1,А2,...АNМ
1,20
i=1,n):=
1 Докажем
что i=1,n):*АI
М Д-во:
По индукции: 1)
n=1, n=2 - верно 2)
Пусть для (n-1) -
верно => докажем
для n: а)
=1
=> приравниваем
1=...==0
=> верно б)
<1
*А1
+...+ *А
+*А=
(1-)((/1-)*А1+...+(/1-)*А)
+ *А
= (1-)*B
+ *А
BМ
- по индуктивному
предположению
АМ
- по условию=>(1-)*B
+ *АМ
Ч.т.д График
Гf = {(x,f(x)):хDf},
Надграфик
UPf={(x,y):y>f(x)} Определение:
Функция f выпукла
<=> UPf - множество
выпукло. Условие
Йенсена:
АIМ
0
i=1,n):=1
=> i=1,n):*АI
М,
xI0,
f(xI)yI
=> i=1,n):*АI
=xI;*yIf(xI)*yI Неравенство
Йенсена: АIМ
0
=1f(xI)*f(xI) 47.Критерий
выпуклости
дифференцируемой
функции.
Теорема:
Пусть f определена
в интервале
(a;b), тогда следующие
условия эквивалентны:
1) f - выпукла в
(a;b) ~
2) x’,xO,x”(a;b)
x’ (f(xO)-f(x’))/(xO-x’)(f(x”)-f(xO))/(x”-xO).
Геометрический
смысл: при сдвиге
вправо угловой
коэффициент
секущей растет. Доказательство: “=>”
AB: k=(y-f(x’))/(xO-x’)(f(xO)-f(x’))/(xO-x’)
=> yf(xO);
AB: k=(f(x”)-y)/(x”-xO)(f(x”)-f(xO))/(x”-xO)
=>yf(xO)
(f(xO)-f(x’))/(xO-x’)(f(x”)-f(xO))/(x”-xO) “<=”
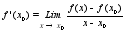 .
.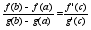
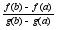 *(g(x)
- g(a))]
*(g(x)
- g(a))]
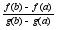 *g’(x)
*g’(x)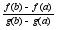 *g’(c)
или f’(c) =
*g’(c)
или f’(c) =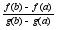 *g’(c).
*g’(c).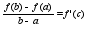
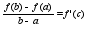
 n
n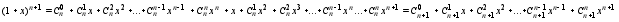
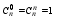
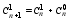 Разложение
Паскаля
Разложение
Паскаля (Записав
коэффициенты
в виде пирамиды
- получим треугольник
Паскаля)
(Записав
коэффициенты
в виде пирамиды
- получим треугольник
Паскаля)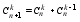
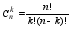 к=0,1,...,n
к=0,1,...,n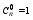 (1+х)0
=
(1+х)0
=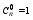
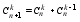 =
=
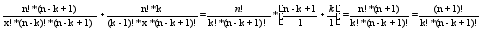 Ч.т.д
Ч.т.д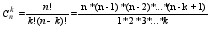
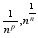 (во всех пределах
n)
(во всех пределах
n)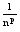 =
0 (p>0)
=
0 (p>0)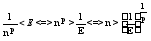 - это означает
что, мы нашли
такое n0=
- это означает
что, мы нашли
такое n0=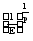 :
n>n0
|
:
n>n0
|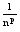 |
|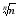 =1
=1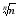 - 1
- 1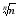 =1+xN
=1+xN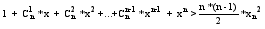
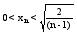 При
n
При
n
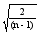 0
=> xN0
(Лемма о зажатой
последовательности)=>Lim
0
=> xN0
(Лемма о зажатой
последовательности)=>Lim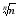 =Lim
(1+xN)=1+0=1
=Lim
(1+xN)=1+0=1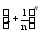 ;
yN=
;
yN=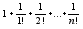 ;
zN=yN
+
;
zN=yN
+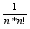
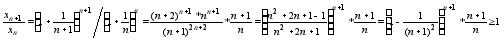
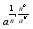 (во
всех пределах
n)
(во
всех пределах
n)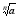 =1,
a>0
=1,
a>0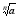 xN+1=
xN+1=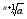
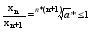 =>
Lim xN=x
=>
Lim xN=x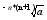
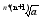
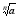
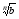 =1
b=1/a =>
=1
b=1/a =>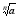 =
1/
=
1/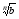 =>
Lim
=>
Lim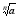 =
1/1 = 1
=
1/1 = 1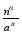 =
0, a>1
=
0, a>1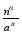 xN+1=
xN+1=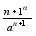
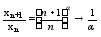 т.к.
Lim
т.к.
Lim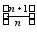 =
Lim
=
Lim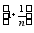 =Lim
=Lim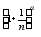 =1
=1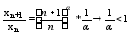 =>
n0:
n>n0
xn+1/xn<1 => СТ x=limxn
=>
n0:
n>n0
xn+1/xn<1 => СТ x=limxn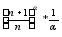
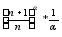 => x = x*1/a => x=0
=> x = x*1/a => x=0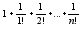 ;
zN=yN
+
;
zN=yN
+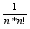
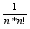 - yN+1 -
- yN+1 -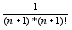 =
=
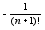 +
+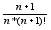 -
-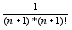 =
=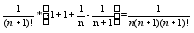
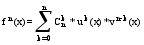
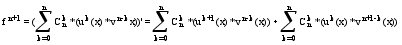
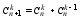 =>
=>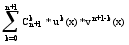 +
uN+1*v0=
+
uN+1*v0=