Реферат: Пределы
Предел.
Число
А наз-ся
пределом
последоват-ти
Xn если
для любого
числа Е>0, сколь
угодно малого,
N0, такое
что при всех
n>N0 будет
выполн-ся нер-во
|Xn-A| Число
А явл-ся пределом
послед-ти Xn, если
для любой
Е-окрестности
(.)А сущ-ет конкретное
число N0,
для кот. любые
точки >N0
попадают в
Е-окрестность
(.)А. Св-ва
послед-ти, имеющей
предел:
1.если
послед-ть имеет
предел, то он
единственный.
Док-во:
предп, что
пределы различны:
lim Xn=a, lim Xn=b (n),
тогда |a-b|=|a-Xn+Xn-b|. Из
lim Xn=a (n)
=>
E/2
N1 n>N1
|a-Xn| 2.теорема
о сжатой переменной.
n>N1 XnZnYn
limXn = lim Yn = a (n)
=>
lim Zn=a (n)
Док-во:
1. из
того, что
lim Xn=a (n)
=> n>N2
|Xn-a| Функция
y=f(x) наз-ся ограниченной
в данной обл-ти
изменения
аргумента Х,
если сущ-ет
положит число
М такое, что
для всех значений
Х, принадлежащих
рассматриваемой
обл-ти, будет
выполн-ся нер-во
|f(x)|M.
Если же такого
числа М не сущ-ет,
то f(x) наз-ся
неограниченной
в данной обл-ти. Бесконечно
малая величина. Величина
Xn наз-ся бесконечно
малой при
n,
если lim Xn = 0 (n).
E>0,
N0, n>N0,
|Xn| Свойства
б.м. величин: 1.Сумма
б.м. величин
есть величина
б.м.
Док-во:
из Xn – б.м.
=>
E/2 N1,
n>N1 |Xn| из
Yn–б.м.=>
E/2 N2,
n>N2 |Yn| 2.Произведение
ограниченной
величины на
б.м. величину
есть величина
б.м.
Док-во:Xn
– огр. величина
=>
K, |Xn|
K,
Yn
– б.м. =>
E/K N0
n>N0 |Yn| |Xn*Yn|=|Xn||Yn| 3.Достаточный
признак существования
предела переменной
величины: если
переменная
величина Xn имеет
конечный предел
А, то эту переменную
величину можно
представить
в виде суммы
этого числа
А и б.м. величины.
lim Xn=a (n)
=> Xn=a+Yn, Yn – б.м.
Док-во:
Из lim Xn=a (n)
=> E
N0
n>N0 |Xn-a| Xn-a=Yn
– б.м. => Xn=a+Yn. Справедливо
и обратное:
если переменную
величину можно
представить
в виде суммы
Xn=a+Yn (Yn – б.м.), то lim Xn=a (n). Xn
– бесконечно
большая n,
если M>0
N0,
n>N0, |Xn|>M
=> M Свойства
б.б. величин: 1.Произведение
б.б. величин
есть величина
б.б. из
Xn – б.б. =>M
N1,
n>N1 |Xn|>M из
Yn – б.б. => M
N2, n>N2
|Yn|>M N0=max(N1,
N2) =>
|Xn*Yn|=|Xn||Yn|>MM=M2>M Lim
XnYn=
(n). 2.Обратная
величина б.м.
есть б.б. Обратная
величина б.б.
есть б.м. lim Xn=
(n)
– б.б. Yn=1/Xn – б.м. Из
lim Xn=
=> M=1/E N0,
n>N0 |Xn|>M
=>n>N0.
|Yn|=1/|Xn|<1/M=E
=>Yn – б.м. => lim Yn=0 (n). 3.Сумма
б.б величины
и ограниченной
есть б.б. величина.
Основные
теоремы о пределах: lim
Xn=a, lim Yn=b => lim (XnYn)=ab
(n) Док-во:
lim Xn=a => Xn=a+n;
lim Yn=b => Yn=b+n; Xn
Yn = (a + n)
(b + n)
= (a
b) + (
n
bn) =>
lim(XnYn)=ab
(n). limXnYn
= lim Xn * lim Yn (n). lim
Xn=a, lim Yn=b (n)
=> lim Xn/Yn = Док-во:
Xn/Yn – a/b = (a+n)/(b+n)
– a/b = (ab+nb–ab–an)/b(b+n)
=(bn-an)/b(b+n)=n
=> Xn/Yn=a/b+n
=>
lim Xn/Yn = a/b = (lim Xn)/(lim Yn) (n).
Пределы
ф-ии непрерывного
аргумента.
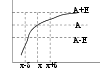
Число А
наз-ся пределом
ф-ии y=f(x) при хx0,
если для любого
Е>0 сколь угодно
малого сущ-ет
такое число
>0,
что при x
будет выпол
|x-x0|<,
будет выполняться
нер-во |f(x) – A| Lim
xx0
f(x)=A
Ф
Lim f(x)=
(xx0).
Ч
I замечательный
предел.
Рассмотрим
окр-ть радиуса
1; обозн угол
МОВ через Х.
Sтреуг
МОА< Sсект
МОА
SтреугМОА=0,5ОА*МВ=0,5*1*sin=0.5sinX.
SсектМОА=0,5*ОА*АМ=0,5*1*х=0,5х.
SтреугСОА=0,5*ОА*АС=0,5*1*tgX=0,5tgX.
SinX
1
Lim cosX=1, lim 1=1 (x0)
=>lim (sinX)/x=1.
Следствия:
1. limx0(tgX)/x=lim(sinX)/x*1/cosX=
=lim(sinX)/x*lim (1/cosX)=1;
2.limx0(arcsinX)/x={arcsinX=t,sint=x,t0}=
=limt0t/sint=1;
3. limx0
(sin x)/x
= lim (Sin
x)/(x)=
=/
limx0(sin
x)/x=/.
II замечательный
предел.
limn(1+1/n)n=?
Бином
Ньютона:
(a+b)n=an+nan-1b+(n(n-1)an-2b2)/2!+...
+(n(n-1)(n-2)(n-3)an-4b4)/4!+...+bn.
(1+1/n)n=1+n1/n+n(n-1)/2!n2+n(n-1)(n-2)/3!n3+...+1/nn=
=2+1/2!(1-1/n)+1/3!(1-1/n)(1-2/n)+1/4!(1-1/n)(1-2/n)(1-3/n)+...+1/nn={послед-ть
возрастающая}<
2+0.5(1-1/n) +1/22(1-1/n)(1-2/n)+1/23(1-1/n)(1-2/n)(1-3/n)+1/2n
< 2+0.5+1/22+1/23+...+1/2n
=2+0.5(1-1/2n)/(1-0.5)=2+1-1/2n=3-1/2n
<3.
2(1+1/n)n<3
=>
limn(1+1/n)n=e.
Следствия:
1.limx+(1+1/x)x=e.
Док-во: nxn+1
=>1/n1/x1/(n+1),
1/n+1
(1/x)+1
1/(n+1) + 1, (1/n+1)x(1/x+1)x(1+1/(n+1))x
(1/n+1)n+1(1+1/x)x(1+1/(n+1))n
limn(1+1/n)n(1+1/n)=e*1=e,
limn(1+1/(n+1))n+1*1/(1+1/(n+1))=e*1/1=e
=> limx+(1+1/x)x=e. Непрерывность. -фун.
y=f(x)
наз. непрерывной
в точке х0,
если сущ. предел
фун. y=f(x)
при хх0
равный значению
фун f(x0).limf(x)=f(x0) Условия: 1.
f(x) – опред ф-ия;
2. limxx0-0f(x)
limxx0+0
f(x) – конечные
пределы; 3.
limxx0-f(x)=limxx0+f(x);
4. limxx0f(x)=f(x0).
Если Х0
т-ка разрыва
и выполн усл-ие
2, то Х0
– 1 род
Если Х0
– 1 род и выполн
усл-ие 3, то разрыв
устран.
Если Х0
т-ка разрыва
и не вып усл-ие
2, то Х0
– 2род. Св-ва
непрерывности
в точке: 1.Если
фун f1(x)
и f2(x)
непрерывны
в точке х0,
то сумма (разность)
y(х)=f1(x)f2(x),
произведение
у(х)=f1(x)*f2(x),
а также отношение
этих фун у(х)=f1(x)/f2(x),
есть непрерывная
фун в точке х0. Док-во
(суммы): По определению
получ limхх0f1(x)=f1(x0)
и limхх0f2(x)=f2(x0)
на основании
св-ва1 можем
написать:
limхх0у(х)=limхх0[f1(x)+f2(x)
]= =limхх0f1(x)+limхх0f2(x)=f1(x0)+f2(x0)=у(х0).
Итак сумма есть
непрерывная
фун.
2.Всякая
непрерывная
фун непрерывна
в каждой точке,
в которой она
определена.
3.Если фун
z=(х)
непрерывна
в точке х=х0,
а фун y=f(z)
непрерывна
в соот-й точке
z0=(х0),
то фун y=f((х))
непрерывна
в точке х0.
Если фун
непрерывна
в каждой точке
некоторого
интервала
(а,в), где а<в, то
говорят, что
фун непреывна
на этом интервале. Если
фун непрерывна
в каждой точке
некоторого
интервала (а,в)
и непрерывна
на концах интервала,
то говорят, что
f(x) непрерывна
на замкнутом
интервале или
отрезке (а,в). Непрерывности
на заданном
промежутке
Ф-ия наз-ся
непрерывной
на пром-ке
(a;b), если
она непрерывн
в кажд т-ке этого
пром-ка.
Свойства(small): 1. достиг
наиб и наим
значения; 2. если
м и М – наиб и
наим знач-ия,
то она достиг
любые значения
м Св-ва
непрерывности
на заданном
промежутке(full): 1.Еслифун
y=f(x) непрерывна
на некотором
отрезке [а,в]
(а<х<в), то на
отрезке [а,в]
найдется по
крайней мере
одна точка х=х1
такая, что значение
фун в этой точке
будут удовл
соот-ю f(x1)f(x),
то значение
фун в этой точке
наз наибольшим
знач фун y=f(x); и
найдется по
крайней мере
такая точка
х2, что значения
фун в этой точке
будут удовл
соот-ю
f(x2)
f(x), то знач фун
в этой точке
наз наименьшим
значением фун
y=f(x). 2.Пусть
фун y=f(x) непрерывна
на отрезке
[а,в] и на концах
отрезка принимает
значения разных
знаков, тогда
м/у точками а
и в найдется
по крайней мере
одна точка х=с,
в которой фун
обращается
в нуль: f(с)=0, а<с<в. 3.Пусть
фун y=f(x) определена
и непрерывна
на отрезке
[а,в]. Если на концах
этого отрезка
фун принимает
значения f(а)=А,
f(в)=В, то каово
бы ни было число
, заключенное
м/у А и В, найдется
такая точка
х=с, заключ м/у
а и в, что f(с)=. Производная. 1.Пусть
y=f(x), xX, x0;
x0+x X
=> y=f(x0)=f(x0+x)-f(x0),
y/x=(f(x0+x)-f(x0))/x. Если
limx0y/x,
то этот предел
наз-ся производн
ф-ии в т-ке Х0.
Если
f(x) имеет производ
в кажд т-ке xX,
то мы можем
брать прозвол
Х, считая его
фиксир, х+хХ.
Limх0(f(x0+x)-f(x0))/x=
=f/(х)=df(x)/dx=dy/dx=y|(x).
2
Производная
фун f(x) в точке
х0 равна
угловому коэф-ту
касательной
к гр-ку фун f(x) в
точке М (х0;f(x0)).
Если т-ка
М будет приближ-ся
к т-ке М0
(при х0),
то секущая
приближ-ся к
касат.
y|(x0)=limх0(f(x0+x)-f(x0))/
/x=limх0y/x=limх0tg==lim0tg=tg0.
L: y-f(x0)=f\(x0)(x-x0)
Nl=y-f(x0)=-(x-x0)/f\(x0).
3. Основ
теоремы о
производных.
1. y=U(x)+V(x),
y|=U|(x)+
V|(x).
Док-во: для х+х
имеем: y+y=(u+u)+(v+v).
Следовательно,
y=u+v,
y/x=u/x+v/x,
y|=limx0y/x
= limx0u/x+
limx0v/x=U|(x)+V/(x).
2. y=uv, y|=u|v+uv|.
Док-во: y+y=(u+u)(v+v),
y=(u+u)(v+v)-uv=uv+uv+uv,
y/x=uv/x+vu/x+uv/x,
y|=
limx0y/x=
limx0uv/x
+ limx0vu/x
+ limx0uv/x={
limx0u=0,
т.к ф-ия дифф-ма
и непрерывна}=u|v+uv|.
3. y=u/v, y|=(u|v-uv|)/v2.
Док-во: y+y=(u+u)/(v+v),
y=(u+u)/(v+v)-u/v=(vu-uv)/v(v+v)
y/x...
4. y=ax,
y|=axln
a. Док-во: ln
y=x ln a, y|/y=ln
a, y|=yln a
y|=axln
a.
Неявно
задан фун и
нахождение
ее производ.
Говорят,
что соот-е F(x;y)=0
задается неявно,
если сущ фун
у=f(x), х принадлежит
отрезку [а,в]
и, если подстав-е
в F(x;y)=0 соот-е обращает
его в тождество()
{F(x;y)=0,у=f(x),х
принадлежит
отрезку [а,в],F(x;f(x))
0}
Правило
нахождения:
Если
F(x;y)=0 задает
фцн неявно, т.е
это будет тождество,
то тождественное
равенство можно
по членно
продифференцировать.
{[F(x;y)]/=0/}
Формула
Лейбница.
y(n)=(uv)(n)=(u)(n)v+nu(n-1)v|+([n(n-1)]/[1*2])*n(n-2)v||+…+uv(n)
Дифференцирование
ф-ии в точке.
Ф-ия y=f(x) наз-ся
дифференцируемой
в т-ке Х0,
если y=Ax+O(x),
где А не зависит
от Х,
О(Х)
– б.м., более
высокого порядка
малости, чем
Х,
когда Х0,
т.е. limx0O(x)/x=0.
АХ
– главная часть
приращения.
Теорема:
y=f(x) дифф-ма
в т-ке Х0
т и тт, когда
она в этой т-ке
имеет конечную
производную
A=f\(x0).
Необход
усл-ие дифф-ти:
если ф-ия
дифф-ма, то она
имеет кон производ.
Дано: y=Ax+O(x) f\(x0)=limx0y/x=
limx0[(Ax+O(x))/x]
= limx0(A+O(x)/x)=A
=> y=f\(x0)x+O(x)
=> limx0y=0
=> f(x) – непрерывна. Достат
усл-ие дифф-ти:
если ф-ия в
заданной т-ке
имеет кон производ,
то она дифф-ма.
Дано: f\(x0)
– число, f\(x0)=limx0y/x
=> y/x=f\(x0)+(x)
{(ч)
– б.м.}, y=f\(x0)x+(x)x
=> y=f\(x0)x+O(x),
т.е. O(x)=(x)x
=> limx0O(x)/x=limx0(x)=0.
Дифференциал
ф-ии это главная
часть приращения,
линейная относит
Х. Приближ
знач ф-ии в некот
т-ке: y=f(x0+x)-f(x0)
=>f(x0+x)=f(x0)+yf(x0)+df(x0)=f(x0)+f\(x0)dx,
dx=x.Бесконечно
большая величина
(lim Xn)/(lim Yn) = a/b.
 выпол
x0-
выпол
x0-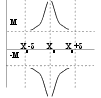 -ия
y=f(x) наз-ся
бесконечно
большой при
xx0
если для М>0
сколь угодно
большого
>0,
что x
|x-x0|<
будет выполняться
нер-во |f(x)|>M, x
x0-
-ия
y=f(x) наз-ся
бесконечно
большой при
xx0
если для М>0
сколь угодно
большого
>0,
что x
|x-x0|<
будет выполняться
нер-во |f(x)|>M, x
x0-![]()
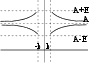 исло
А наз-ся
пределом y=f(x) x,
если для любого
Е>0 можно найти
число К, x
|x|>K |f(x)-A|
исло
А наз-ся
пределом y=f(x) x,
если для любого
Е>0 можно найти
число К, x
|x|>K |f(x)-A|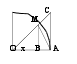
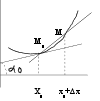 .
Геометр
смысл производ.
.
Геометр
смысл производ.