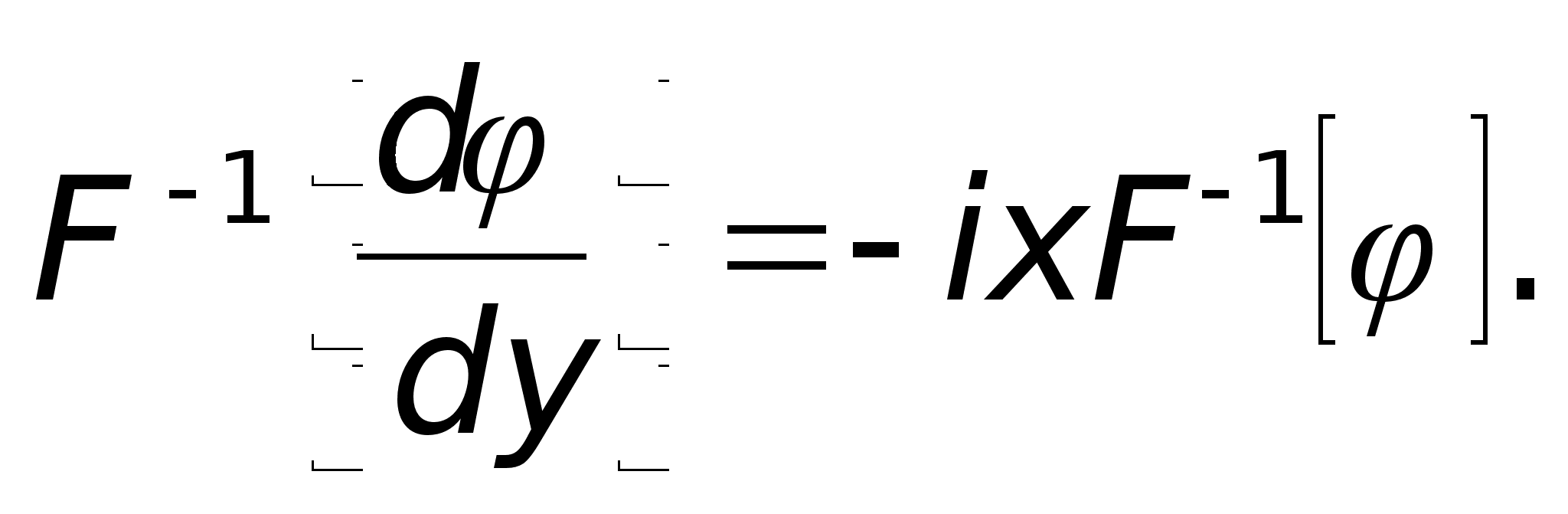Реферат: Преобразование Фурье
Kalmiik-forever
Глава I
Преобразование Фурье.
§1. Класс Шварца.
Преобразование Фурье отображает класс Шварца на себя.
Определение. Следующее множество комплекснозначных функций действительного переменного называется классом Шварца.
.
Класс Шварца иногда называют классом быстро убывающих функций.
Операции обычного сложения и умножения функции на число превращают класс Шварца в линейное векторное пространство:
,S(R), a, bК выполнено a+bS(R).
Отметим несколько простых свойств функций из класса Шварца.
Если (x)S(R),то
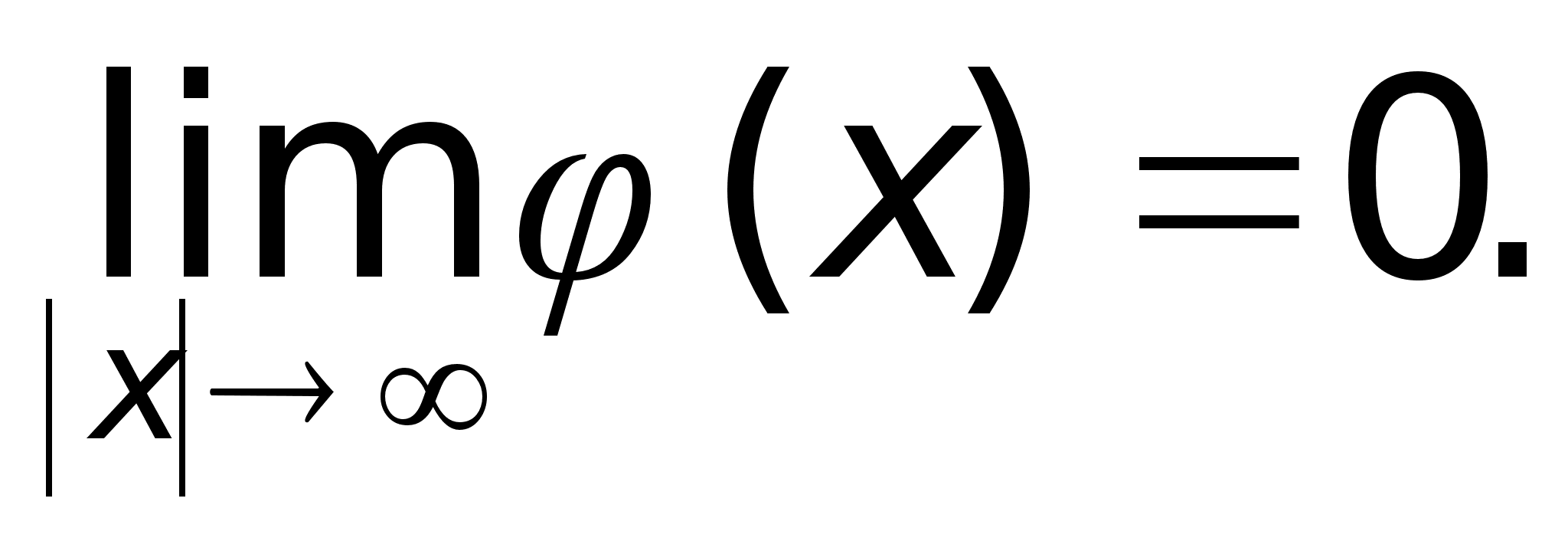
Если (x)S(R),то (x) ограничена на R.
Если (x)S(R),то (x)=x(x)S.
Если (x)S(R) и P(x) – многочлен, то P(x)(x)S.
Если (x)S(R),то
.
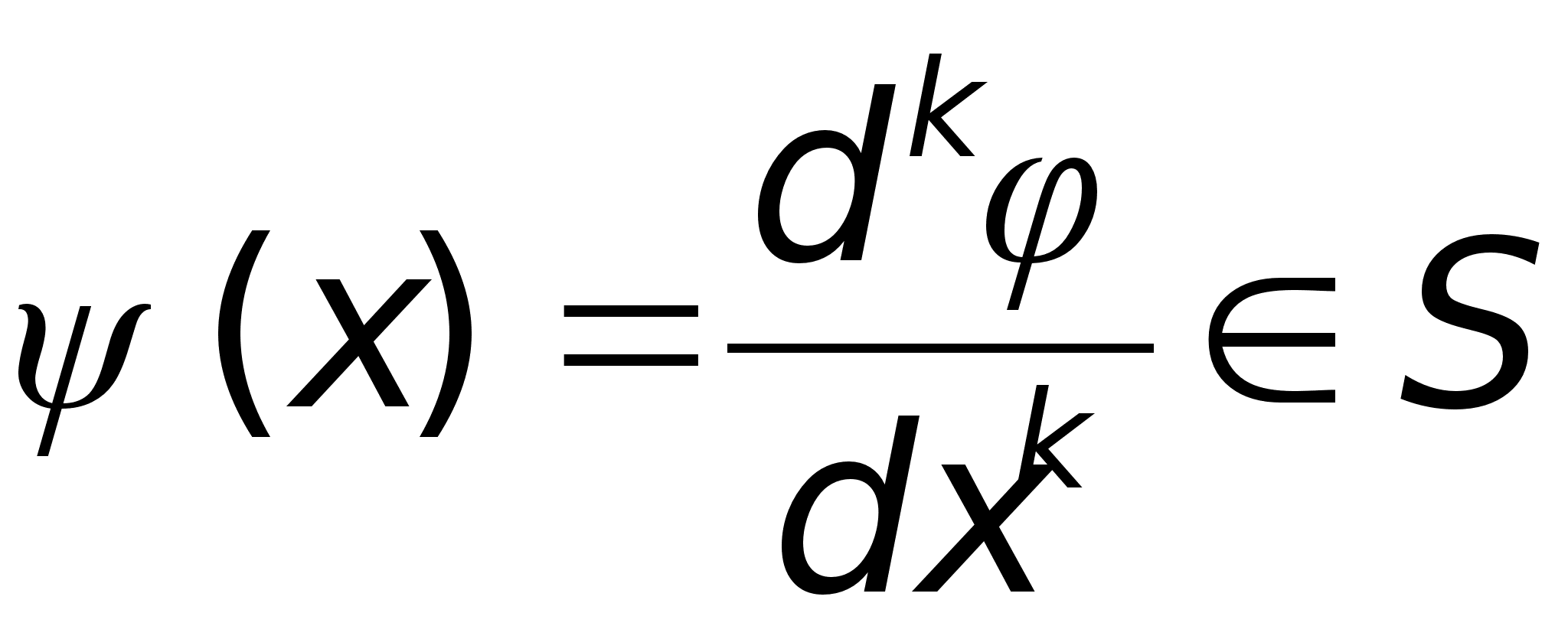Доказательство. Первые два свойства сразу следуют из неравенств
.
Докажем свойство 3). Во первых, =xC∞(R). Далее,
.
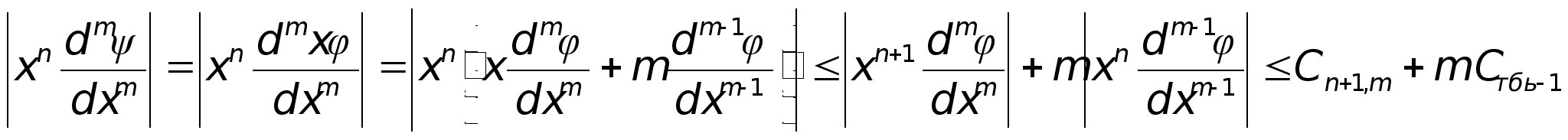Свойство 4) получается из 3) последовательным применением. В самом деле, если P(x)=a0+a1x+…+anxn, то по свойству 3) имеем xiS(R), потому функция P(x)(x)=a0+a1(x)+a2(x2)+…+an(xn) принадлежит классу Шварца ввиду его линейности.
Свойство 5) доказывается аналогично свойству 3).
§2. Одномерное преобразование Фурье.
Определение. Функция
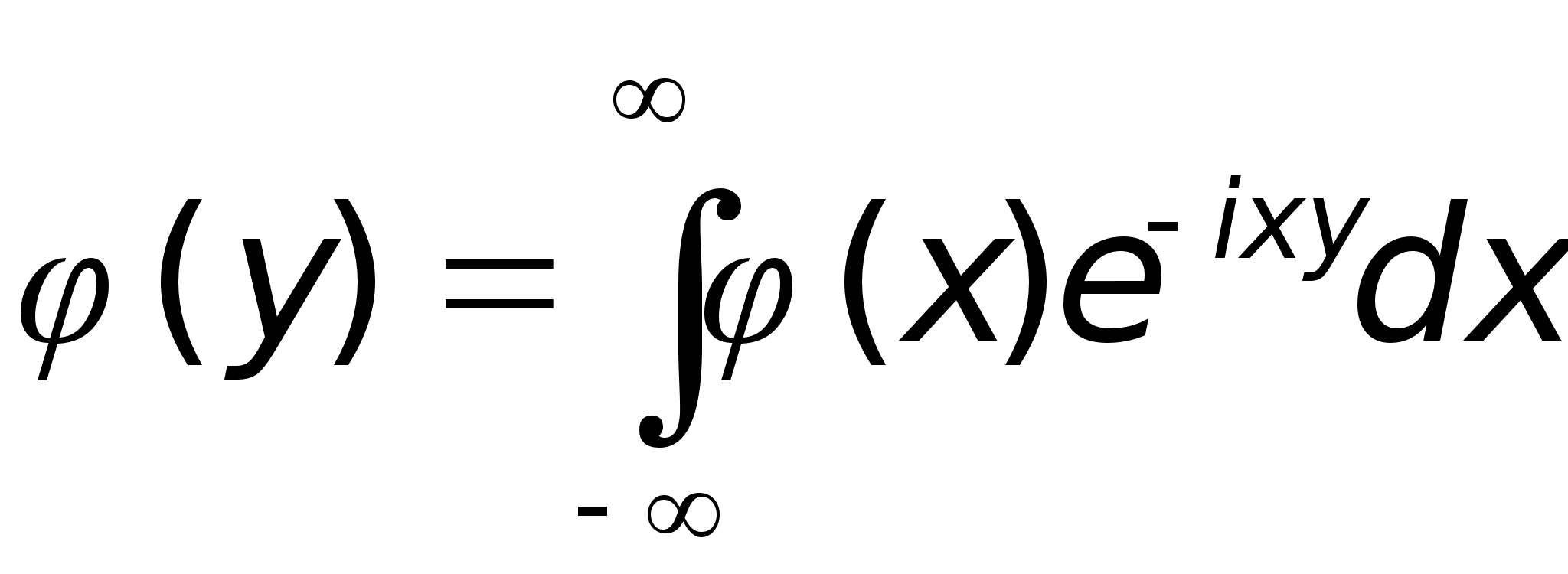(1)
называется преобразованием Фурье функции (x) и обозначается F[]. Ясно, что не для всякой функции (x) интеграл (1) сходится, и потому не для всякой функции определено преобразование Фурье.
Если
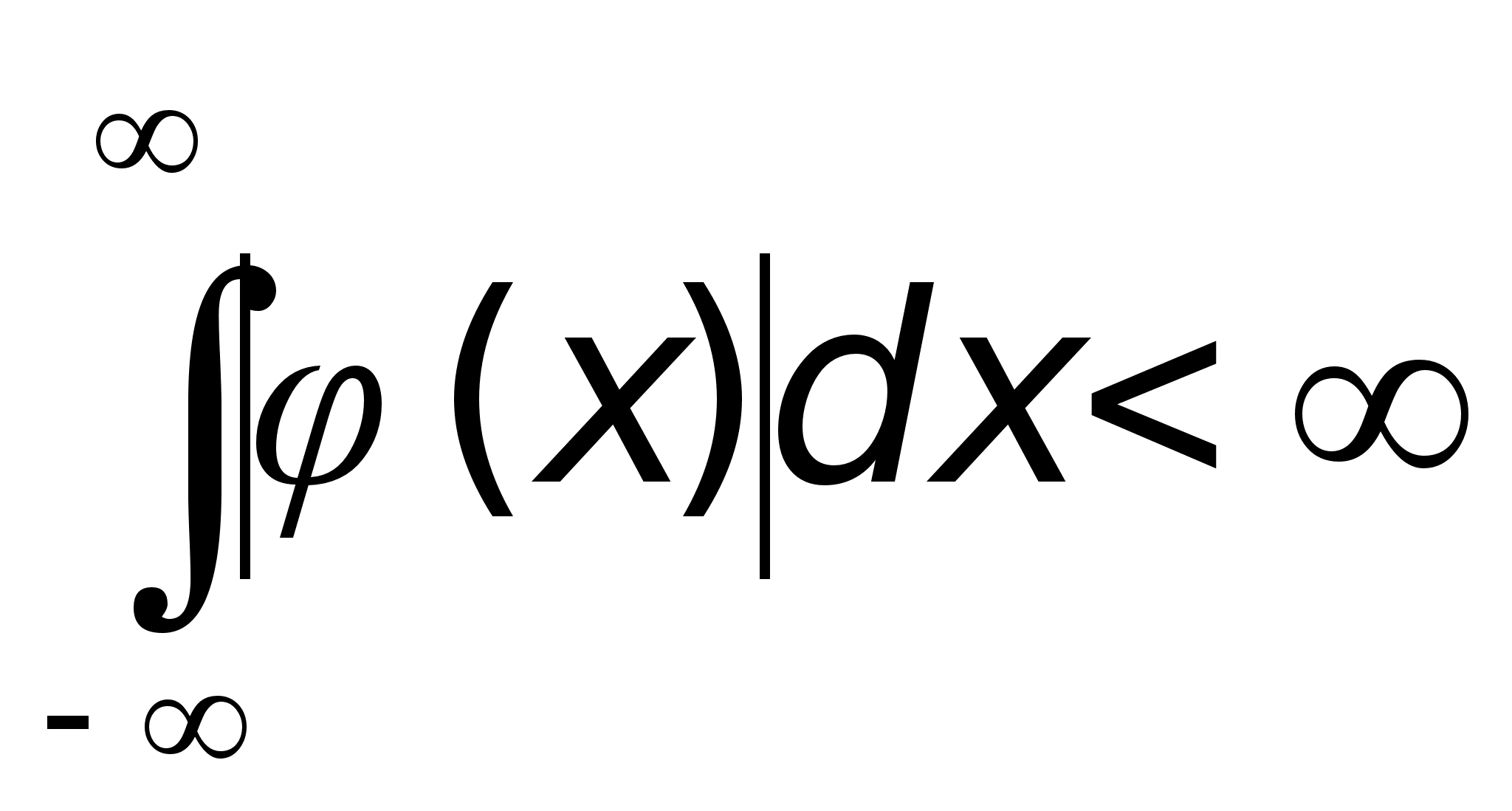(интеграл Лебега),
то будем говорить,
что
принадлежит
пространству
L1(R).
Предложение 1. Преобразование Фурье функции (x) из L1(R) определено и ограничено по модулю на действительной оси.
Доказательство
следует
из равенства
и (1):
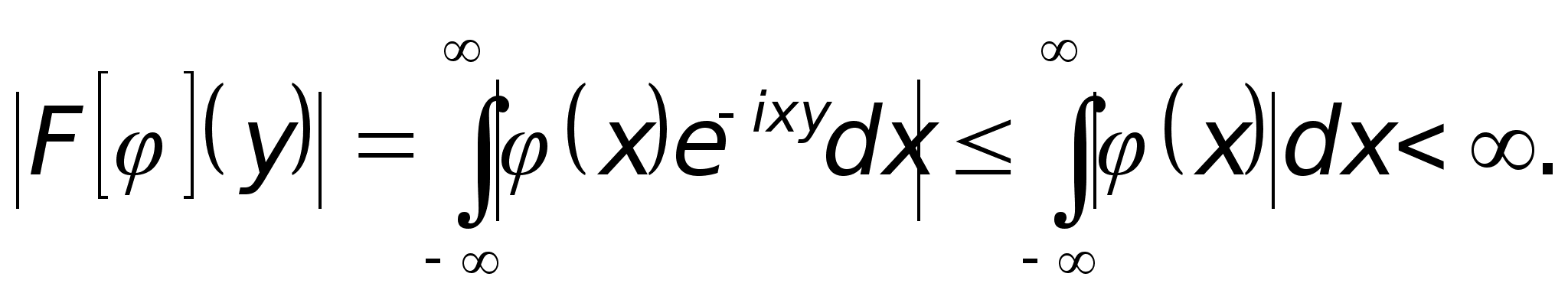
Следствие. Преобразование Фурье определено для функций S(R).
Доказательство. Достаточно доказать, что S(R)L1(R). Заметим, что если S(R), то по свойству 4) функция (1+x2)S(R) и, следовательно, ограничена, а (1+x2)-1L1(R). Поэтому функция (1+x2)(1+x2)-1L1(R).
§3. Свойства преобразований Фурье функций из S(R).
1)
Доказательство получается дифференцированием в (1) под знаком интеграла. Это законно, так как интеграл, полученный после дифференцирования, мажорируется интегралом
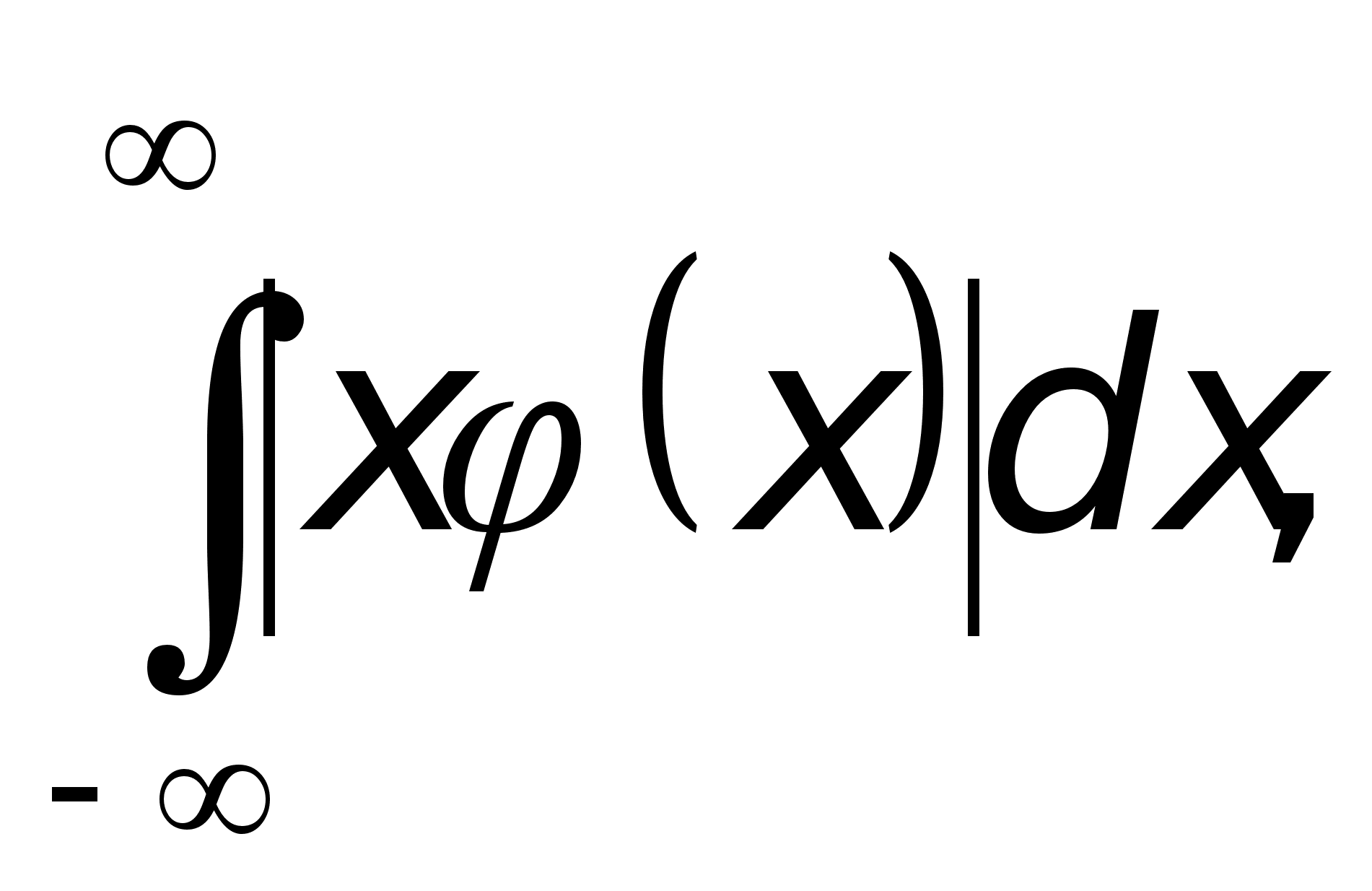
сходимость которого вытекает из свойства 3): x(x)S(R)L1(R).
2) Если S(R), то F[]C(R).
Так как -ixS, то доказательство немедленно вытекает из 1).
Доказательство. Очевидно
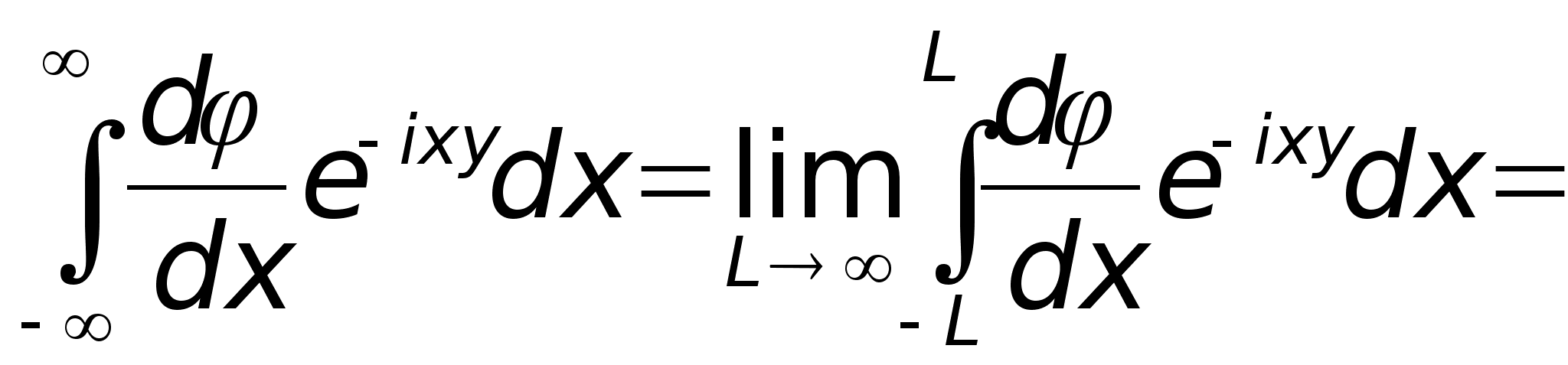
теперь можно интегрировать по частям
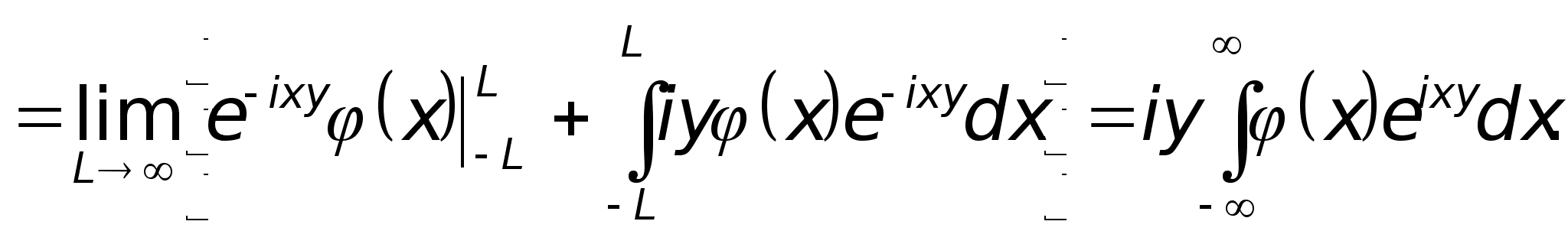
Это и доказывает свойство 3).
Предложение 2. Преобразование Фурье функции из класса Шварца есть снова функция из класса Шварца.
Доказательство. Многократно применяя свойства 1) и 3), устанавливаем
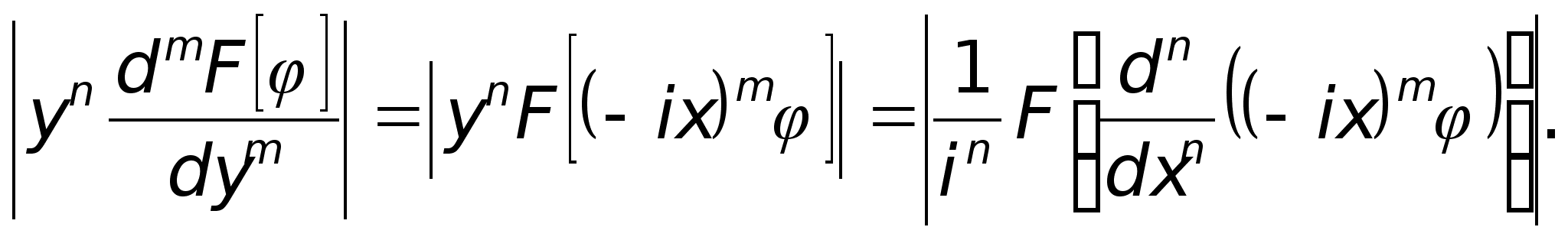
По свойствам 4) и 5) класса Шварца функция
лежит
в классе Шварца
SL1
, и тогда, по
предложению
пункта 2, функция
ограничена
некоторой
постоянной,
которую мы
обозначим Cn,m.
Предложение
доказано.
§4. Обратное преобразование Фурье.
Определение. Функция
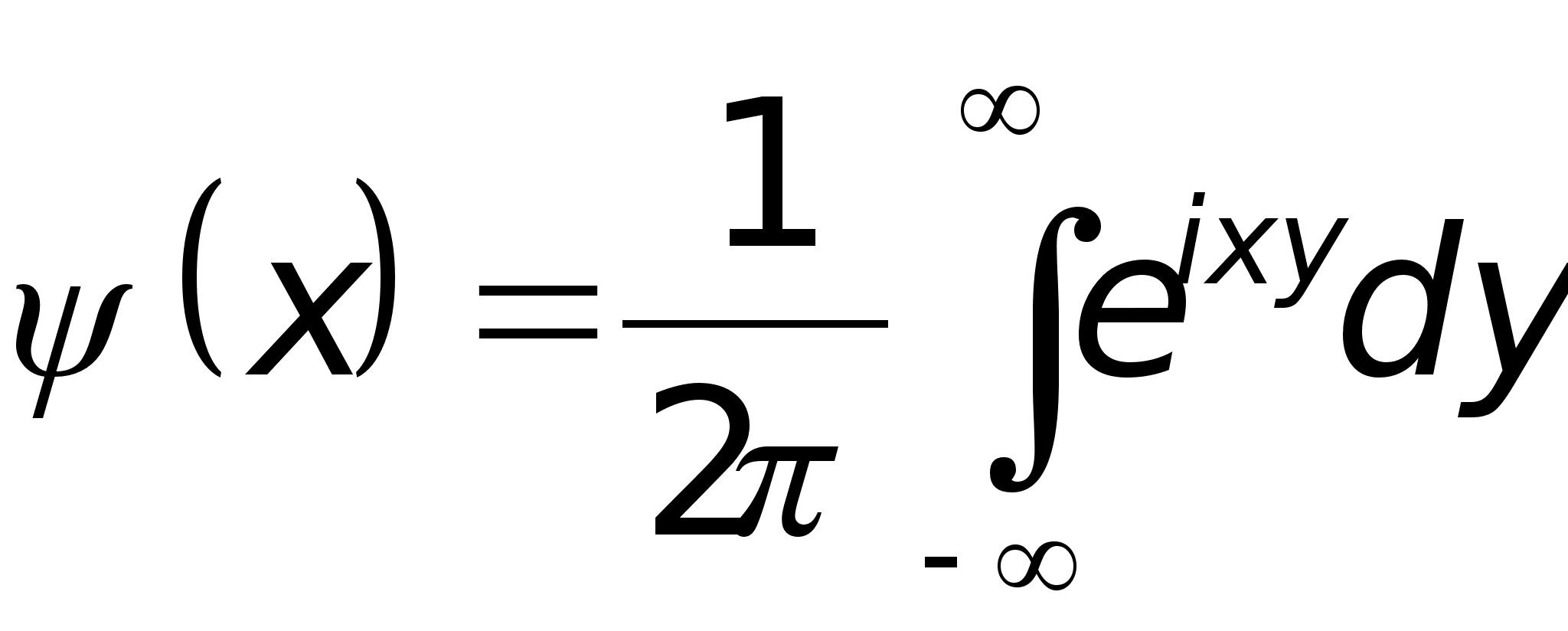
называется обратным преобразованием Фурье функции (y) и обозначается F-1[].
Нетрудно проверить, что обратное преобразование Фурье функций из S(R) обладает свойствами, аналогичными прямому:
Докажем, что F-1[F[]]= для любой функции S. Для этого потребуется
Лемма. Пусть непрерывная функция h(y)L1(R) имеет почти всюду ограниченную производную. Пусть
такой набор точек, что на интервалах (yi,yi+1) функция h класса C2, i=1,2,…,n. Тогда для всех x, отличных от yi, i=1,2,…,n+1, справедливо соотношение
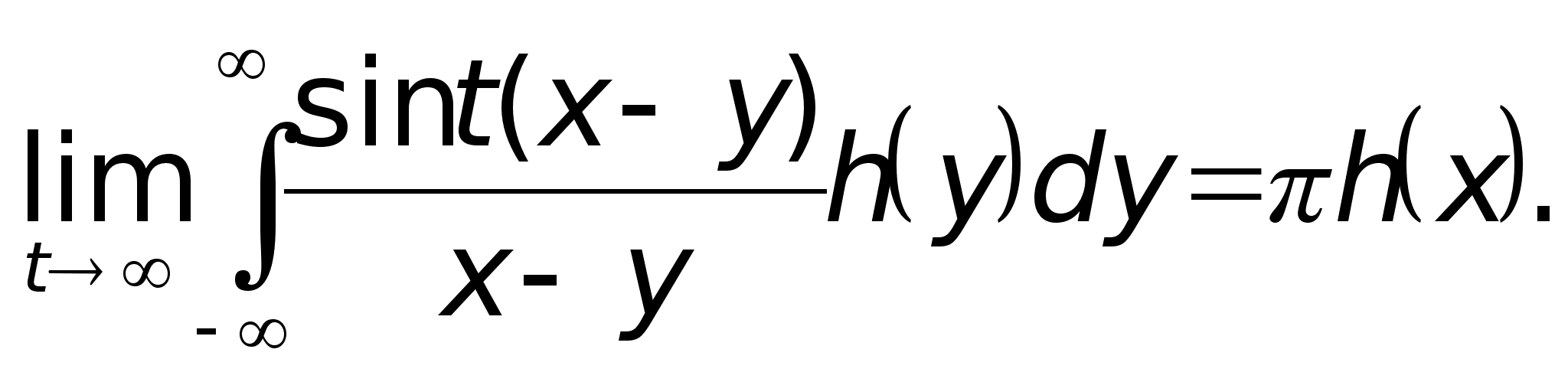
Доказательство. Так как h(y)L1 , то для всякого >0 найдется такое А, что
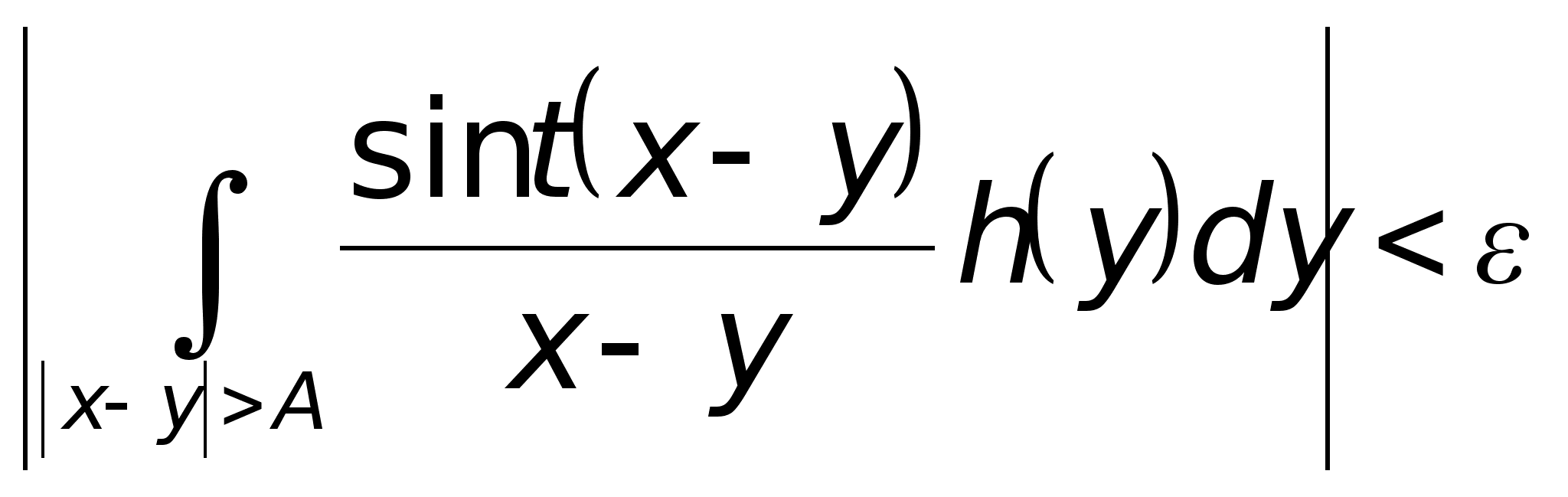
при всех t>0. Заметим, что
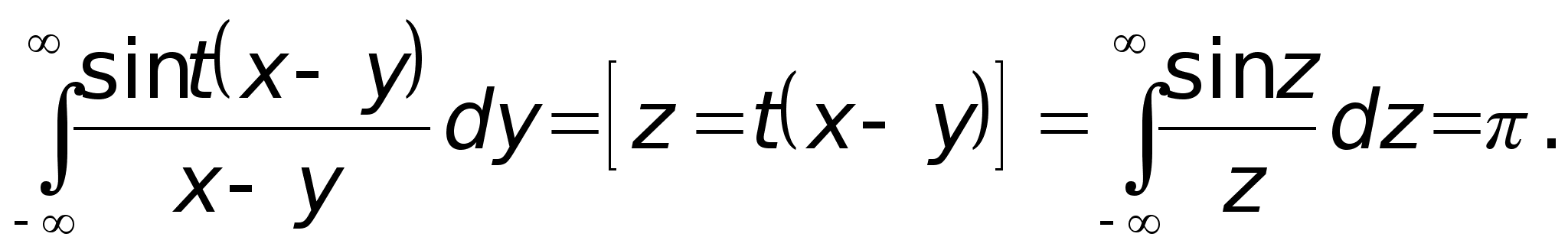(3)
Тогда
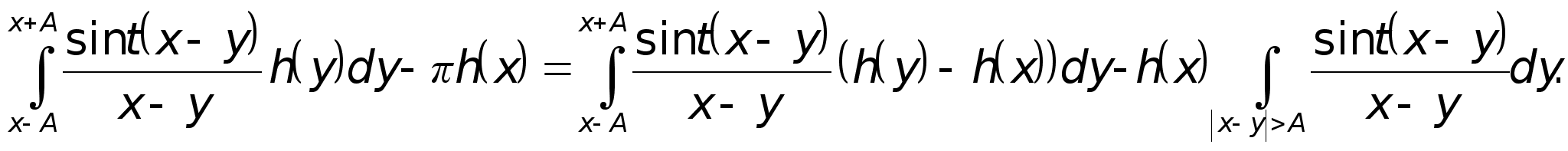
Второе слагаемое в (4) заменой z= t(x - y) приводится к виду
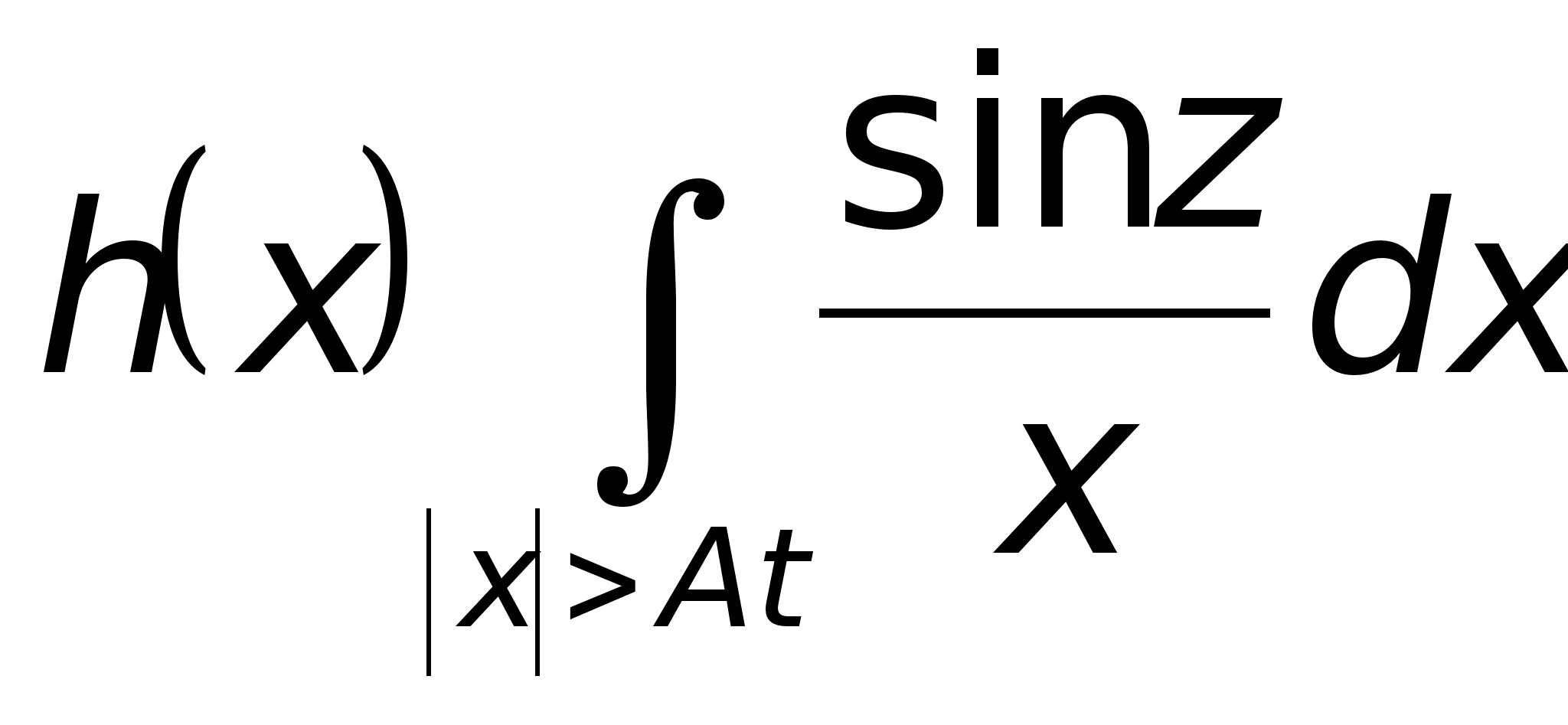
и,
следовательно,
стремится к
нулю при
в силу сходимости
интеграла (3).
Для доказательства
леммы осталось
показать, что
первое слагаемое
в (4) также стремится
.
Введем обозначение
Если h класса C2 в окрестности точки x, то из равенства
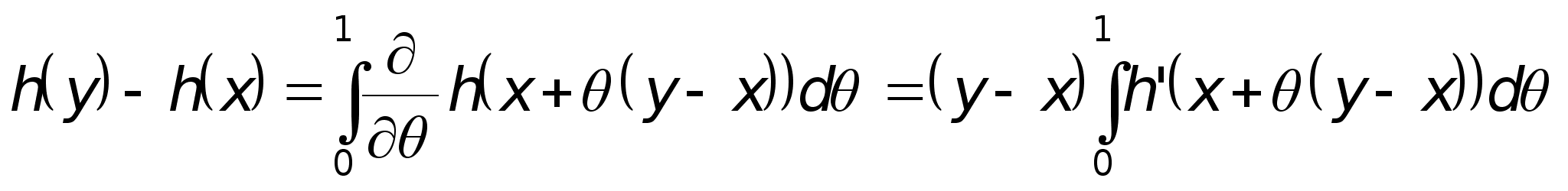
следует дифференцируемость функции g(y) в точке y = x. Итак, g(y) – кусочно-диференцируемая функция. Интегрируя по частям, устанавливаем
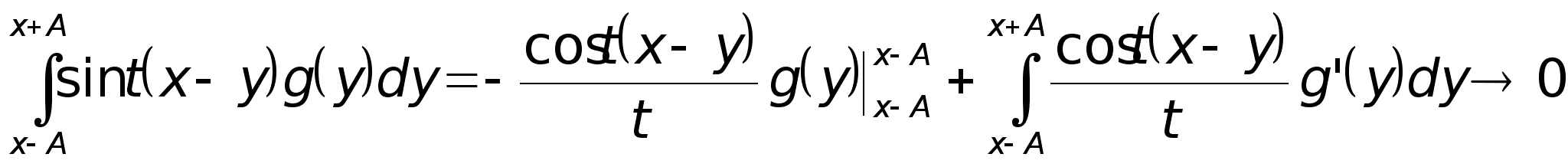
при
Лемма доказана.
Предложение 3. F-1[F[]]= для любого S(R).
Доказательство.
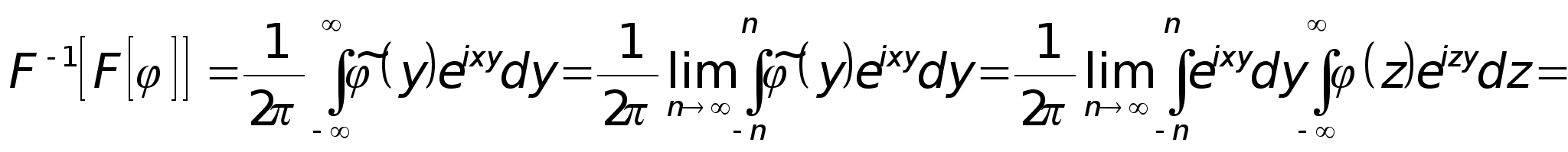
Внутренний интеграл сходится равномерно по y[-n, n], поэтому возможна замена порядка интегрирования.
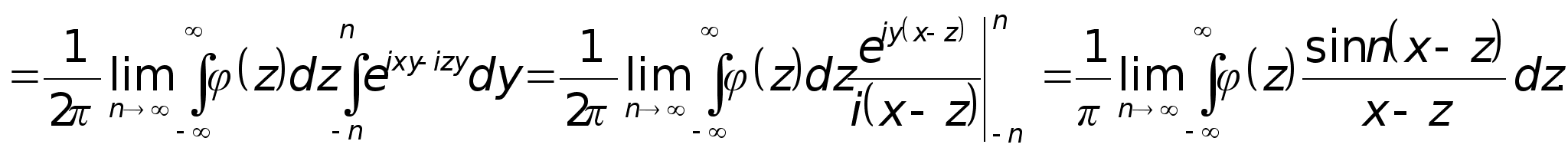
Теперь утверждение следует из леммы.
Из
доказанного
предложения
вытекает, что
преобразование
Фурье взаимно-однозначно
отображает
класс Шварца
в себя. Покажем
что это отображение
“на”. Определим
оператор J
переводящий
функцию (x)
в функцию (-x).
Тогда очевидно
равенство
F=2JF-1,
откуда, умножая
справа на FJ/2
и используясь
равенством
JJ=1,
будем иметь
,
где 1 справа
надо понимать
как тождественное
отображение
в S(R).
Последнее
равенство
означает, что
любая функция
из S(R)
есть преобразование
Фурье некоторой
функции.
§5. Класс Шварца в многомерном случае.
Мультииндексом
=(1,…,n)
будем называть
набор из неотрицательных
целых чисел.
Порядком
мультииндекса
будем называть
число
Глава II
Задача Коши для уравнения теплопроводности.
§1. Постановка задачи коши для уравнения теплопроводности.
Требуется
найти функцию
u(x,t),
непрерывную
при t
0
и x
R
и класса C2
при t>0,
удовлетворяющую
уравнению
(1)
при
t>0,
xR
и начальному
условию
u(x,0)=(x). (2)
Задача (1),(2) имеет, вообще говоря, много решений. Поэтому обычно накладывают дополнительное условие, которому должно удовлетворять решение.
Теорема (Тихонова). Пусть u(x,t) – решение задачи (1),(2) с функцией (x)0. Пусть >0 существует постоянная C>0 такая, что
при всех xR и t0. Тогда u0.
Из
этой теоремы
следует, что
при среди функций,
растущих, грубо
говоря, медленнее
чем
при любом
>0,
не может найтись
более одного
решения задачи
(1),(2).
Эту теорему мы приводим без доказательства, но ниже докажем теорему единственности при более сильных ограничениях.
§2. Формальный поиск решения.
Применим преобразование Фурье
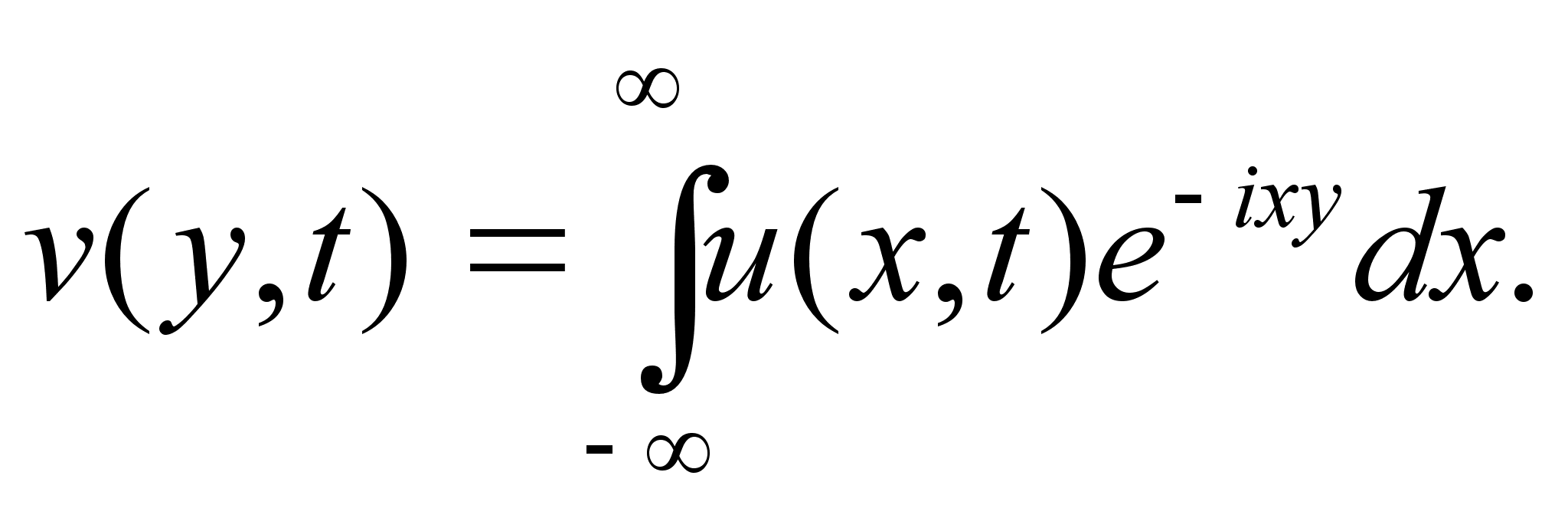(3)
Выкладки этого пункта будем проделывать, не заботясь об обосновании. Дифференцируя (3) по t, устанавливаем:
Кроме того, по свойству 3) преобразования Фурье
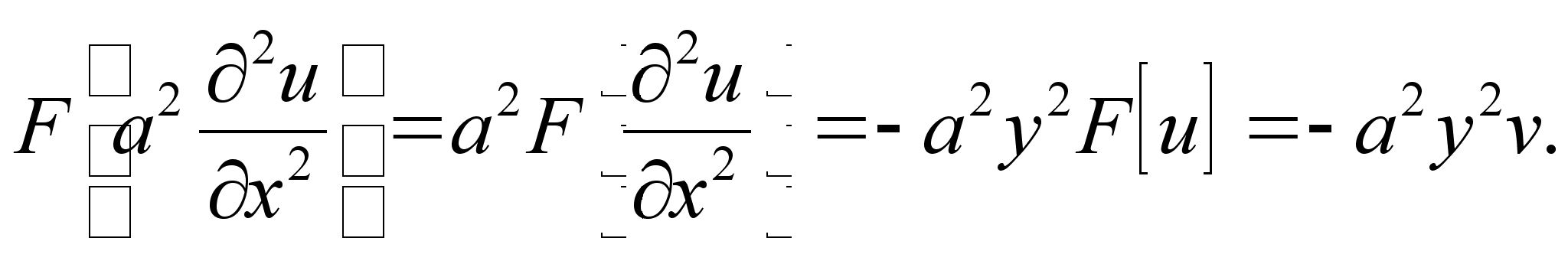
Учитывая (1), имеем
(4)
Решая это обыкновенное дифференциальное уравнение с параметром y, находим
Где g(y) – произвольная функция. Используя (2), определяем g(y):
§3. Решение задачи Коши с начальной функцией из класса Шварца.
Теорема 2. Если S(R), то формула
(5)
дает решение задачи (1), (2), бесконечно дифференцируемое при t0.
Доказательство.
Так как
,
то
при любом t0
и обратное
преобразование
Фурье в формуле
(5) определено.
Дифференцируя
(5) по t, имеем
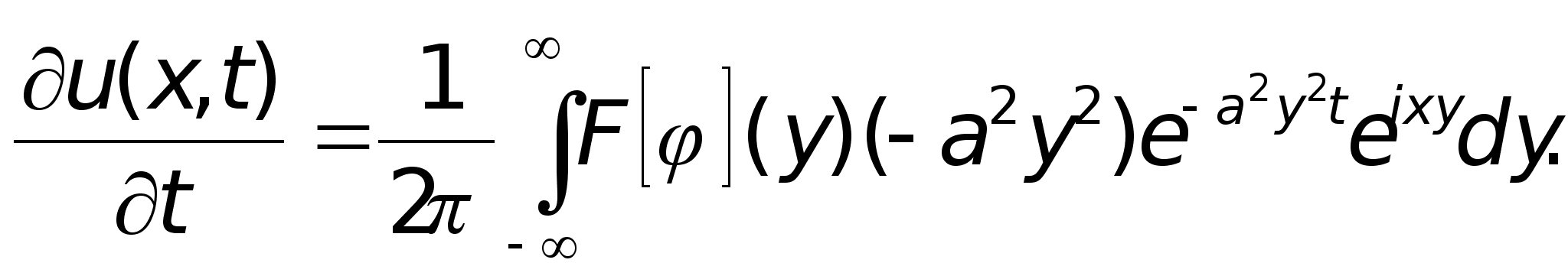(6)
так как
,
то интеграл
(6) сходится
равномерно
при t0,
и дифференцирование
законно. Совершенно
так же доказывается
бесконечная
дифференцируемость
функции u(x,t)
по t и x.
Дифференцируя (5) дважды по x, устанавливаем:
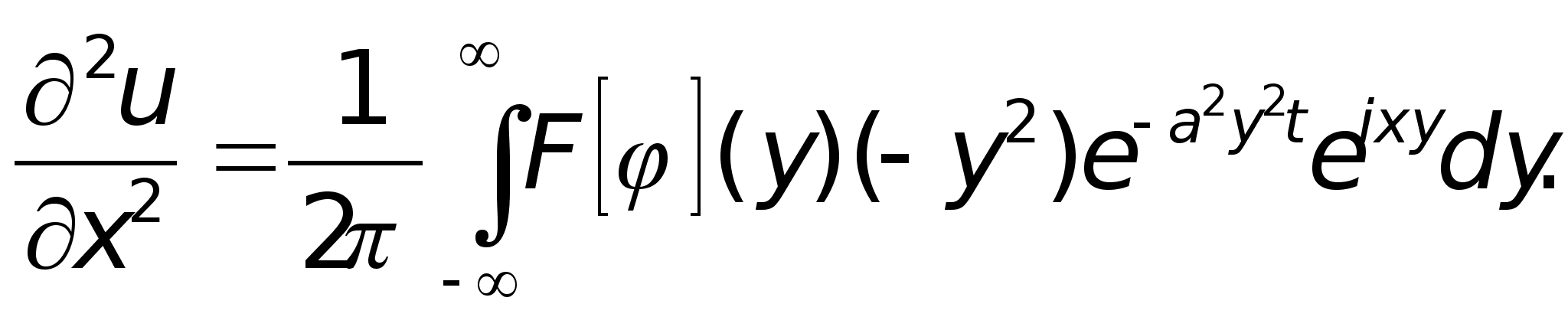(7)
Из формул (6),(7) вытекает, что функция u(x,t) удовлетворяет уравнению (1). Справедливость условия (2) очевидна. Теорема доказана.
§4. Фундаментальное решение уравнения теплопроводности.
Преобразуем формулу (5) к более удобному ”явному” виду. Для этого запишем ее в интегралах
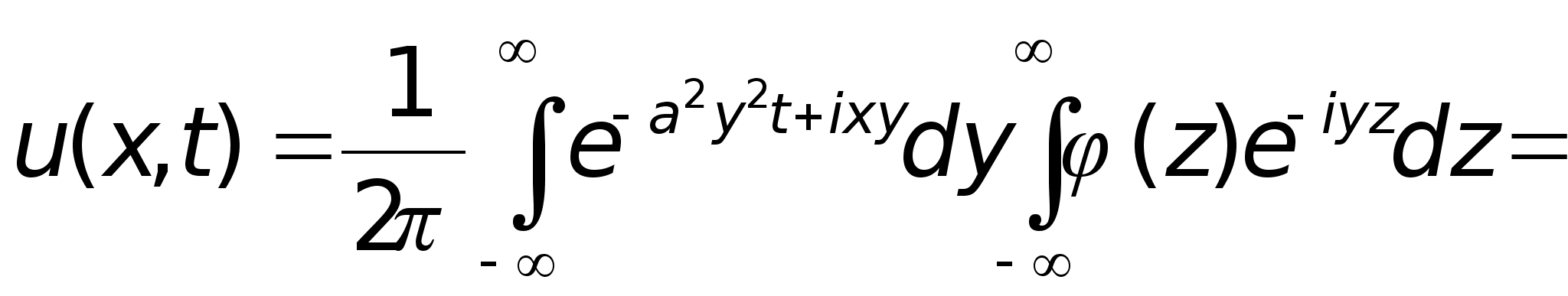
меняем порядок интегрирования
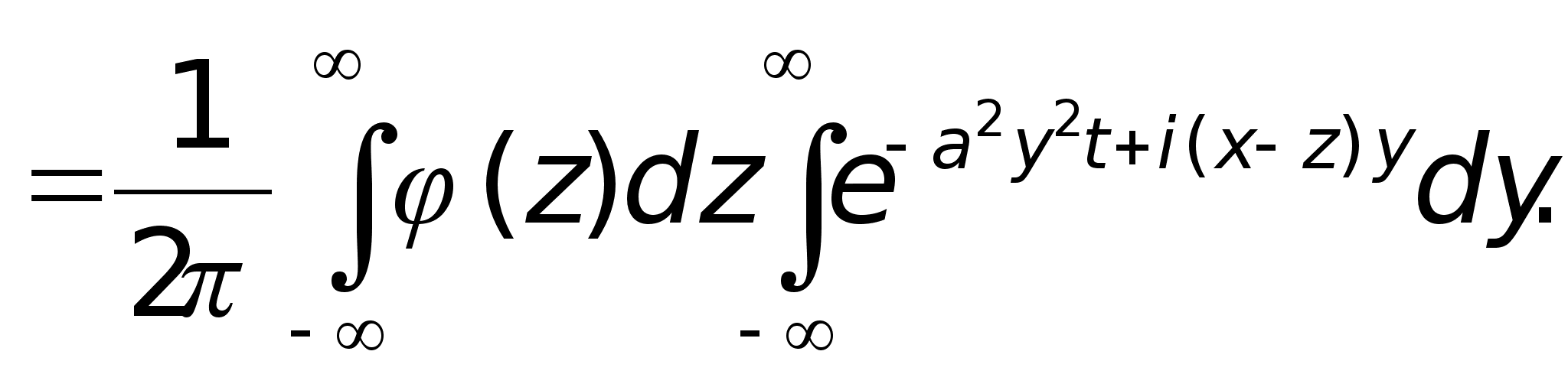(8)
В формуле
(8) внутренний
интеграл есть
преобразование
Фурье от функции
при значении
аргумента
–(x-z),
поэтому из
(9.2) имеем
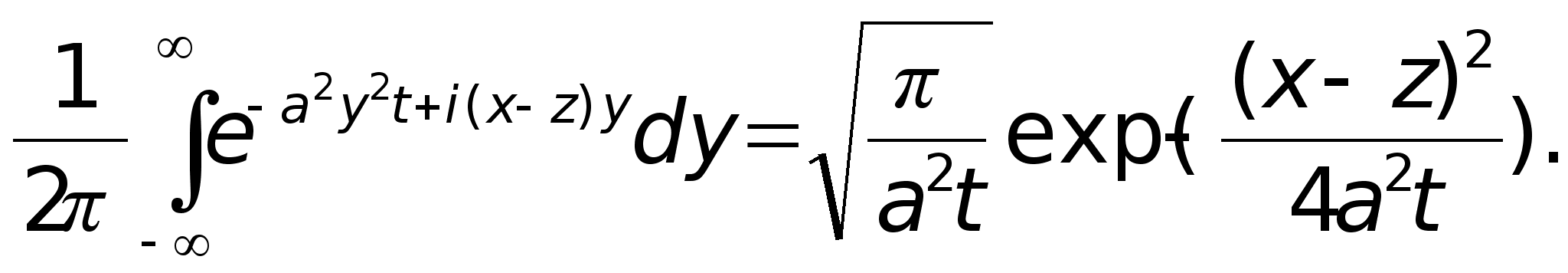
Подставляя это в (8), получим
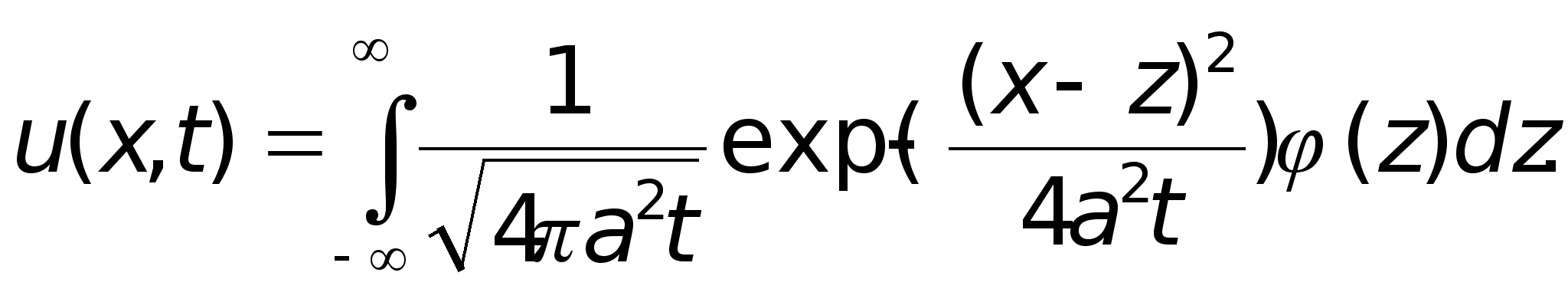(9)
Функцию
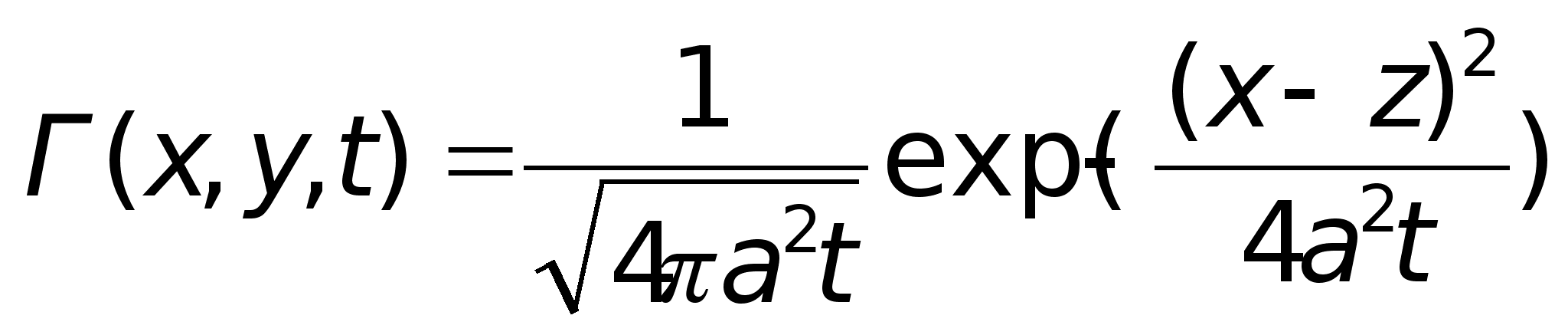
называют фундаментальным решением уравнения теплопроводности. Легко проверяются следующие свойства этой функции:
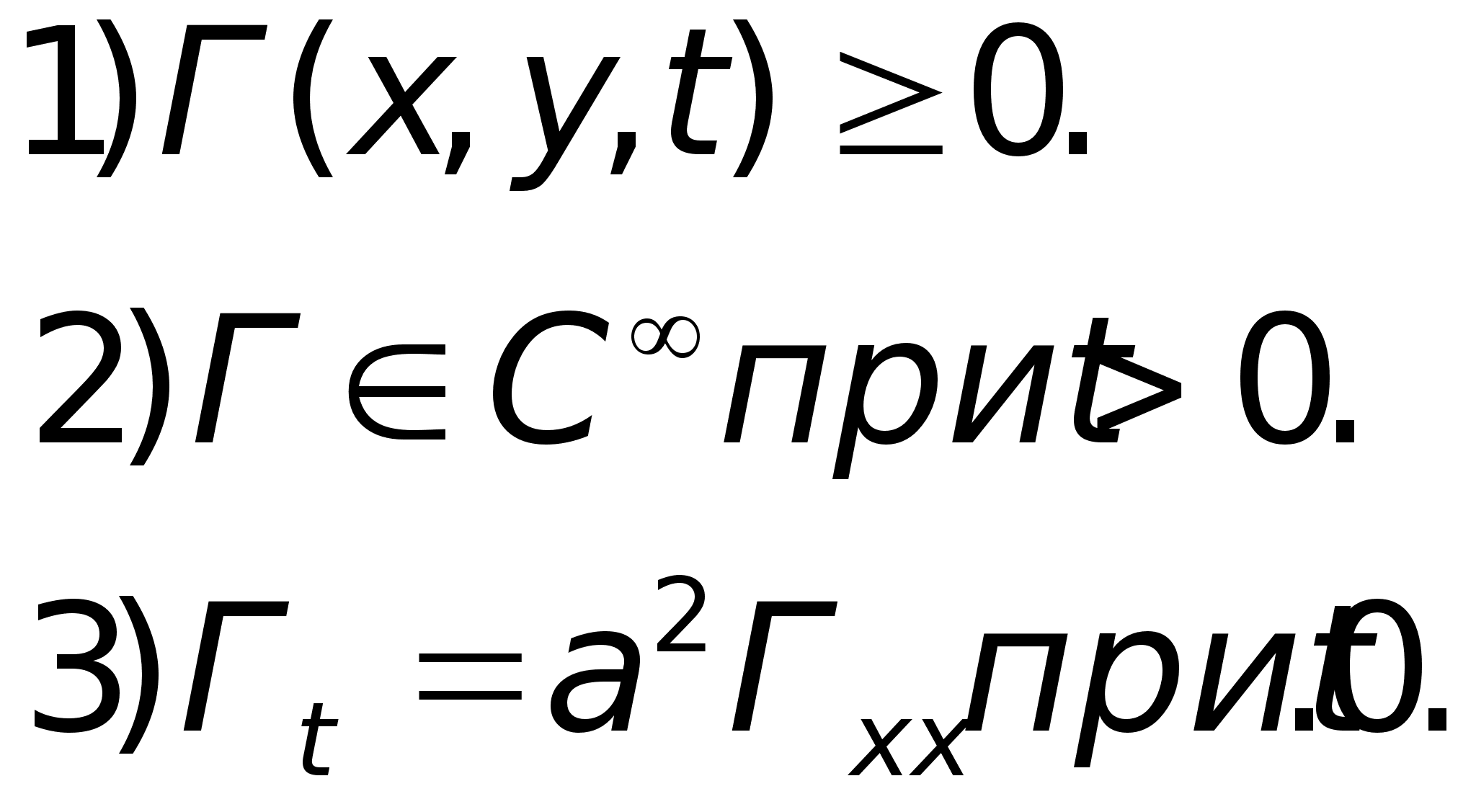
§5. Решение задачи с непрерывной ограниченной начальной функцией.
Теорема 3. Пусть (z) ограничена и непрерывна на вещественной оси. Тогда формула (9) дает решение задачи (1),(2).
Доказательство. Продифференцируем (9) под знаком интеграла
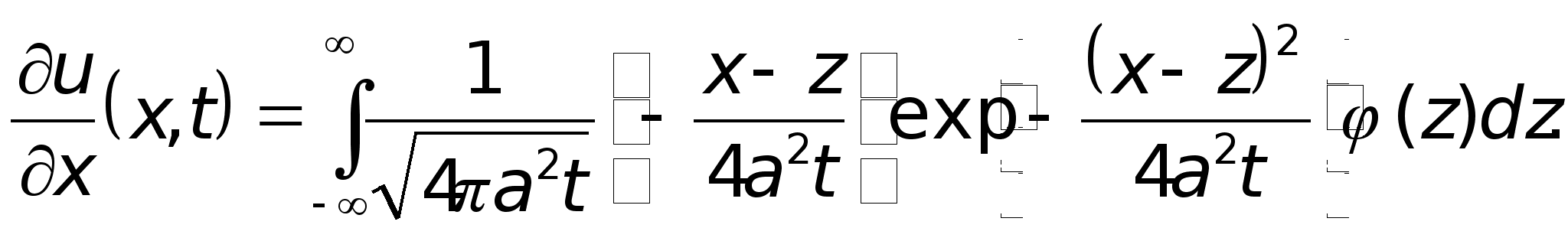(10)
Чтобы обосновать законность такого дифференцирования, достаточно показать равномерную сходимость по x интеграла (10), для чего произведем замену
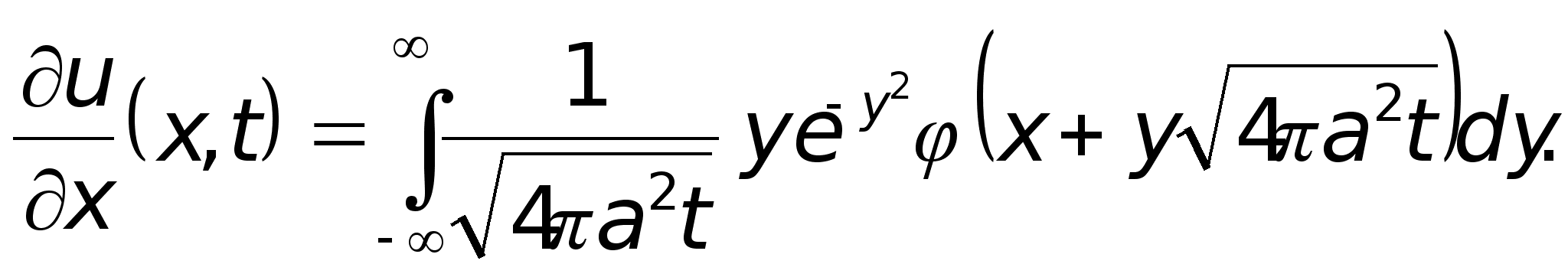
Из ограниченности функции следует равномерная сходимость интеграла как по xR, так и по t>.
Совершенно так же доказывается бесконечная дифференцируемость функции u(x, t) по x и t при t>0. Из свойства 3) фундаментального решения следует, что u есть решение уравнения (1).
Для доказательства (2) снова сделаем замену переменной интегрирования в (9):
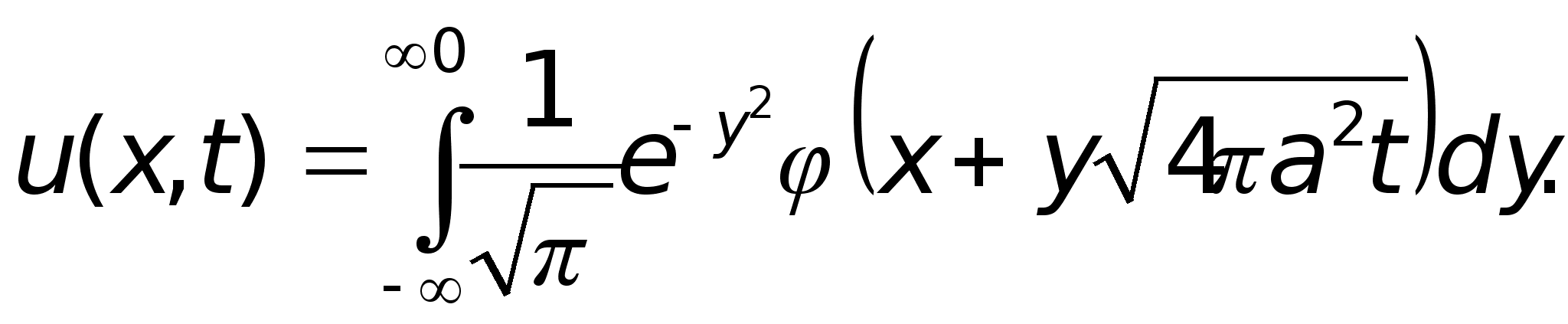
Так как последний интеграл сходится равномерно по x и t, то возможен предельный переход под знаком интеграла
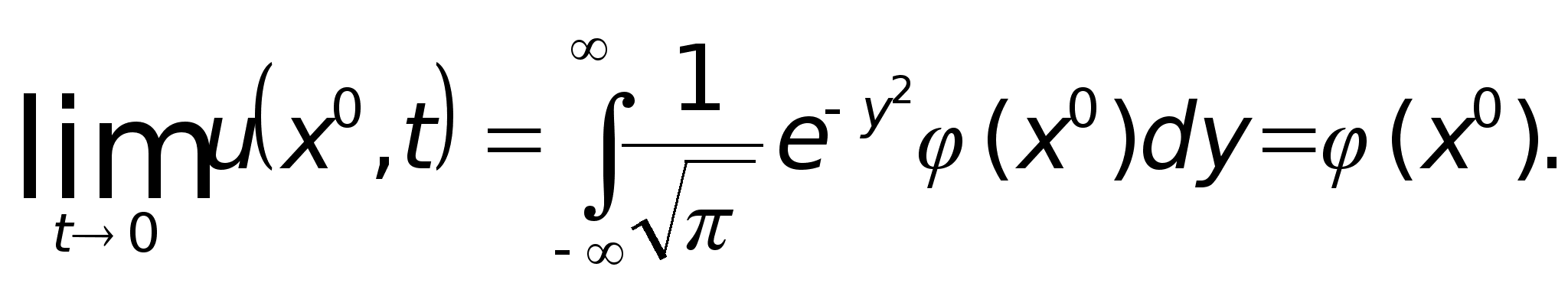
Теорема доказана.
§6. Единственность решения в классе ограниченных функций.
Теорема 4. Пусть ограниченная функция u(x, t) является решением задачи (1), (2) с начальной функцией 0. Тогда u(x, t)0.
Доказательство. Рассмотрим функцию
(x, t)=(x2+3a2t)+u(x, t),
где >0, - любого знака. Легко проверить, что
(11)
Так как функция u ограничена, то функция v(x, y) в области t>0 достигает минимума в некоторой точке (x0, t0). Покажем, что v(x0, t0)0. Пусть, напротив v(x0, t0)<0. Тогда, очевидно, t0>0, так как v(x, 0)0. Как необходимые условия минимума имеем соотношения
которые противоречат (11).
Итак, v(x, t)0 при всех x и t0. При фиксированных x и t,переходя к пределу при 0 в неравенстве
(x2+3a2t)+u(x, t)0,
получаем u(x, y)0. Ввиду произвольности знака отсюда следует u=0.Теорема доказана