Реферат: Преобразования фигур
Малоязовская башкирская гимназия
Геометрия
Реферат
на тему:
“Преобразования фигур”
Выполнил: ученик 10 Б класса
Халиуллин А.Н.
Проверила: Исрафилова Р.Х.
Малояз 2003 год
План:
I. Преобразование.
II. Виды преобразований
1. Гомотетия
2. Подобие
3. Движение
III. Виды движения
1. Симметрия относительно точки
2. Симметрия относительно прямой
3. Симметрия относительно плоскости
4. Поворот
5. Параллельный перенос в пространстве
I. Преобразование - смещение каждой точки данной фигуры каким-нибудь образом, и получение новой фигуры.
II. Виды преобразования в пространстве: подобие, гомотетия, движение.
Подобие
Свойства подобия: 1. Подобие переводит прямые в прямые, полупрямые – в полупрямые, отрезки – в отрезки.
2. Подобие сохраняет углы между полупрямыми
3. Подобие переводит плоскости в плоскости.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Гомотетия
Гомотетия – простейшее преобразование относительно центра O с коэффициентом гомотетии k. Это преобразование, которое переводит произвольную точку X’ луча OX, такую, что OX’ = k*OX.
Свойство гомотетии: 1. Преобразованием гомотетии переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k=1).
Доказательство. Действительно, пусть O – центр гомотетии и a - любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости a. Преобразование гомотетии переводит точку A в точку A’ на луче OA, а точку B в точку B’ на луче OB, причем OA’/OA = k, OB’/OB = k, где k – коэффициент гомотетии. Отсюда следует подобие треугольников AOB и A’OB’. Из подобия треугольников следует равенство соответственных углов OAB и OA’B’, а значит, параллельность прямых AB и A’B’. Возьмем теперь другую прямую AC в плоскости a. Она при гомотетии перейдет а параллельную прямую A’C’. При рассматриваемой гомотетии плоскость aперейдет в плоскость a’, проходящую через прямые A’B’, A’C’. Так как A’B’||AB и A’C’||AC, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, плоскости a и a’ параллельны, что и требовалось доказать.
Движение
Движением - преобразование одной фигуры в другую если оно сохраняет расстояние между точками, т.е. переводит любые две точки X и Y одной фигуры в точки X , Y другой фигуры так, что XY = X Y
Свойства движения: 1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения. Это значит, что если A, B, C, лежащие на прямой, переходят в точки A1,B1,C1. То эти точки также лежат на прямой; если точка B лежит между точками A и C, то точка B1 лежит между точками A1 и C1.
Доказательство. Пусть точка B прямой AC лежит между точками A и C. Докажем, что точки A1,B1,C1 лежат на одной прямой.
Если точка A1,B1,C1 не лежат на прямой, то они являются вершинами треугольника. Поэтому A1C1 < A1B1 + B1C1. По определению движения отсюда следует, что AC<AB+BC. Однако по свойству измерения отрезков AC=AB+BC.
Мы пришли к противоречию. Значит, точка B1 лежит на прямой A1C1. Первое утверждение теоремы доказано.
Покажем теперь, что точка B1 лежит между A1 и C1. Допустим, что точка A1 лежит между точками B1 и C1. Тогда A1B1 + A1C1 = B1C1, и, следовательно, AB+AC=BC. Но это противоречит неравенству AB+BC=AC. Таким образом, точка A1 не может лежать между точками B1 и C1.
Аналогично доказываем, что точка C1 не может лежать между точками A1 и B1.
Так как из трех точек A1,B1,C1 одна лежит между двумя другими, то этой точкой может быть только B1. Теорема доказана полностью.
2. При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки
3. При движении сохраняются углы между полупрямыми.
Доказательство. Пусть AB и AC – две полупрямые, исходящие из точки A, не лежащие на оной прямой. При движении эти полупрямые переходят в некоторые полупрямые A1B1 и A1C1. Так как движение сохраняет расстояние, то треугольники ABC и A1B1C1 равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов BAC и B1A1C1, что и требовалось доказать.
4. Движение переводит плоскость в плоскость.
Докажем это свойство. Пусть a - произвольная плоскость. Отметим на ней любые три точки A, B, C, не лежащие на одной прямой. Проведем через них плоскость a'.
Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a'.
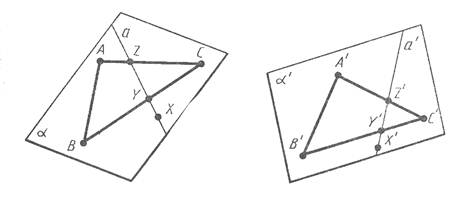 Пусть X - произвольная
точка плоскости a. проведем через нее
какую-нибудь прямую a в плоскости a,
пересекающую треугольник ABXC в двух точках Y и Z. Прямая
а перейдет при движении в некоторую прямую a'. Точки Y и Z
прямой a перейдут в точки Y' и Z',
принадлежащие треугольнику A'B'C', а значит, плоскости a'.
Пусть X - произвольная
точка плоскости a. проведем через нее
какую-нибудь прямую a в плоскости a,
пересекающую треугольник ABXC в двух точках Y и Z. Прямая
а перейдет при движении в некоторую прямую a'. Точки Y и Z
прямой a перейдут в точки Y' и Z',
принадлежащие треугольнику A'B'C', а значит, плоскости a'.
Итак прямая a' лежит в плоскости a'. Точка X при движении переходит в точку X' прямой a', а значит, и плоскости a', что и требовалось доказать.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
III. Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.
Симметрия относительно точки
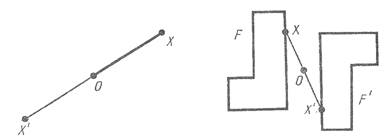 Пусть О - фиксированная точка и X -
произвольная точка плоскости. Отложим на продолжении отрезка OX за
точку O отрезок OX', равный OX.
Точка X' называется симметричной точке X относительно точки O. Точка, симметричная точке O, есть сама
точка O. Очевидно, что точка, симметричная точке X',
есть точка X.
Пусть О - фиксированная точка и X -
произвольная точка плоскости. Отложим на продолжении отрезка OX за
точку O отрезок OX', равный OX.
Точка X' называется симметричной точке X относительно точки O. Точка, симметричная точке O, есть сама
точка O. Очевидно, что точка, симметричная точке X',
есть точка X.
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точке O, называется преобразованием симметрии относительно точки O. При этом фигуры F и F' называются симметричными относительно точки O.
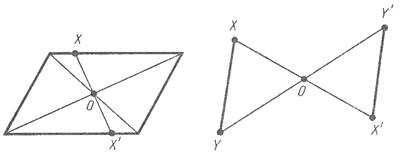 Если преобразование симметрии относительно точки O
переводит фигуру F в себя, то она называется центрально-симметричной,
а точка O называется центром симметрии.
Если преобразование симметрии относительно точки O
переводит фигуру F в себя, то она называется центрально-симметричной,
а точка O называется центром симметрии.
Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей.
Теорема: Преобразование симметрии относительно точки является движением.
Доказательство. Пусть X и Y - две произвольные точки фигуры F. Преобразование симметрии относительно точки O переводит их в точки X' и Y'. Рассмотрим треугольники XOY и X'OY'. Эти треугольники равны по первому признаку равенства треугольника. У них углы при вершине O равны как вертикальные, а OX=OX', OY=OY' по определению симметрии относительно точки O. Из равенства треугольников следует равенство сторон: XY=X'Y'. А значит, что симметрия относительно точки O есть движение. Теорема доказана.
Симметрия относительно прямой
Пусть g - фиксированная прямая. Возьмем произвольную точку X и опустим перпендикуляр AX н прямую g. На продолжении перпендикуляра за точку A отложим отрезок AX', равный отрезку AX. Точка X' называется симметричной точке X относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке X', есть точка X.
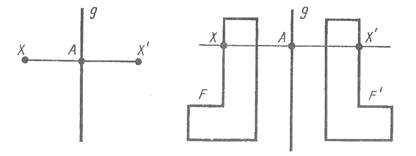 Преобразование фигуры F в
фигуру F', при котором каждая ее точка X
переходит в точку X', симметричную относительно данной прямой g,
называется преобразованием симметрии относительно прямой g.
При этом фигуры F и F' называются симметричными относительно прямой g.
Преобразование фигуры F в
фигуру F', при котором каждая ее точка X
переходит в точку X', симметричную относительно данной прямой g,
называется преобразованием симметрии относительно прямой g.
При этом фигуры F и F' называются симметричными относительно прямой g.
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.
Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, является осями симметрии прямоугольника. Прямые на которых лежат диагонали ромба, является его осями симметрии.
Теорема: Преобразование симметрии относительно прямой является движением.
 Доказательство. Примем данную прямую за ось
у декартовой системы координат. Пусть произвольная точка A (x;y)
фигуры F переходит в точку A' (x';y')
фигуры F'. Из определения симметрии относительно прямой
следует, что у точек A и A' равные ординаты, а абсциссы отличаются только
знаком: x' = -x.
Доказательство. Примем данную прямую за ось
у декартовой системы координат. Пусть произвольная точка A (x;y)
фигуры F переходит в точку A' (x';y')
фигуры F'. Из определения симметрии относительно прямой
следует, что у точек A и A' равные ординаты, а абсциссы отличаются только
знаком: x' = -x.
Возьмем две произвольные точки A (x;y) и B (x;y). Они перейдут в точки A' (-x;y) и B' (-x;y).
Имеем:
AB2=(x2-x1)2+(y2-y1)2
A'B'2=(-x2+ x1) 2+(y2-y1)2
Отсюда видно, что AB=A'B'. А значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.
Симметрия относительно плоскости
Пусть a - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость a и на его продолжении за точку Aоткладываем отрезок AX', равный XA. Точка X' называется симметричной точке X относительно плоскости a, а преобразование, которое переводит X в симметричную ей точку X', называется преобразованием симметрии относительно плоскости a.
Если точка X лежит в плоскости a, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости a переводит фигуру в себя, то фигура называется симметричной относительно плоскости a, а плоскость a называется плоскостью симметрии этой фигуры.
Поворот
 Поворот плоскости около данной точки
называется такое движение, при котором каждый луч, исходящий из точки,
поворачивается на один и тот же угол в одном и том же направлении.
Поворот плоскости около данной точки
называется такое движение, при котором каждый луч, исходящий из точки,
поворачивается на один и тот же угол в одном и том же направлении.
Это значит, что если при поворот около точки O точка
переходит в точку X', то лучи OX и OX' образуют
один и тот же угол, какова бы ни была точка X. Этот угол
называется углом поворота. Преобразование фигур при повороте плоскости
также называется поворотом.
Параллельный перенос в пространстве
Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a,b,c одни и те же для всех точек (x; y; z). Параллельный переносов пространстве задается формулами
x'=x+a, y'=y+b, z'=z+c,
выражающими координаты x', y', z' точки, в которую переходит точка (x; y; z) при параллельном переносе. Так же, как и на плоскости, доказываются следующие свойства параллельного переноса:
1. Параллельные перенос есть движение.
2. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'.
Новым для параллельного переноса в пространстве является следующее свойство:
5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную её плоскость.
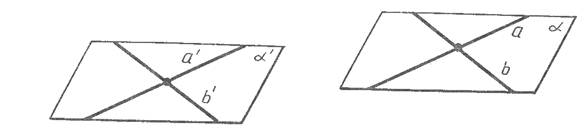
Действительно, пусть a - произвольная плоскость, проведем в этой плоскости две пересекающиеся прямые a и b. При параллельном переносе прямые a и b переходят либо в себя, либо в параллельные прямые a' и b'. Плоскость a переходит в некоторую плоскость a', проходящую через прямые a' и b'. Если плоскость a' не совпадает с a, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, она параллельна a, что и требовалось доказать.
Список использованной литературы:
1. Учебник Геометрии 7-11 классы. А.В. Погорелов
2. Учебник Геометрии 10-11 классы. А.Д. Александров.
| Многомерная геометрия | |
|
ОГЛАВЛЕНИЕ Введение Глава I. Элементы общей теории многомерных пространств § 1. Историческая справка § 2. Понятие векторного многомерного пространства ... Так как при аффинном преобразовании плоскости переходят в плоскости, а параллельные плоскости в параллельные плоскости, это аффинное преобразование переводит весь k- параллелепипед ... Точка А имеет равные координаты: x = y = z (поскольку при повороте пространства, переставляющем оси координат: , и плоскость L и сфера S переходят в себя, а поэтому их общая точка ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... 7а, б) продольная ось ЛА расположена в плоскости горизонта, совпадает с линией ОВ и параллельна главной оси гироскопа. вала" конуса НВ относительно плоскости симметрии вертолета при |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Аффинные преобразования | |
|
Глава I.Понятие о геометрическом преобразовании 1.1 Что такое геометрическое преобразование? Осевая симметрия, центральная симметрия, поворот ... Если на плоскости задана какая-либо фигура F, то множество всех точек, в которые переходят тонки фигуры F при рассматриваемом преобразовании, представляет собой новую фигуру F., В ... Осевая симметрия, поворот (в частности, центральная симметрия) и параллельный перенос имеют то общее, что каждое из этих преобразований переводит любую фигуру F на плоскости в ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Большая коллекция шпор для МАТАНа (1 семестр 1 курс) | |
|
1. Векторы. Действия над векторами. Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n ... Для составления уравнения прямой М1М2 запишем уравнения пучка прямых, проходящих через точку М1: y-y1=k(x-x1). Замечание: можно переходить к пределу под знаком непрерывной функции limf(x)=limg(y) limf(x)=f(x0)=y0 x x x x x x |
Раздел: Рефераты по математике Тип: шпаргалка |
| Геометрические построения на плоскости | |
|
Геометрические построения на плоскости Введение Вам, будущим учителям, в школьном курсе математики придется учить ребят решению задач на построение ... Угол позволяет: а) сделать все построения, выполнимые линейкой; б) через данную точку плоскости провести под углом ѭ к некоторой данной прямой; в) если построены отрезок АВ и ... ГМТ 6. Множество точек плоскости, из которых отрезок АВ виден под углом ѭ, где ѭ = 90o, ѭ = 180o , есть две дуги с общими концами А и В (без точек А и В), симметричные относительно ... |
Раздел: Рефераты по математике Тип: учебное пособие |