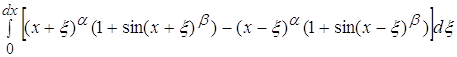Реферат: Свойства усредненной функции с сильной осцилляцией
Министерство образования Российской Федерации
Башкирский государственный педагогический университет
Кафедра математического анализаДипломная квалификационная работа
Автор: Гарипов Ильгиз.
Тема: Свойства усредненной функции с сильной осцилляцией.
К защите допущен ____________
Заведующий кафедрой к.ф. м. н.
доцент Сафаров Т.Г.
Руководитель д.физ-мат. наук. профессор Султанаев Я.Т.
Уфа 2001
Стр.
Введение 3
§ 1 Свойства функции 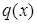 . 4
. 4
§ 2 Свойства функции ![]() и
ее производных. 5
и
ее производных. 5
2.1
![]() 5
5
2.2
![]() 6
6
2.3
![]() где a>0 7
где a>0 7
2.4
![]() 9
9
§ 3 Поведение 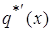 11
11
3.1 ![]() 11
11
3.2
![]() 11
11
3.3
![]() 12
12
3.4
![]() 13
13
§ 4 Поведение 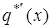 14
14
4.1 ![]() 14
14
4.2
![]() 15
15
4.3
![]() 15
15
4.4
![]() 16
16
Заключение 17
Литература 18
Введение
Пусть ![]() произвольная функция,
определенная на
произвольная функция,
определенная на ![]() , и
, и ![]() при
при ![]()
Введем в рассмотрение
функцию ![]() с помощью следующего равенства:
с помощью следующего равенства:
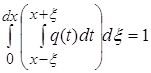 (1)
(1)
Назовем эту функцию
усреднением функции ![]()
Это название оправдано так как из (1) и теоремы о среднем для интегралов можем заключить
![]()
![]()
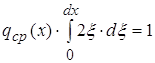
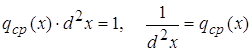
§ 2 Свойства функции 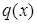 .
.
1.
Если ![]() , при
, при ![]() , то
, то ![]() при
при ![]()
Доказательство:
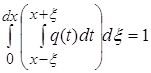 ,
, ![]() ,
, ![]()
![]() " N >0,
" N >0, ![]() :
: ![]()
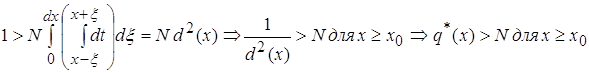
2.
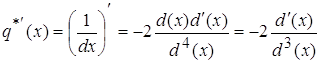 (2)
(2)
3.
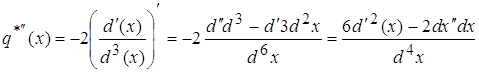 (3)
(3)
Дифференцируя формулу (1) по dx получаем
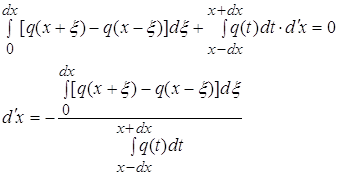 (4)
(4)
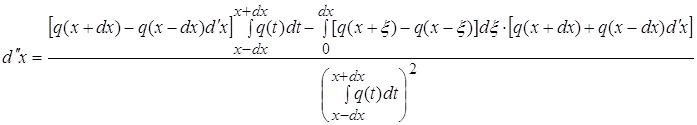 (5)
(5)
§ 2 Свойства
функции ![]() и ее производных.
и ее производных.
I) Рассмотрим вид функции 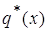 для
случаев когда
для
случаев когда 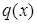 :
:
2.1 ![]()
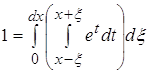
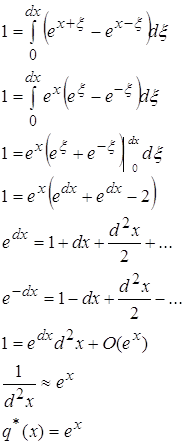
2.2 ![]()
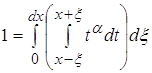
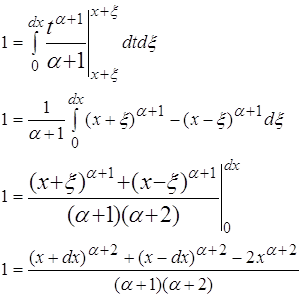
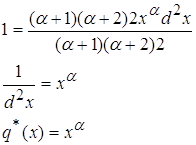
2.3 ![]() где a>0;
где a>0;
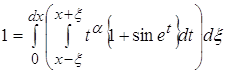
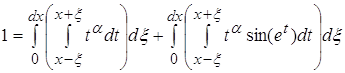
Разделим интеграл на два интеграла и вычислим их отдельно.

Второй интеграл не
оказывает влияния на первый, так как при ![]() функция стремится к 0.
функция стремится к 0.
Доказательство:
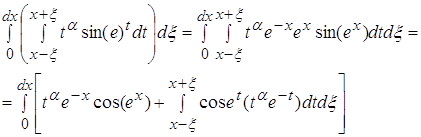
Рассматривая второй интеграл, мы получаем:
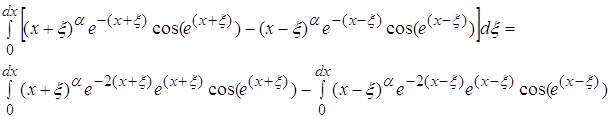
Рассматривая первый интеграл, получаем:
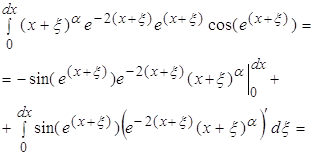
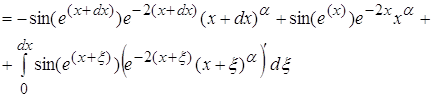
Последние два
слагаемых полученных при интегрировании содержат в произведении ![]() , то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь
интеграл при
, то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь
интеграл при ![]() становится очень малым по сравнению с первой частью. Поэтому
можно считать что при
становится очень малым по сравнению с первой частью. Поэтому
можно считать что при ![]()
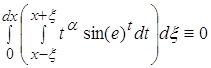
Следовательно:
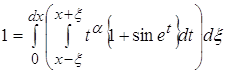
![]()
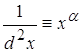
2.4. ![]()
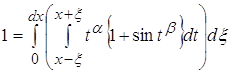
Наложить на![]() ограничение, такое чтобы
ограничение, такое чтобы ![]() присутствие
присутствие ![]() не влияло на поведение функции.
не влияло на поведение функции.
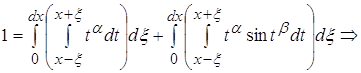
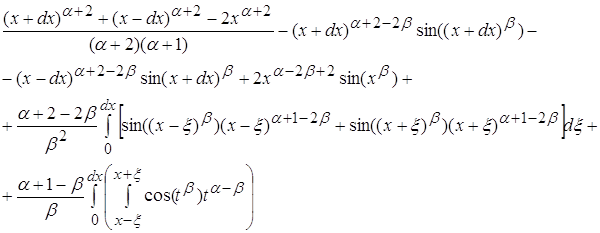
Рассматривая полученное выражение можно заметить что
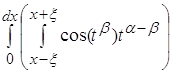
становится пренебрежительно малым по отношению к остальной части
как только ![]() . Ограничение
№1
. Ограничение
№1
В тоже время
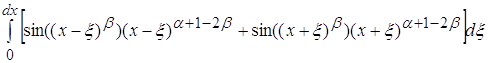
Становится бесконечно малым как
только ![]() . Ограничение №2
. Ограничение №2
Раскрывая в оставшейся части скобки, по Биному Ньютона получаем, что
![]()
должен быть очень малым при ![]() то есть
то есть
![]()
так как ![]() ограниченная функция, к 0 должен
стремится
ограниченная функция, к 0 должен
стремится ![]() .
.
![]()
![]()
![]()
![]() Ограничение
№3
Ограничение
№3
Учитывая ограничения 1, 2, 3 получаем:
![]()
Следовательно, ![]() ограничение на
ограничение на ![]() удовлетворяющее поставленной задаче,
при котором присутствие
удовлетворяющее поставленной задаче,
при котором присутствие ![]() не влияет на поведение функции
не влияет на поведение функции ![]() .
.
§ 3 Рассмотрим поведение функции ![]() для случаев:
для случаев:
3.1) ![]()
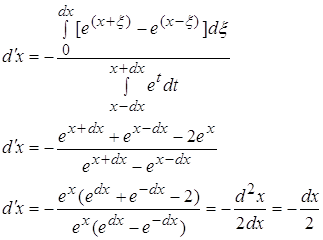
![]()
![]()
3.2) ![]()
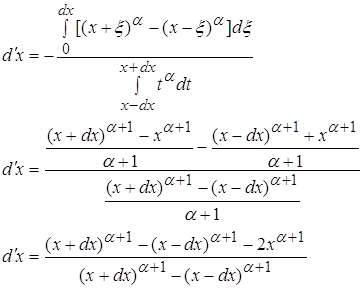
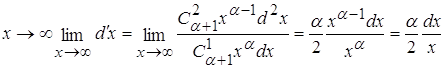
![]()
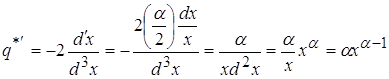
3.3) ![]()
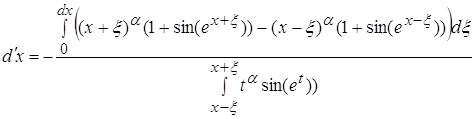
Вычислим отдельно интегральное выражение, стоящее в числителе:
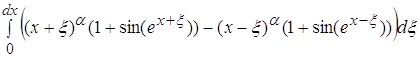 =
=
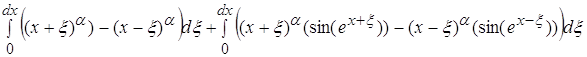 =
=
![]()
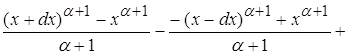
![]()
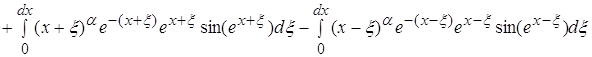
![]()
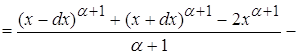
![]()
рассматривая пределы при ![]() видим
что на поведение функции оказывает влияние только главный член
видим
что на поведение функции оказывает влияние только главный член ![]()
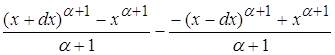
Поведение данной функции при ![]() эквивалентно
поведению функции
эквивалентно
поведению функции
![]() (*)
(*)
Вычислим интеграл в знаменателе:
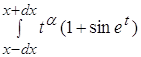 =
=
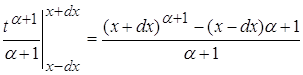
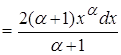
![]() (**)
(**)
Учитывая (*)и (**) получаем
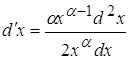
![]()
Следовательно,
по формуле (2) получаем ![]()
3.4
![]()
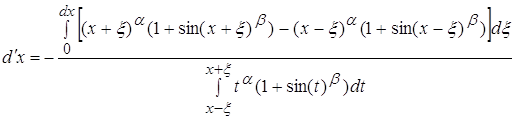
Отдельно вычислим числитель и знаменатель:
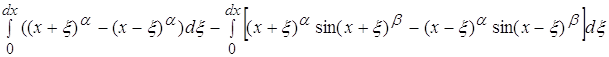
По ранее доказанному в пункте 2.4 мы можем сказать что второй интеграл не оказывает влияния на поведение функции. Поэтому мы можем утверждать, что числитель эквивалентен выражению:
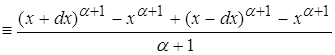
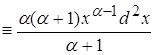
Вычислим знаменатель:
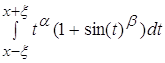
Разделив интеграл на 2 интеграла, мы получаем:
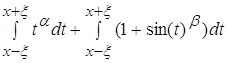
По пункту 2.4 можем вывести что второй интеграл не
влияет на поведение функции при ![]()
Следовательно, знаменатель:
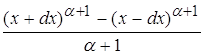
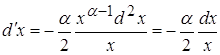
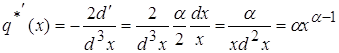
§4.
Рассмотрим поведение второй производной ![]()
Для облегчения вычислений введем обозначения:
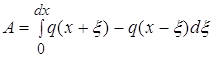
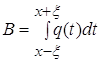
![]()
![]()
При этом формула для ![]() примет
вид
примет
вид 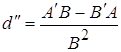 (6)
(6)
4.1 ![]()
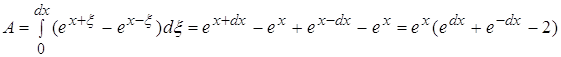
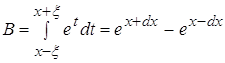
![]()
![]()
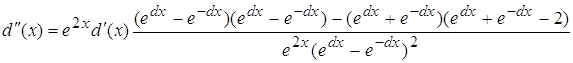
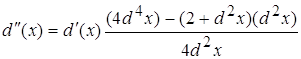
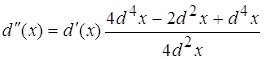
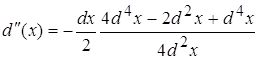
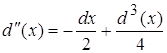
Виду того, что d(x) очень мал то 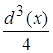 будет несравним с d(x) т.е.
будет несравним с d(x) т.е.
![]()
4.2 ![]()
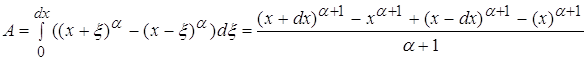
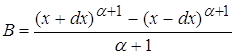
![]()
![]()
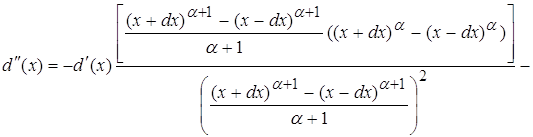
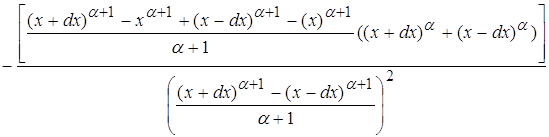
используя равенства, полученные в пункте 2.2 и 3.2, преобразуя данное равенство, приходим к выражению:
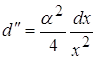
(Все выкладки приводить не буду в виду их громоздкости и сложности для восприятия. Добавлю только что все выкладки, примененные в данном пункте полностью повторяют ограничения и эквивалентные выражения, использованные в пунктах 2.2 и 3.2).
Отсюда следует что ![]()
4.3 ![]()
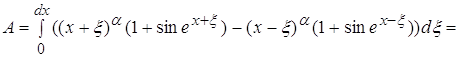
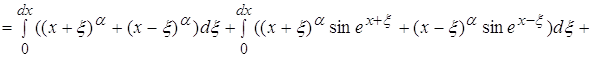
Используя данные, полученные в п.3.3 получаем что
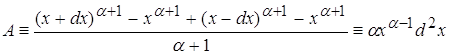
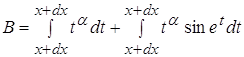
Возвращаясь к п. 3.3 находим:
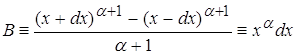
![]()
![]()
Вычисляя ![]() по формуле 6, получаем:
по формуле 6, получаем:
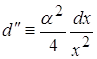
и ![]()
4.4 ![]()
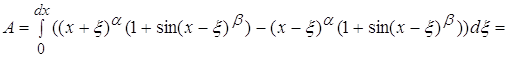
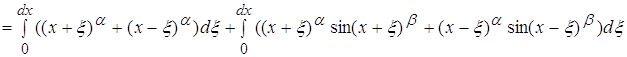
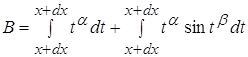
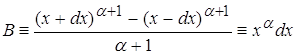
![]()
![]()
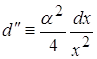
и ![]()
Заключение
В результате проведенного исследования поведения усредненной функции в случае осциллирующих коэфициентов, получены данные приведенные в следующей таблице:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|