Реферат: Температурный расчет с помощью вычислений информационной математики
разрешим первое уравнение относительно y1 , второе - относительно y2 и т.д.
Тогда получим эквивалентную систему
где
при
i<>j
и
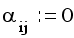при i=j
(i,j=1,2,...,n)
Такую систему будем в дальнейшем называть приведенной.
Метод Зейделя заключается в следующем. Выбрав вектор начального приближения
y(ср)=(y1,y2,...,yn)
подставим его компоненты в правую часть первого уравнения системы и вычислим первую компоненту y`1 нового вектора y`(ср) . В правую часть второго уравнения подставим компоненты (y`1,y2,y3,...,yn) и вычислим вторую компоненту y`2'нового вектора. В третье уравнение подставим (y`1,y`2,y3,...,yn) и т.д. Очевидно,подстановкой в каждое уравнение мы, дойдя до последнего уравнения, обновим все компоненты исходного вектора и получим первое приближение к решению
y`(ср)=(y`1,y`2,y`3,...,y`n)
Далее , взяв в качестве исходного вектор у`(ср) , выполним вторую итерацию и получим y``(ср). Этот процесс будем продолжать до достижения заданной степени точности.
Оценка погрешности приближений процесса Зейделя
Для оценки погрешности прежде всего вычисляют показатель скорости сходимости
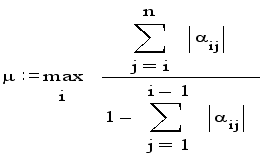
То есть для
каждой строки
матрицы коэффициентов
системы
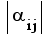вычисляется
сумма модулей
коэффициентов,
лежащих правее
главной диагонали
:
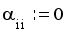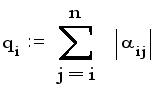
и сумма модулей коэффициентов, лежащих левее главной диагонали:
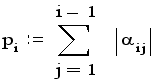
Для каждой i-й строки (i =1,2,...,n ) вычисляется отношение
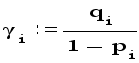
и в качестве
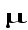берется
максимальное
из этих отношений.
Чем меньше
окажется
,
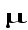тем большей
будет скорость
сходимости.
Для процесса Зейделя справедлива следующая оценка погрешности К-го приближения:
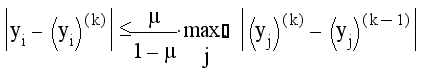(i,j=1,2,...,n)
то есть модуль
отклонения
любого
i -го корня
системы в К-м
приближении
от точного
значения того
же корня
не больше, чем
умноженное
на множитель
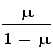максимальное
из приращений
корней, полученных
в результате
перехода от
(K-1)
-го приближения
к К-му.
Если задаться
абсолютной
погрешностью
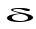и
потребовать
выполнения
условия
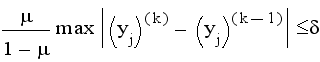(j=1,2,...,n)
то выполнится и условие
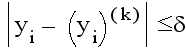(i=1,2,3,...,n),
то есть заданная
степень точности
на К-й итерации
будет достигнута.
На практике
это означает,
что после каждой
итерации необходимо
выделить тот
корень, изменение
которого по
сравнению с
предыдущим
значением
оказалось
наибольшим
по модулю. Модуль
приращения
этого корня
необходимо
умножить на
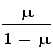и сравнить
результат с
выбранной
абсолютной
погрешностью.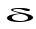
Достаточные условия сходимости процесса Зейделя
Если модули коэффициентов системы удовлетворяют хотя бы одному из условий
(i,j=1,2,3,...,n)
то процесс Зейделя для соответствующей приведенной системы сходится к её единственному решению при любом выборе начального вектсра y(ср) Такие системы называют системами с диагональным преобладанием.
Метод Зейдедя имеет свойство, позволяющее обеспечить сходимость процесса для любых систем уравнений с неособенной матрицей коэфициентов.
Если обе части систем с неособенной матрицей коэфициентов А=[aij] умножить слева на транспонировнную матриц A*[aij] , то будет получена новая, равносильная исходной система, которая называется нормальной. Процесс Зейделя для приведенной системы, полученной из нормальной, всегда сходится независимо от выбора нача льного приближения.
Блок схема.
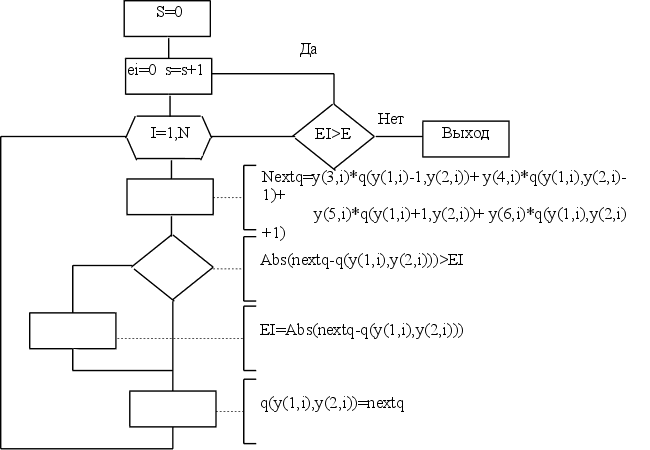
Подпрограмма метода Зейделя.
c-----------------------------------------------------------------
cПОДПРОГРАММА РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ
c
с integer N-входное количество уравнений
c real y(6,N)-входной массив уравнений,содержащий следующие поля:
c y(1,N)-номер точки по оси X
c y(2,N)-номер точки по оси Y
c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))
c y(3,N)=h^2/(2*(h^2+k^2))
c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)
c y(4,N)=k^2/(2*(h^2+k^2))
c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))
c y(5,N)=h^2/(2*(h^2+k^2))
c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)
c y(6,N)=k^2/(2*(h^2+k^2))
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-входной массив начальных значений Y
c real Q(M,P)-выходной массив вычисленых значений Y
c real E-погрешность вычислений
c------------------------------------------------------------------
subroutine zeidel(N,y,M,P,q,E)
integer N,M,P,I,S
real y(6,N),q(M,P),E,EI,NEXTQ
c------------------------------------------------------------------
c вычисление коэфициента сходимости процесса
c mj=y(5,1)+y(6,1)
c и выражения
c km=mj/(1-mj)
C НО Т.К. MJ=0.5 ТО KM=1 И СЛЕДОВАТЕЛЬНО ЕГО МОЖНО ОПУСТИТЬ
c-----------------------------------------------------------------
c KM=(y(5,1)+y(6,1))/(1-y(5,1)+y(6,1))
c------------------------------------------------------------------
c итерации
c S-счетчик итераций
c------------------------------------------------------------------
S=0
1 EI=0.
S=S+1
do I=1,N
NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+
+ y(4,i)*Q(y(1,i),y(2,i)-1)+
+ y(5,i)*Q(y(1,i)+1,y(2,i))+
+ y(6,i)*Q(y(1,i),y(2,i)+1)
c------------------------------------------------------------------
c вычисление погрешности на данной итерации
c------------------------------------------------------------------
if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)
+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))
c print *,'x=',y(1,i),' y=',y(2,i)
q(y(1,i),y(2,i))=NEXTQ
enddo
c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI
if (EI.gt.E)goto 1
c do i=P,1,-1
c print '(21e10.3)',(q(j,i),j=1,M)
c enddo
end
ТЕСТ
В качестве теста выполним одну итерацию для системы , полученной в предыдущем пункте.
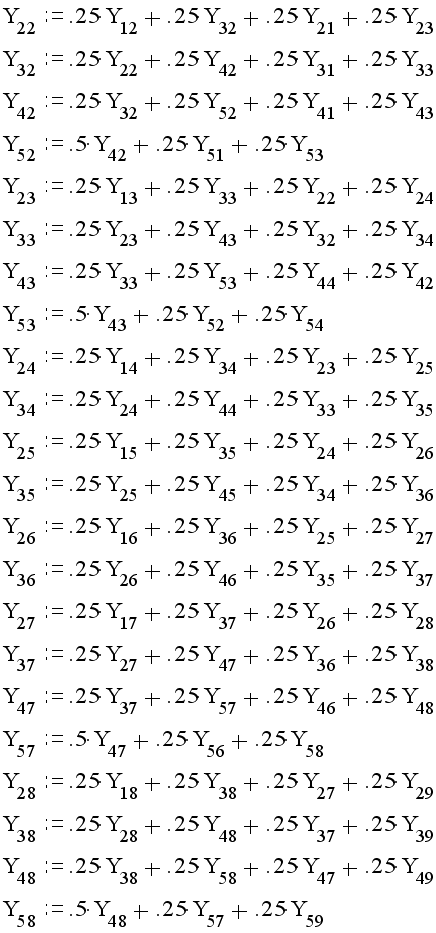
при начальных условиях:
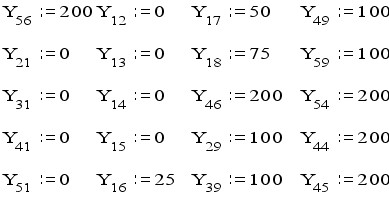
все остальные Yij:=0.
Получается:
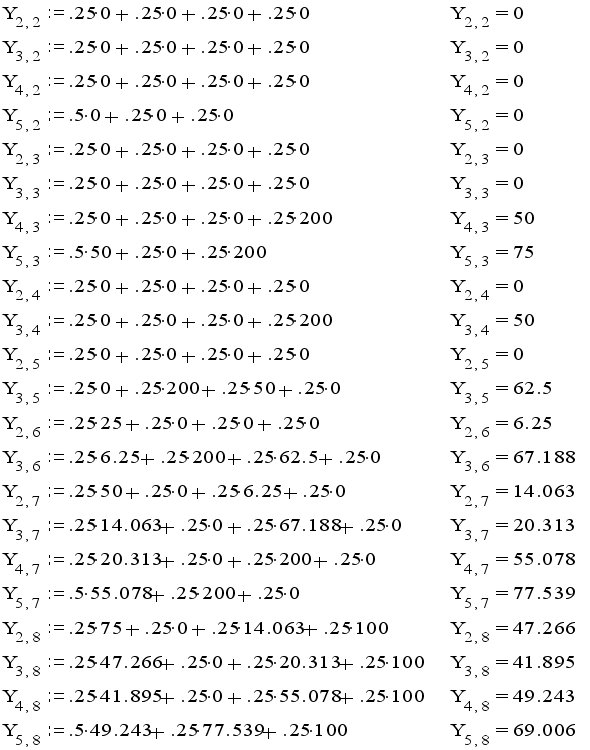
Результат:
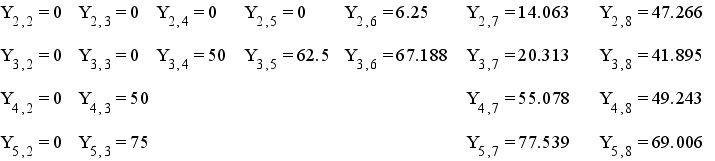
Полный текст программы.
c------------------------------------------------------------------
c ПОДПРОГРАММА СОСТАВЛЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
c МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
c
c real H-шаг по оси X
c real K-шаг по оси Y
c real N-количество уравнений(примерное число,желательно N=M*P)
c real y(6,N)-выходной массив уравнений,содержащий следующие поля:
c y(1,N)-номер точки по оси X
c y(2,N)-номер точки по оси Y
c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))
c y(3,N)=h^2/(2*(h^2+k^2))
c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)
c y(4,N)=k^2/(2*(h^2+k^2))
c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))
c y(5,N)=h^2/(2*(h^2+k^2))
c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)
c y(6,N)=k^2/(2*(h^2+k^2))
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-массив значений Y
c integer N-выходное количество получившихся уравнений
c------------------------------------------------------------------
subroutine mkr(H,K,N,y,M,P,q)
integer M,P,IIX,IIY,NN,N,KR1,KR2,KR3
real y(6,N),H,K,q(M,P),HX,KY
c-----------------------------------------------------------------
c подсчитываю коэфициенты
c h^2/(2*(h^2+k^2))
c и
c k^2/(2*(h^2+k^2))
c-----------------------------------------------------------------
HX=H**2/(2*(H**2+K**2))
KY=K**2/(2*(H**2+K**2))
c-----------------------------------------------------------------
c составление уравнений
c и
c присваивание начальных значений
c
c nn-счетчик уровнений
c iix-номер текущего узла по оси X
c iiy-номер текущего узла по оси Y
c-----------------------------------------------------------------
NN=0
KR1=((P-1)/8)*3+1
KR2=((P-1)/8)*5+1
KR3=((M-1)/4)*3+1
do IIY=2,P-1
do IIX=2,M
if (NN.eq.N)then
print *,'ПЕРЕПОЛНЕНИЕ МАССИВА Y'
stop
endif
c-----------------------------------------------------------------
c проверка границы трубы с жидкостью
c-----------------------------------------------------------------
if ((IIY.ge.KR1).and.(IIY.le.KR2).and.(IIX.ge.KR3)) then
q(IIX,IIY)=200.
c-----------------------------------------------------------------
c проверка симметрии
c-----------------------------------------------------------------
elseif (((IIY.lt.KR1).or.(IIY.gt.KR2)).and.(IIX.eq.M)) then
q(IIX,IIY)=6
NN=NN+1
y(1,NN)=IIX
y(2,NN)=IIY
y(3,NN)=2*HX
y(4,NN)=KY
y(5,NN)=0
y(6,NN)=KY
c-----------------------------------------------------------------
c составление уравнений во внутренних точках фигуры
c-----------------------------------------------------------------
else
q(IIX,IIY)=5
NN=NN+1
y(1,NN)=IIX
y(2,NN)=IIY
y(3,NN)=HX
y(4,NN)=KY
y(5,NN)=HX
y(6,NN)=KY
endif
enddo
enddo
c-----------------------------------------------------------------
c присваивание начальных значений на границе фигуры
c------------------------------------------------------------------
KY=0
KR1=P/2+1
do IIY=1,P
if (IIY.le.KR1)then
q(1,IIY)=0
else
q(1,IIY)=500*KY-100
endif
KY=KY+K
enddo
do IIX=1,M
q(IIX,1)=0
q(IIX,P)=100
enddo
N=NN
end
c-----------------------------------------------------------------
c ПОДПРОГРАММА РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ
c
с integer N-входное количество уравнений
c real y(6,N)-входной массив уравнений,содержащий следующие поля:
c y(1,N)-номер точки по оси X
c y(2,N)-номер точки по оси Y
c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))
c y(3,N)=h^2/(2*(h^2+k^2))
c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)
c y(4,N)=k^2/(2*(h^2+k^2))
c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))
c y(5,N)=h^2/(2*(h^2+k^2))
c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)
c y(6,N)=k^2/(2*(h^2+k^2))
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-входной массив начальных значений Y
c real Q(M,P)-выходной массив вычисленых значений Y
c real E-погрешность вычислений
c------------------------------------------------------------------
subroutine zeidel(N,y,M,P,q,E)
integer N,M,P,I,S
real y(6,N),q(M,P),E,EI,NEXTQ
c------------------------------------------------------------------
c вычисление коэфициента сходимости процесса
c mj=y(5,1)+y(6,1)
c и выражения
c km=mj/(1-mj)
C НО Т.К. MJ=0.5 ТО KM=1 И СЛЕДОВАТЕЛЬНО ЕГО МОЖНО ОПУСТИТЬ
c-----------------------------------------------------------------
c KM=(y(5,1)+y(6,1))/(1-y(5,1)+y(6,1))
c------------------------------------------------------------------
c итерации
c S-счетчик итераций
c------------------------------------------------------------------
S=0
1 EI=0.
S=S+1
do I=1,N
NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+
+ y(4,i)*Q(y(1,i),y(2,i)-1)+
+ y(5,i)*Q(y(1,i)+1,y(2,i))+
+ y(6,i)*Q(y(1,i),y(2,i)+1)
c------------------------------------------------------------------
c вычисление погрешности на данной итерации
c------------------------------------------------------------------
if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)
+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))
c print *,'x=',y(1,i),' y=',y(2,i)
q(y(1,i),y(2,i))=NEXTQ
enddo
c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI
if (EI.gt.E)goto 1
c do i=P,1,-1
c print '(21e10.3)',(q(j,i),j=1,M)
c enddo
end
c------------------------------------------------------------------
c ПОДПРОГРАММА АЛФАВИТНО-ЦИФРОВОГО,МОЗАИЧНОГО
c ВЫВОДА РЕЗУЛЬТАТА
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-входной массив значений Y
c
c
c------------------------------------------------------------------
subroutine outdata(M,P,q)
character
a(11)/'.','+','*','','','-','-','-','','-','-'/
integer M,P,I,J
real q(M,P)
do J=P,1,-1
print '(400A2)',(a(int(q(I,J)/21)+1),I=1,M),
+ (a(int(q(I,J)/21)+1),I=M-1,1,-1)
enddo
do I=1,10
print *,'''',a(I),'''','---> от ',20*(I-1),', до ',
+ 20*I,'(включительно)'
enddo
end
c------------------------------------------------------------------
c ПОДПРОГРАММА ВЫЧИСЛЕНИЯ ОШИБКИ
c real q-массив значений Y с шагом =2*h
c real qq-массив значений Y с шагом =h
c real E-значение погрешности
c
c------------------------------------------------------------------
subroutine mistake(M,P,q,qq,E)
integer M,P,iq,jq,iqq,jqq
real qq(M,P),q(int(M/2)+1,int(P/2)+1),max,E,other
max=0
iq=0
do iqq=1,P,2
iq=iq+1
jq=0
do jqq=1,M,2
jq=jq+1
other=abs(q(jq,iq)-qq(jqq,iqq))
if (other.gt.max)max=other
enddo
enddo
print *,M,' ',P,' ',max/3
if (max/3.lt.E) then
call outdata(M,P,qq)
Stop
endif
end
c------------------------------------------------------------------
c ОСНОВНАЯ ПРОГРАММА
c
c
c------------------------------------------------------------------
integer N/90000/,M,P,flag/0/
real y(6,90000),q(300,300),H/.05/,K/.05/,E/.5/,qq(300,300)
real EZ/.01/
c print *,'Введите шаг вдоль оси X '
c read (*,*)H
c print *,'Введите шаг вдоль оси Y '
c read (*,*)K
c print *,'Введите точность вычислений '
c read (*,*)E
M=.2/H+1
P=.4/K+1
call mkr(H,K,N,y,M,P,q)
call zeidel(N,y,M,P,q,EZ)
111 H=H/2
K=K/2
M=.2/H+1
P=.4/K+1
N=90000
if (flag.eq.0)then
flag=1
call mkr(H,K,N,y,M,P,qq)
call zeidel(N,y,M,P,qq,EZ)
call mistake(M,P,q,qq,E)
else
flag=0
call mkr(H,K,N,y,M,P,q)
call zeidel(N,y,M,P,q,EZ)
call mistake(M,P,qq,q,E)
endif
goto 111
end
Литература.
1. И.С.Березин,Н.П.Жидков ’Методы вычислений’,том 1,М.,1966,632 стр.
2.’ Численные методы решения задач на ЭВМ ’ , Учебное пособие , Г.Н.Рубальченко , К. , 1989 , 148 стр.
3.’Справочник языка ФОРТРАН’ , М.,1996 ,106 стр.
Температурный расчет с помощью вычислений информационной математики.