Реферат: Усложнение решающего правила при управлении в задачах распознавания образов
Бекмуратов К.А.
Рассматривается один из возможных принципов усложнения решающего правила непрерывного пространства признаков, порождаемого опорными объектами конкретного образа. Предложена процедура нахождения предельного значения размерности признакового пространства, в котором возможно кусочно-линейное разделение образов и гарантированы требуемые качество и надежность распознавания, необходимые в системах управления.
В работе [1] описан метод формирования пространства непрерывных признаков, приводящий к безошибочному разделению образов. Введено понятие непрерывного признака и показано, что если набирать пространство только из определенных в [1] признаков, то можно достичь безошибочного разделения образов.
В данной работе так же, как и в [2], рассмотрим случай, когда в пространстве непрерывных признаков размерности n безошибочное разделение обучающей последовательности невозможно.
Пусть
на некотором множестве ![]() мощности
мощности ![]() объектов
объектов ![]() определены подмножества
определены подмножества ![]() при
при ![]() , представляющие собой образы
на обучающей выборке
, представляющие собой образы
на обучающей выборке ![]()
Допустим,
что ![]() - подмножество на
- подмножество на ![]() , соответствующее конкретному
образу
, соответствующее конкретному
образу ![]() , а
, а ![]() - подмножество на
- подмножество на ![]() , соответствующее остальным
, соответствующее остальным ![]() образом
образом ![]()
Требуется
с использованием обучающую выборки ![]() найти
решающее правило
найти
решающее правило ![]() , указывающее
принадлежность любого объекта из
, указывающее
принадлежность любого объекта из ![]() одному
одному
из
заданных образов ![]() или
или ![]() с вероятностью ошибки, не
превышающей
с вероятностью ошибки, не
превышающей ![]() , достигаемой с надежностью
(1-
, достигаемой с надежностью
(1-![]() ), и определить
целесообразности усложнения решающих правил при синтезе непрерывных признаковых
пространств.
), и определить
целесообразности усложнения решающих правил при синтезе непрерывных признаковых
пространств.
Если
обучающая последовательность не может быть безошибочно разделима выбранным
решающим правилом, то в общем случае справедлива теорема Вапника - Червоненкиса
[3], смысл которой состоит в том, что если в n-мерном
пространстве признаков решающее правило совершает ![]() ошибок
при классификации обучающей последовательности длины
ошибок
при классификации обучающей последовательности длины ![]() , то с вероятностью
, то с вероятностью ![]() можно утверждать, что
вероятность ошибочной классификации составит величину, меньшую
можно утверждать, что
вероятность ошибочной классификации составит величину, меньшую ![]() ,
,
![]() ,
,
где N- число всевозможных правил заданного класса, которое можно построить в пространстве заданной размерности.
Предположим,
что в процессе обучения из последовательно поступивших непрерывных свойств относительно
![]() опорных объектов
опорных объектов ![]() синтезирована подсистема
непрерывных признаков. В зависимости от состава случайной и независимой выборки
процесс обучения может остановиться при любом значении n,
но если разделение конкретной обучающей выборки наступило в n-мерном
пространстве, то число N всевозможных решающих правил в
классе не должно превышать числа всех подмножеств множества, состоящего из
элементов, т.е.
синтезирована подсистема
непрерывных признаков. В зависимости от состава случайной и независимой выборки
процесс обучения может остановиться при любом значении n,
но если разделение конкретной обучающей выборки наступило в n-мерном
пространстве, то число N всевозможных решающих правил в
классе не должно превышать числа всех подмножеств множества, состоящего из
элементов, т.е.
![]() ,
,
где
![]() .
.
Логарифмируя получим
![]() (1)
(1)
Если
учесть ![]() , то (1) принимает вид
, то (1) принимает вид
![]()
![]() ,
(2)
,
(2)
где
![]() можно оценить в виде
можно оценить в виде
 (3)
(3)
Подставляя (3) в (2), получаем
![]() (4)
(4)
Используя теорему Вапника-Червоненкиса [3], можно вычислить предельную размерность пространства
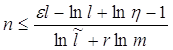 ,
(5)
,
(5)
которая
при заданных ![]() гарантирует требуемые e и h.
гарантирует требуемые e и h.
Пусть
вычислено максимально допустимое значение размерности пространства ![]() в виде (5) и в этом
пространстве фиксирована линейная решающая функция
в виде (5) и в этом
пространстве фиксирована линейная решающая функция
![]() (6)
(6)
Далее,
для того чтобы в процессе обучения синтезировать пространство, в котором
линейное решающее правило (6) безошибочно разделило бы обучающую выборку ![]() длины
длины ![]() , и при этом размерность
пространства не превышала бы
, и при этом размерность
пространства не превышала бы ![]() ,
необходимо на признаки
,
необходимо на признаки ![]() наложить
дополнительные требования. Зная предельную размерность простанства
наложить
дополнительные требования. Зная предельную размерность простанства ![]() (8), можно оценить
минимально допустимую разделяющую силу каждого выбираемого признака
(8), можно оценить
минимально допустимую разделяющую силу каждого выбираемого признака ![]() в виде
в виде
![]()
Минимально допустимая разделяющая сила признака позволяет при синтезе непрерывного пространства использовать не все признаки, а выбирать только те, разделяющая сила которых удовлетворяет неравенству
![]()
Допустим,
что в синтезированном пространстве непрерывных признаков размерности n линейная решающая функция (9) совершает ошибки с частотой ![]() . Тогда рассмотрим
соотношение
. Тогда рассмотрим
соотношение
![]() , (7)
, (7)
где
N* - соответствует решающему правилу, работающему с
частотой ошибки ![]() , N**-
безошибочно разделяющая обучающая последовательность длины
, N**-
безошибочно разделяющая обучающая последовательность длины ![]() .
.![]()
С использованием этого соотношения, можно установить целесообразность усложнения решающего правила в случае, если в пространстве размерности n ещё не достигнуто безошибочное разделение обучающей выборки.
Известно [3], что если вместо линейного правила используется кусочно-линейное и оно безошибочно разделяет обучающую выборку длины l, то в соответствии (7) вместо n следует выбирать величину
n=nk+k , (8)
где k - число линейных решающих правил, составляющих искомое кусочно - линейное правило. Используя соотношения (7) и (8), ответим на вопрос: стоит ли усложнять решение, если линейное правило в пространстве размерности n не обеспечивает безошибочного разделения обучающей выборки. Для этого нужно сделать подстановку:
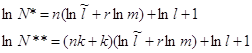 ,
(9)
,
(9)
В этом случае усложнение решающего правила, определяемое числом k, не приведёт к снижению вероятности ошибки, если будет выполнено соотношение (7) после подстановки (8). Из этого условия можно найти такое значение k, выше которого теряет всякий смысл усложнение решающего правила, действующего в пространстве непрерывных признаков размерности n:
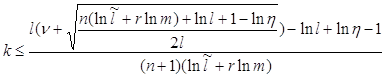 . (10)
. (10)
Таким
образом, если выбирать n и k
согласно (5) и (10), то процедура позволяет, при синтезе пространства,
использовать не все признаки, а выбирать только те, разделяющая сила которых
позволяет при заданных ![]() обеспечить
требуемые значения ε и η.
обеспечить
требуемые значения ε и η.
Список литературы
1. Бекмуратов. К.А. Процедура формирования непрерывных признаковых пространств при последовательном обучении. Узб. Журнал // «Проблемы информатики и энергетики».- 1994.-№4.-С.17-20.
2. К.А. Бекмуратов. Пошаговая проверка целесообразности усложнения решающего правила при последовательном обучении задаче распознавания. Узб. Журнал // «Проблемы информатики и энергетики». -2000. -№1. – С. 16-19.
3. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.(Статистические проблемы обучения). – М.: Наука, 1974. –С. 415.
| Нейрокомпьютерные системы | |
|
Введение. ПОЧЕМУ ИМЕННО ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ? После двух десятилетий почти полного забвения интерес к искусственным нейронным сетям быстро ... Вектор непрерывных входов может представлять собой произвольную точку на плоскости х-у. В этом случае мы имеем дело со способностью сети разбивать плоскость на непрерывные области ... В такой интерпретации "большие" векторы С производят более маленькие величины весов bij, чем "маленькие" вектора С. Это свойство самомасштабирования делает возможным разделение ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Машины, которые говорят и слушают | |
|
УДК 621.391 Рассмотрены современныэ тенденции развития систем автоматического распознавания и синтеза речевых сигналов. Освещены проблемы построения ... Т.К.Винцюк и соавторы [21] показали, что в рамках существующей однодикторной системы фонемного распознавания речи может быть создана многодикторная система распознавания, которую ... Так как автоматическое распознавание 300 - 300 слов в непрерывном речевом потоке - сложная задача, веди использовать обычные математические методы распознавания, то для ее решения ... |
Раздел: Рефераты по кибернетике Тип: реферат |
| Теоретические основы математических и инструментальных методов ... | |
|
Теоретические основы специальности. Оптимизационные методы решения экономических задач. Классическая постановка задачи оптимизации. Оптимизация ... Линейное пространство имеет размерность n (или, коротко, n-мерно), если в нем найдется n линейно независимых элементов, но любые (n+1) элемент линейно зависимы. Итак, любое линейное нормированное пространство можно сделать метрическим пространством указанным выше естественным способом (так, указанные нами нормы в пространстве непрерывных ... |
Раздел: Рефераты по экономико-математическому моделированию Тип: реферат |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... С другой стороны, сингулярное разложение матриц удобно при отображении одного векторного пространства в другое, возможно с иной размерностью. ... вектором a , а nb есть порядок полино-ма,описываемого вектором b. Выход y(n) является линейной комбинацией текущего и пре-дыдущих входов, то есть x(n) x(n-1) ..., и предыдущих |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Достаточно общая теория управления (Расовые доктрины в России: их ... | |
|
Достаточно общая теория управления _ Постановочные материалы учебного курса факультета прикладной математики - процессов управления Санкт ... При формировании совокупности концепций управления, соответствующих вектору целей, размерность пространства параметров вектора состояния увеличивается за счёт приобщения к столбцу ... Преобразователь информации, вырабатывающий управленческое решение, осуществляет выборку информации из памяти, соотнося накопленную памятью информацию с непрерывно поступающей ... |
Раздел: Остальные рефераты Тип: реферат |