Реферат: Формирование действия контроля в процессе работы над вычислительными приемами и навыками у младших школьников
Введение
Главной целью образования считается развитие умственных, интеллектуальных задатков ребёнка.
В связи с этим перед школой возникает важная задача, значимость которой заключается в правильной организации учебной деятельности.
Сущность обучения основана на создании условий, при которых в процессе обучения ребёнок становиться её субъектом, т.е. обучения ради самоизменения. Организация такой деятельности формирует у учащихся умение самостоятельно ставить перед собой учебные задачи; планировать учебную деятельность, выбирать соответствующие учебные действия для её реализации, осуществить контроль по ходу выполняемой работы и умение оценить полученные результаты.
В традиции из целостной структуры учебной работы выпадают именно контроль и оценка со стороны ребёнка, они изымаются и присваиваются учителем, а ученик самоосвобождается от необходимости контролировать и оценивать. В связи с этим учебная работа ребёнка постепенно лишается собственно контролирующего и оценивающего компонентов и, следовательно, внутренней мотивирующей и направляющей основы.
Появление действий контроля означает, что структура учения наполняется всеми компонентами и происходит обобщение способов осуществления отдельных систем учебных действий в целостное образование, обеспечивающее то, что обычно называют умением учиться.
Выполнение действия контроля способствует тому, что учащиеся обращают внимание на содержание собственных действий с точки зрения их соответствия решаемой задаче. Такое отношение школьников к собственным действиям (или рефлексия) служит существенным условием правильности их построения и изменения.
С сожалением приходится констатировать, что учителя уделяют недостаточное внимание обучению учащихся приёмам и способам формирования действия контроля. Это объясняется недостаточностью педагогического опыта, методических рекомендаций, пособий, справочников, направленных на внедрение методических приёмов обучения контролю, отсутствием в программах указаний на необходимость его формирования.
Учитывая научные знания и исследования по данной проблеме, основываясь на современных требованиях к учебному процессу, мы считаем, что овладение учащимися младших классов действия контроля в процессе обучения – является актуальной проблемой, стоящей перед современной школой. Наши наблюдения за деятельностью детей младших классов при формировании вычислительных навыков показали, что они не всегда умеют объяснить, правильно ли найдено значение выражения, не могут обосновать выбор арифметического действия, не могут выполнить проверку. Это говорит о том, что ученики слабо владеют или совсем не владеют умением контролировать себя в процессе решения.
Необходимо отметить, что в обычной практике работы, как правило, преобладает контроль по результату, где проверяется не правильность проведения отдельных операций и их последовательность, умение контролировать каждый свой шаг, а полученный результат.
В существующих пособиях по методике математики для учителей начальных классов авторы определённо указывают на необходимость формирования действия контроля у учащихся в процессе формирования вычислительных навыков. Однако в этих пособиях не раскрывается сущность понятия действия контроля и пути его формирования.
Цель исследования состоит в выявлении эффективных условий формирования действия контроля в процессе работы над вычислительными приёмами и навыками. В соответствии с целями были намечены следующие задачи:
проанализировать психолого-педагогическую литературу по исследуемой проблеме;
изучить сущность действия контроля в учебной деятельности;
провести диагностику сформированности действия контроля у учащихся 3 класса;
разработать и апробировать экспериментальную модель, направленную на развитие действия контроля у младших школьников в процессе работы над вычислительными приёмами и навыками.
Объект исследования: процесс формирования действия контроля.
Предмет исследования: особенности формирования действия контроля в процессе работы над вычислительными навыками.
Теоретический анализ проблемы исследования позволил сформировать следующее предположение: формирование действия контроля будет более эффективным, если:
учитель выделит структурные особенности действия контроля для отдельных вычислительных приёмов;
в процессе обучения будет использоваться система заданий, направленная на усвоение алгоритмов контрольных действий учащимися;
учитель будет ставить перед учащимися задачи на контроль.
Методологической основой исследования явились идеи о теории учебной деятельности (Д.Б. Эльконин, В.В. Давыдов, В.В. Репкин) и поэтапного формирования умственных действий (Н.Ф. Талызина, Л.Я. Гальперин). А также работы М.А. Бантовой, Н.Б. Истоминой, И.А. Аргинской по методике формирования вычислительного навыка.
В исследовании применялись следующие методы: теоретический анализ психолого-педагогической и методической литературы; беседа, опрос, анализ результатов работ учащихся; применение заданий, предназначенных для определения у учащихся уровня общего умения осуществлять действие контроля при работе над вычислительными навыками; эксперимент:
База исследования: школа №25 г. Иркутска, 3 «Д» класс.
1. Особенности контроля в учебной деятельности младших школьников
1.1. Сущность действия контроля, его особенности в младшем школьном возрасте и место в структуре учебной деятельности
Действие контроля мы рассматриваем внутри целостной структуры учебной деятельности школьников, выделенной и описанной Д.Б. Элькониным и В.В. Давыдовым.
Один из важнейших компонентов учебной деятельности – контроль. Согласно мнению Д.Б. Эльконина [39], под контролем следует понимать прежде всего контроль за правильностью и полнотой выполнения операций, входящих в состав действий .
В действии выполняются ориентировочные, исполнительные и контрольные функции. Согласно Н.Ф. Талызиной [37]: «Любое действие человека представляет собой своеобразную микросистему управления, включающую “управляющий орган” (ориентировочную часть действия), исполнительный “рабочий орган” (исполнительная часть действия), следящий и сравнивающий механизм (контрольная часть действия)».
К.Н. Поливанова [29,66] считает, что контроль заключается в определении соответствия других учебных действий условиям и требованиям учебной задачи. Он помогает ученику, меняя операционный состав действий, выявлять их связь с теми или иными особенностями условий решаемой задачи и свойствами получаемого результата. Благодаря этому, контроль обеспечивает нужную полноту операционного состава действий и правильность их выполнения.
В ряде исследований [23], [29], [34], [22] особое внимание уделялось изучению учебного действия контроля. Были выделены несколько его видов (итоговый, пооперационный, планирующий, упреждающий, рефлексивный). В работе Т.А. Матис специально выявились причины плохого формирования этого действия у младших школьников.
Контроль как форма произвольного внимания изучался группой психологов под руководством П.Я. Гальперина [4]. Отмечалось, что всякое внимание есть контроль, но не всякий контроль есть внимание. Это положение соответствует пониманию особенностей контроля в учебной деятельности. Так, по мнению Л.В. Берцфаи [4], если человек сопоставляет своё действие с готовым образцом, то он пользуется контролем в форме произвольного внимания. Но в специфической учебной деятельности, где учащийся осуществляет поиск адекватных способов своего действия (образцов, которых у него ещё нет), он не может пользоваться контролем в форме произвольного внимания. Контроль в учебной деятельности, по мнению Л.В. Берцфаи, К.Н. Поливановой, В.Г. Гомонок состоит в соотнесении предметного действия с конкретными условиями его выполнения и с ожидаемыми результатами. В своих работах данные авторы выделяют упреждающий и рефлексивный контроль. Так, в процессе поиска адекватных способов решения учебной задачи учащимся необходимо во внутреннем плане проиграть различные предполагаемые способы действия и сопоставить их с ожидаемыми результатами. Это упреждающий контроль.
Другой вид контроля учащийся использует, когда ему приходится перестраивать способ действия или строить его заново: в этом случае он не выбирает из известных ему способов какой-либо способ, более адекватный условиям задачи, а самостоятельно, (или с помощью учителя) строит его. Здесь осуществляется рефлексивный контроль.
В.Г. Романко [34] описала основные характеристики формирования у младших школьников рефлексивного контроля при усвоении ими теоретических знаний рефлексивный контроль связан с апробированием детьми ранее освоенного общего способа предметного действия в новых условиях его использования, с поиском нового способа действия применительно к этим условиям.
В соответствии с мнением Д.Б. Эльконина [39], контроль в учебной деятельности бывает двух видов: по результату и по процессу. Контроль по результату осуществляется на основании того, выполнено задание или нет, насколько качественно оно выполнено. Контроль по результату имеет смысл только в том случае, если он возвращается к контролю по процессу, а это встречается только тогда, когда учащийся совершил ошибку. Контроль по процессу предполагает выяснение тех операций, способов, действий, с помощью которых получен результат. Г.Я. Мор [24] отмечает, что для контроля по процессу необходимо знать алгоритм действия ученика, приём работы при выполнении задания. Без такого контроля невозможно выяснить причины многих трудностей. Формирование полноценного контроля возможно только на основе контроля по процессу.
По мнению М.В. Гамезо, действие контроля есть действие сличения, соотнесение учебных действий с образцом, который задаётся извне. Он выделяет три вида контроля: по результату (итоговый контроль), пооперационный и перспективный. Пооперационный (поисковый) контроль более высокий уровень контроля, чем итоговый. Это – коррекция деятельности, слежение за ходом действия, за тем, какое действие выполняется в данный момент, что ещё предстоит делать. Одновременно идёт контроль качества: как выполняется действие, соответствуют ли действия заданным требованиям. Перспективный (планирующий) контроль ещё более совершенный вид саморегуляции. Это корректирование деятельности на несколько операций вперёд, сличение предстоящей деятельности и своих возможностей её выполнения.
По мнению П.К. Анохина, контроль предполагает как бы три звена:
модель, образ потребного, желаемого результата действия;
процесс сличения этого образа и реального действия;
принятие решения о продолжении и коррекции действия.
Все эти три звена и есть структуры внутреннего контроля субъекта деятельности за её реализацией. Каждое звено деятельности, каждое её действие внутренне контролируется. Именно это позволяет нам говорить, что человек является саморегулируемой, самообучающейся, самосовершенствующейся личностью.
Д.Б. Эльконин придаёт действию контроля в процессе решения учебной задачи особое значение. По его предположению, именно оно характеризует всю учебную деятельность как управляемый самим ребёнком произвольный процесс. Произвольность учебной деятельности определяется наличием нескольких не столько намерения нечто сделать и желанием учиться, сколько контролем за выполнением действий в соответствии с образцом. Д.Б. Эльконин [39] полагает, что формирование произвольности основных психических процессов в младшем школьном возрасте, становление произвольности умственных действий детей существенно определяется именно степенью произвольности учебной деятельности. Последняя уже зависит от уровня сформированности входящего в ней действия контроля.
Условием нормального протекания учебных действий является наличие контроля за их выполнением. Согласно мнению Г.В. Репкиной, Е.В. Заики [33], заключается в постоянном прослеживании хода выполнения учебных действий, своевременном обнаружении различных больших и малых погрешностей в их выполнении, а также внесении необходимых корректив в них. Без такого прослеживания и таких корректив деятельность может существенно отклониться от своего русла, что, в конечном счёте, станет препятствием для решения учебной задачи.
Особенности действия контроля у разных учеников могут быть различными, и эти различия могут проявляться в степени автоматизированности его протекания (представляет ли он собой развёрнутое самостоятельное действие или включён в процесс выполнения действий), в его направленности (контролируется процесс выполнения действий или лишь их результаты), в критериях, на основе которых строится контроль (материализованная или идеально представленная схема-образец), во времени его осуществления (после действия, в процессе действия и до его начала) и т.п. Эти и другие характеристики контроля и составляют предмет его диагностики.
Таким образом, под контролем в учебной деятельности понимаются соотнесение предметного действия с конкретными условиями его выполнения и с ожидаемыми результатами. Действие контроля предполагает наличие умения предвидеть результаты своих действий, сопоставляя выполняемые действия с определённым образцом, предотвращать появление ошибок. Сущность действия заключена в соотнесении действий с «образцом» - эталоном действия.
Развитие контроля в учебной деятельности у младших школьников подчиняется, по данным Г.С.Никифорова [25] определённым закономерностям. В начале обучения в школе овладение контролем выступает для детей как самостоятельная форма деятельности, внешняя по отношению к основной задаче.
Постепенно, благодаря многократным и постоянным упражнениям в его осуществлении действие контроля превращается в необходимый элемент учебной деятельности, включённый в процесс её выполнения. Уже с первого класса дети начинают под руководством учителя овладевать действием контроля «учебного» поведения: как надо входить в класс; как правильно сидеть и вставать из-за парты; поднимать руку; собирать портфель. Дети спешат подтвердить результаты, опираясь на мнение преподавателя, родителей. Только во втором, третьем классе действие контроля детей начинает всё более заметно проявляться как «составная часть» учебной деятельности. У школьников начинает всё заметнее проявляться тенденция подвергать действию контроля не только результаты учебной деятельности, но и проверять свои действия в самом процессе её выполнения. К концу младшего школьного возраста у детей постепенно развивается способность к волевой регуляции собственного поведения, умение контролировать свои поступки и в целом подчинять их принятым правилам. На начальном этапе обучения действие контроля реализуется по конкретному образцу, затем по представлению о нём и на завершённом этапе – на основании обобщённого представления образцов. Умение ребёнка самостоятельно сопоставлять результаты выполненных заданий с особенностями производимых действий свидетельствует, по мнению В.В. Давыдова [14], о том, что исходные виды самоконтроля в его учебной деятельности сформированы.
Таким образом, формирование контроля у младших школьников проходит путь от контроля со стороны взрослых (от внешней формы) к собственно самоконтролю (к внутренней форме). Следовательно, в процессе обучения действие контроля постепенно превращается в необходимый элемент учебной деятельности, включённый в процесс её выполнения, контрольное действие приобретает предупредительный и пооперационный характер.
1.2. Критерии и уровни сформированности действия контроля.
В условиях развивающего обучения управление развитием каждого ученика становится непременным условием всей системы организации учебного процесса. Такое управление в первую очередь предполагает выявление картины происходящих в обучении изменений в деятельности каждого отдельного индивида по мере его становления как субъекта учебной деятельности. Иными словами, и учитель становится в позицию непременного осуществления своеобразной исследовательской деятельности: он должен научиться выделять показатели развития учебной деятельности учеников, оценивать ход их изменений, вносить соответствующие коррективы в своё взаимодействие с конкретными учениками и вновь проводить диагностику итогов таких коррекций. К сожалению, к настоящему времени ещё нет таких способов, которые без особых сложностей могли бы быть перенесены в практику работы учителя из научных исследований. И тогда наиболее адекватным методом оказывается наблюдение: при всех его недостатках (некоторые неточности, зависимости результатов от особенностей восприятия и понимания ситуации наблюдателем и др.), именно оно, - а может быть и только оно, - способно дать целостное представление о таком сложном явлении как формулирующаяся учебная деятельность.
Действие контроля состоит в соотнесении предметного действия с конкретными условиями его выполнения и с ожидаемыми результатами.
Действие может характеризоваться различными качественными особенностями, которые позволяют судить о степени его сформированности у ученика. Так, действие контроля может практически полностью отсутствовать, не проявляться при решении учебных задач, - в этом случае можно говорить о его несформированности. Или оно может проявляться лишь в элементарных своих формах, которые свидетельствуют лишь о начальных этапах его формирования. Наконец, действие контроля может обнаружиться в относительно совершенной, развитой форме, являющейся показателем достаточно полной его сформированности.
В качестве сформированности действия контроля можно выделить следующие критерии:
потребность в контроле.
осознание назначения контроля.
умение учащихся обнаруживать ошибки: в действиях своих товарищей, учителя, собственных; в результате действия, в ходе действия;
умение выполнять действие контроля.
имеет желание осуществлять контроль: самостоятельное стремление, по требованию учителя, не испытывает стремления к осуществлению контроля. Ниже приводится перечень уровней сформированности действия контроля по Г.В. Репкиной и Е.В. Заике, выделенные на основе вышеупомянутых критериев.
Первый уровень – отсутствие контроля.
Совершаемые учеником действия и операции никак не контролируются, часто оказываются неправильными, допущенные ошибки не замечаются и не исправляются. Часто допускаются ошибки даже при решении хорошо знакомых задач. Не умеет исправлять ошибку ни самостоятельно, ни по просьбе учителя, т.к. не способен свои действия и их результаты соотнести с заданной схемой действия и обнаружить их соответствие или несоответствие. Некритически относится к указаниям учителя и исправлению ошибок в своих работах, соглашается с любым исправлением, в том числе, когда оно тут же меняется на противоположное. Неоднократно повторяет одни и те же ошибки после их исправления учителем. Не может объяснить, почему действия надо совершать именно так, а не иначе. Не замечает ошибок, допущенных другими учениками. Обращает внимание лишь на нарушение внешних требований («грязно», «загнуты углы»). При просьбе учителя проверить свою работу и исправить ошибки действует хаотично, не придерживаясь никакого плана проверки и не соотнося свои действия ни с какой схемой.
Второй уровень – контроль на уровне непроизвольного внимания.
Контроль выполняется неустойчиво и неосознанно. В его основе лежит неосознаваемая или плохо осознаваемая учеником схема действия, которая зафиксировалась в его непроизвольной памяти за счет многократного выполнения одного и того же действия. Контроль же в форме специального, целенаправленного действия по соотнесению выполняемого учеником процесса решения задачи с усвоенной им схемой действия отсутствует. Ученик действует импульсивно, хаотично, но за счет непроизвольного запоминания схемы действия и непроизвольного внимания как бы предугадывает направление схемы правильных действий, однако не может объяснить, почему следует делать так, а не иначе, легко отказывается от своего решения. Хорошо знакомые действия может совершать безошибочно, а если допустит ошибку, может обнаружить её самостоятельно или по просьбе учителя, однако делает это не систематически. Не может объяснить ни саму ошибку, ни правильный вариант, дает лишь формальные ответы типа: «так неправильно», «так надо». Что касается новых, недостаточно хорошо усвоенных действий, то ошибки в них допускаются часто, и при этом не замечаются и не исправляются.
Третий уровень – потенциальный контроль на уровне произвольного внимания. Выполняя новое задание, ученик может допустить ошибку, однако, если учитель просит его проверить свои действия или найти и исправить ошибку, ученик, как правило, находит её и исправляет и может при этом объяснить свои действия. Вводимые схемы действия осознает и может сличать с ними собственный процесс решения задачи, хотя делает это не всегда, особенно при выполнении новых действий. Выполнив действие без осознаваемого контроля, тут же по просьбе учителя может проконтролировать его ретроспективно и в случае необходимости внести соответствующие исправления. Как самостоятельное, целенаправленное действие, контроль такому ученику доступен и может им выполняться, но происходит это преимущественно только после окончания действий по просьбе учителя. Одновременно совершать новое действие и соотносить его со схемой ребенок затрудняется. Что касается хорошо освоенных или неоднократно повторенных действий, то в них ребенок почти не допускает ошибок, а если допустит, может самостоятельно найти их и исправить. Во всех случаях, исправляя ошибку, ребенок может обосновать свои действия, ссылаясь на усвоенную и осознанную схему действия.
Четвертый уровень – актуальный контроль на уровне произвольного внимания.
В процессе выполнения действия ученик ориентируется на хорошо осознанную и усвоенную им обобщенную схему действия и успешно соотносит с ней процесс решения задачи. Это приводит к тому, что действия выполняются, как правило, безошибочно. Допущенные ошибки обнаруживаются и исправляются самостоятельно, причем случаи повторения одних и тех же ошибок крайне редки. Может правильно объяснить свои действия. Может безошибочно решать большое число разнообразных задач, построенных на основе одного и того же способа действия, умело соотнося их с усвоенной схемой. Осознанно контролируются действия других учеников при совместном выполнении заданий. Однако, столкнувшись с новой задачей или изменением условий действий, требующих корректив в саму схему действия, ученик оказывается беспомощным и не может отступить от заданной схемы. Другими словами, ученик может успешно контролировать не только итог, но и процесс выполнения действия и по ходу его выполнения сверять совершаемые действия с готовой наличной схемой, однако проконтролировать соответствие самой схемы действий имеющимся новым условием он не может.
Пятый уровень – потенциальный рефлексивный контроль.
Столкнувшись с новой задачей, внешне похожей на решавшиеся ранее, ученик точно выполняет учебные действия в соответствии с прежней схемой, не замечая того, что эта схема оказывается неадекватной новым условиям. Допущенные ошибки может обнаружить с помощью учителя и, отвечая на его наводящие вопросы, может объяснить их источник – несоответствие примененного действия новым условиям задачи. Обычно после этого ученик пытается исправить свои действия, перестроить применяемый способ, тем не менее это ему удается сделать только с помощью учителя. Под руководством учителя может переходить к выделению принципов построения плана действий соответствующего типа, то есть устанавливать соотнесение между основаниями выбора и построения способов действия и их обобщенных схем в зависимости от изменения условий.
Задания, соответствующие применяемой схеме действий, как знакомые ему, так и незнакомые, выполняет регулярно и безошибочно, контролируя свои действия непосредственно в процессе выполнения. Уверенно отстаивает результат своих действий, обосновывая его анализом примененных способов.
Шестой уровень – актуальный рефлексивный контроль.
Решая новую задачу, внешне похожую на решаемые ранее, ученик может самостоятельно обнаружить ошибки, возникающие из-за несоответствия применяемого им обобщенного способа действия (или схемы) новым условиям задачи. В связи с этим самостоятельно вносить коррективы в применяемую схему действия за счет поиска и выявления еще более общих оснований действия, т.е. принципов его построения. Другими словами, ученик умеет контролировать не только соответствие выполняемых действий обобщенной их схеме, но и соответствие самой этой обобщенной схемы изменившимся условиям задачи. В ряде случаев ученик может приступать к такой коррекции действий еще до начала их фактического выполнения в соответствии с усвоенной схемой, определив её неадекватность новым условиям заранее, как бы «прокрутив их в уме». Помощь учителя может при этом встречать отрицательно, пытаясь сначала выработать новый способ самостоятельно.
На основе вышеизложенного материала, нами была создана нормативная модель действия контроля в учебной деятельности младших школьников:
потребность в контроле;
осознание назначения контроля;
умение обнаруживать ошибку (свою, своих товарищей, учителя; самостоятельно, в хорошо знакомых действиях, в новых условиях);
умение объяснить ошибку;
умение критически относиться к контролю со стороны других детей, учителя;
умение исправлять ошибку на основе соотнесения хода и результата действия с заданной схемой действия;
умение осуществлять содержательный контроль, обнаружить ошибки по причине несоответствия способа действия и условий задачи;
умение осуществлять межличностный рефлексивный контроль (реконструировать способ действий товарища);
умение осуществлять проверку;
умение составлять план проверки.
1.3. Выводы по главе.
Сущность действия контроля заключена в обязательном сопоставлении действий с «образцом», с эталоном действия.
Формирование действия контроля у младших школьников проходит путь от контроля со стороны взрослых (от внешней формы) к собственно самоконтролю (к внутренней форме). В начале обучения в школе овладение действием контроля выступает как самостоятельная форма деятельности, внешняя по отношению к основной задаче. Постепенно, в процессе обучения действие контроля превращается в необходимый элемент учебной деятельности, включенный в процесс ее выполнения.
Выполнение действия контроля способствует тому, что учащиеся обращают внимание на содержание собственных действий с точки зрения их соответствия решаемой задаче. Такое отношение школьников к собственным действиям служит существенным условием правильности их построения и изменения.
На начальном этапе обучения действие контроля реализуется по конкретному образцу, затем по представлению о нем и на завершающем этапе – на основании обобщенного представления образцов.
2. Возможности формирования действия контроля в процессе работы над вычислительными приёмами и навыками
2.1. Общая характеристика формирования вычислительных приёмов и навыков у младших школьников
Деятельность по овладению вычислительных приёмов можно рассматривать как учебную деятельность, важнейшим компонентом является действие контроля. Под контролем при правильности вычислительных приёмов следует понимать как проверку всей деятельности, направленной на выполнение вычислительных приёмов, так и проверку конечного результата.
В век компьютерной грамотности значимость навыков письменных вычислений, несомненно, уменьшилась. Вместе с тем, научиться быстро и правильно выполнять письменные вычисления важно для младших школьников как в плане продолжающейся работы с числами, так и в плане практической значимости этих навыков для дальнейшего обучения в школе.
Особенность изучения письменных вычислений обусловлена тем, что у детей быстро развивается усталость при работе с числами. Это объясняется большим количеством операций как письменного сложения и вычитания, так и письменного умножения и деления. Избежать быстрой утомляемости и снижения внимания при изучении письменных вычислений поможет чередование различных видов деятельности, отказ от однообразных тренировочных упражнений, обучение приёмам действия контроля. Действие контроля должно присутствовать на каждом этапе выполнения вычислительного приёма. Только в этом случае возможно постоянное прослеживание хода выполнения учебных действий, своевременное обнаружение различных больших и малых погрешностей в их выполнении, а также внесение необходимых корректив в них. Обнаруженная ошибка в процессе вычислений позволит сохранить ребёнку внутренние силы, предотвратить преждевременную усталость. Для контроля в выполнении письменных вычислений целесообразно показать ученикам, как использовать опорные сигнал, например точки, напоминающие о том, что следует учесть перенесённую через разряд единицу. В связи с этим необходимо больше внимания уделять формированию действия контроля в процессе работы над вычислительными приёмами и навыками, так как организационное на уроке математики действие контроля, приводит к концентрации внимания всех учащихся, формирует в практической деятельности каждого ученика умение рассуждать, исключает ошибки в тетрадях, что позволяет совершенствовать умения осознанно выполнять вычислительные приёмы.
Формирование у младших школьников вычислительных навыков остаётся одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий.
В ряде исследований [2], [8] раскрываются основные положения системы формирования вычислительного навыка. Особое внимание было уделено работе М.А. Бантовой, посвящённой изучению данной темы.
Раскроем суть вычислительного приёма. Пусть надо сложить числа 8 и 6. Приём вычисления для этого случая будет состоять из ряда операций:
замена числа 6 суммой удобных слагаемых 2 и 4;
прибавление к числу 8 слагаемого 2;
прибавление к полученному результату, к числу 10, слагаемого 4.
Здесь выбор операций и порядок их выполнения определяется соответствующей теоретической основой приёма – применением свойства прибавления к числу суммы (сочетательное свойство): замена числа 6 суммой удобных слагаемых, затем прибавление к числу 8 последовательно каждого слагаемого. Кроме того, здесь используются и другие знания, например, при выполнении первой операции используется знание состава чисел первого десятка: 10=8+2 и 6=2+4.
Таким образом, можно сказать, что приём вычисления над данными числами складывается из ряда последовательных операций, выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами; причём выбор операций в каждом приёме определяется теми теоретическими положениями, которые используются в качестве теоретической основы.
Вычислительный навык – это высокая степень овладения вычислительными приёмами.
В большинстве случаев уже в начальных классах школы для нахождения результата арифметического действия можно использовать в качестве теоретической основы различные теоретические положения, что приводит к разным приёмам вычислений.
Например:
156=15+15+15+15+15+15=90;
156=(10+5)6=106+56=90;
156=15(23)=(152)3=90.
Теоретической основой для выбора операций, составляющих первый из приведённых приёмов, является конкретный смысл действия умножения; теоретической основой второго приёма – свойство умножения суммы на число, а третьего приёма – свойство умножения числа на произведение. Операции, составляющие приём вычисления, имеют разный характер. Многие из них сами являются арифметическими действиями. Эти операции играю особую роль в процессе овладения вычислительными приёмами: выполнение приёма в свёрнутом плане сводится к выделению и выполнению именно операций, являющихся арифметическими действиями. Поэтому операции, являющиеся арифметическими действиями, можно назвать основными. Например, для случая 164 основными будут операции: 104=40, 64=24, 40+24=64. Все другие операции – вспомогательные.
Число операций составляющих прием, определяется прежде всего выбором теоретической основы вычислительного приема. Например, при сложении чисел 57 и 25 в качестве теоретической основы может выступать свойство прибавления суммы к числу, тогда прием будет включать три операции: замена числа 25 суммой разрядных слагаемых 20 и 5, прибавление к числу 57 слагаемого 20 и прибавление к результату, к 77, слагаемого 5; если же теоретической основой является свойство прибавления суммы к сумме, то прием для того же случая будет включать пять операций: замена числа 75 суммой разрядных слагаемых 50 и 7, замена числа 25 суммой разрядных слагаемых 20 и 5, сложение чисел 7 и 5, сложение полученных результатов 70 и 12. Число операций зависит также от чисел, над которыми выполняются арифметические действия.
Число операций, выполняемых при нахождении результата арифметического действия, может сокращаться по мере овладения приемом. Например, для случаев вида 8+2 на начальной стадии формирования навыка ученик выполняет три операции: замена числа 2 суммой 1 и 1, прибавление числа 1 к 8 , прибавление числа 1 к результату, к 9. Однако после заучивания таблицы сложения ученик выполняет одну операцию – он сразу связывает числа 8 и 2 с числом 10. Как видим, здесь прием как бы перерастает в другой.
Д
Структура вычислительного приёма
ля большей наглядности структуру вычислительного приема мы представили в виде схемы:

Теоретическая основа


Основные операции
Вспомогательные операции

Общеизвестно, что теоретической основой вычислительных приёмов служат определения арифметических действий, свойства действий и следствия, вытекающие из них. Имея это в виду и принимая во внимание методический аспект, можно выделить группы приёмов в соответствии с их общей теоретической основой. Существуют различные классификации вычислительных приёмов. Рассмотрим более детально классификацию вычислительных приёмов, предложенную Бантовой М.А., основанием которой является общность теоретической основы вычислительных приёмов, изучаемых в начальных классах.
Данную классификацию мы представили в виде таблицы.
Таблица 1.
Классификация вычислительных приёмов по общности теоретической основы
|
Группы вычислительных приёмов Теоретическая основа |
Устные | Письменные | |
| Табличные | Внетабличные | ||
|
а2,3,4; 18:6; 23 и т.д. |
||
|
а+5,6,7,8,9 и т.д. |
542; 5420; 273; 144; 81:3; 120:45; 1840 и т.д. |
49+23; 90-36 и т.д. |
|
а-5,6,7,8,9; 21:3 и т.д. | 9-7; 60:3; 54:18 и т.д. | Письменные приёмы деления и умножения |
|
46+19; 255; 300:50 и т.д. |
512-298 и т.д | |
|
а1 |
10+6; 16-10; 1200:100; 4020 и т.д. |
Письменные приёмы деления и умножения |
|
а0 |
а1;
а:1; а0;
|
Как видим, все вычислительные приёмы строятся на той или иной теоретической основе, причём в каждом случае учащийся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительных приёмов.
Это реальная предпосылка овладения учащимися осознанными вычислительными навыками.
Общность подходов каждой группы – есть залог овладения учащимися обобщёнными вычислительными навыками.
Вычислительный навык – это высокая степень овладения вычислительными приёмами. Приобрести вычислительный навык – значит, для каждого случая знать какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро. В качестве сформированности полноценного вычислительного навыка можно выделить следующие критерии: правильность, осознанность, рациональность, обобщённость, автоматизм и прочность. Вместе с тем, учитывая, что ученик при выполнении вычислительного приёма должен отдавать отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом – системой операций, мы относим к основным критериям и степень овладения умением контролировать себя при выполнении вычислительного приёма.
О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению.
Нами были выделены и представлены в таблице уровни и критерии сформированности вычислительного навыка.
Таблица 2.
Критерии и уровни сформированности вычислительного навыка
|
уровни критерии |
высокий | средний | низкий |
| 1. правильность | Ученик правильно находит результат арифметического действия над данными числами. | Ребёнок иногда допускает ошибки в промежуточных операциях. | Ученик часто неверно находит результат арифметического действия, т.е. не правильно выбирает и выполняет операции. |
| 2. осознанность | Ученик осознаёт, на основе каких знаний выбраны операции. Может объяснить решение примера. | Ученик осознаёт на основе каких знаний выбраны операции, но не может самостоятельно объяснить, почему решал так, а не иначе | Ребёнок не осознаёт порядок выполнения операций. |
| 3. рациональность | Ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный приём. Может сконструировать несколько приёмов и выбрать более рациональный. | Ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный приём, но в нестандартных условиях применить знания не может. | Ребёнок не может выбрать операции, выполнение которых быстрее приводит к результату арифметического действия. |
|
4. обобщённость |
Ученик может применить приём вычисления к большему числу случаев, то есть он способен перенести приём вычисления на новые случаи. | Ученик может применить приём вычисления к большему числу случаев только в стандартных условиях. | Ученик не может применить приём вычисления к большему числу случаев. |
| 5. автоматизм | Ученик выделяет и выполняет операции быстро и в свёрнутом виде. | Ученик не всегда выполняет операции быстро и в свёрнутом виде. | Ученик медленно выполняет систему операций, объясняя каждый шаг своих действий. |
| 6. прочность | Ученик сохраняет сформированные вычислительные навыки на длительное время. | Ученик сохраняет сформированные вычислительные навыки на короткий срок. | Ребёнок не сохраняет сформированные вычислительные навыки. |
В качестве одного из показателей полноценного вычислительного навыка мы выделим контроль. При этом мы отдаём себе отчёт в том, что контроль – качественно иной показатель, чем перечисленные выше, а поэтому, его не следует рядопологать с ними. Умение осознанно контролировать выполняемые операции, позволяет формировать вычислительный навык более высокого уровня, чем без наличия этого умения. Это значит, что все ранее раскрытые нами качественные характеристики, проявляются при формировании вычислительного навыка на более высоком уровне. Как видим, умение контролировать себя в процессе формирования вычислительного навыка требует от ученика полноценного, осознанного, обобщённого и самостоятельного владения всеми операциями, определяющими процесс выполнения вычислительного приёма.
Традиционно процесс обучения рассматривается как процесс взаимодействия учителя и учащихся, в ходе которого решаются задачи образования, воспитания и развития. К основным структурным компонентам, раскрывающим его сущность, относят цели обучения, содержание, деятельность преподавания и учения, характер их взаимодействия, принципы, методы, формы обучения.
В традиционном обучении содержание представлено в основном предметными знаниями, умениями, навыками. Интеллектуальные, учебные и другие умения находятся в снятом виде, представлены через предметные действия, не выступают самостоятельным предметом усвоения. Уровень их усвоения служит показателем успешности обучения. Также очевиден репродуктивный уровень представленности учебного содержания в учебниках: это конкретные правила и определения, которые нужно выучить, большое количество тренировочных упражнений, которые выполняются с целью закрепления, наличие образцов выполнения учебных заданий, ведущие к однотипности его выполнения – это концентрический принцип структурирования учебного содержания, где изложение идёт от простого к сложному, от более лёгкого к трудному.
В развивающей системе обучения его содержание выступает средством развития личности ребёнка, следовательно, оно должно соответствовать содержанию развития, отражать его.
По мнению Г.А. Цукерман, взаимоотношения учителя и учащихся в традиционном обучении характеризуется как исполнительские, основанные на одностороннем подражании. Учитель при этом выступает как носитель совершенных образцов, а ребёнок как более или менее успешный имитатор действий взрослого: «Я делаю вслед за учителем. Я делаю сам, как учитель». Для традиционного обучения также характерно отсутствие собственно учебных отношений между детьми на уроках, что объясняется преобладанием фронтального способа организации деятельности детей, при котором все ученики связаны с учителем, общение замкнуто на нем.
Коренным образом меняется содержание деятельности учителя в развивающем обучении. Теперь главная задача учителя – не «донести», «преподнести» и показать учащимся, а организовать совместный поиск решения возникший перед ними задачи. Учитель начинает выступать как режиссёр мини-спектакля, который рождается непосредственно в классе.
Развивающее обучение немыслимо без постоянного учебного общения, при котором учащийся, поняв, чего он не знает, не умеет делать, сам начинает активно действовать, восполняя недостаток знания и включая в этот процесс учителя, как более опытного партнёра. Мнение учителя при этом воспринимается детьми как одна из возможных точек зрения, которую нужно соотнести с собственной точкой зрения и мнениями других учеников. Необходимость такого общения вытекает из природы поисковой, исследовательской деятельности, при которой поиск истины в одиночку невозможен, необходим коллективный поиск, сопровождающийся постоянным обменом мнениями.
Содержание обучения задаёт определённый способ его усвоения, определённый тип учения. В традиционном (объяснительно-иллюстративном) обучении преобладает догматический тип учения, который предполагает репродуктивный способ и уровень усвоения учебного содержания. Основные усилия учеников при этом сосредоточены на восприятии готовых знаний, образцов выполнения действий на их закреплении и воспроизведении. Находясь в ситуации решения какой-либо задачи, школьник, как правило, не старается найти способ решения, а усердно пытается вспомнить решение аналогичных задач. Если вспомнить не удаётся, аналогичная задача не отыскивается, то ученик чаще всего оставляет задачу не решённой или прибегает к другим (не учебным) способом выполнения. Как правило, ученик, оставаясь один на один с учебным материалом, не знает, как преступить к его изучению. Данный тип учения не может обеспечиваться активной мотивацией.
Отсутствие готового для запоминания учебного содержания изменяет позицию ученика в учебном процессе, коренным образом меняет тип учения. Из догматического он преобразуется в эвристический, исследовательский, при котором новое знание открывается учеником самостоятельно или в совместном поиске учителем и учащимся. И.С. Якиманская отмечает, что в условиях развивающего обучения учащиеся самостоятельно добывают знания и способы действия, перестраивают ранее полученные, осуществляют широкий перенос усвоенного на решение новых учебных и практических задач, то есть выполняют в основном не воспроизводящую, а преобразующую деятельность. Развивающие технологии имеют специальные методы, включающие детей в коллективный поиск: это создание проблемных ситуаций, ситуация учебного спора, метод коллизий, метод решения учебных задач.
Например, при формировании вычислительных навыков в традиционной системе рассматривается позиция: делай то, что тебе предлагают, чтобы научиться делать это быстро и правильно. Этот путь предполагает сообщение учащимся образца, алгоритма выполнения операций, на основании которого учащиеся многократно её выполняют. В результате такой репродуктивной деятельности достигается запоминание предложенного алгоритма и вырабатывается запланированный навык, при этом дети часто не осознают, на основе каких знаний выбраны операции и установлен порядок их выполнения.
В системе Л.В. Занкова действует другая позиция: делай для того, чтобы продвинуться в решении стоящей перед тобой математической проблемы или чтобы обнаружить такую проблему. Таким образом, используется косвенный путь формирования навыков, который предполагает включение учеников в продуктивную творческую деятельность, в самостоятельное установление алгоритма операции. Прежде всего, необходимо осознать, что предлагаемый путь является более длинным, и в системе нет стремления к быстрому формированию вычислительных навыков, а отводится большое время на осознание тех теоретических и практических основ, которые лежат в фундаменте предлагаемых способов вычислений. Такое осознание – процесс длительный, и его можно организовать только тогда, когда навык еще не сформировался. Если формирование навыка уже произошло, никакого плодотворного возврата к осознанию его источника не может быть для подавляющего большинства людей. Дети никогда не поймут, зачем нужно размышлять о том, что просто уже делаешь, не задумываясь.
Следующей особенностью является отказ от активной эксплуатации механической памяти при запоминании таких важных основ овладения вычислительными навыками, как таблицы сложения и умножения. В системе основ запоминания этих таблиц является длительная и активная деятельность, требующая постоянного обращения к ним. Именно этой особенностью диктуется то, что каждый ученик имеет право открыто пользоваться таблицами как справочным материалом до тех пор, пока ему это необходимо.
В результате такого подхода к формированию вычислительных навыков дети приобретают прочные и осознанные навыки выполнения математических действий. Когда такая цель достигнута, необходимо перейти к наращиванию скорости выполнения вычислений.
Органическое соединение осознания основ выполнения действий и формирование вычислительных навыков приводит к тому, что материал для работы над вычислительными навыками создается самими детьми, а не дается готовым.
Отличие разных систем обучения заключается не в том, что в одних используется один путь, а в других – другой. В каждой системе присутствуют оба подхода, различие же в том, каково соотношение этих путей. В системе, направленной на общее развитие учащихся, главным является именно косвенный путь формирования навыков, прямой же используется тогда и в той мере, как это необходимо. В связи с этим, системы обучения имеют различные подходы формирования вычислительных навыков. Так, например, традиционная система предполагает ряд этапов, направленных на работу над каждым отдельным приемом:
Подготовка к введению нового приема.
На этом этапе создается готовность к усвоению вычислительного приема, а именно: учащиеся должны усвоить те теоретические положения, на которых основывается теоретический прием. Центральное же звено при подготовке к введению нового приема – овладение учеником основными операциями, которые войдут в новый прием.
Ознакомление с вычислительным приемом.
На этом этапе ученики усваивают суть приема: какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия. Степень самостоятельности учащихся должна увеличиваться при переходе от приема к приему другой группы.
Закрепление знания приема и выработка вычислительного навыка.
На данном этапе учащиеся должны твердо усвоить систему операций, составляющих вычислительный прием, и предельно быстро выполнять эти операции, то есть овладеть вычислительным навыком.
В процессе работы важно предусмотреть ряд стадий в формировании у учащихся вычислительных навыков.
На первой стадии закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производя развернутую запись, если она была предусмотрена на предыдущем этапе. На второй стадии происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции, обосновывают выбор и порядок их выполнения, вслух же они проговаривают выполнение основных операций, то есть промежуточных вычислений. На третьей стадии происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, то есть здесь происходит свертывание и основных операций. Четвертая стадия характеризуется предельным свертыванием выполнения операций: учащиеся выполняют все операции в свернутом плане предельно быстро, то есть они овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений.
Названные стадии не имеют четких границ: одна постепенно переходит в другую.
В системе Л. В. Занкова [2] формирование навыков проходит три принципиально различных этапа.
Первый этап – осознание основных положений, лежащих в фундаменте выполнения операции, создание алгоритма ее выполнения. На этом обязательно прослеживается, оценивается и создается каждый шаг в рассуждениях детей, устные рассуждения переводятся в запись математическими знаками. Отсюда вытекает характерный признак этого этапа - подробная запись выполнения операции, с которой в данный момент работают ученики. На этом этапе практически не используется прямой путь. Он возникает только при выполнении промежуточных, знакомых детям операций. Результатом этого этапа является выработка алгоритма выполнения операции и его осознание.
Главным направлением второго этапа является формирование правильного выполнения операции. Для достижения этой цели необходимо не только использование выработанного на 1 этапе алгоритма выполнения операции, но, может быть, в еще большей степени, свободная ориентация в ее нюансах, умение предвидеть. К чему приведет то или иное изменение компонентов операции. В силу этого на втором этапе используются оба пути формирования навыков, однако косвенный путь продолжает быть ведущим, прямой же используется в качестве подчиненного.
Третий этап формирования навыка нацелен на достижение высокого темпа выполнения операции. Именно на этом этапе на первый план выходит прямой путь формирования навыка. Главная задача учителя – построить работу так, чтобы дети хотели выполнять необходимые вычисления и получали от этого удовольствие.
2.2. Особенности формирования действия контроля в процессе работы над вычислительными приёмами и навыками.
Условием нормального протекания учебных действий является наличие контроля за их выполнением.
В исследовании Т. А. Матис [39] изучались пути формирования рефлексивного контроля в совместной учебной деятельности младших школьников. Было обнаружено, что контроль начинает формироваться у детей при совместном решении учебных задач. Важным условием формирования названного учебного действия стало превращение детьми анализа предметного содержания в анализ собственных способов действия в данном содержании (т.е. осуществление рефлексии этих способов). Особую роль в таком превращении играли знаково-символические схемы, позволяющие детям совместно планировать свои действия и контролировать их выполнение. Распределяя между собой и выполняя поочередно то планирование, то контроль за ним, учащиеся с помощью этих схем могли удерживать обе цели внутри сложного совместного действия. По мере его овладения происходило свертывание планирования и отпадала необходимость внешнего контроля за ним со стороны другого ученика: наблюдалось слияние планирования и контроля в одном индивидуальном действии – рефлексивном контроле.
Работа Г. П. Максимовой [22] интересна тем, что в ней вопросы формирования учебного действия изучались во взаимосвязи с формированием таких мыслительных действий, как рефлексия, анализ и планирование.
В исследовании К. Н. Поливанова [29] обнаружено, что важным условием формирования полноценного контроля служит переход младших школьников от выполнения одного учебного действия к другому (наиболее благоприятное условие – переход от преобразования материала к моделированию его существенного отношения.
Работы данных авторов раскрывают одно общее положение, высказанное Д.Б. Элькониным: «Есть основания полагать, что формирования контроля от контроля за действиями других к контролю за своими собственными действиями».
А. В. Захарова [18] отметила, что выполнение действия контроля способствует тому, что учащиеся обращают внимание на содержание собственных действий с точки зрения их соответствия решаемой задаче. Такое отношение школьников к собственным действиям служит существенным условием правильности их построения и изменения.
Г. А. Цукерман выдвинула гипотезу, согласно которой сотрудничество со сверстниками качественно отличается от сотрудничества со взрослыми и так же, как сотрудничество со взрослыми, является необходимым условием психического развития ребенка. Г. А. Цукерман анализировала взаимодействия детей и их особенности с точки зрения их влияния на психическое развитие в процессе генетико-моделирующего эксперимента. Ее исследования продемонстрировали необходимость кооперации со сверстниками для формирования контрольно-оценочных действий ребенка. Чтобы освоить эти действия, ребенок должен встать на позицию взрослого, а это возможно только при кооперации с другим ребенком, сверстником.
В. В. Рубцов на основе экспериментальных исследований заключает, что кооперация со сверстниками и координация точек зрения – основа происхождения интеллектуальных структур ребенка.
Р. Я. Гузман считает, что для организации полноценного совместного учебного действия очень важны такие формы учебной работы, как взаимная проверка заданий, взаимные задания групп, учебный конфликт, а также обсуждение участниками способов своего действия.
Работы Ю. А. Полуянова, Т. А. Матис, В. В. Рубцова, Г. А. Цукерман выявили специфическую роль конфликта точек зрения школьников в возникновении их учебных дискуссий, роль самих дискуссий в совместной учебной деятельности учащихся. Они отметили, что ситуация конфликта позиций, требующая диалога и дискуссий, выступает важным звеном формирования у школьников умения выделять и учитывать точку зрения других людей при контроле и оценке своих действий.
В соответствии с мнением Д. Б. Эльконина дети прежде всего должны научиться контролировать друг друга и самих себя. Психологи различают два аспекта взаимоконтроля в учебной деятельности по результату и по процессу. Контроль по результату (продукту) осуществляется на основании того, выполнено задание или нет, насколько качественно оно выполнено. Контроль по процессу предполагает выяснение тех операций, способов, действий, с помощью которых получен результат. Взаимоконтроль по процессу вырабатывает умение осуществлять самоконтроль. Согласно Г. Я. Мор [24, 35], организованный на уроке взаимоконтроль и самоконтроль по процессу приводит к концентрации внимания всех учащихся, формирует в практической деятельности каждого ученика умение рассуждать, дает возможность слабым учащимся лучше разобраться в изучаемом материале, дает возможность на каждом уроке осуществлять обратную связь учителя и учеников.
Развитие умственных действий даёт возможность для развития всех структурных элементов учебной деятельности, а следовательно и действия контроля как компонента этой деятельности.
О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны выполняет все операции приводящие к решению.
Умение осознано контролировать выполняемые операции позволяет формировать вычислительные навыки более высокого уровня, чем без наличия этого умения.
Выполнение вычислительного приёма – мыслительный процесс, следовательно, овладение вычислительным приёмом и умение осуществлять контроль за его выполнением, должно происходить одновременно в процессе обучения.
Структура действия контроля должна соответствовать предметному содержанию процесса выполнения вычислительных приёмов, поэтому целесообразно обучать учащихся не только общему способу контроля, но и умению переносить этот способ на конкретные виды вычислительных приёмов.
Важными представляются следующие условия формирования действия контроля в процессе работы над вычислительными приёмами и навыками:
осознание назначения контроля учащимися;
формирование у учащихся контрольных суждений;
постановка учителем перед учащимися задачи на контроль;
совместное планирование действий и контроль за их выполнением;
использование заданий, направленных на усвоение алгоритмов контролирующих действий учащимися;
критическое отношение учащихся к контролю со стороны других детей, учителя;
формирование потребности в действии контроля.
Перечисленные условия формирования действия контроля в процессе работы над вычислительными приёмами и навыками позволят учащимся избежать трудностей в вычислениях, помогут ученикам быть более внимательными в процессе овладения вычислительными приёмами.
2.3. Выводы по главе
Умение выполнять вычислительный прием – есть умение выполнять систему умственных операций, следовательно, контроль – есть умение осознанно контролировать выполняемые операции. При развитии действия контроля на уроках математики, совершенствуется умение осознанно выполнять вычислительные приемы. И, наоборот, в случае отсутствия действия контроля, сформированность вычислительных приемов и навыков имеет низкий уровень. Следовательно, процесс выполнения вычислительного приема и осознанное его контролирование, должны быть двумя сторонами единого процесса, процесса овладения вычислительными приемами и навыками.
Действие контроля, сформированное при овладении одних вычислительных приемов, естественно будет проявляться и при выполнении других вычислительных приемов, поскольку при их решении ученик использует в новой конкретной ситуации те же умственные операции. Усвоенная система операций, составляющая процесс выполнения вычислительного приема, в дальнейшем служит образцом для самостоятельного овладения вычислительным приемом и в то же время позволяет осуществлять пооперационный контроль.
На первых этапах овладения вычислительным приемом пооперационный контроль осуществляется под руководством учителя. Но при целенаправленном формировании умения контролировать выполняемые действия, пооперационный контроль на последнем этапе формирования вычислительных приемов и навыков переходит в самоконтроль, который помогает устранить появление возможных ошибок и вместе с тем повышает качество овладения вычислительными приемами и навыками.
3. Экспериментальная работа по формированию действия контроля в процессе работы над вычислительными приемами и навыками
3.1. Диагностика сформированности действия контроля и вычислительных приемов и навыков
На основе проанализированной литературы нами было проведено исследование с целью выявления уровня сформированности действия контроля. Базой исследования была определена школа – гимназия № 25 г. Иркутска, 3»Д» класс. В исследовании принимал участие весь класс, составе 23 учащихся. В ходе исследования были использованы следующие методы: письменный опрос, беседа, срезы знаний, самостоятельная работа. Нами были выделены следующие задачи исследования: 1. изучить сформированность некоторых свойств действия контроля: а) умение выполнять контроль по результату и желание его осуществлять б) умение обнаружить ошибку (свою, товарищей, учителя), объяснять ее появление в) умение обнаружить ошибку в ходе действия и реконструировать способ действия.
С целью изучения интереса детей к математике, вычислительным приемам нами был проведен письменный опрос, который включал следующие вопросы:
Какие задания тебе нравится выполнять на уроках математики?
Любишь ли ты выполнять вычисления?
С удовольствием ли ты находишь значения выражений?
Какие ошибки чаще всего допускаешь в вычислениях?
Можешь ли самостоятельно найти и исправить ошибки, допущенные в вычислениях?
Нравится ли тебе самостоятельно открывать новые способы вычислений?
Всегда ли делаешь проверку выполняемых вычислений?
Экспериментальные данные, которые отображены в таблице №1 (приложение 1), позволили получить следующие результаты: 69,5 % детей предпочитают находить значения выражений, и делают это с удовольствием, причем 8,6 % из них на сложение и вычитание. Самостоятельно обнаружить и исправить ошибки способны 34 % учащихся (8 человек). Есть основания полагать, что дети не стремятся к выполнению действия контроля по результату.
Для определения уровня сформированности действия контроля была проведена самостоятельная работа, которая состояла из нескольких заданий. Одно из них было направлено на выявление умения осуществлять контроль по результату, стремление выполнять действие контроля.
Содержание: найди значение выражения: 257*8=…. Выполни проверку. Полученные результаты были подвергнуты анализу и представлены в таблице №2 (приложение 2). Экспериментальные данные говорят о том, что 8 человек, что составляет 34,7%, умеют осуществлять контроль по результату, 6 человек испытывают стремление выполнять действие контроля, 14 человек (60, 8 %) осуществляют контроль по требованию учителя.
Второе задание ставило своей целью выявить умение обнаруживать ошибки учителя и объяснять их появление. Для этого было предложено следующее задание: проверь решение выражений. Объясни ход решения:
| | 5006 |
| 7 | |
| 35002 |
| - | 972 | 3 | |
| 9 | 3114 | ||
| - | 7 | ||
| 3 | |||
| - | 4 | ||
| 3 | |||
| - | 12 | ||
| 12 | |||
| 0 |
Наблюдения показали, что 6 человек, что составляет 26%, не смогли обнаружить ошибку учителя и объяснить ее появления.
С целью выявления умения осуществлять контроль по процессу и умения реконструировать решение, учащимся было предложено задание, направленное на выбор правильного решения и исправление неверного:
| | 4831 | | 4831 | | 4831 | - | 504 | 7 | - | 504 | 7 | - | 504 | 7 | |||||
| 9 | 9 | 9 | 42 | 626 | 49 | 72 | 42 | 612 | |||||||||||
| 39429 | 40329 | 40429 | - | 18 | - | 14 | 8 | ||||||||||||
| 14 | 14 | 7 | |||||||||||||||||
| - | 44 | 0 | 14 | ||||||||||||||||
| 42 | 14 | ||||||||||||||||||
| 2 | ост | 0 |
Как показывает анализ данных результатов, только у 14 человек (60,8%) сформировано умение осуществлять контроль по процессу. Реконструировали неверные решения 4 ученика (17,35), что свидетельствует о несформированности данного умения.
Полученные данные были подвергнуты количественному и качественному анализу, и представлена в таблице 3 (приложение 3), на основе которых мы выявили уровни сформированности действия контроля у учащихся.
Гистограмма дает возможность наглядно представить результаты таблицы.

Кол-во учащихся
Уровни сформированности действия контроля
Рис. 1 Сформированность действия контроля экспериментального класса
Проведенный нами анализ приводит к заключению, что у 8.6% учащихся (Андреев Саша, Грицюк Альберт) – отсутствует контроль, 47,8% (11 человек) – контроль на уровне непроизвольного внимания, 30.4% (7 человек) – потенциальный контроль на уровне произвольного внимания, 3человека (Жвакин Сергей, Клещев Артем, Неверова Маша) – актуальный контроль на уровне произвольного внимания.
С целью установления результативности данного эксперимента нами был выбран контрольный класс, в составе 22 человек. В ходе исследования были использованы аналогичные методы. В соответствии с полученными данными мы выявили уровни сформированности действия контроля в данном классе. Результаты диагностики сформированности действия контроля сведены в таблицу №4 (приложение 4).
Г
Количество учащихся
истограмма дает возможность наглядно представить результаты таблицы (см. рис. 2):
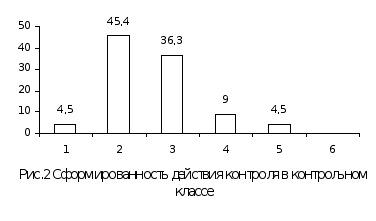
Уровни сформированности действия контроля
По данным гистограммы можно сделать вывод, что у 4,5% (Игнатов Семен) – отсутствует действие контроля, 45,4%(10 человек) – контроль на уровне непроизвольного внимания, 36,3% (8 человек) – потенциальный контроль на уровне произвольного внимания, 9% (Орданов Глеб, Трухин Дмитрий) – актуальный контроль на уровне произвольного внимания, 4,5% (Родникова Таня) – потенциальный рефлексивный контроль.
Вышеизложенные данные говорят о том, что уровни сформированности действия контроля в экспериментальном и контрольном классах существенно не отличаются. Результаты эксперимента показали, что не все ребята осознают назначение контроля, многие не испытывают желания контролировать себя. Действия товарищей. Мы отметили сложность для учеников в заданиях, направленных на реконструирование решения. В деятельности детей в основном преобладает контроль по результату. Многие учащиеся затрудняются обнаружить ошибки в процессе решения, объяснить их источник, доказать правильность своего суждения. Это говорит о том, что ученики слабо владеют или совсем не владеют умением контролировать себя в процессе решения.
Деятельность по овладению вычислительными приемами можно рассматривать как учебную деятельность, важнейшим компонентом которой является действие контроля. Под контролем правильности выполнения вычислительного приема следует понимать как проверку всей деятельности, направленной на выполнение вычислительного приема, так и проверку конечного результата. Следовательно, при развитии действия контроля на уроках математики, совершенствуется умение осознанно выполнять вычислительные приемы. И, наоборот, в случае отсутствия действия контроля, сформированность вычислительных приемов и навыков имеет низкий уровень. Отсюда возникает необходимость выявить уровень сформированности вычислительных приемов и навыков в данном классе.
В ходе исследования мы основывались на заданиях, которые были использованы при выявлении уровня сформированности действия контроля.
На данном этапе мы определяли уровень сформированности таких критериев вычислительного навыка как правильность, которая характеризуется количеством ошибок, допущенных в промежуточных операциях; осознанность – основанная на осознании каких знаний выбраны операции, умение объяснить ход своего решения; прочность – умение сохранить на длительный срок сформированные вычислительные навыки, которые являются промежуточными операциями в алгоритме.
Определить уровень сформированности таких критериев, как рациональность, обобщенность, автоматизм - не удалось, в связи с тем, что рациональность предполагает выбор более рационального приема из нескольких; обобщенность- способность перенести прием вычисления на новые случаи.
Задания, направленные на выявление данных критериев не были включены в исследование. Об автоматизме следует говорить, когда ученик выполняет операции быстро и в свернутом виде, что является не реальным на данном этапе формирования вычислительных приемов и навыков.
Исходя из анализа проведенного среза и беседы, мы представили в таблице №5 (приложение 5) результаты выявления уровней сформированности вычислительных приемов и навыков экспериментального класса.
Д
А – правильность;
В – осознанность;
С – прочность.
анные таблицы для большей наглядности мы представили в виде гистограммы (см. рис. 3):

1 2 3
А
1 2 3
В
1 2 3
С
Количество учащихся
Критерии и уровни сформированности вычислительного навыка
Проведенный нами анализ приводит к заключению, что 30,4% (7 человек) – часто не верно находят результат арифметических действий, допускают много ошибок в промежуточных операциях. 65,2% (15 человек) – осознают, на основе каких знаний выбраны операции, но не могут самостоятельно объяснить, почему решили так, а не иначе. У 26% (6 человек) – промежуточные операции, которые выполняются в алгоритме – сохранены на длительный срок.
С целью осуществления сравнительно – сопоставительного анализа и установления результатов выявленного исходного уровня сформированности вычислительных приемов и навыков, нами была составлена таблица №6 (приложение 6), отражающая результаты выявления уровня сформированности вычислительных приемов в контрольном классе.
Изобразим результаты таблицы в виде гистограммы (см рис. 4):

1 2 3
А
1 2 3
В
1 2 3
С
Количество учащихся
Критерии и уровни сформированности вычислительных навыков
А – правильность;
В – осознанность;
С – прочность.
Исходя из такой обработки данных, полученных при изучении сформированности вычислительного навыка, можно вывести общий коэффициент каждого уровня, что свидетельствует о том, что 54,5% (12 человек) – редко допускают ошибки в промежуточных операциях, 22,7 % - осознают, на основе каких знаний выбраны операции, могут объяснить свое решение, 22,7% - промежуточные операции сохранены на длительный срок.
Таким образом, можно сказать, что существенной разницы между уровнями сформированности вычислительного навыка в контрольном и экспериментальном классах нет.
Полученные данные показывают, что уровень сформированности вычислительных приемов и навыков учащихся при выполнении заданий различен в зависимости от степени овладения приемами действия контроля. Проведенное исследование свидетельствует о том, что причину затруднений учащихся в усвоении арифметических действий следует искать в правильной организации учебного процесса. Один из резервов совершенствования процесса обучения математике – направленность всей методической системы обучения на личность школьников, на их индивидуальные особенности. В связи с этим, необходимо больше внимания уделять организации действия контроля на уроке, так как это приводит к концентрации внимания всех учащихся, формирует умение рассуждать, обнаруживать ошибки в процессе вычислений, позволяет предотвратить преждевременную усталость.
Исходя из вышесказанного, мы считаем, что необходима работа, направленная на развитие умения контролировать свою деятельность в процессе выполнения вычислений, что позволяет совершенствовать не только умение выполнять вычислительные приемы, но и способствует воспитанию осознанного отношения к своей работе.
3.2 Обучающий эксперимент с целью развития действия контроля в процессе работы над вычислительными приёмами и навыками
Анализ психолого – педагогической и методической литературы по проблеме исследования путей и условий развития действия контроля в процессе работы над вычислительными приемами навыками показал, что данная проблема не достаточно исследована на практике. Кроме этого, анализ учебных программ свидетельствует о том, что в традиционной программе уделяется меньше внимания развитию действия контроля, чем в развивающих системах. Таким образом, на основании изученной литературы и выявленного уровня сформированности действия контроля у учащихся школы№ 25 г. Иркутска в классе 3 «Д», нами были выделены следующие задачи: 1) разработать программу экспериментальной работы, направленной на развитие действия контроля в процессе работы над вычислительными приемами и навыками; 2) апробировать программу экспериментальной работы на базе школы №25 г. Иркутска в классе 3 «Д». Содержание программы базируется на следующих принципах:
создание благоприятных условий, способствующих развитию действия контроля.
индивидуальный уровень сформированности действия контроля.
умение контролировать как действия других людей, так и свои собственные.
умение контролировать весь процесс осуществления действия.
Нами была составлена экспериментальная программа в виде таблицы, где представлены этапы исследования, задачи, виды работ, направленные на формирование действия контроля в процессе овладения вычислительными приемами и навыками. (таблица №7 , приложение 7 )
Рассмотрим более детально этапы экспериментальной работы:
1 этап – подготовительный. Включает следующие задачи:
формировать потребность в осуществлении действия контроля.
способствовать осознанию действия контроля.
актуализировать знания о месте действия контроля в учебной деятельности.
обогатить знания о действии контроля.
Для осуществления перечисленных задач была проведена беседа с учащимися о важности действия контроля, о том, зачем нужно контролировать свои действия. Для того, чтобы ученик пришел к необходимости делать проверку, детям предлагалось найти значение выражения и сверить конечный результат с ответом, записанным на доске (неверным).
В процессе работы перед выполнением каждого вычисления была организована установка на контроль.
Ученикам предлагались деформированные выражения, а также задания, выполнить которые было невозможно, не осуществив контроль: выражения, выписанные на доску, были составлены так, что ответ каждого выражения являлся началом какого – то другого.
2 этап – основной. Задача – учить осуществлять проверку по готовому алгоритму; развивать умение учащихся обнаруживать ошибки: в действиях своих товарищей, учителя, собственных, в результате действия, в процессе действия.
С целью приучения контролировать не только собственные действия, но и действия своих товарищей, учителя, дети выполняли вычисление, после чего им предлагалось обменяться тетрадями и проверить вычисления товарища.
В своей работе мы использовали задания, направленные на развитие умения учащихся обнаруживать ошибки, умение объяснять их, выявлять причины их возникновения, такие как: а) решение учителя с преднамеренной ошибкой, б) детям предлагалось найти ошибку и подумать, что привело к появлению ошибки, в) учащиеся задавали такой вопрос отвечающему у доски, чтобы он нашел, исправил и объяснил ошибку. Наша работа была направлена на развитие у детей умение задавать уточняющие вопросы, доказательно рассуждать.
3 этап – заключительный. Задача которого – учить детей самостоятельно разрабатывать алгоритм контрольного действия, ставить учебную задачу на основе контроля.
Мы сочли необходимым показать детям, что существует контроль не только по результату, но и контроль, который охватывает весь процесс осуществления действия (пооперационный). Взаимоконтроль по процессу повышает КПД практической работы, так как почти исключает ошибки в тетради учащихся, формирует речь учащихся, дает возможность слабым учащимся лучше разобраться в изучаемом материале
В ходе работы нам было важно учить детей осуществлять рефлексивный контроль: реконструировать способ действия товарища, учителя, приведший к ошибке.
На данном этапе мы использовали задания, направленные на разработку алгоритма контрольного действия. Работа была реализована не полностью, так как требует больше времени для ее осуществления.
Апробацию программы мы проиллюстрируем на примере некоторых уроков.
Фрагмент урока№1
Задачи по развитию действия контроля:
Формировать потребность в осуществлении действия контроля;
Развивать умение осуществлять контроль по результату;
Развивать умение контролировать действия товарища, собственные действия;
Развивать умение доказательно рассуждать;
|
Экспериментальные комментарии |
Ход урока |
|
2 этап – Повторение вид работы – устный счет Задача для учителя: проверить осознанность, прочность вычислительных приемов относительно устных приемов сложения, деления. Задача для учащихся: Ребята, сегодня мы продолжим говорить о значении действия контроля, выполним задания, направленные на умение складывать числа, оканчивающиеся на 0, повторим устные приемы деления; |
|
Умение осуществлять контроль по результатам (сопоставлять ответы) Умение осуществлять контроль по результату. Развиваем умение обнаруживать ошибки в решениях товарищей. Это помогает в развитии умения находить ошибки в собственных действиях. Развиваем умение доказательно рассуждать. |
Уч. Зад. №1. Практич. Задание: Найдите значения выражений, сопоставив результаты и буквы на цветках, и вы узнаете имя мультипликационного героя, который пришел к нам на урок. Содержание: 270:270=…; 260:130=…; 930:310=…; 420:105=…; 600:120=…; 666:111=…; 280:40=…; 560:70=…;
А Т А К П Е Ш С
5 2 8 7 4 3 6 1 Кто пришел в гости? (Степашка). Как вы это узнали? (Сопоставили результаты выражений и цифры на цветках). Молодцы! Вы очень сообразительны. Мы проверили значения выражений с помощью ответов. Уч. Зад. №2. Ребята, кто знает, какая птица может ходить по дну водоема? Чтобы ответить на этот вопрос, выполните вычисление: Содержание: 250+150+30+120+250=…; Ответы: воробей = 850; оляпка= 800; сорока=700; К нам в гости пришел Незнайка и он утверждает, что по дну водоема может ходить воробей. Вы с ним согласны? Докажите, что Незнайка не прав. Как вы сумели доказать свою правоту? (Выполнили проверку). Как вы считаете, без проверки вы смогли бы доказать свое мнение? Для чего необходима проверка? Итог: Мы не сможем доказать, что решение верно, не будем уверены в достоверности результата, если не выполним проверку, не проконтролируем свои действия. |
Фрагмент урока №2
Задачи по развитию действия контроля:
развивать умение осуществлять парный контроль.
Развивать умение задавать уточняющие вопросы
Развивать умение обнаруживать ошибки в решениях товарищей
Развивать умение осуществлять рефлексивный контроль: реконструировать способ действий, приведший к ошибке.
Развивать умение осуществлять контроль по результату.
|
Экспериментальные комментарии. |
Ход урока |
Развиваем умение осуществлять парный контроль. Развиваем умение обнаруживать ошибки. Развиваем умение осуществлять рефлексивный контроль: реконструировать решения, приведшие к ошибке. Развиваем умение доказательно рассуждать. Развиваем умение развивать контроль по результату, контролировать действие своих товарищей. |
2 этап. Повторение вид работы – устный счет Задача для учителя: проверить устные приемы умножения и деления на однозначные, круглые двузначные и трехзначные числа. Задача для учащихся: Мы повторим устные приемы умножения и деления, продолжим учиться обнаруживать ошибки в вычислениях. Это умение поможет нам не допускать ошибки и вовремя замечать их. Уч. Зад.№1 . Ребята, Чебурашка и Шапокляк прислали нам несколько выражений. Но в конверте все выражения перепутались и теперь мы не знаем, где решения Чебурашки, а где «ловушки» Шапокляк. Поэтому мы не можем быть уверены, что все решения верны, так как Шапокляк любит делать мелкие пакости. Наша задача обсудить выражения и их значения и обнаружить ошибки, если таковые имеются. Содержание: 560:70=80; 360:9=50; 490:90=90; 70 * 9=6500; 30 * 800=2700; 500 * 70=35000; Работаем в парах. Вам необходимо просмотреть все действия, обнаружить ошибки, объяснить их своему соседу и, доказательно рассуждая исправить их. Итак, сколько вычислений прислал Чебурашка? (Одно). Вы смогли обнаружить и устранить «ловушки» Шапокляк? Молодцы! Это поможет нам не допускать ошибки и быть более внимательными. Уч. Зад. №2 Практич. Задание: Найдите значения выражений: Содержание: 7080:20=…; 1020:20=…; 630:30=…; 3050:50=…; 2800:40=…; Ответы для самоконтроля: 308;354;402; 413; 423;484;554; Для того чтобы проверить себя, суммируйте ответы 1 и 2 выражений. Если сумма указана в ответах для самоконтроля, то значения верны, переходите к следующему вычислению. Саша назовет значения 1 и 2 выражений, их сумму, а вы внимательно слушайте и исправляйте по необходимости своего товарища. Итак, мы нашли верные значения, поучились контролировать себя, своих товарищей, исправлять, доказательно рассуждая. |
Фрагмент урока№3
Задачи по развитию действия контроля:
Развивать умение разрабатывать алгоритм контрольного действия.
Развивать умение осуществлять пооперационный контроль.
Развивать умение обнаруживать ошибку в ходе вычислений.
| Экспериментальные комментарии | Ход урока |
Операционный контроль Умение обнаруживать ошибки в вычислениях, объяснять их. Умение разрабатывать алгоритм контрольного действия. Умение контролировать действия своих товарищей. |
3 этап: Закрепление изученного материала. Вид работы – выполнение вычисления Задача для учителя: закреплять умение выполнять письменное деление многозначных чисел, продолжить учить обнаруживать ошибки в вычислениях; Задача для учащихся: Мы продолжим выполнять письменное деление многозначных чисел, поучимся обнаруживать ошибки, объяснять их. Практич. Задача: Злая колдунья Гогера отправила к нам своих злых слуг обезьян. Они принесли выражение, в котором, возможно, есть ошибка. Колдунья уверена, что мы ошибку не найдем и превратимся в глупых учеников. Что нам поможет найти ошибку? (Проверка). Правильно, мы должны поучиться проверять не только результат решения, но и весь процесс выполнения вычисления. Нам необходимо составить алгоритм проверки, с помощью которого мы найдем ошибку. Мы уже составляли подобные алгоритмы, так что думаю, мы справимся с этим. Что нам было важно контролировать в процессе выполнения вычислений? На что нужно обратить внимание? (1. Чтобы определить, правильно мы выделили 1 неполное делимое, нам необходимо отсчитать такое количество цифр в делимом, сколько в делителе. Если число, получившееся в делимом, меньше делителя, значит 1 неполное делимое будет больше делителя на одну цифру. Если число, получившееся в делимом, больше делителя, следовательно, оно является 1 неполным делителем. 2. Чтобы определит, верно ли мы подобрали количество цифр в частном, важно найти 1 неполное делимое и посчитать количество оставшихся разрядов. 3. Чтобы определить, правильно ли подобрана цифра в частном, нужно ее умножить на делитель. Получившееся число должно быть не больше делимого, а остаток меньше делителя. Ваня попробует порассуждать. Остальные внимательно слушают и контролируют ход мыслей своего товарища. Итак, мы справились с заданием, составили алгоритм проверки деления многозначных чисел, который помог нам найти ошибку. Руководствуясь этим алгоритмом, вы сможете выполнять деление чисел без ошибок. |
3.3 Анализ результатов обучающего эксперимента
Задачей контрольного этапа является выявление результатов формирующего эксперимента и эффективности программы экспериментальной работы. Для этого нами, во первых, была проведена диагностическая работа по определению уровня сформированности действия контроля и вычислительного навыка, достигнутого ими в ходе апробации серии уроков. Во вторых, был сделан сравнительно – сопоставительный анализ данных, полученных в ходе исследовательской работы в контрольном и экспериментальном классах на констатирующем и контрольном этапе. Для этого были использованы те же методы, что и на констатирующем этапе.
В начале данной части исследования, нами был проведен срез по выявлению достигнутого уровня сформированности действия контроля.
Для выявления умения осуществлять контроль по результату, детям предлагалось выполнить вычисление, выбрать правильные ответы из всех предложенных.
Содержание: 3172: 13=… ; 4862:11=… ;
Ответы: 244; 385; 442; 546;
Второе задание ставило своей целью выявить умение обнаруживать ошибки учителя и объяснять их появление. Для этого было предложено следующее задание:
Проверь вычисление. Объясни ход решения:
| - | 680 | 5 |
| 5 | 130 | |
| - | 18 | |
| 18 | ||
| 0 |
С целью выявления умения осуществлять контроль по процессу и рефлексивный контроль: реконструировать решение, учащимся было предложено задание, направленное на выбор правильного решения и исправление неверного:
| - | 3650 | 50 | - | 3650 | 50 | |
| 300 | 613 | 350 | 73 | |||
| - | 65 | - | 150 | |||
| 50 | 150 | |||||
| - | 150 | 0 | ||||
| 150 | ||||||
| 0 |
Результаты проведенного среза представлены в таблице №8 (приложение 8) . Если критерий, представленный в таблице присутствовал в ответе ученика, то ставился «+», если не проявлялся, то «-».
По данным таблицы можно сделать следующие выводы: осуществить контроль по результату, выбрать правильные ответы из всех предложенных смогли все учащиеся. Подобные задания выполнялись детьми на формирующем этапе эксперимента и вызывали у них большой интерес.
Обнаружить ошибки учителя смогли 95,6% учеников. Ольховский Эрик не справился с заданием в связи с отсутствием на многих занятиях обучающего эксперимента. В ходе индивидуальной беседы, которая была проведена с каждым учеником, Грицюк. А., Топорков. Ю., Торгашин. В. не смогли объяснить причину появления ошибки.
Следующее задание, целью которого было умение осуществлять пооперационный и рефлексивный контроль, оказалось сложным для учащихся. Реконструировали решение только 69,5% (16 человек). Андреев. С; Леонов. И; Ольховский. Э ; Торгашин. В. не осуществили контроль по процессу.
Большинство детей ограничилось нахождением ошибки в процессе вычисления, не выполнив рефлексивный контроль. Для выявления отношения детей к математике, вычислительным приемам, нами была проведена беседа, экспериментальные данные которой позволили получить следующие результаты: 73,9% выполняют вычисления с удовольствием. Самостоятельно обнаружить ошибку способны 60,8% учащихся. Надо отметить, что дети стремятся к выполнению действия контроля.
Анализ данных проведенного среза и беседы позволили нам выявить и представить в таблице №9 (приложение 9), уровень сформированности действия контроля экспериментального класса.
С целью наглядного изображения эффективности проведенного формирующего эксперимента, мы представили результаты в виде гистограммы (см рис. 5):

Количество учащихся
Уровни сформированности действия контроля
до эксперимента;
после эксперимента


У
Количество учащихся
до эксперимента;
после эксперимента.

Уровни сформированности действия контроля


Таким образом, после проведенного формирующего эксперимента общий уровень сформированности действия контроля в экспериментальном классе повысился, а в контрольном классе существенно не изменился.
Анализ данных проведенного среза и индивидуальная беседа позволили нам выявить уровни сформированности вычислительных навыков в экспериментальном классе.
Таблица 3
Сформированность вычислительных навыков в экспериментальном классе
|
Уровни Критерии |
1, человек |
2, человек |
3, человек |
| Правильность | 0 | 12 | 11 |
| Осознанность | 2 | 15 | 6 |
| Прочность | 1 | 12 | 10 |
Изобразим результаты (см. рис 7):

Количество учащихся
Критерии и уровни сформированности вычислительного навыка
А – правильность;
В – осознанность;
С – прочность.
до эксперимента;
после эксперимента.
1 2 3
А
1 2 3
В
1 2 3
С


Уровни сформированности вычислительных навыков в контрольном классе сведены в таблицу№4
Таблица 4
Сформированность вычислительных навыков в контрольном классе
|
Уровни Критерии |
1, человек |
2, человек |
3, человек |
| Правильность | 5 | 13 | 4 |
| Осознанность | 4 | 14 | 4 |
| Прочность | 3 | 15 | 4 |
Р
А – правильность;
В – осознанность;
С – прочность.
до эксперимента;
после эксперимента.

1 2 3
А
1 2 3
В
1 2 3
С
Количество учащихся
Критерии и уровни сформированности вычислительного навыка


Исходя из такой обработки данных, полученных после формирующего эксперимента, можно отметить, что общий уровень сформированности вычислительного навыка у учащихся контрольного класса практически не изменился, а у учащихся экспериментального класса повысился. Полученные результаты дают основание утверждать об эффективности обучающего эксперимента. В целом можно сказать, что в процессе проведения обучающего эксперимента, у детей наблюдалось более внимательное отношение к действию контроля при выполнении вычислений, повысился интерес к математике, усовершенствовалось умение не только выполнять вычислительные приемы, но и осознанно относиться к своей работе, контролировать действия учителя, товарищей, умение рассуждать, что оказало положительное влияние на процесс работы над вычислительными приемами и навыками.
3.4. Выводы по главе.
Проведенный эксперимент позволяет сделать следующие выводы.
Формирование действия контроля предполагает развитие не только умение соотносить объект контроля с образцом, но и умение самостоятельно выбирать или конструировать такие образцы- критерии успешности выполнения тех или иных действий, критерии достижения той или иной цели. Приемам действия контроля необходимо специально учить.
Развитие умения предвидеть результаты своих действий, отдавая отчет в правильности их выполнения, сопоставляя выполняемые действия с определенным образцом, позволяет не только исправлять ошибки, но и предотвращать возможность их появления.
У учащихся следует формировать умение проверять не только конечный результат выполненной работы, но и весь процесс ее выполнения. Формирование полноценного действия контроля возможно только на основе пооперационного контроля, так как он предполагает выяснение тех операций, способов, действий, с помощью которых получен результат.
В связи с тем, что выполнение вычислительных приемов представляет собой мыслительный процесс и является сложным умственным действием, имеющим свое операционное содержание, то овладение вычислительным приемом и умение осуществлять контроль за его выполнением должно осуществляться одновременно в процессе обучения при правильной организации деятельности учащихся.
Такой подход к формированию действия контроля в процессе работы над вычислительными приемами и навыками позволит учащимся избежать трудности в вычислениях, так как ими будут усвоены все специфические особенности вычислительных приемов.
Заключение
Экспериментальная работа дает возможность сформулировать теоретические выводы и практические рекомендации по формированию действия контроля в процессе работы над вычислительными приемами и навыками у младших школьников.
Действие контроля является необходимым компонентом учебной деятельности.
Сущность действия контроля заключена в обязательном сопоставлении, соотнесении действий с «образцом», - эталоном действия.
Следовательно, целесообразно обучать детей не только пользоваться готовым эталоном для осуществления действия контроля, но и самостоятельно разрабатывать эталон контрольного действия.
Процесс выполнения вычислительного приема и осознанное его контролирование должны быть двумя сторонами единого процесса овладения вычислительным приемом, так как при развитии действия контроля на уроках математики, совершенствуется умение осознанно выполнять вычислительные приемы.
Необходимо обучать учащихся не только общему способу контроля процесса овладения вычислительным приемом, но и умению переносить этот способ на конкретные виды вычислительных приемов.
В предположении нами были выделены условия формирования действия контроля в процессе работы над вычислительными приемами и навыками. Для создания условий мы разработали программу экспериментальной работы, направленную на развитие действия контроля у младших школьников.
Основываясь на программу, мы выделили этапы экспериментальной работы.
Первый этап направлен на стимулирование потребности в осуществлении действия контроля.
Второй этап связан с умением осуществлять проверку по готовому плану, обнаруживать ошибки (в действиях учителя, товарищей, собственных; в результате действия, в ходе действия, в способе действия).
Результаты исследования показали, что с возрастанием уровня сформированности действия контроля усиливается познавательный интерес к уроку математики, совершенствуются вычислительные навыки.
Предположение, выдвинутое в начале исследования, в основном подтвердилось: формирование действия контроля, при соблюдении следующих условий:
выделение структурных особенностей действия контроля для отдельных вычислительных приемов;
использование в процессе обучения системы заданий, направленной на усвоение алгоритмов контрольных действий учащимися;
постановка перед учащимися задачи на контроль,
привело к качественному изменению показателей сформированности действия контроля у младших школьников.
Следовательно, мы можем утверждать, что выделенные нами условия формирования действия контроля в процессе работы над вычислительными приемами и навыками оказались эффективными.
Таким образом, развитие действия контроля в процессе работы над вычислительными приемами и навыками при соблюдении данных условий говорит о том, что разработанная программа экспериментального обучения является эффективным средством формирования структурных компонентов учебной деятельности младших школьников.
Литература
Абрамова Г. С. Возрастная психология. Учебное пособие для студент. вузов.- М.: Академия, 1997 – 638 с.
Аргинская И. И. Математика 3 класс. – Самара, « Корпорация» Федоров», 1997 – 88 с.
Бабанский Ю. К. Оптимизация процесса обучения. Общедидактический аспект. – М.: Педагогика, 1977 – 254 с.
Берцфаи Л. В.. Специфика учебного действия контроля //Вопросы психологии – 1987, - №4 – с. 55 - 60
Берцфаи Л. В., Поливанова К.Н. Диагностика действия контроля // Диагностика учебной деятельности и интеллектуального развития детей. – М., 1981 – с. 29 - 40
Берцфаи Л. В., Романко В. Г. Исследование особенностей рефлексивного контроля. Сообщение 1 // Новые исследования в психологии – 1981, - №2 – с. 68 – 72
Бадма – Гаряева М. В. Развитие вычислительных навыков у учащихся 1 класса // Начальная школа – 1999 - №11 – с.21 – 23
Бантова М. А. Система формирования вычислительных навыков // Начальная школа – 1993 - №11 – с. 38 - 43
Батий Ю. Ю. Самоконтроль учащихся при выполнении заданий // Начальная школа – 1979 - №4 – с.41 – 43
Бахир В. К. Развивающее обучение // Начальная школа – 1997 - №5 – с. 26 – 31
Воронцов А. Б. Некоторые подходы к вопросу контроля и оценки учебной деятельности учащихся // Начальная школа – 1999 - №7 – с.61 – 71
Давыдов В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования. – М.: Педагогика, 1986 – 239 с.
Давыдов В. В. Содержание и строение учебной деятельности школьников. – М., 1978 – 321 с.
Давыдов В.В. Теория развивающего обучения. – М.: ИНТОР, 1996 – 544 с.
Давыдов В. В. Что такое учебная деятельность // Начальная школа – 1999 - №7 – с. 12 – 18
Елагина Л.Н. Самоконтроль и самооценка в процессе обучения математике // Начальная школа – 1082 - №8 – с. 65 – 67
Емельяненко М. В. Система развивающих заданий по теме « Умножение многозначного числа на однозначное» // Начальная школа – 1996 - №12 – с. 47 – 50
Захарова А.В. Развитие контроля и оценки в процессе формирования учебной деятельности//Формирование учебной деятельности школьников. – М., 1982 – 234 с.
Зимняя И. А. Педагогическая психология. – Ростов на Дону: Феникс, 1997 – 476 с.
Камышева И.Н. Пособие для самоконтроля на уроках математики // Начальная школа – 1988 - №10 – с.36 - 37
Леонтьев Л. Н. Деятельность. Сознание. Личность – 2 – е изд. – М., 1977 – 364 с.
Максимова Т.П. Влияние формы кооперации младших школьников на развитие контрольно - оценочных действий.// Развитие мотивационно – познавательной сферы младшего школьника в условиях учебной деятельности. – Волгоград, 1985 – 276 с.
Мальцева К.П. Самоконтроль в учебной работе младшего школьника. – М., 1962 – 389 с.
Мор Г.Я. Формирование навыков самоконтроля и взаимоконтроля у учащихся //Начальная школа – 1993 - №11 – с.38 – 43
Никифоров Г.С. Самоконтроль человека. – М., - с. 90 – 94
Особенности психического развития детей 6 – 7 летнего возраста /Под ред. Д.Б.Эльконина, А.Л.Венгера – М.: Педагогика, 1988 – 137 с.
Петровский В.А., Черепанова Е.М. Индивидуальные особенности самоконтроля при организации внимания//Вопросы психологии. – 1987 - №5 – с.48 – 51
Познавательные процессы и способности в обучении / Под ред. В.Д. Шадрикова. – М.: Просвещение, 1996 – 168 с.
Поливанова К.Н. Психологические формирования действия контроля в учебной деятельности. // Новые исследования в психологии. – 1983, - №1 – с. 65 – 68
Психологическое развитие младших школьников/ Под ред. В.В. Давыдова. – М.: Педагогика, 1990 – с.22—103
Реализация межпредметных и внутрипредметных связей в обучении и воспитании младших школьников: Межвузовский сборник научных трудов. – Л., 1984 – 132 с.
Репкин В.В. Формирование учебной деятельности в младшем школьном возрасте//Начальная школа – 1999 - №7 – с.19 – 24
Репкина Г.В., Заика Е.В. Оценка уровня сформированности учебной деятельности. Томск: Пеленг, 1993 – 62 с.
Романко В.Г. Особенности рефлексивного контроля как учебного действия//Новые исследования в психологии – 1985, - №1 – с.65 – 71
Самоконтроль младших школьников в процессе решения арифметических задач: Методические рекомендации / Сост. Г.М. Соснина. – Иркутск, 1983 – 34с.
Талызина Н.Ф. Педагогическая психология – М.: Академия, 1998 – 497 с.
Талызина Н.Ф. Формирование познавательной деятельности младших школьников. – М.: Просвещение, 1988 – 374 с.
Фридман Л.М., Кулагина М.Ю. Психологический справочник учителя. – М.: Просвещение, 1991 – 287 с.
Эльконин Д.Б. Избранные психологические труды. – М., 1995, - 342 с.
Эльконин Д.Б. К проблеме периодизации психического развития в детском возрасте // Вопросы психологии – 1971, - №4 – с. 57 – 61.
Приложение 1
|
Вопросы Фамилия ученика |
1. Какие задания тебе нравится выполнять по математике | 2. Любишь ли ты выполнять вычисления | 3. Какие ошибки чаще всего допускаешь в вычислениях | 4. Можешь ли самостоятельно найти и исправить ошибки в допущенных вычислениях | 5. Нравится ли открывать новые способы вычисления | 6. Всегда ли делаешь проверку вычисления |
| Бычковский | Вычисления | Да | Никаких | Да | Нет | Нет |
| Ильин | Вычисления | Да | В значении | Иногда | Да | Иногда |
| Исаков | Умножение | Да | Переход через десяток | Да | Да | Нет |
| Грицюк | Сложение | Нет | Обычные | Нет | Иногда | Да |
| Андреев | Задачи | Да | Умножение | Нет | Да | Нет |
| Гичева | Задачи | Да | Значение | Иногда | Нет | Да |
| Козинец | Уравнения | Да | Никаких | Да | Иногда | Да |
| Неверова | Выражения на умножение | Да | Никаких | Иногда | Да | Иногда |
| Оборин | Вычисление | Да | Не знаю | Да | Не знаю | Нет |
| Леонов | Задачи | Да | Не знаю | Нет | Нет | Нет |
| Наумов | Вычисление | Да | Деление | Иногда | Да | Нет |
| Манькова | Вычисление | Да | Никаких | Нет | Иногда | Нет |
| Клещев | Примеры на сложение | Да | Никаких | Да | Да | Да |
| Жвакин | Примеры на вычитание | Да | В табличных случаях | Иногда | Да | Нет |
| Шолхонов | Сложные задачи | Да | Деление | Да | Иногда | Не всегда |
| Топорков | Примеры на сложение | Нет | Никаких | Нет | Нет | Иногда |
| Фролов | уравнения | Да | Не знаю | Иногда | Да | Да |
| Солонин | Задачи | Да | Значение | Иногда | Не всегда | Иногда |
| Подкова | Вычисление | Да | Переход через десяток | Нет | Да | Да |
| Шестопалова | Задачи | Да | Деление | Иногда | Иногда | Да |
| Ольховский | Никакие | Нет | В табличных случаях | Нет | Нет | Нет |
| Подварков | Лёгкие задания | Да | Деление | Иногда | Да | Нет |
| Торгашин | Выражения на умножение | Да | Переход через десяток | Да | Иногда | Да |
Приложение 2
Таблица 2
Выделение исходного уровня сформированности действия контроля в экспериментальном классе
|
Критерии сформированности действия контроля Фамилия ученика |
Осуществление контроля по результату | Умение обнаруживать ошибку учителя | Умение осуществлять пооперационный контроль | Умение реконструировать способ действия |
| Андреев | - | - | - | - |
| Бычковский | + | + | + | - |
| Гичева | + | - | + | + |
| Грицюк | - | - | - | - |
| Жвакин | + | + | + | + |
| Ильин | - | + | + | - |
| Исаков | + | + | + | - |
| Клещев | + | + | + | - |
| Козинец | + | + | + | + |
| Леонов | + | + | + | - |
| Манькова | + | - | - | - |
| Наумов | + | + | - | - |
| Неверова | + | + | + | + |
| Оборин | - | + | - | - |
| Ольховский | - | + | - | - |
| Подварков | - | - | + | - |
| Подкова | + | + | + | - |
| Солонин | + | + | - | - |
| Топорков | - | + | - | - |
| Торгашин | + | - | + | - |
| Фролов | - | + | + | - |
| Шестопалова | + | + | + | - |
| Шолхонов | + | + | + | - |
Приложение 3
Таблица 3
Уровни сформированности действия контроля в экспериментальном классе
| Фамилия Имя ученика | Уровень сформированности действия контроля |
| Андреев Саша | 1 |
| Бычковский Витя | 3 |
| Гичева Катя | 2 |
| Грицюк Альберт | 1 |
| Жвакин Сергей | 4 |
| Ильин Толя | 2 |
| Исаков Валентин | 3 |
| Клещев Артём | 4 |
| Козинец Даша | 3 |
| Леонов Иван | 3 |
| Манькова Катя | 2 |
| Наумов Артём | 2 |
| Неверова Маша | 4 |
| Оборин Сергей | 2 |
| Ольховский Эрик | 2 |
| Подварков Паша | 2 |
| Подкова Юля | 3 |
| Солонин Егор | 2 |
| Топорков Юра | 2 |
| Торгашин Влад | 2 |
| Фролов Женя | 2 |
| Шестопалова Кристина | 3 |
| Шолхонов Дима | 3 |
Приложение 4
Таблица 4
Уровни сформированности действия контроля в контрольном классе
| Фамилия ученика | Уровень сформированности действия контроля |
| Антонов | 3 |
| Амосов | 2 |
| Барабанов | 3 |
| Быков | 3 |
| Барковская | 2 |
| Вершилло | 3 |
| Дроздова | 2 |
| Дробышева | 2 |
| Игнатьев | 3 |
| Купряков | 1 |
| Краснов | 3 |
| Лопатина | 3 |
| Москвитин | 2 |
| Муравьёва | 3 |
| Малинский | 2 |
| Орданов | 4 |
| Румынин | 2 |
| Родникова | 5 |
| Светлакова | 2 |
| Соболев | 2 |
| Трухин | 4 |
| Яблонов | 2 |
Пржене 5
Таблица 5
Уровни сформированности вычислительного навыка в экспериментальном классе
| Фамилия Имя ученика | Уровень сформированности вычислительного навыка: | ||
| Правильность | Осознанность | Прочность | |
| Андреев Саша | 1 | 1 | 1 |
| Бычковский Витя | 2 | 2 | 3 |
| Гичева Катя | 2 | 2 | 2 |
| Грицюк Альберт | 1 | 1 | 1 |
| Жвакин Сергей | 3 | 2 | 2 |
| Ильин Толя | 2 | 2 | 1 |
| Исаков Валентин | 2 | 2 | 3 |
| Клещев Артём | 2 | 2 | 2 |
| Козинец Даша | 2 | 2 | 3 |
| Леонов Иван | 2 | 1 | 2 |
| Манькова Катя | 1 | 1 | 2 |
| Наумов Артём | 1 | 1 | 2 |
| Неверова Маша | 3 | 2 | 3 |
| Оборин Сергей | 1 | 1 | 2 |
| Ольховский Эрик | 2 | 1 | 1 |
| Подварков Паша | 1 | 2 | 2 |
| Подкова Юля | 2 | 3 | 3 |
| Солонин Егор | 2 | 2 | 2 |
| Топорков Юра | 1 | 1 | 1 |
| Торгашин Влад | 2 | 2 | 1 |
| Фролов Женя | 2 | 3 | 2 |
| Шестопалова Кристина | 2 | 2 | 3 |
| Шолхонов Дима | 2 | 2 | 2 |
Приложение 6
Таблица 6
Уровни сформированности вычислительного навыка в контрольном классе
| Фамилия Имя ученика | Уровень сформированности вычислительного навыка: | ||
| Правильность | Осознанность | Прочность | |
| Антонов | 2 | 2 | 2 |
| Амосов | 1 | 1 | 2 |
| Барабанов | 2 | 1 | 2 |
| Быков | 2 | 2 | 3 |
| Барковская | 1 | 2 | 1 |
| Вершилло | 2 | 2 | 3 |
| Дроздова | 1 | 2 | 2 |
| Дробышева | 2 | 2 | 2 |
| Игнатьев | 2 | 2 | 2 |
| Купряков | 1 | 1 | 1 |
| Краснов | 2 | 2 | 2 |
| Лопатина | 2 | 2 | 2 |
| Москвитин | 1 | 1 | 2 |
| Муравьёва | 3 | 2 | 2 |
| Малинский | 2 | 2 | 1 |
| Орданов | 3 | 3 | 3 |
| Румынин | 1 | 1 | 2 |
| Родникова | 3 | 3 | 3 |
| Светлакова | 2 | 2 | 2 |
| Соболев | 2 | 2 | 1 |
| Трухин | 3 | 3 | 3 |
| Яблонов | 2 | 2 | 2 |
Приложение 8
Таблица 8
|
Критерии сформированности действия контроля Фамилия имя ученика |
Умение осуществлять контроль по результату | Умение обнаруживать ошибку учителя | Умение объяснять ошибку | Умение осуществлять контроль по процессу | Умение осуществлять рефлексивный контроль: реконструировать способ действия |
| Андреев Саша | + | + | + | - | - |
| Бычковский Витя | + | + | + | + | + |
| Гичева Катя | + | + | + | + | - |
| Грицюк Альберт | + | + | - | + | + |
| Жвакин Сергей | + | + | + | + | + |
| Ильин Толя | + | + | + | + | + |
| Исаков Валентин | + | + | + | + | - |
| Клещев Артём | + | + | + | + | + |
| Козинец Даша | + | + | + | + | + |
| Леонов Иван | + | + | + | - | - |
| Манькова Катя | + | + | + | + | + |
| Наумов Артём | + | + | + | + | - |
| Неверова Маша | + | + | + | + | + |
| Оборин Сергей | + | + | + | + | + |
| Ольховский Эрик | + | - | - | - | - |
| Подварков Паша | + | + | + | + | + |
| Подкова Юля | + | + | + | + | + |
| Солонин Егор | + | + | + | + | + |
| Топорков Юра | + | + | - | + | + |
| Торгашин Влад | + | + | - | - | - |
| Фролов Женя | + | + | + | + | + |
| Шестопалова Кристина | + | + | + | + | + |
| Шолхонов Дима | + | + | + | + | + |
Приложение 9
Таблица 9
Сформированность действия контроля у учащихся экспериментального класса
| Фамилия Имя ученика | Уровень сформированности действия контроля |
| Андреев Саша | 2 |
| Бычковский Витя | 4 |
| Гичева Катя | 3 |
| Грицюк Альберт | 2 |
| Жвакин Сергей | 4 |
| Ильин Толя | 3 |
| Исаков Валентин | 4 |
| Клещев Артём | 4 |
| Козинец Даша | 4 |
| Леонов Иван | 3 |
| Манькова Катя | 3 |
| Наумов Артём | 3 |
| Неверова Маша | 5 |
| Оборин Сергей | 3 |
| Ольховский Эрик | 2 |
| Подварков Паша | 3 |
| Подкова Юля | 4 |
| Солонин Егор | 3 |
| Топорков Юра | 3 |
| Торгашин Влад | 2 |
| Фролов Женя | 4 |
| Шестопалова Кристина | 5 |
| Шолхонов Дима | 5 |
Приложение 7
Таблица 7
Программа экспериментальной работы
Предмет усвоения |
Этап усвоения |
Задачи, по формированию действия контроля |
Виды работ направленные на формирование действия контроля |
|
применение применение восприятие применение применение |
Первый этап:
|
|
|
осмысление применение применение применение |
Второй этап:
а. В действиях товарищей б. В действиях учителя в. в собственных действиях г. в результате действия;
учить определять причину появления ошибки. |
|
|
образцом решения)
|
||
|
закрепление применение закрепление закрепление |
Третий этап:
|
б. поэлементный анализ ответа ученика. Вызванный к доске ученик отвечает с использованием алгоритма контроля. Остальные слушают, отмечая плюсы и минусы ответа ученика. Затем поднимают сигнальные карточки, кто не согласен по первому пункту алгоритма, по второму и т.д. в. поочерёдное рассуждение. Классу даётся выражение в несколько действий, в котором необходимо расставить их последовательность в соответствии с правилами. Учащиеся работают парами, попеременно объясняя друг другу ход решения выражения г. выражения выписанные на доску составлены так, что ответ каждого является началом какого-то другого
детям предлагается выражение, решённое разными способами (среди которых верные и неверные), необходимо их реконструировать
|
Содержание
| Стр. | ||
| Введение | 3 | |
| 1. | Особенности контроля в учебной деятельности младших школьников | 6 |
| 1.1 | Сущность действия контроля, его особенности в младшем школьном возрасте и место в структуре учебной деятельности | 6 |
| 1.2 | Критерии и уровни сформированности действия контроля | 11 |
| 1.3 | Выводы по главе | 16 |
| 2. | Возможности формирования действия контроля в процессе работы над вычислительными навыками | 17 |
| 2.1 | Общая характеристика формирования вычислительных приёмов и навыков у младших школьников | 17 |
| 2.2 | Особенности формирования действия контроля в работе над вычислительными приёмами и навыками | 29 |
| 2.3 | Выводы по главе | 32 |
| 3. | Экспериментальная работа по формированию действия контроля в процессе работы над вычислительными приёмами и навыками | 33 |
| 3.1 | Диагностика исходного уровня сформированности действия контроля на уроках математики | 33 |
| 3.2 | Обучающий эксперимент с целью развития действия контроля в процессе работы над вычислительными приёмами и навыками | 40 |
| 3.3 | Анализ результатов обучающего эксперимента | 44 |
| 3.4 | Выводы по главе | 49 |
| Заключение | 51 | |
| Литература | 53 | |
| Приложения |
Министерство образования Российской Федерации
Иркутский государственный педагогический университет
Кафедра методики начального образования
Факультет ПиМНО
Специальность «педагогика и методика начального образования»
Курс 5
Дипломная работа
Топорковой Надежды Геннадиевны
Формирование действия контроля в процессе работы над вычислительными приёмами и навыками у младших школьников
Научный руководитель:
Петрова М.А.
к.п.н; доцент.
Консультант: Кабаева Н.Н.
Ст. преподаватель.
Работа допущена
к защите______________________________
Зав. кафедрой__________________________
Дата представления_____________________
Дата возврата__________________________
Дата защиты___________________________
Оценка________________________________
ИРКУТСК 2001
| Педагогические условия формирования умений учебной деятельности ... | |
|
Дипломная работа Педагогические условия формирования умений учебной деятельности младших школьников Оглавление ВВЕДЕНИЕ 1. Сущность умений учебной ... Аналогичную картину наблюдает учитель в отношении сформированности у школьников навыков устного счета. На втором уровне развития умений характерным является такое управление познавательными действиями учеников, когда наряду с инструктажем и показом готовых образцов деятельности ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Математическое мышление младших школьников | |
|
Содержание Введение Глава 1. Теоретические основы развития математического мышления младших школьников с помощью нестандартных задач 1.1 Особенности ... ... воспитательного процесса с целью формирования всесторонне развитой и творчески мыслящей личности младшего школьника во многом зависит от умения ими решать нестандартные задачи. Эффективность и качество обучения математике определяются не только глубиной и прочностью овладения школьниками системой математических знаний, умений и навыков, предусмотренных ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Контроль и самоконтроль знаний и умений младшего школьника | |
|
Министерство образования Российской Федерации Кафедра методики основ естествознания Дипломная работа Контроль и самоконтроль знаний и умений младшего ... Важную роль в воспитании самоконтроля играет контроль со стороны учителя за деятельностью школьников, который обычно направляется на установление полноты выполнения учащимися ... Ученики, получившие одинаковые отметки, могут иметь несравнимые уровни овладения учебным материалом: один недостаточно овладел умением решать задачи, второй - вычислительными ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Психолого-педагогические условия профессионального самоопределения ... | |
|
Психолого-педагогические условия профессионального самоопределения учащихся в процессе обучения биологии СОДЕРЖАНИЕ профессиональное самоопределение ... В целях формирования устойчивой положительной мотивации школьников содержание курсов предпрофильной подготовки может включать сведения из психологии, химии, географии, истории ... Посмотрите на ключ (учитель зарисовывает ключ на доске, ученики сравнивают его со своими ответами) Если вы выполнили верно все задание, то можете поставить себе 10 баллов, если вы ... |
Раздел: Рефераты по психологии Тип: дипломная работа |
| Использование дидактических игр для развития познавательной ... | |
|
ГОУ СПО "Кунгурское педагогическое училище" Использование дидактических игр для развития познавательной деятельности 6-классников на уроках математики ... Дидактические игры и занимательные упражнения, а также использование на уроках раздаточного материала,- необходимое условие успешного обучения математике школьников, так как ... Главное, на что обратить внимание,- необходимость получать информацию о состоянии деятельности учащегося, составляющей умение решать задачи того или иного класса.[12,45-49 ... |
Раздел: Рефераты по математике Тип: дипломная работа |
