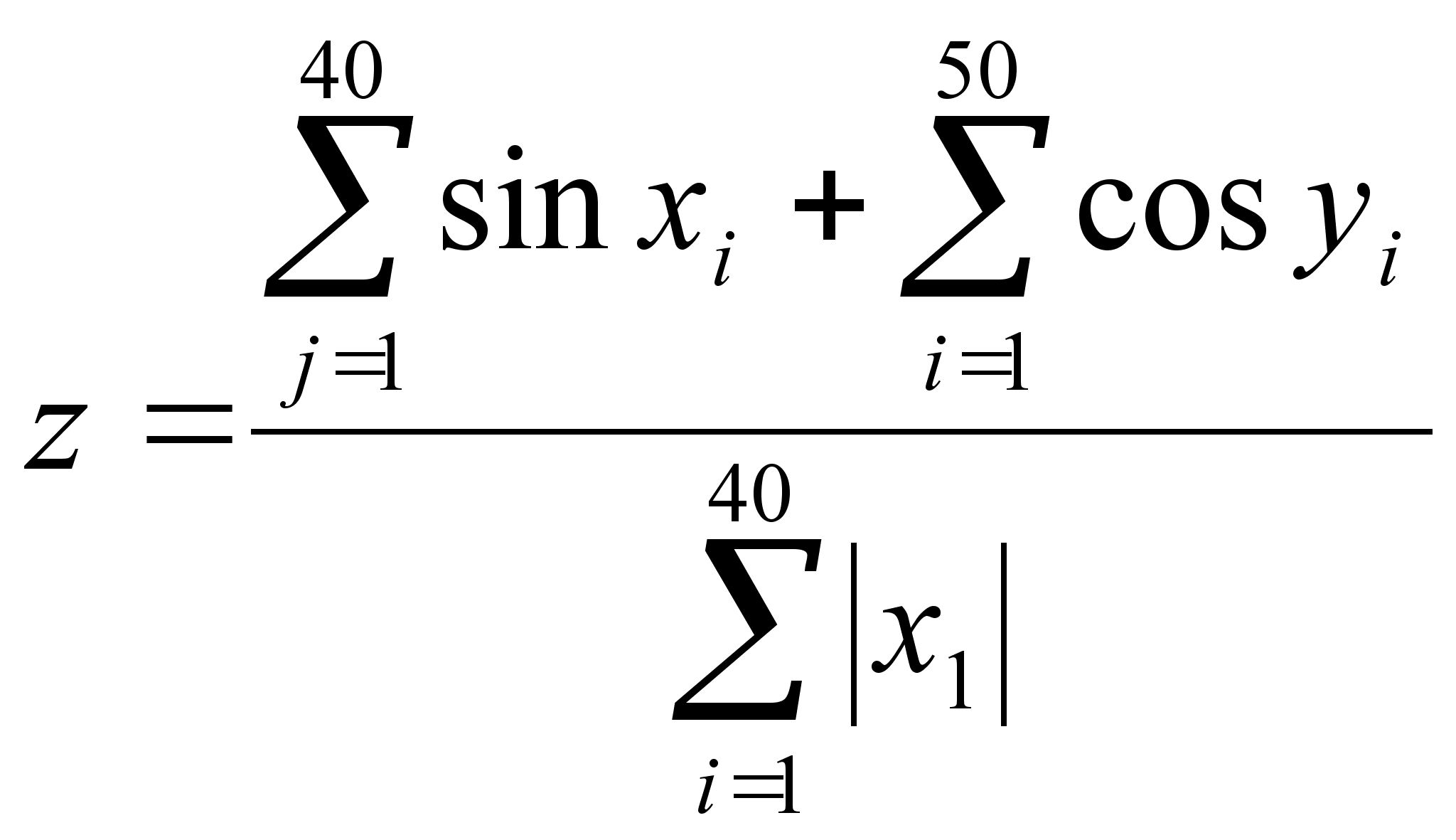Реферат: Лабораторная работа по информатике, вариант №13, с методическим пособием.zip
Целью работы является написание программ на ЭВМ, согласно условию в выбранном варианте, первая программа для задания А, и вторая программа для задания Б. Для написания программ использовался Borland Turbo Pascal версии 7.1. Рассмотрим по очереди эти два задания.
ЗАДАНИЕ А. Необходимо подсчитать количество нулевых элементов для матриц А(N,M) и В(M,N), причём M и N не могут быть больше 20.
Матрицы А и В представляют в машинном исполнении двухмерные массивы, число элементов в которых не может быть больше 20х20=400 элементов по условию. Каждый индекс числа – M и N представляет собой «координату» числа в матрице, по его строке и столбцу, соответственно. Автор программы ввёл в неё выбор количества строк и столбцов для каждой матрицы (массива), дав пользователю возможность выбрать его в пределах от двух до двадцати (по условию). Программа занесения данных в сами массивы построена на цикле оператора FOR, причём если пользователю будет лень вносить данные самостоятельно – программа может сделать это за него посредством генерации случайных чисел и занесения их в массивы, что на современных компьютерах занимает считанные наносекунды. На программу самогенерации-самоввода элементов матриц автор программы ввёл некоторые ограничения во избежании не занесения в них нулевых элементов, что необходимо для проверки правильности работы программы. Если вручную вы можете ввести любое действительное число от -32768 до 32767, то программа самогенерации генерирует целые числа от нуля до двадцати. И, если вы, к примеру, задали в программе размер матриц 2X3, что составляет всего шесть элементов, то вполне вероятно (как показала практика тестирования программы), что в ней будет хотя бы один нулевой элемент, или, попросту – ноль. Подпрограмма подсчёта количества нулевых элементов тоже построена на цикле оператора FOR, и если бы она не была необходима по условию, без неё можно было бы обойтись, включив подсчёт таких элементов в цикл ввода данных / цикл генерации данных, тем самым повысив быстродействие программы. Эта подпрограмма (так же, как и подпрограмма в задании Б) оформлена в виде процедуры.
ЗАДАНИЕ Б. Найти средние значения и стандартные отклонения для элементов массивов X(N), Y(M), причём количество элементов не может быть более 100.
В этом примере реализована та же подпрограмма ввода / генерации данных, что и в задании А, с разницей в массивах – здесь мы имеем одномерные массивы. На программу генерации элементов массивов наложены те же самые ограничения, что и в задании А, с той разницей, что число генерируется в интервале от нуля до ста, а не до двадцати. В подпрограмму вычисления условий задачи внесён тот же цикл оператора FOR, несущий в этом задании вспомогательную функцию вычисления среднего числа массивов в частности. Подпрограмма оформлена в виде отдельной процедуры, как и в задании А, однако без этой процедуры обойтись, как в первом задании, нельзя, так как разбросав её на алгоритмы ввода и генерации данных мы усложняем, запутываем алгоритм программы, снижая тем самым её производительность (быстродействие).
Лабораторная работа №6
Программирование с использованием подпрограмм пользователя.
Задание для самостоятельной работы.
Изучить:
правила записи подпрограмм различных видов и способов обращений к ним;
способы передачи параметров в подпрограмму;
правила записи программ, использующих подпрограммы.
Разработать алгоритм решения задачи.
Составить программу решения задачи.
Подготовить тестовый вариант программы и исходных данных.
Задание к работе
Задание А.
Выполнить на ЭВМ программу, использующую подпрограмму функцию, в соответствии с номером параметра, указанным в таблице.
Проверить правильность выполнения программы с помощью тестового варианта.
|
Вариант Задания |
Условия задачи | Примечания |
| 1 |
Вычислить большие корни кв. уравнений x2-ax+b=0 cy2-dy-f=0 |
Все корни действительные |
| 2 | Подсчитать число точек, находящихся внутри круга радиусом r с центром в начале координат; координаты заданы массивами X(100), Y(100) | Расстояние точки от начала координат вычислять в подпрограмме |
| 3 |
|
Длину стороны энугольников вычислять в подпрограмме |
| 4 | Подсчитать число точек, находящихся внутри круга радиусом r с центром в точке с координатами (1,1); координаты заданы массивами X(80), Y(80) | Расстояние точки от центра круга определять в подпрограмме |
| 5 |
Вычислить z=(v1+v2+v3)/3 , где v1 ,v2,v3, - объёмы шаров с радиусами r1 , r2 и r3 соответственно |
Vi вычислять в подпрограмме |
| 6 | Вычислить суммы положительных элементов массивов X(N), Y(M), Z(K) |
N<=60 M<=60 K<=70 |
| 7 | Вычислить среднее арифметическое положительных элементов для массивов A(N1), B(N2), C(N3) |
N1<=100 N2<=100 N3<=100 |
| 8 |
Подсчитать количество элементов матриц X(10,15) и Y(20,12), удовлетворяющих условиям 0<=xij<=1 и 0<=yij<=1 |
|
| 9 | Вычислить суммы положительных элементов каждой строки для матриц A(10,12) и B(15,10) | |
| 10 |
Вычислить z=(xm1+xm2)/2 , где xm1 и xm2 – наименьшие элементы массивов X1(70), X2(80) |
|
| 11 | Вычислить суммы элементов главных диагоналей матриц A(N,N) B(M,M) |
M<=20 N<=30 |
| 12 |
Вычислить z=(s1+s2)/2, где s1- сумма положительных элементов массива X(50); s2- сумма отрицательных элементов массива Y(60) |
Обе суммы вычислять в одной подпрограмме |
|
13 |
Подсчитать число нулевых элементов для матриц A(N,M) и B(M,N) |
M<=20 N<=20 |
| 14 | Вычислить суммы элементов нижних треугольных матриц для матриц A(15,15) и B(20,20) | |
| 15 | Определить число положительных элементов до первого отрицательного в массивах X(40), Y(50), Z(N) |
N<=50 |
Задание Б.
Выполнить на ЭВМ программу, использующую подпрограмму-процедуру в соответствии с номером, указанным в таблице.
Проверить правильность выполнения программы с помощью тестового варианта .
|
Вариант Задания |
Условие задачи |
Примечания |
| 1 |
Вычислить z = (s1+s2)/k1k2 ,где s1 и k1 – сумма и количество положительных элементов массива X(N); s2 и k2 – сумма и количество положительных элементов массива Y(M). |
M<=100 N<=100 |
| 2 |
Вычислить z = (es1+es2)/k1k2, где s1 и k1 – сумма и количество положительных элементов массива X(100); s2 и k2 – сумма и количество положительных элементов массива Y(80). |
Обе суммы вычислять в одной подпрограмме |
| 3 | Вычислить и запомнить суммы положительных элементов каждой строки матицы A(10,20), B(15,10). | |
| 4 |
Вычислить z = (x1+y1)/(x2-y2), где x1 и x2 – корни уравнения 2x2+x-4 = 0, y1 и y2 – корни уравнения ay2+2y-1 = 0 . |
Все корни действительные |
| 5 | Найти наибольшие элементы и их порядковые номера массивов X(N) и Y(M) |
N<=80 M<=70 |
| 6 | Переписать положительные элементы массива X(100) и Y(80) в массив Z подряд | Запись в массив Z осуществлять в подпрограмме |
| 7 | Найти наименьшие элементы и номера строк и столбцов, в которых они расположены, для матриц A(10,15) и B(15,12) | |
| 8 | Вывести на печать элементы целочисленных матриц N(5,8) и M(10,6), кратные трём | |
|
9
|
Вычислить z, где xi и yi – заданы массивами |
Все суммы вычислять в одной подпрограмме |
| 10 |
Вычислить z = (xmax-ymin)/2, где xmax – максимальный элемент массива X(50); ymin – минимальный элемент массива Y(40) |
xmax и ymin вычислять в одной подпрограмме |
| 11 | Вычислить и запомнить количество отрицательных элементов каждого столбца для матриц A(10,10), B(15,20) | |
| 12 | Вычислить суммы элементов верхней треугольной матрицы для матриц A(10,10), B(15,15) | |
|
13 |
Найти средние значения и стандартные отклонения для элементов массивов X(N), Y(M) |
N<=100 M<=100 |
| 14 | Вычислить суммы и количества элементов, находящихся в интервале от a до b для матриц X(10,8) и Y(10,12) | |
| 15 | Преобразовать массивы X(50) и Y(60), расположив в них подряд только положительные элементы. Вместо остальных элементов записать нули |
Пример выполнения работы
Задание А.
Выполнить на ЭВМ решение задачи. Определить ближайшую к началу координат точку, находящуюся в верхней полуплоскости, и наиболее удалённую точку, лежащую в нижней полуплоскости. Координаты точек, находящихся в верхней полуплоскости , заданы массивами X1(N) и Y1(N), а лежащие в нижней полуплоскости ,- массивами X2(M) и Y2(M), где N<=40, M<=60.
Для каждой точки верхней полуплоскости следует определить расстояние от начала координат. Из этих расстояний необходимо найти наименьшее. Такие же действия выполнить для точек, находящихся в нижней полуплоскости, однако найти наибольшее расстояние от начала координат.
Вычисление расстояний от начала координат и нахождение наименьшего или наибольшего из них выполним в подпрограмме-функции.
Использование
одной подпрограммы
для нахождения
наибольшего
и наименьшего
значений потребует
введения
дополнительного
параметра,
который необходим
для проверки
условия K*R>K*RM.
Если K=1,
то условие R>RM
используется
для нахождения
наибольшего;
если K=
-1, то условие
В подпрограмму
необходимо
передать массивы
координат
точек, их размер,
а также параметр
K,
который может
принимать
значения +1 или
–1. Результат,
полученный
в подпрограмме–функции,
присваивается
её имени. Программа,
реализующая
алгоритм, имеют
вид:
program coord;
usec crt;
const n=40;
type mas =array[1..n] of real;
var i,n : byte;
s : real;
x ,y : mas;
function vec(x,y:mas; n,kx:integer):real;
var j : integer;
r,rm : real;
begin
rm := -1e20;
for j := 1 to n do begin
r := sqrt(sgr(x[i])+sgr(y[i]));
if (kx*r>=kx*rm) then rm := r;
end;
vec := rm
end;
{ исполняемая
часть главной
программы }
begin
textattr:=27;clrscr;
gotoxy(30,2);writeln(‘');
write('Введите
кол-во координат
верхней полуплоскости.
');
readln(n);
writeln('Введите
координаты');
for i :=1 to n do begin
read(x[i]); write(‘ ‘);readln(y[i]);
end;
writeln(‘Ближайшая
точка удалена
на расстояние
=’, s:=vec(x,y,n,-1);
write('Введите
кол-во координат
нижней полуплоскости.
');
readln(n);
writeln('Введите
координаты');
for i :=1 to n do begin
read(x[i]); write(‘ ‘);readln(y[i]);
end;
writeln(‘Наиболее
удаленная точка
находится на
расстояни =’,
s:=vec(x,y,n,1);
end.
Проверить
правильность
выполнения
программы для
массивов, заданных
значениями:
Для верхней
полуплоскости
x={-4,0,3}; y={0,5,4};
Для нижней
полуплоскости
x={-4,0,2}; y={-2,-5,-1};
Для которых
наименьшее
расстояние
от начала координат
в верхней
полуплоскости
s = 4, а наибольшее
- в нижней полуплоскости
s = 5.
Задание Б.
Решить на
ЭВМ задачу.
Переписать
положительные
элементы массивов
X(n),Y(m)
в массив Z подряд.
Запись положительных
элементов в
массив осуществить
в подпрограмме.
Принять ограничения:
n<=100 и m<=100.
В подпрограмме
должна осуществляться
запись положительных
элементов
исходного
массива в массив
результатов.
Для этого
в подпрограмму
необходимо
передать следующие
параметры: имя
и количество
элементов
исходного
массива, имя
и номер элемента
с которого
дописывать
результирующий
массив. Поскольку
в массив результатов
Z записывается
подряд положительные
элементы из
нескольких
массивов, в
списке параметров
должны фигурировать
также: входной
параметр L –
номер ячейки,
начиная с которой
необходимо
осуществлять
запись в массив
результатов.
При первом
обращении к
подпрограмме
в неё необходимо
передать имя
массива Х, количество
его элементов
N; входной параметр
L=1, запись осуществляется
в массив Z, начиная
с элемента с
индексом 1. При
завершении
первого обращения
L
хранит номер
последней
занятой ячейки
в массиве Z.
При втором
обращении
необходимо
передать
соответственно
массив Y,
количество
его элементов
M,
и L=L+1
равной номеру
ячейки преднозначенной
для до записи
в массив Z.
В схеме алгоритма
при первом
обращении к
подпрограмме
параметр L задан
равным нулю,
так как в подпрограмме
перед записью
элемента в
массив z индекс
L
увеличивается
на 1. По этой же
причине при
втором обращении
параметру L
опять увеличивается
на 1, что даёт
возможность
обратиться
к следующей
ячейки массива
Z
при втором
обращении.
Программа,
реализующая
алгоритм, имеют
вид:
program sort (input,output);
uses crt;
{подключение
модуля упровляющего
текстовым
режимом монитора}
const n=200;
type mas:array[1..n] of real;
var i,n,m,l: byte;
x,y,z:mas;
procedure st (var a,c:mas;n:byte;var l:byte);
var j:byte;
begin
for j:=1 to n do
if a[i]>0 then begin
inc(l);
c[l] := a[j];
end;
end;
{ исполняемая
часть главной
программы }
begin
window(1,
1, 80, 25);textattr
:= 27; clrscr;
gotoxy(5,
2);write('Введите кол-во
элементов
массива X');
readln(n);
gotoxy(5,
3);write('Введите значения
массива X');
for i := 1 to n do begin
gotoxy(i*4-2, 5); read(x[i]);
end;
gotoxy(5,
9);write('Введите кол-во
элементов
массива Y');
readln(m);
gotoxy(5,
10);write('Введите значения
массива Y');
for i := 1 to m do begin
gotoxy(i*4-2, 12); read(y[i]);
end;
l := 0;
st(x,z,n,l);
st(y,z,m,l);
gotoxy(5,
15);write(‘Результативный
массив Z’);
for i:=1 to l do begin
gotoxy(i*4-2, 17);write(z[i]);
end;
end.
Данная конкретная
программа в
тестировании
не нуждается,
так как выведенные
на печать результаты
позволяют
однозначно
судить о правильности
выполнения
программы.
Контрольные
вопросы
Указать, при
каких условиях
целесообразно
использование
подпрограмм,
какие выгоды
они представляют
пользователю.
Указать, в
чём отличие
различных
видов подпрограмм
пользователя.
Указать
способы обращения
к подпрограммам
пользователя.
Указать
способы передачи
параматров
в подпрограмму.
Указать, как
организовывать
подпрограмму
без параметров.
Перечислить,
как согласуются
формальные
и фактические
параметры.
Указать
конструкции,
которые могут
быть формальными
и фактическими
параметрами.
Пояснить,
как и куда
осуществляется
выход из подпрограммы.
R