Реферат: Построение интерполяционного многочлена и вычисление по нему значения функции для заданного аргумента
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Международная «Лига развития науки и образования» (Россия)
Международная ассоциация развития науки, образования и культуры России (Италия)
Международный «ИНСТИТУТ УПРАВЛЕНИЯ»
(г. Архангельск)
КУРСОВАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«Информатика и программирование»
Тема : «Построение интерполяционного многочлена и вычисление по нему значения функции для заданного аргумента»
|
Выполнил: студент экономического факультета, группы 12-И Воробьев А.А. Проверил: Горяшин Ю.В. |
Архангельск
2004
Аннотация
Цель курсовой: для функции заданной в таблице построить интерполяционный многочлен и вычислить по нему значение функции для заданного значения аргумента. Составить блок схему алгоритма и программу на одном из языков высокого уровня (С++) для вычисления заданного интерполяционного многочлена. В программе предусмотреть возможности ввода любого числа значений функции для чего организовать хранение ее значении при помощи линейного списка.
Содержание
1. Аннотация
2. Содержание
3. Глава №1
4. Глава №2
5. Заключение
6. Список литературы
7. Приложение
8. Программа
Введение.
Возможность постановки вычислительного эксперимента на ЭВМ приводит к существенному ускорению процессов математизации науки и техники, к постоянному расширению области приложения современных разделов математики. Количественные методы внедряются практически во все сферы человеческой деятельности, что приводит к расширению круга профессий, для которых математическая грамотность становится необходимой. Однако, развитие науки и техники, современная технология производства ставят перед специалистами задачи, для которых либо не возможно, либо крайне громоздко и сложно получение алгоритма классическими методами математического анализа. Отсюда стремление использовать различные численные методы, разрабатываемые вычислительной математикой и позволяющие получить конечный числовой результат с приемлемой для практических целей точностью.
Численный метод решения задачи - это определенная последовательность операций над числами, т.е. вычислительный алгоритм, языком которого являются числа и арифметические действия. Такая примитивность языка позволяет реализовать численные методы на ЭВМ, что делает их мощными и универсальными инструментами исследования. Численные методы используются в тех случаях, когда не удается найти точное решение возникающей математической задачи. Это происходит главным образом, потому, что искомое решение обычно не выражается в привычных для нас элементах или других известных функциях. Даже для достаточно простых математических моделей иногда не удается получить результат решения в аналитической форме. В таких случаях основным инструментом решения многих математических задач выступают численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами, при этом результаты получаются также в виде числовых значений.
Многие численные методы разработаны давно, однако при ручных вычислениях они могли использоваться лишь для решения узкого круга не слишком сложных задач, и только с появлением высоко производительных ЭВМ начался период бурного развития методов вычислительной математики и их внедрения в практику. Численные методы приобрели важнейшее значение как мощное математическое средство решения практических задач в различных областях науки и техники.
Интерполирование, интерполяция,- приближенное или точное нахождение какой-либо величины по известным отдельным значениям или других величин, связанных с ней. В первоначальном понимании- восстановление функции (точное или приближенное) по известным ее значениям или значениям ее производных в заданных отрезках.
Основное применение интерполяции - это вычисление значении табулированной функции для неузловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют «искусством чтения таблиц между строками». (П.Ф. Фильчаков)
Глава 1
Основные направления исследования: разрешимость задачи интерполирования, простейших интерполяционных формул, применение интерполяции для построения приближенных интерполяционных формул, применение интерполяции для построения приближенных и численных методов решения различных задач математики и ее приложений.
Приближенное
представление функций. Интерпояционные функции ![]() на
отрезке
на
отрезке ![]() по значениям ее в узлах
по значениям ее в узлах ![]() сетка
сетка ![]() - означает постоение другой
функции
- означает постоение другой
функции ![]() такой, что
такой, что ![]() В более общей постановке
задача интерполирования функции
В более общей постановке
задача интерполирования функции ![]() состоит
в постоении
состоит
в постоении ![]() не только из условий
совпадения значений функций
не только из условий
совпадения значений функций ![]() и
и ![]() на стеке
на стеке ![]() , но и совпадения в
отдельных узлах производных до какого-то порядка или некоторых других
соотношений, связанных
, но и совпадения в
отдельных узлах производных до какого-то порядка или некоторых других
соотношений, связанных ![]() и
и ![]() .
.
Обычно ![]() стоится в виде
стоится в виде
![]() ,
,
где ![]() -
некоторая заранее выбранная система линейно независимых функций. Такое
интерполирование называется л и н е й н ы м относительно системы
-
некоторая заранее выбранная система линейно независимых функций. Такое
интерполирование называется л и н е й н ы м относительно системы ![]() , а
, а ![]() интерполяционным
многочленом по системе
интерполяционным
многочленом по системе ![]() .
.
Выбор системы ![]() определяется свойством
класса функций, для приближения которого предназначаются интерполяционные
формулы. Например, для приближения
определяется свойством
класса функций, для приближения которого предназначаются интерполяционные
формулы. Например, для приближения ![]() -
периодической функции на
-
периодической функции на ![]() за
за ![]() естественно взять
тригонометрическую систему функций, для приближения на полу оси
естественно взять
тригонометрическую систему функций, для приближения на полу оси ![]() ограниченных или
возрастающих функции- систему рациональных или показательных функций,
учитывающих поведение приближаемых функций на бесконечности и т.д.
ограниченных или
возрастающих функции- систему рациональных или показательных функций,
учитывающих поведение приближаемых функций на бесконечности и т.д.
Чаще всего используя а л г е
б р а и ч е с к о е интерполирование: ![]() .
Существует ряд явных представлений алгебраических интерполяционных многочленов.
Например интерполяционный многочлен Лагранжа имеет вид:
.
Существует ряд явных представлений алгебраических интерполяционных многочленов.
Например интерполяционный многочлен Лагранжа имеет вид:
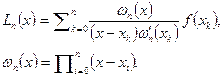
В задаче приближения функции
и на всём отрезке ![]() алгебраическое интерполирование
высокого порядка выполняется сравнительно редко. Алгебраический интерполяционный
процесс не является сходящимся в классе непрерывных на
алгебраическое интерполирование
высокого порядка выполняется сравнительно редко. Алгебраический интерполяционный
процесс не является сходящимся в классе непрерывных на ![]() функций. Обычно
ограничиваются линейным интерполированием по узлам
функций. Обычно
ограничиваются линейным интерполированием по узлам ![]() и
и
![]() на каждом отрезке
на каждом отрезке ![]() или квадратичным по трем
узлам
или квадратичным по трем
узлам ![]() ,
,![]() ,
,![]() на
отрезке
на
отрезке ![]() .
.
Эффективным аппаратом приближения функции являются интерполяционные сплайны, но их построение в ряде частных случаях требует значительных вычислительных затрат.
На практике чаще всего
используются параболические или кубические полиноминальные сплайны. Интерполяция
кубическим сплайном дефекта 1 для функции ![]() относительно
сетки
относительно
сетки ![]() называет функцию
называет функцию ![]() , являющуюся многочленом 3-й
степени на каждом из отрезков
, являющуюся многочленом 3-й
степени на каждом из отрезков ![]() ,
принадлежащую классу дважды непрерывно дифференцируемых функции и
удовлетворяющую условиям
,
принадлежащую классу дважды непрерывно дифференцируемых функции и
удовлетворяющую условиям
![]() .
.
При таком определении
кубического сплайна, он имеет еще свободных параметра, для нахождения которых
на сплайн налагаются дополнительные краевые условия. Например ![]() или
или ![]() и
и ![]() , или некоторые другие.
, или некоторые другие.
Полиномиальный
интерполяционный сплайн произвольной степени m дефекта r определяется как функция ![]() ,
удовлетворяющая, кроме условий
,
удовлетворяющая, кроме условий ![]() и
и ![]() , еще дополнительно условиям
совпадения в узлах сетки значений функции
, еще дополнительно условиям
совпадения в узлах сетки значений функции ![]() и
интерполированной функции
и
интерполированной функции ![]() и их производных
до некоторого порядка.
и их производных
до некоторого порядка.
Часто при обработке
эмпирических данных ![]() коэффициенты
коэффициенты ![]() в
в ![]() определяют исходя из
требования минимизации суммы
определяют исходя из
требования минимизации суммы
![]()
![]() - заданные числа,
- заданные числа, ![]() .
.
Такое построение функции называют интерполированием по методу наименьших квадратов.
Интерполирование функций
многих переменных имеет ряд принципиальных и алгебраических трудностей.
Например в случае алгебраической интерполяции интерполяционный многочлен
Лагранжа фиксированной степени, вообще говоря, не существует для произвольной
схемы различных узлов интерполяции. В частности для функций двух переменных ![]() такой многочлен
такой многочлен ![]() суммарной степени не выше
n может быть построен по узлам
суммарной степени не выше
n может быть построен по узлам ![]() лишь при условии, что эти
узлы не лежат на алгебраической кривой порядка n.
лишь при условии, что эти
узлы не лежат на алгебраической кривой порядка n.
Другой поход к интерполированию
функции многих переменных ![]() стоит в том,
что сначала интерполируется функция по переменной
стоит в том,
что сначала интерполируется функция по переменной ![]() при
фиксированных
при
фиксированных ![]() потом по
следующей переменной при фиксированных
потом по
следующей переменной при фиксированных ![]() и
т.д. интерполяционные сплайны для функций многих переменных определяются по
многомерной сетке при соответствующих изменениях по аналогии с одномерным
случаем.
и
т.д. интерполяционные сплайны для функций многих переменных определяются по
многомерной сетке при соответствующих изменениях по аналогии с одномерным
случаем.
Интерполирование функций и численные методы. Интерполирование функции используется:
1. для замены сложно вычисляемой функции другой, вычисляемой проще
2. для приближенного восстановления функции на всей области задания по значениям её в отдельных точках или по другим известным величинам
3. для получения сглаживающих функций
4. для приближенного нахождения предельных значений функции
5. в задачах ускорения сходимости последовательностей и рядов и в других вопросах.
Общие идеи построения
интерполяционных методов решения уравнения ![]() =0
и систем уравнения
=0
и систем уравнения ![]() ,
одни и те же. Трудности задачи интерполирования функций многих преременных особенно
сказывается при исследовании и практическом использовании такого рода методов
для большого числа уравнений. В основу получении интерполяционных методов
решения уравнения
,
одни и те же. Трудности задачи интерполирования функций многих преременных особенно
сказывается при исследовании и практическом использовании такого рода методов
для большого числа уравнений. В основу получении интерполяционных методов
решения уравнения ![]() =0 положена
замена функции
=0 положена
замена функции ![]() ее интерполяционным
многочленом
ее интерполяционным
многочленом ![]() и последующим решением
уравнения
и последующим решением
уравнения ![]() =0 берутся за
приближенные решении уравнения
=0 берутся за
приближенные решении уравнения ![]() =0
интерполяционный многочлен
=0
интерполяционный многочлен ![]() используется
так же при построении итерационных методов решения уравнения
используется
так же при построении итерационных методов решения уравнения ![]() =0.
=0.
Например взяв за ![]() корень линейного
интерполяционного алгебраического многочлена, построенного по значениям
корень линейного
интерполяционного алгебраического многочлена, построенного по значениям ![]() и
и ![]() в узле
в узле ![]() или по значениям
или по значениям ![]() и
и ![]() в узлах
в узлах ![]() и
и ![]() , приходят соответственно к
методу Ньютона и метода секущих
, приходят соответственно к
методу Ньютона и метода секущих
![]() ,
,
где ![]() -
разделенная разность функций для узлов
-
разделенная разность функций для узлов ![]() и
и
![]() .
.
Другой подход к построению
численных методов решения уравнения ![]() =0
основан на интерполировании обратной функции
=0
основан на интерполировании обратной функции ![]() .
Пусть в качестве интерполяционной формулы для функции
.
Пусть в качестве интерполяционной формулы для функции ![]() взят интерполяционный
алгебраический многочлен Лагранжа
взят интерполяционный
алгебраический многочлен Лагранжа ![]() ,
построенный по узлам
,
построенный по узлам ![]() Тогда за
следующее приближению к корню
Тогда за
следующее приближению к корню ![]() уравнения
уравнения
![]() =0 берется величина
=0 берется величина ![]() .
.
Численное интегрирование. Аппарат интерполирования функции лежит в основе построения многих квадратурных и кубатурных формул. Такого рода формулы строятся путем замены интегрируемой функции на всей области или на её составных частях интерполяционными многочленами того или иного вида и последующим интегрированием этих многочленов. Например квадратурные формулы наивысшей алгебраической степени точности, так называемые квадратурные формулы Гаусса:
![]()
где ![]() -
знакопостоянная весовая функция, получаемая в результате замены функции
-
знакопостоянная весовая функция, получаемая в результате замены функции ![]() интерполяционным
алгебраическим многочленом, построенным по корням
интерполяционным
алгебраическим многочленом, построенным по корням ![]() ортогонального
относительно веса
ортогонального
относительно веса ![]() многочлена
степени n.
многочлена
степени n.
Изложенная выше схема построения формул для приближенного вычисления интегралов применима и в многомерном случае
Формулы численного дифференцирования, в основе которых лежит интерполирование, получаются в результате дифференцирования интерполяционных многочленов. Ввиду неустойчивости задачи численнго дифференцирования относительно ошибок использования значений функций в узлах шаг интерполирования должен согласоваться с погрешносьтью значений функций. Поэтому на практике нередки случаи, когда известная на густой сетке функция используется в данной задаче не во всех точках, а на более редкой сетке.
При численном решении
интегральных уравнений, известная функция ![]() заменяется
в интегральном уравнении каким-либо интерполяционным приближением
(интерполяционным алгебраическим многочленом, интерполяционным сплайном и т.д.)
с узлами интерполирования
заменяется
в интегральном уравнении каким-либо интерполяционным приближением
(интерполяционным алгебраическим многочленом, интерполяционным сплайном и т.д.)
с узлами интерполирования ![]() , а
приближенные значения
, а
приближенные значения ![]() для
для ![]() находятся из системы,
полученной после подстановке вместо независимости переменной x узлов интерполирования
находятся из системы,
полученной после подстановке вместо независимости переменной x узлов интерполирования ![]() . В случае нелинейных интегральных
уравнений приближенные значения
. В случае нелинейных интегральных
уравнений приближенные значения ![]() находятся
соответственно из нелинейной системы.
находятся
соответственно из нелинейной системы.
Интерполяционная формула-
для приближенного вычисления значений функции ![]() ,
основанного вычисления на замене приближаемой функции
,
основанного вычисления на замене приближаемой функции ![]() более простой в каком- то
смысле функцией
более простой в каком- то
смысле функцией
![]()
|
|
|
наперед заданного класса, причем
параметры ![]() выбираются так чтобы
значения
выбираются так чтобы
значения ![]() совпадали с известными заранее
значениями
совпадали с известными заранее
значениями ![]() для данного множества
для данного множества ![]() попаро различных значений
аргумента:
попаро различных значений
аргумента:
такой способ приближенного
представления функций называется интерполированием, а точки ![]() , для которых должны выполняться
условия
, для которых должны выполняться
условия ![]() , - узлами интерполяции.
, - узлами интерполяции.
В ряде случаев (например,
при интерполировании алгебраическими многочленами) параметры ![]() могут быть явно выражены из
системы
могут быть явно выражены из
системы ![]() , и тогда
, и тогда ![]() непосредственно используется
для приближенного вычисления значений функции
непосредственно используется
для приближенного вычисления значений функции ![]() .
.
Интерполяционный процесс- процесс получения
последовательности интерполирующих функций ![]() при
неограниченном возрастании числа n узлов
интерполирования. Если интерполирующие функции
при
неограниченном возрастании числа n узлов
интерполирования. Если интерполирующие функции ![]() представлены
в виде частных сумм некоторого функционального ряда, то последний иногда
называется интерполяционным рядом. Целью построения
интерполяционного полинома чаще всего является, по крайней мере в простейших
первоначальных задачах интерполирования, приближение в каком- то смысле по
средствам интерполирующих функций
представлены
в виде частных сумм некоторого функционального ряда, то последний иногда
называется интерполяционным рядом. Целью построения
интерполяционного полинома чаще всего является, по крайней мере в простейших
первоначальных задачах интерполирования, приближение в каком- то смысле по
средствам интерполирующих функций ![]() , о
которой или имеется неполная информация, или форма которой слишком сложна для
непосредственного использования.
, о
которой или имеется неполная информация, или форма которой слишком сложна для
непосредственного использования.
Интерполяционная формула Эверетта:
Интерполяционные формулы Грегори-
Ньютона построенные по нисходящим или восходящим разностям, наиболее
целесообразно применять в начале или конце таблицы. При этом для достижения высокой
степени точности иногда приходится рассматривать разности, отстоящие достаточно
далеко от интересующих нас значений функции ![]() или
или
![]() . Поэтому на средних
участках таблицы лучше результаты дают интерполяционные формулы, построенные на
базе центральных разностей, то есть разностей, которые ближе всего расположены
к центральной сотке, содержащей
. Поэтому на средних
участках таблицы лучше результаты дают интерполяционные формулы, построенные на
базе центральных разностей, то есть разностей, которые ближе всего расположены
к центральной сотке, содержащей ![]() .
.
К интерполяционным формулам с центральными разностями относятся формулы Гаусса, Стирлинга, Бесселя, Эверетта и многие другие; формула Эверетта получила наибольшее распространение, она была получена 1900 г.:
![]()
где ![]() ;
;
![]() ;
; ![]() .
.
Формуле Эверетта так же можно придать форму, наиболее удобную для вычисления:
![]()
если для ее коэффициентов ввести обозначения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Коэффициенты ![]() удобнее всего вычислять по
следующей рекуррентной формуле, которая непосредственно вытекает из
удобнее всего вычислять по
следующей рекуррентной формуле, которая непосредственно вытекает из ![]() :
:
![]() ;
; ![]() ;
;
![]()
Таблица разностей:
| x | y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
Таблицу можно продолжать строить, в
нашем случае до последнего ![]() , число
разностей зависит от количества значений y. Таблица разностей высчитывается
, число
разностей зависит от количества значений y. Таблица разностей высчитывается
![]() ,
и так далее(можно заметить такую систему в приведенной выше таблице)
,
и так далее(можно заметить такую систему в приведенной выше таблице)
Тестовый пример.
П р и м е р. Функция ![]() задана таблицей на сегменте
задана таблицей на сегменте ![]() . Определим при помощи
интерполяции значение
. Определим при помощи
интерполяции значение ![]() .
.
Р е ш е н и е. По данным значениям функции составляем таблицу разностей (табл. 1), из которых видно, что четвертые разности в данном примере практически равны постоянны, а пятые разности практически равны нулю, и поэтому мы их в дальнейших вычислениях не будем принимать во внимание.
Принимаем ![]() =0,85;
=0,85; ![]() =0,9;
=0,9; ![]() =0,874.
=0,874.
Тогда ![]() =0,8273695;
=0,8273695; ![]() =0,8075238, и, далее, так
как шаг таблицы
=0,8075238, и, далее, так
как шаг таблицы ![]() =0,05, то
=0,05, то
![]()
Т а б л и ц а 2
| x |
|
|
|
|
|
|
|
0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
0.9120049 0.8971316 0.8812009 0.8642423 0.8462874 0.8273695 0.8075238 0.7867871 0.7651977 |
-0.0148733 -0.0159307 -0.0169586 -0.0179549 -0.0189179 -0.0198457 -0.0207367 -0.0215894 |
-0.0010574 -0.0010279 -0.0009963 -0.0009630 -0.0009278 -0.0008910 -0.0008527 |
0.0000295 0.0000316 0.0000333 0.0000352 0.0000368 0.0000383 |
0.0000021 0.0000017 0.0000019 0.0000014 0.0000015 |
-0.0000004 0.0000002 -0.0000005 0.0000001
|
Т а б л и ц а 2
| Эверетта | ||
|
|
|
|
|
0 1 2 |
0.52000 -0.06323 0.01179 |
0.82273695 -0.0009278 0.0000014 |
|
0 1 2 |
0.48000 -0.06157 0.01160 |
0.8075238 -0.0008910 0.0000015 |
|
|
Все вычисления по формуле Эверетта представлены в табл. 2.
Все
необходимые значения разностей(и самой функции, которые мы в табл. 2 обозначили
как разности нулевого порядка ![]() ) взяты
из табл. 1. Первые три строки в табл. 2 заполнены значениями
) взяты
из табл. 1. Первые три строки в табл. 2 заполнены значениями ![]() для
для ![]() и
и ![]() , а последующие три строки
соответственно значениями
, а последующие три строки
соответственно значениями ![]() для
для ![]() и
и ![]() .
.
Перемножив (не
снимая промежуточных результатов) коэффициенты ![]() на
расположенные в той же строке
на
расположенные в той же строке ![]() , мы и
получим искомое значение функции
, мы и
получим искомое значение функции ![]() , как
сумму произведений
, как
сумму произведений
Проверка
производится непосредственно при помощи степенного ряда для рассматриваемой
функции Эверетта 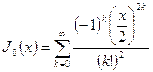 согласно которому
получим
согласно которому
получим ![]()
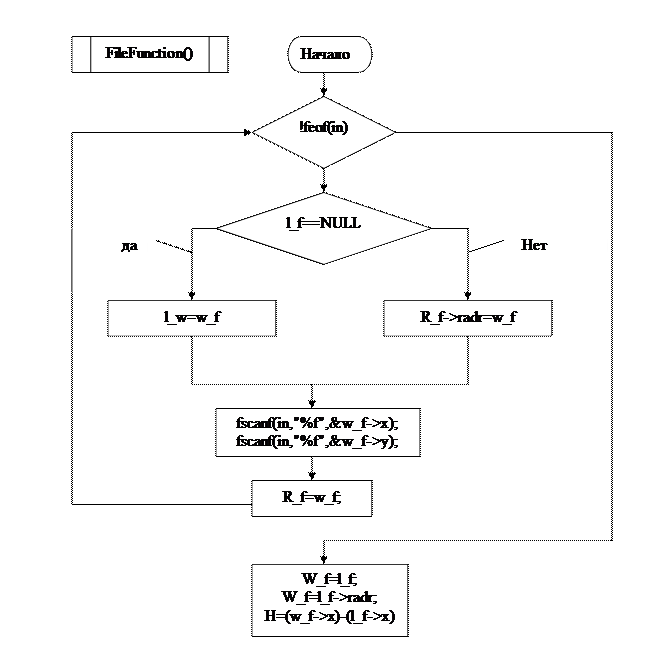
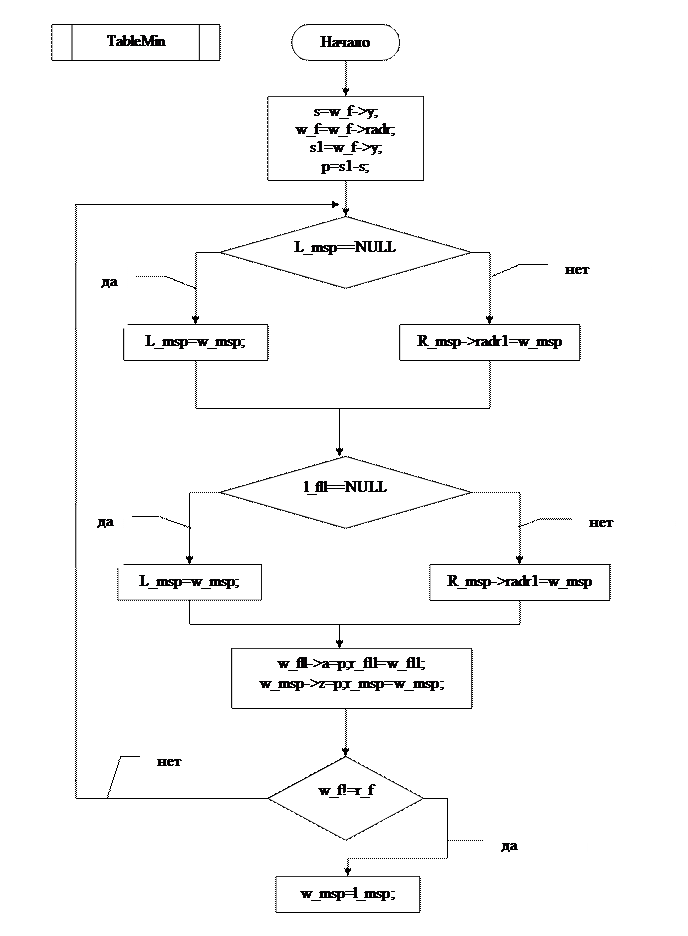
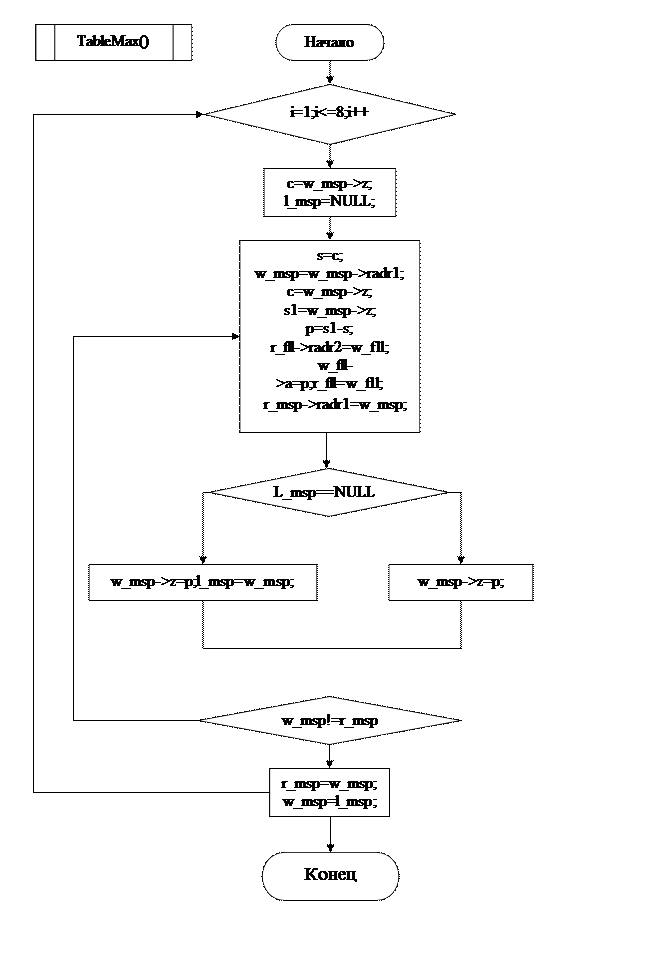
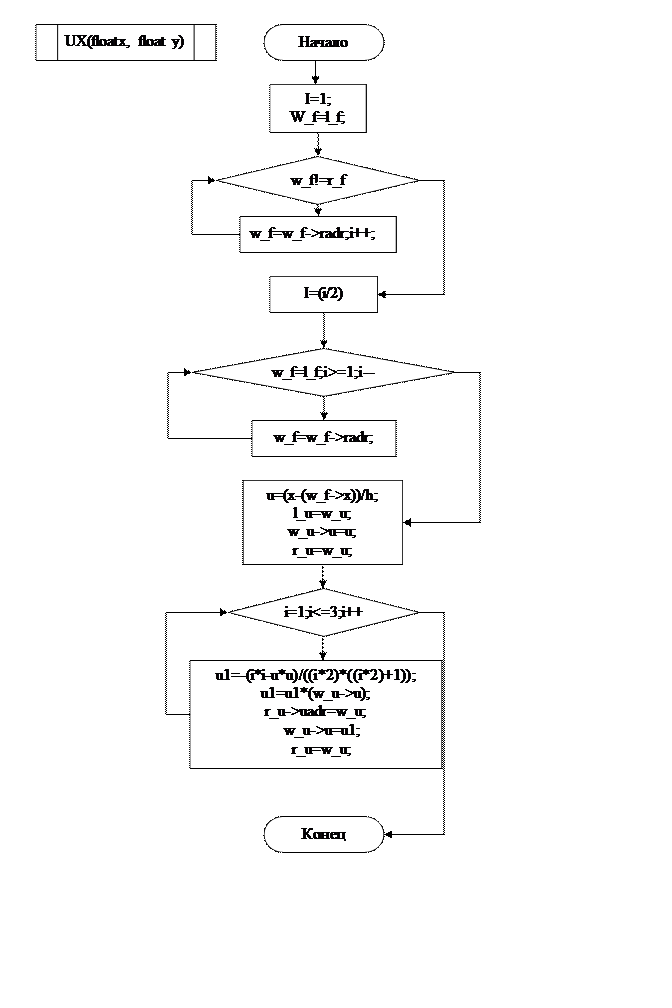
ГЛАВА №2
MAIN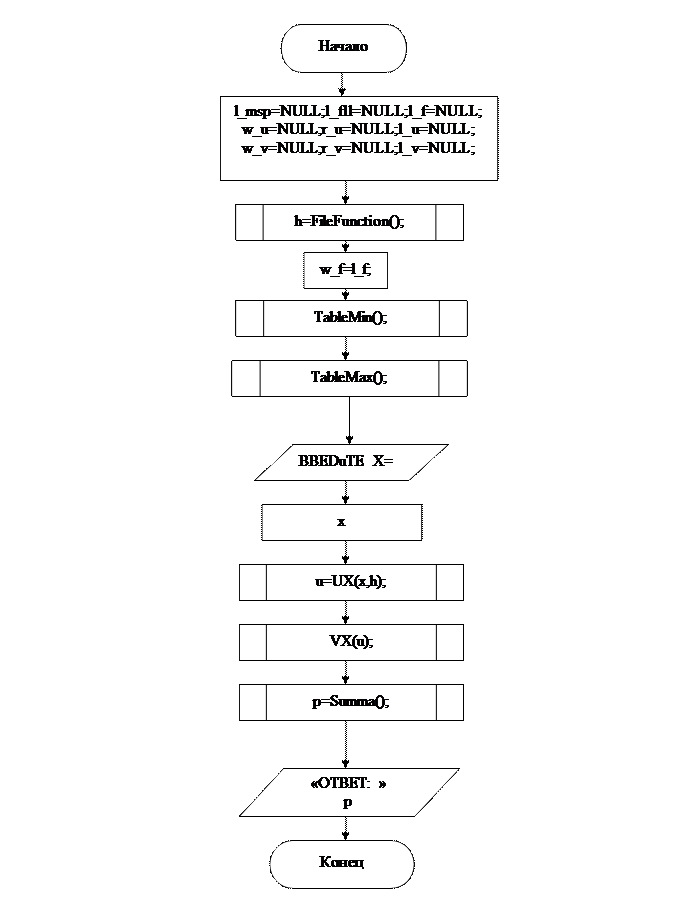





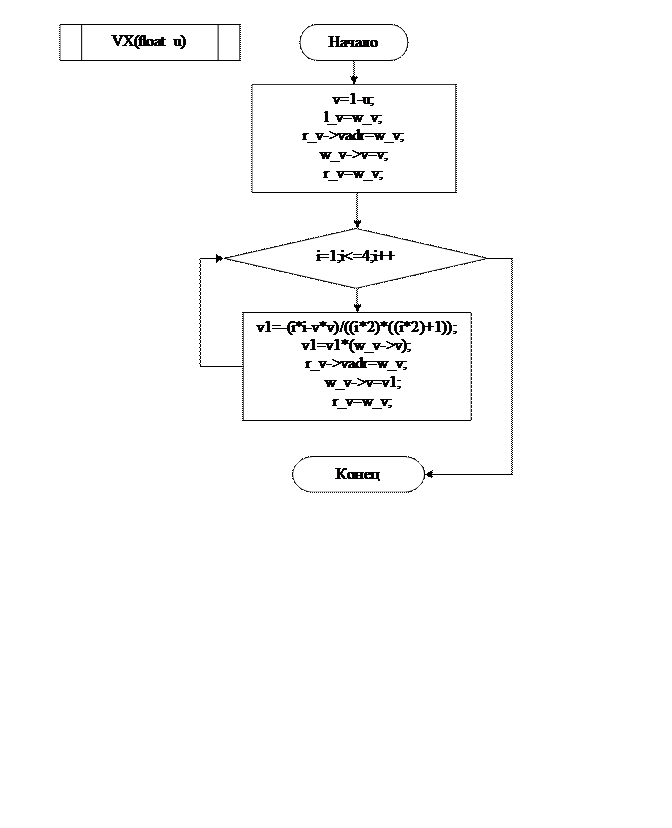

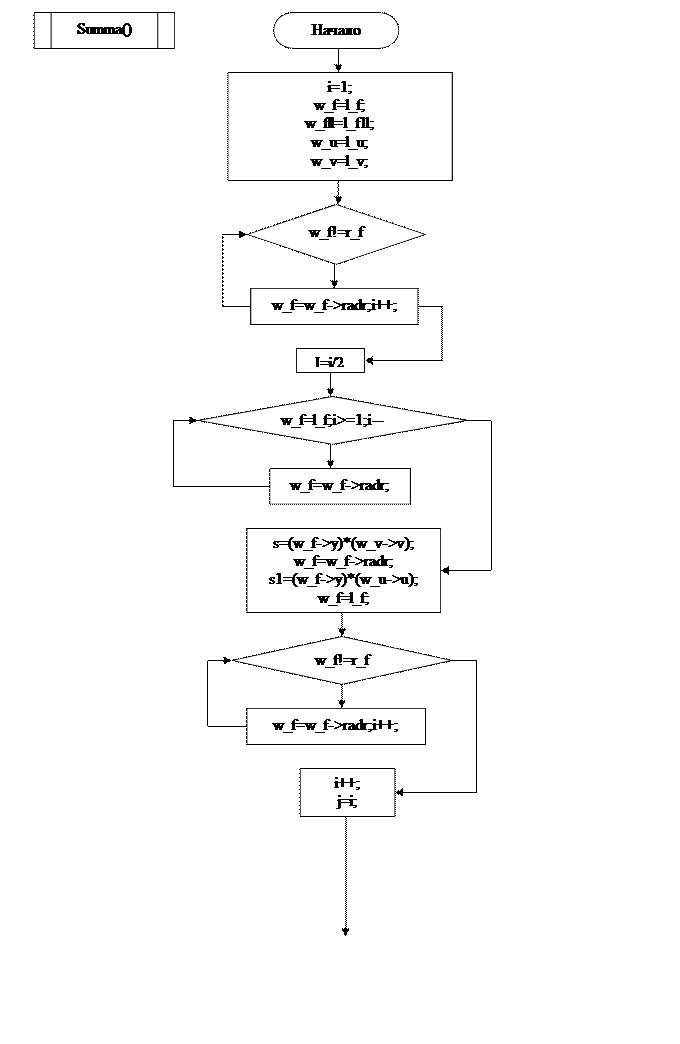

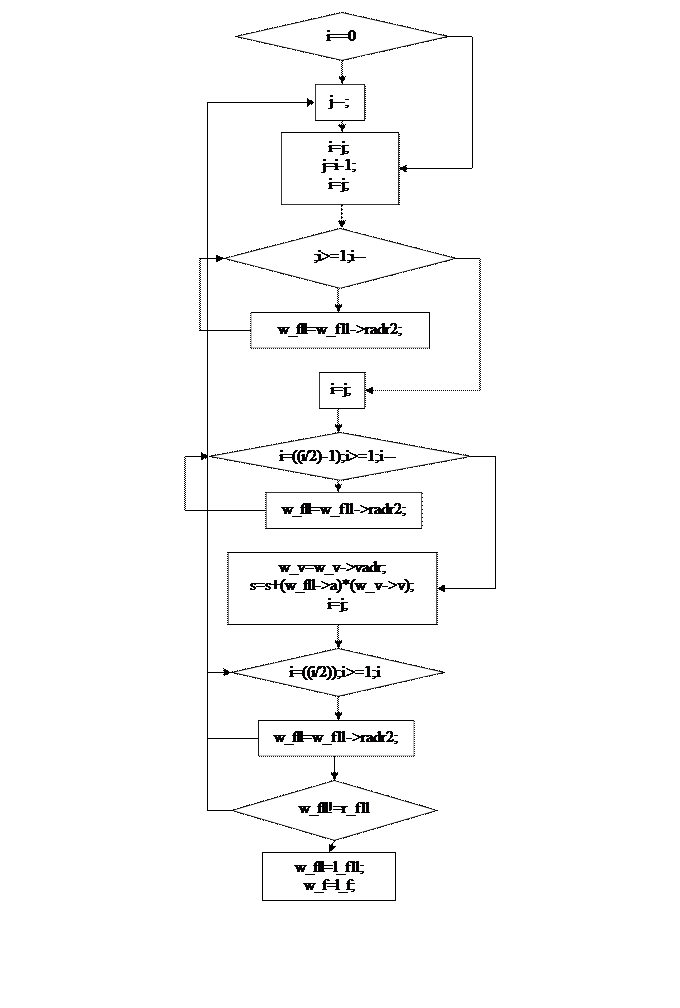

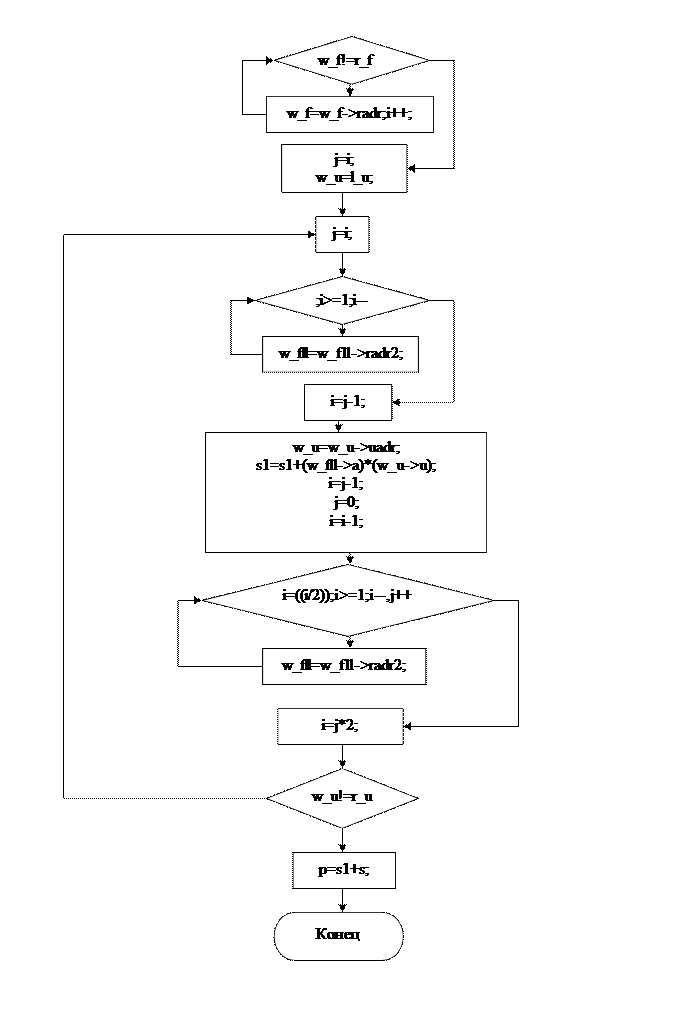

Заключение
Удалось построить интерполяционный многочлен и вычислить по нему значение функции для заданного значения аргумента. Составлена блок схема алгоритма и программа на языке С++ (Приложение) для вычисления заданного интерполяционного многочлена. В программе предусмотрена возможность ввода любого числа значений функции для чего организованно хранение ее значения при помощи линейного списка.
Список литературы
1. Архангельский Н.А. Вычислительные методы алгебры в приемах и задачах. М.: МАИ, 1976.
2. Васильев Ф.П. Численные методы решения экстремальных задачь. М.: Наука,1988.
3. Васильков Ф.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. Пособие. М.: Финансы и статистика, 1999.
4. Фильчаков П.Ф., Справочник по высшей математике. Киев: Наукова думка, 1974.
5. Фильчаков П.Ф., Численные методы. Киев: Наукова думка, 1976.
6. Большая математическая энциклопедия. М.: Олма-Пресс, 2004
7. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
8. Тихонов А.Н., Вводные лекции по прикладной математике. М.: Наука, 1984.
9. Калиткин Н.Н., Численные методы. М.: Наука, 1987.
10. Корн Г., Корн Т. Справочник по математике. М.: Наука, 1984.
| Численные методы решения типовых математических задач | |
|
... УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Тульский государственный университет Кафедра автоматики и телемеханики Численные методы решения ... Чем больше узлов интерполирования на отрезке [x0,xn] , тем точнее интерполяционный многочлен приближает заданную табличную функцию, т.е. тем точнее равенство: В данной работе описаны и реализованы с помощью блок-схем и языка программирования Turbo Pascal базовые задачи вычислительной математики: решение систем линейных алгебраических ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Сравнительный анализ численных методов | |
|
Министерство образования и науки Республики Казахстан Карагандинский государственный технический университет Кафедра САПР Курсовая работа по ... Как видно в узлах интерполяции значение интерполяционного многочлена Лагранжа и исходной функции равны. Основная идея модификации состоит в том, что при вычислении очередного (k+1)-го приближения к известному xi при i>1 используют используются уже найденные приближения к известным x1 ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Практическое применение интерполирования гладких функций | |
|
Специальность "Математические методы в экономике" КУРСОВАЯ РАБОТА Практическое применение интерполирования гладких функций 2010 Содержание Введение 1 ... Такой способ приближения называют интерполяцией или интерполированием. Если являются степенями {1, х, х2, ., хn}, то говорят об алгебраической интерполяции, а функцию называют интерполяционным полиномом и обозначим как: |
Раздел: Рефераты по математике Тип: курсовая работа |
| Уравнения и способы их решения | |
|
Министерство общего и профессионального образования РФ Муниципальное образовательное учреждение Гимназия № 12 сочинение на тему: Уравнения и способы ... Если какой-нибудь корень многочлена является корнем многочлена, то необходимо сравнить из кратности: если кратность корня многочлена больше кратности корня многочлена , то этот ... В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного ... |
Раздел: Рефераты по математике Тип: реферат |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... MATLAB обеспечивает ряд интерполяционных методик, которые позволяют находить компромисс ме-жду точностью представления интерполируемых данных и скоростью вычислений и исполь-зуемой ... diff - Вычисление конечных разностей и приближенное дифференцирование. |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |