Реферат: Эйлеровы и гамильтоновы графы
Выполнил:
Студент 4 курса 4 гр. МФ
Цургулов Алил Гасанович
Научный руководитель:
Якубов А. 3.
Махачкала, 2003 год
§1. Основные понятия и определения 5
§2. Критерий существования эйлерова цикла 5
§3. Алгоритмы построения эйлерова цикла 6
§4. Некоторые родственные задачи 8
§5. Задача китайского почтальона 9
Глава 2. Гамильтоновы циклы 11
§1. Основные понятия и определения 11
§2. Условия существования гамильтонова цикла 11
§3. Задачи связанные с поиском гамильтоновых циклов 13
§4. Методы построения гамильтоновых циклов в графе. 15
§5. Алгебраический метод построения гамильтоновых циклов 15
§6. Метод перебора Робертса и Флореса 16
§8. Улучшение метода Робертса и Флореса 18
§10. Сравнение методов поиска гамильтоновых циклов 21
Глава 3. Задача коммивояжера 23
§2. “Жадный” алгоритм решения ЗК 26
§3. “Деревянный” алгоритм решения ЗК 27
§4. Метод лексикографического перебора 29
§5. Метод ветвей и границ решения ЗК 30
§6. Применение алгоритма Дейкстры к решению ЗК 35
§7. Метод выпуклого многоугольника для решения ЗК 35
§9. Применение генетических алгоритмов 39
Целью моей курсовой работы является описание методов нахождения и построения эйлеровых и всех гамильтоновых циклов в графах, а также сравнительный анализ этих методов. Другая цель решаемая в данной работе — это рассмотрение задачи коммивояжера и методов ее решения (включая эвристические и генетические алгоритмы).
Прежде всего, чтобы внести ясность и уточнить терминологию, хотелось бы дать определения некоторым элементам графа таким, как маршрут, цепь, цикл.
Маршрутом в графе G(V,E) называется чередующаяся последовательность вершин и ребер: v0,e1, … en,vn, в которой любые два соседних элемента инцидентны. Если v0 = vn, то маршрут замкнут, иначе открыт.
Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, ребра) различны, то маршрут называется простой цепью.
Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Граф без циклов называется ациклическим. Для орграфов цепь называется путем, а цикл — контуром.
Глава 1. Эйлеровы циклы
Требуется найти цикл, проходящий по каждой дуге ровно один раз. Эту задачу впервые поставил и решил Леонард Эйлер, чем и заложил основы теории графов, а соответствующие циклы теперь называются эйлеровыми. Фигуры, которые требуется обрисовать, не прерывая и не повторяя линии, также относятся к эйлеровым циклам.
Задача возникла из предложенной Эйлеру головоломки, получившей название "проблема кенигсбергских мостов". Река Прегель, протекающая через Калининград (прежде город назывался Кенигсбергом), омывает два острова. Берега реки связаны с островами так,
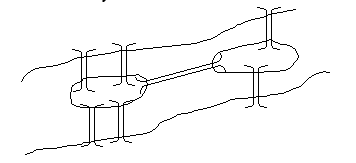
как
это показано
на рисунке.
В головоломке требовалось найти маршрут, проходящий по всем участкам суши таким образом, чтобы каждый из мостов был пройден ровно один раз, а начальный и конечный пункты маршрута совпадали.
§1. Основные понятия и определения
Дадим теперь строгое определение эйлерову циклу и эйлерову графу. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.
Ясно, что эйлеров цикл содержит не только все ребра по одному разу, но и все вершины графа (возможно, по несколько раз). Очевидно также, что эйлеровым может быть только связный граф.
Выберем в качестве вершин графа берега реки, а в качестве ребер - мосты, их соединяющие. После этого задача становится очевидной: требование неосуществимо - чтобы его выполнить, число дуг, приходящих к каждой вершине, должно быть четным. В самом деле, поскольку по одному мосту нельзя проходить дважды, каждому входу на берег должен соответствовать выход.
§2. Критерий существования эйлерова цикла
Что необходимо, чтобы в графе существовал эйлеров цикл? Во-первых, граф должен быть связанным: для любых двух вершин должен существовать путь, их соединяющий. Во-вторых, для неориентированных графов число ребер в каждой вершине должно быть четным. На самом деле этого оказывается достаточно.
Теорема 1. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным.
Доказательство.
Необходимость. Любой эйлеров цикл должен прийти в вершину по одному ребру и покинуть ее по другому, так как любое ребро должно использоваться ровно один раз. Поэтому, если G содержит эйлеров цикл, то степени вершин должны быть четными.
Достаточность. Пусть G — связный неориентированный граф, все вершины которого имеют четную степень. Начнем путь из некоторой произвольной вершины x0 и пойдем по некоторому ранее не использованному ребру к следующей вершине, и так до тех пор, пока не вернемся в вершину x0 и не замкнем цикл. Если все ребра окажутся использованными, то нужный эйлеров цикл построен. Если же некоторые ребра не использованы, то пусть Ф — только что построенный цикл. Так как граф G связен, то цикл Ф должен проходить через некоторую вершину, скажем xi, являющуюся конечной вершиной какого-либо до сих пор не использованного ребра. Если удалить все ребра, принадлежащие Ф, то в оставшемся графе все вершины по-прежнему будут иметь четную степень, так как в цикле Ф должно быть четное число ребер (0 является четным числом), инцидентных каждой вершине.
Начиная теперь с xi, получаем цикл Ф’, начинающийся и оканчивающийся в xi. Если все оставшиеся ранее ребра использованы для цикла Ф’, то процесс окончен. Нужный эйлеров цикл будет образован частью цикла Ф от вершины x0 до xi, затем циклом Ф’ и, наконец, частью цикла Ф от вершины xi до x0. Если же все еще остались неиспользованные ребра, то объединение построенных выше циклов Ф и Ф’ дает новый цикл Ф. Мы снова можем найти вершину xj, принадлежащую циклу и являющуюся концевой вершиной некоторого неиспользованного ребра. Затем мы можем приступить к построению нового цикла Ф’, начинавшегося в xj, и так до тех пор, пока не будут использованы все ребра и не будет получен таким образом эйлеров цикл Ф. Это доказывает теорему.
Хотя доказательство проведено для неориентированных графов, оно сразу переносится на ориентированные, только требование четности заменяется теперь на такое: число входящих в каждую вершину ребер должно быть равно числу выходящих.
Следствие #1.
Для связного эйлерова графа G множество ребер можно разбить на простые циклы.
Следствие #2.
Для того чтобы связный граф G покрывался единственной эйлеровой цепью, необходимо и достаточно, чтобы он содержал ровно 2 вершины с нечетной степенью. Тогда цепь начинается в одной из этих вершин и заканчивается в другой.
§3. Алгоритмы построения эйлерова цикла
Выше был установлен эффективный способ проверки наличия эйлерова цикла в графе. А именно, для этого необходимо и достаточно убедиться, что степени всех вершин четные, что нетрудно сделать при любом представлении графа. Осталось заметить, что предложенный в доказательстве алгоритм линеен, т.е. число действий прямо пропорционально числу ребер.
Алгоритм построения эйлерова цикла в эйлеровом графе.
Вход: эйлеров граф G(V,E), заданный матрицей смежности. Для простоты укажем, что Г[v]— множество вершин, смежных с вершиной v.
Выход: последовательность вершин эйлерова цикла.
S:=Ш {стек для хранения вершин}
select
v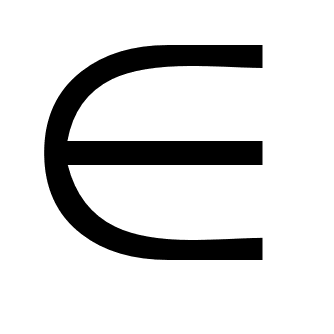 V
{произвольная
вершина}
V
{произвольная
вершина}
v→S {положить v в стек S}
while S≠Ш do
v←S; v→S {v — верхний элемент стека}
if Г[v]=Ш then
v←S;
yield v
else
select
u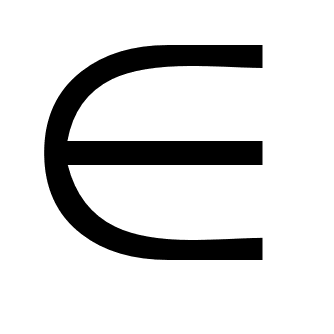 Г[v]
{взять первую
вершину из
списка смежности}
Г[v]
{взять первую
вершину из
списка смежности}
u→S {положить u в стек}
Г[v]:=Г[v]\{u}; Г[u]:=Г[u]\{v} {удалить ребро (v,u)}
end if
end while
Обоснование алгоритма.
Принцип действия этого алгоритма заключается в следующем. Начиная с произвольной вершины, строим путь, удаляя ребра и запоминая вершины в стеке, до тех пор пока множество смежности очередной вершины не окажется пустым, что означает, что путь удлинить нельзя. Заметим, что при этом мы с необходимостью придем в ту вершину, с которой начали. В противном случае это означало бы, что вершина v имеет нечетную степень, что невозможно по условию. Таким образом, из графа были удалены ребра цикла, а вершины цикла были сохранены в стеке S. Заметим, что при этом степени всех вершин остались четными. Далее вершина v выводится в качестве первой вершины эйлерова цикла, а процесс продолжается, начиная с вершины, стоящей на вершине стека.
Мне бы хотелось привести здесь еще один алгоритм построения эйлерова цикла в эйлеровом графе — это Алгоритм Флёри, он позволяет пронумеровать ребра исходного графа так, чтобы номер ребра указывал каким по счету это ребро войдет эйлеров цикл.
Алгоритм Флёри:
1. Начиная с любой вершины v присваиваем ребру vu номер 1. Вычеркиваем это ребро из списка ребер и переходим к вершине u.
2. Пусть w - вершина, в которую мы пришли в результате выполнения 1 шага алгоритма и k - номер, присвоенный очередному ребру на этом шаге. Выбираем произвольное ребро инцидентное вершине w, причем мост выбираем только в крайнем случае, если других возможностей выбора ребра не существует. Присваиваем ребру номер k+1 и вычеркиваем его. Процесс длится до тех пор, пока все ребра не вычеркнут.
Примечание: Мостом называется ребро, удаление которого лишает данный граф связности, т.е. увеличивает число компонент связности.
Пример:
П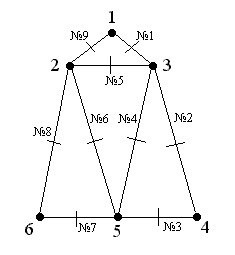
риведем
теперь строгое
обоснование
корректности
алгоритма Флёри
построения
эйлерового
цикла в данном
эйлеровом
графе.
Теорема 2. Пусть G(V,E) — эйлеров граф. Тогда следующая процедура всегда возможна и приводит к построению эйлерова цикла графа G(V,E).
Выходя из произвольной вершины, идем по ребрам графа произвольным образом, соблюдая при этом следующие правила:
Стираем ребра по мере их прохождения (вместе с изолированными вершинами, которые при этом образуются);
На каждом шаге идем по мосту только в том случае, когда нет других возможностей.
Доказательство.
Убедимся сначала, что указанная процедура может быть выполнена на каждом этапе. Пусть мы достигли некоторой вершины v, начав с вершины u, v ≠ u. Удалив ребра пути из v в u, видим, что оставшийся граф G1 связен и содержит ровно две нечетных вершины v и u. Согласно следствию #2 из теоремы 1 граф G1 имеет эйлеров путь P из v в u. Поскольку удаление первого ребра инцидентного u пути P либо не нарушает связности G1, либо происходит удаление вершины u и оставшийся граф G2 связен с двумя нечетными вершинами, то отсюда получаем, что описанное выше построение всегда возможно на каждом шаге. (Если v = u, то доказательство не меняется, если имеются ребра, инцидентные u). Покажем, что данная процедура приводит к эйлерову пути. Действительно, в G не может быть ребер, оставшихся не пройденными после использования последнего ребра, инцидентного u, поскольку в противном случае удаление ребра, смежного одному из оставшихся, привело бы к несвязному графу, что противоречит условию 2).
§4. Некоторые родственные задачи
Сразу же укажем ряд вопросов, связанных с тем, имеется ли в неориентированном графе эйлеров цикл. Например,
Каково наименьшее число цепей или циклов необходимое для того, чтобы каждое ребро графа G содержалось точно в одной цепи или в одном цикле? Очевидно, что если G имеет эйлеров цикл или эйлерову цепь, то ответом будет число один.
Р
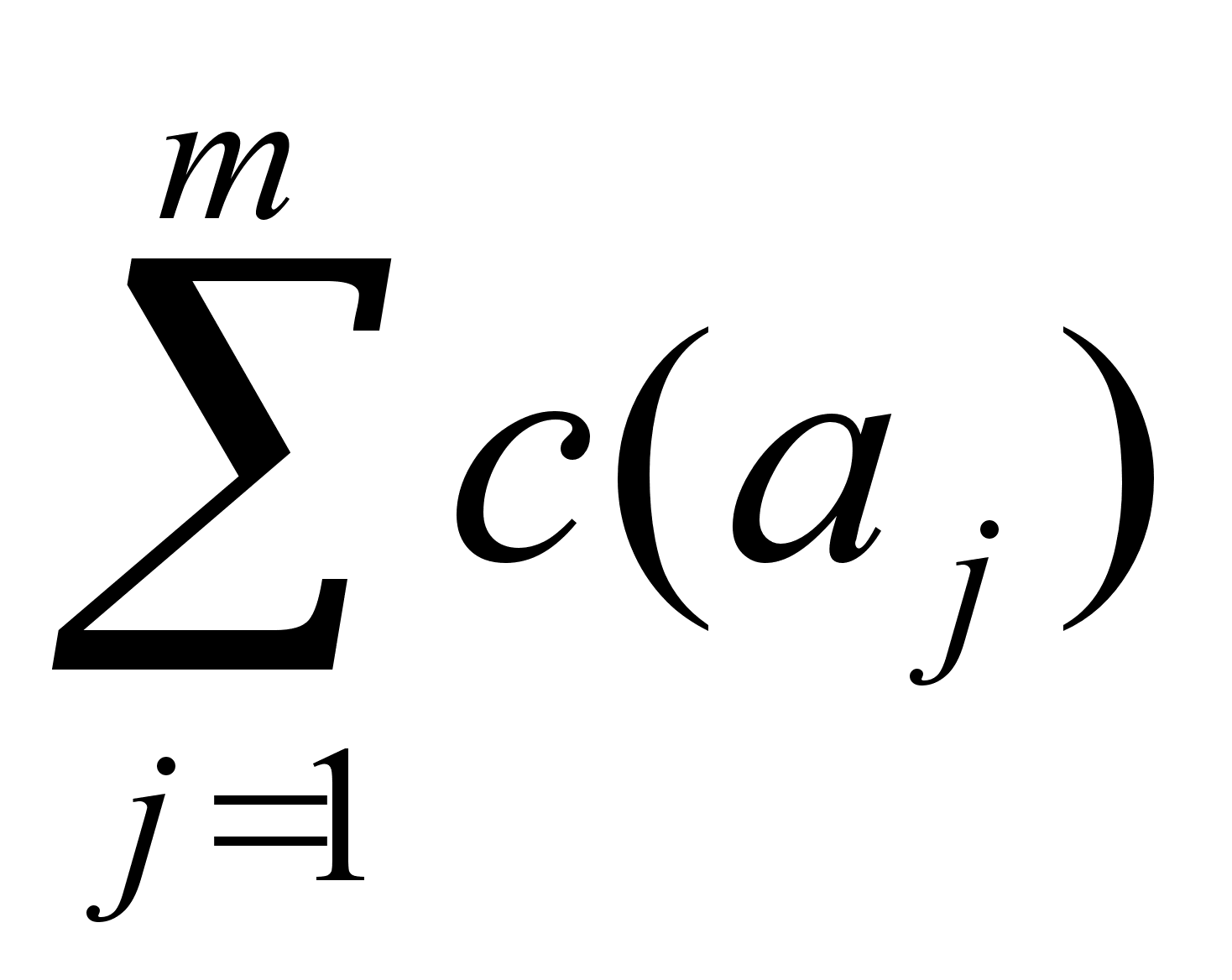
ебрам графа G приписаны положительные веса. Требуется найти цикл, проходящий через каждое ребро графа G по крайней мере один раз и такой, что для него общий вес (а именно сумма величин njc(aj), где число nj показывает, сколько раз проходилось ребро aj, а c(aj) — вес ребра) минимален. Очевидно, что если G содержит эйлеров цикл, то любой такой цикл будет оптимальным, так как каждое ребро проходится по один раз и вес этого цикла равен тогда
Сформулированная выше задача 2) называется задачей китайского почтальона, и ее решение имеет много потенциальных приложений, как например:
Сбор мусора. Рассмотрим проблему сбора домашнего мусора. Допустим, что определенный район города обслуживается единственной машиной. Ребра графа G представляют дороги, а вершины — пересечения дорог. Величина c(aj) — вес ребра — будет соответствовать длине дороги. Тогда проблема сбора мусора в данном районе сводится к нахождению цикла в графе G, проходящего по каждому ребру G по крайней мере один раз. Требуется найти цикл с наименьшим километражем.
Доставка молока или почты. Еще две задачи, когда требуется определить маршрут, проходящий хотя бы один раз по каждой из улиц, возникают при доставке молока или почты. Здесь задача состоит в нахождении маршрута, минимизирующего общий километраж (или время, стоимость и т.д.).
Проверка электрических, телефонных или железнодорожных линий. Проблема инспектирования распределенных систем (лишь некоторые из которых названы выше) связана с непременным требованием проверки всех «компонент». Поэтому она также является проблемой типа 2) или близка к ней.
§5. Задача китайского почтальона
Р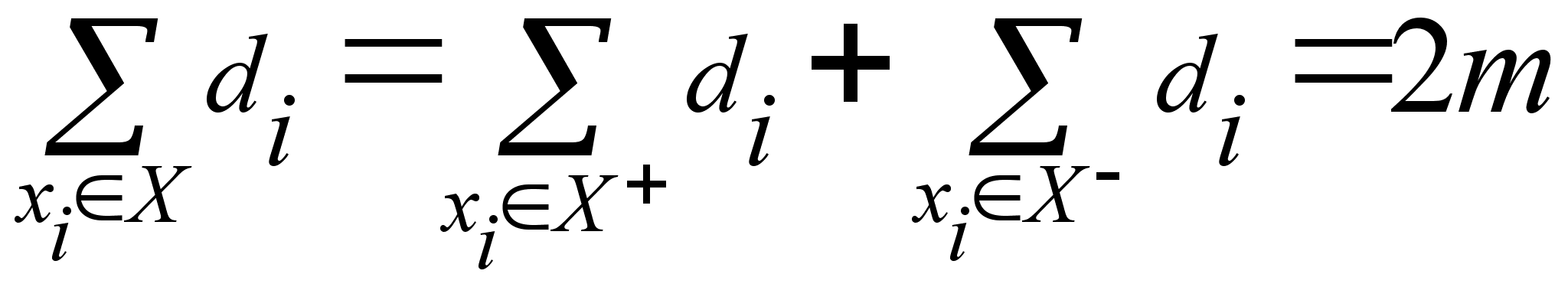
ассмотрим
неориентированный
граф G(X,A).
Среди вершин
из X некоторые
вершины (скажем
из множества
X+) будут
иметь четные
степени, а остальные
(из множества
X-=X\X+)
— нечетные
степени. Сумма
степеней di
всех вершин
xi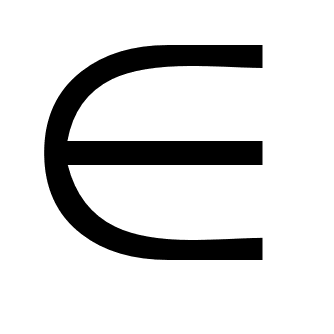 X
равна удвоенному
числу ребер
в A (т.к. каждое
ребро добавляет
по единице к
степеням двух
его концевых
вершин) и поэтому
равна четному
числу 2m.
Следовательно,
и так как первая
сумма четна,
то вторая сумма
также четна.
Но все di
в последней
сумме нечетны,
значит число
|X-| вершин
нечетной степени
четно.
X
равна удвоенному
числу ребер
в A (т.к. каждое
ребро добавляет
по единице к
степеням двух
его концевых
вершин) и поэтому
равна четному
числу 2m.
Следовательно,
и так как первая
сумма четна,
то вторая сумма
также четна.
Но все di
в последней
сумме нечетны,
значит число
|X-| вершин
нечетной степени
четно.
Пусть M —
множество таких
цепей (скажем
μij) в G
между концевыми
вершинами xi
и xj
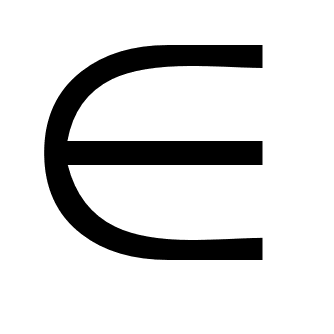 X-, что
никакие две
цепи не имеют
одинаковых
конечных вершин,
т.е. цепи соединяют
различные пары
вершин из X-
и покрывают
все вершины
множества X-.
Число цепей
μij в M
равно 1/2|X-|
и всегда цело,
если конечно
оно определено.
Предположим
теперь, что все
ребра, образующие
цепь μij,
теперь удвоены
(добавлены
искусственные
ребра). Так поступаем
с каждой цепью
μij
X-, что
никакие две
цепи не имеют
одинаковых
конечных вершин,
т.е. цепи соединяют
различные пары
вершин из X-
и покрывают
все вершины
множества X-.
Число цепей
μij в M
равно 1/2|X-|
и всегда цело,
если конечно
оно определено.
Предположим
теперь, что все
ребра, образующие
цепь μij,
теперь удвоены
(добавлены
искусственные
ребра). Так поступаем
с каждой цепью
μij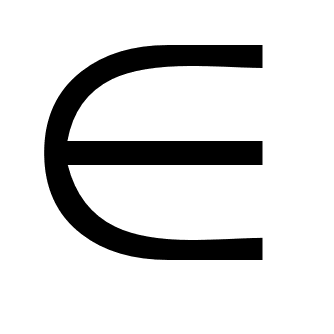 M
и полученный
граф обозначим
через G-(M).
Так как некоторые
ребра из G
могут входить
более чем в
одну цепь μij,
то некоторые
ребра из G-(M)
могут быть
(после того как
добавлены все
«новые» цепи
μij) утроены,
учетверены
и т.д.
M
и полученный
граф обозначим
через G-(M).
Так как некоторые
ребра из G
могут входить
более чем в
одну цепь μij,
то некоторые
ребра из G-(M)
могут быть
(после того как
добавлены все
«новые» цепи
μij) утроены,
учетверены
и т.д.
Теорема 3. Для любого цикла, проходящего по G, можно выбрать множество M, для которого граф G-(M) имеет эйлеров цикл, соответствующий первоначально взятому циклу в графе G. Это соответствие таково, что если цикл проходит по ребру (xi, xj) из G l раз, то в G-(M) существует l ребер (одно реальное и l-1 искусственных) между xi и xj, каждое из которых проходится ровно один раз эйлеровым циклом из G-(M). Справедливо и обратное утверждение.
Доказательство.
Если цикл проходит
по графу G,
то по крайней
мере одно ребро,
инцидентное
каждой вершине
xi
нечетной степени,
должно проходиться
дважды. (Ребро,
проходимое
дважды, можно
рассматривать
как два параллельных
ребра — одно
реальное и одно
искусственное
— и каждое из
них проходится
один раз). Пусть
это ребро (xi,
xk). В
случае нечетности
степени dk
вершины xk
графа G
добавление
искусственного
ребра прежде
всего сделает
dk
четным, и значит
только ребро
(xi,xk)
нужно будет
проходить
дважды, если
ограничиться
рассмотрением
лишь вершин
xi и
xk. В
случае когда
dk
четно, добавление
искусственного
ребра сделает
dk
нечетным, а
второе ребро
выходящее из
xk
должно быть
пройдено дважды
(т.е. добавляется
еще одно искусственное
ребро). Такая
ситуация сохраняется
до тех пор, пока
не встретится
вершина нечетной
степени, о чем
говорилось
выше. Следовательно,
чтобы удовлетворить
условию возвращения
в вершину xi,
нужно дважды
пройти всю цепь
из xi
в некоторую
другую вершину
нечетной степени
xr
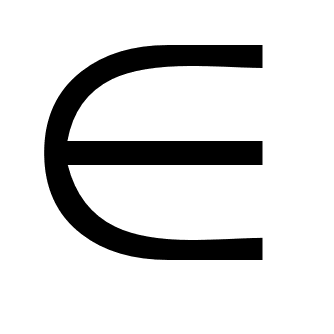 X-. Это
автоматически
приводит к
выполнению
условия прохождения
вершины xr.
Аналогично
обстоит дело
для всех других
вершин xi
X-. Это
автоматически
приводит к
выполнению
условия прохождения
вершины xr.
Аналогично
обстоит дело
для всех других
вершин xi
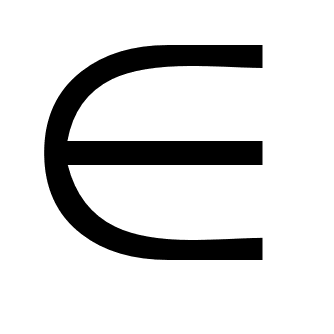 X-. Это
значит что все
множество M
цепей из G,
определенное
выше, должно
проходится
дважды, и так
как отсюда
вытекает, что
каждое ребро
из G-(M)
должно проходиться
один раз, то
теорема доказана.
X-. Это
значит что все
множество M
цепей из G,
определенное
выше, должно
проходится
дважды, и так
как отсюда
вытекает, что
каждое ребро
из G-(M)
должно проходиться
один раз, то
теорема доказана.
Алгоритм решения задачи китайского почтальона немедленно следует из доказанной теоремы, так как все, что для этого необходимо, состоит в нахождении множества цепей M* (цепного паросочетания для множества вершин нечетной степени), дающего наименьший дополнительный вес. Цикл наименьшего веса, проходящий по G, будет иметь вес, равный сумме весов всех ребер из G плюс сумма весов ребер в цепях из M*. Это то же самое, что и сумма весов всех ребер — реальных и искусственных — графа G-(M*).
Описание алгоритма решения задачи китайского почтальона:
Пусть [cij] — матрица весов ребер G. Используя алгоритм нахождения кратчайшей цепи, образуем |X-|*|X-| — матрицу D=[dij], где dij — вес цепи наименьшего веса, идущей из некоторой вершины xi
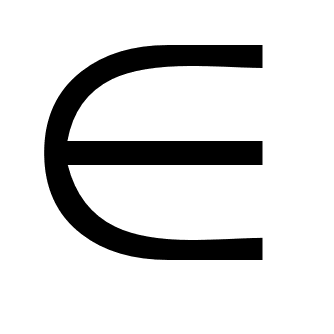 X-
в другую вершину
xj
X-
в другую вершину
xj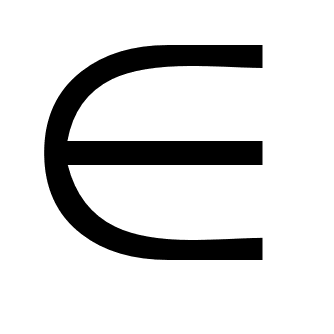 X-.
X-.Найдем то цепное паросочетание M* для множества X-, которое дает наименьший вес (в соответствии с матрицей весов D). Это можно сделать эффективно с помощью алгоритма минимального паросочетания.
Если вершина xα сочетается с другой вершиной xβ, то определим цепь μαβ наименьшего веса (из xα в xβ), соответствующую весу dαβ, делая шаг 1. Добавим искусственные ребра в G, соответствующие ребрам из μαβ, и проделаем это для всех других цепей из множества M*, в результате чего получится граф G-(M*).
Сумма весов всех ребер графа G-(M*), найденная с использованием матрицы [cij] (вес искусственного ребра берется равным весу параллельного ему реального ребра), равна минимальному весу цикла, проходящего по G. При этом число прохождений цикла по ребру (xi,xj) равно общему числу параллельных ребер между xi и xj в G-(M*).
Покажем, что указанный выше алгоритм строит минимальный цикл. Для этого следует заметить, что поскольку на шаге 2 мы используем минимальное паросочетание, никакие две кратчайшие цепи μij и μpq при таком паросочетании (скажем, идущие из xi в xj и из xp в xq) не могут иметь общего ребра. Если бы они имели общее ребро (xa, xb), то сочетание вершин xi и xq (использующее подцепи от xi к xb и от xb к xq) и сочетание пары вершин xp и xj (использующее подцепи от xp к xa и от xa к xj) давало бы общее паросочетание веса 2cab, меньшего чем вес первоначального паросочетания, что противоречит предположению о минимальности исходного паросочетания. Следовательно, граф G-(M*)не должен содержать более двух параллельных ребер между любыми двумя вершинами, т.е. оптимальный цикл не проходит ни по какому ребру графа G более чем два раза.
Н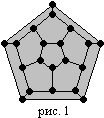 азвание
«гамильтонов
цикл» произошло
от задачи
«Кругосветное
путешествие»
предложенной
ирландским
математиком
Вильямом Гамильтоном
в 1859 году. Нужно
было, выйдя из
исходной вершины
графа, обойти
все его вершины
и вернуться
в исходную
точку. Граф
представлял
собой укладку
додекаэдра,
каждой из 20 вершин
графа было
приписано
название крупного
города мира.
азвание
«гамильтонов
цикл» произошло
от задачи
«Кругосветное
путешествие»
предложенной
ирландским
математиком
Вильямом Гамильтоном
в 1859 году. Нужно
было, выйдя из
исходной вершины
графа, обойти
все его вершины
и вернуться
в исходную
точку. Граф
представлял
собой укладку
додекаэдра,
каждой из 20 вершин
графа было
приписано
название крупного
города мира.
§1. Основные понятия и определения
Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Граф, который содержит простой путь, проходящий через каждую его вершину, называется полугамильтоновым. Это определение можно распространить на ориентированные графы, если путь считать ориентированным.
Гамильтонов цикл не обязательно содержит все ребра графа. Ясно, что гамильтоновым может быть только связный граф и, что всякий гамильтонов граф является полугамильтоновым. Заметим, что гамильтонов цикл существует далеко не в каждом графе.
Замечание.
Любой граф G
можно превратить
в гамильтонов
граф, добавив
достаточное
количество
вершин. Для
этого, например,
достаточно
к вершинам
v1,…,vp
графа G
добавить вершины
u1,…,up
и множество
ребер {(vi,ui)}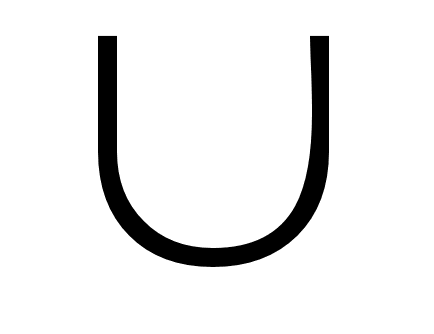 {(ui,vi+1)}.
{(ui,vi+1)}.
Степенью вершины v называется число ребер d(v), инцидентных ей, при этом петля учитывается дважды. В случае ориентированного графа различают степень do(v) по выходящим дугам и di(v) — по входящим.
§2. Условия существования гамильтонова цикла
В отличии от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет. Более того, задача проверки существования гамильтонова цикла оказывается NP-полной. Большинство известных фактов имеет вид: «если граф G имеет достаточное количество ребер, то граф является гамильтоновым». Приведем несколько таких теорем.
Теорема Дирака.
Если в графе
G(V,E)
c n вершинами
(n ≥ 3) выполняется
условие d(v)
≥ n/2 для любого
v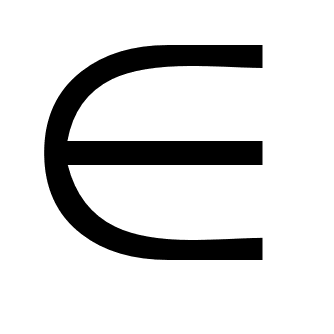 V,
то граф G
является
гамильтоновым.
V,
то граф G
является
гамильтоновым.
Доказательство.
От противного. Пусть G — не гамильтонов. Добавим к G минимальное количество новых вершин u1, … ,un, соединяя их со всеми вершинами G так, чтобы G’:= G + u1 + … + un был гамильтоновым.
Пусть v, u1,
w, … ,v —
гамильтонов
цикл в графе
G’, причем
v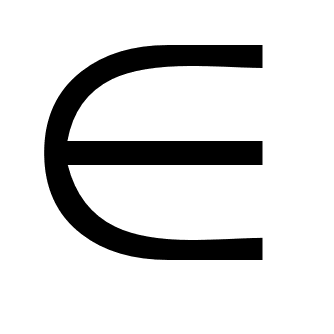 G,
u1
G,
u1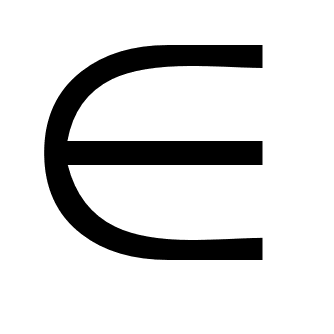 G’,
u1
G’,
u1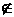 G.
Такая пара
вершин v
и u1 в гамильтоновом
цикле обязательно
найдется, иначе
граф G был
бы гамильтоновым.
Тогда w
G.
Такая пара
вершин v
и u1 в гамильтоновом
цикле обязательно
найдется, иначе
граф G был
бы гамильтоновым.
Тогда w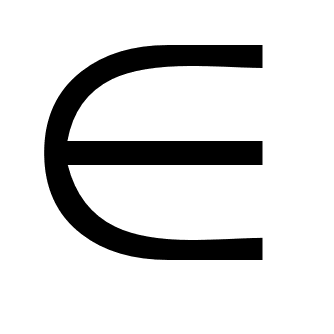 G,
w
G,
w
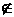 {u1,…,un},
иначе вершина
u1 была
бы не нужна.
Более того,
вершина v
несмежна с
вершиной w,
иначе вершина
u1 была
бы не нужна.
{u1,…,un},
иначе вершина
u1 была
бы не нужна.
Более того,
вершина v
несмежна с
вершиной w,
иначе вершина
u1 была
бы не нужна.
Далее, если в цикле v,u1,w, … ,u’,w’, … ,v есть вершина w’, смежная с вершиной w, то вершина v’ несмежна с вершиной v, так как иначе можно было бы построить гамильтонов цикл v,v’, … ,w,w’, … ,v без вершины u1, взяв последовательность вершин w, … ,v’ в обратном порядке. Отсюда следует, что число вершин графа G’, не смежных с v, не менее числа вершин, смежных с w. Но для любой вершины w графа G d(w) ≥ p/2+n по построению, в том числе d(v) ≥ p/2+n. Общее число вершин (смежных и не смежных с v) составляет n+p-1. Таким образом, имеем:
n+p-1 = d(v)+d(V) ≥ d(w)+d(v) ≥ p/2+n+p/2+n = 2n+p.
Следовательно, 0 ≥ n+1, что противоречит тому, что n > 0.
Теорема Оре. Если число вершин графа G(V,E) n ≥ 3 и для любых двух несмежных вершин u и v выполняется неравенство:
d(u)+d(v)
≥ n и
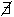 (u,v)
(u,v)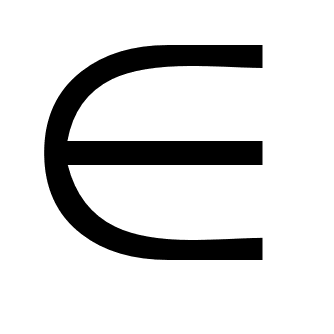 E,
то граф G
— гамильтонов.
E,
то граф G
— гамильтонов.
Граф G имеет гамильтонов цикл если выполняется одно из следующих условий:
Условие Поша: d(vk) ≥ k+1 для k < n/2.
Условие Бонди: из d(vi) ≤ i и d(vk) ≤ k => d(vi)+d(vk)≥n (k≠i)
Условие Хватала: из d(vk) ≤ k ≤ n/2 => d(vn-k) ≥ n-k.
Далее, известно, что почти все графы гамильтоновы, то есть
г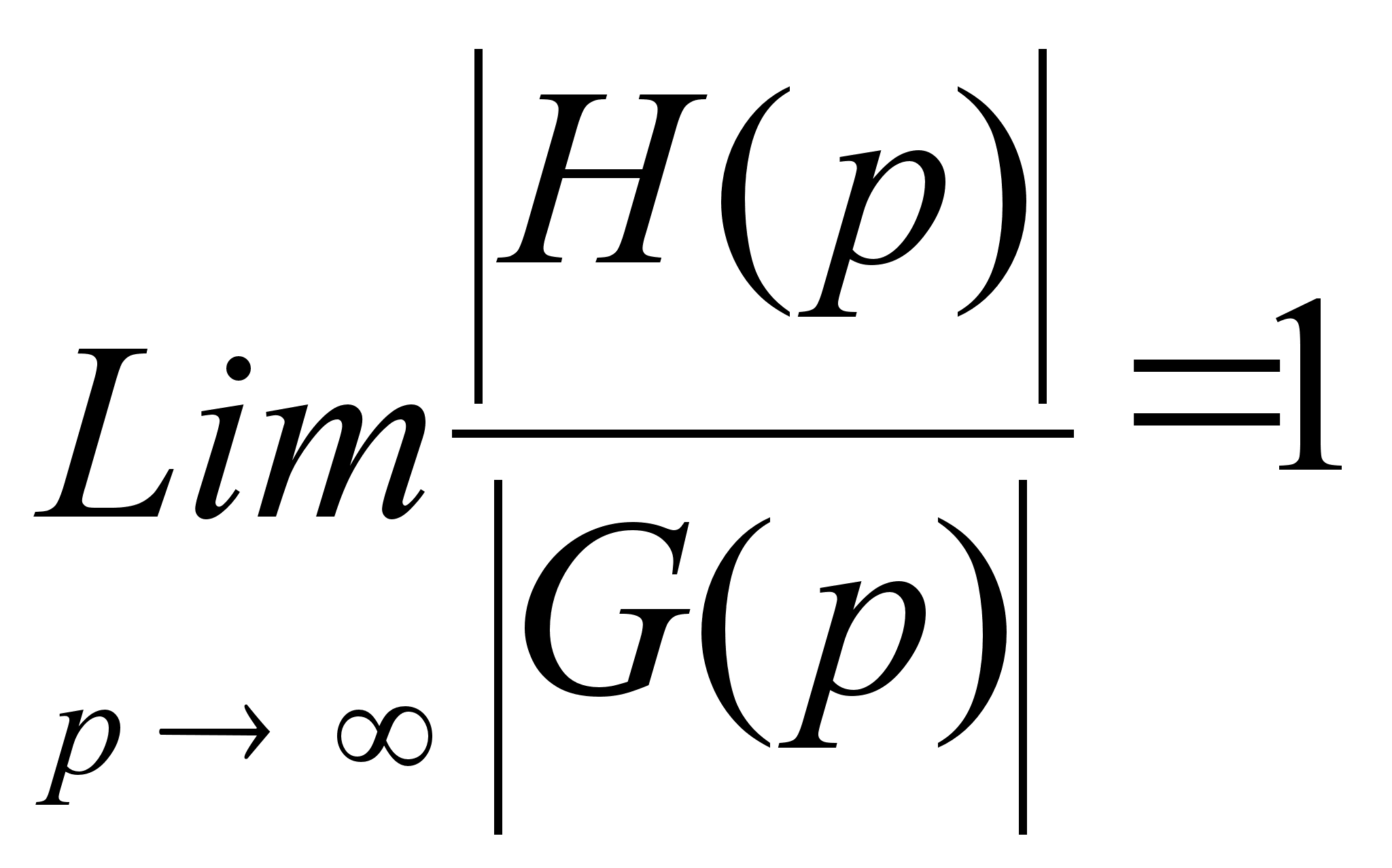
де
H(p) —
множество
гамильтоновых
графов с p
вершинами, а
G(p) —
множество всех
графов с p
вершинами.
Таким образом,
задача отыскания
гамильтонова
цикла или
эквивалентная
задача коммивояжера
являются практически
востребованными,
но для нее неизвестен
(и, скорее всего
не существует)
эффективный
алгоритм решения.
Пример графа, когда не выполняется условие теоремы Дирака, но граф является гамильтоновым.
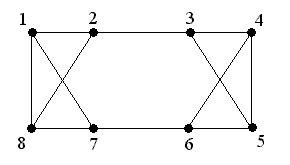
N = 8; d(vi) = 3; 3 ≥ 8/2 = 4 не гамильтонов граф, но существует гамильтонов цикл: M = (1, 2, 3, 4, 5, 6, 7, 8, 1)
§3. Задачи связанные с поиском гамильтоновых циклов
В ряде отраслей промышленности возникает следующая задача планирования. Нужно произвести n продуктов, используя единственный тип аппаратуры. Аппарат должен быть перенастроен после того как был произведен продукт pi (но до того как начато производство продукта pj), в зависимости от комбинации (pi,pj). Стоимость перенастройки аппаратуры постоянна и не зависит от производимых продуктов. Предположим, что эти продукты производятся в непрерывном цикле, так что после производства последнего из n продуктов снова возобновляется в том же фиксированном цикле производство первого продукта.
Возникает вопрос о том, может ли быть найдена циклическая последовательность производства продуктов pi (i=1,2,…,n), не требующая перенастройки аппаратуры. Если представить эту задачу в виде ориентированного графа, то ответ на поставленный вопрос зависит от того, имеет ли этот ориентированный граф гамильтонов цикл или нет.
Если не существует циклической последовательности продуктов, не требующей перенастройки аппаратуры, то какова должна быть последовательность производства с наименьшими затратами на перенастройку, т.е. требующая наименьшего числа необходимых перенастроек?
Таким образом мы рассмотрим следующие две задачи.
Задача 1. Дан ориентированный граф G, требуется найти в G гамильтонов цикл (или все циклы), если существует хотя бы один такой цикл.
Задача 2. Дан полный ориентированный цикл G, дугам которого приписаны произвольные веса C=[cij], найти такой гамильтонов цикл, который имеет наименьший общий вес. Следует отметить, что если ориентированный граф G не полный, то его можно рассматривать как полный ориентированный граф, приписывая отсутствующим дугам бесконечный вес.
Алгоритмы решения задачи коммивояжера и ее вариантов имеют большое число практических приложений в различных областях человеческой деятельности. Рассмотрим, например, задачу в которой грузовик выезжает с центральной базы для доставки товаров данному числу потребителей и возвращается назад на базу. Стоимость перевозки пропорциональна пройденному грузовиком расстоянию, и при заданной матрице расстояний между потребителями маршрут с наименьшими транспортными затратами получается как решение соответствующей задачи коммивояжера. Аналогичные типы задач возникают при сборе почтовых отправлений из почтовых ящиков, составлении графика движения школьных автобусов по заданным остановкам и т.д. Задача очень легко обобщается и на тот случай, когда доставкой (сбором) занимаются несколько грузовиков, хотя эту задачу можно также переформулировать как задачу коммивояжера большей размерности. Другие приложения включают составление расписания выполнения операций на машинах, проектирование электрических сетей, управление автоматическими линиями и т.д.
Очевидно, что сформулированная выше задача (1) является частным случаем задачи (2). В самом деле, приписывая случайным образом дугам заданного ориентированного графа G конечные веса, получаем задачу коммивояжера. Если решение для этой задачи, т.е. кратчайший гамильтонов цикл, имеет конечное значение, то это решение является гамильтоновым циклом ориентированного графа G (т.е. ответом на задачу 1). Если же решение имеет бесконечное значение, то G не имеет гамильтонова цикла.
С другой стороны можно дать еще одну интерпретацию задачи 1). Рассмотрим снова полный ориетированный граф G1 с общей матрицей весов дуг [cij] и рассмотрим задачу нахождения такого гамильтонова цикла, в котором самая длинная дуга минимальна. Эту задачу можно назвать минимаксной задачей коммивояжера. Тогда классическую задачу коммивояжера в той же терминологии можно было бы назвать минисуммной задачей коммивояжера. Покажем теперь, что задача (1) действительно эквивалентна минимаксной задаче коммивояжера.
В вышеупомянутом полном ориентированном графе G1 мы можем наверняка найти гамильтонов цикл. Пусть это будет цикл Ф1, и пусть вес самой длинной его дуги равен ĉ1. Удалив из G1 любую дугу, вес которой не меньше ĉ1, получим ориентированный граф G2. Найдем в ориентированном графе G2 гамильтонов цикл Ф2, и пусть вес его самой длинной дуги равен ĉ2. Удалим из G2 любую дугу, вес которой не меньше ĉ2, и так будем продолжать до тех пор, пока не получим ориентированный граф Gm+1, не содержащий никакого гамильтонова цикла. Гамильтонов цикл Фm в Gm (с весом ĉm) является тогда по определению решением минимаксной задачи коммивояжера, так как из отсутствия гамильтонова цикла в Gm+1 следует, что в G1 не существует никакого гамильтонова цикла, не использующего по крайней мере одну дугу с весом, большим или равным ĉm.
Таким образом, алгоритм нахождения гамильтонова цикла в ориентированном графе решает также минимаксную задачу коммивояжера. Наоборот, если мы располагаем алгоритмом решения последней задачи, то гамильтонов цикл в произвольном ориентированном графе G может быть найден с помощью построения полного ориентированного графа G1 с тем же самым множеством вершин, что и в G, дугам которого, соответствующим дугам из G, приписаны единичные веса, а остальным дугам — бесконечные веса. Если решение минимаксной задачи коммивояжера для G1 имеет конечный вес (на самом деле равный единице), то в графе G может быть найден соответствующий гамильтонов цикл. Если же решение имеет бесконечный вес, то в графе G не существует никакого гамильтонова цикла. Следовательно, две указанные задачи можно рассматривать как эквивалентные, поскольку было продемонстрировано, что алгоритм нахождения гамильтонова цикла позволяет решать минимаксную задачу коммивояжера и наоборот.
Ввиду того, что обе сформулированные выше задачи (1) и (2) часто встречаются в практических ситуациях и (как мы увидим позже) задачу (1) саму по себе решить намного проще, чем как подзадачу задачи (2), мы обе эти задачи рассмотрим по отдельности.
§4. Методы построения гамильтоновых циклов в графе.
Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе G гамильтонов цикл. Критерии существования, данные выше, представляют теоретический интерес, но являются слишком общими и не пригодны для произвольных графов, встречающихся на практике. Алгебраические методы определения гаильтоновых циклов не могут быть применены с более чем несколькими десятками вершин, так как они требуют слишком большого времени работы и большой памяти компьютера. Более приемлемым является способ Робертса и Флореса, который не предъявляет чрезмерных требований к памяти компьютера, но время в котором зависит экспоненциально от числа вершин в графе. Однако другой неявный метод перебора имеет для большинства типов графов очень небольшой показатель роста времени вычислений в зависимости от числа вершин. Он может быть использован для нахождения гамильтоновых циклов в очень больших графах. Ниже будут описаны алгебраический метод, перебор с возвратами, его улучшение, мультицепной метод.
§5. Алгебраический метод построения гамильтоновых циклов
Этот метод
включает в себя
построение
всех простых
цепей с помощью
последовательного
перемножения
матриц. «Внутреннее
произведение
вершин» цепи
x1, x2,
… ,xk-1,
xk
определяется
как выражение
вида x2*x3*
… xk-1,
не содержащее
две концевые
вершины x1
и xk.
«Модифицированная
матрица смежности»
B=[β(i,j)]
— это (nЧn)-
матрица, в которой
β(i,j) —
xj,
если существует
дуга из xi
в xj
и нуль в противном
случае. Предположим
теперь, что у
нас есть матрица
PL
= [pL(i
,j)], где pL(i,j)
— сумма внутренних
произведений
всех простых
цепей длины
L (L≥1) между
вершинами xi
и xj
для xi≠xj.
Положим pL(i,i)=0
для всех i.
Обычное алгебраическое
произведение
матриц B*PL
= P’L+1
= [p’L+1(s,t)]
определяется
как
т.е. p’L+1(s,t)
является суммой
внутренних
произведений
всех цепей из
xs в
xt
длины l+1.
Так как все
цепи из xk
в xt,
представленные
внутренними
произведениями
из pL(k,t),
являются простыми,
то среди цепей,
получающихся
из указанного
выражения, не
являются простыми
лишь те, внутренние
произведения
которых в pL(k,t)
содержат вершину
xs.
Таким образом,
если из p’L+1(s,t)
исключить все
слагаемые,
содержащие
xs
(а это можно
сделать простой
проверкой), то
получим pL+1(s,t).
Матрица PL+1=[pL+1(s,t)],
все диагональные
элементы которой
равны 0, является
тогда матрицей
всех простых
цепей длины
L+1.
В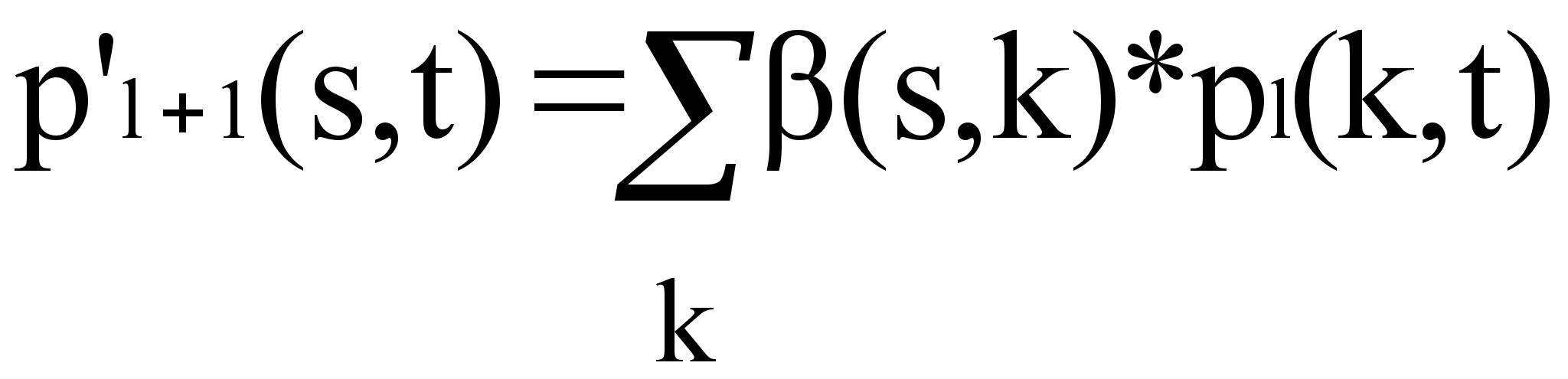
ычисляя
затем B*PL+1,
находим PL+2
и т.д., пока не
будет построена
матрица Pn-1,
дающая все
гамильтоновы
цепи (имеющие
длину n-1)
между всеми
парами вершин.
Гамильтоновы
циклы получаются
тогда сразу
из цепей в Pn-1
и тех дуг из
G, которые
соединяют
начальную и
конечную вершины
каждой цепи.
С другой стороны,
гамильтоновы
циклы даются
членами внутреннего
произведения
вершин, стоящими
в любой диагональной
ячейке матрицы
B*Pn-1
(все диагональные
элементы этой
матрицы одинаковые).
Очевидно, что в качестве начального значения матрицы P (т.е. P1) следует взять матрицу смежности A графа, положив все ее диагональные элементы равными нулю.
Недостатки этого метода совершенно очевидны. В процессе умножения матриц (т.е. когда L увеличивается) каждый элемент матрицы PL будет состоять из все большего числа членов вплоть до некоторого критического значения L, после которого число членов снова начнет уменьшаться. Это происходит вследствие того, что для малых значений L и для графов, обычно встречающихся на практике, число цепей длины L+1, как правило, больше, чем число цепей длины L, а для больших значений L имеет место обратная картина. Кроме того, так как длина каждого члена внутреннего произведения вершин увеличивается на единицу, когда L увеличивается на единицу, то объем памяти, необходимый для хранения матрицы PL, растет очень быстро вплоть до максимума при некотором критическом значении L, после которого этот объем снова начинает уменьшаться.
Небольшая модификация вышеприведенного метода позволяет во много раз уменьшить необходимый объем памяти и время вычислений. Так как нас интересуют только гамильтоновы циклы и, как было отмечено выше, они могут быть получены из членов внутреннего произведения любой диагональной ячейки матрицы B*Pn-1, то необходимо знать только элемент pn-1(1,1). При этом на каждом этапе не обязательно вычислять и хранить всю матрицу PL, достаточно лишь найти первый столбец PL. Эта модификация уменьшает необходимый объем памяти и время вычислений в n раз. Однако даже при использовании этой модификации программа для ЭВМ, написанная на языке PL/1, который позволяет построчную обработку литер и переменное распределение памяти, не была способна найти все гамильтоновы циклы в неориентированных графах с более чем примерно 20 вершинами и средним значением степени вершины, большим 4. Использовался компьютер IBM 360/65 с памятью 120 000 байтов. Более того, даже для графа с вышеуказанными «размерами» данный метод использовал фактически весь объем памяти и время вычислений равнялось 1.8 минуты. Не такое уж незначительное время для столь небольшого графа.
§6. Метод перебора Робертса и Флореса
В противоположность алгебраическим методам, с помощью которых пытаются найти сразу все гамильтоновы циклы и при реализации которых приходится хранить поэтому все цепи, которые могут оказаться частями таких циклов, метод перебора имеет дело с одной цепью, непрерывно продлеваемой вплоть до момента, когда либо получается гамильтонов цикл, либо становится ясно, что эта цепь не может привести к гамильтонову циклу. Тогда цепь модифицируется некоторым систематическим способом (который гарантирует, что в конце концов будут исчерпаны все возможности), после чего продолжается поиск гамильтонова цикла. В этом способе для поиска требуется очень небольшой объем памяти и за один раз находится один гамильтонов цикл.
Следующая схема перебора, использующая обычную технику возвращения, была первоначально предложена Робертсом и Флоресом. Начинают с построения (kЧn)-матрицы M=[mij], где элемент mij есть i-я вершина (скажем xq), для которой в графе G(X,Г) существует дуга (xj,xq). Вершины xq во множестве Г(xj) можно упорядочить произвольно, образовав элементы j-го столбца матрицы M. Число строк k матрицы M будет равно наибольшей полустепени исхода вершины.
Метод состоит в следующем. Некоторая начальная вершина (скажем, x1) выбирается в качестве отправной и образует первый элемент множества S, которое каждый раз будет хранить уже найденные вершины строящейся цепи. К S добавляется первая вершина (например, вершина a) в столбце x1. Затем к множеству S добавляется первая возможная вершина (например, вершина b) в столбце a, потом добавляется к S первая возможная вершина (например, вершина c) в столбце b и т.д. Под «возможной» вершиной мы понимаем вершину, еще не принадлежащую S. Существуют две причины, препятствующие включению некоторой вершины на шаге r во множество S = {x1,a,b,c, … ,xr-1,xr}:
В столбце xr нет возможной вершины.
Цепь, определяемая последовательностью вершин в S, имеет длину n-1, т.е. является гамильтоновой цепью.
В случае 2) возможны следующие случаи:
В графе G существует дуга (xr,x1), и поэтому найден гамильтонов цикл.
Дуга (xr,x1) не существует и не может быть получен никакой гамильтонов цикл.
В случаях (1) и (2b) следует прибегнуть к возвращению, в то время как в случае (2a) можно прекратить поиск и напечатать результат (если требуется найти только один гамильтонов цикл), или (если нужны все такие циклы) произвести печать и прибегнуть к возвращению.
Возвращение состоит в удалении последней включенной вершины xr из S, после чего остается множество S = {x1,a,b,c, … ,xr-1}, и добавлении к S первой возможной вершины, следующей за xr, в столбце xr-1 матрицы M. Если не существует никакой возможной вершины, делается следующий шаг возвращения и т.д.
Поиск заканчивается в том случае, когда множество S состоит только из вершины x1 и не существует никакой возможной вершины, которую можно добавить к S, так что шаг возвращения делает множество S пустым. Гамильтоновы циклы, найденные к этому моменту, являются тогда всеми гамильтоновыми циклами, существующими в графе.
Рассмотрим пример поиска гамильтонова цикла в графе переборным методом Робертса и Флореса.
Пример:
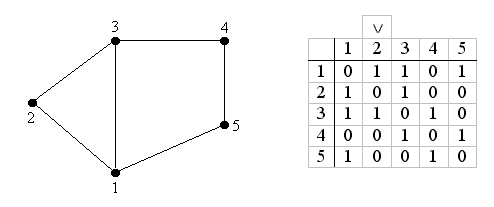
"2"
1) S = {1}
2) S = {1, 2}
3)
S = {1, 2, 3}
4) S = {1, 2, 3, 4}
5) S = {1, 2, 3, 4, 5} - Г
4→3 4→5
6) S = {1, 2, 3, 4}
7) S = {1, 2,
3} 3→1 3→2 3→4
8) S = {1, 2}
9) S = {1}
"3"
10) S = {1, 3}
3→2
11) S = {1, 3, 2}
2→1
12) S = {1, 3}
2→3
13) S = {1, 3, 4}
3→4 4→5
14) S = {1, 3, 4, 5, 4}
5→нет
15) S = {1,
3, 4}
16) S = {1, 3}
17) S = {1}
"5"
18) S =
{1, 5}
19) S = {1, 5, 4}
20) S = {1, 5, 4, 3}
21) S = {1, 5,
4, 3, 2} - Г
22) S = {1, 5, 4,
3}
23) S = {1, 5, 4}
24) S = {1, 5}
25) S = {1}
26) S = Ш
§8. Улучшение метода Робертса и Флореса
Рассмотрим
улучшение
основного
переборного
метода Робертса
и Флореса. Допустим,
что на некотором
этапе поиска
построенная
цепь задается
множеством
S = {x1,x2,
… ,xr}
и что следующей
вершиной, которую
предполагается
добавить к S,
является x*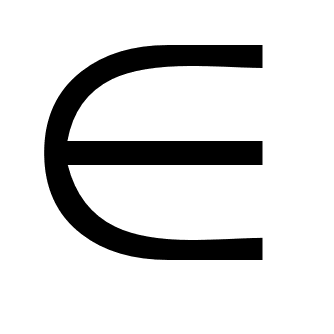 S.
Рассмотрим
теперь две
следующие
ситуации, в
которых вершина
является
изолированной
в подграфе,
остающемся
после удаления
из G(X,Г)
всех вершин,
образующих
построенную
до этого цепь.
S.
Рассмотрим
теперь две
следующие
ситуации, в
которых вершина
является
изолированной
в подграфе,
остающемся
после удаления
из G(X,Г)
всех вершин,
образующих
построенную
до этого цепь.
Если существует такая вершина x
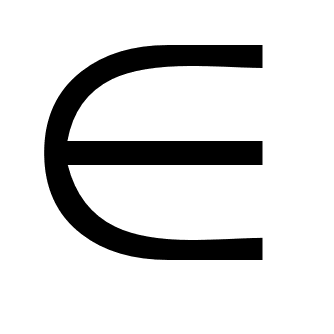 X\S,
что x
X\S,
что x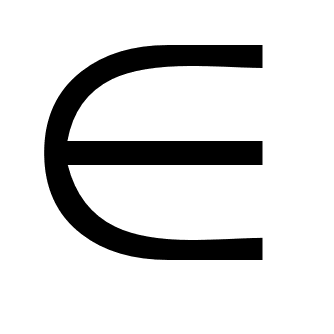 Г(xr)
и Г-1(x)
Г(xr)
и Г-1(x)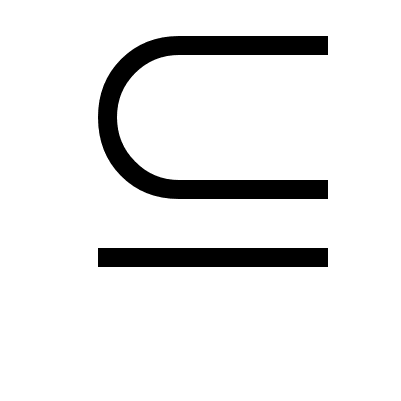 S, то, добавляя
к S любую
вершину x*,
отличную от
x, мы не сможем
в последующем
достигнуть
вершины x
ни из какой
конечной вершины
построенной
цепи, и, значит,
эта цепь не
сможет привести
нас к построению
гамильтонова
цикла. Таким
образом, в этом
случае x
является
единственной
вершиной, которую
можно добавить
к S для
продолжения
цепи.
S, то, добавляя
к S любую
вершину x*,
отличную от
x, мы не сможем
в последующем
достигнуть
вершины x
ни из какой
конечной вершины
построенной
цепи, и, значит,
эта цепь не
сможет привести
нас к построению
гамильтонова
цикла. Таким
образом, в этом
случае x
является
единственной
вершиной, которую
можно добавить
к S для
продолжения
цепи.Если существует такая вершина x
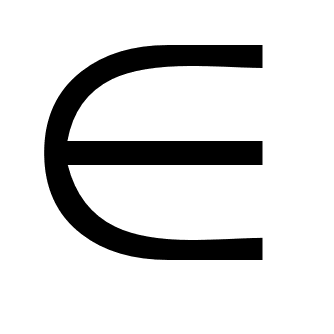 X\S,
что x
X\S,
что x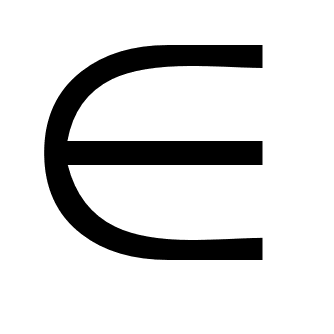 Г-1(x1)
и Г(x)
Г-1(x1)
и Г(x)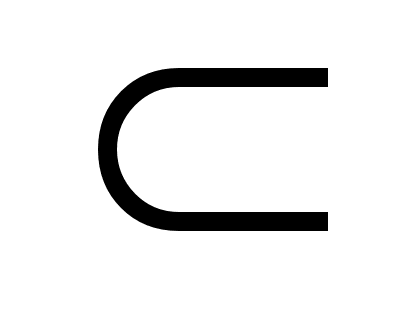 S
S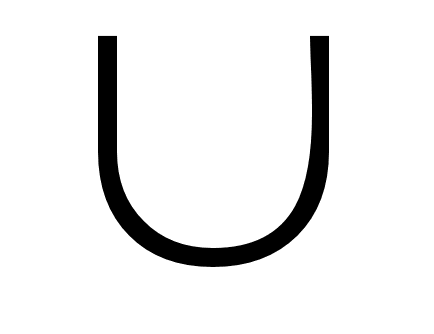 {x*}
для некоторой
другой вершины
x*, то x*
не может быть
добавлена к
S, так как
тогда в остающемся
подграфе не
может существовать
никакой цепи
между x и
x1. Цепь,
определяемая
множеством
S
{x*}
для некоторой
другой вершины
x*, то x*
не может быть
добавлена к
S, так как
тогда в остающемся
подграфе не
может существовать
никакой цепи
между x и
x1. Цепь,
определяемая
множеством
S
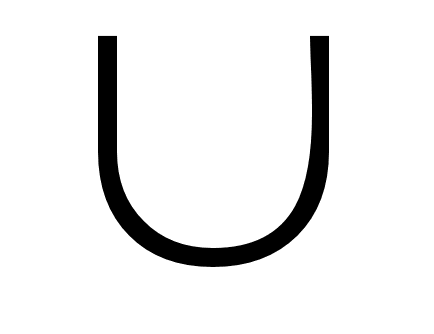 {x*}, не может
поэтому привести
к гамильтонову
циклу, а в качестве
кандидата на
добавление
к множеству
S следует
рассмотреть
другую вершину,
отличную от
x*.
{x*}, не может
поэтому привести
к гамильтонову
циклу, а в качестве
кандидата на
добавление
к множеству
S следует
рассмотреть
другую вершину,
отличную от
x*.
Проверка условий (a) и (b) будет, конечно, замедлять итеративную процедуру, и для небольших графов (менее чем с 20 вершинами) не получается никакого улучшения первоначального алгоритма Робертса и Флореса. Но для больших графов эта проверка приводит к заметному сокращению необходимого времени вычислений, уменьшая его обычно в 2 или более раз.
§9. Мультицепной метод
После внимательного изучения операций алгоритма перебора Робертса и Флореса становится очевидным, что даже после сделанного улучшения не слишком много внимания уделяется оставшейся части графа, в которой берется последовательность вершин, продолжающих построенную цепь. Обычно построение цепи S0 в процессе поиска (S0 рассматривается и как упорядоченное множество вершин, и как обычное множество) подразумевает существование еще каких-то цепей в других частях графа. Эти предполагаемые цепи либо помогают быстрее построить гамильтонов цикл, либо указывают на отсутствие такого цикла, содержащего цепь S0, что позволяет сразу прибегнуть к возвращению.
Метод, описанный ниже, был предложен первоначально для неориентированных графов; здесь дается его небольшое видоизменение для ориентированных графов. Метод состоит в следующем.
Допустим, что на некотором этапе поиска построена цепь S0 и возможны цепи S1, S2, … . Рассмотрим какую-либо «среднюю» вершину одной из этих цепей (слово «средняя» здесь означает любую вершину, отличную от начальной и конечной). Поскольку эта вершина уже включена в цепь с помощью двух дуг, то очевидно, что все другие дуги, входящие или выходящие из такой вершины, могут быть удалены из графа. Для любой начальной вершины вышеуказанных цепей можно удалить все дуги, исходящие из нее (за исключением дуги, включающей эту вершину в цепь), а для любой конечной вершины можно удалить все дуги, оканчивающиеся в ней (опять-таки за исключением дуги, включающей ее в цепь). Кроме того, за исключением случая, когда существует только одна цепь (скажем, S0), проходящая через все вершины графа G (т.е когда S0 — гамильтонова цепь), любая имеющаяся дуга, ведущая из конца любой цепи в начальную вершину этой же цепи, может быть удалена, так как такая дуга замыкает не гамильтоновы циклы.
Удаление всех этих дуг даст граф — со всеми «средними» вершинами цепей, в котором только одна дуга оканчивается в каждой вершине и только одна дуга исходит из нее. Все эти «средние» вершины и дуги, инцидентные им, удаляются из G, а вместо них для каждой цепи вводится единственная дуга, идущая от начальной вершины цепи до ее конечной вершины. В результате всего этого получается редуцированный граф Gk(Xk,Гk), где k — индекс, показывающий номер шага поиска.
Рассмотрим теперь продолжение цепи S0 (сформированной в результате поиска), осуществляемое путем добавления вершины xj, которая является возможной в смысле алгоритма Робертса и Флореса, т.е. в Gk существует дуга, исходящая из конечной вершины цепи S0 — обозначим эту вершину e(S0) — и входящая в вершину xj. Добавление xj к S0 осуществляется так:
Сначала удаляются из Gk все необходимые дуги, т.е.
все дуги, оканчивающиеся в xj или исходящие из e(S0), за исключением дуги (e(S0), xj);
все дуги, выходящие из xj в начальную вершину пути S0;
если окажется, что xj является начальной вершиной другой цепи Sj, то следует удалить также любую дугу, идущую из конечной вершины цепи Sj в начальную вершину цепи S0.
Обозначим граф, оставшийся после удаления всех дуг, через G’k(Xk,Гk’).
Если существует вершина x в графе G’k, не являющаяся конечной ни для одной из цепей S0, S1, … и которая после удаления дуг имеет полустепень захода, равную единице, т.е. |Г-1k’(x)|=1, то выкинуть все дуги, исходящие из вершины v= Г-1k’(x), за исключением дуги (v, x).
Если существует вершина x графа G’k, не являющаяся начальной ни для какой цепи и которая после удаления дуг имеет полустепень исхода, равную единице, т.е. |Гk’(x)|=1, то выкинуть все дуги, исходящие из вершины x, за исключением дуги (x, Гk’(x)).
Перестроить все цепи и удалить дуги, ведущие из конечных в начальные вершины.
Повторить шаг 2 до тех пор, пока можно удалять дуги.
Удалить из оставшегося графа G’k все вершины, полустепени захода и исхода которых равны единице, т.е. вершины, которые стали теперь «средними» вершинами цепей. Это удаление производится так, как это было описано выше, в результате чего получается новый редуцированный граф Gk+1, заменяющий предыдущий граф Gk.
Совершенно очевидно, что если добавление вершины xj к цепи S0 делает полустепень захода или полустепень исхода (или обе) некоторой вершины x в конце шага 2 равной нулю, то не существует никакого гамильтонова цикла. В этом случае вершина xj удаляется из множества S0 и в качестве другой вершины xj, позволяющей продолжить цепь S0, выбирается некоторая другая вершина из множества Гk’[e(S0)]. И так до тех пор, пока не будет исчерпано все множество Гk’[e(S0)] и придется прибегнуть к возвращению (т.е. e(S0) удаляется из S0 и заменяется другой вершиной и т.д.). Отметим, что операция возвращения предполагает хранение достаточной информации об удаленных дугах в шагах 1 и 2 на каждом этапе k, чтобы можно было по графу Gk+1 восстановить граф Gk при любых k, если приходится прибегать к возвращению.
Если (на некотором этапе) в конце шага 2 установлено, что только одна цепь проходит далее через все вершины, то в этом случае существование гамильтонова цикла может быть выявлено непосредственно. Если цикл при этом не найден (или если он найден, но надо найти все гамильтоновы циклы), то нужно прибегнуть к возвращению.
Лучший вычислительный путь состоит в том, чтобы при каждой итерации шага 2 (за исключением последней) проверять отличие от нуля полустепеней захода и исхода всех вершин графа G’k. Поэтому как только одна из них станет равной нулю, сразу же применяется операция возвращения, и если найдена гамильтонова цепь, то получается и гамильтонов цикл без проверки существования дуги возврата.
Если не возникает ни один из вышеупомянутых случаев, т.е. если (на некотором этапе k) в конце шага 2 остается более чем одна цепь и все полустепени являются ненулевыми, то нельзя еще сделать никаких выводов. Тогда вершина xj добавляется к S0 и выбирается другая вершина для дальнейшего продолжения цепи. Шаги 1, 2, 3 повторяются, начиная с нового редуцированного графа.
§10. Сравнение методов поиска гамильтоновых циклов
В этом параграфе сравниваются первоначальный вариант алгоритма Робертса и Флореса, его улучшенный вариант и мультицепной метод. Эти три метода мы будем сравнивать по необходимому времени вычислений для нахождения одного гамильтонова цикла, если таковой существует, или доказательства его отсутствия. Проверка была проведена на случайно выбранных графах, степени вершин которых лежат в предписанных границах. Всего было использовано около 200 графов, для которых приводятся средние результаты. Во всех графах оказались гамильтоновы циклы.
Ниже на рисунке 1 показана зависимость требуемого алгоритмом Робертса и Флореса времени вычисления от числа вершин графа; степени вершин лежат в пределах 3 — 5. Ввиду сильных вариаций требуемого времени для графов одинаковых размеров приводятся три ломанные, характеризующие среднее, максимальное и минимальное время, полученное для различных графов с одинаковым числом вершин. Следует заметить, что на рисунке 1 применен полулогарифмический масштаб, что говорит об экспоненциальном характере зависимости. Формула, дающая приближенную зависимость времени T от числа вершин n графа со степенями вершин в пределах 3 — 5, такова:
T = 0.85·10-4 · 100.155n (секунд на CDC6600).
Улучшенный вариант алгоритма Робертса и Флореса не намного лучше первоначального алгоритма. Необходимое время вычисления в нем все еще зависит (более или менее) экспоненциально от n. Зависимость отношения времен вычисления при использовании этих двух алгоритмов для неориентированных графов со степенями вершин 3 — 5 приведена на рисунке 2. Из этого рисунка видно, что «улучшенный» вариант в действительности хуже для графов малых размеров, хотя для больших графов (с более чем 20 вершинами) он позволяет сэкономить более 50% времени вычисления.
По отношению к тому же вышеупомянутому множеству графов мультицепной алгоритм оказался очень эффективным. Это видно из рисунка 3, на котором показано необходимое для этого алгоритма время вычисления (здесь применен линейный масштаб). График показывает, что время растет очень медленно в зависимости от числа вершин и поэтому алгоритм применим для очень бльших графов.
Другим преимуществом этого метода является очень слабая вариация времени для различных графов одинакового размера, и поэтому можно оценит с разумной степенью доверительности время вычисления, необходимое для различных задач.
Кроме того, эксперименты показывают, что для графов, степени вершин которых лежат в вышеприведенных пределах 3 — 5, метод по существу не чувствителен к степеням вершин. Вычислительные результаты, показанные на рисунках 1-3, относятся к поиску одного гамильтонова цикла в графе.
Небезынтересно
сказать несколько
слов о вычислениях
с тремя алгоритмами,
когда искались
все гамильтоновы
циклы. Так, для
неориентированного
графа с 20 вершинами
со степенями
вершин 3 — 5, потребовалось
2 сек, чтобы найти
все гамильтоновы
циклы, следуя
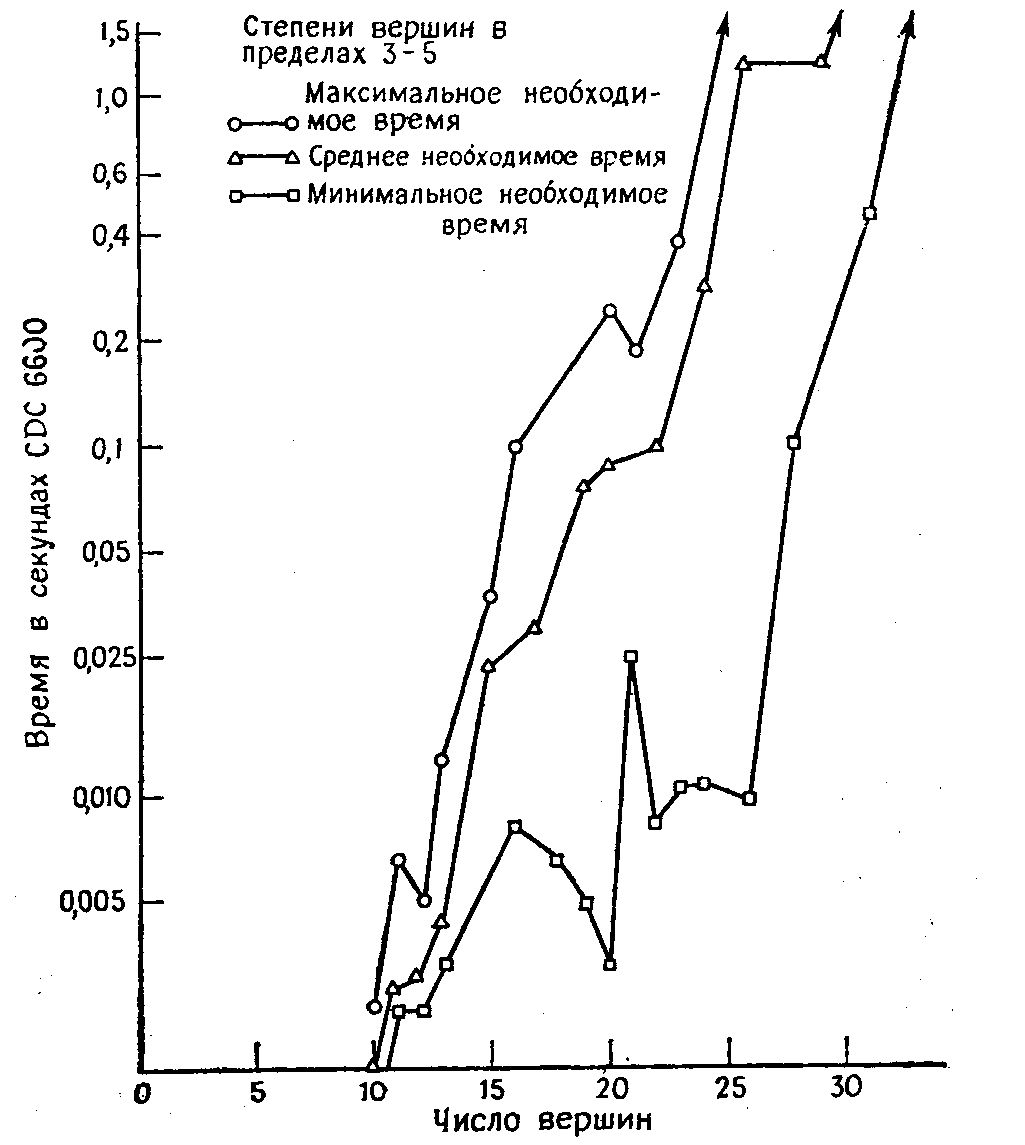
Рис.1 Вычислительная реализация алгоритма Робертса и Флореса
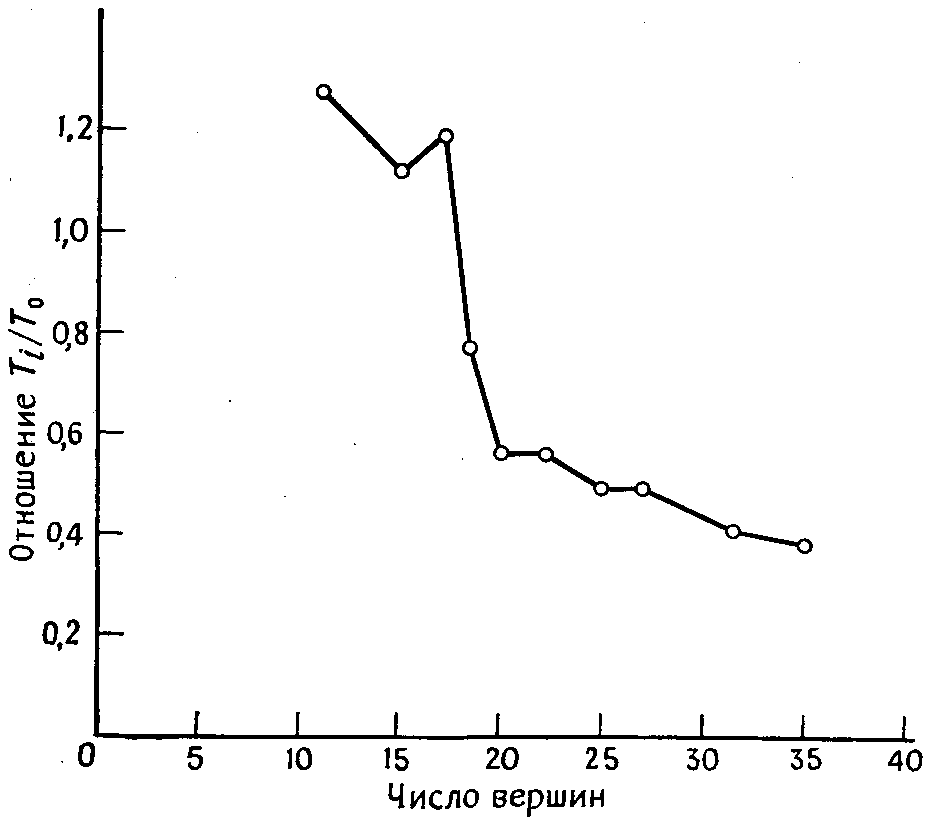
Рис.2 Реализация улучшенного алгоритма Робертса и Флореса
Время вычисления: T0-основной алгоритм, T1-улучшенный алгоритм
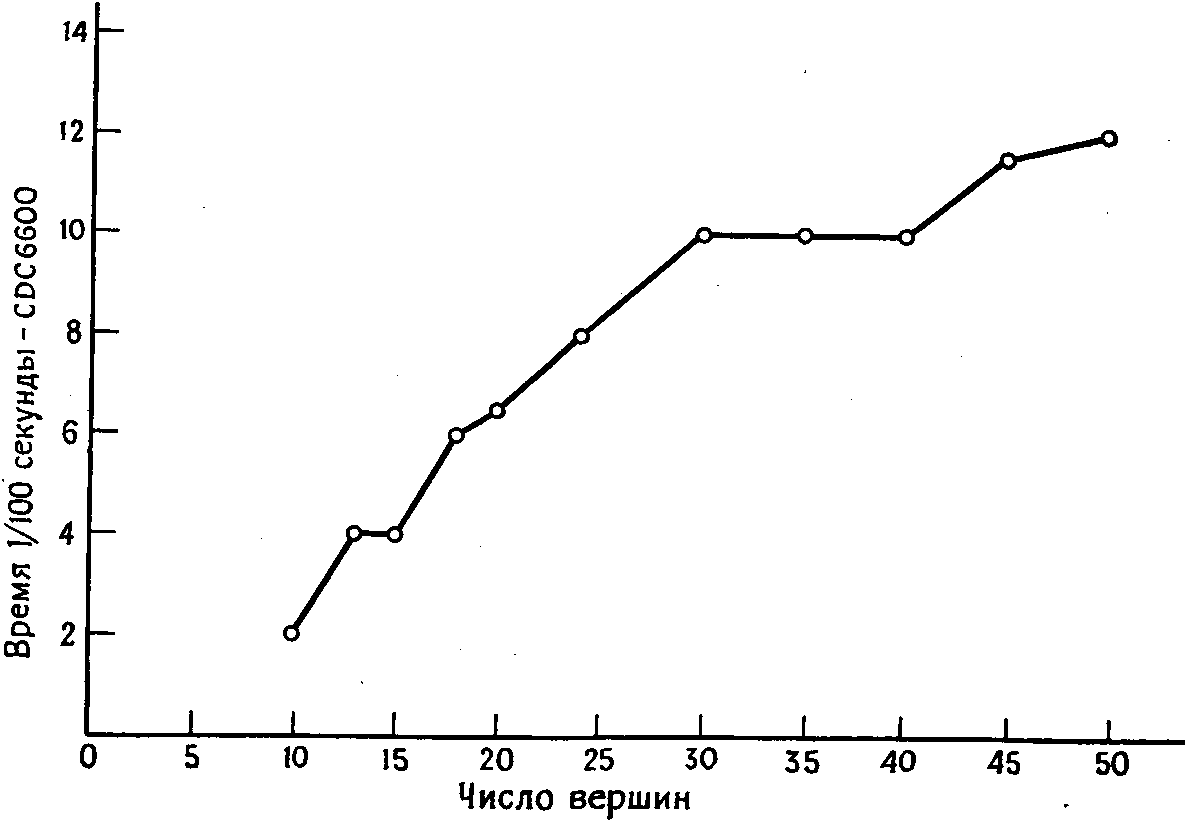
алгоритму Робертса и Флореса (этих циклов оказалось 18). Улучшенный вариант того же алгоритма потребовал 1.2 сек, а мультицепной алгоритм — 0.07 сек. Вычисления проводились на ЭВМ CDC6600.
Глава 3. Задача коммивояжера
Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё, как об Великую теорему Ферма обламывали зубы лучшие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы. Ниже будет показано, что решение ЗК методом полного перебора оказывается практически неосуществимым даже для сравнительно небольших задач. Более того, известно, что ЗК принадлежит к числу NP-полных задач.
§1. Общее описание
Постановка задачи следующая.
Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по одному разу в неизвестном порядке города 1,2,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jТ=(1,2,…,n). Тур коммивояжера может быть описан циклической перестановкой t=(j1,…,jn, j1), причём все j1,…,jn – разные номера; повторяющийся в начале и в конце j1, показывает, что перестановка зациклена. Расстояния между парами вершин Сij образуют матрицу С. Далее введем n2 альтернативных переменных xij, принимающих значение 0, если переход из i-го пункта в j-ый не входит в маршрут и 1 в противном случае. Условия прибытия в каждый пункт и выхода из каждого пункта только по одному разу выражаются равенствами (1) и (2).
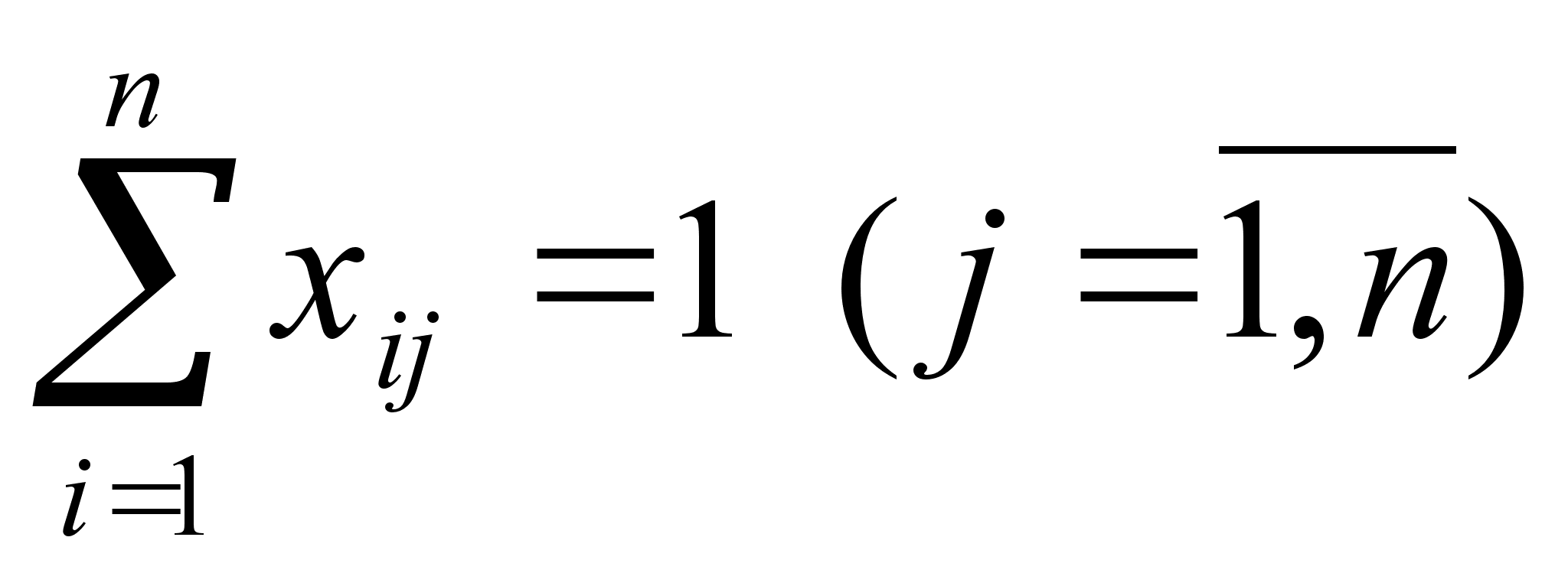 (1)
(1)
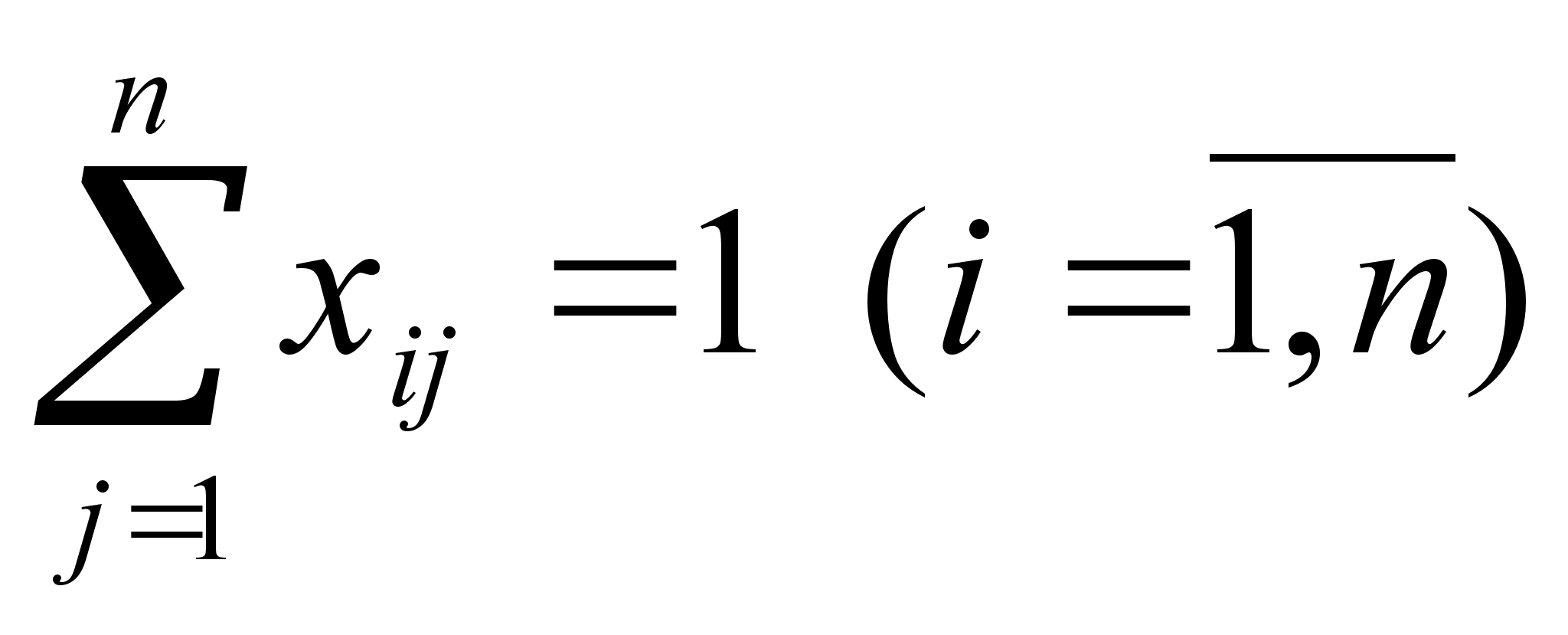 (2)
(2)
Для обеспечения
непрерывности
маршрута вводятся
дополнительно
n переменных
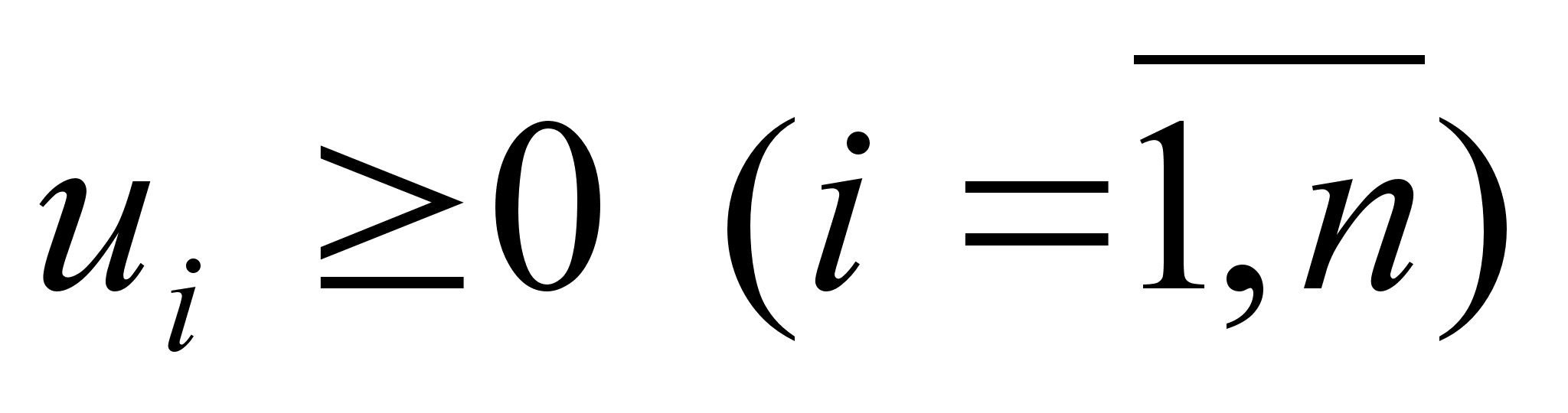 и n2 дополнительных
ограничений
(3).
и n2 дополнительных
ограничений
(3).
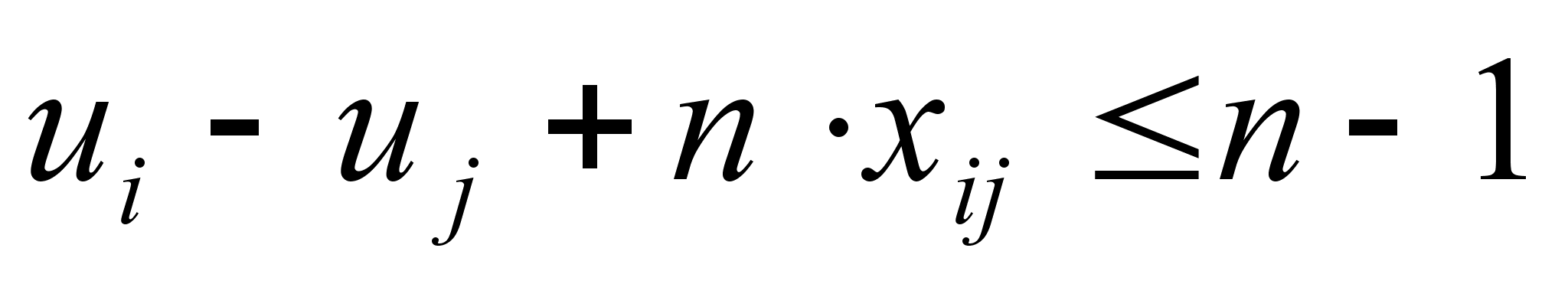 (3)
(3)
Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать суммарную протяженность маршрута F, которая запишется в следующем виде:
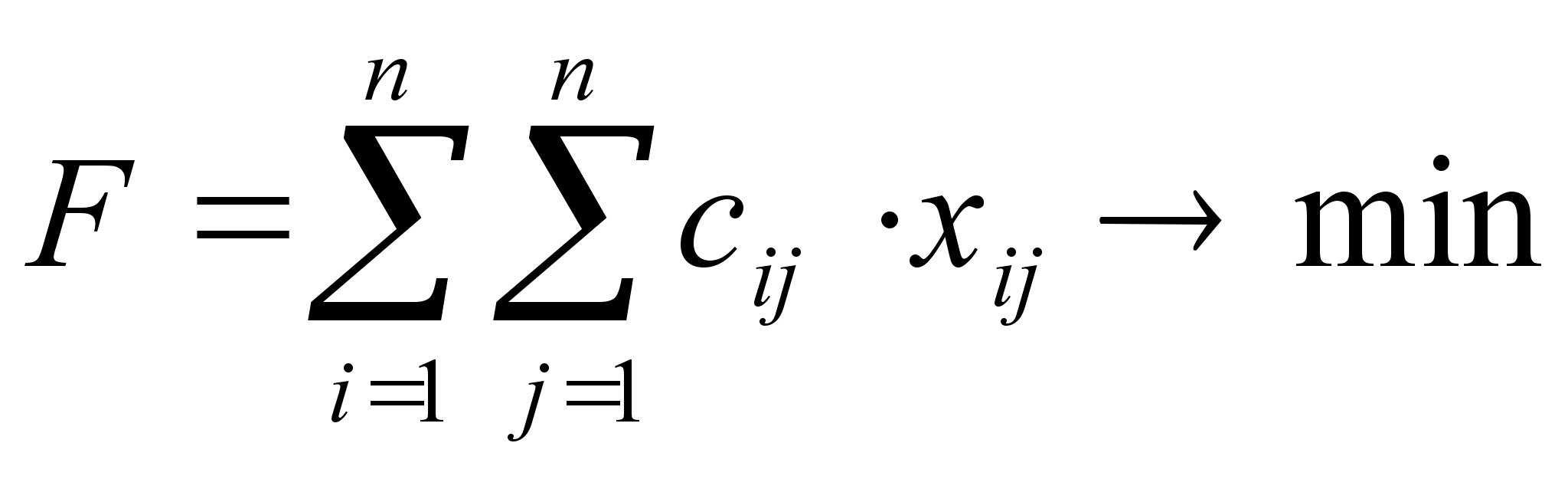 (4)
(4)
Относительно математической формулировки ЗК уместно сделать два замечания. Первое, в постановке Сij означали расстояния, поэтому должны выполняться следующие условия:
неотрицательными, т.е. для всех jТ:
Cij 0;
Cjj = ∞ (5)
(последнее равенство означает запрет на петли в туре),
симметричными, т.е. для всех i, j:
Сij = Сji (6)
удовлетворять неравенству треугольника, т.е. для всех:
Cij + Cjk Cik (7)
В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (5)-(7) не удовлетворяют. Особенно часто нарушается условие (7) (например, если Сij – не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому мы будем различать два варианта ЗК: симметричную задачу, когда условие (7) выполнено, и несимметричную - в противном случае. Условия (5)-(7) по умолчанию мы будем считать выполненными.
Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j1,j2,…,jn,j1) и t’=(j1,jn,…,j2,j1) имеют разную длину и должны учитываться оба. Всего разных туров очевидно (n-1)!
Зафиксируем на первом и последнем месте в циклической перестановке номер j1, а оставшиеся n-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.
Можно представить, что X состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j) проведено, если xij=0 и не проведено, если xij=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).
Доказательство, что модель (1-4) описывает задачу о коммивояжере.
Условие (2) означает, что коммивояжер из каждого города выезжает только один раз; условие (3) - въезжает в каждый город только один раз; условие (4) - обеспечивает замкнутость маршрута, содержащего N городов, и не содержащего замкнутых внутренних петель.
Рассмотрим
условие (4) подробнее.
Применим метод
доказательства
от противного,
то есть предположим,
что условие
(4) выполняется
для некоторого
подцикла T из
R городов, где
R
Так как
то N·R
(N -1), где R < N, R
0.
Следовательно,
не существует
замкнутого
подцикла с
числом городов
меньшим, чем
N.
Покажем, что
существует
Ui, которое для
замкнутого
цикла, начинающегося
в некотором
начальном
пункте, удовлетворяют
условию (4). При
всех Xij (j-й город
не посещается
после i-го) в (4)
имеем Ui-Uj
N-1, что допустимо
в силу произвольных
Ui и Uj.
Пусть на некотором
R-ом шаге i-й город
посещается
перед j-м, то есть
Xij = 1. В силу
произвольности
значений Ui
и Uj положим
Ui = R, а Uj = R+1, тогда
из (4) имеем:
Ui-Uj+N·Xij
R-(R-1)+N = N-1
Итак, существуют
такие конечные
значения для
Ui и Uj, что для
маршрута, содержащего
N городов, условие
(4) удовлетворяется
как неравенство
или строгое
равенство. А
следовательно,
модель (1)-(4) описывает
задачу о коммивояжере.
В терминах
теории графов
симметричную
ЗК можно сформулировать
так:
Дана полная
сеть с n
вершинами,
длина ребра
(i,j)=
Сij. Найти
гамильтонов
цикл минимальной
длины.
В несимметричной
ЗК вместо «цикл»
надо говорить
«контур», а
вместо «ребра»
- «дуги», «стрелки».
Некоторые
прикладные
задачи формулируются
как ЗК, но в них
нужно минимизировать
длину не гамильтонова
цикла, а гамильтоновой
цепи. Такие
задачи называются
незамкнутыми.
Некоторые
модели сводятся
к задаче о нескольких
коммивояжерах,
но мы здесь их
рассматривать
не будем.
Жадный алгоритм
– алгоритм
нахождения
наикратчайшего
расстояния
путём выбора
самого короткого,
ещё не выбранного
ребра, при условии,
что оно не образует
цикла с уже
выбранными
рёбрами. “Жадным”
этот алгоритм
назван потому,
что на последних
шагах приходится
жестоко расплачиваться
за жадность. П
В пользу процедуры
“иди в ближайший”
можно сказать
лишь то, что
при старте из
одного города
она не уступит
стратегии “иди
в дальнейший”.
Как видим, жадный
алгоритм ошибается.
Можно ли доказать,
что он ошибается
умеренно, что
полученный
им тур хуже
минимального,
положим, в 1000 раз?
Мы докажем, что
этого доказать
нельзя, причем
не только для
жадного алгоритма,
а для алгоритмов
гораздо более
мощных. Но сначала
нужно договориться,
как оценивать
погрешность
неточных алгоритмов,
для определенности,
в задаче минимизации.
Пусть fB
- настоящий
минимум, а fA
- тот квазиминимум,
который получен
по алгоритму.
Ясно, что
fA/
fB≥1,
но это – тривиальное
утверждение,
что может быть
погрешность.
Чтобы оценить
её, нужно «зажать»
отношение
оценкой сверху:
fA/fB
≥ 1+nε (8)
где, как обычно
в высшей математике,
ε≥0, но, против
обычая, может
быть очень
большим. Величина
ε и будет служить
мерой погрешности.
Если алгоритм
минимизации
будет удовлетворять
неравенству
(8), мы будем говорить,
что он имеет
погрешность
ε.
Предположим
теперь, что
имеется алгоритм
А решения ЗК,
погрешность
которого нужно
оценить. Возьмем
произвольный
граф G(V,E)
и по нему составим
входную матрицу
ЗК:
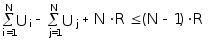 .
.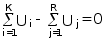 ,
,
§2. “Жадный”
алгоритм решения
ЗК
 осмотрим,
как поведет
себя при решении
ЗК жадный алгоритм.
Здесь алгоритм
превратится
в стратегию
“иди в ближайший,
в который еще
не входил, город”.
Жадный алгоритм,
очевидно, бессилен
в этой задаче.
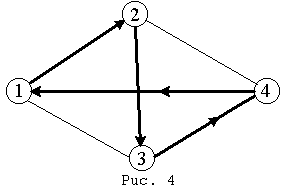
Рассмотрим
для примера
сеть на рис. 2,
представляющую
узкий ромб.
Пусть коммивояжер
стартует из
города 1. Алгоритм
“иди вы ближайший
город” выведет
его в город 2,
затем 3, затем
4; на последнем
шаге придется
платить за
жадность, возвращаясь
по длинной
диагонали
ромба. В результате
получится не
кратчайший,
а длиннейший
тур.
осмотрим,
как поведет
себя при решении
ЗК жадный алгоритм.
Здесь алгоритм
превратится
в стратегию
“иди в ближайший,
в который еще
не входил, город”.
Жадный алгоритм,
очевидно, бессилен
в этой задаче.
Рассмотрим
для примера
сеть на рис. 2,
представляющую
узкий ромб.
Пусть коммивояжер
стартует из
города 1. Алгоритм
“иди вы ближайший
город” выведет
его в город 2,
затем 3, затем
4; на последнем
шаге придется
платить за
жадность, возвращаясь
по длинной
диагонали
ромба. В результате
получится не
кратчайший,
а длиннейший
тур.
Если в графе
G есть гамильтонов
цикл, то минимальный
тур проходит
по этому циклу
и fB
= n. Если алгоритм
А тоже всегда
будет находить
этот путь, то
по результатам
алгоритма можно
судить, есть
ли гамильтонов
цикл в произвольном
графе. Однако,
не переборного
алгоритма,
который мог
бы ответить,
есть ли гамильтонов
цикл в произвольном
графе, до сих
пор никому не
известно. Таким
образом, наш
алгоритм А
должен иногда
ошибаться и
включать в тур
хотя бы одно
ребро длины
1+nε. Но тогда
fA
(n-1)+(1+nε)
так что fA/fB
= 1+nε, т.е.
превосходит
погрешность
ε на заданную
неравенством
(8). О величине
ε в нашем рассуждении
мы не договаривались,
так что ε может
быть произвольно
большим.
С[i,j]={
1, если
ребро (i,j)
принадлежит
Е
1+nε,
в противном
случае
Таким образом доказана следующая теорема.
Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.
Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (7).
§3. “Деревянный” алгоритм решения ЗК
Теперь можно обсудить алгоритм решения ЗК через построение кратчайшего остовного дерева. Для краткости будет называть этот алгоритм “деревянным”.
Вначале обсудим свойство спрямления. Рассмотрим какую-нибудь цепь, например, на рис. 5. Если справедливо неравенство треугольника, то d[1,3] d[1,2]+d[2,3] и d[3,5] d[3,4]+d[4,5]. Сложив эти два неравенства, получим:
d[1,3]+d[3,5]d[1,2]+d[2,3]+d[3,4]+d[4,5].
По неравенству треугольника получим: d[1,5] d[1,3]+d[3,5]. Окончательно,
d[1,5] d[1,2]+d[2,3]+d[3,4]+d[4,5]
Итак, если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи. Это обобщение расхожего убеждения, что прямая короче кривой.
Вернемся к ЗК и опишем решающий ее “деревянный” алгоритм.
Построим на входной сети ЗК кратчайшее остовное дерево и удвоим все его ребра. Получим граф G – связный и с вершинами, имеющими только четные степени.
Построим эйлеров цикл в G, начиная с вершины 1, цикл задается перечнем вершин.
Просмотрим перечень вершин, начиная с 1, и будем зачеркивать каждую вершину, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.
П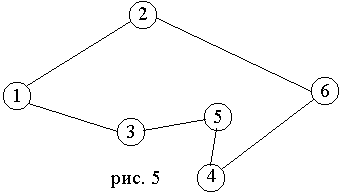 ример
1. Дана полная
сеть, показанная
на рис.5. Найти
тур “жадным”
и “деревянным”
алгоритмами.
ример
1. Дана полная
сеть, показанная
на рис.5. Найти
тур “жадным”
и “деревянным”
алгоритмами.
Р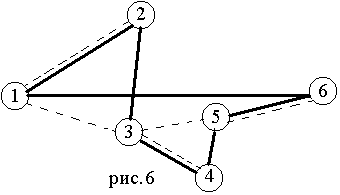 ешение.
ешение.
1. “Жадный” алгоритм (иди в ближайший город из города 1) дает тур 1–(4)–3-(3)–5-(5)–4–(11)–6–(10)–2–(6)–1, где без скобок показаны номера вершин, а в скобках – длины ребер. Длина тура равна 39, тур показана на рис. 5.
2. “Деревянный” алгоритм вначале строит остовное дерево, показанное на рис. 6 штриховой линией, затем эйлеров цикл 1-2-1-3-4-3-5-6-5-3-1, затем тур 1-2-3-4-5-6-1 длиной 43, который показан сплошной линией на рис. 6.
Теорема. Погрешность “деревянного” алгоритма равна 1.
Доказательство. Возьмем минимальный тур длины fB и удалим из него максимальное ребро. Длина получившейся гамильтоновой цепи LHC меньше fB. Но эту же цепь можно рассматривать как остовное дерево, т. к. эта цепь достигает все вершины и не имеет циклов. Длина кратчайшего остовного дерева LMT меньше или равна LHC. Имеем цепочку неравенств
fB > LHC LMT (9)
| — |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
— | 6 | 4 | 8 | 7 | 14 |
|
2 |
6 | — | 7 | 11 | 7 | 10 |
|
3 |
4 | 7 | — | 4 | 3 | 10 |
|
4 |
8 | 11 | 4 | — | 5 | 11 |
|
5 |
7 | 7 | 3 | 5 | — | 7 |
|
6 |
14 | 10 | 10 | 11 | 7 | — |
Умножая (9) на два и соединяя с (10), получаем цепочку неравенств
2fB > 2LHC 2LMT fA (11)
Т.е. 2fB>fA, fA/fB>1+; =1. Теорема доказана.
Таким образом, мы доказали, что “деревянный” алгоритм ошибается менее, чем в два раза. Такие алгоритмы уже называют приблизительными, а не просто эвристическими.
§4. Метод лексикографического перебора
Известно еще несколько простых алгоритмов, гарантирующих в худшем случае =1. Для того, чтобы найти среди них алгоритм поточнее, зайдем с другого конца и для начала опишем “brute-force enumeration” - “перебор грубой силой”, как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с n городами требует при полном переборе рассмотрения (n-1)!/2 туров в симметричной задаче и (n-1)! Туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро:
| 5! | 10! | 15! | 20! | 25! | 30! | 35! | 40! | 45! | 50! |
|
~102 |
~106 |
~1012 |
~1018 |
~1025 |
~1032 |
~1040 |
~1047 |
~1056 |
~1064 |
Говорят, что перестановка (a1,…,an) лексикографически предшествует перестановке (b1,…,bn), если существует k ≤ n ak < bk и для любого i > k ai = bi.
Пусть имеется некоторый алфавит и наборы символов алфавита (букв), называемые словами. Буквы в алфавите упорядочены: например, в русском алфавите порядок букв абя (символ читается “предшествует”). Если задан порядок букв, можно упорядочить и слова. Скажем, дано слово u=(u1,u2,…,um) – состоящее из букв u1,u2,…,um — и слово v=(v1,v2,…,vb). Тогда если u1v1, то и uv, если же u1=v1, то сравнивают вторые буквы и т.д. Этот порядок слов и называется лексикографическим. Рассмотрим, скажем, перестановки из пяти элементов, обозначенных цифрами 1…5. Лексикографически первой перестановкой является 1-2-3-4-5, второй 1-2-3-5-4,… ,последней 5-4-3-2-1. Нужно осознать общий алгоритм преобразования любой перестановки в непосредственно следующую за ней.
Правило такое: скажем, дана перестановка 1-3-5-4-2. Нужно двигаться по перестановке справа налево, пока впервые не увидим число, меньшее, чем предыдущее (в примере это 3 после 5). Это число, Pi-1 надо увеличить, поставив вместо него какое-то число из чисел, расположенных правее, от Pi до Pn. Число большее, чем Pi-1, несомненно, найдется, так как Pi-1 < Pi. Если есть несколько больших чисел, то, очевидно, надо ставить меньшее из них. Пусть это будет Pj, j > i-1. Затем число Pi-1 и все числа от Pi до Pn, не считая Pj нужно упорядочить по возрастанию. В результате получится непосредственно следующая перестановка, в примере — 1-4-2-3-5. Потом получится 1-4-2-5-3 (тот же алгоритм, но упрощенный случай) и т.д.
Нужно понимать, что в ЗК с n городами не нужны все перестановки из n элементов. Потому что перестановки, скажем, 1-3-5-4-2 и 3-5-4-2-1 (последний элемент соединен с первым) задают один и тот же тур, считанный сперва с города 1, а потом с города 3. Поэтому нужно зафиксировать начальный город 1 и присоединять к нему все перестановки из остальных элементов. Этот перебор даст (n-1)! разных туров, т.е. полный перебор в несимметричной ЗК (мы по-прежнему будем различать туры 1-3-5-4-2 и 1-2-4-5-3).
Если мы решим, поставленную в примере 1 задачу коммивояжера, методом лексикографического перебора, то получим следующий тур 1-2-6-5-4-3-1 длиной 36.
§5. Метод ветвей и границ решения ЗК
К идее метода ветвей и границ приходили многие исследователи, но Литтл с соавторами на основе указанного метода разработали удачный алгоритм решения ЗК и тем самым способствовали популяризации подхода. С тех пор метод ветвей и границ был успешно применен ко многим задачам, для решения ЗК было придумано несколько других модификаций метода, но в большинстве случаев излагается пионерская работа Литтла.
Т.к. желательно усовершенствовать перебор, применив разумную идею, ниже будет описан алгоритм, который реализует простую, но широко применимую и очень полезную идею.
Общая идея тривиальна: нужно разделить огромное число перебираемых вариантов на классы и получить оценки (снизу – в задаче минимизации, сверху – в задаче максимизации) для этих классов, чтобы иметь возможность отбрасывать варианты не по одному, а целыми классами. Трудность состоит в том, чтобы найти такое разделение на классы (ветви) и такие оценки (границы), чтобы процедура была эффективной.
Входные данные.
Алгоритм метода ветвей и границ предназначен для нахождения минимального гамильтонова контура на графе с N вершинами. В матрице расстояний задачи коммивояжера если между вершинами i и j нет дуги, то ставится символ "бесконечность". Этот же символ ставится по диагонали, что означает запрет на возвращение в вершину, через которую уже проходил контур.
Идея алгоритма.
Основная идея метода состоит в том, что вначале строят нижнюю границу длин множества гамильтоновых контуров ω0. Затем множество контуров разбивается на два подмножества таким образом, чтобы первое подмножество ω1ij состояло из гамильтоновых контуров, содержащих некоторую дугу (i,j), а другое подмножество ω1not ij не содержало этой дуги. Для каждого из подмножеств определяются нижние границы по тому же правилу, что и для первоначального множества гамильтоновых контуров. Полученные нижние границы подмножеств ω1ij и ω1not ij оказываются не меньше нижней границы всего множества гамильтоновых контуров, т.е.
Ф(ω0)<=Ф1ij,
Ф(ω0)<=Ф1not ij
Сравнивая нижние границы Ф1ij и Ф1not ij, можно выделить среди них то, которое с большей вероятностью содержит гамильтонов контур минимальной длины.
Затем одно из подмножеств ω1ij или ω1not ij по аналогичному правилу разбивается на два новых ω2ij и ω2ij. Для них снова отыскиваются нижние границы Ф2ij и Ф2not ij и т.д. Процесс ветвления продолжается до тех пор, пока не отыщется единственный гамильтонов контур. Его называют первым рекордом. Затем просматривают оборванные ветви. Если их нижние границы больше длины первого рекорда, то задача решена. Если же есть такие, для которых нижние границы меньше, чем длина первого рекорда, то подмножество с наименьшей нижней границей подвергается дальнейшему ветвлению, пока не убеждаются, что оно не содержит лучшего гамильтонова контура.
Если же такой найдется, то анализ оборванных ветвей продолжается относительно нового значения длины контура. Его называют вторым рекордом. Процесс решения заканчивается, когда будут проанализированы все подмножества.
Для практической реализации метода ветвей и границ применительно к задаче коммивояжера нужно указать прием определения нижних границ подмножеств и разбиения множества гамильтоновых контуров на подмножества (ветвление).
Определение нижних границ
Если к элементам любого ряда матрицы задачи коммивояжера (строке или столбцу) прибавить или вычесть из них некоторое число, то от этого оптимальность плана не изменится. Длина же любого гамильтонова контура изменится на данную величину.
Для того, чтобы найти нижнюю границу вычтем из каждой строки число, равное минимальному элементу этой строки, вычтем из каждого столбца число, равное минимальному элементу этого столбца. Полученная матрица называется приведенной по строкам и столбцам. Сумма всех вычтенных чисел называется константой приведения.
Константа приведения может быть выбрана в качестве нижней границы длины гамильтоновых контуров.
Разбиение множества контуров на подмножества
Для выделения претендентов на включение в множество дуг, по которым производится ветвление, рассмотрим в приведенной матрице все элементы, равные нулю. Найдем степени θij нулевых элементов этой матрицы. Степень нулевого элемента cij равна сумме минимальных элементов в строке i и столбце j при блокировании перехода (i,j) бесконечностью. С наибольшей вероятностью искомому гамильтонову контуру принадлежат дуги с максимальной степенью нуля.
Для получения матрицы контуров, включающей дугу (i,j) вычеркиваем в матрице строку i и столбец j, а чтобы не допустить образования не гамильтонова контура заменяем элемент замыкающий текущую цепочку на бесконечность.
Множество контуров, не включающих дугу (i,j) получаем путем замены элемента cij на бесконечность.
| - | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | - | 0 | 0 | 3 | 3 | 6 |
| 2 | 0 | - | 1 | 4 | 1 | 0 |
| 3 | 1 | 2 | - | 0 | 0 | 3 |
| 4 | 4 | 5 | 0 | - | 1 | 3 |
| 5 | 4 | 2 | 0 | 1 | - | 0 |
| 6 | 7 | 1 | 3 | 3 | 0 | - |
| 2 | 1 | 4 | ||||
| табл. 4 |
| - | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | - | 2 | 0 | 4 | 3 | 10 | 4 |
| 2 | 0 | - | 1 | 5 | 1 | 4 | 6 |
| 3 | 1 | 4 | - | 1 | 0 | 7 | 3 |
| 4 | 4 | 7 | 0 | - | 1 | 7 | 4 |
| 5 | 4 | 4 | 0 | 2 | - | 4 | 3 |
| 6 | 7 | 3 | 3 | 4 | 0 | - | 7 |
| табл. 3 |
| - | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | - | 6 | 4 | 8 | 7 | 14 |
| 2 | 6 | - | 7 | 11 | 7 | 10 |
| 3 | 4 | 7 | - | 4 | 3 | 10 |
| 4 | 8 | 11 | 4 | - | 5 | 11 |
| 5 | 7 | 7 | 3 | 5 | - | 7 |
| 6 | 14 | 10 | 10 | 11 | 7 | - |
| табл. 2 |
Повторно запишем матрицу:
Вычитание константы из элементов любой строки или столбца матрицы С, не изменяет минимальный тур.
Для алгоритма нам будет удобно получить побольше нулей в матрице С, не получая там, однако, отрицательных чисел. Для этого мы вычтем из каждой строки ее минимальный элемент (это называется приведением по строкам, см. табл. 3), а затем вычтем из каждого столбца матрицы, приведенной по строкам, его минимальный элемент, получив матрицу, приведенную по столбцам (см. табл.4).
Прочерки по диагонали означают, что из города i в город i ходить нельзя. Заметим, что сумма констант приведения по строкам равна 27, сумма по столбцам 7, сумма сумм равна 34.
Тур можно задать системой из шести подчеркнутых (выделенных другим цветом) элементов матрицы С, например, такой, как показано на табл. 2. Подчеркивание элемента означает, что в туре из i-го элемента идут именно в j-ый. Для тура из шести городов подчеркнутых элементов должно быть шесть, так как в туре из шести городов есть шесть ребер. Каждый столбец должен содержать ровно один подчеркнутый элемент (в каждый город коммивояжер въехал один раз), в каждой строке должен быть ровно один подчеркнутый элемент (из каждого города коммивояжер выехал один раз); кроме того, подчеркнутые элементы должны описывать один тур, а не несколько меньших циклов. Сумма чисел подчеркнутых элементов есть стоимость тура. В таблице 2 стоимость равна 36, это тот минимальный тур, который получен лексикографическим перебором.
Теперь будем рассуждать от приведенной матрицы в табл. 2. Если в ней удастся построить правильную систему подчеркнутых элементов, т.е. систему, удовлетворяющую трем вышеописанным требованиям, и этими подчеркнутыми элементами будут только нули, то ясно, что для этой матрицы мы получим минимальный тур. Но он же будет минимальным и для исходной матрицы С, только для того, чтобы получить правильную стоимость тура, нужно будет обратно прибавить все константы приведения, и стоимость тура изменится с 0 до 34. Таким образом, минимальный тур не может быть меньше 34. Мы получили оценку снизу для всех туров.
Теперь приступим к ветвлению. Для этого проделаем шаг оценки нулей. Рассмотрим нуль в клетке (1,2) приведенной матрицы. Он означает, что цена перехода из города 1 в город 2 равна 0. А если мы не пойдем из города 1 в город 2? Тогда все равно нужно въехать в город 2 за цены, указанные во втором столбце; дешевле всего за 1 (из города 6). Далее, все равно надо будет выехать из города 1 за цену, указанную в первой строке; дешевле всего в город 3 за 0. Суммируя эти два минимума, имеем 1+0=1: если не ехать «по нулю» из города 1 в город 2, то надо заплатить не меньше 1. Это и есть оценка нуля. Оценки всех нулей поставлены на табл. 5 правее и выше
нуля (оценки нуля, равные нулю, не ставились).
Выберем максимальную из этих оценок (в примере есть несколько оценок, равных единице, выберем первую из них, в клетке (1,2)).
Итак, выбрано нулевое ребро (1,2). Разобьем все туры на два класса – включающие ребро (1,2) и не включающие ребро (1,2). Про второй класс можно сказать, что придется приплатить еще 1, так что туры этого класса стоят 35 или больше.
Что касается первого класса, то в нем надо рассмотреть матрицу в табл. 6 с вычеркнутой первой строкой и вторым столбцом.
Дополнительно в уменьшенной матрице поставлен запрет в клетке (2,1), т. к. выбрано ребро (1,2) и замыкать преждевременно тур ребром (2,1) нельзя.
| 1 | 3 | 4 | 5 | 6 |
| 2 | 1 | 4 | 1 | 0 |
| 3 |
01 |
- | 1 | 3 |
| 4 | 0 | 1 | - | 0 |
| 5 | 3 | 3 |
01 |
- |
| табл. 8 |
| - | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | - |
01 |
0 | 3 | 3 | 6 |
| 2 |
01 |
- | 1 | 4 | 1 | 0 |
| 3 | 1 | 2 | - |
01 |
0 | 3 |
| 4 | 4 | 5 |
01 |
- | 1 | 3 |
| 5 | 4 | 2 | 0 | 1 | - | 0 |
| 6 | 7 | 1 | 3 | 3 |
01 |
- |
| табл. 5 |
| - | 1 | 3 | 4 | 5 | 6 |
| 2 |
01 |
1 | 4 | 1 | 0 |
| 3 | 1 | - |
01 |
0 | 3 |
| 4 | 4 |
01 |
- | 1 | 3 |
| 5 | 4 | 0 | 1 | - | 0 |
| 6 | 7 | 3 | 3 |
01 |
- |
| - | 1 | 3 | 4 | 5 | 6 |
| 2 |
01 |
1 | 4 | 1 | 0 |
| 3 |
03 |
- |
01 |
0 | 3 |
| 4 | 3 |
01 |
- | 1 | 3 |
| 5 | 3 | 0 | 1 | - | 0 |
| 6 | 6 | 3 | 3 |
01 |
- |
| табл. 7 |
Уменьшенную матрицу можно привести на 1 по первому столбцу, так что каждый тур, ей отвечающий, стоит не меньше 35. Результат наших ветвлений и получения оценок показан на рис.6.
Кружки представляют
классы: верхний
кружок – класс
всех тур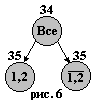 ов;
нижний левый
– класс всех
туров, включающих
ребро (1,2); нижний
правый – класс
всех туров, не
включающих
ребро (1,2). Числа
над кружками
– оценки снизу.
ов;
нижний левый
– класс всех
туров, включающих
ребро (1,2); нижний
правый – класс
всех туров, не
включающих
ребро (1,2). Числа
над кружками
– оценки снизу.
Продолжим ветвление в положительную сторону: влево - вниз. Для этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7 есть
| - | 3 | 4 | 6 |
| 2 | 1 | 3 |
03 |
| 4 |
03 |
- | 3 |
| 5 | 0 |
03 |
0 |
| табл. 10 |
| - | 3 | 4 | 5 | 6 |
| 2 | 1 | 3 | 1 | 0 |
| 4 |
01 |
- | 1 | 3 |
| 5 | 0 |
02 |
- | 0 |
| 6 | 3 | 2 |
03 |
- |
| табл. 9 |
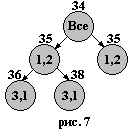 5+3=38.
Для оценки
левой нижней
вершины на рис.
7 нужно вычеркнуть
из матрицы
C[1,2] еще строку
3 и столбец 1,
получив матрицу
C(1,2),(3,1) на табл.
8. В эту матрицу
нужно поставить
запрет в клетку
(2,3), так как уже
построен фрагмент
тура из ребер
(1,2) и (3,1), т.е. [3,1,2] и нужно
запретить
преждевременное
замыкание
(2,3). Эта матрица
приводится
по столбцу на
1 (табл. 9), таким
образом, каждый
тур соответствующего
класса (т.е. тур,
содержащий
ребра (1,2) и (3,1)) стоит
36 и более.
5+3=38.
Для оценки
левой нижней
вершины на рис.
7 нужно вычеркнуть
из матрицы
C[1,2] еще строку
3 и столбец 1,
получив матрицу
C(1,2),(3,1) на табл.
8. В эту матрицу
нужно поставить
запрет в клетку
(2,3), так как уже
построен фрагмент
тура из ребер
(1,2) и (3,1), т.е. [3,1,2] и нужно
запретить
преждевременное
замыкание
(2,3). Эта матрица
приводится
по столбцу на
1 (табл. 9), таким
образом, каждый
тур соответствующего
класса (т.е. тур,
содержащий
ребра (1,2) и (3,1)) стоит
36 и более.
Оцениваем теперь нули в приведенной матрице C[(1,2),(3,1)] нуль с максимальной оценкой 3 находится в клетке (6,5). Отрицательный вариант имеет оценку 38+3=41. Для получения оценки положительного варианта убираем строчку 6 и столбец 5, ставим запрет в клетку (5,6), см. табл. 10. Эта матрица неприводима. Следовательно, оценка положительного варианта не увеличивается (рис.8).
| - | 3 | 4 |
| 4 | 0 | - |
| 5 | 0 | 0 |
| табл. 11 |
В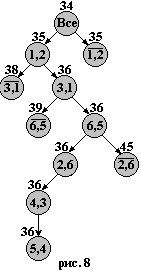 матрицу надо
добавить запрет
в клетку (5,3), ибо
уже построен
фрагмент тура
[3,1,2,6,5] и надо запретить
преждевременный
возврат (5,3). Теперь,
когда осталась
матрица 2х2 с
запретами по
диагонали,
достраиваем
тур ребрами
(4,3) и (5,4). Мы не зря
ветвились, по
положительным
вариантам.
Сейчас получен
тур: 1→2→6→5→4→3→1
стоимостью
в 36. При достижении
низа по дереву
перебора класс
туров сузился
до одного тура,
а оценка снизу
превратилась
в точную стоимость.
матрицу надо
добавить запрет
в клетку (5,3), ибо
уже построен
фрагмент тура
[3,1,2,6,5] и надо запретить
преждевременный
возврат (5,3). Теперь,
когда осталась
матрица 2х2 с
запретами по
диагонали,
достраиваем
тур ребрами
(4,3) и (5,4). Мы не зря
ветвились, по
положительным
вариантам.
Сейчас получен
тур: 1→2→6→5→4→3→1
стоимостью
в 36. При достижении
низа по дереву
перебора класс
туров сузился
до одного тура,
а оценка снизу
превратилась
в точную стоимость.
Итак, все классы, имеющие оценку 36 и выше, лучшего тура не содержат. Поэтому соответствующие вершины вычеркиваются. Вычеркиваются также вершины, оба потомка которой вычеркнуты. Мы колоссально сократили полный перебор. Осталось проверить, не содержит ли лучшего тура класс, соответствующий матрице С[Not(1,2)], т.е. приведенной матрице С с запретом в клетке 1,2, приведенной на 1 по столбцу (что дало оценку 34+1=35). Оценка нулей дает 3 для нуля в клетке (1,3), так что оценка отрицательного варианта 35+3 превосходит стоимость уже полученного тура 36 и отрицательный вариант отсекается.
Для получения оценки положительного варианта исключаем из матрицы первую строку и третий столбец, ставим запрет (3,1) и получаем матрицу. Эта матрица приводится по четвертой строке на 1, оценка класса достигает 36 и кружок зачеркивается. Поскольку у вершины «все» убиты оба потомка, она убивается тоже. Вершин не осталось, перебор окончен. Мы получили тот же минимальный тур, который показан подчеркиванием на табл. 2.
Удовлетворительных теоретических оценок быстродействия алгоритма Литтла и родственных алгоритмов нет, но практика показывает, что на современных ЭВМ они часто позволяют решить ЗК с n = 100. Это огромный прогресс по сравнению с полным перебором. Кроме того, алгоритмы типа ветвей и границ являются, если нет возможности доводить их до конца, эффективными эвристическими процедурами.
§6. Применение алгоритма Дейкстры к решению ЗК
Одним из вариантов решения ЗК является вариант нахождения кратчайшей цепи, содержащей все города. Затем полученная цепь дополняется начальным городом – получается искомый тур.
Известно множество простых алгоритмов. Один из них – алгоритм Дейкстры, предложенный Дейкстрой ещё в 1959г. Этот алгоритм решает общую задачу:
В ориентированной, неориентированной или смешанной сети найти кратчайший путь между двумя заданными вершинами.
При небольшой модификации алгоритм Дейкстры позволяет найти кратчайшие пути из данной вершины во все остальные. Матрица расстояний Dik задаёт длины дуг dik между i-ой и k-ой вершинами; если такой дуги нет, то dik присваивается большое число Б, равное “машинной бесконечности”. Алгоритм Дейкстры имеет квадратичную сложность O(n2).
Таким образом, для решения ЗК нужно n раз применить алгоритм Дейкстры следующим образом.
Возьмём произвольную пару вершин j,k. Исключим непосредственное ребро D[j,k]. С помощью алгоритма Дейкстры найдём кратчайшее расстояние между городами j,…,k. Пусть это расстояние включает некоторый город m. Имеем часть тура j,m,k. Теперь для каждой пары соседних городов (в данном примере – для j,m и m,k) удалим соответственное ребро и найдём кратчайшее расстояние. При этом в кратчайшее расстояние не должен входить уже использованный город.
Далее аналогично находим кратчайшее расстояние между парами вершин алгоритмом Дейкстры, до тех пор, пока все вершины не будут задействованы. Соединим последнюю вершину с первой и получим тур. Чаще всего это последнее ребро оказывается очень большим, и тур получается с погрешностью, однако алгоритм Дейкстры можно отнести к приближённым алгоритмам.
§7. Метод выпуклого многоугольника для решения ЗК
Рассмотрим рис. 9-10 и попытаемся найти в них кратчайшие туры. Очевидно, что кратчайший тур не должен содержать пересекающихся ребёр (в противном случае, поменяв вершины при пересекающихся рёбрах местами, получим более короткий тур). В первом случае кратчайшим является тур 1-2-4-5-3-1, а во втором – тур 1-2-3-4-5-1. Анализируя множество других аналогичных расположении пяти и более городов, можно сделать следующее общее предположение:
Если можно
построить
выпуклый
многоугольник,
по периметру
к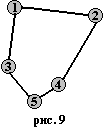
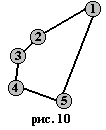 оторого
лежат все города,
то такой выпуклый
многоугольник
является кратчайшим
туром.
оторого
лежат все города,
то такой выпуклый
многоугольник
является кратчайшим
туром.
Однако не всегда
можно построить
выпуклый
многоугольник,
по периметру
которого лежали
бы все города.
Велика вероятность
того, что некоторые
города не войдут
в выпуклый
многоугольник.
Такие города
будем называть
“центральными”.
Так как построить
выпуклый
многоугольник
довольно легко,
то задача сводится
к тому, чтобы
включить в тур
в виде выпуклого
многоугольника
все центральные
города с минимальными
потерями. Пусть
имеется массив
T[n+1],
содержащий
в себе номера
городов по
порядку, которые
должен посетить
коммивояжер,
т. е. вначале
коммивояжер
должен посетить
город T[1],
затем T[2],
потом T[3] и
т.д., причём
T[n+1]=T[1]
(коммивояжер
должен вернуться
в начальный
город). Тогда,
если выполняется
равенство i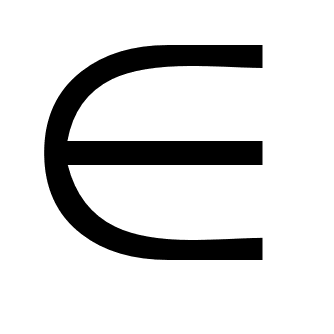 [1,2..n] C[T[i],p]+
C[p,T[i+1]]–C[T[I],T[i+1]]
= min, то центральный
город с номером
p нужно
включить в тур
между городами
T[i] и
T[i+1]. Проделав
эту операцию
для всех центральных
городов, в результате
получим кратчайший
тур. Для задачи,
решённой нами
методом ветвей
и границ, этот
алгоритм даёт
правильное
решение.
[1,2..n] C[T[i],p]+
C[p,T[i+1]]–C[T[I],T[i+1]]
= min, то центральный
город с номером
p нужно
включить в тур
между городами
T[i] и
T[i+1]. Проделав
эту операцию
для всех центральных
городов, в результате
получим кратчайший
тур. Для задачи,
решённой нами
методом ветвей
и границ, этот
алгоритм даёт
правильное
решение.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
13 | 6 | 13 | 14 | 15 | 14 | 16 | |
|
2 |
13 | 11 | 11 | 8 | 13 | 17 | 14 | |
|
3 |
6 | 11 | 5 | 6 | 11 | 7 | 11 | |
|
4 |
13 | 11 | 5 | 2 | 6 | 7 | 6 | |
|
5 |
14 | 8 | 6 | 2 | 6 | 5 | 6 | |
|
6 |
15 | 13 | 11 | 6 | 6 | 13 | 5 | |
|
7 |
14 | 17 | 7 | 7 | 5 | 13 | 9 | |
|
8 |
16 | 14 | 11 | 6 | 6 | 5 | 9 | |
| табл. 13 |
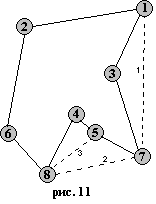
Одним из возможных недостатков такого алгоритма является необходимость знать не матрицу расстояний, а координаты каждого города на плоскости. Если нам известна матрица расстояний между городами, но неизвестны их координаты, то для их нахождения нужно будет решить n систем квадратных уравнений с n неизвестными для каждой координаты. Уже для 6 городов это сделать очень сложно. Если же, наоборот, имеются координаты всех городов, но нет матрицы расстояний между ними, то создать эту матрицу несложно. Это можно легко сделать в уме для 5-6 городов. Для большего количества городов можно воспользоваться возможностями компьютера, в то время как промоделировать решение системы квадратных уравнений на компьютере довольно сложно.
На основе вышеизложенного можно сделать вывод, что этот алгоритм, наряду с деревянным алгоритмом и алгоритмом Дейкстры, можно отнести к приближённым (хотя за этим алгоритмом ни разу не было замечено выдачи неправильного варианта).
§8. Генетические алгоритмы
Пусть дана некоторая сложная функция (целевая функция), зависящая от нескольких переменных, и требуется найти такие значения переменных, при которых значение функции максимально. Задачи такого рода называются задачами оптимизации и встречаются на практике очень часто.
Г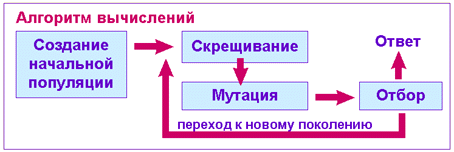 енетический
алгоритм - это
простая модель
эволюции в
природе, реализованная
в виде компьютерной
программы. В
нем используются
как аналог
механизма
генетического
наследования,
так и аналог
естественного
отбора. При
этом сохраняется
биологическая
терминология
в упрощенном
виде. Вот как
моделируется
генетическое
наследование:
енетический
алгоритм - это
простая модель
эволюции в
природе, реализованная
в виде компьютерной
программы. В
нем используются
как аналог
механизма
генетического
наследования,
так и аналог
естественного
отбора. При
этом сохраняется
биологическая
терминология
в упрощенном
виде. Вот как
моделируется
генетическое
наследование:
|
Хромосома |
Вектор
(последовательность)
из нулей и
единиц. |
|
Индивидуум
= |
Набор хромосом = вариант решения задачи. |
|
Кроссовер |
Операция, при которой две хромосомы обмениваются своими частями. |
|
Мутация |
Случайное изменение одной или нескольких позиций в хромосоме. |
Чтобы смоделировать эволюционный процесс, сгенерируем вначале случайную популяцию - несколько индивидуумов со случайным набором хромосом (числовых векторов). Генетический алгоритм имитирует эволюцию этой популяции как циклический процесс скрещивания индивидуумов и смены поколений.
Жизненный цикл популяции - это несколько случайных скрещиваний (посредством кроссовера) и мутаций, в результате которых к популяции добавляется какое-то количество новых индивидуумов. Отбором в генетическом алгоритме называется процесс формирования новой популяции из старой популяции, после чего старая популяция погибает. После отбора к новой популяции опять применяются операции кроссовера и мутации, затем опять происходит отбор, и так далее.
Отбор в генетическом алгоритме тесно связан с принципами естественного отбора в природе следующим образом:
|
Приспособленность |
Значение целевой функции на этом индивидууме. |
|
Выживание наиболее |
Популяция следующего поколения формируется в соответствии с целевой функцией. Чем приспособленнее индивидуум, тем больше вероятность его участия в кроссовере, т.е. размножении. |
Таким образом, модель отбора определяет, каким образом следует строить популяцию следующего поколения. Как правило, вероятность участия индивидуума в скрещивании берется пропорциональной его приспособленности. Часто используется так называемая стратегия элитизма, при которой несколько лучших индивидуумов переходят в следующее поколение без изменений, не участвуя в кроссовере и отборе. В любом случае каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность индивидуумов перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации берут наилучшего из найденных индивидуумов.
Генетический
алгоритм - новейший,
но не единственно
возможный
с пособ
решения задач
оптимизации.
С давних пор
известны два
основных пути
решения таких
задач - переборный
и локально-градиентный.
У этих методов
свои достоинства
и недостатки,
и в каждом конкретном
случае следует
подумать, какой
из них выбрать.
пособ
решения задач
оптимизации.
С давних пор
известны два
основных пути
решения таких
задач - переборный
и локально-градиентный.
У этих методов
свои достоинства
и недостатки,
и в каждом конкретном
случае следует
подумать, какой
из них выбрать.
Рассмотрим достоинства и недостатки стандартных и генетических методов на примере классической задачи коммивояжера (TSP - traveling salesman problem). Суть задачи состоит в том, чтобы найти кратчайший замкнутый путь обхода нескольких городов, заданных своими координатами. Оказывается, что уже для 30 городов поиск оптимального пути представляет собой сложную задачу, побудившую развитие различных новых методов (в том числе нейросетей и генетических алгоритмов).
Каждый вариант
решения (для
30 городов) - это
числовая строка,
где на j-ом месте
стоит номер
j-ого по порядку
обхода города.
Таким образом,
в этой задаче
30 параметров,
причем не все
комбинации
значений допустимы.
Естественно,
первой идеей
является полный
п еребор
всех вариантов
обхода.
еребор
всех вариантов
обхода.
Переборный
метод наиболее
прост по своей
сути и тривиален
в программировании.
Для поиска
оптимального
решения (точки
максимума
целевой функции)
требуется
последовательно
вычислить
значения целевой
функции во всех
возможных
точках, запоминая
максимальное
решение. Недостатком
этого метода
является большая
вычислительная
стоимость. В
частности, в
задаче коммивояжера
потребуется
просчитать
длины более
1 030
вариантов
путей, что совершенно
нереально.
Однако, если
перебор всех
вариантов за
разумное время
возможен, то
можно быть
абсолютно
уверенным в
том, что найденное
решение действительно
оптимально.
030
вариантов
путей, что совершенно
нереально.
Однако, если
перебор всех
вариантов за
разумное время
возможен, то
можно быть
абсолютно
уверенным в
том, что найденное
решение действительно
оптимально.
Второй популярный
способ основан
на методе
градиентного
спуска. При
этом вначале
выбираются
некоторые
случайные
значения параметров,
а затем эти
значения постепенно
изменяют, добиваясь
наибольшей
скорости роста
целевой функции.
Дост игнув
локального
максимума,
такой алгоритм
останавливается,
поэтому для
поиска глобального
оптимума потребуются
дополнительные
усилия.
игнув
локального
максимума,
такой алгоритм
останавливается,
поэтому для
поиска глобального
оптимума потребуются
дополнительные
усилия.
Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же - глобальный). Легко видеть, что задача коммивояжера унимодальной не является.
Типичная практическая задача, как правило, мультимодальна и многомерна, то есть содержит много параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение.
Однако, комбинируя переборный и градиентный методы, можно надеяться получить хотя бы приближенное решение, точность которого будет возрастать при увеличении времени расчета.
Генетический
алгоритм представляет
собой именно
такой комбинированный
метод. Механизмы
с крещивания
и мутации в
каком-то смысле
реализуют
переборную
часть метода,
а отбор лучших
решений - градиентный
спуск. На рисунке
показано, что
такая комбинация
позволяет
обеспечить
устойчиво
хорошую эффективность
генетического
поиска для
любых типов
задач.
крещивания
и мутации в
каком-то смысле
реализуют
переборную
часть метода,
а отбор лучших
решений - градиентный
спуск. На рисунке
показано, что
такая комбинация
позволяет
обеспечить
устойчиво
хорошую эффективность
генетического
поиска для
любых типов
задач.
Итак, если на
некотором
множестве
задана с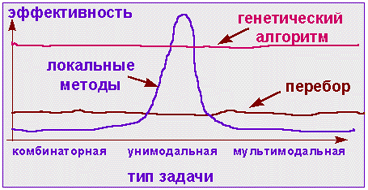 ложная
функция от
нескольких
переменных,
то генетический
алгоритм - это
программа,
которая за
разумное время
находит точку,
где значение
функции достаточно
близко к максимально
возможному.
Выбирая приемлемое
время расчета,
мы получим одно
из лучших решений,
которые вообще
возможно получить
за это время.
ложная
функция от
нескольких
переменных,
то генетический
алгоритм - это
программа,
которая за
разумное время
находит точку,
где значение
функции достаточно
близко к максимально
возможному.
Выбирая приемлемое
время расчета,
мы получим одно
из лучших решений,
которые вообще
возможно получить
за это время.
§9. Применение генетических алгоритмов
Определим теперь понятия, соответствующие мутации и кроссинговеру в генетическом алгоритме.
Мутация — это преобразование хромосомы, случайно изменяющее одну или несколько ее позиций (генов). Наиболее распространенный вид мутаций — случайное изменение только одного из генов хромосомы.
Кроссинговер (в литературе по генетическим алгоритмам также употребляется название кроссовер или скрещивание) — это операция, при которой из двух хромосом порождается одна или несколько новых хромосом. В простейшем случае кроссинговер в генетическом алгоритме реализуется так же, как и в биологии (см. рис. 1). При этом хромосомы разрезаются в случайной точке и обмениваются частями между собой. Например, если хромосомы (1, 2, 3, 4, 5) и (0, 0, 0, 0, 0) разрезать между третьим и четвертым генами и обменять их части, то получатся потомки (1, 2, 3, 0, 0) и (0, 0, 0, 4, 5).
Блок-схема генетического алгоритма изображена на рис. 1. Вначале генерируется начальная популяция особей (индивидуумов), т.е. некоторый набор решений задачи. Как правило, это делается случайным образом. Затем мы должны смоделировать размножение внутри этой популяции. Для этого случайно отбираются несколько пар индивидуумов, производится скрещивание между хромосомами в каждой паре, а полученные новые хромосомы помещаются в популяцию нового поколения. В генетическом алгоритме сохраняется основной принцип естественного отбора — чем приспособленнее индивидуум (чем больше соответствующее ему значение целевой функции), тем с большей вероятностью он будет участвовать в скрещивании. Теперь моделируют в нескольких случайно выбранных особях нового поколения изменяются некоторые гены. Затем старая популяция частично или полностью уничтожается и мы переходим к рассмотрению следующего поколения. Популяция следующего поколения в большинстве реализаций генетических алгоритмов содержит столько же особей, сколько начальная, но в силу отбора приспособленность в ней в среднем выше. Теперь описанные процессы отбора, скрещивания и мутации повторяются уже для этой популяции и т. д.
В каждом следующем поколении мы будем наблюдать возникновение совершенно новых решений нашей задачи. Среди них будут как плохие, так и хорошие, но благодаря отбору число хороших решений будет возрастать. Заметим, что в природе не бывает абсолютных гарантий, и даже самый приспособленный тигр может погибнуть от ружейного выстрела, не оставив потомства. Имитируя эволюцию на компьютере, мы можем избегать подобных нежелательных событий и всегда сохранять жизнь лучшему из индивидуумов текущего поколения — такая методика называется “стратегией элитизма”.
Чтобы использовать генетический алгоритм для решения практических задач, необходимо рассматривать более сложные варианты введенных выше понятий. Поясним это на примере задачи коммивояжера для 20 городов.
В качестве индивидуумов будем рассматривать маршруты обхода. Информацию о маршруте можно записать в виде одной хромосомы — вектора длины 20, где в первой позиции стоит номер первого города на пути следования, затем — номер второго города и т. д. Первое затруднение возникает, когда мы пытаемся определить мутации для таких хромосом — стандартная операция, изменяющая только одну позицию вектора, недопустима, так как приводит к некорректному маршруту. Но можно определить мутацию как перестановку значений двух случайно выбранных генов. При таком преобразовании путь следования меняется только в двух городах.
Найденный маршрут, вероятно, не является самым оптимальным, но близок к нему по длине — как правило, генетические алгоритмы “ошибаются” не более чем на 5—10%. Этот недостаток компенсируется для комбинаторных задач относительно высокой скоростью работы — в нашем примере ответ был получен за 25 секунд. На практике генетические алгоритмы нередко используют совместно с другими методами, которые позволяют повысить их точность.
Эксперименты показали, что погрешность разработанного алгоритма не зависит от погрешности начального решения и составляет (максимальные значения) для ориентированных графов - 5%, для неориентированных 1%. Причем в 90% случаев алгоритм находил точное решение. Эксперименты проводились для графов с количеством вершин, меньшим 75 (где было возможным нахождение точного решения).
В.М. Бондарев, В.И. Рублинецкий, Е.Г. Качко. Основы программирования, 1998 г.
Н. Кристофидес. Теория графов: алгоритмический подход, Мир, 1978 г.
Ф.А. Новиков. Дискретная математика для программисто Птер, 2001 г.
В.А. Носов. Комбинаторика и теория графов, МГТУ, 1999 г.
О. Оре. Теория графов, Наука, 1982 г.
www.codenet.ru
www.algolist.ru
1000 76 43 38 51 42 19 80
42 1000 49 26 78 52 39 87
48 28 1000 36 53 44 68 61
72 31 29 1000 42 49 50 38
30 52 38 47 1000 64 75 82
66 51 83 51 22 1000 37 71
77 62 93 54 69 38 1000 26
42 58 66 76 41 52 83 1000