Реферат: Задача обработки решеток
Содержание
| Введение | 3 |
| 1.1 Задача обработки решетки | 5 |
| 1.2 Продолжаемость | 9 |
| 1.2.1 Спектральные основы и совместные множества | 9 |
| 1.2.2 Сопряженно-симметричные функции и их векторное представление | 10 |
| 1.2.3 Õàðàêòåðèñòèêè ïðîäîëæàåìîñòè | 11 |
| 1.3 Граница и внутренняя часть | 15 |
| 1.3.1 Функции спектральной плотности мощности | 15 |
| 1.3.2 Дискретизация спектральной основы | 16 |
| 1.4 Метод Писаренко | 18 |
| 1.4.1 Метод Писаренко для решеток датчиков | 18 |
| 1.4.2 Вычисление оценки Писаренко | 22 |
| Резюме | 25 |
| 2.1. Интегральное уравнение для открытого резонатора с осесимметричным диском | 26 |
| 2.2 Интегральное уравнение открытого резонатора с диэлектрическим диском, несоосным с зеркалами [72] | 32 |
| Заключение, перспективы | 39 |
| 3 Метод СВЧ контроля параметров полимеров | 40 |
| Литература | 45 |
| ПриложениЯ | 47 |
| Приложение А | 48 |
| Приложение В | 50 |
| Приложение С | 52 |
| Иллюстрации | 54 |
Рассматривается вкратце задача обработки решеток и формулируется задача абстрактной спектральной оценки. Эта задача включает оценку многомерного спектра мощности частотно-волнового вектора по измерениям корреляционной функции и знанию спектральной основы.
Исследование согласующихся по корреляции спектральных оценок приводит к вопросу продолжаемости : существует ли любой положительный спектр на спектральной основе, который в точности согласует данное множество корреляционных выборок? Для ответа на этот вопрос разработана математическая структура, в рамках которой следует анализировать и разрабатывать алгоритмы спектральной оценки.
Метод спектральной оценки Писаренко, который моделирует спектр в виде импульсов плюс шумовая компонента, распространяется со случая временной последовательности на более общий случай обработки решеток. Оценку Писаренко получают как решение линейной задачи оптимизации, которая может быть решено при использовании линейного алгоритма программирования, к примеру, симплекс - метода.
Введение
Подобно тому, как спектр мощности стационарной временной последовательности описывает распределение мощности в зависимости от частоты, спектр мощности частотно-волнового вектора однородного и стационарного волнового поля описывает распределение мощности в зависимости от волнового вектора и временной частоты или, что эквивалентно, в зависимости от направления распространения и временной частоты. Спектр частота - волновой вектор или информация, которая может быть получена из него, является важной во многих применениях. В радиоастрономии и гидролокации могут быть основаны на информации, содержащейся в оценке спектра мощности. Следовательно, оценка спектра мощности по данным решетки датчиков представляет больной практический интерес.
Раздел II содержит краткий обзор волновых нолей и решеток датчиков, а также введение в задачу спектральной оценки. Рассматриваются альтернативные математические представления спектров мощности, как мер и как функций спектральной плотности. В разделе II вводится термин корешетки, множества разделений вектора и временных запаздываний, для которых доступны корреляционные выборки, и спектральной основы, области частоты-пространства волнового, вектора, содержащей мощность. к которой чувствительны датчики. Никакой особой структуры не предполагается как и для корешетки. Так и для спектральной основы. Раздел II завершается Формулировкой абстрактной задачи: оценкой спектра мощности при условии того, что он положителен на спектральной основе и равен нулю вне ее, а также обладает некоторыми известными корреляциями для разделений в корешетке. Хотя и проще многих задач, встречаемых на практике, ключевые характеристики, которые отличают задачу решетки, от задачи спектральной оценки мощности временной последовательности, сохраняются : многомерность частотной переменной и неравномерность корешетки.
При условии этой формулировки проблемы естественно рассматривать спектральные оценки, которые согласуются с известной информацией: спектральные оценки, положительные на спектральной основе и равные нулю вне её, в точности согласующиеся с измеренными корреляциями, .исследование таких, согласованных с корреляцией, спектральных оценок ставит два главных вопроса. Первый и более фундаментальный вопрос касается существования любой такой оценки. Эта проблема, продолжаемости имеет глубокие исторические корни [1] и недавно была поднята Дикинсоном [2] относительно двумерной спектральной оценки по методу максимальной энтропии, а также является темой некоторых недавних работ Цибенко[3 - 4]. Проблема продолжаемости исследуется в разделе III. Характеризуются продолжаемые множества корреляционных измерений. Рассматривается также их зависимость от спектральной основы и эффект дискретизации спектральной основы. В попытке ответить на вопрос о продолжаемости разработана необходимая математическая структура, позволяющая анализировать специальные методы спектральной оценки и разрабатывать алгоритмы для их вычисления.
Вторым поднятым вопросом является вопрос единственности:
имеется ли единственная согласованная с. корреляцией спектральная оценка и, если нет, как выбрать нужную ? Действительно, единственная оценка не существует, за исключением весьма специальных случаев; задача метода спектральной оценки состоит в выборе одного из ансамбля спектров, удовлетворяющего согласованию корреляции, положительности и ограничениям спектральной основы. Раздел IУ касается метода Писаренко [5] , который включает моделирование корреляционных измерений в виде суммы двух компонентов. Один, шумовой компонент известной спектральной формы, но неизвестной амилитуды, делается настолько большим, насколько это возможно без превращения второго компонента в непродолжаемый. Показано, что спектральная оценка по методу Писаренко решает линейную задачу оптимизации. Решение этой задачи оптимизации будет всегда существовать, если корреляционные измерения являются продолжаемыми. Показало, что тактически метод Писаренко тесно связан с вопросом продолжаемости и алгоритм вычисления оценки Писаренко будет также служить в качестве теста продолжаемости. Показано, что оценка Писаренко не является всегда единственной в общем случае, хотя она единственна для случая временной последовательности, где задача линейной оптимизации сводится к задаче на собственные значения.
1.1. Задача обработки решетки
Вообразим многомерную однородную
среду, поддерживающую волновое поле с комплексными значениями u(x, t) и содержащую решетку датчиков. Волновое
паче будет предполагаться однородным и стационарным, так что его статистики
второго порядка описываются корреляционной санкцией r , или эквивалентно, спектром мощности ![]() [6].
[6].
![]() (2.1)
(2.1)
Представление спектра мощности, посредством положительной
меры ![]() обеспечивает необходимую гибкость для того, чтобы
иметь дело с диапазоном спектральных оснований унифицированным образом и
обрабатывать спектры, которые содержат импульсы: конечная мощность при
единственном волновом векторе.
обеспечивает необходимую гибкость для того, чтобы
иметь дело с диапазоном спектральных оснований унифицированным образом и
обрабатывать спектры, которые содержат импульсы: конечная мощность при
единственном волновом векторе.
В инженерной литературе более
принято представлять спектр мощности посредством положительной функции
спектральной плотности ![]() . В этом
представлении
. В этом
представлении
![]() (2.2)
(2.2)
где ![]() -
некоторая фиксированная мера, которая позволяет интерпретировать выражение
/2.2/ в виде многомерной поверхности или объемного интеграла, возможно
взвешенного, над частотно-волновым векторным пространством.
-
некоторая фиксированная мера, которая позволяет интерпретировать выражение
/2.2/ в виде многомерной поверхности или объемного интеграла, возможно
взвешенного, над частотно-волновым векторным пространством.
Если дана 'функция спектральной
плотности мощности ![]() , то возможно
определить соответствующую положительную меру путем требования, чтобы мера
подмножества В частотно-волнового векторного пространства равнялась интегралу
функции спектральной плотности по В:
, то возможно
определить соответствующую положительную меру путем требования, чтобы мера
подмножества В частотно-волнового векторного пространства равнялась интегралу
функции спектральной плотности по В:
![]() (2.3)
(2.3)
Теперь будет сформулирована простая задача спектральной оценки. Особое внимание будет уделено моделированию свойств процесса сбора данных, которые являются общими для многих задач обработки решеток. Эти свойства включают измерение корреляционной функции при конечном числе неравномерно распределенных точек и ограничения на область пространства частоты-воктора волны, в котором может присутствовать мощность.
Каждый из ПИП производит временную функцию, которая является волновым полем U, подвергнутым выборке в точке пространства. Совокупность временных функций, образуемых всеми ПИП, выход или отклик решетки, должна быть обработана с тем, чтобы обеспечить оценку спектра мощности частоты-волнового вектора. Стохастический характер волнового поля неизменно приводит к случайным 'изменениям любой спектральной оценки, основанной на выходе решетки. Чтобы противодействовать этому эффекту, спектральные оценки часто базируются на устойчивых статистиках, получаемых с выхода решетки. Обычным примером такой статистики является корреляционная оценка, вычисляемая посредством умножения выхода одного ПИП на задержанный во времени выход второго ПИП с усреднением по времени. Эта обработка дает в результате оценку корреляционной функции с временной задержкой, соответствующей запаздыванию во времени и пространственным разделением, которое является вектором расстояния между ПИП. Процесс усреднения обеспечивает статистически стабильные оценки корреляции, что дает в результате статистическую стабильность спектральной оценки, основанной на этих корреляционных оценках. Важно отметить, что оценки корреляций доступны только для конечного множества междатчиковых расстояний и временных задержек [8]. Тема ошибок корреляционных оценок не будет затрагиваться. Эта. статья касается скорее свойств множеств истинных корреляционных выборок и спектральных оценок, основанных на корреляционных выборка.
Предполагается известным, что спектр заключен в ограниченной области пространства частота-волновой вектор, спектральной основе. Снаружи этой основы предполагается, что спектр равен нулю. Ограниченная спектральная основа может естественно возникнуть несколькими путями. Например, в среде, которая поддерживает скалярные волны, известный источник, среда и характеристики датчика могут быть использованы для построения соответствующей спектральной основы. Источник может иметь известную временную ширину полосы или известную конечную угловую протяженность. Соотношение дисперсии и затухание в среде ограничивает область пространства частота-волновой вектор, в которой может присутствовать мощность. ПИП могут иметь конечную временную полосу могут быть направленными. Все эти эффекты могут моделироваться посредством предположения о том, что мощность отсутствует снаружи определенной области пространства частота-волновой вектор. Известная спектральная основа, базирующаяся на физике частной задачи, представляет собой важную априорную информацию, которая может быть использовала в .задаче спектральной оценки.
Во многих применениях значительно больше данных доступно во временном измерении, чем в пространственном измерении. В этих случаях удобно отделить временную переменную посредством анализа Фурье временной последовательности выхода каждого датчика, а затем произвести раздельную спектральную опенку волнового вектора для каждой временной частоты путем использования коэффициентов Фурье в качестве данных для спектрального оценивателя волнового вектора. Таким образом задача оценки стимулируется для комплексных данных, даже хотя физические волновые поля имеют
вещественные значения. К счастью, обычный анализ Фурье
является часто удовлетворительным, когда данные избыточны, а также неявным при
узкополосном характере многих датчиков. Там, где ограниченные данные во
временное измерении делают упомянутый выше подход не практичным, а доступными
являются широкополосные решетки датчиков, полная задача может трактоваться
посредством включения временных переменных ![]() и
и
![]() в векторы
в векторы ![]() и k. Тогда
и k. Тогда ![]() будет
описывать разделение как в пространстве, так и во времени, a k волновой
вектор пространства-времени. Будем полагать, что принят один из этих двух
подходов; следовательно временные переменные
будет
описывать разделение как в пространстве, так и во времени, a k волновой
вектор пространства-времени. Будем полагать, что принят один из этих двух
подходов; следовательно временные переменные ![]() и
и
![]() будут опущены.
будут опущены.
Простым примером модели спектральной оценки, разработанной выше, является решетка ПИП, состоящая из одинаковым образом ориентированных ИП.
Пример 2.1: решетка из трех ИП.
Представим, что решетка ИП, показанная на рис.1, используется для приема
единственной временной частоты ![]() ,
соответствующей длине волны
,
соответствующей длине волны ![]() .
.
ИП с диаметром d имеет полосу пропускания, которая грубо описывается выражением
![]() .
.
Полагая, что волновое поле удовлетворяет соотношению дисперсии
для однородной, недиспергирующей среды, основанием для спектральной оценки должна быть полярная шапка, описываемая двумя уравнениями
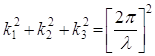
![]()
и показанная на рис.2
Совместным множеством для этой задачи является только множество всех 3-мерных пространственных разделений между ИП в решетке.
1.2 Продолжаемость
В последнем разделе была построена простая модель задачи обработки решетки: если даны некоторые корреляционные измерения и спектральная основа, получить спектральную оценку. Естественно использование известной информации о спектре для ограничения спектральной оценки требованием того, чтобы она была согласована с измеренными корреляциями, положительной и ограниченной спектральной основой. Такие, спектральные оценки называются спектральными оценками согласованными с корреляцией.
Исследование спектральных оценок, согласованных с корреляцией подымает фундаментальный вопрос о существовании. Если задана, конечная совокупность измеренных корреляций и спектральная основа, то существует ли по крайней мере одна согласованная с корреляцией спектральная оценка ? Если такая спектральная оценка существует, то о измеренных корреляциях говорят, что они продолжаемы. /Корреляционная функция, полученная посредством обратного преобразования Фурье согласованной с корреляцией спектральной оценки, является подходящим продолжением корреляционных измерений на все пространственные разделения/. После некоторых необходимых математических определений мы получим ответ на вопрос о существовании путем характеризации множества продолжаемых корреляционных измерений.
1.2.1 Спектральные основы и совместные множества
Вначале необходимо определить
более тщательно термины спектральная основа и совместное множество.
Предполагается, что спектральная основа К является компактным
подмножеством ![]() , т.е. К
замкнуто и ограничено. Предположение относительно компактности К
приводит к некоторым техническим преимуществам: непрерывная функция на
компактном множестве достигает своей нижней и верхней грани. Кроме того,
компактность должна всегда содержаться в физической задаче. Как обсуждалось в
предыдущем разделе, знание источника, среды и характеристик датчиков может быть
использовано для построения соответствующей спектральной основы.
, т.е. К
замкнуто и ограничено. Предположение относительно компактности К
приводит к некоторым техническим преимуществам: непрерывная функция на
компактном множестве достигает своей нижней и верхней грани. Кроме того,
компактность должна всегда содержаться в физической задаче. Как обсуждалось в
предыдущем разделе, знание источника, среды и характеристик датчиков может быть
использовано для построения соответствующей спектральной основы.
Совместное множество ![]() будет определяться, как
конечное подмножество
будет определяться, как
конечное подмножество ![]() со свойствами
со свойствами
I / 0![]() ;
;
II / если ![]()
III / ![]() является множеством линейно
независимых функций на .
является множеством линейно
независимых функций на .
Условие I/ подразумевает знание r(0) полной мощности в спектре.
Условие II/ отражает тот факт, что
корреляционная функция всегда сопряжено симметрична; так, если ![]() известна, то известна и
известна, то известна и ![]() . Условия I/ и II/ совместно подразумевают, что
. Условия I/ и II/ совместно подразумевают, что ![]() имеет вид
имеет вид
![]() (3.1)
(3.1)
Условие II/ гарантирует, что корреляционные измерения независимы; каждое измерение дает новую информацию о спектре.
Если D > 1 , то задача спектральной оценки является
многомерной. Если ![]() и
и ![]() то задача спектральной
оценки является известным случаем временной последовательности и вопрос
продолжаемости сводится к известной задаче тригонометрических моментов [9].
то задача спектральной
оценки является известным случаем временной последовательности и вопрос
продолжаемости сводится к известной задаче тригонометрических моментов [9].
1.2.2 Сопряженно-симметричные функции и их векторное представление
Спектральная основа и совместное
множество естественно предполагает ситуацию векторного пространства для задачи
спектральной оценки, в которой сопряженно-симметричные комплекснозначные
функции на ![]() будут играть центральную
роль. Сопряженно-симметричная функция f на
будут играть центральную
роль. Сопряженно-симметричная функция f на ![]() является
функцией, для которой
является
функцией, для которой ![]() при всех
при всех ![]() . Корреляционные выборки, из
которых должны образовываться спектральные оценки, являются такими функциями.
/Благодаря этой симметрии многие из нижеследующих выражений являются вещественными,
хотя они, ради простоты, были записаны в виде, который предполагает, что они
могут быть комплексно-значными/. Совместное множество
. Корреляционные выборки, из
которых должны образовываться спектральные оценки, являются такими функциями.
/Благодаря этой симметрии многие из нижеследующих выражений являются вещественными,
хотя они, ради простоты, были записаны в виде, который предполагает, что они
могут быть комплексно-значными/. Совместное множество ![]() имеет 2М + I элемент и
таким образом сопряженно-симметричная функция на
имеет 2М + I элемент и
таким образом сопряженно-симметричная функция на ![]() характеризуется
посредством 2М + I независимыми вещественными числами. Так,
сопряженно-симметричная функция на
характеризуется
посредством 2М + I независимыми вещественными числами. Так,
сопряженно-симметричная функция на ![]() может
рассматриваться как вектор в
может
рассматриваться как вектор в ![]() .
/Векторное пространство над вещественными числами выбирается потому, что только
умножение на вещественное число, переводит корреляционную функцию в другую
корреляционную функцию/. Будут использоваться как функциональное обозначение
.
/Векторное пространство над вещественными числами выбирается потому, что только
умножение на вещественное число, переводит корреляционную функцию в другую
корреляционную функцию/. Будут использоваться как функциональное обозначение ![]() так и векторное f.
так и векторное f.
Поскольку ![]() является линейно-независимым
ìíîæåñòâîì функций на K, то отсюда следует, что каждый вектор
p â
является линейно-независимым
ìíîæåñòâîì функций на K, то отсюда следует, что каждый вектор
p â ![]() может быть единственным образом связан ñ вещественно-значным
может быть единственным образом связан ñ вещественно-значным ![]() -полиномом P(k)
íà Ê посредством соотношения
-полиномом P(k)
íà Ê посредством соотношения
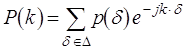 (3.2)
(3.2)
Вектор будет называться
положительным, если ![]() на К. Р
будет обозначать множество этих векторов, связанных с положительными
на К. Р
будет обозначать множество этих векторов, связанных с положительными ![]() -полиномами. Из компактности
К, как можно показать, следует, что Р является выпуклым конусом с
вершиной в начале координат. /Множество С является конусом с вершиной в
начале координат, если
-полиномами. Из компактности
К, как можно показать, следует, что Р является выпуклым конусом с
вершиной в начале координат. /Множество С является конусом с вершиной в
начале координат, если ![]() подразумевает
подразумевает ![]() для всех
для всех ![]() [10]. Конусы являются
важными видами множеств в задаче спектральной оценки, поскольку только
умножение на положительные вещественные числа переводит корреляционную функцию
в другую корреляционную функцию, а
[10]. Конусы являются
важными видами множеств в задаче спектральной оценки, поскольку только
умножение на положительные вещественные числа переводит корреляционную функцию
в другую корреляционную функцию, а ![]() -полином
в другой
-полином
в другой ![]() -полином./
-полином./
Внутреннее произведение вектора r корреляционных выборок и вектора р полиномиальных коэффциентов будет определяться как
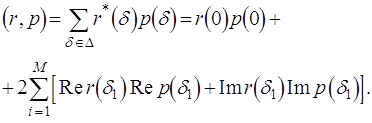 (3.3)
(3.3)
Это внутреннее произведение дает
возможность по новому записать ![]() -полином:
-полином:
![]() , где
, где ![]() обозначает вектор с
компонентами
обозначает вектор с
компонентами ![]() . Отметим также,
что если
. Отметим также,
что если ![]() , то
, то ![]() , что cooтветствует
выражению соотношению Парсеваля.
, что cooтветствует
выражению соотношению Парсеваля.
1.2.3 Характеристики продолжаемости
Пусть Е обозначает
множество продолжаемых векторов корреляции. То есть ![]() , если
, если
![]() (3.4)
(3.4)
для некоторой положительной меры ![]() на К. Из свойств
интеграла следует, что, Е является замкнутым выпуклым конусом с вершиной
в начале координат. Кроме того, сечение по Е при
на К. Из свойств
интеграла следует, что, Е является замкнутым выпуклым конусом с вершиной
в начале координат. Кроме того, сечение по Е при ![]() :
:
![]() (3.5)
(3.5)
является выпуклой оболочкой компактного множества
![]() (3.6)
(3.6)
является выпуклой оболочкой компактного множества
Итак, Е - замкнутый выпуклый конус с вершиной в начале координат, генерируемой посредством А. Эта характеристика продолжаемой корреляция аналогична той, которую дал первоначально Каратеодори в 1907 году для задачи тригонометрических моментов [I]. Важность этого состоит в том, что множество продолжаемых векторов корреляции описывается в терминах простого множества А. Это дает также ясную геометрическую картину продолжаемости и будет полезно в доказательствах.
Вторая характеристика продолжаемости, которая является более полезной при разработке методов спектральной опенки, происходит из того факта, что Е выражается в виде пересечения всех замкнутых полупространств, содержащих его [10]. Эта характеристика включает дуальность, так как полупространства определяются линейными функционалами, т.е. элементами дуального пространства. Замкнутое полупространство определяется посредством вектора q, и вещественного числа с в виде множества
![]() (3.7)
(3.7)
Чтобы определить отдельные полупространства, содержащие Е,
достаточно рассмотреть те корреляционные векторы, которые генерируют Е :
положительные кратные векторов во множестве А. Замкнутое
полупространство содержит Е тогда и только тогда, когда ![]() для каждого
для каждого ![]() и каждого
и каждого ![]() . Поскольку
. Поскольку ![]() можно сделать произвольно
большой, должно быть истинным то, что
можно сделать произвольно
большой, должно быть истинным то, что ![]() ,
т.е. q - член конуса Р.
Наименьшее полупространство, содержащее Е для такого q соответствует выбору с = 0. Итак,
,
т.е. q - член конуса Р.
Наименьшее полупространство, содержащее Е для такого q соответствует выбору с = 0. Итак,
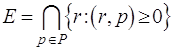 (3.8)
(3.8)
или, словами, следующее.
Теорема о продолжимости : .вектор ![]() является продолжимым тогда
и только тогда, когда
является продолжимым тогда
и только тогда, когда ![]() для всех
положительных p.
для всех
положительных p.
Таким образом, положительные полиномы естественно имеют место в задаче продолжаемости, поскольку они определяют гиперплоскости основы множества Е продолжаемых векторов корреляции. На языке функционального анализа теорема о продолжимости, которая является видом леммы Фаркаша [11], просто констатирует, что Е и Р - положительные сопряженные конусы.[10]. Эта теорема имеет важное следствие относительно перемещения простой характеристики Р, в терминах положительности, на характеристику Е. Хотя введение спектральной основы в рассматриваемую задачу является новым, по существу та же характеристика продолжимости была первоначально использована Кальдероном и Пепинским [l2], и Рудиным [l3].
Рисунок 4 демонстрирует зависимость Е от спектральной основы. Существуют две точки зрения на эту зависимость. Прямая точка зрения отмечает тот факт, что Е является выпуклым конусом, генерированным А; поскольку К уменьшилось, А сжалось и Е теперь меньше, чем на рис.3. Косвенная точка зрения включает ограничения; множество К ограничивает множество Р посредством условия о положительности, а множество Р ограничивает множество P посредством теоремы продолжимости. Итак, когда К сжимается, Р растет, и Е сжимается.
Для случая временной последовательности теорема о продолжимости сводится к тесту положительной определенности теплицевой матрицы, образованной из корреляционных выборок. Следовательно, о продолжимости можно говорить как об общем аналоге положительной определенности.
Пример 3.1 : Случай временной
последовательности; D=1,
![]() .B этом случае, проблема
продолжимости сводится к проблеме тригонометрических моментов [9]. Хотя это и не справедливо в
общем случае, для случая временной последовательности, как следует из
фундаментальной теоремы алгебры, положительный полином может быть факторизован
в виде квадрата модуля М-той степени тригонометрического полинома
.B этом случае, проблема
продолжимости сводится к проблеме тригонометрических моментов [9]. Хотя это и не справедливо в
общем случае, для случая временной последовательности, как следует из
фундаментальной теоремы алгебры, положительный полином может быть факторизован
в виде квадрата модуля М-той степени тригонометрического полинома
![]() .
.
Внутреннее произведение ![]() становится
теплицевой формой в коэффициентах
становится
теплицевой формой в коэффициентах ![]()

Таким образом, требование того,
чтобы внутреннее произведение ![]() было
положительным для всех полиномов сводится к требованию положительной
определенности теплицевой формы, соответствующей корреляционным измерениям.
было
положительным для всех полиномов сводится к требованию положительной
определенности теплицевой формы, соответствующей корреляционным измерениям.
1.3 Граница и внутренняя часть
Необходимо будет делать различие между границей и внутренней частью множеств Е и Р. Рассмотрение метода Писаренко в разделе 17, к примеру, включает векторы на границах Е и Р. Векторы во внутренней части Е и P являются важными тогда, когда затрагиваются пункции спектральной плотности, как например, в методе спектральной опенки по способу максимальной энтропии [l4].
Граница замкнутого множества состоит из тех членов, которые находятся произвольно близко к некоторому вектору снаружи множества. Внутренняя часть замкнутого множества состоит из тех членов, которые не находятся на границе. .
Граница и внутренняя часть конечного измеримого множества не зависит от частного выбора нормы вектора [15]. Кроме того, поскольку Р и Е являются выпуклыми множествами, особенно просто охарактеризовать их внутренний части и границы.
Граница Р, обозначаемая ![]() , состоит из тех положительных
полиномов, которые равны нулю для некоторых
, состоит из тех положительных
полиномов, которые равны нулю для некоторых ![]() .
Внутренняя часть Р, обозначаемая
.
Внутренняя часть Р, обозначаемая ![]() ,
состоит из тех полиномов, которые строго положительны на К.
,
состоит из тех полиномов, которые строго положительны на К.
Положительные полиномы могут быть
использованы для определения границы и внутренней части Е. Граница Е,
обозначаемая ![]() , состоит из тех продолжимых
корреляционных векторов, которые превращают в нуль внутреннее произведение с
некоторым ненулевым положительным полиномом. Внутренняя часть Е,
обозначаемая
, состоит из тех продолжимых
корреляционных векторов, которые превращают в нуль внутреннее произведение с
некоторым ненулевым положительным полиномом. Внутренняя часть Е,
обозначаемая ![]() , состоит из тех
корреляционных векторов, которые делают строго положительными внутренние
произведения с каждым ненулевым положительным полиномом.
, состоит из тех
корреляционных векторов, которые делают строго положительными внутренние
произведения с каждым ненулевым положительным полиномом.
1.3.1 Функции спектральной плотности мощности
Многие методы спектральной оценки
представляют спектр мощности не как меру, а в виде функции спектральной
плотности. Это ведет к модификации задачи продолжимости: если задана
фиксированная положительная конечная мера ![]() ,
которая определяет интеграл
,
которая определяет интеграл
![]() (3.9)
(3.9)
то какие корреляционные векторы ![]() могут быть произведены от
некоторой строго положительной функции
могут быть произведены от
некоторой строго положительной функции ![]() ?
При одном дополнительном ограничении на
?
При одном дополнительном ограничении на ![]() ,
которое легко удовлетворяется на практике, модно показать, что векторы, которые
могут быть представлены таким образом, являются векторами, находящимися во
внутренней части Е. Кроме того, можно показать, что любой век
,
которое легко удовлетворяется на практике, модно показать, что векторы, которые
могут быть представлены таким образом, являются векторами, находящимися во
внутренней части Е. Кроме того, можно показать, что любой век
тор во внутренней части Е может быть представлен в
форме /3.9/ для некоторой непрерывной, строго положительной ![]() .
.
Теорема продолжимости для функций спектральной плотности:
Если каждое соседство каждой точки в К имеет строго
положительную ![]() -меру, то
-меру, то
1/если ![]() равномерно
ограничена относительно нуля по К,
равномерно
ограничена относительно нуля по К,
то
![]() ;
;
2/если ![]() ,
то
,
то
![]()
для некоторой непрерывной, строго положительной функции ![]() .
.
Доказательство этой теоремы содержится в Приложении А.
1.3.2 Дискретизация спектральной основы
Многие представляющие интерес спектральные основы содержат бесконечное число точек. Эти спектральные основы следует часто аппроксимировать в вычислительных алгоритмах посредством конечного числа точек. Поэтому важно понимать эффекты такой аппроксимации.
Рассмотрим дискретную спектральную основу
![]() (3.10)
(3.10)
Мера ![]() на
дискретной основе полностью характеризуется ее значением
на
дискретной основе полностью характеризуется ее значением ![]() в каждой точке. Итак,
обратный интеграл -Фурье сводится к конечной сумме
в каждой точке. Итак,
обратный интеграл -Фурье сводится к конечной сумме
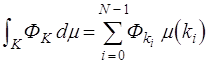 (3.11)
(3.11)
Аналогично, для санкций спектральной плотности
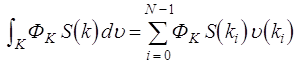 (3.12)
(3.12)
Мера ![]() может
считаться определяющей квадратурное правило для интегралов по спектральной
основе.
может
считаться определяющей квадратурное правило для интегралов по спектральной
основе.
Из определений продолжимых
векторов корреляции и положительных полиномов можно заметить, что, если
спектральная основа образуется посредством выбора конечного числа- точек из
некоторой исходной спектральной основы, то новое множество Е является
выпуклым многогранником, вписанным внутрь исходного множества Е, а новое
множество Р является выпуклым многогранником, описанный вокруг
первоначального множества Р. Следовательно, новое Е меньше исходного
Е, а новое Р больше исходного Р. Достаточно плотная
выборка исходной спектральной основы приведет к многогранникам, которые
аппроксимируют исходные множества с произвольной точностью. Например, на рис.5
показан эффект аппроксимации спектральной основы ![]() четырьмя
выборками
четырьмя
выборками ![]() для
для ![]() . Исходные конусы Е и
Р имеют круговое поперечное сечение при
. Исходные конусы Е и
Р имеют круговое поперечное сечение при ![]() ,
как показано на рис.3. Конусы, соответствующие выборочной основе имеют /оба/
квадратное поперечное сечение. Границы новых и старых конусов пересекаются у
векторов, соответствующих точкам выборки.
,
как показано на рис.3. Конусы, соответствующие выборочной основе имеют /оба/
квадратное поперечное сечение. Границы новых и старых конусов пересекаются у
векторов, соответствующих точкам выборки.
1.4 Метод Писаренко
Писаренко описал метод спектральной оценки временной последовательности, в котором спектр моделируется в виде суммы импульсов штос компонента белого шума [5]. Если компонента белого шума выбирается настолько большой, насколько это возможно, то, как он показал, положение и амплитуды импульсов, необходимые для согласования измеренных корреляций, определяются единственным образом. Метод Писаренко будет выведен для более обшей ориентации ИП и для более общей шумовой компоненты. Связь метода Писаренко с вопросом продолжимости будет продемонстрирована.
Продолженная оценка Писаренко будет получена как решение задачи оптимизации, включающей минимизацию линейного функционала над выпуклой областью, определенной линейными ограничениями.
Решение этой задачи оптимизации существует всегда, но оно может быть не единственным. Получается задача двойственной' оптимизации, которая для случая временных последовательностей приводит к знакомой интерпретации метода Писаренко в виде разработки сглаживающего фильтра с ограничениями по методу наименьших квадратов. И опять, решение этой двойственной задачи существует всегда, но может быть не единственным.
Рассматриваются алгоритмы для вычисления по методу Писаренко. Основная задача оптимизации записывается, для спектральной основы, состоящее из конечного числа точек, в воде линейной программы стандартного вида. Рассматривается применение симплекс-метода для решения этой основной линейной программы. Представлена двойственная линейная программа. Рассматриваются также возможность создания вычислительных алгоритмов, более быстрых, чем симплекс-метод.
1.4.1 Метод Писаренко для решеток датчиков
Основой метода Писаренко является
однозначное разложение /рис.6/ корреляционного вектора ![]() на сумму масштабированного
вектора корреляции шума
на сумму масштабированного
вектора корреляции шума ![]() , во
внутренней части Е, и остаток
, во
внутренней части Е, и остаток ![]() на
границе Е
на
границе Е
![]() (4.1)
(4.1)
Допущение о том, что ![]() находится в
находится в ![]() подразумевает, что такое
разложение произвольного вектора
подразумевает, что такое
разложение произвольного вектора ![]() существует
и единственно. Рассмотрим однопараметрическое семейство корреляционных векторов
существует
и единственно. Рассмотрим однопараметрическое семейство корреляционных векторов
![]() (4.2)
(4.2)
Для ![]() достаточно
положительного
достаточно
положительного ![]() не должен быть
продолжаемым, а для
не должен быть
продолжаемым, а для ![]() достаточно
отрицательного
достаточно
отрицательного ![]() должен быть
продолжимым, так как допущение, что
должен быть
продолжимым, так как допущение, что ![]() подразумевает,
что Е содержит окрестность
подразумевает,
что Е содержит окрестность ![]() .
Выпуклость Е означает, что имеется некоторое наибольшее число
.
Выпуклость Е означает, что имеется некоторое наибольшее число ![]() , такое, что
, такое, что ![]() является продолжимым.
Поскольку имеются произвольно близко к
является продолжимым.
Поскольку имеются произвольно близко к ![]() непродолжимые
векторы,
непродолжимые
векторы, ![]() должен быть на границе Е.
Кроме того, поскольку
должен быть на границе Е.
Кроме того, поскольку ![]() тогда и только
тогда, когда
тогда и только
тогда, когда ![]() продолжим, это разложение
продолжим, это разложение ![]() может 'быть использовало в
качестве теста продолжимости.
может 'быть использовало в
качестве теста продолжимости.
Это однозначное разложение ![]() может быть сформулировано в
виде основной задачи линейной оптимизации на всех положительных спектрах
мощности. Отметим, что
может быть сформулировано в
виде основной задачи линейной оптимизации на всех положительных спектрах
мощности. Отметим, что ![]() имеет по крайней
мере , одно положительное спектральное представление
имеет по крайней
мере , одно положительное спектральное представление ![]() и, что из /4.1/ для
и, что из /4.1/ для ![]() следует
следует
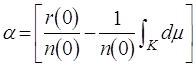 (4.3)
(4.3)
Утверждение того, что ![]() является
наибольшим числом, так что остаток
является
наибольшим числом, так что остаток ![]() продолжаем,
приводит к линейной задаче оптимизации
продолжаем,
приводит к линейной задаче оптимизации
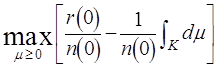 (4.4з)
(4.4з)
так что
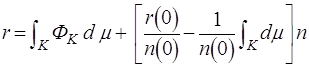 (4.45)
(4.45)
Максимум равен ![]() и он
достигается
и он
достигается ![]() .
.
Поскольку ![]() продолжаемо, оно
соответствует некоторой положительной мере
продолжаемо, оно
соответствует некоторой положительной мере ![]() .
Следовательно /4.1/ принимает вид
.
Следовательно /4.1/ принимает вид
![]() (4.5)
(4.5)
Если ![]() , то
, то ![]() является положительной
мерой, которая согласует корреляционные измерения и которая имеет наиболее
возможную шумовую компоненту.
является положительной
мерой, которая согласует корреляционные измерения и которая имеет наиболее
возможную шумовую компоненту.
Некоторая дополнительная
информация относительно остатка ![]() и его
спектрального представления может быть получена.
и его
спектрального представления может быть получена. ![]() находится
на границе Е; следовательно, он дает нулевое внутреннее произведение с
некоторым ненулевым положительным полиномом
находится
на границе Е; следовательно, он дает нулевое внутреннее произведение с
некоторым ненулевым положительным полиномом
![]() (4.6)
(4.6)
Из этого следует, что основа ![]() должна
быть на нулевом множестве
должна
быть на нулевом множестве ![]() . Или
более точно, основа любого спектрального представления
. Или
более точно, основа любого спектрального представления ![]() должна быть на пересечении
нулевых множеств всех положительных полиномов, которые образуют нулевое
внутреннее произведение с
должна быть на пересечении
нулевых множеств всех положительных полиномов, которые образуют нулевое
внутреннее произведение с ![]() . Это
предполагает окончательный шаг в выводе метода Писаренко; а именно, объединение
остатка
. Это
предполагает окончательный шаг в выводе метода Писаренко; а именно, объединение
остатка ![]() с импульсным
спектром. ^ .
с импульсным
спектром. ^ .
Тот факт, что целевой функционал
основной задачи оптимизации не является строго выпуклым, допускает, что
решение не может в общем случае быть единственным. Решение ![]() основной задачи оптимизации
всегда единственно тогда и только тогда, когда корреляционный вектор на границе
Е имеет единственное спектральное представление. В случае временной
последовательности каждый такой
основной задачи оптимизации
всегда единственно тогда и только тогда, когда корреляционный вектор на границе
Е имеет единственное спектральное представление. В случае временной
последовательности каждый такой ![]() имеет
единственное спектральное представление, как сумма М или меньшего числа
импульсов[5].
имеет
единственное спектральное представление, как сумма М или меньшего числа
импульсов[5].
Пример 4.1: Случай временной
последовательности, ![]() . Как и в примере
3.1, каждый положительный полином может быть факторизован в виде
. Как и в примере
3.1, каждый положительный полином может быть факторизован в виде ![]() для некоторого
тригонометрического полинома М-той, степени
для некоторого
тригонометрического полинома М-той, степени ![]() и
следовательно
и
следовательно ![]() могут быть
равными нуля не более, чем в М точках. Спектр
могут быть
равными нуля не более, чем в М точках. Спектр ![]() , следовательно, должен быть
суммой импульсов в этих точках. Кроме того, поскольку возможно построить
положительный полином, который равен нулю в
, следовательно, должен быть
суммой импульсов в этих точках. Кроме того, поскольку возможно построить
положительный полином, который равен нулю в ![]() произвольно
выбранных точках и нигде больше, то отсюда следует, что
произвольно
выбранных точках и нигде больше, то отсюда следует, что ![]() имеет единственное
спектральное представление в виде суммы импульсов в общих нулях всех
положительных полиномов
имеет единственное
спектральное представление в виде суммы импульсов в общих нулях всех
положительных полиномов ![]() так что
так что ![]() .
.
В более широком смысле, теорема
продолжимости совместно с теоремой Каратеодори [16] показывает,
что имеется по крайней мере одно спектральное представление ![]() в виде суммы не более чем 2М
импульсов.
в виде суммы не более чем 2М
импульсов.
Теорема представления: Если ![]() , то существует
, то существует ![]() и
и ![]() , так что
, так что
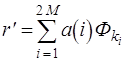 (4.7)
(4.7)
Доказательство теоремы представления можно найти в Приложении В. Это представление и, таким образом, решение основной задачи оптимизации могут быть не единственными. Дальнейшее обсуждение этой проблемы единственности можно найти в Приложений С.
Если ![]() и
местоположения импульсов в единственном решении
и
местоположения импульсов в единственном решении ![]() могут
быть определены для данного
могут
быть определены для данного ![]() , то
амплитуды импульсов могут быть вычислены просто путем решения набора линейных
уравнений. А сейчас мы получим двойственную задачу оптимизации, которая дает
, то
амплитуды импульсов могут быть вычислены просто путем решения набора линейных
уравнений. А сейчас мы получим двойственную задачу оптимизации, которая дает ![]() и
и ![]() , так что
, так что ![]() . Тогда, если
. Тогда, если ![]() имеет единственное
спектральное представление, местоположения импульсов могут быть определены по
нулям
имеет единственное
спектральное представление, местоположения импульсов могут быть определены по
нулям ![]() . Из теоремы продолжимости
следует
. Из теоремы продолжимости
следует
![]() (4.8)
(4.8)
Так как ![]() и
и ![]() , то отсюда следует, что
, то отсюда следует, что ![]() и
и ![]() для всех
для всех ![]() . Кроме того, так как
. Кроме того, так как ![]() для некоторого
для некоторого ![]() , то отсюда следует, что
, то отсюда следует, что
![]() (4.9а)
(4.9а)
на множестве
![]() (4.9b)
(4.9b)
и минимум достигается при ![]() .
Решение этой двойственной задачи может не быть единственным даже в случае
временной последовательности, когда она сводится к задаче собственного вектора,
полученной Писаренко, и приводит к интерпретации метода Писаренко в виде
определения сглаживающего фильтра с ограничениями по методу наименьших
квадратов.
.
Решение этой двойственной задачи может не быть единственным даже в случае
временной последовательности, когда она сводится к задаче собственного вектора,
полученной Писаренко, и приводит к интерпретации метода Писаренко в виде
определения сглаживающего фильтра с ограничениями по методу наименьших
квадратов.
Пример 4.2 : Случай временной последовательности, ![]() . Как в примере /3.1/
. Как в примере /3.1/
 .
.
Кроме того, если ![]() соответствует
белому шуму единичной мощности,
соответствует
белому шуму единичной мощности,
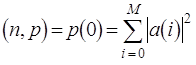 .
.
Таким образом, двойственная задача оптимизации сводится к
нахождению собственного вектора теплицевой матрицы, связанного с ![]() , соответствующего
наименьшему собственному значению. Если имеется несколько таких собственных
векторов, импульсы располагаются в общих нулях соответствующих полиномов. Любой
нормированный собственный вектор, соответствующий минимальному собственному
значению, дает коэффициенты сглаживающего фильтра, сумма квадратов величин
которых ограничена единицей, что дает наименьшую выходную мощность при наличии
входного процесса, корреляции которого описываются
, соответствующего
наименьшему собственному значению. Если имеется несколько таких собственных
векторов, импульсы располагаются в общих нулях соответствующих полиномов. Любой
нормированный собственный вектор, соответствующий минимальному собственному
значению, дает коэффициенты сглаживающего фильтра, сумма квадратов величин
которых ограничена единицей, что дает наименьшую выходную мощность при наличии
входного процесса, корреляции которого описываются ![]() [17].
[17].
1.4.2 Вычисление оценки Писаренко
При разработке алгоритмов вычисления оценки Писаренко можно столкнуться с дискретной спектральной основой
![]()
Для такой основы основная задача /4.4/ может быть переписана в виде линейное программы стандартного вида
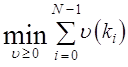 (4.11з)
(4.11з)
так что для ![]()
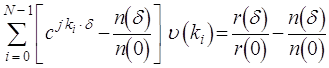 (4.11b)
(4.11b)
с N переменными и 2М ограничениями. Минимум равен ![]() и достигается для
и достигается для ![]() . Основная теорема линейного
программирования 18 эквивалентна теореме представления в этом случае. При
условии, что для этой линейной программы существует решение, как показано в
предыдущем разделе, основная теорема гарантирует решение, в котором не более,
чем 2М из
. Основная теорема линейного
программирования 18 эквивалентна теореме представления в этом случае. При
условии, что для этой линейной программы существует решение, как показано в
предыдущем разделе, основная теорема гарантирует решение, в котором не более,
чем 2М из ![]() не равны нулю,
так называемое, базовое решение.
не равны нулю,
так называемое, базовое решение.
Двойственная линейная программа [l5]
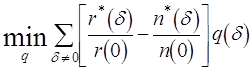 (4.12з)
(4.12з)
так что для ![]()
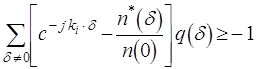 (4.12b)
(4.12b)
эквивалентная двойственной задаче /4.9/ для дискретной спектральной основы, где ограничение
![]() (4.13)
(4.13)
было использовано для исключения ![]() и где
и где ![]() . Её минимум равен
. Её минимум равен ![]() и достигается при
и достигается при ![]() .
.
Основная задача может быть решена при использовании симплекс-метода [18]. Применение симплекс-метода к основной задаче приводит в результате к существенно тому же результату /вычислительному алгоритму/, что и применение, /одинарного/ метода замены к двойственной задаче [19]. Применив соответствующий метод для избежания зацикливания [20], может быть получен алгоритм, который гарантирует сходимость к оптимальному решению за конечное число шагов, хотя его воплощения обычно были медленными .
Задача чебышевской аппроксимации связана с вычислением оценки Писаренко; она может быть сформулирована, как минимизация линейного функционала на выпуклом пространстве, определенном ограничениями типа линейных неравенств [l6]. Она также решалась с использованием симплекс-метода /одинарная замена/. Однако для частной задачи чебышевской аппроксимации непрерывных функций полиномами с одной переменной существует вычислительный метод, который значительно быстрее симплекс-метода, это метод многократной замены Ремеза. Хотя были сделаны попытки распространить этот метод на более общие задачи [21], появившиеся в результате алгоритмы не достаточно хорошо понятны; в частности, не доказана их сходимость.
И наконец, задачи недискретной оптимизации, включенные в вычисление оценки Писаренко, /4.4/ к /4.9/, являются видом, известным, как полубесконечные программы. Как теоретические, так и вычислительные аспекты таких программ рассматриваются в сборнике статей, изданных Геттичем [22].
Резюме
Эта статья связана с тем, что вероятно является наиболее простой и интересной задачей в обработке антенных решеток; оценкой спектра мощности с известной основой при условии, что даны некоторые выборки его корреляционной функции. Хотя и простая, эта задача сохраняет несколько черт, которые являются общими для многих задач обработки решеток: многомерные спектры, корреляционные выборки с неравномерными отчетами и произвольные спектральные основы.
Исследование спектральных оценок, согласованных с корреляцией привели к задаче продолжимости. Были даны две характеристики продолжаемости ста задача, для случая временных последовательностей, известна как задача тригонометрических моментов и ее решение включает рассмотрение положительной определенности корреляционных выборок. Положительная определенность может поэтому рассматриваться как специальный случай продолжимости.
Базируясь на теоретической основе, разработанной при решении задачи продолжаемости, метод Писаренко был распространен со случая временных последовательностей на задачу обработки решетки. Было показано, что метод Писаренко тесно .связан с задачек продолжимости. Было показано, что вычисление оценки Писаренко включает решение линейной задачи оптимизации. Было показало, что решение этой задачи не является единственным в общем случае, хотя оно единственно для случая временной последовательности, где задача линейном оптимизации сводится к задача собственных значений.
Хотя рассмотренная в этой статье задача спектральной оценки была разработала для обработки решетки, теоретическая структура и результирующие алгоритмы должна быть полезными в других многомерных задачах, например, обработке изображений.
2.1 ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ОТКРЫТОГО РЕЗОНАТОРА С ОСЕСИММЕТРИЧНЫМ ДИСКОМ
В § 9.3 было получено интегральное уравнение (9.39) для резонатора с диэлектрическим телом в виде шара. Такая форма диэлектрика хороша для анализа, но неудобна для практики.
Обычно приходится иметь дело с диэлектрическими образцами более сложной формы, в частности с диэлектрическим диском. В такой ситуации получить аналитическое выражение для ядра не удается, однако это не является препятствием для нахождения решения задачи.
Действительно, ядро уравнения для резонатора с шаром (9.39) — это сумма ядра для пустого резонатора и дополнительного члена, представляющего собой поле, рассеянное шаром.
Запишем уравнение для резонатора с диском в аналогичном виде, поскольку физическая картина явлении одна и та же:
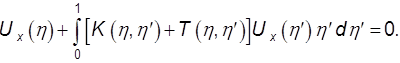 (9.45)
(9.45)
Здесь ![]() - ядро пустого резонатора; Т —
ядро, связанное с рассеянием на диэлектрическом образце. Обсудим, что в
сущности делается при решении уравнения (9.39) методом Галеркина. Для
определенности будем считать, что в качестве базисных и весовых (см.
приложение 2) взяты собственные функции резонатора без шара, которые обозначим
- ядро пустого резонатора; Т —
ядро, связанное с рассеянием на диэлектрическом образце. Обсудим, что в
сущности делается при решении уравнения (9.39) методом Галеркина. Для
определенности будем считать, что в качестве базисных и весовых (см.
приложение 2) взяты собственные функции резонатора без шара, которые обозначим ![]() и будем считать
ортонормированными.
и будем считать
ортонормированными.
С первым слагаемым ядра все ясно, базисные функции являются его собственными, и действие интегрального оператора с таким ядром эквивалентно умножению на постоянную, являющуюся собственным значением пустого резонатора:
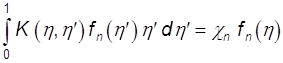 (9.46)
(9.46)
Интегральный оператор со вторым
слагаемым ядра представляет собой магнитное поле тока на зеркалах, рассеянное
шаром. Плотность тока задается в виде ![]() , а рассеянное поле рассчитывается на поверхности
зеркала. При решении (9.39) расчет рассеянного шаром поля проводится
аналитически. Однако ту же процедуру можно произвести численно, и тогда
ограничения на формулу диэлектрического образца в значительной степени снимаются.
, а рассеянное поле рассчитывается на поверхности
зеркала. При решении (9.39) расчет рассеянного шаром поля проводится
аналитически. Однако ту же процедуру можно произвести численно, и тогда
ограничения на формулу диэлектрического образца в значительной степени снимаются.
Для расчета рассеянного поля будем применять интегральное уравнение (3.85). Диэлектрический образец может быть произвольным телом вращения, в частности диском.
После этих общих соображений рассмотрим процедуру решения (9.45) последовательно. Функция U(x) ищется в виде
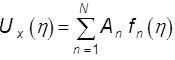 (9.47)
(9.47)
В соответствии с методом Галеркина
(см. приложение 2) подставляем (9.47) в (9.45), затем умножаем на ![]() и повторно интегрируем по
образующей зеркала. С учетом ортонормированности базисных функций имеет
однородную СЛАУ
и повторно интегрируем по
образующей зеркала. С учетом ортонормированности базисных функций имеет
однородную СЛАУ
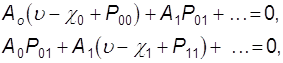 (9.48)
(9.48)
где ![]() -
собственные числа уравнения невозмущенного резонатора [см. (9.46)].
-
собственные числа уравнения невозмущенного резонатора [см. (9.46)].
Элементы матрицы СЛАУ выражаются интегралами
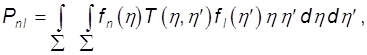 (9.49)
(9.49)
Последнюю формулу надо понимать как символическую. Она эквивалентна процедуре расчета рассеянного поля, описанной выше. Остановимся на ней подробнее.
Вначале необходимо найти поле на
поверхности диэлектрического тела, созданное током вида ![]() на зеркалах. Это можно было
бы сделать с помощью (3.8), (3.9), однако есть более простой путь, если
ограничиться рассмотрением тел небольших, на порядок меньших диаметра зеркал.
Тогда можно воспользоваться приближенным выражением для поля в резонаторе,
соответствующим приближенным функциям токов на зеркалах. На рис. 9.6
представлены графики распределения токов на зеркалах, соответствующие низшему
типу колебаний
на зеркалах. Это можно было
бы сделать с помощью (3.8), (3.9), однако есть более простой путь, если
ограничиться рассмотрением тел небольших, на порядок меньших диаметра зеркал.
Тогда можно воспользоваться приближенным выражением для поля в резонаторе,
соответствующим приближенным функциям токов на зеркалах. На рис. 9.6
представлены графики распределения токов на зеркалах, соответствующие низшему
типу колебаний ![]() и колебанию,
имеющему вариацию по радиусу
и колебанию,
имеющему вариацию по радиусу ![]() . Резонатор конфокальный с параметром
. Резонатор конфокальный с параметром
![]() . Вблизи оси плотность тока,
описываемая гиперсфероидальными функциями (кривые 1), практически не отличаются
от экспоненциальной функции, умноженной на полиномы Лагерра (кривые 2),
т. е. от гауссова пучка [68]. Радиальное распределение отличается только
масштабом по радиусу.
. Вблизи оси плотность тока,
описываемая гиперсфероидальными функциями (кривые 1), практически не отличаются
от экспоненциальной функции, умноженной на полиномы Лагерра (кривые 2),
т. е. от гауссова пучка [68]. Радиальное распределение отличается только
масштабом по радиусу.
Таким образом, будем описывать поле в резонаторе вблизи его центра приближенным .выражением в виде гауссова пучка
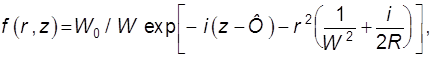 (9.50)
(9.50)
где
![]() ;
;
R - радиус кривизны волнового фронта; W — радиус «освещенного пятна» в пучке. Последняя величина определяется как радиус, на
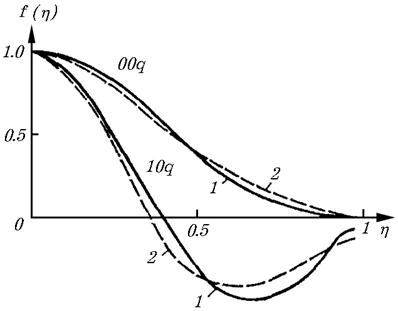
Рис. 9.6. Сравнение точных и приближенных кривых для гиперсфероидальных функций:
1 - точные, 2 - приближенные кривые
котором интенсивность пучка
спадает в е раз по отношению к центру пучка. Характерной величиной для
каждого пучка является наименьший радиус «пятна» ![]() .
Применительно к резонатору - это радиус «пятна» в центре, который связан с
длиной резонатора 1:
.
Применительно к резонатору - это радиус «пятна» в центре, который связан с
длиной резонатора 1:
![]() (9.51)
(9.51)
1 Как и ранее, все длины предполагаются умноженными на волновое число, которое здесь соответствует действительной части собственной частоты невозмущенного резонатора.
Величины W и R медленно меняются вдоль резонатора:
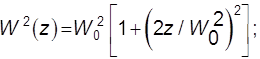 (9.52)
(9.52)
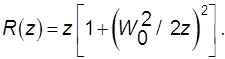 (9.53)
(9.53)
В центре резонатора ![]() Естественно в резонаторе
существуют не один, а два встречных гауссовых пучка, и вблизи центра поле
основной моды в приближении гауссова пучка имеет вид
Естественно в резонаторе
существуют не один, а два встречных гауссовых пучка, и вблизи центра поле
основной моды в приближении гауссова пучка имеет вид
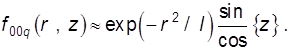 (9.54)
(9.54)
На зеркале ![]() для конфокальной геометрии
резонатора в соответствии с (9.51)—(9.53)
для конфокальной геометрии
резонатора в соответствии с (9.51)—(9.53) ![]() ,
и распределение тока имеет вид1
,
и распределение тока имеет вид1
![]() (9.55);
(9.55);
Для следующего колебания «1, 0, q» поле в центре резонатора представляется формулой
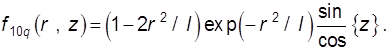 (9.56)
(9.56)
и на зеркалах
![]() (9.57)
(9.57)
Таким образом, поле в резонаторе без образца, соответствующее различным модам, в приближении гауссова пучка нетрудно записать. Оно играет роль первичного поля для задачи возбуждения диэлектрического образца.
Вычисляем эквивалентные токи на
поверхности диэлектрика в предположении, что основная поляризация поля ![]() . В обозначениях § 3.3
имеем:
. В обозначениях § 3.3
имеем:
1 Напомним, что в открытых резонаторах с круглыми зеркалами принята
следующая индексация мод : первый индекс - число вариаций по R, второй - число вариаций по ![]() , а третий - число вариаций
по
, а третий - число вариаций
по ![]()
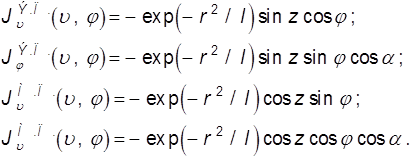 (9.58)
(9.58)
Теперь необходимо возвратиться к
азимутальным гармоникам вида ![]() , поскольку ЭВМ — программы для
диэлектрических тел вращения сделаны применительно к ним. Первичные токи
представляют собой сумму первой и минус первой гармоник. Каждую из них можно
выделить, используя формулу Эйлера. В результате решения задачи возбуждения
диэлектрического тела, а конкретно диска, получаем значения эквивалентных токов
в дискретных и достаточно часто расположенных точках образующей. Зависимость
от
, поскольку ЭВМ — программы для
диэлектрических тел вращения сделаны применительно к ним. Первичные токи
представляют собой сумму первой и минус первой гармоник. Каждую из них можно
выделить, используя формулу Эйлера. В результате решения задачи возбуждения
диэлектрического тела, а конкретно диска, получаем значения эквивалентных токов
в дискретных и достаточно часто расположенных точках образующей. Зависимость
от ![]() этих токов известная. Если
объединить токи первой и минус первой гармоник, она будет такой же, как и у
первичных токов (9.58).
этих токов известная. Если
объединить токи первой и минус первой гармоник, она будет такой же, как и у
первичных токов (9.58).
Следующий этап — вычисление
рассеянных диском полей на зеркалах. Для этого используются формулы (3.8),
(3.9). Выра жения для элементов тензорной функции Грина следует упрос тить, как
и при выводе уравнений (9.5)—(9.8), т. е. положить ![]() , а для функции
, а для функции ![]() использовать асимптотическую
формулу (9.22). Последняя содержит множитель, учитывающий набег фазы на
половине размера резонатора (расстояние от образца до одного из зеркал). Такой
же набег фаз имеется в первичном для диэлектрического образца поле. Этот сдвиг
присутствует также в (9.56) и (9.57). Все это позволяет вынести за знак
интеграла множитель
использовать асимптотическую
формулу (9.22). Последняя содержит множитель, учитывающий набег фазы на
половине размера резонатора (расстояние от образца до одного из зеркал). Такой
же набег фаз имеется в первичном для диэлектрического образца поле. Этот сдвиг
присутствует также в (9.56) и (9.57). Все это позволяет вынести за знак
интеграла множитель ![]() , такой же, как и
из основного ядра. Этот множитель, как и ранее, дает основную частотную
зависимость. Ядра без него от частоты зависят слабо, и в них частота полагается
равной действительной части собственной частоты пустого генератора.
, такой же, как и
из основного ядра. Этот множитель, как и ранее, дает основную частотную
зависимость. Ядра без него от частоты зависят слабо, и в них частота полагается
равной действительной части собственной частоты пустого генератора.
Теперь уже можно вычислить
элементы матрицы (9.48). Для определения элемента ![]() берется
рассеянное поле, возбужденное нулевой модой пустого резонатора, т. е.
берется
рассеянное поле, возбужденное нулевой модой пустого резонатора, т. е. ![]() , затем оно в соответствии
с (9.49) домножается на (9.55) и интегрируется. При этом необходимо помнить,
что базисные функции предполагались нормированными. Поэтому функцию (9.55)
необходимо предварительно пронормировать. В силу осевой симметрии системы поверхностный
интеграл (9.49) можно представить в координатах вращения. Интеграл по
, затем оно в соответствии
с (9.49) домножается на (9.55) и интегрируется. При этом необходимо помнить,
что базисные функции предполагались нормированными. Поэтому функцию (9.55)
необходимо предварительно пронормировать. В силу осевой симметрии системы поверхностный
интеграл (9.49) можно представить в координатах вращения. Интеграл по ![]() берется аналитическим, а по
радиальной координате
берется аналитическим, а по
радиальной координате ![]() - численно.
Остальные элементы
- численно.
Остальные элементы ![]() отыскиваются
точно так же.
отыскиваются
точно так же.
Далее решается задача на собственные значения, а затем с помощью формул (9.40) и (9.41) находятся изменения добротности и сдвиг частоты.
2.2 ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОТКРЫТОГО РЕЗОНАТОРА С ДИЭЛЕКТРИЧЕСКИМ ДИСКОМ, НЕСООСНЫМ С ЗЕРКАЛАМИ [72]
При проведении измерений параметров диэлектрика образец в виде диска часто удобнее расположить несоосно с зеркалами и, в частности, так, чтобы оси резонатора и диска были перпендикулярны (рис. 9.7). Такое расположение диска нарушает осевую симметрию задачи. В общем случае отход от осевой симметрии очень -сильно усложняет решение, поскольку теряется основное преимущество систем вращения — независимость отдельных азимутальных гармоник полей.
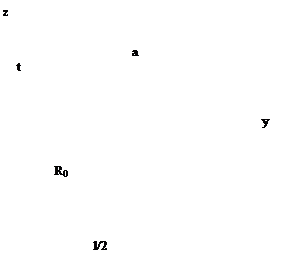
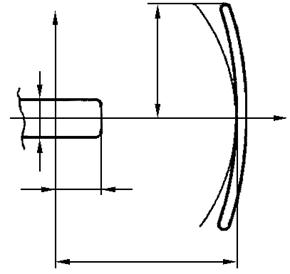
Рис. 9.7. Геометрия открытого резонатора с несоосными зеркалом и диском
Однако в рассматриваемой задаче анализа полей в высокодобротном открытом резонаторе несоосность вносит технические, но не принципиальные затруднения. Действительно, для измерений параметров диэлектрический образец берется небольшим по сравнению с размерами резонатора. Поэтому его внесение в резонатор не приводит к переходу к другой моде, а лишь несколько меняет добротность и резонансную частоту той моды, которая существовала без диэлектрика. Таким образом, за счет фильтрующих свойств резонатора новых азимутальных гармоник не появляется и основная трудность в несоосных системах вращения снимается. Надо лишь следить за тем, чтобы на других азимутальных гармониках у пустого резонатора не было поблизости от частоты рабочей моды других высокодобротных мод.
Метод решения задачи остается в общих чертах тем же, что и в предыдущем параграфе, но с некоторыми усложнениями. Главное из них — это необходимость введения двух систем координат вращения: одной, связанной с зеркалами резонатора (ось вращения у}, и второй, связанной с диэлектрическим телом (ось вращения z) (рис. 9.7). Поле, рассеянное диском, не обладает теперь осевой симметрией по отношению к зеркалам, что существенно затрудняет интегрирование по поверхности зеркал, необходимое при применении метода Галеркина.
Рассмотрим теперь этапы решения задачи. Как и ранее, в методе Галеркина в качестве базиса используются собственные функции пустого резонатора, а точнее, их приближенное представление в виде гауссова пучка.
Пусть центр диска по-прежнему совпадает с центром резонатора, а ось его симметрии повернута на 90° по отношению к оси резонатора (см. рис. 9.6). Решение начинается с нахождения азимутальных гармоник падающего по отношению к диску поля и соответствующих ему первичных токов.
Падающее поле вблизи диска выражается функциями (9.54) и (9.56), которые с учетом изменившейся системы координат запишем так:
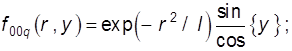 (9.59)
(9.59)
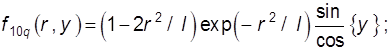 (9.60)
(9.60)
Положим, что основная поляризация поля в резонаторе ![]() . Эквивалентные токи в координатах вращения,
связанных с диском, тогда имеют вид:
. Эквивалентные токи в координатах вращения,
связанных с диском, тогда имеют вид:
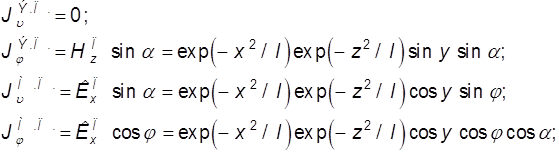 (9.61)
(9.61)
Здесь, как и в (9.58), использованы обозначения § 3.3. Переход от декартовых к координатам вращения дает
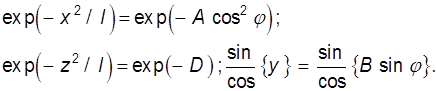 (9.62)
(9.62)
Коэффициенты А, В
и D зависят от формы поверхности, на которой находится точка наблюдения.
На плоском торце ![]() (
(![]() - радиус диска,
- радиус диска, ![]() - его толщина); на
цилиндрической поверхности
- его толщина); на
цилиндрической поверхности ![]() .
.
Воспользуемся малостью
диэлектрического тела по сравнению с размерами резонатора, т. е. учтем, что ![]() или
или ![]() и
и
![]() . Это позволяет представить
экспоненты двумя членами ряда Тейлора
. Это позволяет представить
экспоненты двумя членами ряда Тейлора
![]() . (9.63)
. (9.63)
После этого токи записываются в виде
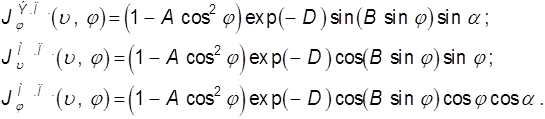 (9.64)
(9.64)
Для следующего типа колебаний «10 q» выражения для первичных токов имеют тот же вид, но A1=3A, D1=3D, B1=B. Далее поля разлагаются в ряд Фурье. Поскольку тело невелико, можно ограничиться небольшим числом гармоник. Используя формулы для коэффициентов ряда Фурье и интегральное представление функции Бесселя (9.21), получаем выражения для гармоник падающих токов. При этом в силу симметрии в случае синфазных токов на зеркалах присутствуют только нечетные гармоники, что соответствует максимуму поля резонатора в области диска:
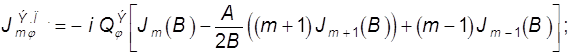
 (9.65)
(9.65)
Здесь
![]() .
.
Переход к отрицательным индексам происходит так же, как и ранее.
После вычисления первичных токов используется алгоритм решения задачи возбуждения тела вращения, основанный на уравнении (3.85). Результат получается в виде распределения азимутальных гармоник плотностей эквивалентных токов на поверхности диэлектрика.
Далее по этому распределению
нетрудно рассчитать рассеянное поле всюду и в том числе на поверхности
зеркала. Как и в § 9.4, это поле и определяет элементы матрицы однородной СЛАУ
(9.48). Расчет ведется в тех же приближениях с учетом изменившейся системы
координат. В частности, асимптотическая формула для функции ![]() в этих координатах имеет
вид
в этих координатах имеет
вид
![]() . (9.66)
. (9.66)
Существенные затруднения вызывает вычисление интегралов (9.49), определяющих элементы матрицы СЛАУ (9.48).
Интеграл здесь поверхностный, т.
е. двойной, и численное интегрирование требует больших затрат времени ЭВМ.
Выходом из положения является аналитическое вычисление одного из интегралов.
Для этого можно воспользоваться тем, что в направлении, перпендикулярном оси ![]() (см. рис. 9.7), каждая из
азимутальных гармоник рассеянного поля имеет синусоидальную зависимость.
Формально удобно вести это интегрирование по декартовой координате
(см. рис. 9.7), каждая из
азимутальных гармоник рассеянного поля имеет синусоидальную зависимость.
Формально удобно вести это интегрирование по декартовой координате ![]() в пределах от
в пределах от ![]() до
до ![]() . Зависимость поля будет
синусоидальной только на окружности с центром, совпадающим с диском1.
Отличие этой окружности от меридиональной линии зеркала учтем только в фазе.
Поправочный множитель, как показывает геометрический расчет, имеет вид
. Зависимость поля будет
синусоидальной только на окружности с центром, совпадающим с диском1.
Отличие этой окружности от меридиональной линии зеркала учтем только в фазе.
Поправочный множитель, как показывает геометрический расчет, имеет вид ![]() .
.
Зависимость поля каждой гармоники
от ![]() на зеркале может быть
представлена только в числах, поэтому интеграл по
на зеркале может быть
представлена только в числах, поэтому интеграл по ![]() в
пределах -
в
пределах - ![]() берется численно. Таким путем
приходим к интегралу
берется численно. Таким путем
приходим к интегралу
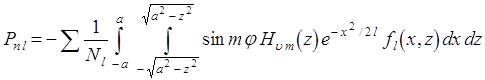 (9.67)
(9.67)
где ![]() —
гиперсфероидальные функции, которые берутся в приближении гауссова пучка, т. е.
в виде (9.55) и (9.57).
—
гиперсфероидальные функции, которые берутся в приближении гауссова пучка, т. е.
в виде (9.55) и (9.57).
Формула (9.67) учитывает векторный
характер поля. Все расчеты ведутся в предположении, что основная поляризация в
резонаторе ![]() и, следовательно,
и, следовательно, ![]() . В рассеянном поле при
использовании метода Галеркина надо брать ту же поляризацию. Она в координатах
вращения, связанных с диском, представляет собой
. В рассеянном поле при
использовании метода Галеркина надо брать ту же поляризацию. Она в координатах
вращения, связанных с диском, представляет собой ![]() .
Интеграл по
.
Интеграл по ![]() , как уже говорилось,
можно взять аналитически. Не останавливаясь на подробностях, их можно найти в
[72], заметим, что этот интеграл можно свести к неполной гамма-функции. Для
вычисления последней имеются быстро сходящиеся ряды. Нахождение одномерного
интеграла по
, как уже говорилось,
можно взять аналитически. Не останавливаясь на подробностях, их можно найти в
[72], заметим, что этот интеграл можно свести к неполной гамма-функции. Для
вычисления последней имеются быстро сходящиеся ряды. Нахождение одномерного
интеграла по ![]() численным методом труда не
представляет.
численным методом труда не
представляет.
Рассмотрим
некоторые результаты расчетов. Качественно они такие же, как и в случае шара (§
9.3). С ростом действительной части диэлектрической проницаемости ![]() диска растет смещение
частоты (рис. 9.8,а). Мнимая часть
диска растет смещение
частоты (рис. 9.8,а). Мнимая часть ![]() , т. е.
, т. е. ![]() , на эту величину влияет
слабо. Изменение обратной величины к добротности
, на эту величину влияет
слабо. Изменение обратной величины к добротности ![]() также увеличивается с ростом
также увеличивается с ростом ![]() за счет рассеяния на диске.
Мнимая часть проницаемости заметно влияет 'на изменение добротности только при
за счет рассеяния на диске.
Мнимая часть проницаемости заметно влияет 'на изменение добротности только при
![]() , когда омические потери в
образце соизмеримы с потерями резонатора за счет рассеяния на диске (рис.
9.8,6).
, когда омические потери в
образце соизмеримы с потерями резонатора за счет рассеяния на диске (рис.
9.8,6).
1 Окружность показана на рис. 9.7 тонкой линией
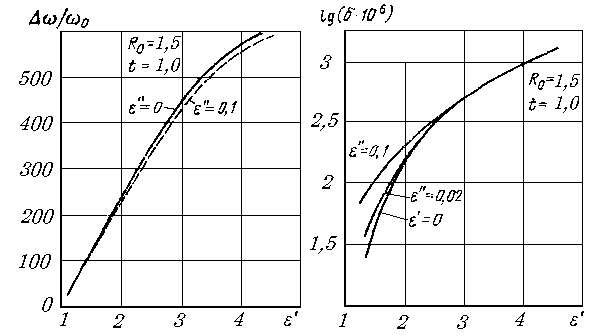
| a) | б) |
Рис. 9.8. Сдвиг резонансной частоты и изменение
добротности открытого резонатора с диском как функция ![]() диска
диска
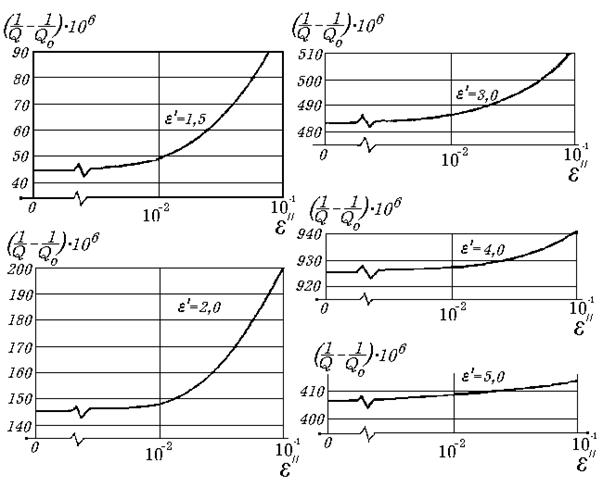
Рис. 9.9 Изменение добротности
открытого резонатора с диском как функция ![]() диска
диска
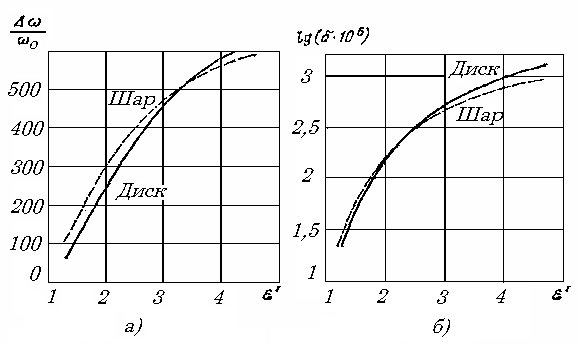
Рис. 9.10. Сравнение параметров резонатора с диэлектрическим шаром и диском
К тому же выводу приходим,
рассматривая параметр ![]() как функцию
как функцию ![]() для различных значений
для различных значений ![]() . Видно, что с увеличением
. Видно, что с увеличением ![]() кривая становится все более
пологой и извлечение информация об
кривая становится все более
пологой и извлечение информация об ![]() диэлектрического
образца становится все более проблематичным (рис. 9.9).
диэлектрического
образца становится все более проблематичным (рис. 9.9).
Если считать, что 10%-ная доля
омических потерь еще различима на фоне потерь на рассеяние, то в области ![]() можно измерить
можно измерить ![]() порядка
порядка ![]() , а при
, а при ![]() только величины
только величины ![]() .
.
Таким образом, методом открытого резонатора можно измерять потери только очень плохих диэлектриков. Расчет связи параметров диэлектрика и характеристик резонатора для шара все же проще, чем для диска. Поэтому встает вопрос, нельзя ли установить соответствие между образцами в форме шара и диска. В качестве параметра соответствия естественно взять объем диэлектрического образца. С этой целью были рассчитаны смещения собственной частоты и изменение обратной величины добротности для шара и диска с одинаковым объемом. Оказалось (рис. 9.10), что эти зависимости, качественно одинаковые, количественно различаются заметно. Поэтому для получения приемлемой точности измерений необходимо тарировочные кривые строить на основе адекватной математической модели.
ЗАКЛЮЧЕНИЕ, ПЕРСПЕКТИВЫ
Метод интегральных уравнений в электродинамике появился сравнительно недавно и быстро завоевал популярность. Этому способствовал целый ряд его преимуществ: простота метода и, следовательно, его доступность; единство подходов к решению весьма широкого круга задач; удобство реализации в виде вычислительных программ алгоритмов, на нем основанных, и, наконец, высокая степень универсальности.
Остановимся на указанных чертах метода несколько подробнее. Единство подходов к большому кругу задач означает, как видно из гл. 2 и 3, что интегральные уравнения, эквивалентные различным граничным задачам электродинамики, составляются по одному и тому же стереотипу. При этом для задач на телах вращения нет необходимости проходить стадию уравнений для произвольных тел. Истокообразные представления (3.8) и (3.9) вместе с формулами для элементов тензорной функции Грина позволяют" легко и быстро, примерно так же как из крупных блоков строят дома, составлять необходимые уравнения.
Те же «крупные блоки» в виде
подпрограмм для ![]() -функции для
элементов тензора Грина и решения систем линейных алгебраических уравнений
позволяют достаточно быстро и просто компоновать программы для всех
сформулированных в книге задач и для многих других. Те же подпрограммы дают
возможность после численного решения уравнений найти поле в любой точке
пространства.
-функции для
элементов тензора Грина и решения систем линейных алгебраических уравнений
позволяют достаточно быстро и просто компоновать программы для всех
сформулированных в книге задач и для многих других. Те же подпрограммы дают
возможность после численного решения уравнений найти поле в любой точке
пространства.
3 МЕТОД СВЧ КОНТРОЛЯ ПАРАМЕТРОВ ПОЛИМЕРОВ
Для контроля технологических параметров полимеров (качества смещения, определение включений, вязкости) находят применение радиоволновые метода СВЧ. Рассмотрим метод, который характеризуется определением объёмной эффективной площади рассеяния ( ЭПР ).
ЭПР это площадь поперечного
сечения некоторого фиктивного тела, которое рассеивает электромагнитную в одну,
ЭПР существенно зависит от формы м ориентации тела, от его материала ЭПР,
разрешаемого объема ![]() заполненного
частицами ( элементарными отражателями), выражается произведением
заполненного
частицами ( элементарными отражателями), выражается произведением ![]() . Так для реальных
полимерных материалов требуется знать распределение частиц во размерам
. Так для реальных
полимерных материалов требуется знать распределение частиц во размерам ![]() размеры частиц в единице
объёма распределены по
размеры частиц в единице
объёма распределены по ![]() групп и в 1-й
группе содержится частиц с аффективной площадью рассеяния
групп и в 1-й
группе содержится частиц с аффективной площадью рассеяния ![]() , то удельная объёмная ЭПР
, то удельная объёмная ЭПР
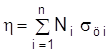 (1)
(1)
ЭПР одной сферической частицы, диаметр ![]() которой много меньше длины
волны, определяется формулой
которой много меньше длины
волны, определяется формулой ![]()
![]() (2)
(2)
Коэффициент 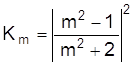 ,
выраженный через комплексный показатель преломления
,
выраженный через комплексный показатель преломления ![]() изменяется
от
изменяется
от ![]() для частиц наполнителя.
для частиц наполнителя.
Практически для большинства объектов полимерных структур
с наполнителем удельную ЭПР можно выразить формулой
 (3)
(3)
Множитель
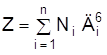 (4)
(4)
можно назвать отражаемостью, которая зависит от концентрации и размера частиц в разрезаемом элементе.
Изменение базы волны ври отражении
можно определить из отпадения напряженностей поля падающей (![]() ) и отраженной (
) и отраженной (![]() ) волн:
) волн:
![]() , (5)
, (5)
Модель этой комплексной величины ![]() , имеющей размерность длины,
определяет интенсивность отражения. Аргумент указывает на изменение фазы волны
при отражении.
, имеющей размерность длины,
определяет интенсивность отражения. Аргумент указывает на изменение фазы волны
при отражении.
Если рассматривать прием и передачу на одну и туже антенну, т.е. одинаковой ( согласованной) поляризацией, умножим выражение на комплексно сопряженную величину
![]() ,
,
В результате получаем
![]()
Это означает, что если эффективная
площадь ![]() - площадь квадрата, то
модель эффективной длины
- площадь квадрата, то
модель эффективной длины ![]() - это
сторона того квадрата;
- это
сторона того квадрата; ![]() - - точное
расстояние до источника, определяющего фазу колебаний
- - точное
расстояние до источника, определяющего фазу колебаний ![]() .
.
Для поляризованного колебания
напряженность регулярного электромагнитного поля выражается вектором ![]() , который вращается с
угловой скоростью
, который вращается с
угловой скоростью ![]() и конец которого
описывает эллипс в плоскости перпендикулярной направлению распространения. Если
распространение происходит в направлении оси
и конец которого
описывает эллипс в плоскости перпендикулярной направлению распространения. Если
распространение происходит в направлении оси ![]() прямоугольной
системы координат
прямоугольной
системы координат ![]() , определяемой
ортами
, определяемой
ортами ![]() ,то эллиптически
поляризованная волна выражается составляющими к полностью описывается четырьмя
параметрами: амплитуда
,то эллиптически
поляризованная волна выражается составляющими к полностью описывается четырьмя
параметрами: амплитуда ![]() , и фазами
, и фазами ![]() y. Однако не все эти параметры характеризуют
поляризацию. Одинаково поляризованными называются волны, у которых эллипсы
поляризации подобны и одинаково ориентированы. Абсолютное значение амплитуд,
влияющие лишь на размеры эллипсов поляризации, начальная фаза
y. Однако не все эти параметры характеризуют
поляризацию. Одинаково поляризованными называются волны, у которых эллипсы
поляризации подобны и одинаково ориентированы. Абсолютное значение амплитуд,
влияющие лишь на размеры эллипсов поляризации, начальная фаза ![]() , одинаковая для обеих
составляющих, ив является поляризационными характеристиками.
, одинаковая для обеих
составляющих, ив является поляризационными характеристиками.
Следовательно состояние поляризации плоской волны можно полностью определить двумя параметрами (рис.1 ).
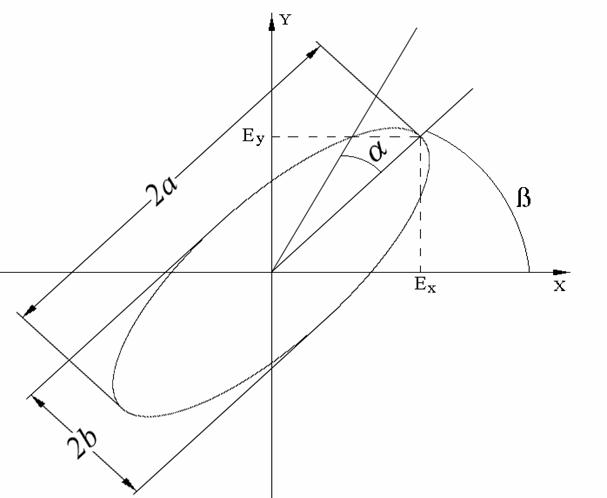
Рис.1 Эллиптически поляризованная плоская волна
В качестве таких параметров могут
служить отношение амплитуд ![]() и сдвиг
фаз y ортогональных составляющих;
отношение амплитуд часто заменяют углом
и сдвиг
фаз y ортогональных составляющих;
отношение амплитуд часто заменяют углом ![]() .
Поляризацию можно также задать величинами, непосредственно характеризующими
форму и ориентацию эллипса: отношение главных осей эллипса
.
Поляризацию можно также задать величинами, непосредственно характеризующими
форму и ориентацию эллипса: отношение главных осей эллипса ![]() углом
углом ![]() и углом наклона главной
оси
и углом наклона главной
оси ![]() (рис.1).
(рис.1).
Система координат ![]() , в которой представлено
поляризованное колебание, может быть задана парой единичных взаимно
перпендикулярных векторов
, в которой представлено
поляризованное колебание, может быть задана парой единичных взаимно
перпендикулярных векторов ![]() ,
, ![]() . Такие ортогональные
векторы - орты - называются поляризованным базисом.
. Такие ортогональные
векторы - орты - называются поляризованным базисом.
В поляризованном базисе ( ![]() ,
, ![]() ) вектор можно представить
выражением
) вектор можно представить
выражением
![]()
где ![]() ,
, ![]() и
и ![]() ,
, ![]() - модули и фазы комплексных
амплитуд, составляющих напряженности электрического поля
- модули и фазы комплексных
амплитуд, составляющих напряженности электрического поля ![]() соответственно. Если
соответственно. Если ![]() , то поляризация линейна,
при
, то поляризация линейна,
при ![]() она эллиптическая. При
круговой поляризации амплитуды составляющих одинаковы, а фазы сдвинуты на 90°.
она эллиптическая. При
круговой поляризации амплитуды составляющих одинаковы, а фазы сдвинуты на 90°.
Поляризационные преобразования при отражении можно представить уравнениями
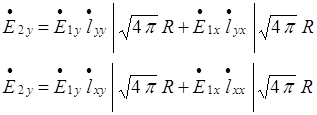
связывающими ортогональные составляющие напряженности ноля
падающей (![]() ) и отраженной (
) и отраженной (![]() ) волн, взятых в одном и том
же поляризационном базисе (
) волн, взятых в одном и том
же поляризационном базисе (![]() ). Пару
этих выражений можно записать в матричной форме.
). Пару
этих выражений можно записать в матричной форме.
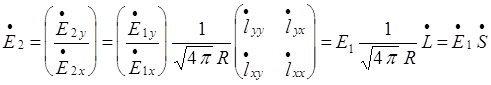
Таблицу комплексных величин
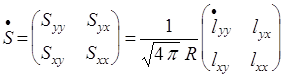
называют матрицей рассеяния. В данной записи матрица рассеяния образована поляризационными составляющими эффективной длины цели.
В дальнейшем будем рассматривать в качестве основной характеристики цели матрицу эффективной длины
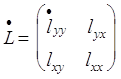
Матрицу эффективной длины целесообразно представить в виде
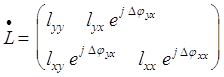
где ![]()
Таким образом, чтобы получить
матрицу эффективной длины цели для однокомпозиционной схемы измерения ( т.е.
антенна является приемной к передающей достаточно найти значения модулей
матрицы ![]() и размерностей их
аргументов
и размерностей их
аргументов ![]() .Для этог0 осуществляют
излечение и прием сигналов для двух составляющих выбранного поляризационного
базиса раздельно.
.Для этог0 осуществляют
излечение и прием сигналов для двух составляющих выбранного поляризационного
базиса раздельно.
При излучении электромагнитных
воли вертикальной поляризации и при приеме вертикально и горизонтально
поляризованных составляющих отраженного сигнала, можно измерить модули ![]() и разность фаз
и разность фаз ![]() . При излучении величин с
горизонтальной линейной поляризацией находят соответственно
. При излучении величин с
горизонтальной линейной поляризацией находят соответственно ![]() и
и ![]() . Основная трудность
появляется при прямом измерении разности фаз
. Основная трудность
появляется при прямом измерении разности фаз ![]() .
Для этого требуется излучать раздельно по времени либо по частоте два
зондирующих колебания: с горизонтальной и вертикальной поляризацией.
.
Для этого требуется излучать раздельно по времени либо по частоте два
зондирующих колебания: с горизонтальной и вертикальной поляризацией.
ЛИТЕРАТУРА
1. Фок В. А. Дифракция на выпуклом теле. - ЖЭТФ, 1945, т. 15, № 12, с. 693 - 698
2. Васильев Е. Н. Возбуждение гладкого идеально проводящего тела вращения. - Изв. Вузов СССР. Сер. Радиофизика, 1959, т. 2, № 4, с. 588 - 601.
3. Андерсеан А. Д. Рассеяние на цилиндрах с произвольным поверхностным импедансом. - ТИИЭР, 1965, т. 53, № 8, с. 1007-1013.
4. Хенл Х., Мауэ А., Вестпфаль К. Теория дифракции. - М.: Мир, 1964. - 428 с.
5. Марков Г. Т., Чаплин А. Ф. Возбуждение электромагнитных волн. - М.: Радио и связь, 1983 - 296 с.
6. Арнольд В. И. Обыкновенные дифференциальные уравнения. - М.: Наука, 1984. - 271 с.
7. Тихонов А. Н., Самарский А. А. Уравнения математической физики. - М.: Наука, 1972. - 735 с.
8. Вычислительные методы в электродинамике / Под ред. Р. Миттры. - М.: Мир, 1977. - 485 с.
9. Панасюк В. В., Саврук М. П., Назарчук З. Т. Метод сингулярных интегральных уравнений в двухмерных задачах дифракции. - Киев: Наукова думка, 1984. - 343 с.
10. Михлин С. Г. Вариационные методы в математической физике. - М.: Наука, 1970, - 420 с.
11. Хижняк Н. А. Функция Грина уравнений Максвелла для неоднородных сред. - ЖТФ, 1958, т. 28,№ 7, с. 1592 - 1604.
12. Кравцов В. В. Интегральные уравнения в задачах дифракции. - В кн.: Вычислительные методы и программирование. - М.: Изд-во МГУ, 1966, вып. У, с. 260 - 293.
13. Васильев Е. Н., Гореликов А. И., Фалунин А. А. Тензорная функция Грина координатах вращения. - В кн.: Сб. научно-методических статей по прикладной электродинамике. - М.: Высшая школа, 1980, вып. 3, с. 3 - 24.
14. Белостоцкий В. В., Васильев Е. Н. Интегральное уравнение сферического открытого резонатора с диэлектрическим шаром. - В кн.: Вычислительные методы и программирование. - М.: Высшая школа, 1978, вып. 2, с. 101 - 111
15. Васильев Е. Н., Серегина А. Р., Седельникова З. В. Дифракция плоской волны на теле вращения, частично покрытом слоем диэлектрика. - Изв. Вузов СССР. Сер. Радиофизика, 1981, т. 24, № 6, с. 753 - 758
16. Хемминг Р. В. Численные методы. - М.: Наука, 1972. - 400 с.
17. Васильев Е. Н., Малов В. В., Солохудов В. В. Дифракция поверхностной волны на открытом конце круглого полубесконечного диэлектрического волновода. - Радиотехника и электроника, 1985, т. 30, № 5, с. 925 - 933.
18. Фокс А., Ли Т. Резонансные типы колебаний в интерферометре квантового генератора. - В кн.: Лазеры. - М.: ИЛ, 1963. - 155 с.
19. Каценеленбаум Б. 3., Сивов А. Н. Строгая постановка задачи о свободных и вынужденных колебаниях открытого резонатора. - Радиотехника и электроника, 1967, т. 12, 11, с. 1184- 1193.
20. Вайнштейн Л. А. Открытые резонаторы и открытые волноводы. - М.: Сов. радио, 1966. - 475 с.
21. Slерiаn В. Ргоbаtе spheroidal wave function, fourier analisis and uncertainly - 1У. Extension to many dimension, generalised prolate spheroidal functions. - Bell System Techn. J., 1964, v. 143, . 11, р. 1042- 1055.
ПРИЛОЖЕНИЯ
Приложение А
Теорема продолжимости для функций спектральной плотности
Это приложение относится к теореме
продолжимости для функций спектральной плотности, обсуждавшихся в разделе Ш-Е.
Подразумевается, что каждая окрестность каждой точки в К имеет строго
положительную ![]() -меру. Это условие
гарантирует, что корреляционные векторы, соответствующие импульсам в К,
могут быть аппроксимированы посредством корреляционных векторов,
соответствующим непрерывным, строго положительным функциям спектральной
плотности.
-меру. Это условие
гарантирует, что корреляционные векторы, соответствующие импульсам в К,
могут быть аппроксимированы посредством корреляционных векторов,
соответствующим непрерывным, строго положительным функциям спектральной
плотности.
Теорема продолжимости для
спектральных функций плотности : Если каждая окрестность каждой точки в К
имеет строго положительную меру ![]() , то
, то
1/если ![]() равномерно
ограничено от нуля по К, то
равномерно
ограничено от нуля по К, то
![]() ,
,
2/если ![]() ,
то
,
то
![]()
для некоторых непрерывных, строго положительных функций ![]() .
.
Доказательство : Первое
утверждение может быть доказано посредством рассмотрения отображения
ограниченной функции ![]() на вектор
на вектор ![]() , определяемый путем
, определяемый путем
![]() (А1)
(А1)
То, что ![]() имеет равномерное
ограничение от ноля означает, что для некоторого
имеет равномерное
ограничение от ноля означает, что для некоторого ![]() для
всех
для
всех ![]() . Поскольку Функции
. Поскольку Функции ![]() являются
линейно-незазисимыми функциями на К и, так как каждая окрестность каждой
точки в К содержит множество со строго положительной мерой, то отсюда
следует, что отражением множества ограниченных
являются
линейно-незазисимыми функциями на К и, так как каждая окрестность каждой
точки в К содержит множество со строго положительной мерой, то отсюда
следует, что отражением множества ограниченных ![]() -полиномов
-полиномов
![]() (А2)
(А2)
при /A1/, является окрестность О. Поэтому отражением
![]() (А3)
(А3)
является подмножество Е, которое находится в
окрестности ![]() .
.
Следовательно, ![]() .
.
Второе утверждение может быть
доказано посредством рассмотрения множества ![]() корреляционных
векторов, соответствующих функциям спектральной плотности, которые являются
интегрируемыми, непрерывными и строго положительными /следовательно, с
ограничением от нуля/,
корреляционных
векторов, соответствующих функциям спектральной плотности, которые являются
интегрируемыми, непрерывными и строго положительными /следовательно, с
ограничением от нуля/,
![]()
![]() является выпуклым и, из доводов,
приведенных выше, следует, что
является выпуклым и, из доводов,
приведенных выше, следует, что ![]() -
открыто. Легко показать., что векторы
-
открыто. Легко показать., что векторы ![]() для
для
![]() находятся в замыкании
находятся в замыкании ![]() . Из теоремы Каратеодори [16] следует, что каждый
. Из теоремы Каратеодори [16] следует, что каждый ![]() может быть записан в виде
положительной суммы 2М + I таких
может быть записан в виде
положительной суммы 2М + I таких ![]() .
Поскольку каждый
.
Поскольку каждый ![]() находится в
замыкании
находится в
замыкании ![]() , то отсюда следует, что
каждый
, то отсюда следует, что
каждый ![]() находится там же. Поэтому
замыканием
находится там же. Поэтому
замыканием ![]() является Е. Два
открытых выпуклых множества с одинаковым замыканием должны быть идентичными.
Поскольку Е находится в замыкании как
является Е. Два
открытых выпуклых множества с одинаковым замыканием должны быть идентичными.
Поскольку Е находится в замыкании как ![]() ,
так и
,
так и ![]() , то отсюда следует, что
, то отсюда следует, что ![]()
Приложение В
Теорема представления
Теорема представления раздела IУ-А является простым распространением теоремы Каратеодори [16] для корреляционных векторов на границе Е с использованием теоремы о продолжимости. Это обобщение "теоремы С" Каратеодори [9, гл. 4] для многократных измерений. Ввиду вывода метода Писаренко в разделе 1У, как линейной программы, теорема представления может также рассматриваться, как вид фундаментальной теоремы линейного программирования. [l8].
Теорема представления: Если ![]() находится на границе Е,
то для некоторых 2М неотрицательных
находится на границе Е,
то для некоторых 2М неотрицательных ![]() и
некоторых
и
некоторых ![]() :
:
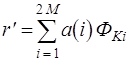 (В1)
(В1)
Доказательство: Рассмотрим
компактное выпуклое множество ![]() ,
которое является выпуклой оболочкой
,
которое является выпуклой оболочкой ![]() . По
теореме Каратеодори,. любой элемент в Е может быть выражен в виде
выпуклой комбинации 2М+1 элементов А
. По
теореме Каратеодори,. любой элемент в Е может быть выражен в виде
выпуклой комбинации 2М+1 элементов А
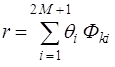 (B2)
(B2)
при ![]() и
и
![]() . Если одно из
. Если одно из ![]() равно нулю, доказательство
завершено. Иначе, поскольку
равно нулю, доказательство
завершено. Иначе, поскольку ![]() находится
на границе
находится
на границе ![]() , имеется некоторый
ненулевой
, имеется некоторый
ненулевой ![]() , такой что
, такой что
 (В3)
(В3)
Итак, для каждого ![]() ,
, ![]() должны быть линейно
зависимыми, следовательно имеются некоторые
должны быть линейно
зависимыми, следовательно имеются некоторые ![]() ,
не все нули, так что
,
не все нули, так что ![]() . Пусть
. Пусть ![]() является числом с
наименьшим значением, так что
является числом с
наименьшим значением, так что ![]() для
некоторого
для
некоторого ![]() .
.
Тогда
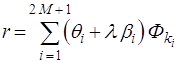 (B4)
(B4)
Один из этих коэффициентов равен
нулю, что делает равным это выражение сумме только 2М членов. Признание
того, что любой элемент Е является масштабированной версией элемента ![]() , завершает доказательство.
, завершает доказательство.
Отметим, что для случая временной
последовательности, ![]() может быть
выражен в виде суммы не более, чем М комплексных экспоненциалов, в то
время, как вышеприведенная теорема гарантирует только представление в терминах 2М
экспоненциалов, Это не недостаток доказательства, а подлинная особенность
проблемы, как показывает следующий одномерный пример.
может быть
выражен в виде суммы не более, чем М комплексных экспоненциалов, в то
время, как вышеприведенная теорема гарантирует только представление в терминах 2М
экспоненциалов, Это не недостаток доказательства, а подлинная особенность
проблемы, как показывает следующий одномерный пример.
Пример BI : ![]() . Предположим, что
. Предположим, что ![]() находится на прямой части
границы и, как показа-
находится на прямой части
границы и, как показа-
но на рис.7. Ясно, что ![]() имеет единственное
представление в виде выпуклой суммы членов А в терминах двух
корреляционных векторов, соответствующих
имеет единственное
представление в виде выпуклой суммы членов А в терминах двух
корреляционных векторов, соответствующих ![]() и
и
![]() ,
,
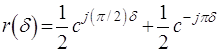
Приложение С
Единственность оценки Писаренко
Как обсуждалось в разделе IУ-А, опенка Писаренко является
единственной, если один и только один спектр может быть связан с каждым
корреляционным вектором на границе Е. Тривиальные проблемы
единственности появляются в результате, если два отдельных ![]() в
в ![]() приводят к одному и тому же
приводят к одному и тому же
![]() . В -более общем смысле
рассмотрим множество корреляционных векторов, соответствующих нулевому
множеству некоторого ненулевого положительного полинома
. В -более общем смысле
рассмотрим множество корреляционных векторов, соответствующих нулевому
множеству некоторого ненулевого положительного полинома ![]()
![]() (С1)
(С1)
Любой вектор ![]() , который превращает в ноль
внутреннее произведение с р ,может быть выражен в виде суммы положительных
составляющих векторов из множества
, который превращает в ноль
внутреннее произведение с р ,может быть выражен в виде суммы положительных
составляющих векторов из множества ![]() . Отсюда
следует, что если это множество является линейно независимыми, то представление
единственно. И наоборот, если это множество линейно зависимо, то можно
построить
. Отсюда
следует, что если это множество является линейно независимыми, то представление
единственно. И наоборот, если это множество линейно зависимо, то можно
построить ![]() на границе Е,
который имеет более одного спектрального представления. Если множество линейно
зависимо, то имеется конечная совокупность ненулевых вещественных чисел
на границе Е,
который имеет более одного спектрального представления. Если множество линейно
зависимо, то имеется конечная совокупность ненулевых вещественных чисел ![]() и
и ![]() , таких что
, таких что
![]() (С2)
(С2)
Поскольку ![]() для всех
для всех ![]() , то должно быть, по крайней
мере, одно
, то должно быть, по крайней
мере, одно ![]() - строго положительное и
одно - строго отрицательное. Итак,
- строго положительное и
одно - строго отрицательное. Итак,
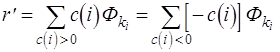 (С3)
(С3)
является ненулевым вектором корреляции на границе Е с, по крайней мере, двумя спектральными представлениями.
Поэтому оценка Писаренко является единственной тогда и только тогда, когда множество корреляционных векторов, соответствующих нулю каждого ненулевого положительного полинома, линейно независимо. В частности, чтобы оценка Писаренко была единственной, никакой ненулевой положительный полином не может иметь более 2М нулей, это условие подобно, хотя и не так строго, условию Хаара [23], которое включает все полиномы, а не только положительные.
Факторизация полиномов в случае
временной последовательности дает сильный результат. В случае временной
последовательности ненулевой положительный полином может иметь не более М
нулей. Кроме того, ненулевой положительный полином может быть построен так, что
он равен нулю в М или менее произвольных точках и больше нигде. Это
означает /Пример 4.I/ , что корреляционный вектор в ![]() имеет
единственное спектральное представление и что этот спектр состоит из и или
менее импульсов. Кроме того, это означает, что любой спектр, состоящий из М
или менее импульсов, имеет корреляционный вектор в
имеет
единственное спектральное представление и что этот спектр состоит из и или
менее импульсов. Кроме того, это означает, что любой спектр, состоящий из М
или менее импульсов, имеет корреляционный вектор в ![]() .
.
Однако, простой пример показывает,, что нет гарантии того, что оценка Писаренко будет единственной в большинстве многомерных ситуаций. Рассмотрим ненулевой положительный полином
![]() (С4)
(С4)
для некоторого ненулевого ![]() .
Нулевое множество
.
Нулевое множество ![]() включает часть
гиперплоскости
включает часть
гиперплоскости
![]() (С5)
(С5)
которая находится в К. Многие спектральные основы, имеющие практический интерес, пересекают эту гиперплоскость в бесконечном числе точек, подразумевая существование некоторого корреляционного вектора на границе Е с неединственным спектральным представлением. Эта проблема неединственности аналогична неединственности в многомерной чебышевской аппроксимации [24].
ИЛЛЮСТРАЦИИ
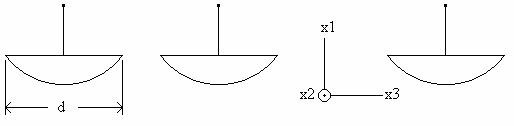
Рис.1 ПИП из трех ИП
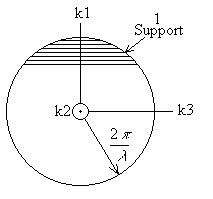
Рис.2 Спектральная основа для решетки ПИП : I - основа
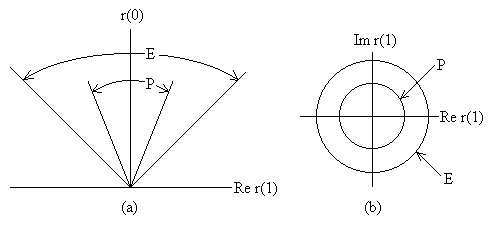
Рис.3 Е и Р для ![]() и
и ![]() . /а/
Сечение Е и Р при
. /а/
Сечение Е и Р при ![]() и /b/ Сечение Е и Р при
и /b/ Сечение Е и Р при ![]() .
.
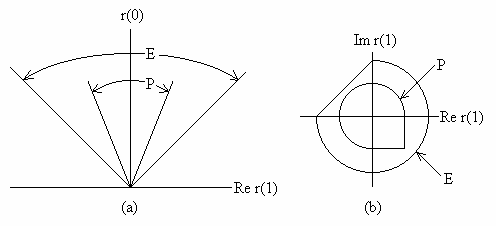
Рис. 4 Е и Р для ![]() и
и ![]() . /а/
Сечение Е и Р при
. /а/
Сечение Е и Р при ![]() и /b/ Сечение Е и Р при
и /b/ Сечение Е и Р при ![]() .
.
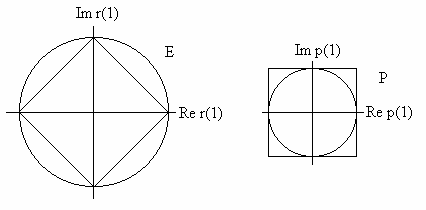
Рис.5 Аппроксимация спектральной
основы посредством выборки ; сечение
при ![]()
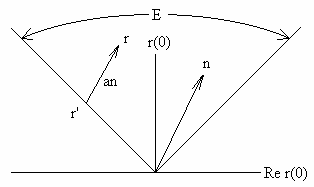
Рис.6 Разложение вектора ![]() на вектор
на вектор ![]() на границе Е плюс
кратное данного вектора
на границе Е плюс
кратное данного вектора ![]() .
.
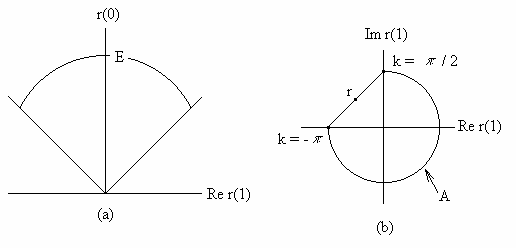
Рис.7 Е для ![]() и
и ![]() . /а/
Сечение по Е при
. /а/
Сечение по Е при ![]() и /b/ Сечение по Е при
и /b/ Сечение по Е при ![]() .
.