Реферат: Расчет настроек автоматического регулятора
Пермский Государственный Технический Университет
Курсовая работа
по предмету: Автоматизация технологических процессов и
производств.
Тема: Расчет настроек автоматического регулятора.
Выполнил: ст-т гр. АТП-93
Никулина Д. В.
Проверил: Бильфельд Н. В.
г. Березники, 1998
Содержание.
1. Координаты кривых разгона.
1.1 Схемы для Ремиконта.
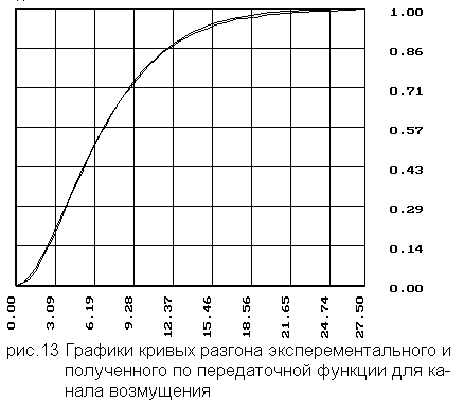
1.2 Координаты и график кривой разгона по возмущению.
1.3 Координаты и график кривой разгона по заданию.
1.4 Координаты и график кривой разгона по управлению.
2. Интерполяция по 3 точкам.
2.1 Линейное сглаживание и график кривой разгона по возмущению.
2.2 Линейное сглаживание и график кривой разгона по заданию.
2.3 Линейное сглаживание и график кривой разгона по управлению.
3. Нормирование кривых разгона.
3.1 Нормирование кривой разгона по возмущению.
3.2 Нормирование кривой разгона по заданию.
3.3 Нормирование кривой разгона по управлению.
4. Аппроксимация методом Симою.
4.1 По возмущению.
4.2 По заданию.
4.3 По управлению.
5. Проверка аппроксимации методом Рунге - Кутта.
5.1 По возмущению.
5.2 По заданию.
5.3 По управлению.
5.4 Сравнение передаточных функций.
5.5 Сравнение кривых разгона.
6. Расчет одноконтурной АСР методом Роточа.
1. Задание
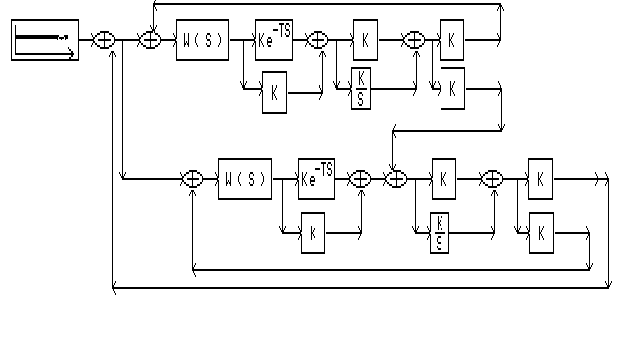
Исследовать работу комбинированной автоматической системы управления в целом и ее отдельных контуров. Провести расчет оптимальных настроечных параметров регуляторов АСР.
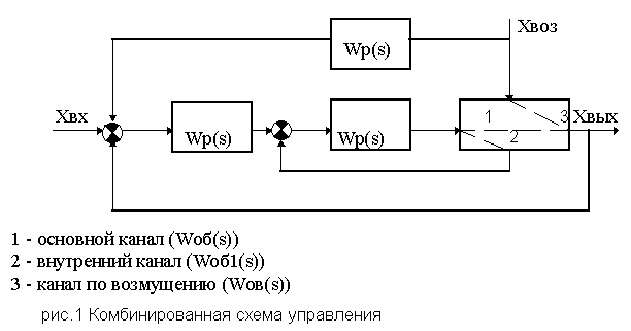
2. Координаты кривой разгона
С помощью программы связи ЭВМ с контроллером снимаем координаты кривой разгона.
Для этого сначала поочередно программируем Ремиконт:
1. по возмущению
2. по заданию
3. по управлению
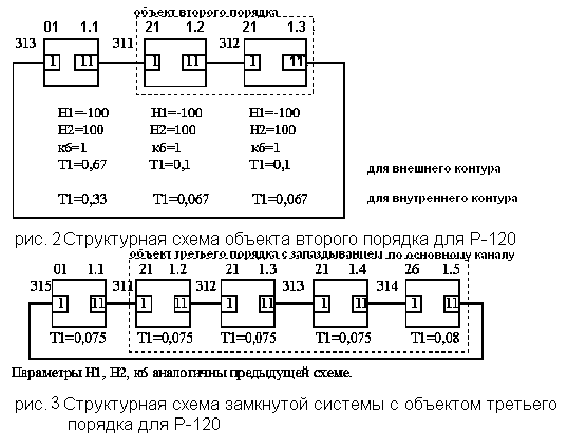
В программе тренды меняя задание добиваемся устойчивости систем.
После того как системы установились приступаем к проведению эксперимента. Для этого устанавливаем алгоблок 11 с которого будем снимать кривую разгона, алгоблок 11 на который будем подавать скачек, амплитуду скачка 10 и интервал времени 0,5.
После просмотра полученных точек кривых разгона удаляем одинаковые.
И строим соответствующие графики.
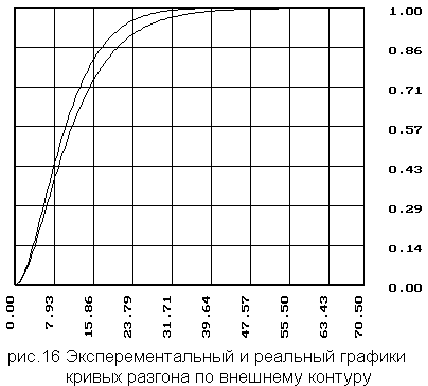
2.1 Координаты и график кривой разгона по каналу возмущения
табл.2.1
|
1 |
0,0000 |
39,0000 |
22 |
11,0000 |
47,1500 |
|
2 |
1,0000 |
39,1500 |
23 |
11,5000 |
47,4500 |
|
3 |
1,5000 |
39,3500 |
24 |
12,0000 |
47,6000 |
|
4 |
2,0000 |
40,0000 |
25 |
12,5000 |
47,7000 |
|
5 |
2,5000 |
40,4000 |
26 |
13,0000 |
47,8500 |
|
6 |
3,0000 |
40,8000 |
27 |
13,5000 |
48,0500 |
|
7 |
3,5000 |
41,2000 |
28 |
14,0000 |
48,1000 |
|
8 |
4,0000 |
42,0500 |
29 |
14,5000 |
48,2000 |
|
9 |
4,5000 |
42,5000 |
30 |
15,0000 |
48,2500 |
|
10 |
5,0000 |
42,9000 |
31 |
15,5000 |
48,4000 |
|
11 |
5,5000 |
43,3000 |
32 |
16,0000 |
48,4500 |
|
12 |
6,0000 |
44,0500 |
33 |
16,5000 |
48,5000 |
|
13 |
6,5000 |
44,4000 |
34 |
17,0000 |
48,5500 |
|
14 |
7,0000 |
44,7500 |
35 |
17,5000 |
48,6500 |
|
15 |
7,5000 |
45,1000 |
36 |
19,0000 |
48,7000 |
|
16 |
8,0000 |
45,6500 |
37 |
19,5000 |
48,7540 |
|
17 |
8,5000 |
45,9000 |
38 |
20,0000 |
48,8000 |
|
18 |
9,0000 |
46,1500 |
39 |
21,5000 |
48,8500 |
|
19 |
9,5000 |
46,4000 |
40 |
22,0000 |
48,9000 |
|
20 |
10,0000 |
46,8000 |
41 |
26,5000 |
48,9500 |
|
21 |
10,5000 |
47,0000 |
42 |
27,0000 |
49,0000 |
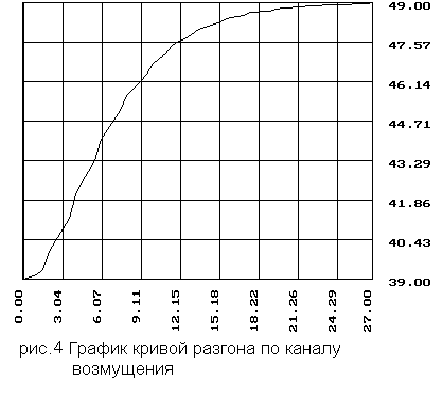
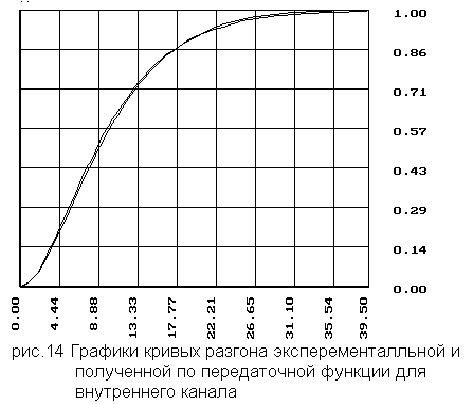
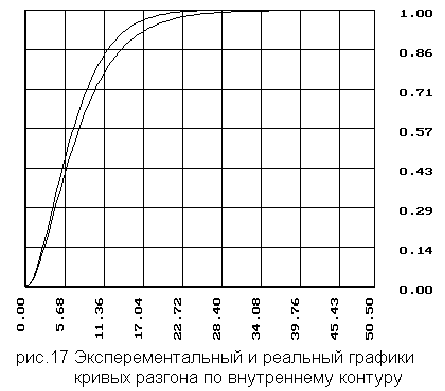
2.2 Координаты и график кривой разгона для внутреннего канала
табл.2.2
|
1 |
0,0000 |
58,0000 |
30 |
15,0000 |
65,9500 |
|
2 |
1,0000 |
58,0500 |
31 |
15,5000 |
66,1000 |
|
3 |
1,5000 |
58,3000 |
32 |
16,0000 |
66,2000 |
|
4 |
2,0000 |
58,4500 |
33 |
16,5000 |
66,4000 |
|
5 |
2,5000 |
58,7000 |
34 |
17,0000 |
66,5000 |
|
6 |
3,0000 |
59,2000 |
35 |
18,5000 |
66,6000 |
|
7 |
3,5000 |
59,4500 |
36 |
18,0000 |
66,6500 |
|
8 |
4,0000 |
59,7000 |
37 |
18,5000 |
66,8000 |
|
9 |
4,5000 |
60,0000 |
38 |
19,0000 |
66,9000 |
|
10 |
5,0000 |
60,6000 |
39 |
19,5000 |
66,9500 |
|
11 |
5,5000 |
60,8500 |
40 |
20,0000 |
67,0500 |
|
12 |
6,0000 |
61,1500 |
41 |
20,5000 |
67,1500 |
|
13 |
6,5000 |
61,4500 |
42 |
21,0000 |
67,2000 |
|
14 |
7,0000 |
62,0000 |
43 |
21,5000 |
67,2500 |
|
15 |
7,5000 |
62,3000 |
44 |
22,0000 |
67,3000 |
|
16 |
8,0000 |
62,5500 |
45 |
22,5000 |
67,3500 |
|
17 |
8,5000 |
62,8000 |
46 |
23,0000 |
67,4000 |
|
18 |
9,0000 |
63,3000 |
47 |
23,5000 |
67,4500 |
|
19 |
9,5000 |
63,5500 |
48 |
24,0000 |
67,5000 |
|
20 |
10,0000 |
63,7500 |
49 |
24,5000 |
67,5500 |
|
21 |
10,5000 |
64,0000 |
50 |
25,0000 |
67,6000 |
|
22 |
11,0000 |
64,4000 |
51 |
26,0000 |
67,6500 |
|
23 |
11,5000 |
64,5500 |
52 |
26,5000 |
67,7000 |
|
24 |
12,0000 |
64,7500 |
53 |
28,0000 |
67,7500 |
|
25 |
12,5000 |
64,9500 |
54 |
29,0000 |
67,8000 |
|
26 |
13,0000 |
65,2500 |
55 |
31,5000 |
67,8500 |
|
27 |
13,5000 |
65,4000 |
56 |
32,0000 |
67,9000 |
|
28 |
14,0000 |
65,5500 |
57 |
39,0000 |
67,9500 |
|
29 |
14,5000 |
65,8500 |
58 |
39,5000 |
68,0000 |
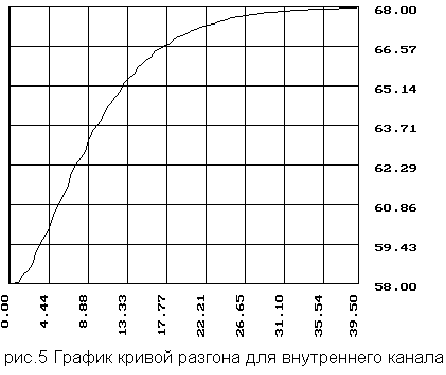
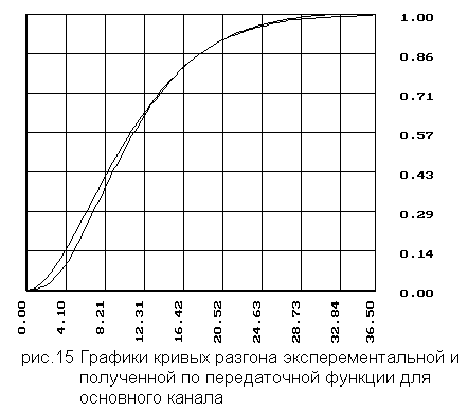
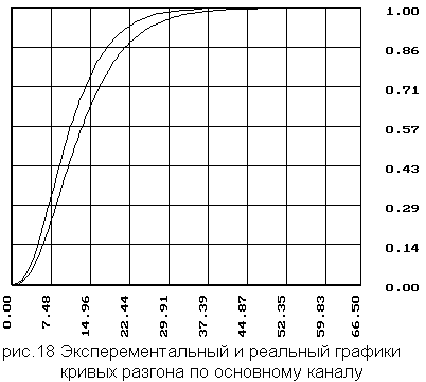
2.3 Координаты и график кривой разгона основного контура
табл 2.3
|
1 |
0,0000 |
50,9500 |
30 |
14,5000 |
58,4000 |
|
2 |
0,5000 |
50,9500 |
31 |
15,0000 |
58,5500 |
|
3 |
1,0000 |
51,0000 |
32 |
15,5000 |
58,7500 |
|
4 |
1,5000 |
51,0500 |
33 |
16,0000 |
59,0000 |
|
5 |
2,0000 |
51,1000 |
34 |
16,5000 |
59,1500 |
|
6 |
2,5000 |
51,2000 |
35 |
17,0000 |
59,2500 |
|
7 |
3,0000 |
51,5000 |
36 |
17,5000 |
59,3500 |
|
8 |
3,5000 |
51,6500 |
37 |
18,0000 |
59,6000 |
|
9 |
4,0000 |
51,8500 |
38 |
18,5000 |
59,6500 |
|
10 |
4,5000 |
52,0500 |
39 |
19,0000 |
59,7500 |
|
11 |
5,0000 |
52,5000 |
40 |
19,5000 |
59,8500 |
|
12 |
5,5000 |
52,8000 |
41 |
20,0000 |
60,0000 |
|
13 |
6,0000 |
53,0500 |
42 |
20,5000 |
60,1000 |
|
14 |
6,5000 |
53,6000 |
43 |
21,0000 |
60,1500 |
|
15 |
7,0000 |
53,9000 |
44 |
21,5000 |
60,2000 |
|
16 |
7,5000 |
54,1500 |
45 |
22,0000 |
60,3000 |
|
17 |
8,0000 |
54,4500 |
46 |
22,5000 |
60,3500 |
|
18 |
8,5000 |
55,0000 |
47 |
23,0000 |
60,4000 |
|
19 |
9,0000 |
55,3000 |
48 |
23,5000 |
60,5000 |
|
20 |
9,5000 |
55,5500 |
49 |
24,0000 |
60,5500 |
|
21 |
10,0000 |
55,8500 |
50 |
25,0000 |
60,6000 |
|
22 |
10,5000 |
56,3500 |
51 |
25,5000 |
60,6500 |
|
23 |
11,0000 |
56,6000 |
52 |
26,0000 |
60,7000 |
|
24 |
11,5000 |
56,8500 |
53 |
27,0000 |
60,7500 |
|
25 |
12,0000 |
57,0500 |
54 |
27,5000 |
60,8000 |
|
26 |
12,5000 |
57,5000 |
55 |
30,0000 |
60,8500 |
|
27 |
13,0000 |
57,7000 |
56 |
30,5000 |
60,9000 |
|
28 |
13,5000 |
57,9000 |
57 |
36,0000 |
60,9500 |
|
29 |
14,0000 |
58,0500 |
58 |
36,5000 |
61,0000 |

3. Интерполяция по трем точкам.
В программе ASR, пользуясь пунктом “интерполировать по 3-м” поочередно считаем кривые разгона и строим соответствующий график.
3.1.Линейное сглаживание и график кривой разгона для внешнего контура
табл. 3.1
|
1 |
0,0000 |
38,9914 |
22 |
11,0000 |
47,2000 |
|
2 |
1,0000 |
39,1667 |
23 |
11,5000 |
47,4000 |
|
3 |
1,5000 |
39,5000 |
24 |
12,0000 |
47,5833 |
|
4 |
2,0000 |
39,9167 |
25 |
12,5000 |
47,7167 |
|
5 |
2,5000 |
40,4000 |
26 |
13,0000 |
47,8667 |
|
6 |
3,0000 |
40,8000 |
27 |
13,5000 |
48,0000 |
|
7 |
3,5000 |
41,3500 |
28 |
14,0000 |
48,1167 |
|
8 |
4,0000 |
41,9167 |
29 |
14,5000 |
48,1833 |
|
9 |
4,5000 |
42,4833 |
30 |
15,0000 |
48,2833 |
|
10 |
5,0000 |
42,9000 |
31 |
15,5000 |
48,3667 |
|
11 |
5,5000 |
43,4167 |
32 |
16,0000 |
48,4500 |
|
12 |
6,0000 |
43,9167 |
33 |
16,5000 |
48,5000 |
|
13 |
6,5000 |
44,4000 |
34 |
17,0000 |
48,5667 |
|
14 |
7,0000 |
44,7500 |
35 |
17,5000 |
48,6333 |
|
15 |
7,5000 |
45,1667 |
36 |
19,0000 |
48,7000 |
|
16 |
8,0000 |
45,5500 |
37 |
19,5000 |
48,7500 |
|
17 |
8,5000 |
45,9000 |
38 |
20,0000 |
48,8000 |
|
18 |
9,0000 |
46,1500 |
39 |
21,5000 |
48,8500 |
|
19 |
9,5000 |
46,4500 |
40 |
22,0000 |
48,9000 |
|
20 |
10,0000 |
46,7333 |
41 |
26,5000 |
48,9500 |
|
21 |
10,5000 |
46,9833 |
42 |
27,0000 |
49,0000 |
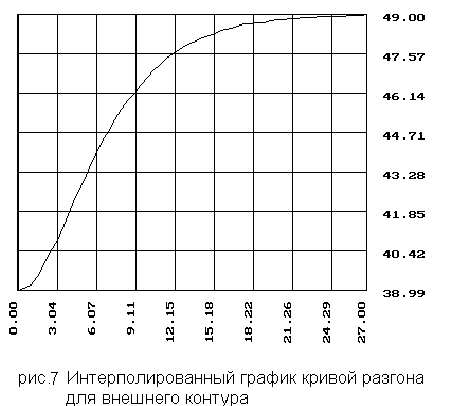
3.2. Линейное сглаживание и график кривой разгона для внутреннего контура
табл 3.2
|
1 |
0,0000 |
57,9667 |
30 |
15,0000 |
65,9667 |
|
2 |
1,0000 |
58,1167 |
31 |
15,5000 |
66,0833 |
|
3 |
1,5000 |
58,2667 |
32 |
16,0000 |
66,2333 |
|
4 |
2,0000 |
58,4833 |
33 |
16,5000 |
66,3667 |
|
5 |
2,5000 |
58,7833 |
34 |
17,0000 |
66,5000 |
|
6 |
3,0000 |
59,1167 |
35 |
18,5000 |
66,5833 |
|
7 |
3,5000 |
59,4500 |
36 |
18,0000 |
66,6833 |
|
8 |
4,0000 |
59,7167 |
37 |
18,5000 |
66,7833 |
|
9 |
4,5000 |
60,1000 |
38 |
19,0000 |
66,8833 |
|
10 |
5,0000 |
60,4833 |
39 |
19,5000 |
66,9667 |
|
11 |
5,5000 |
60,8667 |
40 |
20,0000 |
67,0500 |
|
12 |
6,0000 |
61,1500 |
41 |
20,5000 |
67,1333 |
|
13 |
6,5000 |
61,5333 |
42 |
21,0000 |
67,2000 |
|
14 |
7,0000 |
61,9167 |
43 |
21,5000 |
67,2500 |
|
15 |
7,5000 |
62,2833 |
44 |
22,0000 |
67,3000 |
|
16 |
8,0000 |
62,5500 |
45 |
22,5000 |
67,3500 |
|
17 |
8,5000 |
62,8833 |
46 |
23,0000 |
67,4000 |
|
18 |
9,0000 |
63,2167 |
47 |
23,5000 |
67,4500 |
|
19 |
9,5000 |
63,5333 |
48 |
24,0000 |
67,5000 |
|
20 |
10,0000 |
63,7667 |
49 |
24,5000 |
67,5500 |
|
21 |
10,5000 |
64,0500 |
50 |
25,0000 |
67,6000 |
|
22 |
11,0000 |
64,3167 |
51 |
26,0000 |
67,6500 |
|
23 |
11,5000 |
64,5667 |
52 |
26,5000 |
67,7000 |
|
24 |
12,0000 |
64,7500 |
53 |
28,0000 |
67,7500 |
|
25 |
12,5000 |
64,9833 |
54 |
29,0000 |
67,8000 |
|
26 |
13,0000 |
65,2000 |
55 |
31,5000 |
67,8500 |
|
27 |
13,5000 |
65,4000 |
56 |
32,0000 |
67,9000 |
|
28 |
14,0000 |
65,6000 |
57 |
39,0000 |
67,9500 |
|
29 |
14,5000 |
65,7833 |
58 |
39,5000 |
68,0000 |
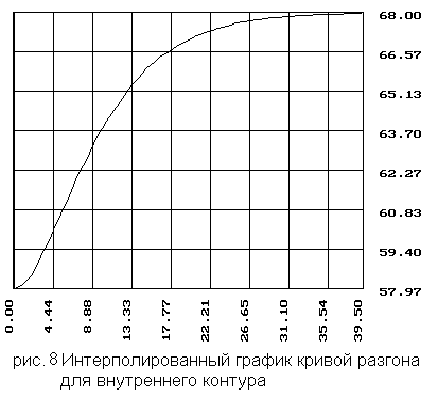
3.3 Линейное сглаживание и график кривой разгона по основному каналу
табл. 3.3
|
1 |
0,0000 |
50,9500 |
30 |
14,5000 |
58,3333 |
|
2 |
0,5000 |
50,9500 |
31 |
15,0000 |
58,5667 |
|
3 |
1,0000 |
51,0000 |
32 |
15,5000 |
58,7667 |
|
4 |
1,5000 |
51,0500 |
33 |
16,0000 |
58,9667 |
|
5 |
2,0000 |
51,1167 |
34 |
16,5000 |
59,1333 |
|
6 |
2,5000 |
51,2667 |
35 |
17,0000 |
59,2500 |
|
7 |
3,0000 |
51,4500 |
36 |
17,5000 |
59,4000 |
|
8 |
3,5000 |
51,6667 |
37 |
18,0000 |
59,5333 |
|
9 |
4,0000 |
51,8500 |
38 |
18,5000 |
59,6667 |
|
10 |
4,5000 |
52,1333 |
39 |
19,0000 |
59,7500 |
|
11 |
5,0000 |
52,4500 |
40 |
19,5000 |
59,8667 |
|
12 |
5,5000 |
52,7833 |
41 |
20,0000 |
59,9833 |
|
13 |
6,0000 |
53,1500 |
42 |
20,5000 |
60,0833 |
|
14 |
6,5000 |
53,5167 |
43 |
21,0000 |
60,1500 |
|
15 |
7,0000 |
53,8833 |
44 |
21,5000 |
60,2167 |
|
16 |
7,5000 |
54,1667 |
45 |
22,0000 |
60,2833 |
|
17 |
8,0000 |
54,5333 |
46 |
22,5000 |
60,3500 |
|
18 |
8,5000 |
54,9167 |
47 |
23,0000 |
60,4167 |
|
19 |
9,0000 |
55,2833 |
48 |
23,5000 |
60,4833 |
|
20 |
9,5000 |
55,5667 |
49 |
24,0000 |
60,5500 |
|
21 |
10,0000 |
55,9167 |
50 |
25,0000 |
60,6000 |
|
22 |
10,5000 |
56,2667 |
51 |
25,5000 |
60,6500 |
|
23 |
11,0000 |
56,6000 |
52 |
26,0000 |
60,7000 |
|
24 |
11,5000 |
56,8333 |
53 |
27,0000 |
60,7500 |
|
25 |
12,0000 |
57,1333 |
54 |
27,5000 |
60,8000 |
|
26 |
12,5000 |
57,4167 |
55 |
30,0000 |
60,8500 |
|
27 |
13,0000 |
57,7000 |
56 |
30,5000 |
60,9000 |
|
28 |
13,5000 |
57,8833 |
57 |
36,0000 |
60,9500 |
|
29 |
14,0000 |
58,1167 |
58 |
36,5000 |
61,0000 |
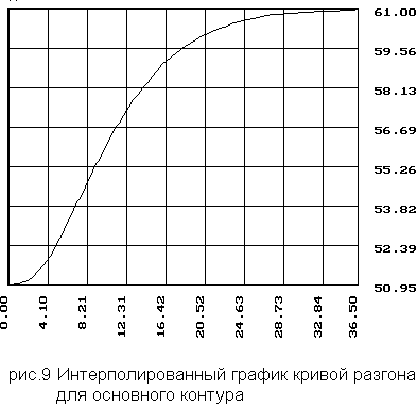
4. Нормирование кривых разгона.
С помощью программы ASR в пункте нормировать последовательно производим нормирование сглаженных кривых и упорядочиваем время начиная с 0,0000, с шагом 0,5 для того чтобы привести полученную динамическую характеристику к единичному виду.
4.1 Нормированная кривая разгона для внешнего контура
табл.4.1
|
1 |
0,0000 |
0,0000 |
22 |
10,5000 |
0,8201 |
|
2 |
0,5000 |
0,0175 |
23 |
11,0000 |
0,8401 |
|
3 |
1,0000 |
0,0508 |
24 |
11,5000 |
0,8585 |
|
4 |
1,5000 |
0,0924 |
25 |
12,0000 |
0,8718 |
|
5 |
2,0000 |
0,1407 |
26 |
12,5000 |
0,8868 |
|
6 |
2,5000 |
0,1807 |
27 |
13,0000 |
0,9001 |
|
7 |
3,0000 |
0,2356 |
28 |
13,5000 |
0,9117 |
|
8 |
3,5000 |
0,2923 |
29 |
14,0000 |
0,9184 |
|
9 |
4,0000 |
0,3489 |
30 |
14,5000 |
0,9284 |
|
10 |
4,5000 |
0,3905 |
31 |
15,0000 |
0,9367 |
|
11 |
5,0000 |
0,4421 |
32 |
15,5000 |
0,9450 |
|
12 |
5,5000 |
0,4921 |
33 |
16,0000 |
0,9500 |
|
13 |
6,0000 |
0,5404 |
34 |
16,5000 |
0,9567 |
|
14 |
6,5000 |
0,5754 |
35 |
17,0000 |
0,9634 |
|
15 |
7,0000 |
0,6170 |
36 |
18,5000 |
0,9700 |
|
16 |
7,5000 |
0,6553 |
37 |
18,0000 |
0,9750 |
|
17 |
8,0000 |
0,6903 |
38 |
18,5000 |
0,9800 |
|
18 |
8,5000 |
0,7152 |
39 |
19,0000 |
0,9850 |
|
19 |
9,0000 |
0,7452 |
40 |
19,5000 |
0,9900 |
|
20 |
9,5000 |
0,7735 |
41 |
20,0000 |
0,9950 |
|
21 |
10,0000 |
0,7985 |
42 |
20,5000 |
1,0000 |
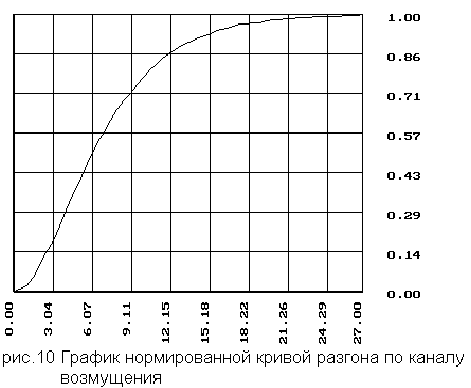
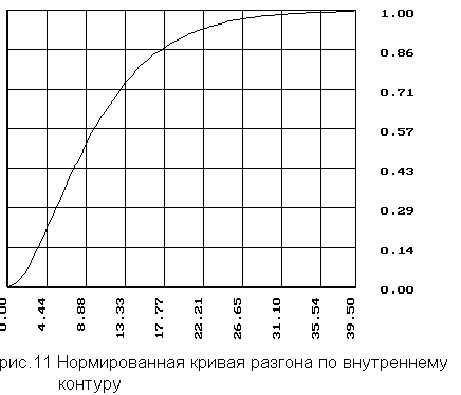
4.2 Нормированная кривая разгона для внутреннего контура
табл.4.2
|
1 |
0,0000 |
0,0000 |
30 |
14,5000 |
0,7973 |
|
2 |
0,5000 |
0,0150 |
31 |
15,0000 |
0,8090 |
|
3 |
1,0000 |
0,0299 |
32 |
15,5000 |
0,8239 |
|
4 |
1,5000 |
0,0515 |
33 |
16,0000 |
0,8372 |
|
5 |
2,0000 |
0,0814 |
34 |
16,5000 |
0,8505 |
|
6 |
2,5000 |
0,1146 |
35 |
17,0000 |
0,8588 |
|
7 |
3,0000 |
0,1478 |
36 |
17,5000 |
0,8688 |
|
8 |
3,5000 |
0,1744 |
37 |
18,0000 |
0,8787 |
|
9 |
4,0000 |
0,2126 |
38 |
18,5000 |
0,8887 |
|
10 |
4,5000 |
0,2508 |
39 |
19,0000 |
0,8970 |
|
11 |
5,0000 |
0,2890 |
40 |
19,5000 |
0,9053 |
|
12 |
5,5000 |
0,3173 |
41 |
20,0000 |
0,9136 |
|
13 |
6,0000 |
0,3555 |
42 |
20,5000 |
0,9203 |
|
14 |
6,5000 |
0,3937 |
43 |
21,0000 |
0,9252 |
|
15 |
7,0000 |
0,4302 |
44 |
21,5000 |
0,9302 |
|
16 |
7,5000 |
0,4568 |
45 |
22,0000 |
0,9352 |
|
17 |
8,0000 |
0,4900 |
46 |
22,5000 |
0,9402 |
|
18 |
8,5000 |
0,5233 |
47 |
23,0000 |
0,9452 |
|
19 |
9,0000 |
0,5548 |
48 |
23,5000 |
0,9502 |
|
20 |
9,5000 |
0,5781 |
49 |
24,0000 |
0,9551 |
|
21 |
10,0000 |
0,6063 |
50 |
24,5000 |
0,9601 |
|
22 |
10,5000 |
0,6329 |
51 |
25,0000 |
0,9651 |
|
23 |
11,0000 |
0,6578 |
52 |
25,5000 |
0,9701 |
|
24 |
11,5000 |
0,6761 |
53 |
26,0000 |
0,9751 |
|
25 |
12,0000 |
0,6993 |
54 |
26,5000 |
0,9801 |
|
26 |
12,5000 |
0,7209 |
55 |
27,0000 |
0,9850 |
|
27 |
13,0000 |
0,7409 |
56 |
27,5000 |
0,9900 |
|
28 |
13,5000 |
0,7608 |
57 |
28,0000 |
0,9950 |
|
29 |
14,0000 |
0,7791 |
58 |
28,5000 |
1,0000 |
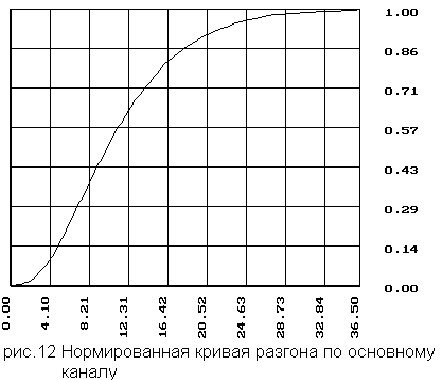
4.3 Нормированная кривая разгона по основному каналу
табл. 4.3
|
1 |
0,0000 |
0,0000 |
30 |
14,5000 |
0,7579 |
|
2 |
0,5000 |
0,0050 |
31 |
15,0000 |
0,7779 |
|
3 |
1,0000 |
0,0100 |
32 |
15,5000 |
0,7977 |
|
4 |
1,5000 |
0,0166 |
33 |
16,0000 |
0,8143 |
|
5 |
2,0000 |
0,0315 |
34 |
16,5000 |
0,8259 |
|
6 |
2,5000 |
0,0498 |
35 |
17,0000 |
0,8408 |
|
7 |
3,0000 |
0,0713 |
36 |
17,5000 |
0,8541 |
|
8 |
3,5000 |
0,0896 |
37 |
18,0000 |
0,8673 |
|
9 |
4,0000 |
0,1177 |
38 |
18,5000 |
0,8756 |
|
10 |
4,5000 |
0,1493 |
39 |
19,0000 |
0,8872 |
|
11 |
5,0000 |
0,1824 |
40 |
19,5000 |
0,8988 |
|
12 |
5,5000 |
0,2189 |
41 |
20,0000 |
0,9088 |
|
13 |
6,0000 |
0,2554 |
42 |
20,5000 |
0,9154 |
|
14 |
6,5000 |
0,2919 |
43 |
21,0000 |
0,9221 |
|
15 |
7,0000 |
0,3201 |
44 |
21,5000 |
0,9287 |
|
16 |
7,5000 |
0,3566 |
45 |
22,0000 |
0,9353 |
|
17 |
8,0000 |
0,3947 |
46 |
22,5000 |
0,9420 |
|
18 |
8,5000 |
0,4312 |
47 |
23,0000 |
0,9486 |
|
19 |
9,0000 |
0,4594 |
48 |
23,5000 |
0,9552 |
|
20 |
9,5000 |
0,4942 |
49 |
24,0000 |
0,9602 |
|
21 |
10,0000 |
0,5290 |
50 |
24,5000 |
0,9652 |
|
22 |
10,5000 |
0,5622 |
51 |
25,5000 |
0,9701 |
|
23 |
11,0000 |
0,5857 |
52 |
25,5000 |
0,9751 |
|
24 |
11,5000 |
0,6153 |
53 |
26,0000 |
0,9801 |
|
25 |
12,0000 |
0,6434 |
54 |
26,5000 |
0,9851 |
|
26 |
12,5000 |
0,6716 |
55 |
27,0000 |
0,9900 |
|
27 |
13,0000 |
0,6899 |
56 |
27,5000 |
0,9950 |
|
28 |
13,5000 |
0,7131 |
57 |
28,0000 |
1,0000 |
|
29 |
14,0000 |
0,7347 |
5. Аппроксимация методом Симою.
С помощью программы ASR в пункту аппроксимации последовательно считаем площади каждой из кривой разгона для последующего получения уравнения передаточной функции.
Для кривой разгона по внешнему контуру для объекта второго порядка получаем следующие данные:
Значения площадей:
F1= 6.5614
F2= 11.4658
F3= -4.5969
F4= -1.1636
F5= 44.0285
F6= -120.0300
Ограничимся
второй площадью.
F1
a1 = F1 + b1 a2
= F2 + b2 + b1 F2 a3
= F3 + b3 + b2 F1 + b1 F2 a1
= 6.5614 + b1 a2
= 11.4658 + b1 6.5614
0 = - 4.5969 + b1 11.4658
Решив систему
получаем : b1 = 0.4
a1 = 6.9614
a2 = 14.0904
Тогда передаточная
функция объекта
второго порядка
по внешнему
контуру имеет
вид:
0.4
s
W(s)=-----------------------------
2
14.0904 s + 6.9614 s + 1
Для кривой
разгона по
внутреннему
контуру для
объекта второго
порядка получаем
следующие
данные:
Значения
площадей:
F1= 9.5539
F2= 24.2986 F3=
-16.7348
F4= -14.7318
F5= 329.7583
F6= -1179.3989
Для определения
передаточной
функции решаем
систему, так
как F3<0.
a1 = 9.5539 + b1 a2
= 24.2986 + 9.5539 b2
0 = -16.7348 + b1 24.2986
Решив систему
получаем : b1 =
0.6887
a1
= 10.2426
a2 = 30.8783
Тогда передаточная
функция объекта
второго порядка
по внутреннему
контуру имеет
вид:
0.6887
s + 1
W(s) =
-----------------------------
2
30.8783s + 10.2426 s + 1
Для кривой
разгона по
заданию для
объкта третьего
порядка с
запаздыванием
получаем следующие
данные:
Значения
площадей:
F1= 10.6679
F2= 38.1160 F3=
30.4228
F4= -46.5445
F5= 168.8606
F6= -33.3020
Так как F3
1 W(s)
=-------------------------------
2
38.1160 s + 10.6679 s + 1
6. Проверка
аппроксимации
методом Рунге
- Кутта.
В программе
ASR в пункте передаточная
функция задаем
полученные
передаточные
функции. И затем
строим графики
экспериментальной
и аналитической
кривых разгона
(по полученной
передаточной
функции).
6.1 Для кривой
разгона по
внешнему контуру
Устанавливаем
для проверки
методом Рунге-Кутта
конечное время
27c, шаг 0,5с.
6.2 Для кривой
разгона по
внутреннему
контуру
Устанавливаем
конечное время
39с, шаг 0,5с.
6.3 Для
кривой разгона
по основному
каналу
При задании
передаточной
функции учитываем
чистое запаздывание
0,08с.
Устанавливаем
конечное время
32с, шаг изменения
0,5с.
Получили,
что кривые
разгона практически
одинаковы,
следовательно
аппроксимация
методом Симою
сделана верно.
6.4 Сравнение
экспериментальных
и исходных
передаточных
функции:
объект
исходная
экспериментальная
передаточная
передаточная
функция
функция
второго
порядка
1
0.6887 s
по возмущению
W(s)= ------------------ W(s)=
-----------------------------
2
2
36 s + 12 s + 1
30,8783 s + 10.2426 s
+ 1
второго
порядка
1
0.4 s
по заданию
W(s)= ------------------------------
W(s)= -------------------------------
2
2
16,1604 s + 8,04
s + 1 14.0904 s + 6.9614 s + 1
третьего
порядка
1
1
с запаздыванием
W(s)= ------------------------------------- W(s)=
-------------------------------
по управлению
3 2
2
91.125 s + 60.75
s + 13.5 s + 1 38.1160 s + 10.6679 s + 1
Анализируя
таблицу можно
сделать вывод
о том, что передаточные
функции второго
порядка практически
одинаковы, а
третьего порядка
значительно
отличаются.
6.5 Сравнение
экспериментальных
и фактических
кривых разгона.
Для исходных
передаточных
функций с помощью
программы ASR,
пунктов аппроксимация
(создать передаточную
функцию и изменить
время) получим
координаты
кривых разгона
и сравним их
с экспериментальной
кривой:
- по внешнему
контуру
- по внутреннему
контуру
- по основному
каналу
Полученные
значению передаточных
функций не
значительно
отличают от
фактических,
что говорит
о достаточно
не большой
погрешности
между фактическими
и экспериментальными
данными.
Расчет
одноконтурной
АСР методом
Роточа.
В программе
Linreg задаем параметры
объекта. Выбираем
в качестве
регулятора
ПИ- регулятор.
И рассчитываем
его настройки: а)
для экспериментальной
передаточной
функции.
В программе
Linreg задаем передаточную
функцию объекта
второго порядка
с запаздыванием.
Выбираем ПИ-регулятор
и определяем
его настройки.
Получаем
kp = 1.0796
Tu = 8.0434
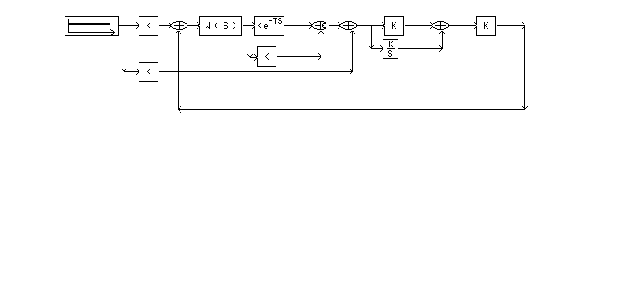
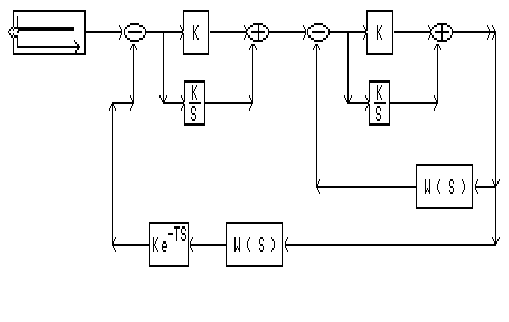
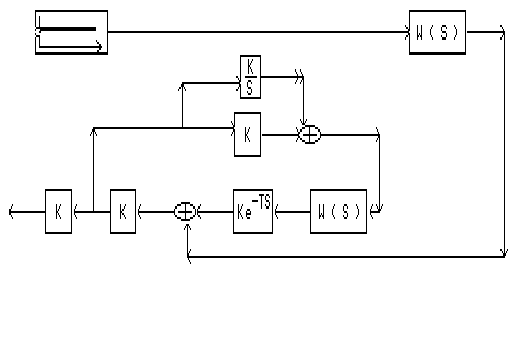
В программе
SIAM пользуясь
следующей
схемой для
одноконтурной
системы
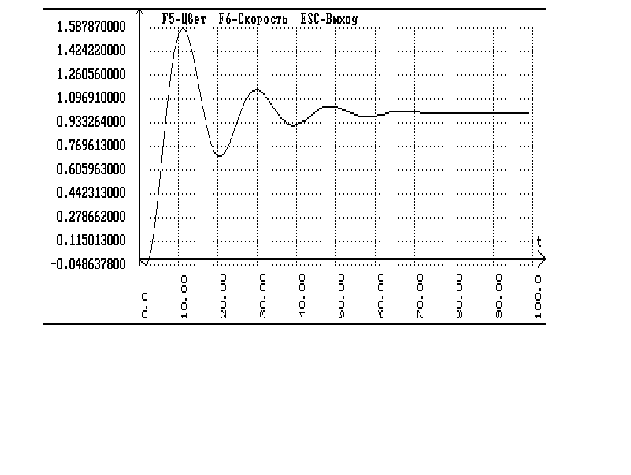
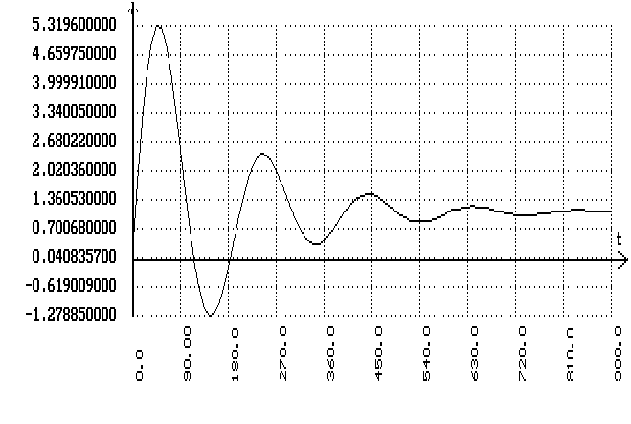
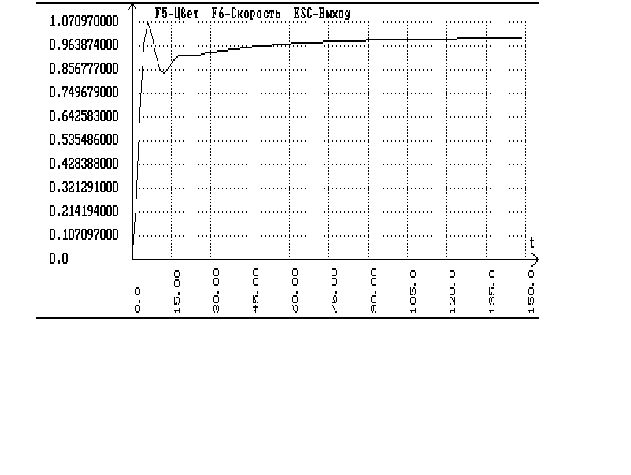
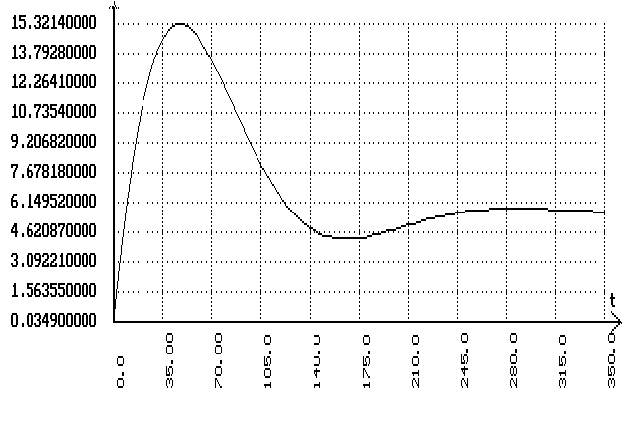
Подаем скачек
на сумматор,
стоящий после
запаздывания
и получаем
график переходного
процесса по
заданию:
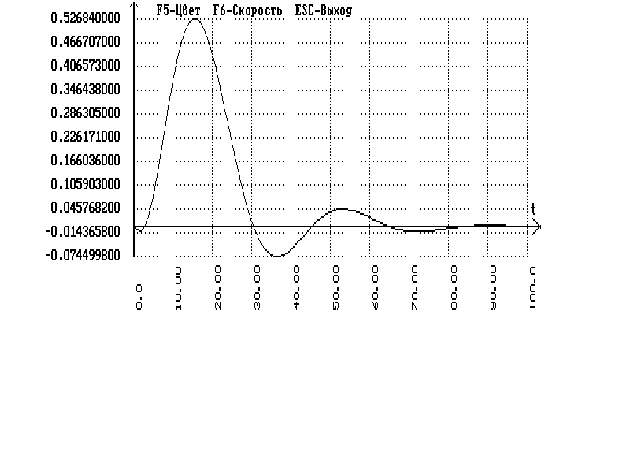
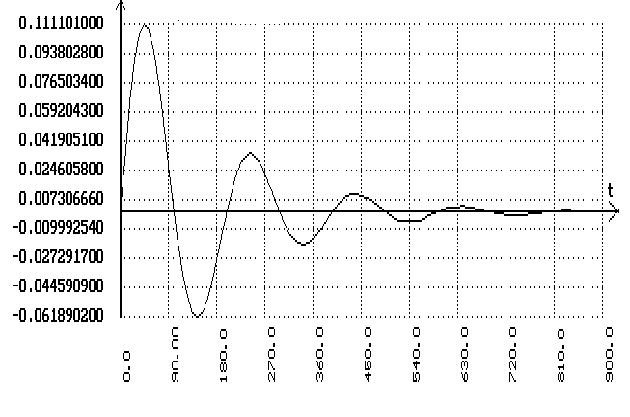
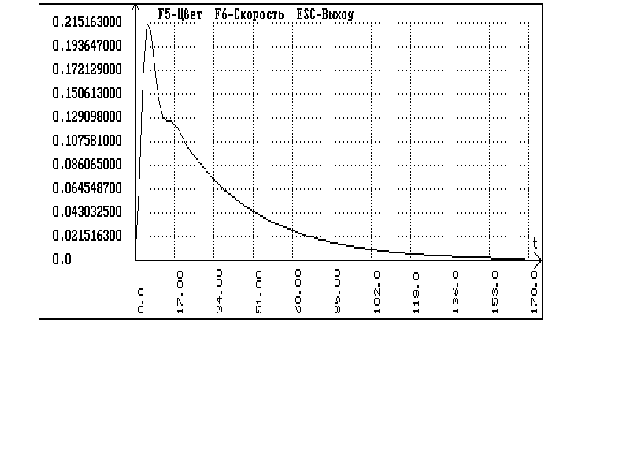
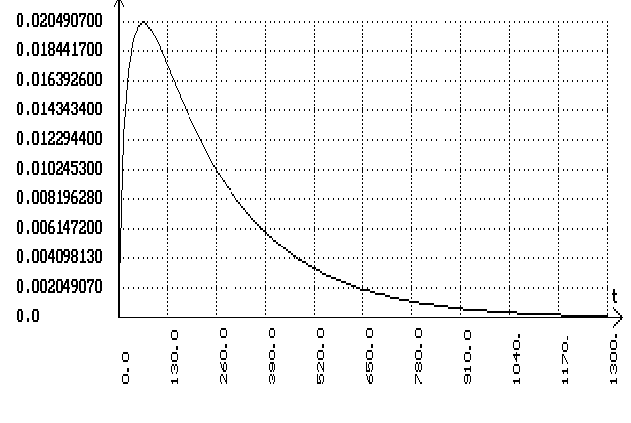
Подаем скачек
на сумматор,
стоящий перед
объектом и
получаем график
переходного
процесса по
возмущению:
б)
для фактической
передаточной
функции
В программе
Linreg задаем передаточную
функцию объекта
третьего порядка
с запаздыванием.
Выбираем ПИ-регулятор
и определяем
его настройки.
Получаем
kp = 0.8743
Tu = 8.3924
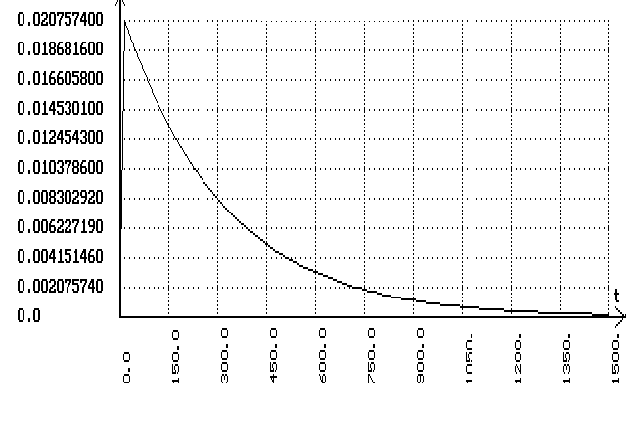
В программе
SIAM пользуясь
схемой для
одноконтурной
системы получаем
- переходный
процесс по
заданию:
Расчет
каскадной АСР
методом Роточа. а)
для экспериментальной
передаточной
функции.
Первоначально
определим
настройки
внутреннего
регулятора
для внутреннего
контура с
передаточной
функцией W1(s).
0.4s +
1 W1(s)
= --------------------------
2
14.0904s + 6.9614s +1
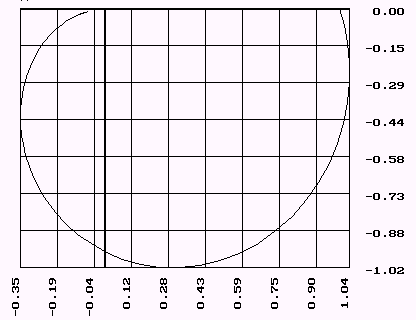
С помощью
программы ASR
получим АФХ
по передаточной
функции и определим
значения u(m,w),
v(m,w), a(m,w), w.
v(m,w) u(m,u) a(m,w) w kp Tu
1,0000
0,0000
0,0000
0,0000
0,0000
0,0000
1,0211
-0,0678
1,0234
0,0100
15,0783
0,0109
1,0360
-0,1398
1,0454
0,0200
7,4774
0,0211
1,0439
-0,2151
1,0659
0,0300
4,9709
0,0307
1,0442
-0,2931
1,0845
0,0400
3,7336
0,0395
1,0361
-0,3728
1,1012
0,0500
3,0067
0,0475
1,0194
-0,4531
1,1156
0,0600
2,5367
0,0547
0,9936
-0,5329
1,1275
0,0700
2,2147
0,0609
0,9587
-0,6108
1,1368
0,0800
1,9877
0,0660
0,9147
-0,6857
1,1431
0,0900
1,1826
0,0701
0,8619
-0,7559
1,1464
0,1000
1,1713
4,4754
0,8008
-0,8203
1,1464
0,1100
1,6386
4,5739
0,7323
-0,8775
1,1429
0,1200
1,1584
0,0749
0,6576
-0,9263
1,1360
0,1300
1,5905
0,0737
0,5778
-0,9658
1,1254
0,1400
1,6169
0,0711
0,4945
-0,9953
1,1114
0,1500
1,6842
0,0668
0,4095
-1,0143
1,0938
0,1600
1,8064
0,0609
0,3243
-1,0229
1,0731
0,1700
2,0137
0,0533
0,2407
-1,0214
1,0493
0,1800
2,3750
0,0438
0,1601
-1,0103
1,0229
0,1900
3,0885
0,0324
0,0840
-0,9906
0,9942
0,2000
5,0095
0,0000
0,0134
-0,9635
0,9635
0,2100
26,1125
0,0034
Так как настройки
регулятора
не могут быть
отрицательными
то ограничимся
3 квадрантом.
И с помощью
программы на
BASIC рассчитаем
оптимальные
настройки для
ПИ - регулятора
методом Стефани
по следующим
формулам:
A^2(m,w)
m 1
Tu
= ------------------------ , kp = ---------- - ----------
w(m^2+1)* v(m,w) v(m,w) u(m,w)
наибольшее
отношение kp/Tu
и будет оптимальными
настройками.
Получили
что kp = 1.712763
Tu = 4.47537
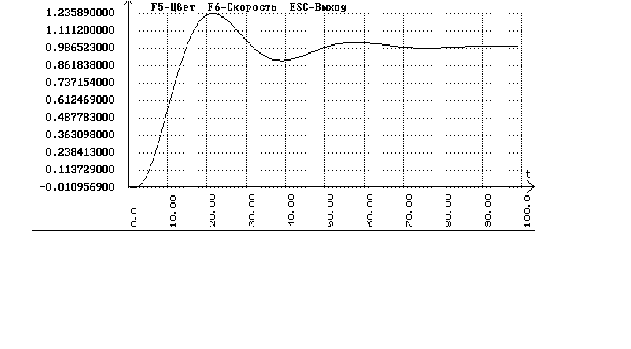
В программе
SIAM с помощью схемы
для одноконтурной
системы без
запаздывания
получаем переходные
процессы по
заданию и по
возмущению:
Сравнивая
график кривой
разгона по
основному
каналу и переходный
процесс внутреннего
контура каскадной
системы делаем
вывод о том,
что за время
запаздывания
основного
контура переходный
процесс во
внутреннем
контуре затухнуть
не успевает,
следовательно
передаточная
функция эквивалентного
объекта имеет
вид:
Wоб(s)
* Wp1(s)
Wоб(s)
= --------------------------- =
1 +
Wоб1(s)
* Wp1(s)
1
1 ---------------------------------
* (1,7128 + ---------- )
2
4,4754s
38,1160s + 10,6679s + 1 --------------------------------------------------------------
=
0,4s + 1 1 1
+ --------------------------- * (1,7128 + ----------)
2
4,4754s
14,0904s + 6,9614s + 1
3 2
107.9987s + 67.4444s + 14.6247s + 1
=
---------------------------------------------------------------------------
5 4 3
2
4116.4785s + 3186.9547s + 969.316s + 138.1861s +
15.7294s + 1
Определяем
настройки
ведущего регулятора.
Для ПИ-регулятора
получаем:
kp = 0.1249
Tu = 5.4148
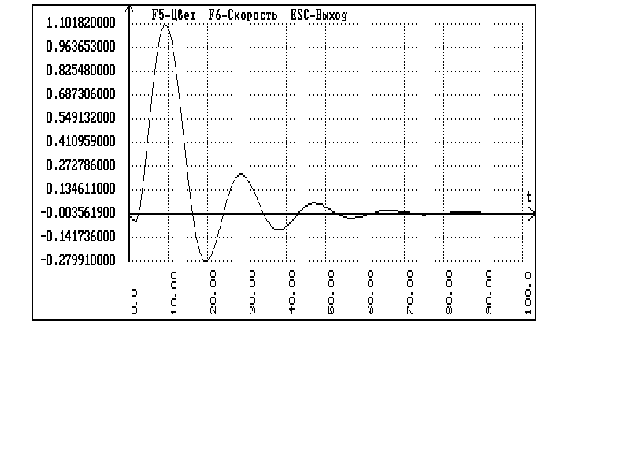
В программе
SIAM с помощью схемы
каскадной
системы получаем
переходный
процесс по
заданию:
С помощью
схемы каскадной
системы получаем
переходный
процесс по
возмущению:
б)
для реальной
передаточной
функции.
Определим
настройки
внутреннего
регулятора
для объекта
второго порядка
с передаточной
функцией
1
W1(s)
=-------------------------
2
16,1604s + 8.04s + 1
Получаем
следующие
настройки
регулятора:
kp = 4.3959
Tu = 6.5957
В программе
SIAM пользуясь
схемой одноконтурной
системы без
запаздывания
получаем графики
переходных
процессов по
заданию и по
возмущению:
Сравнивая
график кривой
разгона по
основному
каналу и переходный
процесс внутреннего
контура каскадной
системы делаем
вывод о том,
что за время
запаздывания
основного
контура переходный
процесс во
внутреннем
контуре затухнуть
не успевает,
следовательно
передаточная
функция эквивалентного
объекта имеет
вид:
Wоб(s)
* Wp1(s)
Wоб(s)
= --------------------------- =
1 +
Wоб1(s)
* Wp1(s)
1
1 ---------------------------------
* (4.3959 + ---------- )
3 2
6.5957s
91.125s + 60.75s + 13.5s
+ 1 --------------------------------------------------------------
=
1 1 1
+ ------------------------ * (4.3959 + ----------)
2
6.5957s
16.1604s + 8.04s + 1
3 2
468.5449s + 249.2673s + 37.0334s + 1 =
--------------------------------------------------------------------------------------------
6
5 4 3
2
42696.154s
+ 49705.969s + 25770.6474s + 7229.3112s + 1076.6779s+71.4868s+ 1
Определяем
настройки
ведущего регулятора.
Для ПИ-регулятора
получаем:
kp = 1.2822
Tu = 6.3952
В программе
SIAM с помощью схем
для каскадной
системы получим
переходные
процессы по
заданию и по
возмущению:
Расчет
комбинированной
АСР. а)
для эксперементальной
передаточной
функции Расчет
компенсирующего
устройства
В программе
SIAM с помощью
смоделированной
схемы комбинированной
системы без
компенсатора
получим соответствующий
переходный
процесс:
Определим
передаточную
функцию фильтра
для структурной
схемы где выход
компенсатора
поступает на
вход регулятора
по формуле:
Wов(s)
Wф(s)
= --------------------- ,
Wоб(s)
* Wр(s)
где Wов(s) - передаточная
функция канала
по возмущению,
Wоб(s) - передаточная
функция объекта,
Wp(s) - передаточная
функция регулятора
0,6887s
+ 1
-----------------------------
2
30.8783 s + 10.2426 s + 1
Wф(s)
= ---------------------------------------------------------- =
1
1
------------------------------- * (1.0796 +
---------- )
2
8.0434 s
38.8783 s + 10.6679 s + 1
4 3
2
232.5099 s + 40.1406 s + 98.6173 s + 8.6837 s
=
-----------------------------------------------------------
3
2
268.1379 s + 119.8220 s + 18.9263 s + 1
Настроечные
параметры
компенсирующего
устройства
будут оптимальными,
если АФХ фильтра
равны нулю при
нулевой и резонансной
частоте. б)
для реальной
передаточной
функции