Реферат: Корреляционно-регрессионный анализ зависимости прибыли 40 банков от их чистых активов
Произвести выборку 40 банков, пользуясь таблицей случайных чисел. Затем по отобранным единицам выписать значения факторного и результативного признаков.
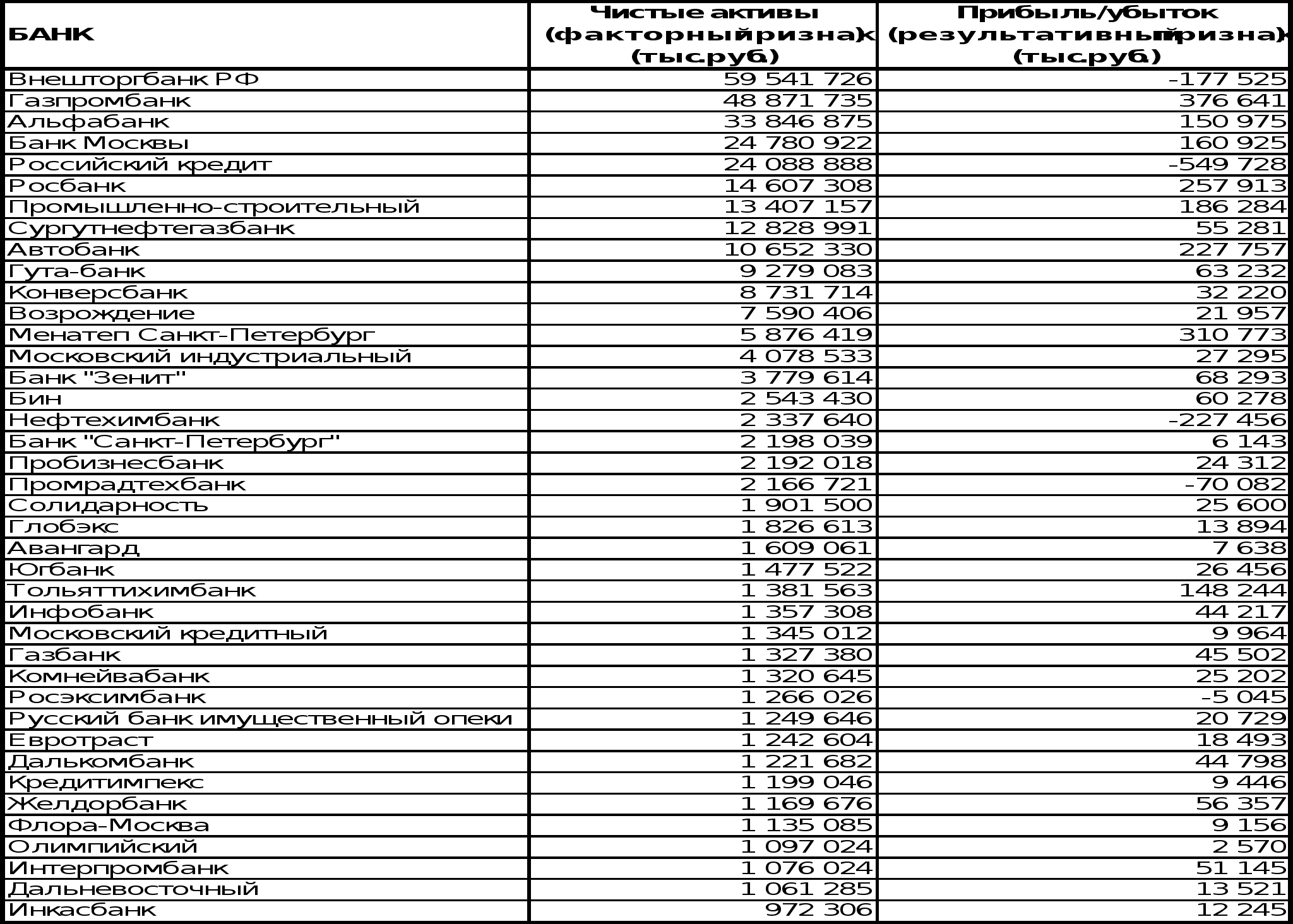
Задание №2.
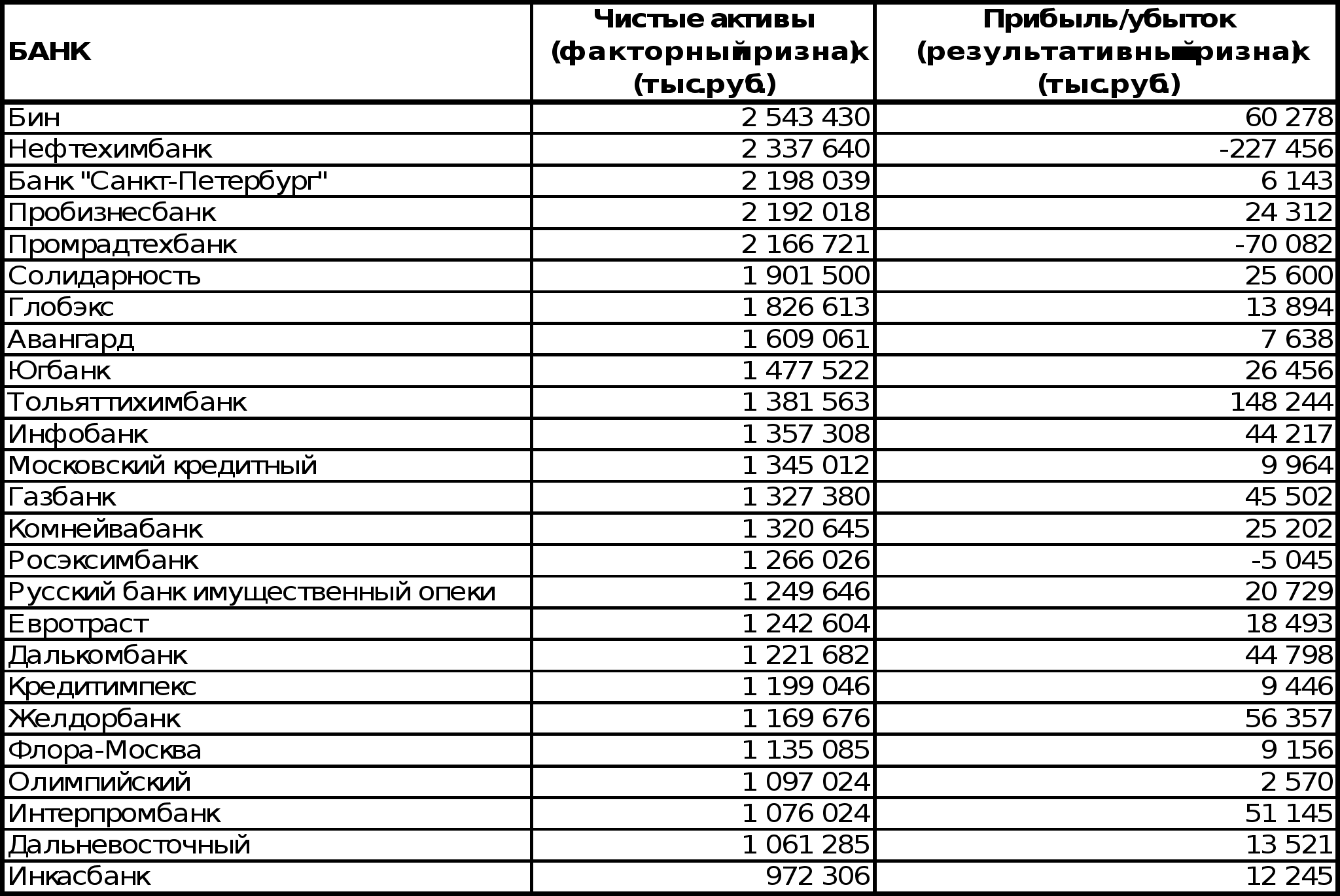
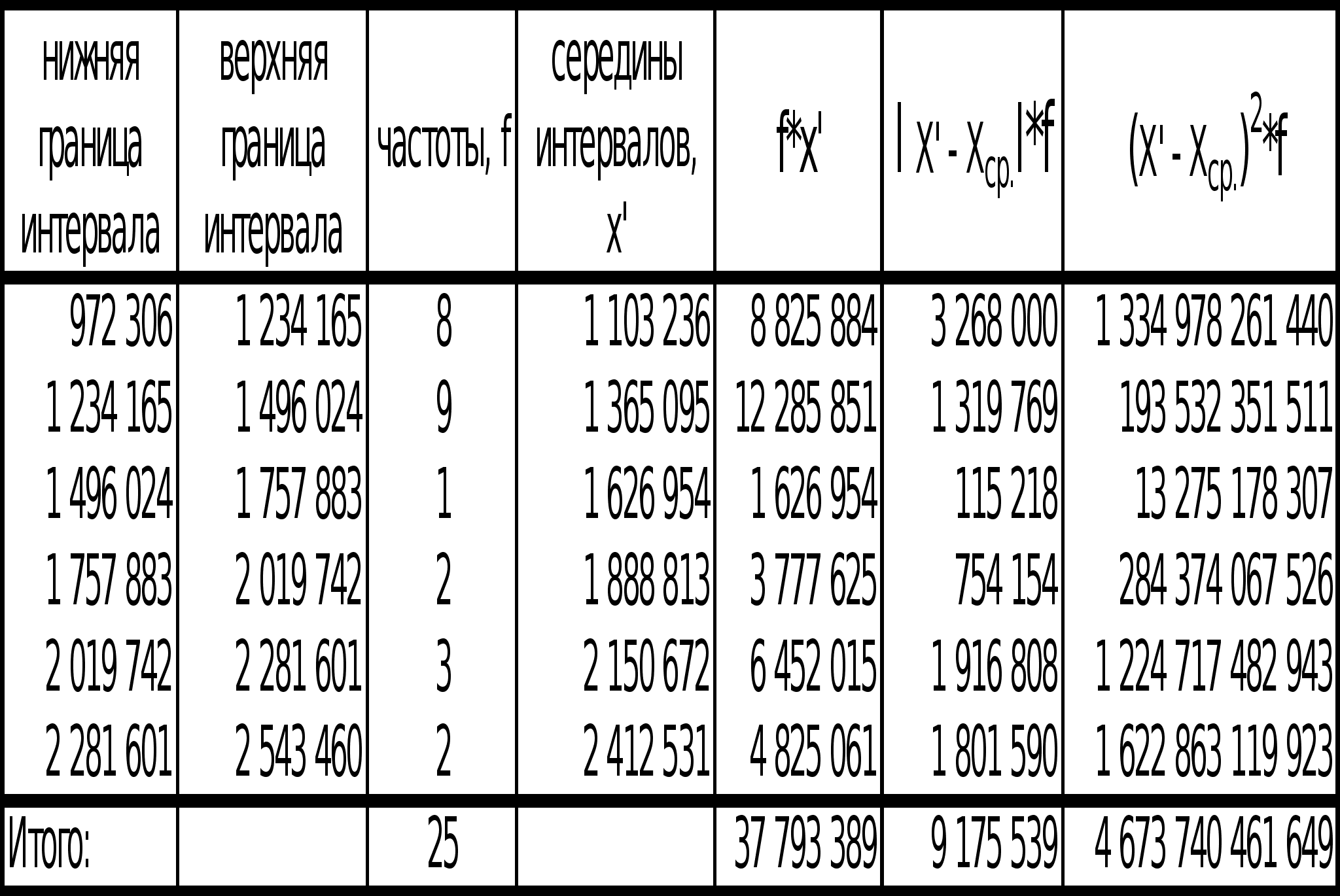
Построить ряд распределения по факторному признаку. Число групп определить по формуле Стерджесса. По построенному ряду распределения рассчитать среднее арифметическое, моду, медиану, показатели вариации. Сформулировать выводы.
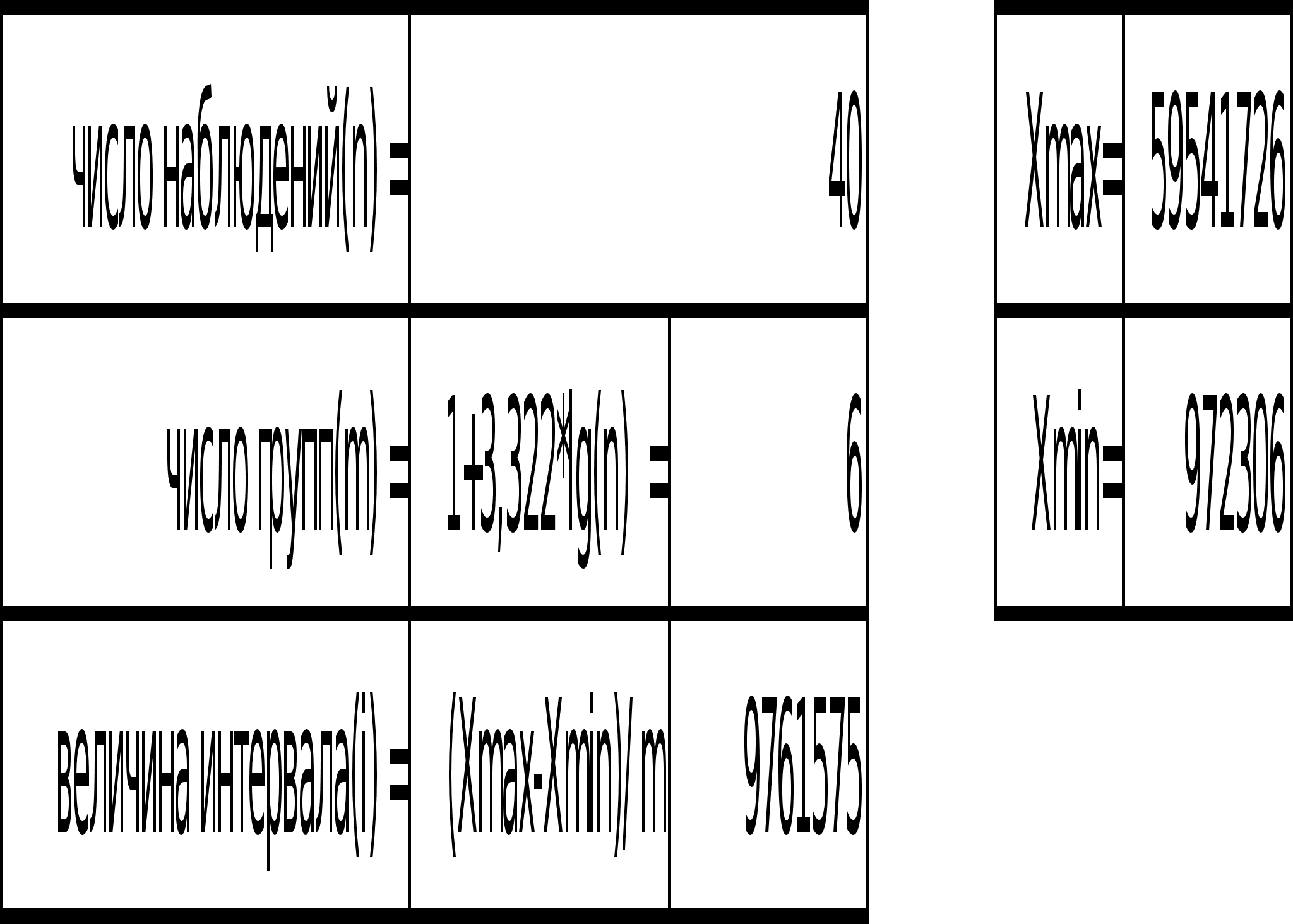
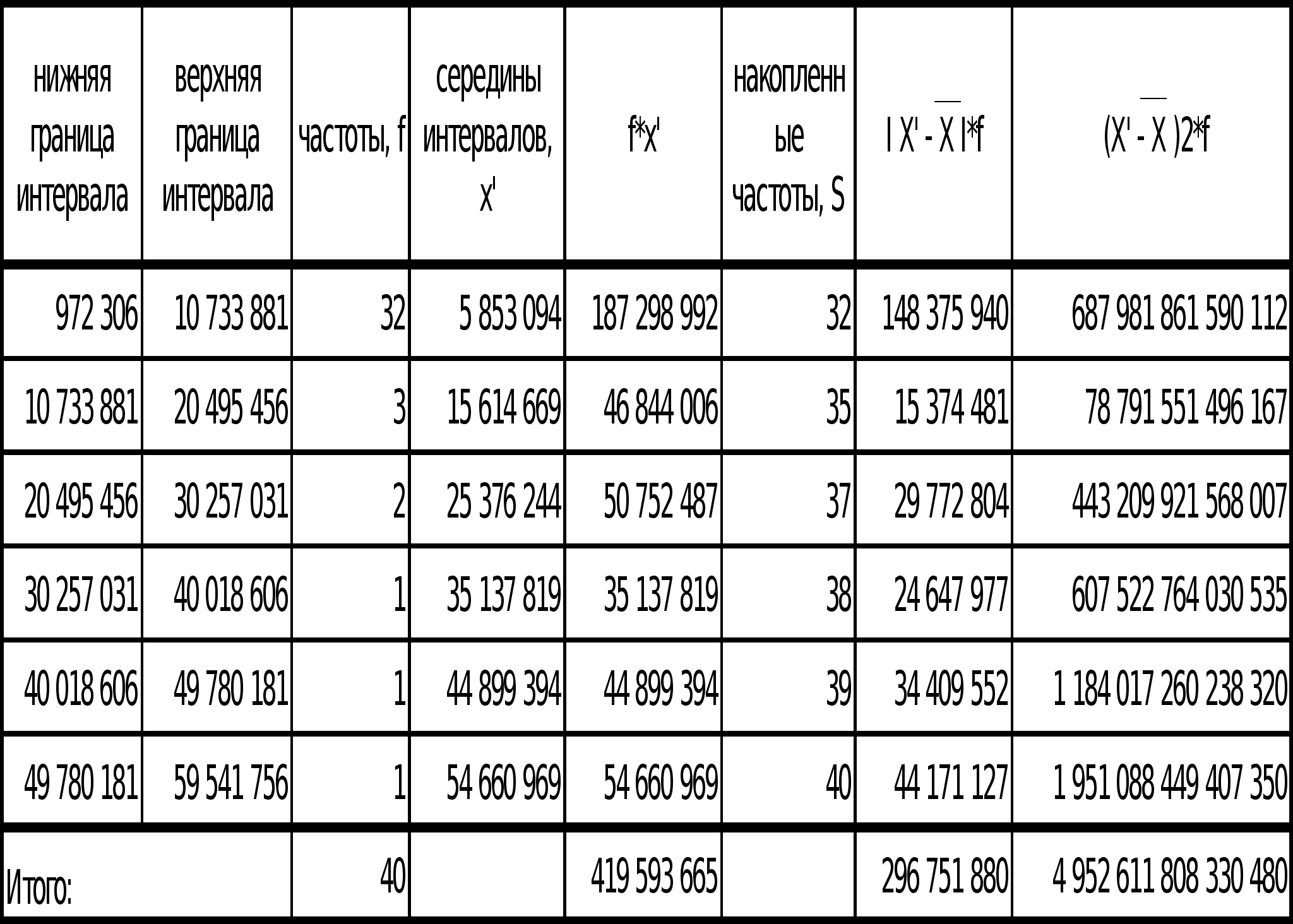
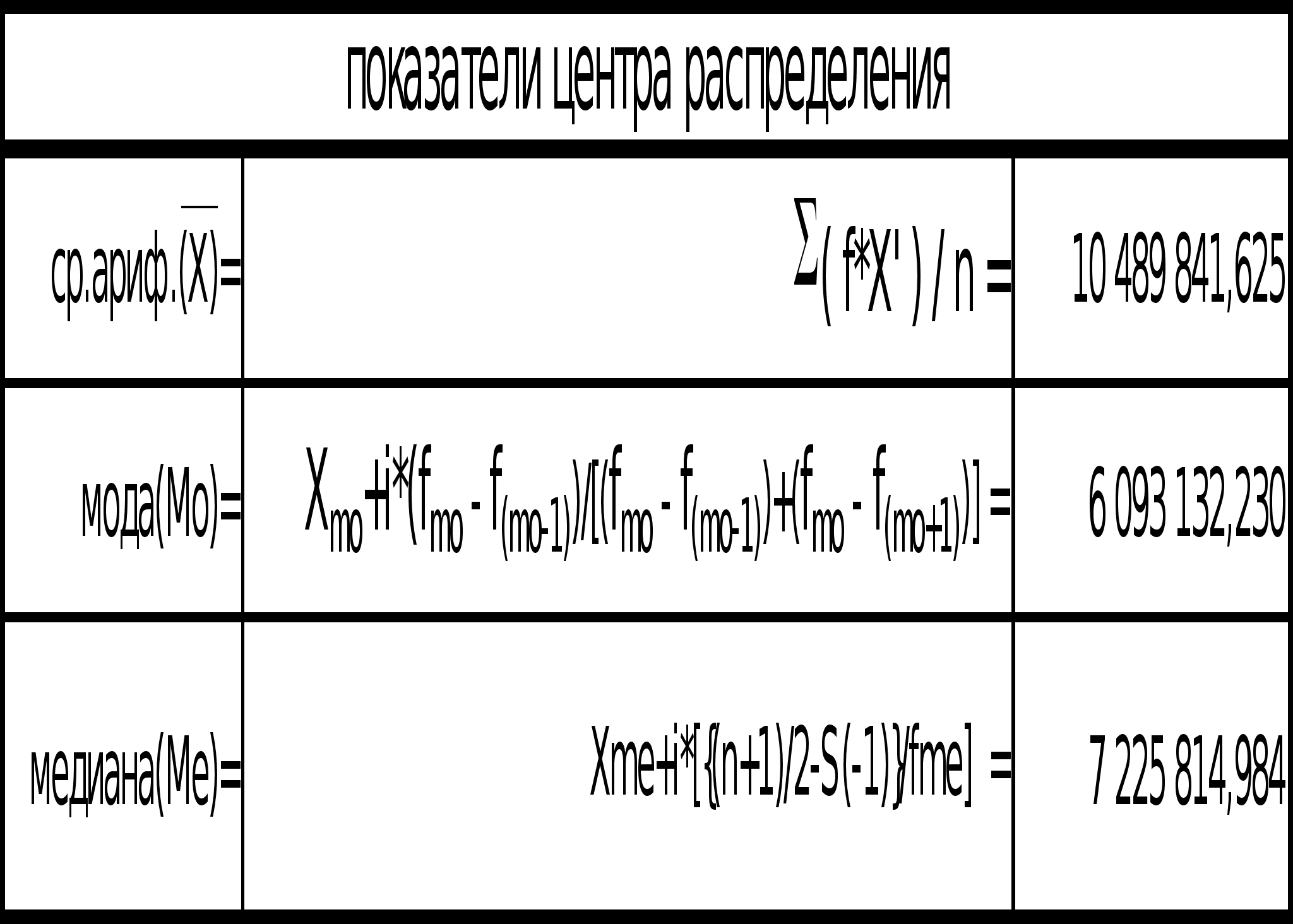

Выводы: Вариация факторного признака (чистых активов) для данной совокупности банков является значительной, индивидуальные значения отличаются в среднем от средней на 11 127 232 тыс. руб., или на 106,08%. Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних. Значение коэффициента вариации (106,08%) свидетельствует о том, что совокупность достаточно неоднородна.
Задание №3
Осуществить проверку первичной информации по факторному признаку на однородность. Исключить резко выделяющиеся банки из массы первичной информации.
Проверка первичной информации по факторному признаку на однородность осуществлялась в несколько этапов по правилу 3 сигм. В результате была получена достаточно однородная совокупность (все единицы лежат в интервале (Xср. - 3 ; Xср. +3), а коэффициент вариации меньше требуемых 33%), которая представлена ниже.
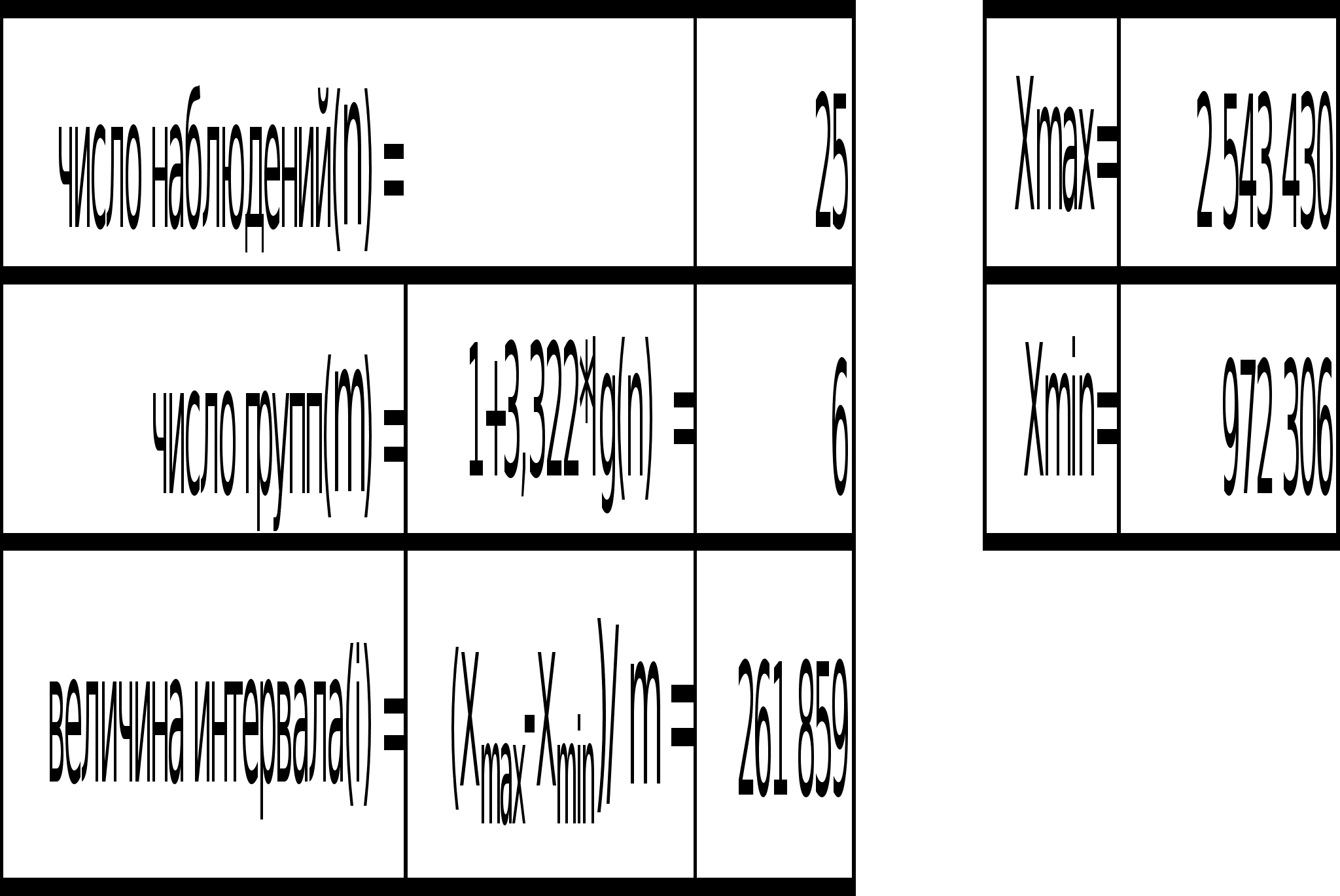
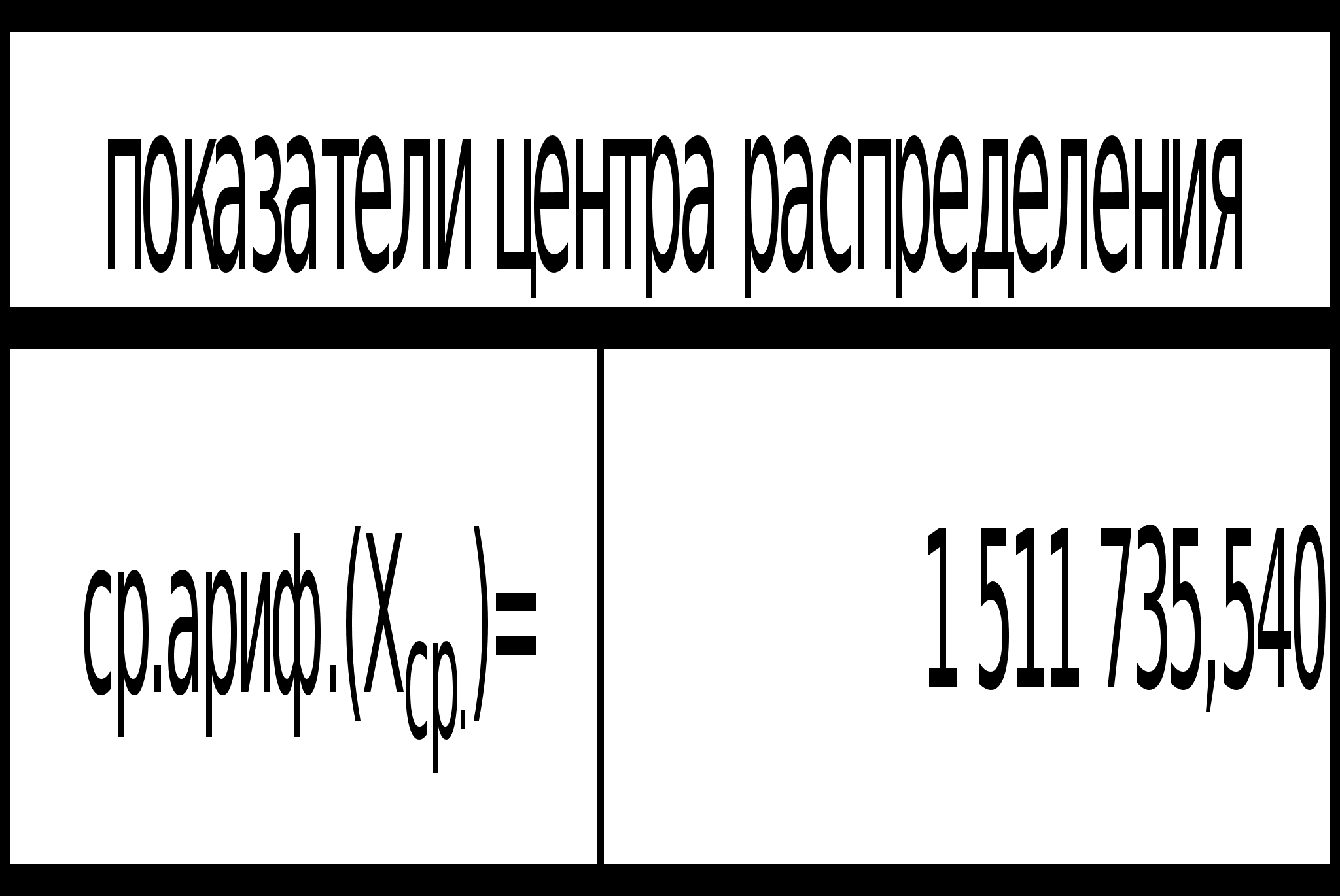


Задание №4
Предполагая, что данные банкам представляют собой 10% простую случайную выборку с вероятностью 0,954 определить доверительный интервал, в котором будет находиться средняя величина факторного признака для генеральной совокупности.
Xср.– Xген.ср. ≤ Xген.ср. ≤ Xср. + Xген.ср.
Где Xср. – средняя выборочной совокупности, Xген.ср. – средняя генеральной совокупности, Xген.ср. – предельная ошибка средней.
Xген.ср. = t * μген.ср.
Где t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки, μген.ср. – величина средней квадратической стандартной ошибки.
Находим t по таблице для удвоенной нормированной функции Лапласа при вероятности 0,954, t = 2.

μген.ср. = ((2*(1- n/N))/n)
Где 2 – дисперсия, n – объем выборочной совокупности, N – объем генеральной совокупности.
N=n/0,1 n=25 N=250 2= 200 301 737 920 Xср. = 1 506 994 (я взял дисперсию и среднюю, рассчитанные по однородной совокупности по не сгруппированным данным)
μген.ср.= 84 917 Xген.ср. = 169 834
Xср.– Xген.ср.= 1 337 161 Xср. + Xген.ср.= 1 676 828
1 337 161 ≤ Xген.ср. ≤1 676 828 - искомый доверительный интервал
В исследовании все размерные величины измеряются тысячами рублей. По причине нехватки места размерность после каждой величины не приводиться.
Задание №5
Проанализировать зависимость результативного признака от факторного признака.
Пункт №1
Установить факт наличия корреляционной зависимости с помощью групповой таблицы и ее направление, дать графическое отображение связи.

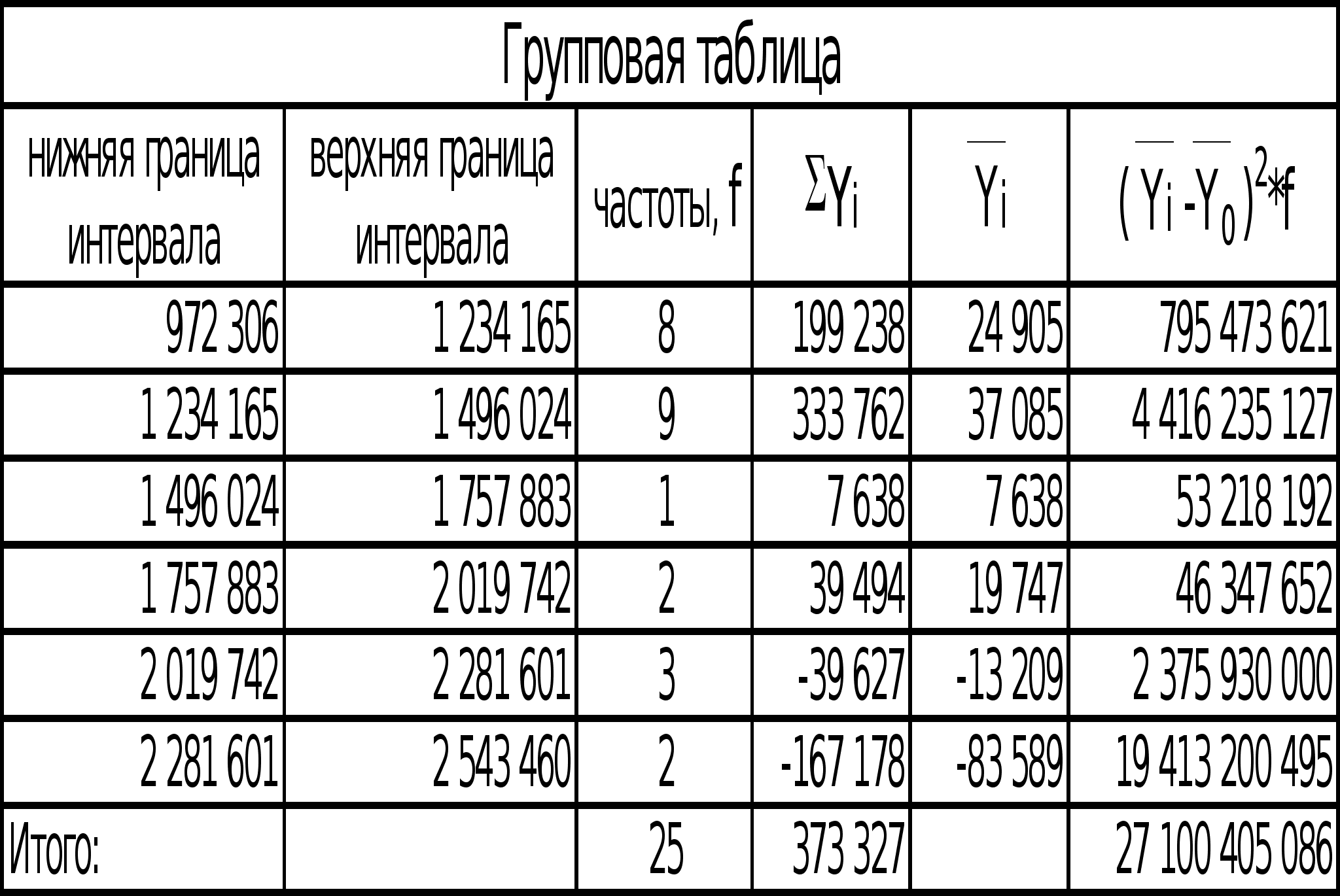
Как видно из данных групповой таблицы, с увеличением величины чистых активов банков уменьшается величина прибыли банков. Эмпирическая линия связи приближается, в общем, к прямой линии. Следовательно, можно предполагать наличие обратной линейной связи.
Пункт №2
Проверить правило сложения дисперсий и сформулировать вывод о степени влияния факторного признака на величину результативного признака.
Нижеследующие показатели были рассчитаны на основе данных групповой таблицы и вспомогательной таблицы (см. приложение 2).
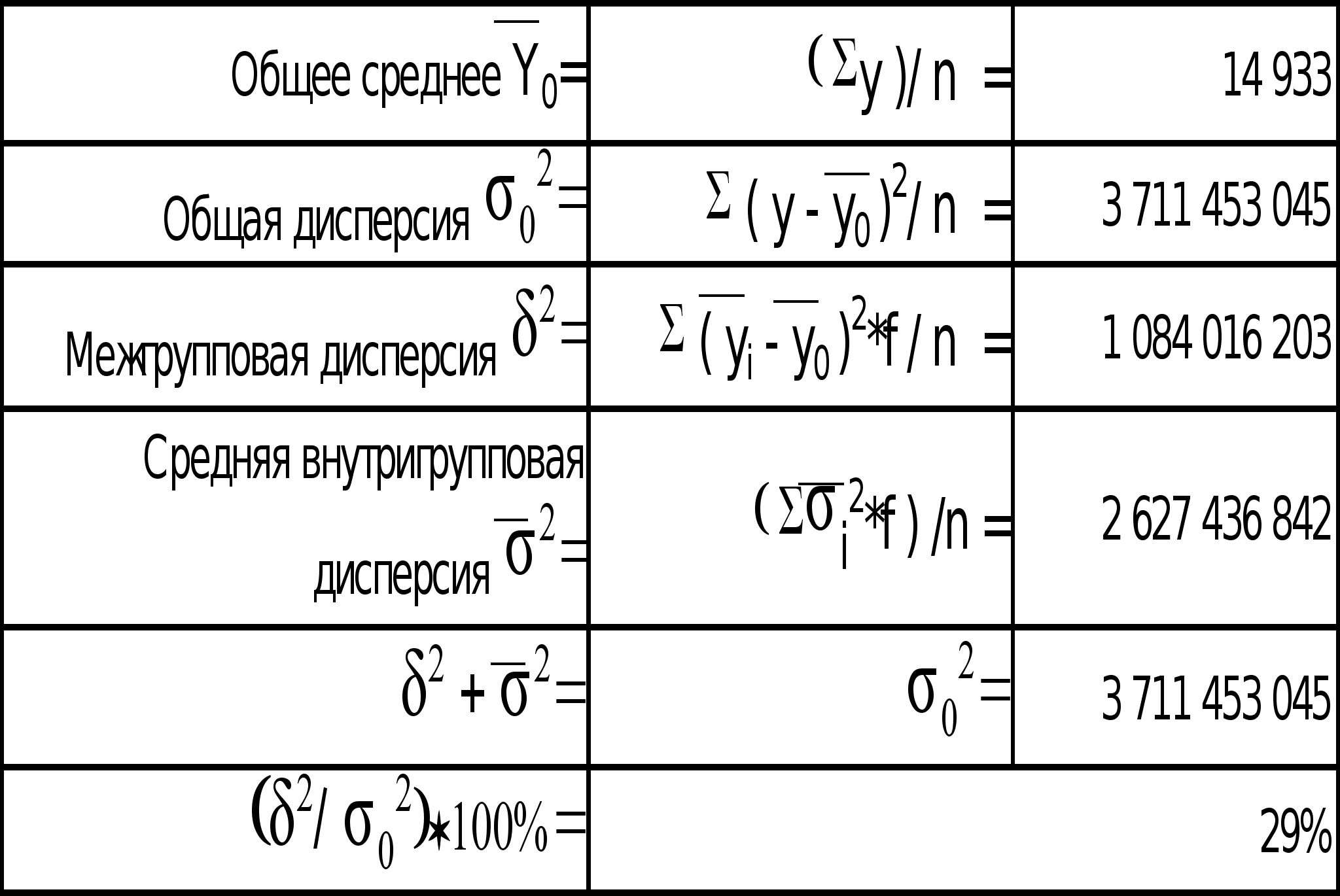
Правило сложения дисперсий проверено: общая дисперсия и сумма межгрупповой и средней внутригрупповой дисперсий совпадают. Из полученных данных можно сделать вывод, что на 29% вариация прибыли банков обусловлена различиями в величине их активов, а на 71% - влиянием прочих факторов. Таким образом, факторный признак (чистые активы банков) имеет среднее влияние на результативный признак (прибыль/убыток).
Пункт №3
Измерить степень тесноты связи с помощью корреляционных отношений, проверить возможность использования линейной функции в качестве формы уравнения связи.
В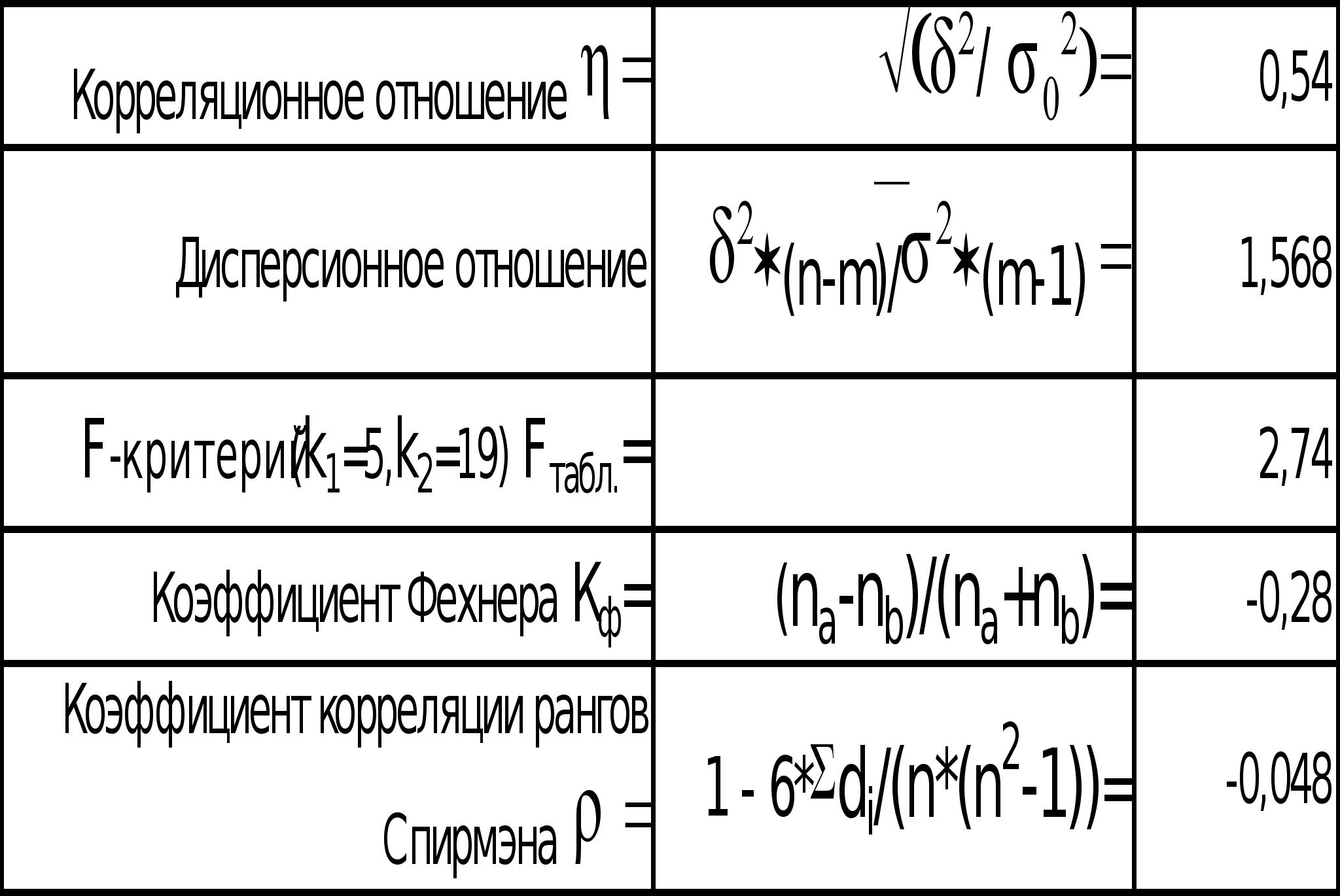
се
нижеследующие
показатели
рассчитаны
с помощью ранее
найденных
данных и данных
вспомогательной
таблицы (см.
приложение
2).
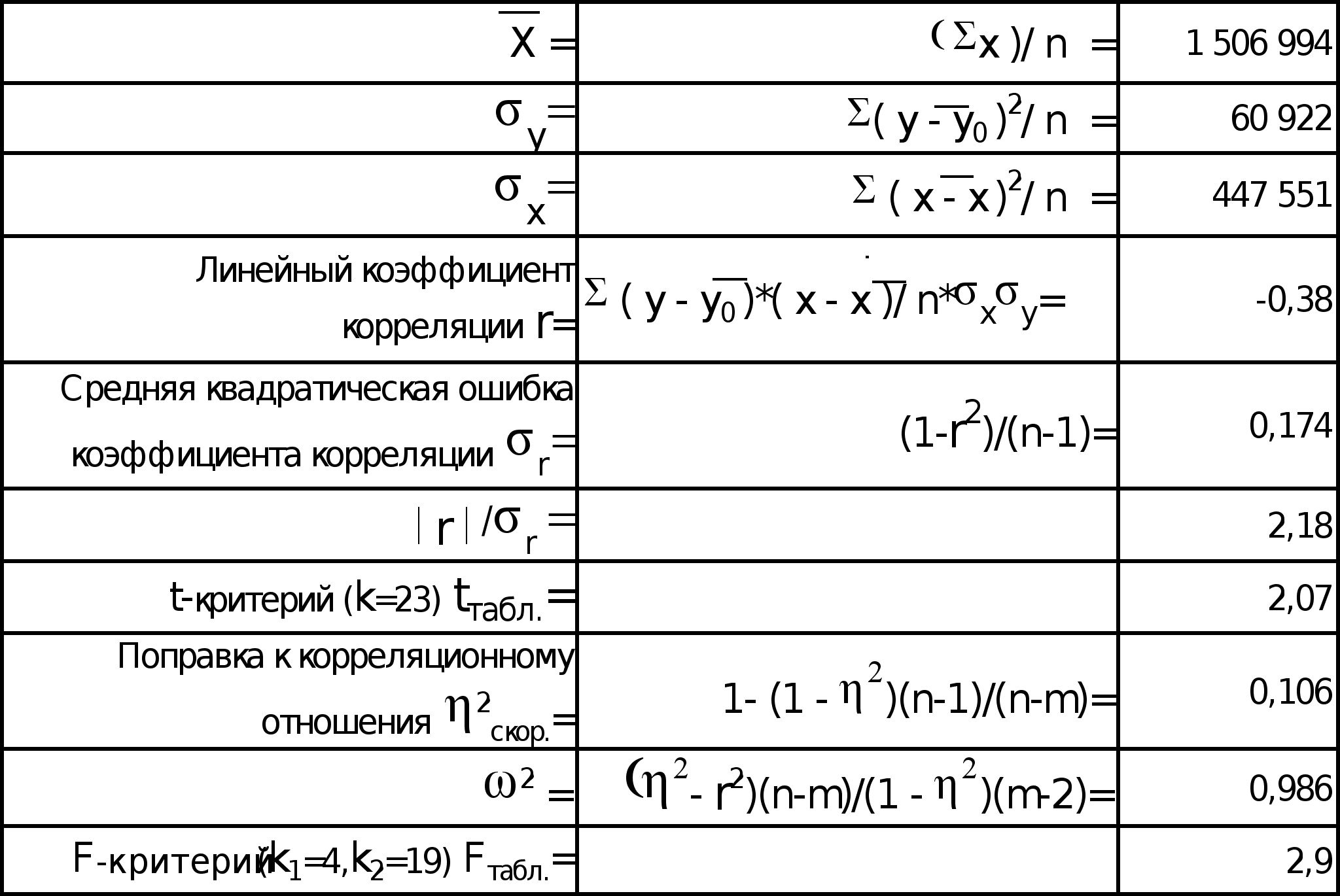
Значение линейного коэффициента корреляции (r = -0,38) свидетельствует об отсутствии тесной связи. Средняя квадратическая ошибка коэффициента корреляции r =0,174, а r /r =2,18, так как r /r > tтабл. (2,18>2,07), то коэффициент корреляции можно считать существенным.
Корреляционное отношение (=0,54) показывает незначительную тесноту связи. Значимость рассчитанного корреляционного отношения оценивается с помощью дисперсионного отношения, равного 1,568. Так как 1,568<2,74 (F-критерий = 2,74), то оценивать тесноту связи с помощью корреляционного отношения нельзя из-за его несущественности.
Рассчитанные здесь же коэффициент Фехнера (Кф= -0,28) и коэффициент корреляции рангов Спирмэна (= -0,048) свидетельствуют о наличие слабой связи. Данные для расчета этих коэффициентов приведены во вспомогательной таблице (см. приложение 2).
Для проверки возможности использования линейной функции определяется величина 2 =0,986, она меньше табличного значения F-критерия (Fтабл.=2,9), поэтому гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается.
Итак, можно утверждать, что между факторным и результативным признаком существует слабая связь. На этом этапе можно было бы остановить исследование, так как очевидно, что был выбран факторный признак, не оказывающий существенного влияния на результативный. И построенная по нему модель связи вряд ли будет качественной и достоверной, и вряд ли будет иметь практическую пользу в экономическом смысле. Но я все же доведу исследование до конца.
Пункт №4
Рассчитать параметры уравнения регрессии, оценить его качество и достоверность, используя среднюю квадратическую ошибку. Дать оценку результатов исследования взаимосвязи в целом.
Определяется модель связи. График эмпирической функции регрессии и величина 2 показывают наличие линейной связи, поэтому используется функция ŷ = a + bx.
b

 =
(xy
– nx
y)/(x2
- n(x)2)=
-0,05
=
(xy
– nx
y)/(x2
- n(x)2)=
-0,05
a
 =
y - bx
= 93 099,35
=
y - bx
= 93 099,35
ŷ = 93 099,35 – 0,05x - модель связи.
Все данные для расчетов содержатся во вспомогательной таблице (см. приложение 2).
Средняя квадратическая ошибка уравнения:
S l
= ((y-ŷ)2/(n-l))
= 58 723, где ŷ
– значения
результативного
признака,
рассчитанные
по уравнению
связи, l –
количество
параметров
уравнения
регрессии.
l
= ((y-ŷ)2/(n-l))
= 58 723, где ŷ
– значения
результативного
признака,
рассчитанные
по уравнению
связи, l –
количество
параметров
уравнения
регрессии.
(Sl / y)100 = (58723/14933)100=393%
Полученное отношение значительно больше 15%, поэтому уравнение достаточно плохо отображает взаимосвязь двух признаков и не может быть использовано в практической работе.
По результатам исследования можно сделать вывод о том, что, хотя теоретически между чистыми активами банков и их прибылями должна существовать прямая тесная связь, на практике же мы показали наличие довольно слабого влияния факторного признака на результативный. Это не совпадение может объясняться рядом причин: во-первых, ошибочными теоретическими предположениями, во-вторых, некачественной, нерепрезентативной выборкой, и, наконец, в-третьих, ошибками, допущенными в исследовании, которых, может быть, не удалось избежать.
| Курс лекций за первый семестр | |
|
Лекции по статистике ЭиУ-228 Новак Артема §1.Понятия статистики, статистическая закономерность и совокупность. 2 §2. Признаки единиц статистической ... Корреляционно-регрессионная модель (КРМ) - такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака. хотя все 5 функций присутствуют в практике КРА, наиболее часто используется линейная зависимость, как наиболее простая и легко поддающаяся интерпретации уравнение линейной ... |
Раздел: Рефераты по статистике Тип: реферат |
| Статистические методы изучения цен и инфляции | |
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Всероссийский Заочный Финансово ... Для изучения вариации используется традиционный методы анализа, основанные на вычислении таких показателей, как размах вариации, среднее линейное отклонение, дисперсия, среднее ... При использовании метода аналитической группировке строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j -й ряда определяется ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Проведение статистического наблюдения | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГЛАЗОВСКИЙ ИНЖЕНЕРНО - ЭКОНОМИЧЕСКИЙ ИНСТИТУТ (филиал) ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ... б) показатели вариации распределения (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации). - выборочная дисперсия (дисперсия признака в выборочной совокупности); |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Определение статистических данных | |
|
Задача 1 За отчетный период имеются данные о розничном товарообороте и издержках обращения по магазинам торга: № магазина Объем розничного ... 1) средний процент норм выработки для всего цеха; 2) среднее линейное отклонение; 3) дисперсию и среднее квадратическое отклонение; 4) коэффициент вариации. Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак Y) и оснащенностью заводов основными производственными фондами (факторный признак ... |
Раздел: Рефераты по экологии Тип: контрольная работа |
| Шпаргалки | |
|
Основные методы стат. анализа. Абсолютные и относительные величины как обобщающие стат. показатели. 1. Понятие, значение и способы измерения ... внутригрупповая - отраж. случ. вариации (часть вариации, возн. под влиянием неучтенных факторов, не зависящая от факторного признака, полож. в основу группировки). = среднему ... Это - корреляционные связи (хар-ся тем, что сред вел. результативного признака измен-ся под воздействием изм-я многих факторных признаков. |
Раздел: Рефераты по статистике Тип: реферат |