Реферат: Статистика
Предмет и метод статистической науки.
1. Предмет статистики. Актуальность и место этой науки в современных условиях.
2. Основные категории статистики.
3. Метод статистики.
4. Задачи статистической науки.
1. Предмет статистики. Актуальность и место этой науки в современных условиях.
Статистика как наука сформировалась в результате слияния двух самостоятельных направлений: немецкого описательного государствоведения и английской политической арифметики. С немецкой стороны основатели: Шлецер, Ахенваль и с английской стороны В. Петти (17-18 века).
Значительный вклад в развитие статистики внес Адольф Кетле (первая половина 19 века). Он соединил в одно две ветви. Во второй половине 19 века - земские статисты.
Начало 20 века – активное внедрение математики в статистику.
Статистика как наука изучает количественную сторону массовых социально-экономических явлений в неразрывной связи с их качеством.
Существуют два вида количественных закономерностей:
- Динамические закономерности – характеризуют однозначную зависимость между причиной и следствием (характерно для естественных наук);
- Статистические закономерности – характеризуют неоднозначные зависимости между причиной и следствием. Они проявляются только как тенденция в массовых явлениях.
Статистика как наука неразрывно связана с другими общественными науками (экономической теорией, финансами и кредитом, экономикой предприятий и т.д.). Она заимствует у этих наук основные экономические категории и опирается на фундаментальные законы этих наук. Со своей стороны статистика предлагает этим наукам целую систему статистических методов и обеспечивает их результатами анализов количественных закономерностей.
Статистика тесно связана с математической статистикой и теорией вероятности, так как сердцевину статистической методологии составляют методы математической статистики.
2. Основные категории статистики.
К числу основных категорий в статистике относятся:
- Признак;
- Статистическая совокупность;
- Единица совокупности;
- Вариация и др.
Признак – это свойство, характерная черта явления, подлежащая статистическому изучению. Признаки классифицируются:
- Качественные (атрибутивные);
- Количественные.
Качественные признаки – выражают существенное неотъемлемое свойство предмета. Противоположные качественным признаки называют альтернативными (например, мужчина – женщина).
Любой качественный признак можно свести к альтернативному (например, студент обучающийся на «отлично» – студент не обучающийся на «отлично»).
Признаки, отдельные значения которых различаются по величине, называются количественными (например, возраст, рост, вес).
Признаки, исходя из их значения для характеристики изучаемого явления делятся на существенные и несущественные. Деление это условное и определяется целью исследования.
Статистическая совокупность – это множество явлений, имеющих один или несколько общих признаков и отличающихся между собой по значениям других признаков.
Каждое отдельное явление, подлежащее статистическому изучению, называется единицей совокупности.
Объективность результатов статистического анализа зависит от степени однородности статистической совокупности. Качественно и количественно однородной считается совокупность, единицы которой имеют общие качественные признаки и близкие по значениям количественные (существенные) признаки.
3. Метод статистики.
В основе статистической методологии лежит диалектический метод.
Диалектика рассматривает явления во взаимосвязи и во взаимозависимости, в динамике, обнаруживает причинно-следственные связи, выделяет главное и второстепенное. Принципы, категории и законы диалектики нашли отражение в конкретных статистических методах.
Статистическим преломлением закона перехода количественных изменений в качественные является закон больших чисел, который лежит в основе статистической методологии. Он гласит, что статистическая закономерность может проявляться с достаточной очевидностью только при массовом статистическом наблюдении, а полученные выводы тем более надежны, чем многочисленней объект исследования.
Доказано, что индивидуальные случайные отклонения от некоторого закономерного для данной совокупности процесса или уровня явления при достаточно большом числе единиц совокупности взаимопогашаются. В результате обнаруживаются причинно-следственные связи или измеряется типичный уровень явлений.
4. Задачи статистической науки.
Задачи статистики можно условно разделить на две группы:
- Постоянные (долговременные);
- Актуальные.
Постоянные задачи:
1) Обеспечить органы управления государством, регионами, отраслями и отдельными предприятиями своевременной полной и достоверной информацией, необходимой для принятия решения;
2) Информировать общественность о явлениях и процессах, происходящих в обществе.
Актуальные задачи формируются исходя из потребности общества и экономики на современном этапе:
Получение объективной информации о деятельности хозяйственных структур с учетом теневого сектора;
Создание автоматизированных баз данных о деятельности текущих хозяйственных структур с возможностью санкционированного доступа к ним для получения информации, необходимой для решения текущих хозяйственных задач;
Прогнозирование развития важных социально-экономических процессов и явлений;
Распространение выборочных обследований во всех секторах общественной и экономической жизни;
Проведение организационно-методологической работы по постепенному переходу на систему национальных счетов.
Организация статистики (как области практической деятельности).
Принципы:
1. Это единая система организации статистики в стране. Это единая система показателей, единая методология их расчета, единая форма отчетности, единые сроки и формы их представления.
2. Соответствие статистических органов государственному устройству и административному территориальному делению страны (то есть Россия, Есть Госкомстат).
3. Увязка в единую систему показателей и форм бухгалтерской и статистической отчетности.
Есть статистическая комиссия ООН, которая осуществляет разработку международной статистической методологии и систем сопоставимых статистических показателей, осуществляет методическую и консультативную деятельность (помощь) органам ООН по вопросам сбора и обработки информации.
Исполнительный орган – статистическое бюро секретариата ООН.
Международный статистический институт – общественная организация, членами которой являются национально-статистические организации и наиболее видные ученые различных стран мира, которые занимаются обобщением научных исследований в различных странах мира.
Системы статистических показателей.
1. Понятие статистического показателя. Сущность системы статистических показателей.
2. Классификация статистических показателей.
1. Понятие статистического показателя. Сущность системы статистических показателей.
Статистический показатель – это качественно определенная переменная величина, количественно характеризующая объект исследования или его свойства. Качественную определенность обеспечивает набор признаков, содержащихся в его определении. Количественная определенность показателя связана с признаками места и времени.
В процессе развития экономики показатели видоизменяются, появляются новые показатели, ликвидируются ранее действующие.
Учитывая сложный взаимосвязный характер социально-экономических явлений, их нельзя охарактеризовать с помощью одного или нескольких разрозненных статистических характеристик. Необходима система взаимоувязанных статистических показателей, представляющих собой статистическую модель экономики и общества.
2. Классификация статистических показателей.
Статистические показатели делятся на однородные группы по различным признакам.
По степени охвата совокупности:
- Индивидуальные;
- Групповые;
- Общие.
В зависимости от того, каким образом статистический показатель характеризует изучаемую совокупность:
- Абсолютные;
- Относительные;
- Средние.
Абсолютные характеризуют масштабы, объем изучаемого явления, различают:
- Натуральные;
- Денежные;
- Трудовые.
Натуральные характеризуют объект в натуральных единицах измерения. Для соизмерения объектов с различными потребительскими свойствами применяют условно натуральные единицы измерения. Пересчет в натуральные показатели осуществляется с помощью коэффициентов, характеризующих отношение фактических потребительских свойств товара к некоторому условному эталону. Иногда пересчет осуществляется применительно к товарам, выпущенным в различных по объему упаковках. Система условно натуральных показателей преобладала в административно-командной экономике.
Денежные – показатели в денежном измерении.
Трудовые – показатели применяются для измерения затрат труда, производительности труда, потерь рабочего времени.
Относительные показатели – представляют соотношение двух и более статистических характеристик, измеряется в коэффициентах, процентах. Виды:
Относительные величины динамики (показывают изменение явления во времени) – это частное отделение текущего отчетного показателя на значение аналогичного показателя в прошлом:
- Базисные;
- Цепные.
Базисные в
качестве базы сравнения один и тот же уровень показателя в прошлом 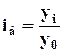 .
.
Цепные –
отношение текущего показателя и показателя предыдущего периода  .
.
Между цепными и базисными относительными величинами динамики существует определенная взаимосвязь. Базисная относительная величина динамики равна произведению цепных относительных величин динамики, взятых в виде коэффициентов за весь анализируемый период.
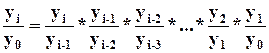
Относительная величина планового задания 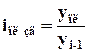 , где
, где ![]() - планируемый уровень,
- планируемый уровень, ![]() - предплановый уровень.
- предплановый уровень.
Относительная величина выполнения плана 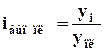 ,
где
,
где ![]() - фактический или отчетный показатель.
- фактический или отчетный показатель.
Произведение относительной величины выполнения плана на относительную величину планового задания дает относительную величину динамики.
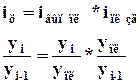
Относительная величина структуры показывает отношение части к целому (доля) 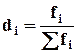 , где
, где ![]() - часть,
- часть, ![]() - целое.
- целое.
Относительная величина координации показывает соотношение частей целого между собой 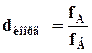 .
.
Относительная величина интенсивности – это соотношение двух разнородных величин ![]() .
.
Чаще всего эти величины используются для характеристики интенсивности производства, потребления какого-либо товара.
Статистическое наблюдение.
1. Понятие статистического наблюдения и его место в статистическом исследовании.
2. Программно-методологические и организационные вопросы статистического наблюдения.
3. Классификация видов статистического наблюдения.
4. Ошибки наблюдения. Пути повышения точности статистического наблюдения.
1. Понятие статистического наблюдения и его место в статистическом исследовании.
Статистическое исследование можно условно разделить на 3 этапа:
1) Непосредственный сбор данных или статистическое наблюдение.
2) Сводка и группировка статистических данных.
3) Статистический анализ, то есть исследование статистических закономерностей, то есть обнаружение взаимосвязей, выявление тенденций развития явления во времени.
Все этапы связаны между собой. Опытный исследователь начинает сбор данных, заранее предполагая, как он их будет обобщать, и какие закономерности могут быть выявлены в результате исследования.
Не всякий сбор данных – это статистическое наблюдение.
Статистическое наблюдение – это научно-обоснованный планомерно-организованный и, как правило, систематический сбор данных о процессах и явлениях общественной жизни.
Информация, полученная в ходе наблюдения должна быть полной, достоверной и отвечающей цели исследования, то есть только то, что нужно.
2. Программно-методологические и организационные вопросы статистического наблюдения.
Основные категории:
1. Объект наблюдения – статистическая совокупность, о которой должны быть собраны интересующие исследователя данные.
2. Единица статистического наблюдения – это составной элемент объекта наблюдения, который подвергается исследованию. Каждая единица должна обладать набором признаков, которые регистрируются в процессе наблюдения.
3. Программа статистического наблюдения – перечень признаков подлежащих регистрации. Программа должна включать наиболее существенные признаки исходя из цели исследования и качественных особенностей объекта наблюдения. Программа должна быть предельно лаконична, так как включение каждого дополнительного признака увеличивает затраты на сбор и обработку информации прямо пропорционально числу единиц наблюдения. Для оставления программы необходимо хорошо знать специфику объекта наблюдения. Составляя программу необходимо одновременно продумать план обработки информации, готовить макеты сводок и статистических таблиц.
4. Для регистрации собранных данных используется формуляр – специально подготовленный бланк, имеющий обычно титульную, адресную и содержательную части. В титульной части содержится наименование обследования, организация, проводящая обследование, и кем и когда утвержден формуляр. Адресная часть содержит наименование, местонахождение объекта исследования и др. реквизиты, позволяющие его идентифицировать. В зависимости от построения содержательной части различают два вида формуляра:
- Бланк-карточка, который составляется на каждую единицу наблюдения;
- Бланк-список, который составляется на группу единиц наблюдения.
У каждого из формуляров есть свои достоинства и недостатки.
Бланк-карточка удобен для ручной обработки, но связан с дополнительными затратами в оформлении титульной и адресной книги.
Бланк-список применяется для автоматической обработки и экономий затрат на подготовку титульной и адресной частей.
Для сокращения затрат на сводку и ввод данных целесообразно использовать машины, читающие формуляры. Вопросы содержательной части формуляра должны быть сформулированы таким образом, чтобы на них можно было получить однозначные, объективные ответы. Лучший вопрос это тот, на который можно ответить «Да» или «Нет». Нельзя включать в формуляр вопросы, на которые трудно или нежелательно отвечать. Нельзя соединять в одной формулировке два разных вопроса. Для оказания помощи опрашиваемых в правильном понимании программы и отдельных вопросов составляются инструкции. Они могут быть как на бланке формуляра, так и в виде отдельной книги.
Чтобы направить ответы респондента в правильное русло применяются статистические подсказы, то есть готовые варианты ответов. Они бывают полные и неполные. Неполные дают респонденту возможность для импровизации.
5. Время наблюдения – продолжительность календарного периода, за который собираются данные об объекте, а так же сезон непосредственного проведения наблюдения.
6. Период проведения наблюдения (регистрации) – время непосредственного сбора данных. Период наблюдения прямо пропорционален сложности объекта наблюдения, динамичности его наблюдения, численности объекта исследования и обширности программы наблюдения.
7. Критический момент – момент времени, по состоянию на который регистрируются данные. Устанавливается при исследовании динамично изменяющегося объекта.
8. Для успешного проведения массового статистического наблюдения составляется организационный план наблюдения. В нем указываются органы наблюдения, время, период и критический момент наблюдения, а так же мероприятия по подготовке и обучению кадров, подготовке бланков формуляров и инструкции, мероприятий по сбору и обработке информации и представлению итогов исследования. Все мероприятия расписаны по срокам с указанием исполнителей, ответственных за мероприятия.
3. Классификация видов статистического наблюдения.
Любое наблюдение, в конечном счете, осуществляется в одной из двух основных формах:
- Статистической отчетности;
- Специально организованное наблюдение.
В условиях административно-командной системы основной формой была отчетность.
Отчетность – система сбора предприятиями, учреждениями и организациями сведений о своей деятельности и обязательно представление их статистическим органами или вышестоящей организации в установленные сроки в виде отчетов, выполненных по утвержденной форме.
Источником информации для отчетности служат данные первичного и бухгалтерского учета. Первичный учет – регистрация фактов по мере их возникновения.
Различают отчетность:
- Общегосударственная отчетность собирается органами общегосударственной статистики по всем хозяйственным структурам не зависимо от формы их собственности и отраслевой принадлежности;
- Ведомственная отчетность собирается для нужд управления в рамках министерств или других многофилиальных организаций.
Так же различают:
- Общая отчетность содержит показатели, характерные для всех хозяйственных структур независимо от их отраслевой или ведомственной принадлежности;
- Специализированная отчетность содержит показатели типичные для конкретной отрасли или вида деятельности.
По времени наблюдения различают:
- Годовая отчетность содержит данные за год;
- Текущая отчетность – квартальная, полугодовая, месячная и т.д.
Для рыночной экономики основной источник информации это специально организованное наблюдение.
По времени проведения различают:
· Текущее наблюдение;
· Непрерывное наблюдение ведется за состоянием и движением населения, за деятельностью предприятий;
· Прерывное наблюдение может быть:
~ Периодическое наблюдение проводится через относительно равные промежутки времени, повторяющееся;
~ Единовременное наблюдение – по мере необходимости.
По степени охвата совокупности бывает:
· Сплошное наблюдение – охватывает всю совокупность (генеральную совокупность);
· Несплошное наблюдение – исследование части совокупности, но с обязательным распространением результатов на всю совокупность, может быть:
~ Выборочный метод – наиболее разработанный и распространенный метод, при котором отбор из генеральной совокупности осуществляется таким образом, чтобы у каждой единицы были равные шансы попасть в выборку;
~ Метод основного массива – это выбор для исследования наиболее представленной части генеральной совокупности;
~ Монографическое наблюдение – это выбор и детальное исследование наиболее типичной единицы наблюдения.
Данные исследования могут быть получены путем:
· Непосредственного наблюдения – данные регистрируются непосредственным наблюдателем на месте их возникновения;
· Документальное наблюдение – источником являются документы;
· Опрос – наблюдение, при котором регистрируются устные и письменные ответы респондента.
По способу организации различают:
· Экспедиционный способ наблюдения, это непосредственное наблюдение, осуществляемое специалистами или специально обученными лицами, наиболее дорогой и трудоемкий способ;
· Самоисчисление или саморегистрация – данные заполняются респондентом, а специалист его консультирует и осуществляет последующий контроль;
· Анкетный способ – предполагает самостоятельное заполнение респондентами распространенных между них анкет. Наиболее неточный способ. Эффективен только тогда, когда сами респонденты заинтересованы в анкетировании;
· Корреспондентный способ – предусматривает сбор и регистрацию информации об объекте наблюдения специально созданной сетью корреспондентов;
· Явочный способ – способ, при котором опрашиваемый сообщает информацию, явившись в органы ее регистрации.
4. Ошибки наблюдения. Пути повышения точности статистического наблюдения.
Ошибки наблюдения по источникам и причинам возникновения можно разделить на две группы:
1) Ошибки регистрации;
2) Ошибки репрезентативности.
Ошибки регистрации связаны с неправильным установлением и/или отражением фактов в процессе наблюдения, могут быть:
· Случайные ошибки регистрации, которые возникают из-за невнимательности или усталости регистратора или респондента;
· Систематические ошибки регистрации, которые бывают:
~ Преднамеренные ошибки, которые возникают из-за нежелания респондента дать объективную информацию;
~ Непреднамеренные систематические ошибки возникают из-за недостаточной квалификации регистраторов.
Ошибки репрезентативности возникают при несплошном наблюдении из-за несоответствия составов генеральной и отобранной совокупностей, бывают:
· Случайные ошибки, которые характерны для выборочного метода и обусловлены волею случая;
· Систематические ошибки возникают из-за неправильно проведенного отбора.
Случайные ошибки поддаются расчету с помощью специальных методов, систематические не поддаются.
Для предотвращения ошибок применяются:
· Логический контроль – проверка логической совместимости собранных данных;
· Арифметический контроль – подсчет и проверка итогов по строкам и столбцам, проверка значений расчетных показателей.
Сводка. Группировка.
1. Понятие и назначение статистической сводки.
2. Сущность и понятие статистической группировки.
3. Определение интервалов.
4. Виды статистических группировок.
5. Понятие и виды статистических таблиц.
1. Понятие и назначение статистической сводки.
Сводка – это второй этап статистического исследования, собранные и проверенные данные должны систематизироваться таким образом, чтобы можно было обнаружить взаимосвязи между признаками, тенденции развития явления во времени или описать характер статистических распределений.
Сводку понимают в узком и широком смысле. Сводка в широком смысле касается содержательной стороны этого процесса, это распределение собранной информации по группам и подгруппам, подбор системы показателей, характеризующих эти группы и подгруппы, составление макетов статистических таблиц. Эта сторона обработки информации тесно связана со спецификой предмета исследования.
Сводка в узком смысле это технические операции по распределению данных по группам, по распределению их по таблицам и подсчет итогов.
Сводка бывает:
- Централизованная сводка – сбор информации осуществляется на местах и собранные данные передаются в центр для обработки. Достоинства: возможность более глубокого анализа без потерь информации, применение мощной вычислительной техники и современного программного обеспечения, участие высококвалифицированных специалистов. Недостатки: на местах не могут воспользоваться в полной мере результатами анализа, снижается оперативность обработки.
- Децентрализованная сводка – обработка информации на местах с передачей сводных данных в вышестоящие организации. В этом случае часть первичной информации и аналитических возможностей утрачивается, но ускоряется процесс обработки.
В современных условиях при наличии сканирующей, вычислительной техники, программного обеспечения - техническая сторона сводки утрачивает первостепенное значение, появляется возможность для более глубокого анализа.
2. Сущность и понятие статистической группировки.
Группировка – объединение единиц статистической совокупности в количественные однородные группы в соответствии со значениями одного или нескольких признаков.
Один из наиболее распространенных и древних статистических методов (применяется более 300 лет). Группировки составляются:
- Для выявления социально-экономических типов явлений;
- Для отражения структуры совокупности;
- Для обнаружения взаимосвязи социально-экономических явлений.
Бывают:
- Группировки по количественным признакам;
- Группировки по качественным признакам.
3. Определение интервалов.
Требования при определении величины интервала:
1. Интервалы должны выбираться таким образом, чтобы состав выделенных групп был количественно и качественно однороден, но группы различались между собой.
2. Интервалы не должны быть слишком малыми, так как при этом образуется большое число малочисленных групп, по которым нельзя обнаружить закономерности, а внутри групп не действует закон больших чисел.
3. Интервалы не должны быть слишком большими, так как это приводит к образованию неоднородных групп, искажению истинного характера, распределения и взаимосвязи.
4. Считается, что величина интервалов и число выделяемых групп зависят от численности статистической совокупности и вариаций изучаемого признака, чем больше численность и выше колеблемость исходных данных, тем больше групп мы должны и можем выделить.
Группировка осуществляется поэтапно. Вначале определяется примерное число групп, затем величина интервала. Строится 1й вариант группировки, потом при необходимости уточняется. Для определения числа групп может применяться формула Стерджесса:
![]() ,
где N - численность совокупности, r – число групп.
,
где N - численность совокупности, r – число групп.
Величина интервала определяется по формуле: ![]() , где xmax, xmin –
соответствующие максимальное и минимальное значения признаков совокупности, с
– величина интервала. Полученный результат округляется.
, где xmax, xmin –
соответствующие максимальное и минимальное значения признаков совокупности, с
– величина интервала. Полученный результат округляется.
Равные интервалы группировки применяются для однородных совокупностей, а для социально-экономических явлений чаще применяются неравноинтервальные группировки.
Если крайнее значение единиц совокупности значительно отличается по величине от остальных, применяются группировки с открытыми границами интервалов.
Пример: Группировка по уровню среднемесячного дохода на одного члена семьи.
| Среднедушевой доход, руб. | Число семей, в % к итогу |
| До 700 | 25,0 |
| 701-1500 | 19,1 |
| 1501-500 | 50,7 |
| Свыше 5000 | 5,2 |
| Итого | 100 |
Первый интервал с открытой нижней границей, последний интервал с открытой верхней границей. Величина первого интервала принимается равной величине следующего за ним интервала (не более чем). Величина последнего интервала с открытой верхней границей принимается равной величине предпоследнего интервала.
4. Виды статистических группировок.
В соответствии с задачами группировки подразделяются на:
- Типологические группировки служат для выявления социально-экономических типов явлений.
- Структурные группировки предназначены для выявления структуры совокупности, то есть соотношение между частями целого.
Пример: Группировка рабочих цеха по профессии.
| Профессия |
Численность в % к итогу |
| Токари | 35 |
| Фрезеровщики | 10 |
| Слесари | 40 |
| Прочие | 15 |
| Итого | 100 |
- Аналитические группировки позволяют установить, в какой мере изменение значений одного из признаков (признак-фактор), влияя на вариацию другого (результативного) признака.
Пример: Аналитическая группировка магазинов по величине торговой площади.
|
Группа магазинов с торговой площадью, кв. м |
Число магазинов |
Средний уровень издержек, в % к товарообороту |
| До 200 | 12 | 28,7 |
| От 200 до 400 | 23 | 24,5 |
| От 400 до 600 | 17 | 21,3 |
| Свыше 600 | 15 | 18,7 |
Группировка показывает обратную связь между торговой площадью и издержками магазина в расчете на 100 руб. товарооборота.
- Комбинационные группировки применяются в тех случаях, когда для выявления социально-экономического типа недостаточно одного признака. Комбинационные группировки строятся по иерархической системе, когда группы, выделенные по одному признаку, делятся на подгруппы по значениям других признаков.
Пример: Группировка промышленных предприятий по стоимости основных фондов и среднесписочной численности работников.
|
Группы предприятий по стоимости основных фондов, тыс. руб. |
В том числе с численностью рабочих, чел. |
Число предприятий |
| До 500 | До 50 | 7 |
| 51-100 | 4 | |
| 101-500 | 2 | |
| 501-1000 | - | |
| Свыше 1000 | - | |
| 501-1000 | До 50 | 1 |
| 51-100 | 3 | |
| 101-500 | 4 | |
| 501-1000 | 4 | |
| Свыше 1000 | - |
Построение комбинационной группировки требует многочисленной совокупности, в противном случае при образовании большого числа групп появляются малочисленные и пустые интервалы.
Недостаток комбинационной группировки: устраняет многомерные группировки, появившиеся в 60-70 годах прошлого века.
- Многомерные группировки предназначены для выделения групп однородных по совокупности признаков.
Для решения этой задачи применяются различные математические алгоритма, общая идея которых заключается в разбиении исходного множества на непересекающиеся подмножества (кластеры, таксоны), элементы, которые либо подобны друг другу, либо наименее удалены друг от друга в N-мерном пространстве признаков.
5. Понятие и виды статистических таблиц.
Статистическая таблица – наиболее рациональная и распространенная форма представления статистических данных. Существует примерно 300 лет.
Любая статистическая таблица состоит из ряда элементов.
Пересечение строк и столбцов называется скелетом таблицы. Если включить в скелет таблицы заголовки граф и строк, получим макет таблицы, который отражает основную цель ее построения. Макеты таблиц обязательно составляются на этапе подготовки программы статистической сводки, для уточнения программ и схемы обработки собранной информации. По аналогии с грамматикой, содержание таблицы делится на подлежащее и сказуемое. Подлежащим таблицы считается объект исследования, сказуемым – перечень признаков, характеризующих объект исследования.
В зависимости от характера разработки подлежащего таблицы делятся на:
- Простые таблицы;
- Групповые таблицы;
- Комбинационные таблицы.
В подлежащем простых таблиц содержатся либо перечень единиц наблюдений, либо показатели времени, либо отдельные территории. В зависимости от этого различают:
- Перечневые простые таблицы;
- Хронологические простые таблицы;
- Территориальные простые таблицы.
Подлежащее групповых таблиц содержит группировку по одному признаку, а комбинационных по нескольким признакам.
Сказуемое таблица может быть:
- Простым – содержит перечень признаков, характеризующих подлежащее;
- Комбинированным – содержит группировку признаков, характеризующих подлежащее.
При составлении таблиц рекомендуется соблюдать ряд общепринятых требований:
1. Таблица не должна быть слишком громоздкой, перенасыщенной показателями, лучше построить 2-3 простых таблиц;
2. Общий заголовок таблицы должен лаконично отображать ее содержание, определять место и время, к которому относятся статистические данные;
3. Территориальные единицы в подлежащем даются в алфавитном порядке, а даты в хронологическом порядке;
4. Кратко формулируются заголовки граф и строк, и в них указываются единицы измерения. Общая единица измерения указывается в общем заголовке;
5. Все показатели таблицы даются с одинаковой точностью, если значение показателя не имеет смысла ставится «х», если отсутствует «-», если данные не известны «….», если величина очень мала «0,0…»;
6. Таблицы могут сопровождаться примечаниями со ссылками на источники информации и методы расчета данных.
Ряды распределения.
1. Понятие и виды рядов распределения.
2. Частотные характеристики рядов распределения.
3. Графическое изображение рядов распределения.
1. Понятие и виды рядов распределения.
Ряд распределения – упорядоченная совокупность значений признака.
Бывают ряды распределения:
- Качественных признаков (атрибутивные ряды распределения);
- Количественных признаков (вариационные ряды распределения).
Любой ряд состоит из 2 видов элементов:
- Вариантов ряда (значения признака);
- Его частотной характеристики.
Атрибутивные ряды характеризуют распределение качественных признаков, например распределение рабочих по полу, профессии, образованию.
Вариационные ряды обычно упорядочиваются в соответствии с увеличением значений количественного признака.
Они бывают дискретные и интервальные. Варианты дискретного ряда – это дискретно прерывно изменяющиеся значения признак, обычно это результат подсчета.
Пример: Распределение мужских костюмов, реализованных магазинами за месяц по размерам.
|
Размер костюма |
Число проданных костюмов, шт. |
| 44 | 12 |
| 46 | 31 |
| 48 | 127 |
| 50 | 215 |
| 52 | 164 |
| 54 | 91 |
| 56 | 47 |
| 58 | 28 |
| 60 | 11 |
| Итого | 726 |
Интервальные ряды предназначены для анализа распределения непрерывно изменяющегося признака, значение которого чаще всего регистрируется путем измерения или взвешивания. Варианты такого ряда – это группировка.
Пример: Распределение покупок в продуктовом магазине по сумме.
| Сумма покупки, руб. | Число покупок |
| До 50 | 37 |
| 50,1-100 | 78 |
| 100,1-150 | 111 |
| 150,1-200 | 105 |
| 200,1-250 | 68 |
| Свыше 250 | 49 |
| Итого | 448 |
Если в атрибутивных и дискретных вариационных рядах частотная характеристика относится непосредственно к варианту ряда, то в интервальных к группе вариантов.
Поскольку в расчетах группа должна быть представлена обычно одним вариантом, в качестве этого варианта условно выбирается середина каждого интервала.
Такой подход возможен исходя из гипотезы о равномерном распределении вариантов внутри каждого интервала.
Интервальный ряд, таким образом, преобразуется в дискретный, варианты которого – это середины соответствующих интервалов. Середины закрытых интервалов определяются как полусумма нижней и верхней границы интервала.
Середина первого интервала с открытой нижней границей
определяется по формуле ![]() , где xВ1 – верхняя граница первого интервала, c2 – второй интервал.
, где xВ1 – верхняя граница первого интервала, c2 – второй интервал.
Середина последнего интервала определяется по формуле ![]() , где xнn – нижняя
граница n-го интервала, сn-1 – предыдущий интервал (предпоследний).
, где xнn – нижняя
граница n-го интервала, сn-1 – предыдущий интервал (предпоследний).
2. Частотные характеристики рядов распределения.
Различают абсолютные и относительные частотные характеристики.
Абсолютная характеристика – частота, показывает, сколько раз встречается в совокупности данный вариант ряда. Достоинство частоты – простота, недостаток – невозможность сравнительного анализа рядов распределения разной численности.
Для подобных сравнений применяют относительные частоты или частости, которые рассчитываются по формуле:
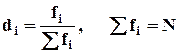 ,
где N – численность
совокупности.
,
где N – численность
совокупности.
Это относительная величина структуры (по форме).
Сумма частостей равна 1.
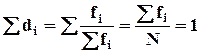
Если частости выражены в процентах или в промилях их суммы равны соответственно 100 или 1000.
В неравных интервальных рядах распределения частотные характеристики зависят не только от распределения вариантов ряда, но и от величины интервала при прочих равных условиях расширение границ интервала приводит к увеличению наполненности групп.
Для анализа рядов распределения с неравными интервалами используют показатели плотности:
Абсолютная плотность:  , где fi – частота, ci - величина интервала – показывает, сколько единиц в
совокупности приходится на единицу величины соответствующего интервала.
Абсолютная плотность позволяет сопоставлять между собой насыщенность различных
по величине интервалов ряда. Абсолютные плотности не позволяют, однако,
сравнивать ряды распределения разной численности.
, где fi – частота, ci - величина интервала – показывает, сколько единиц в
совокупности приходится на единицу величины соответствующего интервала.
Абсолютная плотность позволяет сопоставлять между собой насыщенность различных
по величине интервалов ряда. Абсолютные плотности не позволяют, однако,
сравнивать ряды распределения разной численности.
Для подобных сравнений применяются относительные
плотности: 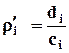 , где di – частости
(доли), ci - величины соответствующих интервалов – показывает,
какая часть (доля) совокупности приходится на единицу величины соответствующего
интервала.
, где di – частости
(доли), ci - величины соответствующих интервалов – показывает,
какая часть (доля) совокупности приходится на единицу величины соответствующего
интервала.
3. Графическое изображение рядов распределения.
Графическое изображение рядов распределения дает наглядное представление о закономерностях распределения.
Дискретный ряд изображается на графике в виде ломаной линии – полигона распределения.
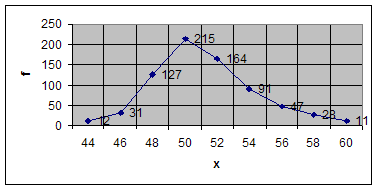
Интервальные ряды изображаются в виде гистограмм распределения (то есть столбиков диаграмм) при этом основанием каждого прямоугольника служит величина соответствующего интервала, а высотой его частотная характеристика.
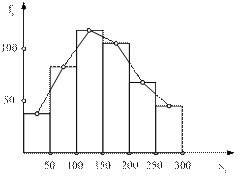
Любая гистограмма может быть преобразована в полигон распределений, для этого необходимо соединить между собой отрезками прямой вершины ее прямоугольников.
При графическом изображении рядов с неравными интервалами по оси ординат откладываются абсолютные или относительные плотности.
Поскольку  , то
, то ![]() и площадь каждого
прямоугольника такой гистограммы равна частоте соответствующего интервала, а
общая площадь гистограммы равна численности совокупности.
и площадь каждого
прямоугольника такой гистограммы равна частоте соответствующего интервала, а
общая площадь гистограммы равна численности совокупности.
![]()
Если на графике откладываются относительные плотности 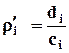 , то
, то ![]() , то площадь каждого
прямоугольника равна частости соответствующего интервала, а общая площадь
гистограммы равна 1.
, то площадь каждого
прямоугольника равна частости соответствующего интервала, а общая площадь
гистограммы равна 1.
При равноинтервальной группировке графики распределений составленные по частотам, частостям и плотностям, подобны друг другу.
Графики распределений с неравными интервалами различаются в зависимости от того, по какой частотной характеристике они строятся.
Для характеристики рядов распределения применяют так же графики накопленных частот или куммуляты.
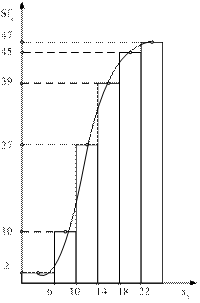
Пример: Распределение хозяйств по урожайности зерновых.
|
Урожайность, га |
Число хозяйств,
|
Накопленная частота,
|
| До 6 | 2 | 2 |
| 6-10 | 8 | 10 (2+8) |
| 10-14 | 17 | 27 (10+17) |
| 14-18 | 12 | 39 (12+27) |
| 18-22 | 6 | 45 (6+39) |
| Свыше 22 | 2 | 47 (25+2) |
| Итого | 47 |
Накопленная частота – это сумма частот данного и всех предшествующих интервалов.
Куммулята позволяет определить, какая часть совокупности обладает значениями изучаемого признака не превышающими заданного предела, а какая часть – наоборот – превышает этот предел.
Средние величины.
1. Понятие средней величины.
2. Средняя арифметическая величина и ее расчет прямым способом.
3. Свойства средней арифметической величины.
4. Практическое использование свойств средней арифметической.
5. Степенные средние.
6. Мода и процентили.
1. Понятие средней величины.
Уровень любого показателя формируется под воздействием существенных закономерных для данного явления, а так случайных причин. Поскольку случайных причин множество и их действия носят стихийный разнонаправленный характер, необходимо нивелировать (устранить) результат такого воздействия, для того чтобы определить типичный закономерный для данных условий места и времени уровень показателей. Таким уровнем является средняя величина.
Средняя – это обобщающая характеристика количественно и качественно однородной совокупности в определенных условиях. Среднее определяется по какому-либо признаку. Среднее проявляется в результате действия закона больших чисел, когда в массовых совокупностях индивидуальные отклонения от типичного уровня взаимопогашаются. Среднее позволяет заменить множество значений показателей одним типичным, что значительно упрощает последующий анализ явлений.
Средняя является объективной характеристикой только для однородных явлений. Средние для неоднородных совокупностей называются огульными и могут применяться только в сочетании с частными средними однородных совокупностей.
Средняя применяется в статистических исследованиях для оценки сложившегося уровня явления, для сравнения между собой нескольких совокупностей по одному и тому же признаку, для исследования динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений.
Средние широко применяются в различных плановых, прогнозных, финансовых расчетах.
2. Средняя арифметическая величина и ее расчет прямым способом.
Средняя арифметическая – наиболее распространенный на практике вид средних. Различают 2 вида арифметических средних:
- Невзвешенную (простую);
- Взвешенную.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по
формуле: ![]() , где
, где ![]() -
сумма вариантов, N – их число – применяется обычно для совокупностей
численностью N
-
сумма вариантов, N – их число – применяется обычно для совокупностей
численностью N![]() 15.
15.
Для массовых статистических совокупностей
рассчитывается взвешенная средняя арифметическая по формуле: 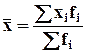 , где
, где ![]() - частоты.
- частоты.
Пример: Расчет средней выработки рабочими токарного цеха.
|
Количество деталей, изготовленных рабочим за смену, шт. |
Число рабочих, чел., |
|
Объем производства,
|
| До 300 | 3 | 290 | 870 |
| 300-320 | 9 | 310 | 2790 |
| 320-340 | 15 | 330 | 4950 |
| 340-360 | 12 | 350 | 4200 |
| 360-380 | 6 | 370 | 2220 |
| Свыше 380 | 6 | 390 | 2340 |
| Итого | 51 | 17370 |
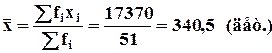
Из таблицы:
1. Средняя величина всегда тяготеет к вариантам с наибольшими частотами.
2. Средняя величина может не совпадать ни с одним из вариантов дискретного ряда.
3. Средняя величина находится внутри интервала значений вариантов ряда.
Сумма ![]() помимо
чисто математического, как правило, имеет смысловое значение, наличие
смыслового значения – один из способов проверки правильности выбора средней.
помимо
чисто математического, как правило, имеет смысловое значение, наличие
смыслового значения – один из способов проверки правильности выбора средней.
Даже если варианты ряда представлены целыми числами, среднее может быть смешанным числом, иногда такой результат логически неправомерен. В этом случае его надо округлять, переводить в проценты или в промили.
3. Свойства средней арифметической величины.
Свойства средней важны для понимания механизма расчета этого показателя, а так же для разработки ряда более сложных статистических методик.
Свойства:
1.
Если из всех вариантов ряда
вычесть или ко всем вариантам добавить постоянное число, то средняя
арифметическая соответственно уменьшится или увеличится на это число. ![]() .
.
2.
Если все варианты ряда умножить
или разделить на постоянное число, то средняя арифметическая соответственно увеличится
или уменьшится в это число раз. 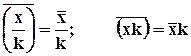 .
.
3.
Если все частоты увеличить или
уменьшить в постоянное число раз, то средняя от этого не изменится. 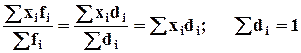 .
.
4.
Сумма отклонений всех вариантов
ряда от средней арифметической равна 0. (Нулевое свойство средней). ![]() .
.
5.
Общая средняя совокупности равна
средней арифметической из частных средне взвешенных по объемам частных
совокупностей. 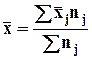 , где
, где ![]() - средняя арифметическая частных групп,
- средняя арифметическая частных групп, ![]() - численность соответствующих групп,
- численность соответствующих групп, ![]() - общая средняя.
- общая средняя.
6. Сумма квадратов отклонений всех вариантов ряда от средней арифметической меньше суммы квадратов их отклонений от любого другого постоянного числа.
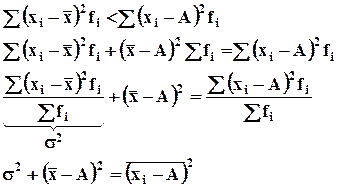
Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии плюс квадрат разности между средней и этим числом А.
Данное свойство положено в основу метода наименьших квадратов, который широко применяется в исследовании статистических взаимосвязей.
4. Практическое использование свойств средней арифметической.
Свойства средней арифметической используются так же для упрощения методики ее расчета. В условиях малопроизводительной вычислительной техники эта методика обеспечивала значительную экономию времени и труда. В настоящее время данная методика служит наглядным образцом иллюстрации свойств средней.
Упрощенная методика расчета средней арифметической
(по данным о выработке рабочих токарей).
|
|
|
|
|
|
|
| 290 | 3 | -40 | -2 | 1 | -2 |
| 310 | 9 | -20 | -1 | 3 | -3 |
| 330 | 15 | 0 | 0 | 5 | 0 |
| 350 | 12 | 20 | 1 | 4 | 4 |
| 370 | 6 | 40 | 2 | 2 | 4 |
| 390 | 6 | 60 | 3 | 2 | 6 |
| 51 | 17 | 9 |
Данный метод называется так же методом расчета от условного нуля. В качестве условного нуля выбирается произвольное постоянное число А. Обычно это вариант ряда с наибольшей частотой. А=330.
Рассчитываем среднюю по новым вариантам: 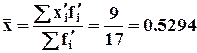 .
.
Пользуясь свойствами средней переходим от условного ![]() к
фактической средней величине
к
фактической средней величине ![]() .
.
5. Степенные средние.
Средняя арифметическая величина является частным случаем, который называется степенной средней.
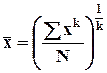 -
для несгруппированных данных;
-
для несгруппированных данных;
 -
для сгруппированных данных.
-
для сгруппированных данных.
Последовательно придавая k дискретное значение 0, 1, 2, 3, … и т.д. получим различные виды средних.
Если k=-1 степенные средние приобретают вид средней гармонической.
 -
для несгруппированных данных;
-
для несгруппированных данных;
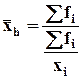 -
для сгруппированных данных.
-
для сгруппированных данных.
Пример: В течение рабочей смены 3 рабочих изготовляли детали. 1й рабочий затрачивая на изготовление 1 детали – 6 мин., 2й – 8 мин., 3й – 7,5 мин. Определить средние затраты времени на изготовление 1 детали.
Среднюю арифметическую взвешенную нельзя использовать для расчета, так как каждый из рабочих изготавливал за смену разное количество деталей. В числителе формулы отражается количество человеко-силы, а в знаменателе условное количество деталей, изготавливаемых за смену.
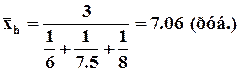
Пример: Продавец в течении нескольких дней продавал на рынке морковь. В первые 4 дня цена составляла 6 руб./кг, в последние 5 дней цена поднялась до 7 руб., а оставшаяся морковь была продана за 4,50 руб./кг. Поскольку данные о товарообороте отсутствуют, то для решения задачи применяется средняя гармоническая взвешенная:
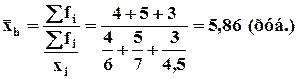
При этом число дней продаж моркови по различным ценам рассматривается как показатель условного товарооборота.
Средняя гармоническая применяется в тех случаях, когда частоты ряда выражены в неявном виде.
Если величина k=0, то степенная средняя приобретает вид средней геометрической.
![]() для
несгруппированных данных;
для
несгруппированных данных;
![]() для
сгруппированных данных.
для
сгруппированных данных.
Средняя геометрическая применяется в тех случаях, когда отдельные варианты ряда резко отличаются от остальных.
Наиболее часто формулу средней геометрической используют для определения средних валютных курсов, эффективности валютных курсов, реальной эффективности валютных курсов (международная финансовая статистика).
Если k=1 степенная средняя принимает вид средней арифметической, взвешенной и невзвешенной.
Если k=2, средняя квадрата.
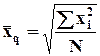 для
несгруппированных данных;
для
несгруппированных данных;
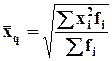 -
для сгруппированных данных.
-
для сгруппированных данных.
Результаты статистического исследования зависят от того, насколько верно избран вид средней. Расчет средних, выполненных на основе одних и тех же данных разными способами дает различные результаты.
В курсе математической статистики доказано, что чем ниже степень средней, тем меньше ее величина. Это называется правилом мажорантности средней.
| k | -1 | 0 | 1 | 2 | |||
|
|
|
< |
|
< |
|
< |
|
Доказано так же, что чем интенсивней колеблются значения вариантов ряда, тем больше разница между ними.
6. Мода и процентили.
Наряду со средними для характеристики распределения применяют такие показатели как мода и процентили, которые дополняют характеристику (обобщающую) и позволяют сравнивать между собой и находить различия в рядах с одинаковыми средними.
Мода – это наиболее часто встречающийся вариант ряда.
В дискретных рядах распределения модой является вариант, имеющий максимальную частотную характеристику.
В интервальных рядах мода определяется в два этапа. В начале определяется интервал, содержащий моду (модальный интервал), а затем рассчитывается значение моды по формуле:
 ,
где
,
где ![]() -
нижняя граница модального интервала, i – величина этого интервала,
-
нижняя граница модального интервала, i – величина этого интервала, ![]() ,
, ![]() ,
, ![]() -
частоты модального, предшествующего ему и следующего за ним интервалов.
-
частоты модального, предшествующего ему и следующего за ним интервалов.
Для последней таблицы (данные о выработке рабочих токарей):
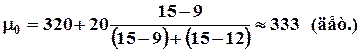
Медиана (вид процентиля), который занимает серединное положение в ряду распределения. Медиана определяется по формуле:
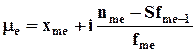 ,
где
,
где ![]() -
нижняя граница интервала, содержащего медиану (интервал определяется по
накопленной частоте, первой превышающей 50% суммы частот (в дальнейшем для
квартилей, децилей – 25%, 75%, 0,1%, 0,2% и т.д.)), i – величина этого интервала,
-
нижняя граница интервала, содержащего медиану (интервал определяется по
накопленной частоте, первой превышающей 50% суммы частот (в дальнейшем для
квартилей, децилей – 25%, 75%, 0,1%, 0,2% и т.д.)), i – величина этого интервала, ![]() -
номер медианы,
-
номер медианы, ![]() - накопленная частота интервала, предшествующего
медиане,
- накопленная частота интервала, предшествующего
медиане, ![]() - частота медианного интервала.
- частота медианного интервала.
Поскольку медиана разновидность процентиля то данная формула носит универсальный характер, она может применяться для определения квартилей (Q) и децилей (d).
Квартили (четверти) отсекают от совокупности соответственно 25%, 50% и 75%.
Децили отсекают от совокупности соответственно 10%, 20%, 30% и т.д.
На первом этапе определяется номер процентиля по формуле:
![]() -
для ряда четным числом единиц;
-
для ряда четным числом единиц;
![]() -
с нечетным числом единиц.
-
с нечетным числом единиц.
![]() -
номер процентиля (порядковый),
-
номер процентиля (порядковый), ![]() - индекс процентиля (выражается десятичной дробью) (
- индекс процентиля (выражается десятичной дробью) (![]() ), N – численность совокупности.
), N – численность совокупности.
Расчет моды и процентилей
на примере группировки магазинов по сумме товарооборота.
|
Группы магазинов с торговой площадью, кв. м |
Число магазинов,
|
Накопленная частота,
|
| До 100 | 6 | 6 |
| 100-200 | 12 | 18 |
| 200-300 | 27 | 45 |
| 300-400 | 13 | 58 |
| 400-500 | 8 | 66 |
| Свыше 500 | 5 | 71 |
| Итого | 71 |
Накопленная частота – это сумма частот данного и всех предшествующих ему интервалов.
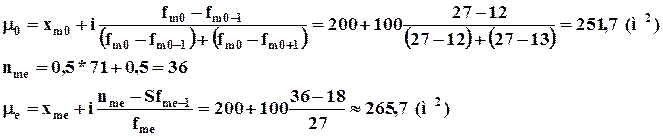
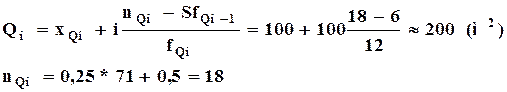
Четверть всех магазинов имеет площадь менее 200 кв. метров, а остальные 75% более 200 кв. метров.
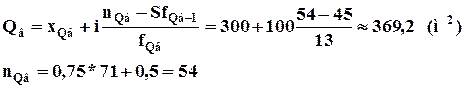
Три четверти магазинов имеют торговые площади не превышающие 369,2 кв. метров, остальные больше.
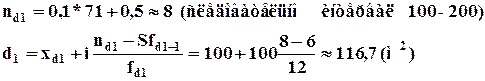
Показатели вариации.
1. Понятие вариации и роль ее изучения в статистических исследованиях.
2. Измерители вариации.
3. Прямой способ расчета показателей вариации.
4. Свойства дисперсии и среднего квадратического отклонения.
5. Упрощенный способ расчета дисперсии и средне квадратического отклонения.
6. Относительные показатели вариации.
7. Стандартизация данных.
8. Моменты распределения.
9. Показатели асимметрии и эксцесса.
10. Средняя арифметическая и дисперсия альтернативного признака.
1. Понятие вариации и роль ее изучения в статистических исследованиях.
Вариация – это колеблемость значений признака у отдельных единиц совокупности.
Наличию вариации обязана своим появлением статистика. Большинство статистических закономерностей проявляется через вариацию. Изучая вариацию значений признака в сочетании с его частотными характеристиками, мы обнаруживаем закономерности распределения (например: население по возрасту, студентов по уровню оценок).
Рассматривая вариацию одного признака параллельно с изменением другого, мы обнаруживаем взаимосвязи между этими признаками или их отсутствие (например: зависимость между торговой площадью и товарооборотом).
Вариации в статистике проявляются двояко, либо через изменения значений признака у отдельных единиц совокупности, либо через наличие или отсутствие изучаемого признака у отдельных единиц совокупности.
Изучение вариации в статистике имеет как самостоятельную цель, так и является промежуточным этапом более сложных статистических исследований.
2. Измерители вариации.
Простейшим показателем вариации является размах
колебаний: ![]() .
.
Достоинство этого показателя простота расчета, возможность использования для оценки вариации однородных совокупностей. Недостаток – неприемлемость для неоднородных совокупностей с редкими выбросами крайних значений признака.
Частично недостатки этого показателя устраняет межквартельный
размах: ![]() . Однако, он характеризует
вариацию только половины совокупности.
. Однако, он характеризует
вариацию только половины совокупности.
Для учета колеблемости всех значений признака применяют показатели среднего линейного отклонения, дисперсии и средне квадратического отклонения.
Средне линейное отклонение – среднее значение отклонений всех вариантов ряда от средней арифметической (иногда от моды или медианы):
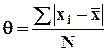 -
для несгруппированных данных;
-
для несгруппированных данных;
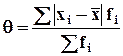 -
для сгруппированных данных.
-
для сгруппированных данных.
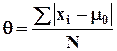
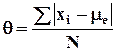
Аналогичным по смыслу среднему линейному отклонению является показатель дисперсии и рассчитываемый на его основе показатель средне квадратического отклонения.
Дисперсия – рассеивание, данный показатель характеризует рассеивание значений признака относительно его средней величины.
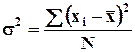 - для несгруппированных данных;
- для несгруппированных данных;
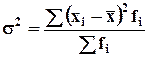 -
для сгруппированных данных.
-
для сгруппированных данных.
Дисперсия – средне квадратическое отклонение всех вариантов ряда от средней арифметической. Если извлечь квадратный корень из дисперсии, получим средне квадратическое отклонение.
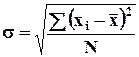 -
для несгруппированных данных;
-
для несгруппированных данных;
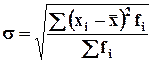 -
для сгруппированных данных.
-
для сгруппированных данных.
Несмотря на логическое сходство, дисперсия является более чувствительной к вариации и, следовательно, чаще применяемый показатель.
3. Прямой способ расчета показателей вариации.
Расчет показателей вариации заработной платы работников завода.
| Группы со среднемесячной з/п, руб. |
Число раб-в, |
|
|
|
|
|
|
| До 1500 | 30 | 750 | 22500 | 1909,09 | 57272,7 | 3644628 | 109338843 |
| 1501-3000 | 75 | 2250 | 168750 | 409,09 | 30681,8 | 167355 | 12551653 |
| 3001-4500 | 45 | 3750 | 168750 | 1090,91 | 49090,9 | 1190083 | 53553719 |
| Свыше 4501 | 15 | 5250 | 78750 | 2590,91 | 38863,6 | 6712810 | 100692149 |
| Итого | 165 | 438750 | 175909 | 276136364 |
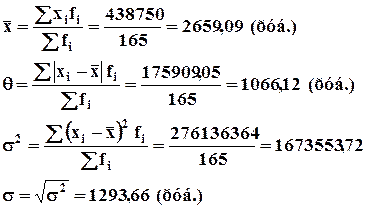
Заработная плата каждого из работников в среднем отклоняется от средне заработной платы на 1066,12 руб.
Средне квадратическое отклонение ![]() заметно больше, чем
аналогичный ему по смыслу среднее линейное отклонение.
заметно больше, чем
аналогичный ему по смыслу среднее линейное отклонение.
4. Свойства дисперсии и среднего квадратического отклонения.
Так же как и средняя дисперсия обладает рядом свойств, имеющих важное значение для понимания сущности этого показателя, методологии его расчета и практического использования для разработки более совершенных статистических методов.
Свойства дисперсии и средне квадратическое отклонение:
1)
Если все варианты ряда уменьшить
или увеличить на постоянное число, то величина дисперсии и средне
квадратического отклонения не изменится. ![]() ;
;
2)
Если все варианты ряда умножить
или разделить на постоянное число, дисперсия соответственно увеличится или
уменьшится в квадрат этого числа раз, а средне квадратическое отклонение в это
число раз. 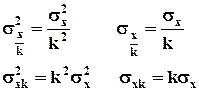 ;
;
3) Если часd>82,7
1107,4
265,3
40 563,44
2 674,30
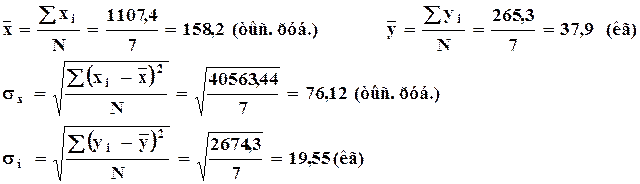
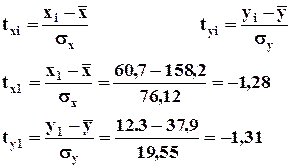
При стандартизации сгруппированных данных наряду с масштабированием вариантов ряда величинами соответствующих средне квадратических отклонений частоты этих рядов пересчитываются в частости.
Стандартизацию данных проводят, когда варианты сравниваемых рядов отличаются единицами измерения и порядком.
Стандартизация является важнейшим статистическим промежуточным этапом.
Стандартизация используется так же хорошо в теории выборочного метода.
8. Моменты распределения.
Моменты распределения составляют алгоритмическую основу многих статистических методов. Различают:
- Произвольные (общий случай);
- Начальные;
- Центральные;
- Стандартные (частный случай).
Выделяют:
- Взвешенные;
- Невзвешенные.
Произвольным моментом k-го порядка называется среднее значение k-ой степени отклонения всех вариантов ряда от произвольного постоянного числа.
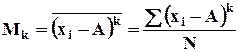 -
для несгруппированных данных;
-
для несгруппированных данных;
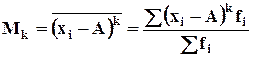 -
для сгруппированных данных.
-
для сгруппированных данных.
При этом k принимает целочисленное значение от 1 до 4.
Если А=0, то произвольный момент преобразуется в начальный момент.
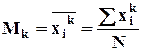 -
для несгруппированных данных;
-
для несгруппированных данных;
при k=1 M1=![]()
при k=2 M2=![]()
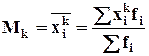 - для сгруппированных данных.
- для сгруппированных данных.
Если А=![]() ,
произвольный момент преобразуется в центральный момент распределения.
,
произвольный момент преобразуется в центральный момент распределения.
 -
для несгруппированных данных;
-
для несгруппированных данных;
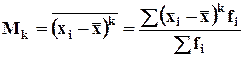 -
для сгруппированных данных.
-
для сгруппированных данных.
При k=1 M1=0
При k=2 M2=![]()
Стандартные моменты это начальные моменты из стандартных отклонений.
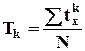 -
для несгруппированных данных;
-
для несгруппированных данных;
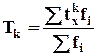 -
для сгруппированных данных.
-
для сгруппированных данных.
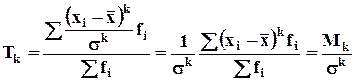
Стандартный момент k-го порядка это отношение центрального момента того же порядка к средне квадратическому отклонению в k-ой степени.
Так же как средняя арифметическая величина и дисперсия, центральные и стандартные моменты обладают рядом свойств, которые по сути ближе всего к свойствам дисперсии.
9. Показатели асимметрии и эксцесса.
При анализе распределений помимо графического изображения характер распределения можно выяснить, рассчитывая такие показатели, как асимметрия и эксцесс.
В качестве показателя асимметрии используют стандартный момент 3-го порядка. Если распределение симметрично относительно средней то показатель асимметрии равен нулю.
g width="107" height="52" src="images/5772474.gif">,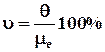 .
.
Коэффициенты вариации определенные по различным основаниям не одинаковы, поэтому, сопоставляя вариации разных совокупностей, нужно использовать коэффициенты вариации, рассчитанные по одной и той же величине.
Коэффициент вариации является так же количественной
мерой однородности совокупности. Принято считать, что если ![]() , то совокупность
количественно однородна. Чем меньше, тем лучше.
, то совокупность
количественно однородна. Чем меньше, тем лучше.
7. Стандартизация данных.
Коэффициенты вариации являются сводными оценками вариаций различных совокупностей. Однако они не позволяют сопоставить между собой значения признака у отдельных или групп единиц разных совокупностей.
Для подобных сравнений прибегают к стандартизации вариантов разных совокупностей по формулам:
 ,
где
,
где ![]() ,
, ![]() - это стандартизированные
значения вариантов ряда x и y
соответственно. В процессе стандартизации мы переходим от измерения вариантов в
натуральных или стоимостных единицах к их измерению величинами соответствующих
средне квадратических отклонений.
- это стандартизированные
значения вариантов ряда x и y
соответственно. В процессе стандартизации мы переходим от измерения вариантов в
натуральных или стоимостных единицах к их измерению величинами соответствующих
средне квадратических отклонений.
Пример: Стандартизация данных о доходах на одного члена семьи и среднедушевом потреблении мяса.
|
Доход на одного члена семьи, тыс. руб./год, |
Среднедушевое потребление мяса, |
|
|
|
|
|
|
| 60,7 | 12,3 | -97,5 | -25,6 | 9 506,25 | 655,36 | -1,28 | -1,31 |
| 84,2 | 19,1 | -74 | -18,8 | 5 476,00 | 353,44 | -0,97 | -0,96 |
| 112,4 | 23,1 | -45,8 | -14,8 | 2 097,64 | 219,04 | -0,60 | -0,76 |
| 144,5 | 35,6 | -13,7 | -2,3 | 187,69 | 5,29 | -0,18 | -0,12 |
| 180,1 | 49,5 | 21,9 | 11,6 | 479,61 | 134,56 | 0,29 | 0,59 |
| 240,9 | 57,3 | 82,7 | 19,4 | 6 839,29 | 376,36 | 1,09 | 0,99 |
| 284,6 | 68,4 | 126,4 | 30,5 | 15 976,96 | 930,25 | 1,66 | 1,56 |
|
1107,4 |
265,3 |
40 563,44 |
2 674,30 |
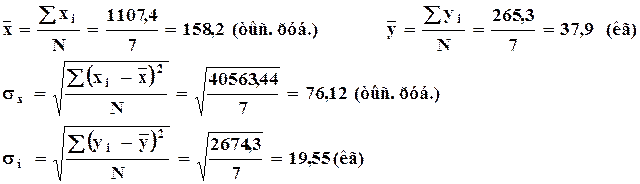
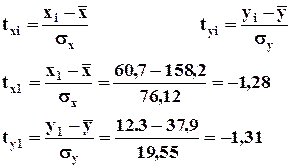
При стандартизации сгруппированных данных наряду с масштабированием вариантов ряда величинами соответствующих средне квадратических отклонений частоты этих рядов пересчитываются в частости.
Стандартизацию данных проводят, когда варианты сравниваемых рядов отличаются единицами измерения и порядком.
Стандартизация является важнейшим статистическим промежуточным этапом.
Стандартизация используется так же хорошо в теории выборочного метода.
8. Моменты распределения.
Моменты распределения составляют алгоритмическую основу многих статистических методов. Различают:
- Произвольные (общий случай);
- Начальные;
- Центральные;
- Стандартные (частный случай).
Выделяют:
- Взвешенные;
- Невзвешенные.
Произвольным моментом k-го порядка называется среднее значение k-ой степени отклонения всех вариантов ряда от произвольного постоянного числа.
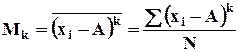 -
для несгруппированных данных;
-
для несгруппированных данных;
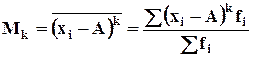 -
для сгруппированных данных.
-
для сгруппированных данных.
При этом k принимает целочисленное значение от 1 до 4.
Если А=0, то произвольный момент преобразуется в начальный момент.
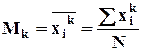 -
для несгруппированных данных;
-
для несгруппированных данных;
при k=1 M1=![]()
при k=2 M2=![]()
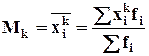 - для сгруппированных данных.
- для сгруппированных данных.
Если А=![]() ,
произвольный момент преобразуется в центральный момент распределения.
,
произвольный момент преобразуется в центральный момент распределения.
 -
для несгруппированных данных;
-
для несгруппированных данных;
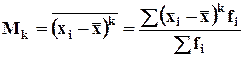 -
для сгруппированных данных.
-
для сгруппированных данных.
При k=1 M1=0
При k=2 M2=![]()
Стандартные моменты это начальные моменты из стандартных отклонений.
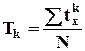 -
для несгруппированных данных;
-
для несгруппированных данных;
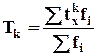 -
для сгруппированных данных.
-
для сгруппированных данных.
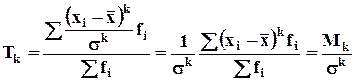
Стандартный момент k-го порядка это отношение центрального момента того же порядка к средне квадратическому отклонению в k-ой степени.
Так же как средняя арифметическая величина и дисперсия, центральные и стандартные моменты обладают рядом свойств, которые по сути ближе всего к свойствам дисперсии.
9. Показатели асимметрии и эксцесса.
При анализе распределений помимо графического изображения характер распределения можно выяснить, рассчитывая такие показатели, как асимметрия и эксцесс.
В качестве показателя асимметрии используют стандартный момент 3-го порядка. Если распределение симметрично относительно средней то показатель асимметрии равен нулю.
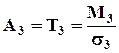
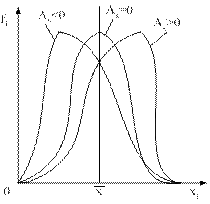
Если показатель асимметрии больше 0, то есть преобладают положительные отклонения от среднего, то наблюдается правосторонняя асимметрия, то есть преобладание в совокупности вариантов ряда превышающих среднюю.
Если же показатель асимметрии меньше 0, налицо левосторонняя асимметрия, то есть превышение численности вариантов ряда меньше чем средняя.
Показатель эксцесса характеризует степень колеблемости исходных данных, чем сильнее вариация, тем более пологой является кривая распределения и наоборот, чем однороднее совокупность, тем в большей степени варианты ряда сконцентрированы около средней и тем более островершинней будет кривая распределения.
В качестве эталона высоты распределения в статистике принимается кривая нормального распределения. Доказано, что стандартный момент 4-го порядка у этой кривой равен 3.
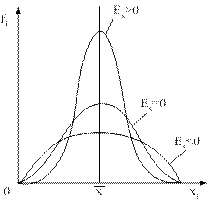
10. Средняя арифметическая и дисперсия альтернативного признака.
Альтернативный признак – тот которым обладает или не обладает единица совокупности.
Наличие альтернативного признака обозначают 1, а
отсутствие – 0. Если численность совокупности – N, а M –
число единиц, обладающих изучаемым признаком, то ![]() -
доля единиц, обладающих изучаемым признаком. Соответственно
-
доля единиц, обладающих изучаемым признаком. Соответственно ![]() - доля единиц таким
признаком не обладающих.
- доля единиц таким
признаком не обладающих.
Предположим
|
|
|
| 1 | p |
| 0 | q |
| 1 |
p+q=1
![]()
Средняя арифметическая альтернативного признака равна p.
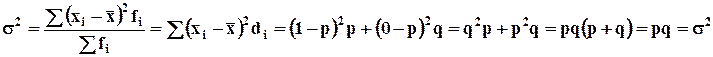
Дисперсия альтернативного признака ![]() .
.
Пример: N=10, M=4
N-M=6

Максимальное значение дисперсии для неоднородных
совокупностей ![]() .
.
Выборочный метод.
1. Сущность выборочного метода и его практическое значение.
2. Ошибка выборки.
3. Малая выборка.
4. Определение оптимальной численности выборки.
5. Распространение результатов выборочного распределения на генеральную совокупность.
6. Классификация способов отбора.
7. Организация отбора различными способами и оценка надежности полученных результатов.
8. Моментное выборочное наблюдение.
1. Сущность выборочного метода и его практическое значение.
Выборочный метод – это основной способ сбора информации в условиях развитой рыночной экономики.
Выборка – разновидность несплошного наблюдения, позволяющего определить показатели всей совокупности (генеральной совокупности) на основе изучения ее части. При этом отобранная часть формируется с учетом положений теории вероятности и математической статистики.
Выборка имеет многовековую историю, но ее математическая составляющая получила развитие во 2й половине 19-20 века. Значительный вклад в формирование теории выборки внесли русские статистики. В СССР господствовало сплошное статистическое наблюдение в виде отчетности. Выборка охватывала только:
- Оценку качества продукции;
- Наблюдение за ценами на городских колхозных рынках;
- Наблюдение за семейными бюджетами;
- Изучение спроса.
За рубежом в то время преобладало выборочное обследование. Сплошное наблюдение охватывало только таможенную статистику, налогообложение и периодически проводимые переписи населения, и промышленные цензы.
Достоинства выборки.
При правильно организованном выборочном обследовании изучается не более 20-25% совокупности, обычно 10% и то много. На лицо огромная экономия времени и средств. При этом благодаря работе статистиков – профессионалов значительно повышается точность наблюдений (нередко она выше, чем при сплошном наблюдении). Однако, параметры выборки в силу объективных причин могут отличаться от соответствующих параметров генеральной совокупности, поэтому результаты выборочного исследования распространяются на генеральную совокупность с определенной вероятностью.
Не всякое несплошное наблюдение – это научно-обоснованная выборка.
Для получения надежных результатов необходимо тщательно готовить выборку. Подготовка включает следующие этапы:
1. Обоснование целесообразности проведения выборки;
2. Подготовка программы выборки;
3. Решение организационных вопросов выборки;
4. Определение способа отбора и численности выборки, обеспечивающих репрезультативность ее результатов.
5. Проведение отбора единиц генеральной совокупности.
6. Сводка полученных результатов и расчет параметров выборки.
7. Определение ошибок выборки.
8. Распространение параметров выборки на генеральную совокупность.
Главная задача выборки:
- Вычисление ожидаемой ошибки выборки, то есть разницы между одноименными характеристиками выборочной и генеральной совокупности;
- Определение доверительной вероятности того, что ошибка репрезультативности не превысит некоторого заранее заданного значения;
- Расчет численности выборки, обеспечивающей с заданной вероятностью необходимую точность исследований.
2. Ошибка выборки.
Возникает из-за различий в вариации значений изучаемого признака у единиц выборочной и генеральной совокупности. Поскольку при соблюдении требований случайного отбора все единицы генеральной совокупности имеют равные шансы попасть в выборку, состав выборки может значительно изменяться при повторении испытаний. Соответственно будут меняться параметры выборки, и возникать ошибки выборки. Ошибки выборки неизбежны, они вытекают из сути метода. Ошибки выборки не могут быть постоянными при повторении отбора.
Ошибка выборки в статистике это некоторая средняя величина или обобщающая характеристика, ошибок полученных при многократном повторении испытаний.
![]()
![]() W - P
W - P
![]() -
ошибка выборки;
-
ошибка выборки;
![]() -
выборочная средняя;
-
выборочная средняя;
![]() -
генеральная средняя;
-
генеральная средняя;
W – доля единиц, обладающих изучаемым признаком в выборочной совокупности (выборочная доля);
P - доля единиц, обладающих изучаемым признаком в генеральной совокупности.
Величина ошибок зависит от способа отбора. В математической статистике доказано, что средняя ошибка выборки (математическое ожидание средней ошибки выборки) – это среднеквадратическое отклонение распределения выборочной средней величины.
Ошибка выборки определяется: 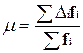
В математической статистике доказано, что средняя
ошибка собственно случайного повторного отбор рассчитывается: 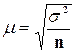 , где
, где
![]() - средняя ошибка выборки;
- средняя ошибка выборки;
![]() - дисперсия генеральной совокупности;
- дисперсия генеральной совокупности;
![]() - численность выборки.
- численность выборки.
Если исследуется выборочная доля при повторном отборе
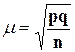 , где
, где ![]() - дисперсия биномиального распределения.
- дисперсия биномиального распределения.
Результаты повторного отбора подчиняются закону биномиального распределения.
При бесповторном отборе результаты многократной
выборки и распределения ошибок подчиняются гипергеометрическому распределению,
и формула средней ошибки имеет вид: 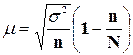 ,
соответственно для выборочной доли
,
соответственно для выборочной доли 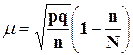 .
.
При выборках большой численности, когда ![]() из массовых генеральных
совокупностей (
из массовых генеральных
совокупностей (![]() ) для расчета
ошибок выборки можно использовать формулу повторного отбора.
) для расчета
ошибок выборки можно использовать формулу повторного отбора.
В формулах средней ошибки выборки присутствует генеральная дисперсия. Однако, она, как правило, неизвестна. Если мы проводим выборку для того, чтобы изучить только часть совокупности, мы не можем знать генеральную дисперсию. Исключение составляют только выборки, проводимые для контроля результата сплошного наблюдения.
Однако, математической статистикой доказано, что если выборка производится из нормального распределения совокупности генеральная и выборочная дисперсия связаны между собой следующим образом:
|
|
||||
Из формулы видно, что достаточно большой выборке (n-1)®n, а ![]() , откуда s2» S2. Поэтому для расчета средних ошибок выборки на
практике используют выборочные дисперсии.
, откуда s2» S2. Поэтому для расчета средних ошибок выборки на
практике используют выборочные дисперсии.
|
|
||||
Если многократно проводить выборки из одной и той же генеральной совокупности, то конкретному размеру ошибки выборки будет соответствовать та или иная статистическая вероятность ее появления.
Вероятности конкретного размера ошибок подсчитать невозможно (нецелесообразно), гораздо важнее знать, что ошибка наблюдений не выйдет за определенные пределы.
|
|
t=1, 2, 3
По формуле Чебышева, если
t=1 r³0
t=2 r³0,75
t=3 r³0,89
Эта формула для условий повторного отбора.
Академик Марков доказал, что предельная теорема справедлива и для бесповторного отбора.
Академик Ляпунов доказал, что вероятности предельных ошибок многочисленных выборок подчиняются закону нормального распределения, следовательно, для определения вероятностей нахождения ошибки выборки в заданных пределах можно использовать интегральную формулу Лапласа.
Площадь кривой ±s 0,6827
2s 0,9545
3s 0,9973
Отсюда, если доверительный коэффициент t=1, то вероятность того, что предельная ошибка выборки не будет больше, чем средняя ошибка, которая составляет 0,683.
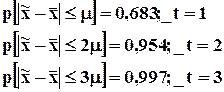
Вероятный интервал изменения генеральной средней или доли в статистике принято называть доверительным интервалом.
Пример: Для анализа жирности молока из партии в 1000 фляг было отобрано и проверено 30. Средний процент жирности в проверенных флягах составил 3,51%, при среднеквадратическом отклонении 0,35. С вероятностью 0,954 определить доверительный интервал средней жирности партии молока (если выборка бесповторная).
|
n=30
![]() =3,51%
=3,51%
S=0,35%
Если мы расширим допустимые пределы точности, то вероятностная надежность результата будет выше, а точность ниже.
Если p=0,997 то t=3, а D=0,19 тогда ожидаемая жирность молока в генеральной совокупности должна
составить ![]() .
.
3. Малая выборка.
В процессе статистических исследований нередко приходится ограничивать объем выборки, особенно в тех случаях, когда исследования единиц совокупности приводит к их разрушению.
В статистике доказано, что даже в выборке весьма малого объема (20-30, а иногда 4-5 единиц) позволяют получить приемлемые для анализа результаты. Проблема малых выборок была решена в 1908г. английским статистиком У.Гассетом (псевдоним Студент). Он сумел определить зависимость между величиной доверительного коэффициента t, а так же численностью малой выборки n с одной стороны, и вероятностью нахождения ошибки выборки в заданных пределах с другой стороны. Эта зависимость получила название – распределение Стьюдента. Для упрощения расчетов имеются специальные таблицы значений критериев Стьюдента (стр. 372 «Практикума по теории статистики»).
n=n-1 – число степеней свободы.
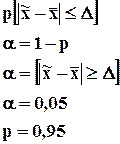
Малая выборка определяется по формуле
|
|
||||
|
|
- число степеней свободы.
Пример: Ежедневные затраты времени 15 работников на поездки туда и обратно составляют в среднем 1,7 часа. Определить пределы, в которых находится среднее время поездки на работу и обратно.
|
![]() =1,7 часа
=1,7 часа
S2=0,134
P=0,95
4. Определение оптимальной численности выборки.
Трудовые и материальные затраты на проведение выборки напрямую зависят от ее численности, поэтому чрезвычайно важно до оптимума сохранить численность выборки, так чтобы не утратить ее точность.
Поиск оптимальной численности выборки удобно
осуществлять на основе формул средней и предельной ошибок. Из формулы средней
ошибки случайного повторного отбора видно, что величина средней ошибки обратно
пропорциональна квадратному корню из численности выборки (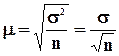 ). Чтобы сократить среднюю
ошибку в 2 раза, нужно численность выборки увеличить в 4 раза. Используя
формулу предельной ошибки выборки
). Чтобы сократить среднюю
ошибку в 2 раза, нужно численность выборки увеличить в 4 раза. Используя
формулу предельной ошибки выборки ![]() можно
найти численность
можно
найти численность ![]() . Это оптимальная
численность выборки для случайного повторного отбора.
. Это оптимальная
численность выборки для случайного повторного отбора.
Пример: Для определения среднего размера банковского вклада сроком на 91 день необходимо провести повторный отбор из совокупности в 2500 договоров. Какое количество договоров необходимо отобрать, чтобы с вероятностью 0,954 предельная ошибка выборки не превысила 25 руб.
|
p=0,954
D=25 руб.
n-?
s2=8900
Наличие в формуле оптимальной численности генеральной
дисперсии ![]() приводит на первый взгляд к парадоксу: зачем нам
проводить выборку, если известна генеральная дисперсия (а, следовательно, и
генеральная средняя). Однако на практике генеральная дисперсия обычно не
известна, вместо нее используют выборочную дисперсию предыдущего обследования,
так как дисперсия как показатель является более устойчивой, чем сами варианты,
на основе которых она рассчитана.
приводит на первый взгляд к парадоксу: зачем нам
проводить выборку, если известна генеральная дисперсия (а, следовательно, и
генеральная средняя). Однако на практике генеральная дисперсия обычно не
известна, вместо нее используют выборочную дисперсию предыдущего обследования,
так как дисперсия как показатель является более устойчивой, чем сами варианты,
на основе которых она рассчитана.
Если отбор осуществляется бесповторно, то численность выборки для такого отбора рассчитывается по формуле:
|
Для
предыдущего примера: ![]()
Результаты близки, так как очень велика генеральная совокупность.
Если в условиях задачи присутствует предельная ошибка выборочной доли, то формула:
|
- для повторного отбора;
- для бесповторного отбора.
Пример: В целях изучения спроса на спортивную обувь периодически проводился опрос 1500 спортсменов. Какова должна быть численность случайного бесповторного отбора, чтобы с p=0,954 ошибка выборки доли спортсменов, предпочитающих обувь с верхом из натуральной кожи, не превысила 0,05, если известно, что ранее этой обуви отдавали предпочтение 65% спортсменов.
|
p=0,954 (t=2)
D=0,05
w=65%=0,65
n-?
5. Распространение результатов выборочного распределения на генеральную совокупность.
Для этих целей используется два метода:
- Метод прямого пересчета;
- Метод поправочных коэффициентов.
Метод прямого пересчета применяется для определения по данным о выборочной доле величины интервала, в пределах которого в генеральной совокупности с заданной вероятностью находится число единиц, обладающих изучаемым признаком.
|
w=0,975 (97,5%)
p=0,954
D=0,005 (0,5%)
Основное назначение метода поправочных коэффициентов – уточнение данных сплошного массового наблюдения посредством выборочных проверок. Обычно такие проверки осуществляются инструкторами-контролерами по результатам проведенных переписей.
Пример: По результатам контрольного обхода счетного участка инструктором-контролером получены уточненные сведения о численности населения 589 человек вместо 572 зарегистрированных счетчиков. Всего на территории инструкторского участка по данным переписи проживало 3893 человека.

- скорректированная численность.
6. Классификация способов отбора.
Методология и результаты расчета основных параметров выборки непосредственно зависят от способа отбора единиц из генеральной совокупности.
Способ отбора – это определенная система организации выборочного исследования. Применение того или иного способа зависит от цели исследования условий выборки, специфики объекта исследования, необходимой точности и оперативности результатов и от средств выделенных на исследования.
Все способы отбора разделяются на 3 вида:
- Индивидуальный;
- Групповой;
- Комбинированный.
При индивидуальном виде отбирают отдельные единицы совокупности.
При групповом виде отбирают группы, серии единиц совокупности (например: выбрали из контейнера несколько ящиков и все их проверили).
Комбинированный способ сочетает индивидуальный и групповой.
Если выборочная совокупность получена сразу, отбор называют одноступенчатым.
При наличии нескольких последовательных этапов отбора – выборка считается многоступенчатой.
Единица отбора меняется на каждой ступени. В отличии от многоступенчатой – многофазная выборка сохраняет одну и ту же единицу на всех стадиях отбора. Однако программа наблюдения постепенно расширяется.
В зависимости от применяемой схемы отбора различают:
- Повторный;
- Бесповторный.
Каждый из видов отбора может осуществляться следующими способами:
1. Собственно случайным;
2. Механическим;
3. Типическим (стратефицированным);
4. Серийным (гнездовым);
5. Комбинированным.
7. Организация отбора различными способами и оценка надежности полученных результатов.
Различные способы отбора отличаются неодинаковой методикой формирования выборки и различными алгоритмами расчета ошибок репрезентативности.
Собственно случайный отбор организуется таким образом, чтобы у всех единиц генеральной совокупности были равные возможности попасть в выборку. Это обеспечивается отбором по жребию, по таблицам случайных чисел или с помощью генераторов случайных чисел. Независимо от того, как будут отбирать единицы, их обязательно нумеруют. При отборе по жребию эти номера наносятся на карточки, шары и т.п., которые затем тщательно перемешиваются и из них наугад отбирается количество карточек, равное численности отбора.
Таблица случайных чисел это матрица 4 или 5 чисел, каждая цифра которой не зависит от остальных цифр данного числа и других чисел. В зависимости от численности выборки из таблицы выбираются одно, двух, трех или четырехзначное число. Числа можно отбирать по столбцам или строкам таблицы (начиная с любой строки или столбца) заранее заданным алгоритмом отбора.
В компьютерах и некоторых калькуляторах имеется генератор случайных чисел, который выводит на экран случайные числа.
Средняя ошибка собственно случайного повторного или бесповторного отбора определяется по формуле: см. пункт (2).
Механический отбор это направленная выборка из совокупности, предварительно упорядоченной по существующему или несуществующему признаку.
На первом этапе генеральная совокупность упорядочивается по какому-либо признаку. Независимо от признака при механическом отборе устанавливается пропорция отбора по формуле: N/n.
Если совокупность сгруппирована по несущественному признаку, то безразлично, с какой единицы начинать отбор.
Если совокупность сгруппирована или упорядочена по существенному признаку, то отбор следует начинать с середины первой группы.
Средняя ошибка механического отбора рассчитывается по формулам для случайного отбора. Это справедливо, когда отбор производился из совокупности, упорядоченной по несущественному признаку.
Если же совокупность была упорядочена по существенному признаку, то такой способ расчета несколько завышает среднюю ошибку выборки.
В данном случае можно было использовать среднюю из внутригрупповых дисперсий, а не общую дисперсию.
Типическая выборка (стратефицированная). При этой выборке генеральная совокупность вначале разбивается на типичные группы (страты), из которых производится случайный отбор единиц. Такая выборка гарантирует представительство всех типичных групп выборочной совокупности, что снижает ошибку выборки. Существуют пропорциональный и непропорциональный способы типического отбора.
При пропорциональном способе из каждой группы отбирается число единиц пропорциональное либо численности группы, либо внутригрупповой вариации изучаемого признака.
При типическом повторном отборе пропорциональном численности групповая средняя ошибка выборки определяется по формуле:

- средняя ошибка выборки для бесповторного отбора;
Если исследуется доля единиц совокупности, обладающих изучаемым признаком, то средние ошибки и дисперсия:
|
- для повторного отбора;
- для бесповторного отбора.
Пример: Для изучения средних цен одного блюда в предприятии общественного питания произведена 10% выборка пропорциональная численности групп.
| Предприятия |
Численность выборки, |
Средняя цена, |
Внутригрупповая дисперсия, |
|
|
| Закусочные | 21 | 19,3 | 68,2 | 405,3 | 1432,2 |
| Кафе | 24 | 42,5 | 151,45 | 1020 | 3634,8 |
| Рестораны | 15 | 63,2 | 342,5 | 948 | 5137,5 |
| 60 | 39,56 | 2373,3 | 10204,5 |
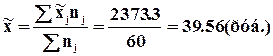
Для расчетов нужно рассчитать среднюю из внутригрупповых дисперсий:
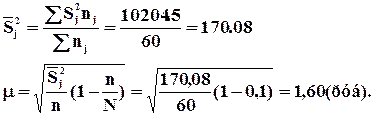
Предельная
ошибка типической выборки с p=0,954 ![]()
Доверительный интервал средней цены блюда 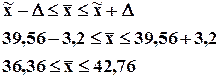
В 954 случаях из 1000 средняя цена блюда в генеральной совокупности будет не ниже 36 руб. 36 коп. и не выше 42 руб. 76 коп.
Оптимальная численность типической выборки пропорциональна численности групп, определяется по формулам:
|
- для повторного отбора;
- для бесповторного отбора.
Каковая должна быть численность выборки, чтобы с p=0,954 можно было бы утверждать, что предельная ошибка не превысит 3 руб. 50 коп.
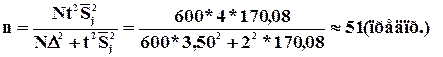
![]()
Численность, подлежащая отбору из отдельных типических групп, рассчитывается по формуле:
|
Из 600 предприятий – 210 закусочных, 240 кафе, 150 ресторанов.
![]()
Наиболее из точных пропорциональных способов типического отбора является отбор пропорциональной вариации значений признака в группах. Данный отбор целесообразен при наличии генеральных внутригрупповых дисперсий. Это возможно, когда выборка осуществляется для контроля данных сплошного наблюдения или когда имеются данные предшествующего сплошного наблюдения.
Численность выборочных групп определяется по формуле:
|
|
||||
Средняя ошибка выборки бесповторного типического отбора пропорциональна вариации признака в группах. Определяется по формуле:
|
Данный способ отбора дает ошибку меньшую, чем отбор пропорциональный численности групп.
Наиболее общим случаем является непропорциональный типический отбор. При произвольных пропорциях формирования типических выборочных групп средняя ошибка выборки рассчитывается по формуле:
|
|
||||
При этом, ошибки средние выборки по группам определяются по формулам:
|
- для повторного отбора;
- для бесповторного отбора.
Серийный или гнездовой отбор – это случайный выбор групп единиц с последующим сплошным наблюдением внутри отобранных серий. Данная выборка применяется преимущественно для контроля качества товаров, когда целесообразно вскрывать и исследовать отдельные упаковки. Это разновидность направленного отбора, способствующего снижению ошибки выборки. Благодаря сплошному исследованию гнезд частные дисперсии не оказывают влияние на ошибку репрезентативности, которая зависит только от вариации серийных средних, то есть от межгрупповой дисперсии, определяется по формуле:
|
|
||||
Средняя ошибка серийной выборки определяется по формулам:
|
|
- для бесповторного отбора.
Пример:
при проверке качества обуви партии 500 коробов отобрано в случайном порядке и
проверено 10 пар обуви. Число стандартных пар в коробах распределялось
следующим образом. ![]()
| № коробов | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Итого |
|
Число стандартных пар в коробе
( |
48 | 45 | 50 | 49 | 47 | 48 | 50 | 46 | 48 | 49 | 480 |
|
|
2304 | 2025 | 2500 | 2401 | 2209 | 2304 | 2500 | 2116 | 2304 | 2401 | 23054 |
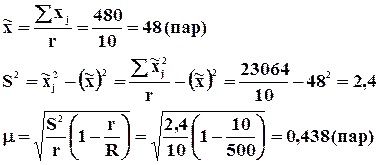
Если становится задача с вероятностью 0,954 определить
число стандартных пар обуви в коробе и доверительные интервалы доли стандартной
обуви в партии, то предельная ошибка выборки ![]() .
Доверительный интервал числа пар в генеральной совокупности определяется по
формуле:
.
Доверительный интервал числа пар в генеральной совокупности определяется по
формуле:
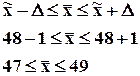
Доля стандартной обуви ![]() /
/
Комбинированная выборка – это сочетание группового и индивидуального отбора единиц наблюдения. Чаще всего сочетается серийный и собственно случайный отбор.
Ошибка выборки комбинированного отбора складывается из ошибок выборки ожидаемых по каждому способу отбора, входящему в комбинацию. Обычно применяют бесповторную комбинированную выборку, хотя теоретически возможен повторный комбинированный отбор. Комбинированная выборка по своей природе является многоступенчатой. Несмотря на простоту методологии многоступенчатого отбора, расчет его ошибки достаточно сложен и определяется по формуле:
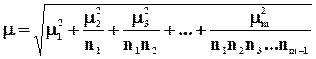 для
равночисленного отбора на каждой ступени.
для
равночисленного отбора на каждой ступени.
|
8. Способ моментных наблюдений.
Метод моментных (мгновенных) наблюдений разработан в 1938 году английским статистиком Типлетом для выборочного изучения производственного процесса. Метод применяется для групповых фотографий затрат рабочего времени и времени работы оборудования, когда наблюдатель периодически обходя рабочие места по заранее установленному маршруту регистрирует в специальном бланке, чем занят рабочий в конкретный момент времени, работает он в данный момент или отдыхает.
Метод моментных наблюдений – это выборка во времени, где генеральной совокупностью является фонд рабочего времени объекта наблюдения, то есть коллектива работников или группы единиц оборудования. Выборочная совокупность складывается из периодов времени регистрации состояния объекта исследования.
Групповые фотографии обеспечивают многократное снижение затрат по сравнению с индивидуальными фотографиями, так как не требуют постоянного присутствия наблюдателя на каждом рабочем месте в течении всего рабочего дня. Метод эффективен для оценки труда коллектива работников, выполняющих однородные операции.
Первым этапом организации мгновенных наблюдений является определение численности выборки, то есть необходимого числа момента регистрации.
|
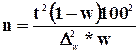
Пример:
для изучения использования рабочего времени 20 официантов методом мгновенных
наблюдений проводится групповая фотография рабочего времени. По норме время
работы должно составлять 8/10 установленной продолжительности рабочего дня (![]() ). Допустимый предел
отклонений
). Допустимый предел
отклонений ![]() . Вероятностная надежность
0,954. Надо определить доверительный интервал доли времени работы в
установленной продолжительности рабочего дня.
. Вероятностная надежность
0,954. Надо определить доверительный интервал доли времени работы в
установленной продолжительности рабочего дня.
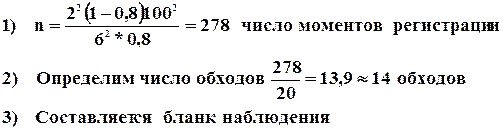
| № рабочего места | Порядковые номера обходов | Итоги регистрации | |||||||
| 1 | 2 | 3 | 4 | … | 13 | 14 | Работал | Не работал | |
| 1 | Н | Н | Н | 10 | 4 | ||||
| 2 | Н | Н | Р | 12 | 2 | ||||
| 3 | Р | Р | Р | 11 | 3 | ||||
| 4 | … | … | … | ||||||
| … | … | … | … | ||||||
| 19 | Н | Н | Р | ||||||
| 20 | Н | Н | |||||||
|
Всего Работал |
2 | 4 | 9 | 210 | |||||
| Не работал | 18 | 16 | 11 | 70 |
Доля рабочего времени по данным обследования ![]() .
.
Средняя ошибка выборки 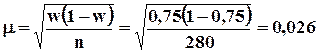 .
.
Предельная ошибка с вероятностью 0,954 ![]() .
.
Доля времени работы по данным исследований
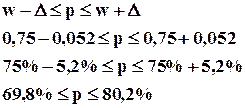
Статистическое исследование взаимосвязей.
1. Виды взаимосвязей и цели их статистического изучения.
2. Классификация методов исследования взаимосвязей.
3. Парная регрессия.
4. Измерения тесноты взаимосвязи.
5. Множественная корреляция и регрессия.
1. Виды взаимосвязей и цели их статистического изучения.
Изучение причинно-следственных зависимостей между фактами – важнейшая задача анализа социально-экономических явлений. Это необходимо для принятия обоснованных управленческих решений. Изучение зависимостей – это сложнейшая задача, поскольку социально-экономические явления сами по себе сложны и многообразны. Кроме того, полученные выводы носят вероятностный характер, так как они делаются на основе данных, представляющих собой выборку во времени или пространстве.
Статистические методы изучения зависимости построены с учетом особенностей изучаемых закономерностей. Статистика изучает преимущественно стохастические связи, когда одному значению признака-фактора соответствует группа значений результативного признака. Если с изменением значений признака-фактора изменяются среднегрупповые значения результативного признака, то такие связи называют корреляционными. Не всякая стохастическая зависимость является корреляционной. Если каждому значению факторного признака соответствует строго определенное значение результативного признака, то такая зависимость функциональная. Ее называют еще полной корреляцией. Неоднозначные корреляционные зависимости называют неполной корреляцией.
По механизму взаимодействия различают:
- Непосредственные связи – когда причина прямо влияет на следствие;
- Косвенные связи – когда между причиной и следствием существуют ряд промежуточных признаков (например, влияние возраста на заработок).
По направлениям различают:
- Прямые связи – когда значение факторного и результативного признаков изменяются в одном направлении;
- Обратные связи – когда значения факторного и результативного признаков изменяются в разных направлениях.
Бывают:
- Прямолинейные (линейные) связи – выражены прямой линией;
- Криволинейные связи – выражены параболой, гиперболой.
По числу взаимосвязанных признаков различают:
- Парные связи – когда анализируется взаимосвязь двух признаков (факторного и результативного);
- Множественные связи – характеризуют влияние нескольких признаков на один результативный.
По силе взаимодействия различают:
- Слабые (заметные) связи;
- Сильные (тесные) связи.
Задача статистики определить наличие, направление, форму и тесноту взаимосвязи.
2. Классификация методов исследования взаимосвязей.
Для изучения зависимости применяются различные статистические методы. Поскольку зависимости в статистике проявляются через вариацию признаков, то и методы в основном измеряют и сопоставляют вариацию факторного и результативного признаков.
Для изучения функциональных зависимостей в статистке применяют балансовый и индексный методы. Сущность балансового метода выражается формулой:
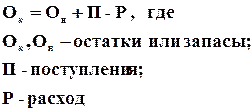
Данная форма может характеризовать движение материальных, денежных средств, ценностей.
Индексный метод применяется для анализа динамики и сравнения обобщающих показателей, а так же факторов, влияющих на изменение уровней этих показателей.
Изучение неполной корреляции осуществляется двумя группами методов, которые можно определить, как нематематические и математические. Нематематические методы:
- Метод параллельных рядов;
- Метод аналитических группировок;
- Графический метод.
Метод параллельных рядов применяется для определения наличия и направления взаимосвязи при немногочисленных совокупностях (15-20 единиц). При этом методе значение факторного признака располагается в порядке возрастания или убывания и параллельно с ними отражаются соответствующие значения результативного признака. Сопоставляя ряды значений, устанавливается зависимость.
Метод аналитической группировки применяется в случаях, когда совокупность достаточно велика и параллельные ряды не позволяют обнаружить зависимость. Этот метод – это разбиение исходных данных на группы в соответствии со значением признака фактора и расчет для каждой группы соответствующего среднегруппового значения результативного признака с тем, чтобы обнаружить взаимосвязь. Аналитические группировки обычно используются для однородных совокупностей, поэтому в них применяются чаще всего равные интервалы.
Пример: зависимость между суммой товарооборота магазина и уровнем издержек обращения.
| Группы магазинов с товарооборотом, тыс. руб. | Количество магазинов | Уровень издержек обращения в процентах к итогу |
| До 20 (10) | 3 | 35,2 |
| 20,1 – 40 (30) | 5 | 32,4 |
| 40,1 – 60 (50) | 8 | 25,2 |
| Свыше 60 (70) | 2 | 21,3 |
Группировка показывает, что с ростом товарооборота падает значение результативного признака. Налицо обратная зависимость. Если изобразить результаты группировки на графике, получим эмпирическую линию регрессии. Интервалы значений факторного признака заменяются средними групповыми показателями.

Эмпирическая линия регрессии показывает примерную форму и направление взаимосвязи.
При построении аналитической группировки надежность ее результатов зависит от того, какое число групп мы можем выделить, не натолкнувшись ни на одно исключение в предполагаемом характере взаимосвязи.
Помимо эмпирической линии регрессии, непосредственно определяющей форму и направление взаимосвязей, существует корреляционное поле, на котором отражаются параметрические данные. По корреляционному полю так же можно судить о характере взаимосвязи. Если точки сконцентрированы около диагонали идущей слева направо, снизу вверх – то связь прямая. Если около другой диагонали – обратная. Если точки рассеяны по всему полю графика – связь отсутствует.
При построении аналитической группировки важно правильно определить величину интервала. Если в результате первичной группировки связь не проявляется отчетливо, можно укрупнить интервал. Однако, укрупняя интервалы, можно иногда обнаружить связь даже там, где ее нет. Поэтому при построении аналитической группировки руководствуются правилом: чем больше групп мы можем выделить, не натолкнувшись ни на одно исключение, тем надежнее наша гипотеза о наличии и форме связи.
Нематематические методы дают приближенную оценку о наличии, формы и направлении связи. Более глубокий анализ осуществляется с помощью математических методов, которые развились на базе методов, применяемых статистиками - нематематиками:
- Регрессионный анализ, позволяющий выразить с помощью уравнения форму взаимосвязи.
- Корреляционный анализ используется для определения тесноты или силы взаимосвязи признаков. Корреляционные методы делят:
- Параметрические методы, которые дают оценку тесноты связи непосредственно на базе значений факторного и результативного признаков;
- Непараметрические методы – дают оценку на основе условных оценок признаков.
Оценка тесноты криволинейных зависимостей дается после расчета параметра уравнения регрессии. Поэтому такой метод называется корреляционно-регрессивным.
Если анализируется зависимость одного факторного и результативного признаков, то в этом случае имеем дело с парной корреляцией и регрессией. Если анализируются несколько факторных и результативных признаков – это множественная корреляция и регрессия.
3. Парная регрессия.
Регрессия – это линия, характеризующая наиболее общую тенденцию во взаимосвязи факторного и результативного признаков.
Предполагается, что аналитическое уравнение выражает подлинную форму зависимости, а все отклонения от этой функции обусловлены действием различных случайных причин. Так как изучаются корреляционные связи, изменению факторного признака соответствует изменение среднего уровня результативного признака. При построении аналитических группировок мы рассматривали эмпирическую линию регрессии. Однако, эта линия не пригодна для экономического моделирования и ее форма зависит от произвола исследователя. Теоретически линия регрессии в меньшей степени зависит от субъективизма исследователя, однако, здесь так же может быть произвол при выборе формы или функции взаимосвязи. Считается, что выбор функции должен опираться на глубокое знание специфики предмета исследования.
На практике чаще всего применяются следующие формы регрессионных моделей:
-
Линейная ![]() ;
;
-
Полулогарифметическая кривая ![]() ;
;
-
Гипербола ![]() ;
;
-
Парабола второго порядка ![]() ;
;
-
Показательная функция ![]() ;
;
-
Степенная функция ![]() .
.
Помимо содержательного подхода существует формальная оценка адекватности подобранной регрессионной модели. Лучшей из них считается та, которая наименее удалена от исходных данных.
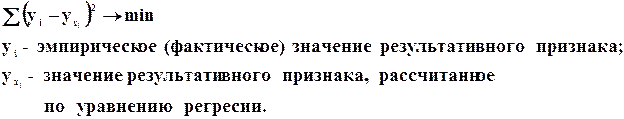
Данное свойство средней, гласящее, что сумма квадратов отклонений всех вариантов ряда от средней арифметической меньше суммы квадратов их отклонений от любого другого числа, положено в основу метода наименьших квадратов, позволяющего рассчитать параметры избранного уравнения регрессии таким образом, чтобы линия регрессии была в среднем наименее удалена от эмпирических данных.
Пример: данная система двух уравнений с двумя неизвестными а0 и а1 позволяет определить точное значение коэффициентов линейной регрессии.
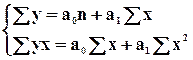
Анализ формы и параметров взаимосвязи между ценой килограмма репчатого лука и объемом его продаж.
|
Цена 1 кг лука, руб. |
Объем продаж, кг |
Товарооборот, руб. |
|
|
|
|
|
|
| 3 | 175 | 525 | 9 | -107,73 | 205,68 | -30,68 | 941,26 | 30625 |
| 3,5 | 200 | 700 | 12,25 | -125,69 | 187,73 | 12,28 | 150,68 | 40000 |
| 4 | 180 | 720 | 16 | -143,64 | 169,77 | 10,23 | 104,65 | 32400 |
| 4,5 | 150 | 675 | 20,25 | -161,60 | 151,82 | -1,815 | 3,29 | 22500 |
| 5 | 160 | 800 | 25 | -179,55 | 133,86 | 26,14 | 683,30 | 25600 |
| 5,5 | 120 | 660 | 30,25 | -197,51 | 115,91 | 4,09 | 16,77 | 14400 |
| 6 | 85 | 510 | 36 | -215,46 | 97,95 | -12,95 | 167,70 | 7225 |
| 6,5 | 90 | 585 | 42,25 | -233,42 | 80,00 | 10,00 | 100,10 | 8100 |
| 7 | 50 | 350 | 49 | -251,37 | 62,04 | -12,04 | 144,96 | 2500 |
| 7,5 | 40 | 300 | 56,25 | -269,33 | 44,09 | -4,09 | 16,69 | 1600 |
| 8 | 25 | 200 | 64 | -287,28 | 26,13 | -1,13 | 1,28 | 625 |
| 60,5 | 1275 | 6025 | 360,25 | -2172,56 | 1274,96 | 0,045 | 2330,68 | 185575 |
Предположим, что связь между ценой и объемом реализации лука линейная. Тогда для расчета параметров а0 и а1 необходимо решить систему уравнений
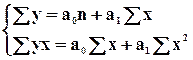 ,
,
подставляя расчетные значения в систему нормальных уравнений и решая ее. Одним из методов получим коэффициенты уравнения линейной регрессии.

![]() -
уравнение регрессии или функция, характеризующая теоретическую зависимость
объемов продаж лука от цены на него. Знак минус указывает на обратную
зависимость.
-
уравнение регрессии или функция, характеризующая теоретическую зависимость
объемов продаж лука от цены на него. Знак минус указывает на обратную
зависимость.
Параметр а0 характеризует условное значение результативного признака при нулевом значении факторного признака (условный объем продаж лука при нулевой цене на него).
Параметры уравнения регрессии оцениваются на
вероятностную надежность. Для этого величина каждого из параметров сравнивается
с соответствующей средней ошибкой выборки, то есть 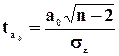 ,
где
,
где ![]() - расчетное значение
критерия Стьюдента, а
- расчетное значение
критерия Стьюдента, а ![]() - остаточное
среднеквадратическое отклонение, характеризующее вариацию эмпирических значений
результативного признака относительно соответствующих им теоретических значений
(вариацию около линии регрессии).
- остаточное
среднеквадратическое отклонение, характеризующее вариацию эмпирических значений
результативного признака относительно соответствующих им теоретических значений
(вариацию около линии регрессии).
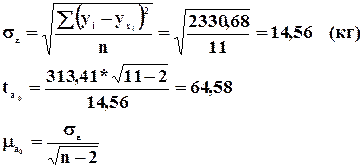
Расчетное значение t критерия
сравнивается с табличным значением для ![]() степеней
свободы и заданной вероятности. Если p=0,95
степеней
свободы и заданной вероятности. Если p=0,95 ![]() то
табличное значение равно t=2,262, то есть
то
табличное значение равно t=2,262, то есть ![]() ,
следовательно, параметр а0 с вероятностью 0,95 надежен. Параметр а1
оценивается по формуле:
,
следовательно, параметр а0 с вероятностью 0,95 надежен. Параметр а1
оценивается по формуле:
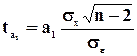 ,
где
,
где ![]() - это показатель вариации
факторного признака.
- это показатель вариации
факторного признака.
В нашем примере ![]() удобнее
всего рассчитывать по формуле:
удобнее
всего рассчитывать по формуле:
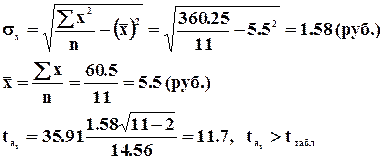
Параметры уравнения регрессии надежны, следовательно,
с вероятностью 0,95 можно утверждать, что полученное уравнение регрессии ![]() объективно отражает форму
зависимости между ценой и объемом продаж лука.
объективно отражает форму
зависимости между ценой и объемом продаж лука.
По данным регрессионного анализа можно рассчитать коэффициент эластичности, характеризующий пропорцию взаимосвязи между вариацией факторного и результативного признаков.
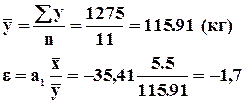
Коэффициент эластичности показывает, что с ростом цены на 1%, объем реализации лука снижается на 1,7%.
4. Измерения тесноты связи.
Методы измерения тесноты взаимосвязи условно делятся на непараметрические и параметрические.
Непараметрические методы применяются для измерения тесноты связи качественных и альтернативных признаков, а так же количественных признаков, распределение которых отличается от нормального распределения.
Для измерения связи альтернативных признаков применяются коэффициент ассоциации Дэвида Юла и коэффициент контингенции Карла Пирсона. Для расчета этих показателей применяется следующая матрица взаимного распределения частот.
a, b, c, d – частоты взаимного распределения признаков.
|
1 признак 2 признак |
ДА | НЕТ |
| ДА | a | b |
| НЕТ | c | d |
При прямой связи частоты сконцентрированы по диагонали a-d, при обратной связи по диагонали b-c, при отсутствии связи частоты практически равномерно распределены по всему полю таблицы.
Коэффициент ассоциации ![]()
Пример: проанализируем зависимость между полом и фактом совершения покупки посетителями магазина.
|
1 признак 2 признак |
М | Ж |
Итого |
| Купил | 24 | 32 | 56 |
| Не купил | 16 | 28 | 44 |
| Итого | 40 | 60 |
![]()
Наблюдается очень слабая прямая связь между полом и фактом свершения покупки. Предельное абсолютное значение коэффициента может быть близко к единице.
Коэффициент ассоциации непригоден для расчета в том случае, если одна из частот по диагонали равна 0. В этом случае применяется коэффициент контингенции, который рассчитывается по формуле:
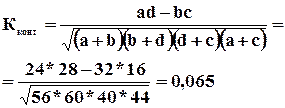
Коэффициент контингенции также указывает на практическое отсутствие связи между признаками (его величина всегда меньше Кас).
Если значения признака распределены более чем по 2 группам, то для определения тесноты связи применяют коэффициенты взаимной сопряженности признаков Пирсона, Чупрова и др.
Показатель Пирсона определяется по формуле  , где
, где ![]() - показатель взаимной
сопряженности признаков, который рассчитывается на основе матрицы взаимного
распределения частот.
- показатель взаимной
сопряженности признаков, который рассчитывается на основе матрицы взаимного
распределения частот.
| 1 гр. | 2 гр. | 3 гр. | Итого | |
| 1 гр. |
s11 |
s12 |
s13 |
n1 |
| 2 гр. |
s21 |
s22 |
s23 |
n2 |
| 3 гр. |
s31 |
s32 |
s33 |
n3 |
| Итого |
m1 |
m2 |
m3 |
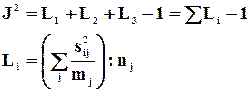
Пример: рассмотрим зависимость между величиной магазина и формой обслуживания.
| Самообслуживание | Традиционное | Итого | |
|
Мелкие магазины |
12 | 45 | 57 |
| Средние | 19 | 10 | 29 |
| Крупные | 14 | 4 | 18 |
| Итого | 45 | 59 |
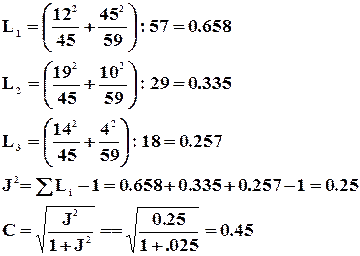
Коэффициент свидетельствует о наличии заметной связи между величиной магазина и формой его обслуживания. Более точным показателем тесноты связи является коэффициент Чупрова, который определяется по формуле:
 ,
где
,
где ![]() - соответственно число
групп, выделенных по каждому признаку. В нашем примере:
- соответственно число
групп, выделенных по каждому признаку. В нашем примере:
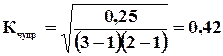
Непараметрические методы измерения тесноты взаимосвязи количественных признаков были первыми из методов измерения тесноты взаимосвязи. Впервые попытался измерить тесноту связи в 30-ч годах 19 века французский ученый Гиррий. Он сопоставлял между собой среднегрупповые значения факторного и результативного признаков. При этом абсолютные значения заменялись их отношениями к некоторым константам. Полученные результаты ранжировались в порядке возрастания. О наличии или отсутствии связи Гиррий судил сопоставляя ранее по группам и подсчитывая количество совпадений и несовпадений рангов. Если преобладало число совпадений – связь считалась прямой. Несовпадение – обратной. При равенстве совпадений и несовпадений – связь отсутствовала.
Методика Гиррий была использована Фехнером при разработке своего коэффициента, а так же Спирменом при разработке коэффициента корреляции рангов.
Расчет коэффициента Фехнера.
|
Цена 1 кг лука, руб. |
Объем продаж, кг |
Знаки отклонений | Сравнение знаков | |
|
|
|
|||
| 3 | 175 | -2,5 | 59,1 | н |
| 3,5 | 200 | -2 | 84,1 | н |
| 4 | 180 | -1,5 | 64,1 | н |
| 4,5 | 150 | -1 | 34,1 | н |
| 5 | 160 | -0,5 | 44,1 | н |
| 5,5 | 120 | 0 | 4,1 | с |
| 6 | 85 | 0,5 | -30,9 | н |
| 6,5 | 90 | 1 | -25,9 | н |
| 7 | 50 | 1,5 | -65,9 | н |
| 7,5 | 40 | 2 | -75,9 | н |
| 8 | 25 | 2,5 | -90,9 | н |
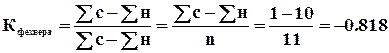
Коэффициент указывает на наличие весьма тесной обратной связи.
На ряду с коэффициентом Фехнера для измерения взаимосвязи количественных признаков применяются коэффициенты корреляции рангов. Наиболее распространенным среди них является коэффициент корреляции рангов Спирмена.
Пример: вычисление коэффициента Спирмена для измерения тесноты взаимосвязи между товарооборотом и уровнем издержек обращения в магазинах.
|
Однодневный товарооборот, тыс. руб.
|
Издержки в % к товарообороту
|
Ранги |
Разность рангов
|
|
|
|
|
|
||||
| 18 | 20,5 | 1 | 4 | -3 | 9 |
| 23 | 23,4 | 2 | 6 | -4 | 16 |
| 29 | 21,2 | 3 | 5 | -2 | 4 |
| 45 | 18,9 | 4 | 2 | 2 | 4 |
| 78 | 19,2 | 5 | 3 | 2 | 4 |
| 93 | 17,5 | 6 | 1 | 5 | 25 |
| Всего | 62 |
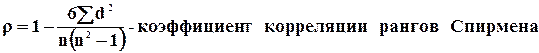
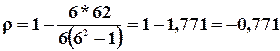
Коэффициент корреляции рангов может принимать значение в пределах от –1 (обратная связь, близкая к функциональной) до +1 (прямая связь, близкая к функциональной).
Непараметрические методы учитывают направления изменений значений признаков, но не зависят от того, насколько интенсивно колеблются значения результативного признака в результате изменения факторного признака. Это позволяют сделать параметрические методы.
Для измерения тесноты линейной взаимосвязи применяется коэффициент корреляции. Базовая форма коэффициента корреляции следующая:
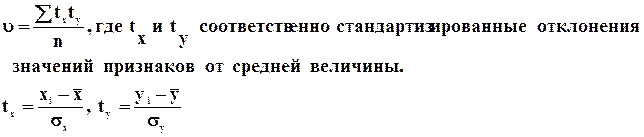
Фактически, коэффициент корреляции – это среднее произведения нормативных отклонений:

Если связь между признаками отсутствует, то
результативный признак не варьирует при изменении факторного признака,
следовательно ![]() . Такой же
результат получается при сбалансированности сумм отрицательных и положительных
произведений.
. Такой же
результат получается при сбалансированности сумм отрицательных и положительных
произведений.
Обычно для расчета коэффициента корреляции применяются формулы, использующие те показатели, которые уже рассчитывались при определении параметров уравнения регрессии. Наиболее удобной для расчетов является формула:
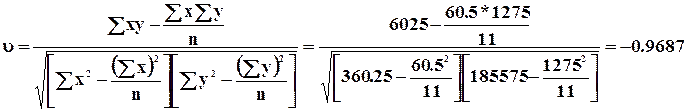
Величина коэффициента корреляции свидетельствует о наличии очень тесной обратной связи между признаками. Качественная оценка тесноты связи дается с помощью шкалы Чедока.
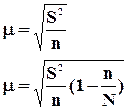
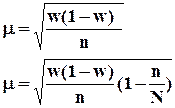

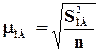
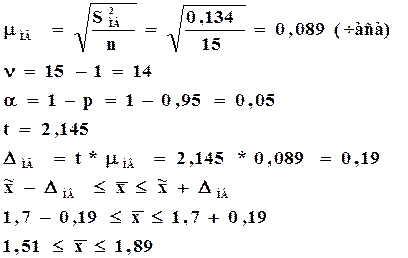
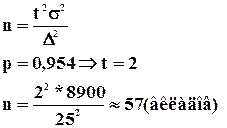


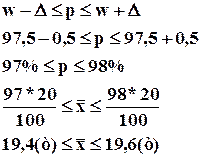
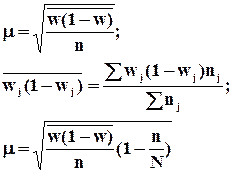
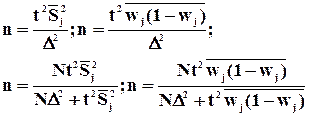
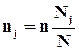

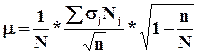
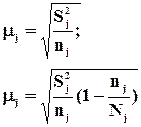
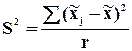
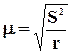
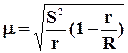
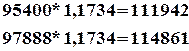
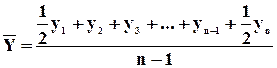
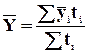 ,
где
,
где 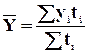 ,
где
,
где 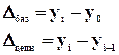
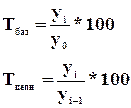
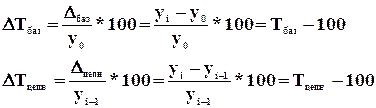
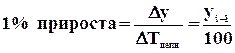 .
.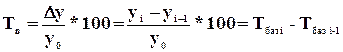
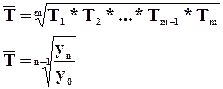
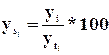 ,
где
,
где 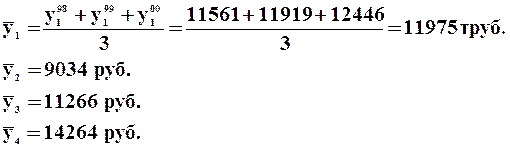
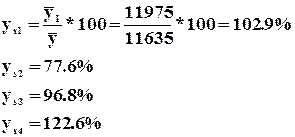
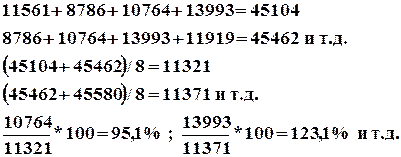
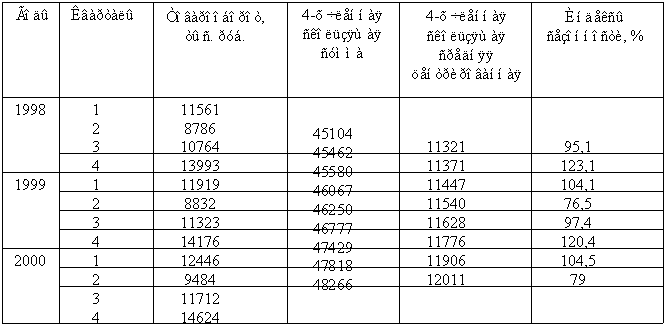
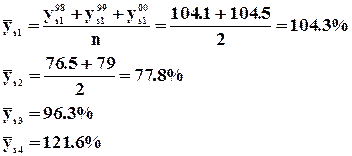
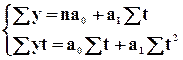


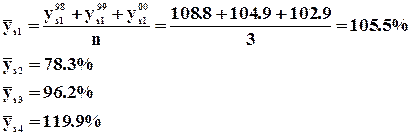
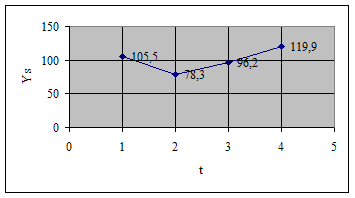
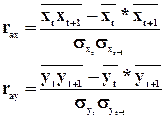
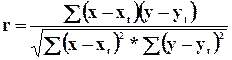 ,
где
,
где 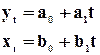 ,
где x, y – соответственно фактические значения уравнений
факторного и результативного признаков.
,
где x, y – соответственно фактические значения уравнений
факторного и результативного признаков.
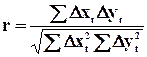 .
.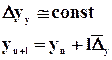 ,
где
,
где 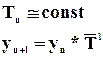 ,
где
,
где 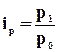 , где
, где 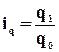 ,
динамики количества проданного или произведенного товара;
,
динамики количества проданного или произведенного товара;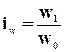 ;
; .
.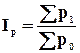 .
Недостаток этого сводного индекса – он не учитывал разницу цен на не одинаковые
товары и структуру товарооборота.
.
Недостаток этого сводного индекса – он не учитывал разницу цен на не одинаковые
товары и структуру товарооборота.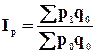 ,
где
,
где  (122,4%).
Этот индекс показывает, что в отчетном периоде, по сравнению с базисным, цены
на товары, приобретенные в прошлом, выросли в среднем на 22,4%.
(122,4%).
Этот индекс показывает, что в отчетном периоде, по сравнению с базисным, цены
на товары, приобретенные в прошлом, выросли в среднем на 22,4%. .
.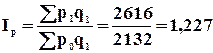 (122,7%).
(122,7%).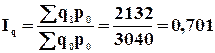 (70,1%) – он показывает динамику количества проданных товаров. В отчетном
периоде по сравнению с базисным физический объем (количество проданных товаров)
снизилось почти на 30% или
(70,1%) – он показывает динамику количества проданных товаров. В отчетном
периоде по сравнению с базисным физический объем (количество проданных товаров)
снизилось почти на 30% или 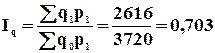 (70,3%).
(70,3%).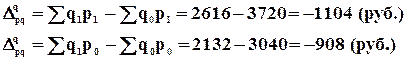
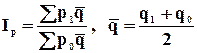 , где
, где  , где
, где 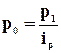 , а
, а 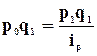 .
.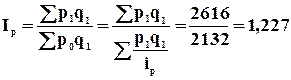 .
.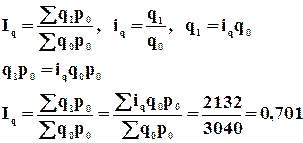
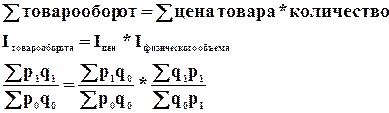
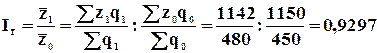 (92,97%)
(92,97%)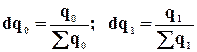 ).
).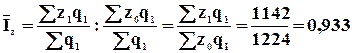 (93,3%). (аналог индекса Пааше).
(93,3%). (аналог индекса Пааше).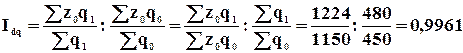 (99,61%).
(99,61%).