Реферат: Статистика
 Часть 1.
Часть 1.
Имеются данные о количестве заявок, поступающие на АТП по дням:
Первоначальный ряд:
| 5 | 14 | 7 | 2 | 8 | 10 | 2 | 6 | 12 | 3 |
| 5 | 7 | 9 | 4 | 3 | 11 | 12 | 7 | 8 | 5 |
| 12 | 7 | 11 | 14 | 3 | 12 | 8 | 10 | 8 | 3 |
| 13 | 11 | 8 | 8 | 2 | 9 | 8 | 5 | 14 | 4 |
| 10 | 12 | 6 | 8 | 2 | 8 | 7 | 9 | 2 | 8 |
| 4 | 6 | 13 | 5 | 3 | 12 | 2 | 5 | 7 | 9 |
| 5 | 7 | 2 | 9 | 5 | 6 | 14 | 4 | 7 | 7 |
| 10 | 10 | 5 | 11 | 8 | 3 | 2 | 9 | 10 | 14 |
| 10 | 7 | 4 | 2 | 8 | 7 | 14 | 6 | 8 | 11 |
| 13 | 8 | 12 | 3 | 11 | 2 | 7 | 9 | 9 | 8 |
Ранжированный ряд:
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 |
| 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 5 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 | 8 |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 9 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 11 | 11 |
| 11 | 11 | 11 | 11 | 12 | 12 | 12 | 12 | 12 | 12 |
| 12 | 13 | 13 | 13 | 14 | 14 | 14 | 14 | 14 | 14 |
Величина вариации
R=xmax-xmin=14-2=12
Величина интервала:
i=![]()
|
xi |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|
fi |
10 | 7 | 5 | 9 | 5 | 12 | 15 | 8 | 7 | 6 | 7 | 3 | 6 |
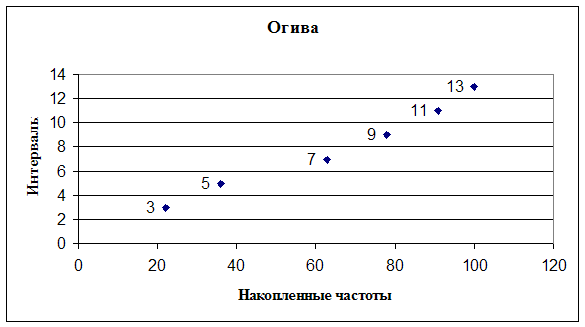
Составим таблицу для накопительных частот:

|
xi |
fi |
Sfi |
| 2¸4 | 22 | 0+22=22 |
| 4¸6 | 14 | 22+14=36 |
| 6¸8 | 27 | 36+27=63 |
| 8¸10 | 15 | 63+15=78 |
| 10¸12 | 13 | 78+13=91 |
| 12¸14 | 9 | 91+9=100 |
Средняя ошибка выборки:
Для дискретного ряда:
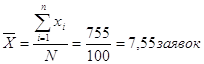
Для интервального ряда построим таблицу:
|
Интервалы по xi |
Центр интервала |
fi |
xi*fi |
| 2¸4 | 3 | 22 | 66 |
| 4¸6 | 5 | 14 | 70 |
| 6¸8 | 7 | 27 | 189 |
| 8¸10 | 9 | 15 | 135 |
| 10¸12 | 11 | 13 | 143 |
| 12¸14 | 13 | 9 | 117 |
|
Sfi=100 |
Sxi*fi=720 |
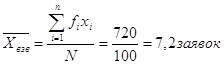
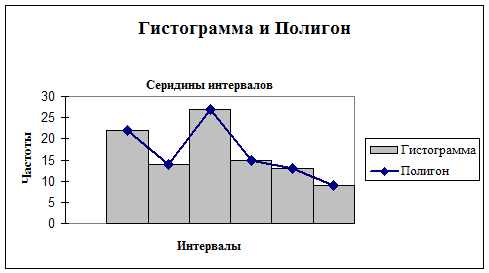
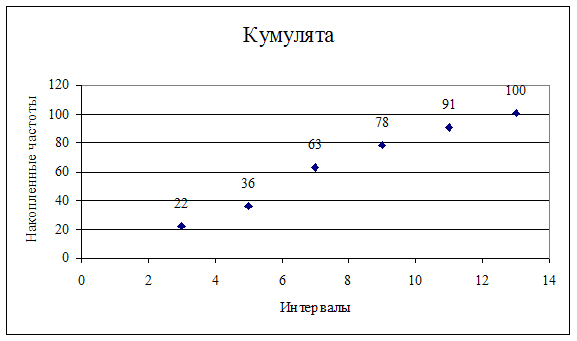
Наглядное изображение вариационного ряда

|
Интервалы по хi |
Середина интервалов |
fi |
| |
|
yt |
Теорет.
|
Кумулятивная частота |
|
|
| Факт. | Теорет. | ||||||||
| 2¸4 | 3 | 22 | 4,2 | 1,33 | 0,1647 | 10,3 | 22 | 10,3 | 11,7 |
| 4¸6 | 5 | 14 | 2,2 | 0,70 | 0,3123 | 19,5 | 36 | 29,8 | 6,2 |
| 6¸8 | 7 | 27 | 0,2 | 0,06 | 0,3982 | 24,9 | 63 | 54,7 | 8,3 |
| 8¸10 | 9 | 15 | 1,8 | 0,57 | 0,3391 | 21,2 | 78 | 75,9 | 2,1 |
| 10¸12 | 11 | 13 | 3,8 | 1,20 | 0,1942 | 12,1 | 91 | 88,0 | 3,0 |
| 12¸14 | 13 | 9 | 5,8 | 1,84 | 0,0734 | 4,6 | 100 | 92,6 | 7,4 |
|
38,6 |
 |

l=![]() =
=![]() =1,17,
=1,17,
где l - критерий согласия;
P(l)=0,1122
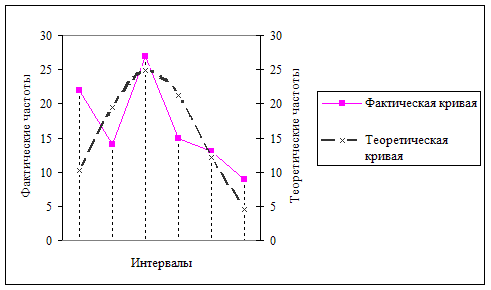
С вероятностью 0,1122 можно утверждать, что отклонения фактических частот от теоретических в этом примере являются случайными. Следовательно, можно считать, что в основе фактического распределения лежит закон нормального распределения.
Среднее линейное отклонение к коэффициенту вариации:
r=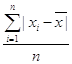 ,
,
r=18/8=2,25
Относительное линейное отклонение:
nr=![]() *100%=
*100%=![]() *100%=31%
*100%=31%
Относительное квадратичное отклонение:
ns=![]() *100%=
*100%=![]() *100%=42%
*100%=42%
Мода.
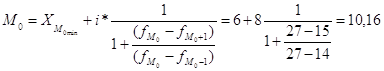
Медиана
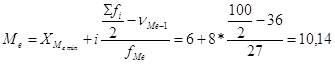
ЧастьII Анализ корреляционных зависимостей.

Исходный ряд |
|
|||||
| №п/п |
Xi |
Yi |
№п/п |
Xi |
Yi |
|
| 1 | 20 | 11 | 26 | 5 | 6 | |
| 2 | 8 | 7 | 27 | 10 | 5 | |
| 3 | 5 | 4 | 28 | 10 | 6 | |
| 4 | 10 | 8 | 29 | 4 | 4 | |
| 5 | 10 | 9 | 30 | 15 | 9 | |
| 6 | 15 | 7 | 31 | 13 | 4 | |
| 7 | 10 | 7 | 32 | 12 | 8 | |
| 8 | 10 | 5 | 33 | 12 | 4 | |
| 9 | 5 | 3 | 34 | 15 | 4 | |
| 10 | 10 | 10 | 35 | 6 | 3 | |
| 11 | 10 | 10 | 36 | 17 | 3 | |
| 12 | 5 | 6 | 37 | 2 | 3 | |
| 13 | 11 | 11 | 38 | 10 | 4 | |
| 14 | 4 | 4 | 39 | 12 | 5 | |
| 15 | 10 | 9 | 40 | 12 | 6 | |
| 16 | 7 | 5 | 41 | 13 | 6 | |
| 17 | 8 | 7 | 42 | 11 | 4 | |
| 18 | 25 | 14 | 43 | 11 | 4 | |
| 19 | 11 | 12 | 44 | 13 | 12 | |
| 20 | 4 | 4 | 45 | 5 | 4 | |
| 21 | 8 | 5 | 46 | 6 | 4 | |
| 22 | 7 | 3 | 47 | 4 | 4 | |
| 23 | 4 | 4 | 48 | 3 | 1 | |
| 24 | 20 | 7 | 49 | 4 | 4 | |
| 25 | 5 | 7 | 50 | 7 | 3 |
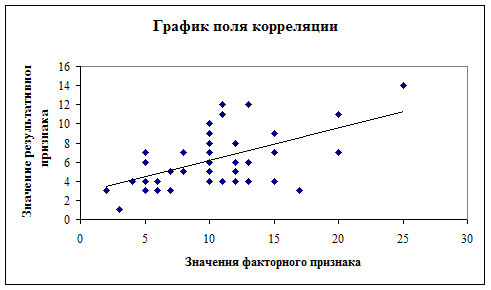
Линейная зависимость
| Ранжированный ряд | |||||
| №п/п |
Xi |
Yi |
№п/п |
Xi |
Yi |
| 1 | 1 | 2 | 26 | 5 | 10 |
| 2 | 3 | 3 | 27 | 5 | 10 |
| 3 | 3 | 4 | 28 | 6 | 10 |
| 4 | 3 | 4 | 29 | 6 | 10 |
| 5 | 3 | 4 | 30 | 6 | 10 |
| 6 | 3 | 4 | 31 | 6 | 10 |
| 7 | 3 | 4 | 32 | 6 | 10 |
| 8 | 4 | 4 | 33 | 7 | 11 |
| 9 | 4 | 5 | 34 | 7 | 11 |
| 10 | 4 | 5 | 35 | 7 | 11 |
| 11 | 4 | 5 | 36 | 7 | 11 |
| 12 | 4 | 5 | 37 | 7 | 12 |
| 13 | 4 | 5 | 38 | 7 | 12 |
| 14 | 4 | 5 | 39 | 8 | 12 |
| 15 | 4 | 6 | 40 | 8 | 12 |
| 16 | 4 | 6 | 41 | 9 | 13 |
| 17 | 4 | 7 | 42 | 9 | 13 |
| 18 | 4 | 7 | 43 | 9 | 13 |
| 19 | 4 | 7 | 44 | 10 | 15 |
| 20 | 4 | 8 | 45 | 10 | 15 |
| 21 | 4 | 8 | 46 | 11 | 15 |
| 22 | 4 | 8 | 47 | 11 | 17 |
| 23 | 5 | 10 | 48 | 12 | 20 |
| 24 | 5 | 10 | 49 | 12 | 20 |
| 25 | 5 | 10 | 50 | 14 | 25 |
|
xi |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 11 | 12 | 13 | 15 | 17 | 20 | 25 |
| fi | 1 | 1 | 6 | 6 | 2 | 3 | 3 | 10 | 4 | 4 | 3 | 3 | 1 | 2 | 1 |
|
yi |
1 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 14 |
| fi | 1 | 15 | 5 | 5 | 6 | 2 | 3 | 2 | 2 | 2 | 1 |
 iy=1,86
iy=1,86
ix=3,29
n=7
2. Построение комбинаторной таблицы

|
xi |
2¸5,29 | 5,29¸8,58 | 8,58¸11,87 | 11,87¸15,16 | 15,16¸18,45 | 18,45¸21,74 | 21,74¸25,03 |
|
yi |
|||||||
| 1¸2,86 | 1 | ||||||
| 2,86¸4,72 | 3,3,3,3,3,3,4,4,4,4,4,4,4, | 4,4,4,4,4,4,4,4 | |||||
| 4,72¸6,58 | 5,5,5,5,5,6,6,6,6,6, | ||||||
| 6,58¸8,44 | 7,7,7,7 | 7,7,8,8 | |||||
| 8,44¸10,3 | 9,9,9,10,10 | ||||||
| 10,3¸12,16 | 11 | 11 | 12,12 | ||||
| 12,16¸14,02 | 14 | ||||||
| Число наблюдений | 14 | 8 | 14 | 10 | 1 | 2 | 1 |
З. Нахождение теоретической формы связи.
Найдем ординату эмпирической линии регрессии
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Составим вспомогательную таблицу

| № п/п | x | y |
y2 |
x2 |
xy |
Yt |
| 1 | 2,00 | 3,36 | 11,29 | 4,00 | 6,72 | 2,76 |
| 2 | 5,29 | 4,00 | 16,00 | 27,98 | 21,16 | 4,66 |
| 3 | 8,58 | 5,93 | 35,16 | 73,62 | 50,88 | 6,55 |
| 4 | 11,87 | 8,80 | 77,44 | 140,90 | 104,46 | 8,44 |
| 5 | 15,16 | 11,00 | 121,00 | 229,83 | 166,76 | 10,33 |
| 6 | 18,45 | 12,00 | 144,00 | 340,40 | 221,40 | 12,23 |
| 7 | 21,74 | 14,00 | 196,00 | 472,63 | 304,36 | 14,12 |
| S | 83,09 | 59,09 | 600,89 | 1289,35 | 875,74 | 59,09 |
Уравнение
прямой ![]()
ì a0*n+a1*Sx=Sy
í
îa0*Sx+a1*Sx2=Sx*y
a0=1,61 , а1=0,58
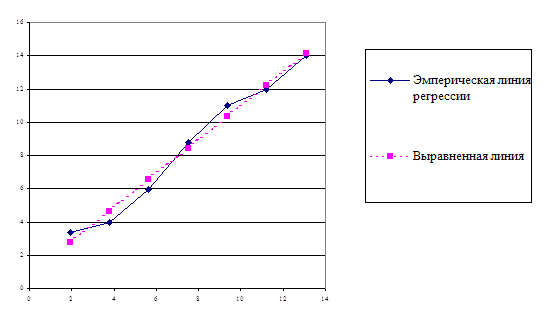
Расчет коэффициента корреляции

|
x |
y |
(x- |
(y- |
(x- |
(x- |
(y- |
| 2 | 3,36 | -9,87 | -5,08 | 50,15 | 97,42 | 25,82 |
| 5,29 | 4 | -6,58 | -4,44 | 29,22 | 43,30 | 19,73 |
| 8,58 | 5,93 | -3,29 | -2,51 | 8,26 | 10,82 | 6,31 |
| 11,87 | 8,8 | 0,00 | 0,36 | 0,00 | 0,00 | 0,13 |
| 15,16 | 11 | 3,29 | 2,56 | 8,42 | 10,82 | 6,55 |
| 18,45 | 12 | 6,58 | 3,56 | 23,42 | 43,30 | 12,66 |
| 21,74 | 14 | 9,87 | 5,56 | 54,86 | 97,42 | 30,90 |
| S | 174,34 | 303,07 | 102,09 |
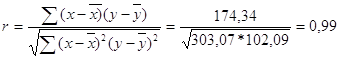
-1<0,99<+1 Þ зависимость между x и y прямая
